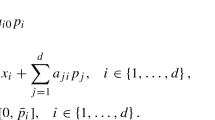On fairness of systemic risk measures

Abstract

In our previous paper “A unified approach to systemic risk measures via acceptance sets” (Mathematical Finance, 2018), we have introduced a general class of systemic risk measures that allow random allocations to individual banks before aggregation of their risks. In the present paper, we prove a dual representation of a particular subclass of such systemic risk measures and the existence and uniqueness of the optimal allocation related to them. We also introduce an associated utility maximisation problem which has the same solution as the minimisation problem associated to the systemic risk measure. In addition, the optimiser in the dual formulation provides a risk allocation which is fair from the point of view of the individual financial institutions. The case with exponential utilities which allows explicit computation is treated in detail.

1 Introduction

Consider a vector $\mathbf{X}=(X^1,\dots ,X^N)\in L^0(\mathrm{\Omega },\mathcal{F},\mathbb{P};{\mathbb{R}}^N)$ of $N$ random variables denoting a configuration of risky (financial) factors at a future time $T$ associated to a system of $N$ financial institutions/banks. One of the first proposals in the framework of risk measures to measure the systemic risk of $\mathbf{X}$, see Chen et al. [16], was to consider the map

$$\rho (\mathbf{X}):=inf\{m\in \mathbb{R}:\mathrm{\Lambda }(\mathbf{X})+m\in \mathbb{A}\},$$

(1.1)

where $\mathrm{\Lambda }:{\mathbb{R}}^N\to \mathbb{R}$ is an aggregation rule that aggregates the $N$-dimensional risk factors into a univariate risk factor, and $\mathbb{A}\subseteq L^0(\mathrm{\Omega },\mathcal{F},\mathbb{P};\mathbb{R})$ is an acceptance set of real-valued random variables. As within the framework of univariate monetary risk measures, systemic risk might again be interpreted as the minimal cash amount that secures the system when it is added to the total aggregated system loss ${\Lambda } (\mathbf{X})$, given that ${\Lambda } (\mathbf{X})$ allows a monetary loss interpretation. Note, however, that in (1.1), systemic risk is the minimal capital added to secure the system after aggregating individual risks. It might be more relevant to measure systemic risk as the minimal cash amount that secures the aggregated system by adding the capital into the single institutions before aggregating their individual risks. This way of measuring systemic risk can be expressed by

$$\rho (\mathbf{X}):=inf\{\sum _{i=1}^N{m}^i:\mathbf{m}=(m^1,\dots ,m^N)\in {\mathbb{R}}^N,\mathrm{\Lambda }(\mathbf{X}+\mathbf{m})\in \mathbb{A}\}.$$

(1.2)

Here, the amount $m^{i}$ is added to the financial position $X^{i}$ of institution $i\in \{1,\dots ,N\}$ before the corresponding total loss ${\Lambda } (\mathbf{X}+\mathbf{m})$ is computed (we refer to Armenti et al. [3], Biagini et al. [7] and Feinstein et al. [27]).

One of the main novelties of our paper [7] was the possibility of adding to $\mathbf{X}$ not merely a vector $\mathbf{m}=(m^1,\dots ,m^N)\in {\mathbb{R}}^N$ of deterministic cash amounts, but more generally a random vector $\mathbf{Y}\in \mathcal{C}$ for some given class $\mathcal{C}$. In particular, the main example considered in [7], and studied further in this paper, is given by choosing the aggregation function

$$ {\Lambda } (\mathbf{x})=\sum _{n=1}^{N}u_{n}(x^{n}) $$

(1.3)

for utility functions $u_{n}$, $n=1,\dots ,N$, the acceptance set

$$\mathbb{A}=\{Z\in L^1(\mathrm{\Omega },\mathcal{F},\mathbb{P};\mathbb{R}),\mathbb{E}[Z]\ge B\}$$

for a given constant $B$, and the class $\mathcal{C}$ such that

$$\mathcal{C}\subseteq {\mathcal{C}}_{\mathbb{R}}\cap \mathcal{L},\text{where }{\mathcal{C}}_{\mathbb{R}}:=\{\mathbf{Y}\in L^0(\mathrm{\Omega },\mathcal{F},\mathbb{P};{\mathbb{R}}^N):\sum _{n=1}^N{Y}^n\in \mathbb{R}\},$$

(1.4)

where the subspace $\mathcal{L}\subseteq L^0(\mathrm{\Omega },\mathcal{F},\mathbb{P};{\mathbb{R}}^N)$ will be specified later. Here, the notation ${\sum }_{n=1}^N{Y}^n\in \mathbb{R}$ means that $\sum _{n=1}^{N}Y^{n}$ is ℙ-a.s. equal to some deterministic constant in ℝ, even though each single $Y^{n}$, $n=1, \dots ,N$, is a random variable. Under these assumptions, the systemic risk measure considered in [7] takes the form

$$\rho (\mathbf{X}):=inf\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in \mathcal{C}\subseteq {\mathcal{C}}_{\mathbb{R}},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}$$

(1.5)

and can still be interpreted as the minimal total cash amount ${\sum }_{n=1}^N{Y}^n\in \mathbb{R}$ needed today to secure the system by distributing the cash at the future time $T$ among the components of the risk vector $\mathbf{X}$. However, while the total capital requirement $\sum _{n=1}^{N}Y^{n}$ is determined today, contrary to (1.2), the individual allocation $Y^{i}(\omega )$ to institution $i$ does not need to be decided today, but in general depends on the scenario $\omega$ realised at time $T$. This total cash amount $\rho (\mathbf{X})$ is computed today through the formula $\sum _{n=1} ^{N}\rho ^{n}(\mathbf{X})=\rho (\mathbf{X})$, where each ${\rho }^n(\mathbf{X})\in \mathbb{R}$ is the risk allocation of each bank, as explained in Definition 1.2 below. Thus, one prominent example that can be modelled by considering random allocations is the default fund of a CCP¹ that is liable for any participating institution. We come back to this mechanism in Sect. 5.

By considering scenario-dependent allocations, we are also taking into account possible dependencies among the banks, as the budget constraints in (1.5) do not depend only on the marginal distribution of $\mathbf{X}$, as it would happen for deterministic $Y^{n}$.

Definition 1.1

A scenario-dependent allocation $\mathbf{Y}_{\mathbf{X}}=\mathbf{(}Y _{\mathbf{X}}^{n})_{n=1,\dots ,N}\in \mathcal{C}$ is called a systemic optimal allocation for $\rho (\mathbf{X})$ defined in (1.5) if it satisfies $\rho (\mathbf{X})=\sum _{n=1}^{N}Y_{ \mathbf{X}}^{n}$ and $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y_{\mathbf{X}}^n))]\ge B$.

As two of the main results of the paper,

• we study in Sect. 3 the dual formulation of the systemic risk measure (1.5) as

  $$\rho (\mathbf{X})=\underset{\mathbf{Q}\in \mathcal{D}}{max}(\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-X^n]-{\alpha }_B(\mathbf{Q})),$$

  (1.6)

  where $\mathbf{Q}:=(Q^{1},\dots ,Q^{N})$, the penalty function $\alpha _{B}$ and the domain $\mathcal{D}$ are specified in Sect. 3. In particular, we establish existence and uniqueness of the optimiser $\mathbf{Q_{X}} \in \mathcal{D}$ of (1.6).

• we show in Sect. 4 existence and uniqueness of the systemic optimal allocation $\mathbf{Y}_{\mathbf{X}}$ for the systemic risk measure (1.5).

We now associate to the risk minimisation problem (1.5) a related utility maximisation problem that plays a central role in this paper, namely

$$\pi (\mathbf{X}):=sup\left\{\mathbb{E}\right[\sum _{n=1}^N{u}_n(X^n+Y^n)]:\mathbf{Y}\in \mathcal{C}\subseteq {\mathcal{C}}_{\mathbb{R}},\sum _{n=1}^N{Y}^n\le A\}.$$

(1.7)

If we interpret $\sum _{n=1}^{N}u_{n}(X^{n}+Y^{n})$ as the aggregated utility of the system after allocating $\mathbf{Y}$, then $\pi ( \mathbf{X})$ can be interpreted as the maximal expected utility of the system over all random allocations $\mathbf{Y}\in \mathcal{C}$ such that the aggregated budget constraint $\sum _{n=1}^{N}Y^{n}\leq A$ holds for a given constant $A$. In the following, we may write $\rho ( \mathbf{X})=\rho _{B}(\mathbf{X})$ and $\pi (\mathbf{X})=\pi _{A}( \mathbf{X})$ to express the dependence on the minimal level of expected utility $B\in \mathbb{R}$ and maximal budget level $A\in \mathbb{R}$, respectively. We shall see in Sect. 4.1 that $B=\pi _{A}( \mathbf{X})$ if and only if $A=\rho _{B}(\mathbf{X})$, and in these cases, the two problems $\pi _{A}(\mathbf{X})$ and $\rho _{B}( \mathbf{X})$ have the same unique solution $\mathbf{Y_{\mathbf{X}}}$. From this, we infer that once a level $\rho (\mathbf{X})$ of total systemic risk has been determined, then

• the systemic optimal allocation$\mathbf{Y}_{\mathbf{X}}$for$\rho$maximises the expected system utility among all random allocations of total cost less than or equal to$\rho (\mathbf{X})$.

Once the total systemic risk has been identified as $\rho (\mathbf{X})$, the second essential question is how to allocate the total risk to the individual institutions.

Definition 1.2

We say that a vector ${({\rho }^n(\mathbf{X}))}_{n=1,\dots ,N}\in {\mathbb{R}}^N$ is a systemic risk allocation of $\rho ( \mathbf{X})$ if it fulfils $\sum _{n=1}^{N}\rho ^{n}(\mathbf{X})=\rho ( \mathbf{X})$.

The requirement $\sum _{n=1}^{N}\rho ^{n}(\mathbf{X})=\rho (\mathbf{X})$ is known as the “full allocation” property; see for example Brunnermeier and Cheridito [13]. In the case of deterministic allocations $\mathbf{Y}\in {\mathbb{R}}^N$, i.e., $\mathcal{C}={\mathbb{R}}^N$, the optimal deterministic $\mathbf{Y}_{\mathbf{X}}$ represents a canonical risk allocation $\rho ^{n}(\mathbf{X}):=Y_{ \mathbf{X}}^{n}$. For general (random) allocations $\mathbf{Y}\in \mathcal{C}\subseteq {\mathcal{C}}_{\mathbb{R}}$, we no longer have such a canonical way to determine $\rho ^{n}(\mathbf{X})$; however, we shall provide evidence that a good choice is

$${\rho }^n(\mathbf{X}):={\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]\text{for }n=1,\dots ,N,$$

(1.8)

where $\mathbf{Q}_{\mathbf{X}}$ is the optimiser of the dual problem (1.6). To this end, suppose a probability vector $\mathbf{Q}=(Q^{1},\dots ,Q^{N})$ is given for the system and consider an alternative formulation of the systemic utility maximisation problem in terms of the valuation provided by $\mathbf{Q}$, namely

$${\pi }^{\mathbf{Q}}(\mathbf{X})={\pi }_A^{\mathbf{Q}}(\mathbf{X}):=sup\left\{\mathbb{E}\right[\sum _{n=1}^N{u}_n(X^n+Y^n)]:\mathbf{Y}\in \mathcal{L},\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]\le A\}.$$

(1.9)

Note that in (1.9) (as well as in (1.10) below), the allocation $\mathbf{Y}$ belongs to a vector space ℒ of random variables (introduced later) without requiring that $\mathbf{Y}\in {\mathcal{C}}_{\mathbb{R}}$ (which would mean that the componentwise sum is equal to a deterministic quantity). Thus for $\pi ^{\mathbf{Q}}(\mathbf{X})$, we maximise the expected systemic utility among all $\mathbf{Y}\in \mathcal{L}$ satisfying the budget constraint ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]\le A$. Similarly, we can introduce a systemic risk measure in terms of the vector $\mathbf{Q}$ of probability measures by

$${\rho }^{\mathbf{Q}}(\mathbf{X})={\rho }_B^{\mathbf{Q}}(\mathbf{X}):=inf\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]:\mathbf{Y}\in \mathcal{L},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}.$$

(1.10)

For $\rho ^{\mathbf{Q}}(\mathbf{X})$, we thus look for the minimal systemic cost ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]$ among all $\mathbf{Y}\in \mathcal{L}$ under the acceptability constraint $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]\ge B$.

A priori, $\rho$ and $\rho ^{\mathbf{Q}}$ defined in (1.5) and (1.10) are quite different objects: even if they both subsume the same systemic budget constraint, $\rho$ is defined only through the computation of the cash amount ${\sum }_{n=1}^N{Y}^n\in \mathbb{R}$, while in $\rho ^{\mathbf{Q}}$ the risk is defined by calculating the value (or the cost) of the random allocations, ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]$. A similar comparison applies to $\pi$ and $\pi ^{\mathbf{Q}}$.

Remark 1.3

To better understand the above comparison, we make an analogy with the classical (univariate) utility maximisation from terminal wealth in securities markets. Let $\mathcal{K}:=\{ (H.S)_{T}: H\mathcal{\ } \text{admissible}\}$, where $(H.S)_{T}$ is the stochastic integral, and let $U(x)=sup\{\mathbb{E}[u(x+K)]:K\in \mathcal{K}\}$ be the utility from the initial wealth $x\in \mathbb{R}$ when optimally investing in the securities $S$ adopting admissible strategies $H$. In this case, there is no need to introduce a cost operator, as we are investing in replicable contingent claims having by definition initial value $x$. On the other hand, $U^Q(x)=sup\{\mathbb{E}[u(x+K)]:{\mathbb{E}}_Q[K]\le 0\}$ is the optimal utility function when a probability vector $Q$ is given. A priori, the two problems are of different nature, unless one shows (see [6]) that for a particular probability measure $Q_{x}$, the two problems have the same value and $U(x)=U^{Q_{x}}(x)= \min _{Q\in \mathcal{M}}U^{Q}(x)$, where ℳ is the set of martingale measures. From the mathematical point of view, once the minimax martingale measure $Q_{x}$ is determined, $U^{Q_{x}}(x)$ is easier to solve than $U(x)$, and the solution to $U^{Q_{x}}(x)$ can then be used to find the solution to $U(x)$. Also for the financial application, one may use $Q_{x}$ to compute the fair price (see [21] and [23, Remark 3.2.2]) of a contingent claim $C$ by computing ${\mathbb{E}}_{Q_x}[C]$.

In view of the analogy in the above remark, we also prove in this paper that

• (i) the optimiser $\mathbf{Q}_{\mathbf{X}}=(Q_{\mathbf{X}}^{1}, \dots , Q_{\mathbf{X}}^{N})$ of the dual problem (1.6) satisfies

  $$ \rho _{B}(\mathbf{X})=\rho _{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X}), \qquad \pi _{A}(\mathbf{X})=\pi _{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X}); $$

• (ii) all four problems have the same (unique) solution $\mathbf{Y_{\mathbf{X}}}$ when $A:=\rho _{B}(\mathbf{X})$;

• (iii) $\mathbf{Q}_{\mathbf{X}}$ provides a systemic risk allocation $({\mathbb{E}}_{Q_{\mathbf{X}}^1}[Y_{\mathbf{X}}^1],\dots ,{\mathbb{E}}_{Q_{\mathbf{X}}^N}[Y_{\mathbf{X}}^N])$ with

  $$\sum _{n=1}^N{\mathbb{E}}_{Q_{{\mathbf{X}}^n}}[Y_{\mathbf{X}}^n]={\rho }_B(\mathbf{X});$$

  (1.11)

• (iv) and

  $$ \rho _{B}(\mathbf{X})=\max _{\mathbf{Q}\in \mathcal{D}}\rho _{B}^{ \mathbf{Q}}(\mathbf{X})=\rho _{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X}), $$

  where the domain $\mathcal{D}$ is defined in (3.3) below and replaces, in analogy with utility maximisation, the set of martingale measures.

Hence $\rho _{B}^{\mathbf{Q}_{\mathbf{X}}}$ is a valid alternative to $\rho _{B}$ (same value and solution), and this justifies its use to compute the systemic risk. In addition, (1.11) shows that the operator assigned by ${\mathbb{E}}_{{\mathbf{Q}}_{\mathbf{X}}}[\cdot ]$ evaluates the risk component $Y_{\mathbf{X}}^{n}$ of the optimal allocation according to $\rho _{B}$ (not only to $\rho _{B}^{\mathbf{Q} _{\mathbf{X}}}$) and proves that the definition in (1.8) provides indeed a systemic risk allocation for $\rho (\mathbf{X})$. In Sect. 5, we further elaborate on this interpretation, we study in detail the properties of the systemic risk probability vector $\mathbf{Q}_{\mathbf{X}}$, and we provide in particular for the marginal risk contribution the formula

$$\frac{d}{d\epsilon }\rho (\mathbf{X}+\epsilon \mathbf{V}){|}_{\epsilon =0}=-\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[V^n]\text{for }\mathbf{V}\in \mathcal{L}.$$

We also discuss certain properties inferred from the above results that argue for the fairness of the systemic risk allocation.

Based on the above exposition, we structure the remaining part of the paper as follows. In Sect. 2, we introduce the technical setting within Orlicz spaces and the main assumptions, and we show that our optimisation problems are well posed. In Sect. 3, we study the dual representation (1.6) of the systemic risk measure. Notably, existence and uniqueness of the dual optimiser $\mathbf{Q}_{\mathbf{X}}$ are proved in Proposition 3.1; see also Corollary 4.13 in Sect. 4. In Sect. 4, we deal with existence and uniqueness of solutions of the primal problems (1.5), (1.7) and (1.9), (1.10). To guarantee existence, we need to enlarge the environment and consider appropriate spaces of integrable random variables. In Sect. 5, we derive cash-additivity and risk marginal contribution properties of the systemic risk measure $\rho (\mathbf{X})$, and fairness properties of the optimal allocations $\rho ^{n}(\mathbf{X})$. The case with exponential utilities and grouping of institutions is treated in detail in Sect. 6, where additional sensitivity and monotonicity properties are established as well.

We conclude this section with a literature overview on systemic risk. In Craig and von Peter [20], Boss et al. [12] and Cont et al. [19], one can find empirical studies on banking networks, while interbank lending has been studied via interacting diffusions and a mean-field approach in several papers like Fouque and Sun [30], Fouque and Ichiba [28], Carmona et al. [15], Kley et al. [37], Battiston et al. [5]. Among the many contributions on systemic risk modelling, we mention the classical contagion model proposed by Eisenberg and Noe [26], the default model of Gai and Kapadia [33], the illiquidity cascade models of Gai and Kapadia [32], Hurd et al. [36] and Lee [39], the asset fire sale cascade model by Cifuentes et al. [18] and Caccioli et al. [14], as well as the model in Weber and Weske [45] that additionally includes cross-holdings. Further works on network modelling are Amini et al. [1], Rogers and Veraart [43], Amini et al. [2], Gleeson et al. [34], Battiston and Caldarelli [4], Detering et al. [24] and Detering et al. [25]. See also the references therein. For an exhaustive overview on the literature on systemic risk, we refer the reader to the recent volumes of Hurd [35] and of Fouque and Langsam [29].

2 The setting

We now introduce the setting and discuss some fundamental properties of our systemic risk measures. Given a probability space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$, we consider the space of random vectors

$$L^0:=L^0(\mathbb{P};{\mathbb{R}}^N):=\{\mathbf{X}=(X^1,\dots ,X^N):X^n\in L^0(\mathrm{\Omega },\mathcal{F},\mathbb{P};\mathbb{R}),n=1,\dots ,N\}.$$

The measurable space $( \Omega ,\mathcal{F})$ is fixed throughout the paper and does not appear in the notations. Unless we need to specify a different probability, we also suppress ℙ from the notations and simply write $L^0({\mathbb{R}}^N)$. In addition, we sometimes suppress ${\mathbb{R}}^d$, $d=1,\dots ,N$, in the notation of the vector spaces when the dimension of the random vector is clear from the context. We assume that $L^0({\mathbb{R}}^N)$ is equipped with the componentwise order relation, i.e., $\mathbf{X}_{1} \geq \mathbf{X}_{2}$ if $X_{1}^{i}\geq X_{2}^{i}$ ℙ-a.s. for $i=1,\dots ,N$.

When $\mathbf{Q}=(Q^{1},\dots ,Q^{N})\$ is a vector of probability measures on $( \Omega ,\mathcal{F})$, we set $L^{1}( \mathbf{Q}):=\{\mathbf{X}=(X^{1},\ldots ,X^{N}): X^{n}\in L^{1}(Q^{n}), n=1,\dots ,N\}$. Unless differently stated, all inequalities between random vectors are meant to be ℙ-a.s. inequalities.

A vector $\mathbf{X}=(X^{1},\ldots ,X^{N})\in L^{0}$ denotes a configuration of risky factors at a future time $T$ associated to a system of $N$ entities.

2.1 Orlicz setting

We consider systemic risk measures defined on Orlicz spaces; see Rao and Ren [40, Chap. III, Sect. 3.4 and Chap. IV, Sects. 4.2 and 4.4] for further details on Orlicz spaces. This presents several advantages. From a mathematical point of view, it is a more general setting than $L^{\infty }$, but at the same time it simplifies the analysis since the topology is order-continuous and there are no singular elements in the dual space. Furthermore, it has been shown by Biagini and Frittelli [9] that the Orlicz setting is natural to embed utility maximisation problems, as the natural integrability condition $\mathbb{E}[u(X)]>-\mathrm{\infty }$ is implied by $\mathbb{E}[\varphi (X)]<+\mathrm{\infty }$; see below. Univariate convex risk measures on Orlicz spaces have been introduced and studied by Cheridito and Li [17] and Biagini and Frittelli [10].

Let $u:\mathbb{R}\to \mathbb{R}$ be a concave and increasing function with $\lim _{x\rightarrow -\infty }\frac{u(x)}{x}=+ \infty$. Consider $\phi (x):=-u(-|x|)+u(0)$. Then $\varphi :\mathbb{R}\to [0,+\mathrm{\infty })$ is a strict Young function, meaning that it is finite-valued, even and convex on ℝ with $\phi (0)=0$ and $\lim _{x\rightarrow +\infty } \frac{\phi (x)}{x}=+\infty$. The Orlicz space $L^{\phi }$ and Orlicz heart $M^{\phi }$ are respectively defined by

$$\begin{array}{rl}{L}^{\varphi }& :=\{X\in L^0(\mathbb{R}):\mathbb{E}[\varphi (\alpha X)]<+\mathrm{\infty }\text{ for some }\alpha >0\},\\ M^{\varphi }& :=\{X\in L^0(\mathbb{R}):\mathbb{E}[\varphi (\alpha X)]<+\mathrm{\infty }\text{ for all }\alpha >0\},\end{array}$$

and they are Banach spaces when endowed with the Luxemburg norm. The topological dual of $M^{\phi }$ is the Orlicz space $L^{\phi ^{\ast }}$, where the convex conjugate $\phi ^{\ast }$ of $\phi$ defined by ${\varphi }^{\ast }(y):={sup}_{x\in \mathbb{R}}(xy-\varphi (x)),y\in \mathbb{R}$, is also a strict Young function. Note that

$$\mathbb{E}[u(X)]>-\mathrm{\infty }\text{if }\mathbb{E}[\varphi (X)]<+\mathrm{\infty }.$$

(2.1)

Remark 2.1

It is well known that $L^{\mathrm{\infty }}(\mathbb{P};\mathbb{R})\subseteq M^{\varphi }\subseteq L^{\varphi }\subseteq L^1(\mathbb{P};\mathbb{R})$. In addition, from the Fenchel inequality $xy\leq \phi (x)+\phi ^{\ast }(y)$, we obtain for any probability measure $Q\ll \mathbb{P}$ that

$$(\alpha |X|)\left(\lambda \frac{dQ}{d\mathbb{P}}\right)\le \varphi (\alpha |X|)+{\varphi }^{\ast }\left(\lambda \frac{dQ}{d\mathbb{P}}\right),$$

and we immediately deduce that $\frac{dQ}{d\mathbb{P}}\in L^{{\varphi }^{\ast }}$ implies $L^{\varphi }\subseteq L^1(Q;\mathbb{R})$.

Given utility functions $u_1,\dots ,u_N:\mathbb{R}\to \mathbb{R}$ satisfying the above conditions with associated Young functions $\phi _{1},\dots ,\phi _{N}$, we define

$$ \mathcal{L} = M^{{\Phi } }:=M^{\phi _{1}}\times \cdots \times M ^{\phi _{N}}, \qquad L^{{\Phi } }:=L^{\phi _{1}}\times \cdots \times L^{\phi _{N}}. $$

(2.2)

2.2 Assumptions and some properties of $\rho$

We consider systemic risk measures $\rho :M^{{\Phi } }\rightarrow [-\infty , +\infty ]$ with

$$\rho (\mathbf{X}):=inf\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in \mathcal{C}\subseteq {\mathcal{C}}_{\mathbb{R}},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}$$

(2.3)

as in (1.5), where the notation $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]\ge B$ also implicitly means that ${\sum }_{n=1}^N{u}_n(X^n+Y^n)\in L^1(\mathbb{P})$ and the linear space ${\mathcal{C}}_{\mathbb{R}}$ was introduced in (1.4). Note that there is no loss of generality in assuming $u_{n}(0)=0$ (simply replace $B$ with $B-\sum _{n=1}^{N}u_{n}(0)$).

The following are standing assumptions for the rest of the paper.

Assumption 2.2

1) ${\mathcal{C}}_0\subseteq {\mathcal{C}}_{\mathbb{R}}$ and $\mathcal{C}=\mathcal{C}_{0}\cap M^{{\Phi } }$ is a convex cone which satisfies ${\mathbb{R}}^N\subseteq \mathcal{C}\subseteq {\mathcal{C}}_{\mathbb{R}}$.

2) For all $n=1,\dots ,N$, $u_n:\mathbb{R}\to \mathbb{R}$ is increasing, strictly concave, differentiable and satisfies the Inada conditions

$$ u_{n}^{\prime }(-\infty ):=\lim _{x\rightarrow -\infty }u_{n}^{\prime }(x)=+\infty , \qquad u_{n}^{\prime }(+\infty ):=\lim _{x\rightarrow +\infty }u_{n}^{\prime }(x)=0. $$

3) $B<{\Lambda } (+\infty )$, i.e., there exists $\mathbf{M}\in {\mathbb{R}}^N$ such that $\sum _{n=1}^{N}u_{n}(M^{n}) \geq B$.

4) For all $n=1,\dots ,N$, it holds for any probability measure $Q\ll \mathbb{P}$ that

$$\mathbb{E}\left[v_n\left(\frac{dQ}{d\mathbb{P}}\right)\right]<\mathrm{\infty }\text{if and only if}\mathbb{E}\left[v_n\left(\lambda \frac{dQ}{d\mathbb{P}}\right)\right]<\mathrm{\infty },\mathrm{\forall }\lambda >0,$$

where $v_n(y):={sup}_{x\in \mathbb{R}}(u_n(x)-xy)$.

Also, from the Fenchel inequality $u_n(X)\le X\frac{dQ}{d\mathbb{P}}+v_n(\frac{dQ}{d\mathbb{P}})$ ℙ-a.s., we immediately deduce that if $X\in L^{1}(Q)$ and $\mathbb{E}[v_n(\frac{dQ}{d\mathbb{P}})]<\mathrm{\infty }$ for some probability measure $Q\ll \mathbb{P}$, then $\mathbb{E}[u_n(X)]<+\mathrm{\infty }$. Some further useful properties of $v_{n}$ are collected in Lemma A.5.

Item 4) in Assumption 2.2 is related to the reasonable asymptotic elasticity condition on utility functions, which was introduced by Schachermayer [44]. The assumption in 4), even though quite weak (see [8, Sect. 2.2]), is fundamental to guarantee the existence of solutions to classical utility maximisation problems (see [44] and [8]). In this paper, it is necessary in Sect. A.3 and for the results of Sect. 4.

Remark 2.3

Note that the duality results presented in Propositions 3.1 and 3.3 below hold true even under the following weaker assumptions on the utility functions: For all $n=1,\dots ,N$, $u_{n}$ is increasing, concave and $\lim _{x\rightarrow -\infty }\frac{u _{n}(x)}{x}=+\infty$.

The domain of $\rho$ is defined by ${\mathrm{dom}}(\rho ):=\{ \mathbf{X} \in M^{{\Phi } }: \rho (\mathbf{X})<+\infty \}$. The proof of the following proposition, which exploits the behaviour of $u_{n}$ at $-\infty$, is given in Appendix A.1.

Proposition 2.4

(a) For all$\mathbf{X} \in M^{{\Phi } }$, we have$\rho (\mathbf{X})>-\infty$. Moreover, the map$\rho :M^{\mathrm{\Phi }}\to \mathbb{R}\cup \{+\mathrm{\infty }\}$defined in (2.3) is finite-valued, monotone decreasing, convex, continuous and subdifferentiable on the Orlicz heart$M^{{\Phi } }= {\mathrm{dom}}(\rho )$.

(b) Furthermore, we have for$\mathbf{X}\in {\mathrm{dom}}( \rho )$that

$$\rho (\mathbf{X})={\rho }^{=}(\mathbf{X}):=inf\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in \mathcal{C},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]=B\}.$$

If there exists an optimal allocation$\mathbf{Y}_{\mathbf{X}}= (Y _{\mathbf{X}}^{1},\dots ,Y_{\mathbf{X}}^{N}) \in \mathcal{C}_{0} \cap M^{{\Phi } }$of$\rho (\mathbf{X})$, then it is unique.

We complete this subsection by introducing one relevant example for the set of admissible random elements, which we denote by $\mathcal{C} ^{(\mathbf{n})}$.

Definition 2.5

For $h\in \{ 1,\dots ,N\}$, let $\mathbf{n}:=(n^1,\dots ,n^h)\in {\mathbb{N}}^h$ satisfy $\ n^{m-1}< n^{m}$ for $m=1, \dots ,h$, $n^{0}:=0$ and $n^{h}:=N$. Set $I_{m}:=\{ n^{m-1}+1,\dots ,n^{m}\}$ for $m=1,\dots ,h$. We now introduce the family of allocations $\mathcal{C}^{(\mathbf{n})}=\mathcal{C}_{0}^{( \mathbf{n})}\cap M^{{\Phi } }$, where

$$\begin{array}{rl}{\mathcal{C}}_0^{(\mathbf{n})}=\{\mathbf{Y}\in L^0({\mathbb{R}}^N):& \mathrm{\exists }d=(d_1,\dots ,d_h)\in {\mathbb{R}}^h\text{ with}\\ & \sum _{i\in I_m}{Y}^i=d_m\text{ for }m=1,\dots ,h\}\subseteq {\mathcal{C}}_{\mathbb{R}}.\end{array}$$

(2.4)

Definition 2.5 models a cluster $C=(C_{1},\dots ,C_{h})$ of financial institutions which is a partition of $\{ X^{1},\dots ,X^{N} \}$. The constraint on $\mathbf{Y}$ is that the components of $\mathbf{Y}$ must sum up to a real number in each element $C_{i}$ of the cluster, i.e., ${\sum }_{j:X^j\in C_i}{Y}^j\in \mathbb{R}$.

For a given $\mathbf{n}:=(n^{1},\dots ,n^{h})$, the values $(d_{1}, \dots ,d_{h})$ may change, but the number of elements in each of the $h$ groups $I_{m}$ is fixed by $\mathbf{n}$. It is then easily seen that $\mathcal{C}^{(\mathbf{n})}$ is a linear space containing ${\mathbb{R}}^N$ and closed with respect to convergence in probability. We point out that the family $\mathcal{C}^{(\mathbf{n})}$ admits two extreme cases:

(i) The strongest restriction occurs when $h=N$, i.e., we consider exactly $N$ groups, and in this case ${\mathcal{C}}^{(\mathbf{n})}={\mathbb{R}}^N$ corresponds to the deterministic case.

(ii) On the opposite side, we can have only one group, $h=1$, and ${\mathcal{C}}^{(\mathbf{n})}={\mathcal{C}}_{\mathbb{R}}\cap M^{\mathrm{\Phi }}$ is the largest possible class corresponding to an arbitrary random injection $\mathbf{Y} \in M^{{\Phi } }$ with the only constraint ${\sum }_{n=1}^N{Y}^n\in \mathbb{R}$.

3 Dual representation of $\rho$

We now investigate the dual representation of systemic risk measures of the form (2.3). When $\mathbf{Z}\in M^{{\Phi } }$ and $\mathbf{\xi }\in L^{{\Phi } ^{\ast }}$, we set $\mathbb{E}[\xi \mathbf{Z}]:={\sum }_{n=1}^N\mathbb{E}[{\xi }^n{Z}^n]$, and for $\frac{d\mathbf{Q}}{d\mathbb{P}}\in L_{+}^{{\mathrm{\Phi }}^{\ast }}$, ${\mathbb{E}}_{\mathbf{Q}}[\mathbf{Z}]={\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Z^n]$. We frequently identify the density $\frac{dQ}{d\mathbb{P}}$ with the associated probability measure $Q\ll \mathbb{P}$.

Proposition 3.1

For any$\mathbf{X} \in M^{{\Phi } }$,

$${\rho }_B(\mathbf{X})=\underset{\mathbf{Q}\in \mathcal{D}}{max}(\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-X^n]-{\alpha }_B(\mathbf{Q})),$$

(3.1)

where the penalty function is given by

$${\alpha }_B(\mathbf{Q}):=\underset{\mathbf{Z}\in \mathcal{A}}{sup}\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-Z^n],$$

(3.2)

with$\mathcal{A}:=\{\mathbf{Z}\in M^{\mathrm{\Phi }}:{\sum }_{n=1}^N\mathbb{E}[u_n(Z^n)]\ge B\}$and

$$\begin{array}{rl}\mathcal{D}:=\mathrm{dom}({\alpha }_B)\cap \{\frac{d\mathbf{Q}}{d\mathbb{P}}\in L_{+}^{{\mathrm{\Phi }}^{\ast }}:& Q^n[\mathrm{\Omega }]=1\mathit{\text{ for all }}n\mathit{\text{ and}}\\ & \sum _{n=1}^N({\mathbb{E}}_{Q^n}[Y^n]-Y^n)\le 0\mathit{\text{ for all }}\mathbf{Y}\in {\mathcal{C}}_0\cap M^{\mathrm{\Phi }}\},\end{array}$$

(3.3)

where${\mathrm{dom}}(\alpha _{B}):=\{\mathbf{Q}=(Q^{1}, \dots , Q^{N}) : Q^{n} \ll P \ \textit{for all}\ n \ \textit{and}\ \alpha _{B}(\mathbf{Q})<+ \infty \}$.

(i) Suppose that for some$i,j\in \{ 1,\dots ,N\}$, $i\neq j$, we have$\pm (e_{i}1_{A}-e_{j}1_{A})\in \mathcal{C}$for all$A\in \mathcal{F}$. Then

$$\begin{array}{rl}\mathcal{D}=\mathrm{dom}({\alpha }_B)\cap \{\frac{d\mathbf{Q}}{d\mathbb{P}}\in L_{+}^{{\mathrm{\Phi }}^{\ast }}:& Q^n[\mathrm{\Omega }]=1\mathit{\text{ for all }}n,Q^i=Q^j\mathit{\text{ and}}\\ & \sum _{n=1}^N({\mathbb{E}}_{Q^n}[Y^n]-Y^n)\le 0\mathit{\text{ for all }}\mathbf{Y}\in \mathcal{C}\}.\end{array}$$

(ii) Suppose that$\pm (e_{i}1_{A}-e_{j}1_{A})\in \mathcal{C}$for all$i,j$and all$A\in \mathcal{F}$. Then

$$\mathcal{D}=\mathrm{dom}({\alpha }_B)\cap \{\frac{d\mathbf{Q}}{d\mathbb{P}}\in L_{+}^{{\mathrm{\Phi }}^{\ast }}:Q^1[\mathrm{\Omega }]=1\mathit{\text{ and }}{Q}^n=Q^1\mathit{\text{ for all }}n\}.$$

Proof

The dual representation (3.1) is a consequence of Proposition 2.4, Theorem A.2 and Propositions 3.9 and 3.11 in [31], taking into consideration that $\mathcal{C}$ is a convex cone, the dual space of the Orlicz heart $M^{{ \Phi } }$ is the Orlicz space $L^{{\Phi } ^{\ast }}$ and $M ^{{\Phi } }={\mathrm{dom}}(\rho )$. Note that by Theorem A.2, the dual elements $\mathbf{\xi }\in L_{+}^{{ \Phi } ^{\ast }}$ are positive, but a priori not normalised. However, we get $\mathbb{E}[{\xi }^n]=1$ by taking $\mathbf{Y}=\pm e_j\in {\mathbb{R}}^N$ and using $\sum _{n=1}^{N}(\xi ^{n}(Y^{n})-Y ^{n})\leq 0$ for all $\mathbf{Y}\in \mathcal{C}$, so that $\xi ^{j}(1)-1\leq 0$ and $\xi ^{j}(-1)+1\leq 0$ imply $\xi ^{j}(1)=1$. This shows the form of the domain $\mathcal{D}$ in (3.3).

(i) Take $\mathbf{Y}:=e_{i}1_{A}-e_{j}1_{A}\in \mathcal{C}$. From $\sum _{n=1}^{N} ( E_{Q^{n}} [Y^{n}] -Y^{n})\leq 0$, we obtain $Q^{i}[A]-1_{A}-Q^{j}[A]+1_{A}\leq 0$, i.e., $Q^{i}[A]-Q^{j}[A]\leq 0$ and similarly taking $\mathbf{Y}:=-e_{i}1_{A}+e_{j}1_{A}\in \mathcal{C}$, we get $Q^{j}[A]-Q^{i}[A]\leq 0$.

(ii) From (i), we obtain $Q^{i}=Q^{j}$. In addition, as ${\sum }_{n=1}^N{Y}^n\in \mathbb{R}$, we get

$$\sum _{n=1}^N({\mathbb{E}}_Q[Y^n]-Y^n)={\mathbb{E}}_Q\left[\sum _{n=1}^N{Y}^n\right]-\sum _{n=1}^N{Y}^n=0.$$

 □

Proposition 3.1 guarantees the existence of a maximiser $\mathbf{Q}_{\mathbf{X}}$ to the dual problem (3.1) and that $\alpha _{B}(\mathbf{Q}_{\mathbf{X}})<+\infty$. Uniqueness is proved in Corollary 4.13 below.

Definition 3.2

Fix any $\mathbf{X} \in M^{{\Phi } }$. A solution of the dual problem (3.1) is a vector $\mathbf{Q}_{ \mathbf{X}}=(Q_{\mathbf{X}}^{1},\dots ,Q_{\mathbf{X}}^{N})$ of probability measures verifying $\frac{d{\mathbf{Q}}_{\mathbf{X}}}{d\mathbb{P}}\in \mathcal{D}$ and

$${\rho }_B(\mathbf{X})=\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]-{\alpha }_B({\mathbf{Q}}_{\mathbf{X}}).$$

(3.4)

A vector $\mathbf{Q}$ of probability measures having density in $\mathcal{D}$ could be viewed, in the systemic $N$-dimensional one-period setting, as the counterpart of the notion of (ℙ-absolutely continuous) martingale measures. Indeed, because $\mathbf{Y}\in {\mathcal{C}}_0\subseteq {\mathcal{C}}_{\mathbb{R}}$, ${\sum }_{n=1}^N{Y}^n\in \mathbb{R}$ is the total amount to be allocated to the $N$ institutions, and then the total cost or value ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]$ should at most be equal to $\sum _{n=1} ^{N}Y^{n}$, for any “fair” valuation operator ${\mathbb{E}}_{\mathbf{Q}}[\cdot ]$, which is the case if $\frac{d\mathbf{Q}}{d\mathbb{P}}\in \mathcal{D}$.

There exists a simple relation among $\rho _{B}$, $\rho _{B}^{ \mathbf{Q}}$ and $\alpha _{B}(\mathbf{Q})$ defined in (2.3), (1.10) and (3.2), respectively.

Proposition 3.3

We have

$${\rho }_B^{\mathbf{Q}}(\mathbf{X})=-\sum _{n=1}^N{\mathbb{E}}_{Q^n}[X^n]-{\alpha }_B(\mathbf{Q})$$

(3.5)

and

$${\rho }_B(\mathbf{X})=\underset{\frac{d\mathbf{Q}}{d\mathbb{P}}\in \mathcal{D}}{max}{\rho }_B^{\mathbf{Q}}(\mathbf{X})={\rho }_B^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X}),$$

(3.6)

where$\mathbf{Q}_{\mathbf{X}}$is a solution of the dual problem (3.1).

Proof

We have

$$\begin{array}{rl}-{\alpha }_B(\mathbf{Q})& =inf\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Z^n]:\mathbf{Z}\in M^{\mathrm{\Phi }}\text{ and }\sum _{n=1}^N\mathbb{E}[u_n(Z^n)]\ge B\}\\ & =inf\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[X^n+Y^n]:\mathbf{Y}\in M^{\mathrm{\Phi }}\text{ and}\sum _{n=1}^N\mathbb{E}[u_n(X^n+Y^n)]\ge B\}\\ & =\sum _{n=1}^N{\mathbb{E}}_{Q^n}[X^n]+{\rho }_B^{\mathbf{Q}}(\mathbf{X}),\end{array}$$

which proves (3.5). Then from (3.5) and (3.4), we deduce that

$${\rho }_B^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})=-\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[X^n]-{\alpha }_B({\mathbf{Q}}_{\mathbf{X}})={\rho }_B(\mathbf{X}),$$

and from (3.1) and (3.5), we get $\rho _{B}( \mathbf{X})=\max _{\mathbf{Q}\in \mathcal{D}}\rho _{B}^{\mathbf{Q}}( \mathbf{X})$. □

Proposition 3.4

If$\alpha _{B}(\mathbf{Q})<+\infty$, the penalty function in (3.2) can be written as

$${\alpha }_B(\mathbf{Q}):=\underset{\mathbf{Z}\in \mathcal{A}}{sup}\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-Z^n]=\underset{\lambda >0}{inf}(-\frac{1}{\lambda }B+\frac{1}{\lambda }\sum _{n=1}^N\mathbb{E}[v_n\left(\lambda \frac{d{Q}^n}{d\mathbb{P}}\right)\left]\right),$$

(3.7)

and$\mathbb{E}[v_n(\lambda \frac{d{Q}^n}{d\mathbb{P}})]<\mathrm{\infty }$for all$n$and all$\lambda >0$. In addition, the infimum is attained in (3.7), i.e.,

$${\alpha }_B\left(\mathbf{Q}\right)=\sum _{n=1}^N\mathbb{E}\left[\frac{d{Q}^n}{d\mathbb{P}}{v}_n^{\prime }\left({\lambda }^{\ast }\frac{d{Q}^n}{d\mathbb{P}}\right)\right],$$

(3.8)

where${\lambda }^{\ast }>0$is the unique solution of the equation²

$$-B+\sum _{n=1}^N\mathbb{E}\left[v_n\left(\lambda \frac{d{Q}^n}{d\mathbb{P}}\right)\right]-\lambda \sum _{n=1}^N\mathbb{E}\left[\frac{d{Q}^n}{d\mathbb{P}}{v}_n^{\prime }\left(\lambda \frac{d{Q}^n}{d\mathbb{P}}\right)\right]=0.$$

(3.9)

Proof

See Appendix A.2. □

Example 3.5

Consider the grouping of Definition 2.5. As $\mathcal{C}^{( \mathbf{n})}$ is a linear space containing ${\mathbb{R}}^N$, the dual representation (3.1) applies. In addition, we have in each group that $\pm (e_{i}1_{A}-e_{j}1_{A})\in \mathcal{C}^{(\mathbf{n})}$ for all $i,j$in the same group and for all $A\in \mathcal{F}$. Therefore in each group, the components $Q^{i}$, $i\in I_{m}$, of the dual elements are all the same, i.e., $Q^{i}=Q^{j}$ for all $i,j\in I_{m}$, and the representation (3.1) becomes

$$\begin{array}{rl}{\rho }_B(\mathbf{X})& =\underset{\mathbf{Q}\in \mathcal{D}}{max}(\sum _{m=1}^h\sum _{k\in I_m}({\mathbb{E}}_{Q^m}[-X^k])-{\alpha }_B(\mathbf{Q}))\\ & =\underset{\mathbf{Q}\in \mathcal{D}}{max}(\sum _{m=1}^h{\mathbb{E}}_{Q^m}[-{\bar{X}}_m]-{\alpha }_B(\mathbf{Q})),\end{array}$$

(3.10)

with

$$\mathcal{D}:=\mathrm{dom}({\alpha }_B)\cap \{\frac{d\mathbf{Q}}{d\mathbb{P}}\in L_{+}^{{\mathrm{\Phi }}^{\ast }}:Q^i=Q^j\text{ for all }i,j\in I_m,Q^i[\mathrm{\Omega }]=1\}$$

(3.11)

and $\overline{X}_{m}:=\sum _{k\in I_{m}}X^{k}$. Indeed,

$$\begin{array}{rl}\sum _{n=1}^N({\mathbb{E}}_{Q^n}[Y^n]-Y^n)& =\sum _{m=1}^h\sum _{k\in I_m}({\mathbb{E}}_{Q^m}[Y^k]-Y^k)\\ & =\sum _{m=1}^h\left({\mathbb{E}}_{Q^m}\right[\sum _{k\in I_m}{Y}^k]-\sum _{k\in I_m}{Y}^k)=0,\end{array}$$

as ${\sum }_{k\in I_m}{Y}^k=d_m\in \mathbb{R}$. If we have only one single group, all components of a dual element $\mathbf{Q}\in \mathcal{D}$ are the same. If $\mathbf{Q}=(Q^{1},\dots ,Q^{n})_{n=1, \dots ,N}$ is in $\mathcal{{D}}$ defined in (3.11), then $({\mathbb{E}}_{{\mathbf{Q}}_1}[Y_{\mathbf{X}}^1],\dots ,{\mathbb{E}}_{{\mathbf{Q}}_N}[Y_{\mathbf{X}}^N])$ is a systemic risk allocation as in Definition 1.2, i.e.,

$$\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y_{\mathbf{X}}^n]=\sum _{m=1}^h\sum _{k\in I_m}{\mathbb{E}}_{Q^m}[Y_{\mathbf{X}}^k]=\sum _{m=1}^h{\mathbb{E}}_{Q^m}\left[\sum _{k\in I_m}{Y}_{\mathbf{X}}^k\right]=\sum _{m=1}^h{d}_m=\rho (\mathbf{X}).$$

(3.12)

Example 3.6

Consider $u_n:\mathbb{R}\to \mathbb{R}$, $u_{n}(x)=-e^{- \alpha _{n}x}/\alpha _{n}$, $\alpha _{n}>0$, for each $n$ and let $B<0$. Then $v_{n}^{\prime }(y)=\frac{1}{\alpha _{n}}\ln y$. From the first order condition (3.9), we obtain that the minimiser is ${\lambda }^{\ast }=-\frac{B}{\beta }$ with $\beta :=\sum _{n=1}^{N}\frac{1}{ \alpha _{n}}$. Therefore (3.8) gives

$${\alpha }_B(\mathbf{Q})=\sum _{n=1}^N\mathbb{E}\left[\frac{d{Q}^n}{d\mathbb{P}}{v}_n^{\prime }\left({\lambda }^{\ast }\frac{d{Q}^n}{d\mathbb{P}}\right)\right]=\sum _{n=1}^N\frac{1}{{\alpha }_n}(H(Q^n|\mathbb{P})+ln(-\frac{B}{\beta })),$$

(3.13)

where $H(Q^n|\mathbb{P}):=\mathbb{E}[\frac{d{Q}^n}{d\mathbb{P}}ln\frac{d{Q}^n}{d\mathbb{P}}]$ is the relative entropy.

4 Existence of solutions

In this section, we deal with existence and uniqueness of optimal allocations for $\rho _{B}(\mathbf{X})$ and the other related primal optimisation problems introduced in Sect. 1. Throughout this section, we assume $\mathbf{X}\in M^{{ \Phi } }$ and that $\mathbf{Q}=(Q^{1},\dots ,Q^{N})$ satisfies $Q^n\ll \mathbb{P}$, $\frac{d\mathbf{Q}}{d\mathbb{P}}\in L^{{\mathrm{\Phi }}^{\ast }}$ and $\alpha _{B}(\mathbf{Q})<+\infty$, or equivalently $\rho _{B}^{\mathbf{Q}}(\mathbf{X})>-\infty$. Recall from Proposition 3.4 that this implies $\mathbb{E}[v_n(\lambda \frac{d{Q}^n}{dP})]<+\mathrm{\infty }$ for all $n$ and all $\lambda >0$. Set

$$L^1(\mathbb{P},\mathbf{Q}):=(L^1(\mathbb{P};{\mathbb{R}}^N)\cap L^1(\mathbf{Q};{\mathbb{R}}^N))\supseteq L^{\mathrm{\Phi }}\supseteq M^{\mathrm{\Phi }}\text{,}$$

(4.1)

where the inclusions follow from Remark 2.1 and $\frac{d\mathbf{Q}}{d\mathbb{P}}\in L^{{\mathrm{\Phi }}^{\ast }}$.

Without loss of generality, we may assume that $u_{i}(0)=0$, $1\leq i\leq N$, and observe that then

$$ u_{i}(x)=u_{i}(x^{+})+u_{i}(-x^{-}). $$

(4.2)

When the utility functions $u_{n}$ are of exponential type, the Orlicz heart $M^{{\Phi } }$ is sufficiently large and contains the optimal allocation $\mathbf{Y}_{\mathbf{X}}$ to $\rho _{B}(\mathbf{X})$; see Sect. 6. This of course also happens for general utility functions on a finite probability space.

As shown in Sect. 4.3, in general, we cannot expect to find the solution $\mathbf{Y}_{\mathbf{Q}}$ for the problem $\rho _{B}^{\mathbf{Q}}(\mathbf{X})$ in the space $M^{{\Phi } }$, but only in the larger space $L^{1}(\mathbf{Q})$, and this motivates the introduction of several extended problems. Let $B\in \mathbb{R}$ and define

$$\begin{array}{rcl}{\tilde{\rho }}_B^{\mathbf{Q}}(\mathbf{X})& :=& inf\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]:\mathbf{Y}\in L^1(\mathbb{P},\mathbf{Q}),\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\},\\ {\hat{\rho }}_B^{\mathbf{Q}}(\mathbf{X})& :=& inf\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]:\mathbf{Y}\in L^1(\mathbf{Q}),\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\},\\ {\tilde{\rho }}_B(\mathbf{X})& :=& inf\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}.\end{array}$$

Analogously, we define $\widetilde{\pi }_{A}^{\mathbf{Q}}(\mathbf{X})$, $\widehat{\pi }_{A}^{\mathbf{Q}}(\mathbf{X})$ and $\widetilde{\pi } _{A}(\mathbf{X})$ for $A\in \mathbb{R}$ by using the optimisation (1.9). We show in (4.8) and (4.9) below that these extensions from $M^{{\Phi } }$ to integrable random variables do not change the optimal values.

In order to prove the existence of an optimal allocation for $\widetilde{\rho }_{B}(\mathbf{X})$, we proceed in several steps. In Theorem 4.10, we first prove the existence of a solution $\widehat{\mathbf{Y}}_{\mathbf{Q}}\in L^{1}(\mathbf{Q})$ for $\widehat{\rho }_{B}^{\mathbf{Q}}(\mathbf{X})$. Then in Proposition 4.11, we show that when it exists, the optimiser to $\rho _{B}( \mathbf{X})$ or to $\widetilde{\rho }_{B}(\mathbf{X})$ coincides with $\widehat{\mathbf{Y}}_{\mathbf{Q}_{\mathbf{X}}}\in L^{1}(\mathbf{Q} _{\mathbf{X}})$. The next key step is to show the existence of $\mathbf{Y}\in L^1(\mathbb{P})$ which is, as specified in Theorem 4.14, a candidate solution to the extended problem and then to prove that $\mathbf{Y}\in L^{1}(\mathbf{Q}_{\mathbf{X}})$. In a final step (see Theorem 4.19, Proposition 4.22 and Corollary 4.23), we prove that $\rho _{B}(\mathbf{X})= \widetilde{\rho }_{B}(\mathbf{X})$ and that the above $\mathbf{Y}\in L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$, hereafter denoted with $\tilde{\mathbf{Y}}_{\mathbf{X}}$, is an optimiser of the extended problem $\widetilde{\rho }_{B}(\mathbf{X})$ and hence coincides with $\widehat{\mathbf{Y}}_{\mathbf{Q}_{\mathbf{X}}}$.

4.1 On $\rho _{B}(\mathbf{X})$ and $\pi _{A}(\mathbf{X})$

Recall that under Assumption 2.2, $\mathcal{C}$ is a convex cone so that if $\mathbf{Y}\in \mathcal{C}$, then $\mathbf{Y}+ \mathbf{\delta }\in \mathcal{C}$ for every deterministic $\delta \in {\mathbb{R}}^N$. Note that $\rho _{B}^{\mathbf{Q}}( \mathbf{X})<+\infty$ and $\pi _{A}^{\mathbf{Q}}(\mathbf{X})>-\infty$.

Proposition 4.1

(a) $B=\pi _{A}(\mathbf{X})$if and only if$A=\rho _{B}( \mathbf{X})$.

(b) If$B=\widetilde{\pi }_{A}(\mathbf{X})$, then$A= \widetilde{\rho }_{B}(\mathbf{X})$.

(c) If$A=\rho _{B}(\mathbf{X})$and there exists a solution to one of the two problems$\pi _{A}(\mathbf{X})$or$\rho _{B}(\mathbf{X})$, then it is the unique solution to both problems.

Proof

(a) “⇐” Let $A=\rho _{B}(\mathbf{X})$ and suppose first that $\pi _{A}(\mathbf{X})>B$. Then there exists $\tilde{\mathbf{Y}} \in \mathcal{C}_{0}\cap M^{{\Phi } }$ such that $\sum _{n=1} ^{N}\tilde{Y}^{n}\leq A$ and $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+{\tilde{Y}}^n)]>B$. The continuity of $u_{n}$ and $\mathbb{E}[u_n(Z^n)]>-\mathrm{\infty }$ for all $\mathbf{Z}\in M^{{\Phi } }$ imply that there exist ${\varepsilon }>0$ and $\widehat{\mathbf{Y}}:= \tilde{\mathbf{Y}}-{\varepsilon }\mathbf{1} \in \mathcal{C}_{0}\cap M ^{{\Phi } }$ such that $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+{\hat{Y}}^n)]\ge B$ and $\sum _{n=1}^{N}\widehat{Y}^{n}< A$. This is in contradiction to $A=\rho _{B}(\mathbf{X})$.

Suppose now that $\pi _{A}(\mathbf{X})< B$. Then there must exist $\delta >0$ such that we have $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]\le B-\delta$ for all $\mathbf{Y}\in \mathcal{C}_{0}\cap M^{{\Phi } }$ such that $\sum _{n=1}^{N}Y ^{n}\leq A$. As $A=\rho _{B}(\mathbf{X})$, for all ${\varepsilon }>0$, there exists $\mathbf{Y}_{{\varepsilon }}\in \mathcal{C}_{0}\cap M ^{{\Phi } }$ such that $\sum _{n=1}^{N}Y_{{\varepsilon }}^{n} \leq A+{\varepsilon }$ and $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y_{\epsilon }^n)]\ge B$. For any $\eta \geq {\varepsilon }\geq \sum _{n=1}^{N}Y_{{\varepsilon }}^{n}-A$, we get

$$ \sum _{n=1}^{N}\bigg(Y_{{\varepsilon }}^{n}-\frac{\eta }{N}\bigg) \leq A+{\varepsilon }-\eta \leq A. $$

Due to $\mathbb{E}[u_n(Z^n)]>-\mathrm{\infty }$ for all $\mathbf{Z}\in M ^{{\Phi } }$ and the continuity of $u_{n}$, we may select ${\varepsilon }>0$ and $\eta \geq {\varepsilon }$ small enough so that $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y_{\epsilon }^n-\frac{\eta }{N})]>B-\delta$. As $\widehat{\mathbf{Y}}:=(Y_{{\varepsilon }} ^{n}-\frac{\eta }{N})_{n}\in \mathcal{C}_{0}\cap M^{{\Phi } }$, we obtain a contradiction.

“⇒” Let $B=\pi _{A}(\mathbf{X})$ and suppose first that $\rho _{B}(\mathbf{X})< A$. Then there must exist $\tilde{\mathbf{Y}} \in \mathcal{C}_{0}\cap M^{{\Phi } }$ such that $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+{\tilde{Y}}^n)]\ge B$ and $\sum _{n=1} ^{N}\widetilde{Y}^{n}< A$. Then there exist ${\varepsilon }>0$ and $\widehat{\mathbf{Y}}:=\tilde{ \mathbf{Y}}+{\varepsilon \mathbf{1}}\in \mathcal{C}_{0}\cap M^{{ \Phi } }$ such that $\sum _{n=1}^{N}\widehat{Y}^{n}\leq A$ and $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+{\hat{Y}}^n)]>B$. This is in contradiction to $B=\pi _{A}(\mathbf{X})$.

Suppose now that $\rho _{B}(\mathbf{X})>A$. Then there must exist $\delta >0$ such that we have $\sum _{n=1}^{N}Y^{n}\geq A+ \delta$ for all $\mathbf{Y}\in \mathcal{C}_{0}\cap M^{{ \Phi } }$ such that $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]\ge B$. As $B=\pi _{A}(\mathbf{X})$, for all ${\varepsilon }>0$, there exists $\mathbf{Y}_{{\varepsilon }}\in \mathcal{C}_{0}\cap M^{{ \Phi } }$ such that $\sum _{n=1}^{N}Y_{{\varepsilon }}^{n}\leq A$ and $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y_{\epsilon }^n)]>B-\epsilon$. Define

$${\eta }_{\epsilon }:=inf\{a>0:\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y_{\epsilon }^n+\frac{a}{N})]\ge B\}$$

and note that $\eta _{{\varepsilon }}\downarrow 0$ if ${\varepsilon } \downarrow 0$. Take ${\varepsilon }>0$ such that $\eta _{{\varepsilon }}<\delta$. Then for any $0<\beta <\delta -\eta _{{\varepsilon }}$, we have $\sum _{n=1}^{N}(Y_{{\varepsilon }}^{n}+\frac{ \eta _{{\varepsilon }}+\beta }{N})\leq A+\eta _{{\varepsilon }}+\beta < A+ \delta$ as well as $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y_{\epsilon }^n+\frac{{\eta }_{\epsilon }+\beta }{N})]\ge B$. As $(Y_{{\varepsilon }}^{n}+\frac{\eta _{{\varepsilon }}+\beta }{N}) \in \mathcal{C}_{0}\cap M^{{\Phi } }$, we obtain a contradiction.

(b) This follows in the same way as “⇒” in (a), replacing $M^{{\Phi } }$ with $L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$.

(c) Suppose there exists $\mathbf{Y}\in \mathcal{C}_{0}\cap M^{{ \Phi } }$ which is a solution to problem (1.5). As $A:=\rho _{B}(\mathbf{X})$, then $\sum _{n=1}^{N}Y^{n}=A$ and the constraint in problem (1.7) is fulfilled for $\mathbf{Y}$. By (a), $B={\pi }_A(\mathbf{X})\ge \mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]\ge B$ and we deduce that $\mathbf{Y}$ is a solution to problem (1.7). Suppose there exists $\mathbf{Y}\in \mathcal{C}_{0} \cap M^{{\Phi } }$ which is a solution to problem (1.7) and set $B:=\pi _{A}(\mathbf{X})$. Then $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]=B$ and the constraint in problem (1.5) is fulfilled for $\mathbf{Y}$. By (a), $A=\rho _{B}( \mathbf{X})\leq \sum _{n=1}^{N}Y^{n}\leq A$ and we deduce that $\mathbf{Y}$ is a solution to problem (1.5). As $\rho _{B}( \mathbf{X})$ admits at most one solution by Proposition 2.4, the same must be true for $\pi _{A}(\mathbf{X})$. □

Proposition 4.2

(a) $B=\pi _{A}^{\mathbf{Q}}(\mathbf{X})$if and only if$A=\rho _{B}^{\mathbf{Q}}(\mathbf{X})$.

(b) If$B=\widetilde{\pi }_{A}^{ \mathbf{Q}}(\mathbf{X})$, then$A=\widetilde{\rho }_{B}^{\mathbf{Q}}(\mathbf{X })$. Similarly, if$B=\widehat{\pi }_{A}^{\mathbf{Q}} (\mathbf{X})$, then$A=\widehat{\rho }_{B}^{\mathbf{Q}}(\mathbf{X})$.

(c) If$A=\rho _{B}^{\mathbf{Q}}(\mathbf{X})$and$B=\pi _{A} ^{\mathbf{Q}}(\mathbf{X})$and there exists a solution to one of the two problems$\pi _{A}^{\mathbf{Q}}(\mathbf{X})$or$\rho _{B}^{\mathbf{Q}}( \mathbf{X})$, then it is the unique solution to both problems.

(d) In (c), we may replace$\pi _{A}^{\mathbf{Q}}$, $\rho _{B}^{\mathbf{Q}}$with$\widetilde{\pi }_{A}^{\mathbf{Q}}$, $\widetilde{\rho }_{B}^{\mathbf{Q}}$or with$\widehat{\pi }_{A}^{ \mathbf{Q}}$, $\widehat{\rho }_{B}^{\mathbf{Q}}$.

Proof

Use step by step the same arguments as in the proof of Proposition 4.1, replacing $\sum _{n=1}^{N}Y^{n}$ with ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]$. The uniqueness in (c) is a consequence of Remark 4.9. □

When using $\mathbf{Q}=\mathbf{Q}_{\mathbf{X}}$, we have already proved that $\rho _{B}(\mathbf{X})=\rho _{B}^{\mathbf{Q}_{\mathbf{X}}}( \mathbf{X})$. Similarly:

Corollary 4.3

Let$A:=\rho _{B}(\mathbf{X})$. Then$\pi _{A}(\mathbf{X})=\pi _{A}^{ \mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$.

Proof

As $A={\rho }_B(\mathbf{X})\in \mathbb{R}$, Proposition 3.3 gives $A=\rho _{B}(\mathbf{X})=\rho _{B}^{\mathbf{Q}_{\mathbf{X}}}( \mathbf{X})$. By Proposition 4.1 (a), respectively Proposition 4.2 (a), we deduce that $B=\pi _{A}(\mathbf{X})$, resp. $B=\pi _{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$, hence $\pi _{A}( \mathbf{X})=\pi _{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$. □

4.2 On the optimal values

The main contribution of this section is to show that the optimal values coincide, see (4.8) and (4.9) below, and that, see (4.11) below,

$${\pi }_A^{\mathbf{Q}}(\mathbf{X})=\underset{{\sum }_{n=1}^N{a}^n=A}{max}\sum _{n=1}^N{U}_n(a^n),A\in \mathbb{R},$$

where

$$U_n(a^n):=sup\{\mathbb{E}[u_n(X^n+W)]:W\in M^{{\varphi }_n},{\mathbb{E}}_{Q^n}[W]\le a^n\}$$

(4.3)

and $\mathbf{a}\in {\mathbb{R}}^N$. In the sequel, we write $U_{n}^{Q_{n}}(a^{n})$ when we need to emphasise the dependence on $Q^{n}$. Note that $\mathbb{E}[u_n(X^n+W)]\le u_n(\mathbb{E}[X^n+W])<+\mathrm{\infty }$ for all $X^n,W\in M^{{\varphi }_n}\subseteq L^1(\mathbb{P};\mathbb{R})$. The conditions $X^{n},W\in M^{\phi _{n}}$ imply that we have $\mathbb{E}[u_n(X^n+W)]>-\mathrm{\infty }$, from which it follows that $U_{n}(a^{n})>-\infty$. As $\frac{d\mathbf{Q}}{dP}\in L^{{\Phi } ^{\ast }}$, $W\in M^{\phi _{n}}$ implies $W\in L^{1}(Q^{n})$ and the problem (4.3) is well posed. Due to the monotonicity and concavity of $u_{n}$, the function $U_{n}$ is monotone increasing, concave and continuous on ℝ and we may replace in its definition the inequality with an equality sign. However, in general, the solution to (4.3) only exists on a larger domain, as suggested by the well-known result reported in Proposition A.6. This leads us to introduce the auxiliary problems

$$\begin{array}{rl}{\hat{U}}_n(a^n)& :=sup\{\mathbb{E}[u_n(X^n+W)]:W\in L^1(Q^n),{\mathbb{E}}_{Q^n}[W]\le a^n\},\\ {\tilde{U}}_n(a^n)& :=sup\{\mathbb{E}[u_n(X^n+W)]:W\in L^1(\mathbb{P},Q^n),{\mathbb{E}}_{Q^n}[W]\le a^n\},\end{array}$$

where $L^1(\mathbb{P},Q^n)$ is defined as in (4.1). The following proposition is a multi-dimensional version of well-known utility maximisation problems. Its proof is based on the extended Namioka–Klee theorem and deferred to Appendix A.4.

Proposition 4.4

We have that

$$ U_{n}(a^{n})=\widetilde{U}_{n}(a^{n})=\widehat{U}_{n}(a^{n})< +\infty , $$

(4.4)

$$\begin{array}{rl}& \mathit{\text{if }}{U}_n(a^n)<u_n(+\mathrm{\infty }),\mathit{\text{ then }}{U}^n:\mathbb{R}\to \mathbb{R}\mathit{\text{ is differentiable, }}\\ & U_n(-\mathrm{\infty })=-\mathrm{\infty },U_n^{\prime }>0,U_n^{\prime }(-\mathrm{\infty })=+\mathrm{\infty },U_n^{\prime }(+\mathrm{\infty })=0,\end{array}$$

(4.5)

and

$$U_n(a^n)=\underset{\lambda >0}{inf}(\lambda ({\mathbb{E}}_{Q^n}[X^n]+a^n)+\mathbb{E}[v_n\left(\lambda \frac{d{Q}^n}{dP}\right)\left]\right).$$

(4.6)

We now show that the optimal values are the same.

Lemma 4.5

Let$A:=\rho _{B}^{\mathbf{Q}}(\mathbf{X})$and$\pi _{A}^{\mathbf{Q}}( \mathbf{X})<+\infty$. Then

$$\begin{array}{rl}{\pi }_A^{\mathbf{Q}}(\mathbf{X})& =sup\left\{\mathbb{E}\right[\sum _{n=1}^N{u}_n(X^n+Y^n)]:\mathbf{Y}\in M^{\mathrm{\Phi }},\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]=A\}\\ & =:{\pi }_A^{\mathbf{Q},=}(\mathbf{X})\end{array}$$

(4.7)

and

$$\begin{aligned} \pi _{A}^{\mathbf{Q}}(\mathbf{X}) =&\sup _{\sum _{n=1}^{N}a^{n}=A}\sum _{n=1}^{N}U_{n}(a^{n})=\widetilde{\pi }_{A}^{\mathbf{Q}}(\mathbf{X})= \widehat{\pi }_{A}^{\mathbf{Q}}(\mathbf{X}), \end{aligned}$$

(4.8)

$$\begin{aligned} \rho _{B}^{\mathbf{Q}}(\mathbf{X}) =&\widetilde{\rho }_{B}^{ \mathbf{Q}}(\mathbf{X})=\widehat{\rho }_{B}^{\mathbf{Q}}(\mathbf{X}). \end{aligned}$$

(4.9)

Proof

Clearly, $+\infty >\pi _{A}^{\mathbf{Q}}(\mathbf{X})\geq \pi _{A}^{ \mathbf{Q,=}}(\mathbf{X})$. By way of contradiction, suppose that $\pi _{A}^{\mathbf{Q}}(\mathbf{X})>\pi _{A}^{\mathbf{Q,=}}(\mathbf{X})$ and take $\varepsilon >0$ such that $\pi _{A}^{\mathbf{Q}}( \mathbf{X})-\varepsilon >\pi _{A}^{\mathbf{Q,=}}(\mathbf{X})$. By the definition of $\pi _{A}^{\mathbf{Q}}(\mathbf{X})$, there exists $\mathbf{Y}\in M^{{\Phi } }$ satisfying ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]<A$ as well as $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]>{\pi }_A^{\mathbf{Q}}(\mathbf{X})-\epsilon$. Take $\widetilde{Y}^{n}=Y^{n}+\delta$, $\delta \in {\mathbb{R}}_{+}$, such that ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[{\tilde{Y}}^n]=A$. Then

$$\begin{array}{rl}{\pi }_A^{\mathbf{Q},=}(\mathbf{X})& \ge \mathbb{E}[\sum _{n=1}^N{u}_n(X^n+{\tilde{Y}}^n)]\ge \mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\\ & >{\pi }_A^{\mathbf{Q}}(\mathbf{X})-\epsilon >{\pi }_A^{\mathbf{Q},=}(\mathbf{X}),\end{array}$$

which is a contradiction. Hence (4.7) holds true. Note that

$$M^{\mathrm{\Phi }}=\{\mathbf{Y}=\mathbf{a}+\mathbf{Z}:\mathbf{a}\in {\mathbb{R}}^N\text{ and }\mathbf{Z}\in M^{\mathrm{\Phi }}\text{ such that }{\mathbb{E}}_{Q^n}[Z^n]=0\text{ for each }n\}.$$

Indeed, take $\mathbf{Y} \in M^{{\Phi } }$ and let $a^n:={\mathbb{E}}_{Q^n}[Y^n]\in \mathbb{R}$ and $Z^{n}:=Y^{n}-a^{n} \in M^{\phi _{n}}$. Then

$$\begin{array}{rl}{\pi }_A^{\mathbf{Q}}(\mathbf{X})& =sup\left\{\mathbb{E}\right[\sum _{n=1}^N{u}_n(X^n+Y^n)]:\mathbf{Y}\in M^{\mathrm{\Phi }},\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]=A\}\\ & =\underset{{\sum }_{n=1}^N{a}^n=A,Z^n\in M^{{\varphi }_n},{\mathbb{E}}_{Q^n}[Z^n]=0\mathrm{\forall }n}{sup}\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+a^n+Z^n)]\\ & =\underset{{\sum }_{n=1}^N{a}^n=A}{sup}\sum _{n=1}^N\underset{Y^n\in M^{{\varphi }_n},{\mathbb{E}}_{Q^n}[Y^n]=a^n}{sup}\mathbb{E}[u_n(X^n+Y^n)]\\ & =\underset{{\sum }_{n=1}^N{a}^n=A}{sup}\sum _{n=1}^N{U}_n(a^n),\end{array}$$

(4.10)

which shows the first equality in (4.8). Then $\pi _{A}^{ \mathbf{Q}}(\mathbf{X})=\widetilde{\pi }_{A}^{\mathbf{Q}}(\mathbf{X})= \widehat{\pi }_{A}^{\mathbf{Q}}(\mathbf{X})$ are consequences of (4.4) and the decompositions analogous to the one just obtained for $\pi _{A}^{\mathbf{Q}}(\mathbf{X})$ in (4.10). If $A:=\rho _{B}^{\mathbf{Q}}(\mathbf{X})>-\infty$, then $B=\pi _{A}^{ \mathbf{Q}}(\mathbf{X})$ by Proposition 4.2 (a). Hence $B=\pi _{A}^{\mathbf{Q}}(\mathbf{X})=\widetilde{\pi }_{A}^{\mathbf{Q}}( \mathbf{X})=\widehat{\pi }_{A}^{\mathbf{Q}}(\mathbf{X})$, and from Proposition 4.2 (b), we obtain $A:=\widetilde{\rho }_{B} ^{\mathbf{Q}}(\mathbf{X})=\widehat{\rho }_{B}^{\mathbf{Q}}(\mathbf{X})$, hence (4.9). □

Proposition 4.6

Let$A:=\rho _{B}^{\mathbf{Q}}(\mathbf{X})$and$\pi _{A}^{\mathbf{Q}}( \mathbf{X})\!<\!+\infty$. There exists a solution$a_{\ast }\in {\mathbb{R}}^N$to problem (4.8), namely

$${\pi }_A^{\mathbf{Q}}(\mathbf{X})=\underset{a\in {\mathbb{R}}^N\mathit{\text{with }}{\sum }_{n=1}^N{a}^n=A}{sup}\sum _{n=1}^N{U}_n(a^n)=\sum _{n=1}^N{U}_n(a_{\ast }^n)\mathit{\text{and}}\sum _{n=1}^N{a}_{\ast }^n=A.$$

(4.11)

Proof

Fix $\delta >0$ and let ${\mathbf{a}}_m={(a_m^1,\dots ,a_m^N)}_{m\in \mathbb{N}}$ be an approximating sequence for the supremum in (4.11). Then $\sum _{n=1}^{N}U_{n}(a_{m}^{n})\geq \pi _{A}^{ \mathbf{Q}}(\mathbf{X})-\delta =: C$ and $\sum _{n=1}^{N}a_{m}^{n}=A$ for large enough $m$. Then (4.11) is a consequence of the continuity of $U_{n}$ and of Lemma 4.7 below, which guarantees that $\mathbf{a}_{m}$ belongs to a compact set in ${\mathbb{R}}^N$. □

Lemma 4.7

Set$K:=\{\mathbf{a}\in {\mathbb{R}}^N:{\sum }_{n=1}^N{a}^n\le A,{\sum }_{n=1}^N{U}_n(a^n)\ge B\}$for arbitrary constants$A$, $B\in \mathbb{R}$. Then$K$is a bounded closed set in${\mathbb{R}}^N$.

Proof

See Appendix A.4. □

We now turn to the uniqueness of the solution to problem (3.2). The proof is in Appendix A.4 and uses the same arguments as in the proof of Proposition 2.4.

Lemma 4.8

The penalty function can be written as

$$\begin{array}{rcl}{\alpha }_B(\mathbf{Q})& =& sup\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-Z^n]:\mathbf{Z}\in M^{\mathrm{\Phi }},\sum _{n=1}^N\mathbb{E}[u_n(Z^n)]=B\}\\ & =& sup\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-Z^n]:\mathbf{Z}\in L^1(\mathbb{P},\mathbf{Q}),\mathbb{E}[\sum _{n=1}^N{u}_n(Z^n)]\ge B\},\end{array}$$

(4.12)

and there exists at most one $\mathbf{Z}\in L^1(\mathbb{P},\mathbf{Q})$ satisfying

$${\alpha }_B(\mathbf{Q})=\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-Z^n]\mathit{\text{and}}\sum _{n=1}^N\mathbb{E}[u_n(Z^n)]\ge B.$$

(4.13)

Remark 4.9

From (4.9) and (3.5), we have

$${\hat{\rho }}_B^{\mathbf{Q}}(\mathbf{X})={\tilde{\rho }}_B^{\mathbf{Q}}(\mathbf{X})={\rho }_B^{\mathbf{Q}}(\mathbf{X})=-\sum _{n=1}^N{\mathbb{E}}_{Q^n}[X^n]-{\alpha }_B(\mathbf{Q}).$$

Hence with a proof similar to the one of Lemma 4.8, we may replace the inequality with an equality sign in the budget constraint in the definition of $\rho _{B}^{\mathbf{Q}}(\mathbf{X})$, $\widetilde{\rho }_{B}^{\mathbf{Q}}(\mathbf{X})$ and $\widehat{\rho } _{B}^{\mathbf{Q}}(\mathbf{X})$, and show the uniqueness of the optimiser $\mathbf{Y}$ in $\rho _{B}^{\mathbf{Q}}(\mathbf{X})$, $\widetilde{\rho }_{B}^{\mathbf{Q}}(\mathbf{X})$ and $\widehat{\rho } _{B}^{\mathbf{Q}}(\mathbf{X})$.

4.3 On the solution of $\widehat{\rho }^{ \mathbf{Q}}$ and comparison of solutions

Theorem 4.10

Suppose$\alpha _{B}(\mathbf{Q})<+\infty$. Consider the random vector$\widehat{\mathbf{Y}}_{\mathbf{Q}}$given by

$${\hat{Y}}_{\mathbf{Q}}^n:=-X^n-v_n^{\prime }\left({\lambda }^{\ast }\frac{d{Q}^n}{d\mathbb{P}}\right),$$

where${\lambda }^{\ast }$is the unique solution to (3.9). Then$\widehat{{Y}}_{\mathbf{Q}}^{n}\in L^{1}(Q ^{n})$, $u_n(X^n+{\hat{Y}}_{\mathbf{Q}}^n)\in L^1(\mathbb{P})$, $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+{\hat{Y}}_{\mathbf{Q}}^n)]=B$and

$$\begin{array}{rl}{\rho }_B^{\mathbf{Q}}(\mathbf{X})& =inf\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]:\mathbf{Y}\in M^{\mathrm{\Phi }},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}\\ & =\sum _{n=1}^N{\mathbb{E}}_{Q^n}[{\hat{Y}}_{\mathbf{Q}}^n]\end{array}$$

(4.14)

$$\begin{array}{rl}& =min\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]:\mathbf{Y}\in L^1(\mathbf{Q}),\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}\\ & ={\hat{\rho }}_B^{\mathbf{Q}}(\mathbf{X}),\end{array}$$

(4.15)

so that$\widehat{\mathbf{Y}}_{\mathbf{Q}}$is the solution for$\widehat{\rho }_{B}^{\mathbf{Q}}(\mathbf{X})$.

Proof

Note that $\rho _{B}^{\mathbf{Q}}(\mathbf{X})>-\infty$ as $\alpha _{B}( \mathbf{Q})<+\infty$. The integrability conditions hold thanks to the results stated in Appendix A.3. From (3.5) and the expression (3.8) for the penalty, we compute

$$\begin{array}{rcl}{\rho }_B^{\mathbf{Q}}(\mathbf{X})& =& -\sum _{n=1}^N{\mathbb{E}}_{Q^n}[X^n]-{\alpha }_B(\mathbf{Q})\\ & =& \sum _{n=1}^N{\mathbb{E}}_{Q^n}[-X^n-v_n^{\prime }\left({\lambda }^{\ast }\frac{d{Q}^n}{d\mathbb{P}}\right)]=\sum _{n=1}^N{\mathbb{E}}_{Q^n}[{\hat{Y}}_{\mathbf{Q}}^n].\end{array}$$

We show that $\widehat{{Y}}_{\mathbf{Q}}^{n}$ satisfies the budget constraint

$$\begin{array}{rcl}\sum _{n=1}^N\mathbb{E}[u_n(X^n+{\hat{Y}}_{\mathbf{Q}}^n)]& =& \sum _{n=1}^N\mathbb{E}\left[u_n\right(-v_n^{\prime }\left({\lambda }^{\ast }\frac{d{Q}^n}{d\mathbb{P}}\right)\left)\right]\\ & =& \sum _{n=1}^N\mathbb{E}\left[v_n\right({\lambda }^{\ast }\frac{d{Q}^n}{d\mathbb{P}}\left)\right]-{\lambda }^{\ast }\sum _{n=1}^N{\mathbb{E}}_{Q^n}\left[v_n^{\prime }\right({\lambda }^{\ast }\frac{d{Q}^n}{d\mathbb{P}}\left)\right]\\ & =& B\end{array}$$

due to $u(-v^{\prime }(y))=v(y)-yv^{\prime }(y)$ by Lemma A.5 and (3.9). Finally, from (4.9), it follows that $\rho _{B}^{\mathbf{Q}}(\mathbf{X})=\widehat{ \rho }_{B}^{\mathbf{Q}}(\mathbf{X})$, and Remark 4.9 implies uniqueness. □

When solutions to both problems $\rho _{B}(\mathbf{X})$ and $\rho _{B} ^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$ exist, they coincide.

Proposition 4.11

Let$\mathbf{Y}_{\mathbf{X}}\in \mathcal{C}_{0}\cap M^{{\Phi } }$be the optimal allocation for$\rho _{B}(\mathbf{X})$and$\mathbf{Q}_{\mathbf{X}}$a solution to the dual problem (3.1). Then$\mathbf{Y}_{\mathbf{X}}= \widehat{{\mathbf{Y}}}_{\mathbf{Q}_{\mathbf{X}}}$, i.e.,

$$Y_{\mathbf{X}}^n={\hat{Y}}_{{\mathbf{Q}}_{\mathbf{X}}}^n:=-X^n-v_n^{\prime }\left({\lambda }^{\ast }\frac{d{Q}_{\mathbf{X}}^n}{d\mathbb{P}}\right).$$

Proof

Note that $\mathbf{Y}_{\mathbf{X}}$ satisfies

$$\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y_{\mathbf{X}}^n)]\ge B,$$

(4.16)

$$\begin{aligned} \sum _{n=1}^{N}Y_{\mathbf{X}}^{n} =& \rho _{B}(\mathbf{X}), \end{aligned}$$

(4.17)

$$\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]\le \sum _{n=1}^N{Y}_{\mathbf{X}}^n,$$

(4.18)

as $\mathbf{Y}_{\mathbf{X}}\in \mathcal{C}$ and $\mathbf{Q}_{ \mathbf{X}}\in \mathcal{D}$. From (4.14), (3.5), (3.4) and (4.17), we deduce that

$$\begin{array}{rl}\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[{\hat{Y}}_{{\mathbf{Q}}_{\mathbf{X}}}^n]={\rho }_B^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})& =-\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[X^n]-{\alpha }_B({\mathbf{Q}}_{\mathbf{X}})\\ & ={\rho }_B(\mathbf{X})=\sum _{n=1}^N{Y}_{\mathbf{X}}^n.\end{array}$$

(4.19)

As $\mathbf{Y}_{\mathbf{X}}$ satisfies (4.16), the definition of $\rho _{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$ gives

$$\sum _{n=1}^N{Y}_{\mathbf{X}}^n={\rho }_B(\mathbf{X})={\rho }_B^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})\le \sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n],$$

which shows together with (4.18) that

$$\sum _{n=1}^N{Y}_{\mathbf{X}}^n=\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n].$$

(4.20)

From (4.19) and (4.20), we then deduce that

$$\begin{array}{rcl}{\alpha }_B({\mathbf{Q}}_{\mathbf{X}})& =& -\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[X^n+{\hat{Y}}_{{\mathbf{Q}}_{\mathbf{X}}}^n],\\ {\alpha }_B({\mathbf{Q}}_{\mathbf{X}})& =& -\sum _{n=1}^N({\mathbb{E}}_{Q_{\mathbf{X}}^n}[X^n]+Y_{\mathbf{X}}^n)=-\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[X^n+Y_{\mathbf{X}}^n].\end{array}$$

As both $\mathbf{X}+\mathbf{Y}_{\mathbf{X}}$ and $\mathbf{X}+ \widehat{\mathbf{Y}}_{\mathbf{Q}_{\mathbf{X}}}$ satisfy the budget constraints associated to $\alpha _{B}(\mathbf{Q}_{\mathbf{X}})$ in (4.13), this implies that $\alpha _{B}(\mathbf{Q}_{\mathbf{X}})$ is attained by both $\mathbf{X}+\mathbf{Y}_{\mathbf{X}}$ and $\mathbf{X}+\widehat{\mathbf{Y}}_{\mathbf{Q}_{\mathbf{X}}}$. The uniqueness shown in Lemma 4.8 allows us to conclude that $\mathbf{Y}_{\mathbf{X}}=\widehat{\mathbf{Y}}_{\mathbf{Q}_{\mathbf{X}}}$. □

Remark 4.12

Theorem 4.19 below proves the existence of ${\tilde{\mathbf{Y}}}_{\mathbf{X}}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$ satisfying (4.16)–(4.18) with $\tilde{\mathbf{Y}}_{\mathbf{X}}$ instead of $\mathbf{Y}_{\mathbf{X}}$. Then the above proof shows that $\tilde{\mathbf{Y}}_{\mathbf{X}}=\widehat{\mathbf{Y}}_{ \mathbf{Q}_{\mathbf{X}}}$. Similarly, Corollary 4.13 below holds for such ${\tilde{\mathbf{Y}}}_{\mathbf{X}}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$.

We now show that the maximiser of the dual representation is unique.

Corollary 4.13

Suppose there exists an optimal allocation$\mathbf{Y}_{\mathbf{X}}$to$\rho _{B}(\mathbf{X})$. Then the solution$\mathbf{Q}_{\mathbf{X}}=(Q _{\mathbf{X}}^{1},\dots ,Q_{\mathbf{X}}^{N})$of the dual problem (3.1) is unique.

Proof

Suppose $\mathbf{Q}_{1}$, $\mathbf{Q}_{2}$ are two optimisers of the dual problem (3.1). Then we have $\alpha _{B}( \mathbf{Q}_{1})<+\infty$, $\alpha _{B}(\mathbf{Q}_{2})<+\infty$ and by Proposition 4.11 and Remark 4.12, for each $n$,

$$-X^n-v_n^{\prime }\left({\lambda }_1^{\ast }\frac{d{Q}_1^n}{d\mathbb{P}}\right)={\hat{Y}}_{{\mathbf{Q}}_1}^n=Y_{\mathbf{X}}^n={\hat{Y}}_{{\mathbf{Q}}_2}^n=-X^n-v_n^{\prime }\left({\lambda }_2^{\ast }\frac{d{Q}_2^n}{d\mathbb{P}}\right)\mathbb{P}\text{-a.s.}$$

As $v_{n}^{\prime }$ is invertible, we conclude that ${\lambda }_1^{\ast }\frac{d{Q}_1^n}{d\mathbb{P}}={\lambda }_2^{\ast }\frac{d{Q}_2^n}{d\mathbb{P}}$ ℙ-a.s., which then implies $Q_{1}^{n}=Q_{2}^{n}$ as $\mathbb{E}[\frac{d{Q}_1^n}{d\mathbb{P}}]=\mathbb{E}[\frac{d{Q}_2^n}{d\mathbb{P}}]=1$. □

4.4 On the existence of the optimal allocation for ${\widetilde{\rho }_{B}}$

4.4.1 A first step

We first show that $\rho _{B}$ reaches its infimum at some $\mathbf{Y}\in L^1(\mathbb{P};{\mathbb{R}}^N)$.

Theorem 4.14

For$\mathcal{C}\subseteq {\mathcal{C}}_{\mathbb{R}}\cap M^{\mathrm{\Phi }}$and for any$\mathbf{X}\in M^{{\Phi } }$, there exist$\mathbf{Y}$in$L^1(\mathbb{P};{\mathbb{R}}^N)$such that

$$\begin{array}{rl}& \sum _{n=1}^N{Y}^n\in \mathbb{R},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B,\\ & {\rho }_B(\mathbf{X}):=inf\{\sum _{n=1}^N{Z}^n:\mathbf{Z}\in \mathcal{C},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Z^n)]\ge B\}=\sum _{n=1}^N{Y}^n\end{array}$$

and a sequence${({\mathbf{Y}}_k)}_{k\in \mathbb{N}}\subseteq \mathcal{C}$with$\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y_k^n)]\ge B$and$\mathbf{Y}_{k}\rightarrow \mathbf{Y}$ ℙ-a.s.

Remark 4.15

We note that the random vector $\mathbf{Y}$ in Theorem 4.14 satisfies all the conditions for being the optimal allocation for $\rho _{B}(\mathbf{X})$, except for the integrability condition $\mathbf{Y}\in M^{{\Phi } }$, which is replaced by $\mathbf{Y}\in L^1(\mathbb{P};{\mathbb{R}}^N)$. Furthermore, $\mathbf{Y}=\lim _{k\to \infty }\mathbf{Y}_{k}$$\mathbb{P}\text{-a.s.}$ for $\mathbf{Y}_{k} \in \mathcal{C}_{0}\cap M^{{ \Phi } }$. If we assume that $\mathcal{C}_{0}$ is closed in $L^0(\mathbb{P})$, which is a reasonable assumption and holds true if $\mathcal{C}=\mathcal{C}^{(\mathbf{n})}$, in which case $\mathcal{C} _{0}^{(\mathbf{n})}$ is defined in (2.4), then $\mathbf{Y}$ also belongs to $\mathcal{C}_{0}$, but in general not to $\mathcal{C}$ (as $M^{{\Phi } }$ is in general not closed for ℙ-a.s. convergence). A special case is when the cardinality of $\Omega$ is finite and the set $\mathcal{C}$ is closed for ℙ-a.s. convergence; under these assumptions, $\mathbf{Y}$ belongs to $\mathcal{C}$ and $\mathbf{Y=Y}_{\mathbf{X}}= \mathbf{\widehat{Y}}_{\mathbf{Q}_{\mathbf{X}}}$. In Sect. 4.4.2, we show when $\mathbf{Y}$ also belongs to ${\mathcal{C}}_0\cap L^1({\mathbf{Q}}_{\mathbf{X}};{\mathbb{R}}^N)$.

Proof of Theorem 4.14

Take a sequence ${({\mathbf{V}}_k)}_{k\in \mathbb{N}}\in {\mathcal{C}\subseteq \mathcal{C}}_{\mathbb{R}}\cap M^{\mathrm{\Phi }}\subseteq L^1(\mathbb{P};{\mathbb{R}}^N)$ such that $\mathbb{R}\ni c_k:={\sum }_{n=1}^N{V}_k^n\downarrow {\rho }_B(\mathbf{X})$ as $k\rightarrow \infty$ and $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+V_k^n)]\ge B$. The sequence ${({\mathbf{V}}_k)}_{k\in \mathbb{N}}$ is bounded for the $L^1(\mathbb{P};{\mathbb{R}}^N)$-norm if and only if so is the sequence ${({\mathbf{X}+\mathbf{V}}_k)}_{k\in \mathbb{N}}$. Given the decomposition into positive and negative parts

$$\sum _{n=1}^N\mathbb{E}[|X^n+V_k^n|]=\sum _{n=1}^N\mathbb{E}[{(X^n+V_k^n)}^{+}]+\sum _{n=1}^N\mathbb{E}[{(X^n+V_k^n)}^{-}],$$

(4.21)

we define the index sets

$$\begin{array}{rcl}{N}_{\mathrm{\infty }}^{+}& =& \{n\in \{1,\dots ,N\}:\underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\mathbb{E}[{(X^n+V_k^n)}^{+}]=+\mathrm{\infty }\},\\ N_b^{+}& =& \{n\in \{1,\dots ,N\}:\underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}sup}\mathbb{E}[{(X^n+V_k^n)}^{+}]<+\mathrm{\infty }\}\end{array}$$

and similarly $N_{\infty }^{-}$ and $N_{b}^{-}$ for the negative parts. We can split (4.21) as

$$\begin{array}{rl}& \sum _{n\in N_{\mathrm{\infty }}^{+}}{E}_{\mathbb{P}}[{(X^n+V_k^n)}^{+}]+\sum _{n\in N_b^{+}}{E}_{\mathbb{P}}[{(X^n+V_k^n)}^{+}]\\ & +\sum _{n\in N_{\mathrm{\infty }}^{-}}{E}_{\mathbb{P}}[{(X^n+V_k^n)}^{-}]+\sum _{n\in N_b^{-}}{E}_{\mathbb{P}}[{(X^n+V_k^n)}^{-}].\end{array}$$

If the sequence ${({\mathbf{X}+\mathbf{V}}_k)}_{k\in \mathbb{N}}$ is not $L^1(\mathbb{P};{\mathbb{R}}^N)$-bounded, then one of the sets $N_{\infty }^{+}$ or $N_{\infty }^{-}$ must be nonempty and then, because of the constraint $\sum _{n=1}^{N}V_{k}^{n}=c_{k}$, both $N_{\infty }^{+}$ and $N_{\infty }^{-}$ must be nonempty. From Lemma A.1 (a), Jensen’s inequality and (4.2) give

$$\begin{array}{rcl}B& \le & \sum _{n=1}^N\mathbb{E}[u_n(X^n+V_k^n)]\le \sum _{n=1}^N{u}_n(\mathbb{E}[X^n+V_k^n])\\ & =& \sum _{n=1}^N{u}_n(\mathbb{E}[(X^n+V_k^n{)}^{+}])+\sum _{n=1}^N{u}_n(-\mathbb{E}[(X^n+V_k^n{)}^{-}])\\ & \le & b(\sum _{n\in N_{\mathrm{\infty }}^{+}}\mathbb{E}[{(X^n+V_k^n)}^{+}]+\sum _{n\in N_b^{+}}\mathbb{E}[{(X^n+V_k^n)}^{+}])\\ & & -2b(\sum _{n\in N_{\mathrm{\infty }}^{-}}\mathbb{E}[{(X^n+V_k^n)}^{-}]+\sum _{n\in N_b^{-}}\mathbb{E}[{(X^n+V_k^n)}^{-}])+\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\\ & =& b(c_k+\sum _{n=1}^N\mathbb{E}[X^n])+\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\\ & & -b(\sum _{n\in N_{\mathrm{\infty }}^{-}}\mathbb{E}[{(X^n+V_k^n)}^{-}]+\sum _{n\in N_b^{-}}\mathbb{E}[{(X^n+V_k^n)}^{-}]),\end{array}$$

which is a contradiction as the second sum in the last term is not bounded from above. Hence our minimising sequence ${({\mathbf{V}}_k)}_{k\in \mathbb{N}}$ has bounded $L^1(\mathbb{P};{\mathbb{R}}^N)$-norm and we may apply a Komlós compactness argument as in [22, Theorem 1.4]. Applying this to the sequence ${({\mathbf{V}}_k)}_{k\in \mathbb{N}}\subseteq \mathcal{C}$, we can find for all $k$ some $\mathbf{Y}_{k}\in {\mathrm{conv}}(\mathbf{V} _{i},i\geq k)\subseteq \mathcal{C}$, as $\mathcal{C}$ is convex, such that $(\mathbf{Y}_{k})$ converges ℙ-a.s. to some $\mathbf{Y}\in L^1(\mathbb{P};{\mathbb{R}}^N)$. Observe that by construction, $\sum _{n=1}^{N}Y_{k}^{n}$ is ℙ-a.s. a real number, and as a consequence, so is $\sum _{n=1}^{N}Y^{n}$. As $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+V_k^n)]\ge B$, also the $\mathbf{Y}_{k}$ satisfy this constraint and therefore $\rho _{B}(\mathbf{X})\leq \sum _{n=1}^{N}Y_{k}^{n}$.

Recall that $\mathbf{Y}_{k}=\sum _{i\in J_{k}}\lambda _{i}^{k} \mathbf{V}_{i}\in {\mathrm{conv}}(\mathbf{V}_{i},i\geq k)$; so there are convex weights $(\lambda _{i}^{k})_{i\in J_{k}}$ with $\lambda _{i}^{k}>0$ and $\sum _{i\in J_{k}}\lambda _{i}^{k}=1$, where $J_{k}$ is a finite subset of $\{k,k+1,\dots \}$. For any fixed $k$, we compute

$$\begin{aligned} \sum _{n=1}^{N}Y_{k}^{n} &=\sum _{n=1}^{N}\bigg( \sum _{i\in J_{k}}\lambda _{i} ^{k}V_{i}^{n}\bigg) _{j}=\sum _{i\in J_{k}}\lambda _{i}^{k}\bigg( \sum _{n=1}^{N}V_{i}^{n}\bigg) \\ &=\sum _{i\in J_{k}}\lambda _{i}^{k}c_{i}\leq c_{k}\bigg( \sum _{i \in J_{k}}\lambda _{i}^{k}\bigg) =c_{k}, \end{aligned}$$

(4.22)

and from $\rho _{B}(\mathbf{X})\leq \sum _{n=1}^{N}Y_{k}^{n}\leq c_{k}$, we then deduce that $\sum _{n=1}^{N}Y^{n}=\rho _{B}(\mathbf{X})$.

We now show that $\mathbf{Y}$ also satisfies the budget constraint. If all utility functions are bounded from above, this is an immediate consequence of Fatou’s lemma since

$$\begin{array}{rl}\sum _{n=1}^N\mathbb{E}[-u_n(X^n+Y^n)]& =\sum _{n=1}^N\mathbb{E}\left[\underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\right(-u_n(X^n+Y_k^n)\left)\right]\\ & \le \underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\sum _{n=1}^N\mathbb{E}[-u_n(X^n+Y_k^n)]\le -B.\end{array}$$

In the general case, recall first that the sequence $(\mathbf{V}_{k})$ is bounded in $L^1(\mathbb{P};{\mathbb{R}}^N)$, and the argument used in (4.22) shows that

$${\parallel \mathbf{X}+{\mathbf{Y}}_k\parallel }_1\le {\parallel {\mathbf{X}\parallel }_1+\underset{k\in \mathbb{N}}{sup}{\parallel \mathbf{V}}_k\parallel }_1,$$

hence ${sup}_{k\in \mathbb{N}}{\parallel \mathbf{X}+{\mathbf{Y}}_k\parallel }_1<\mathrm{\infty }$. We now need to exploit the Inada condition at $+\infty$. Applying Lemma A.1 (b) to the utility functions $u_{n}$, assumed null in 0, we get

$$-u_n(x)+\epsilon x^{+}+b(\epsilon )\ge 0,\mathrm{\forall }x\in \mathbb{R}.$$

Plugging $\mathbf{X}+\mathbf{Y}$ into the expression above and applying Fatou’s lemma, we have

$$\begin{array}{rl}& \mathbb{E}[\sum _{n=1}^N-u_n(X^n+Y^n)+\epsilon {(X^n+Y^n)}^{+}+b(\epsilon )]\\ & =\mathbb{E}\left[\underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\right(\sum _{n=1}^N-u_n(X^n+Y_k^n)+\epsilon {(X^n+Y_k^n)}^{+}+b(\epsilon )\left)\right]\\ & \le \underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\sum _{n=1}^N\mathbb{E}[-u_n(X^n+Y_k^n)+\epsilon {(X^n+Y_k^n)}^{+}+b(\epsilon )]\\ & \le -B+\epsilon \left(\underset{k\in \mathbb{N}}{sup}{\parallel \mathbf{X}+{\mathbf{Y}}_k\parallel }_1\right)+b(\epsilon ).\end{array}$$

As the term $b(\varepsilon )$ cancels in the above inequality, we conclude that for all $\varepsilon >0$,

$$\mathbb{E}[\sum _{n=1}^N-u_n(X^n+Y^n)]\le -B+\epsilon (\underset{k\in \mathbb{N}}{sup}{\parallel \mathbf{X}+{\mathbf{Y}}_k\parallel }_1-\sum _{n=1}^N\mathbb{E}[{(X^n+Y^n)}^{+}]),$$

and since ${sup}_{k\in \mathbb{N}}{\parallel \mathbf{X}+{\mathbf{Y}}_k\parallel }_1<\mathrm{\infty }$, we obtain $\mathbb{E}[{\sum }_{n=1}^N-u_n(X^n+Y^n)]\le -B$ so that $\mathbf{Y}$ satisfies the constraint. □

4.4.2 Second step: the optimal allocation is in $L^{1}(\mathbf{Q}_{\mathbf{X}})$

We now prove further integrability properties of the random vector $\mathbf{Y}$ in Theorem 4.14.

Lemma 4.16

The random vector$\mathbf{Y}$in Theorem 4.14satisfies$\mathbf{Y}^{-} \in L^{1}(\mathbf{Q}_{\mathbf{X}})$.

Proof

Using (4.2) and $\phi _{j}(x):=-u_{j}(-|x|)$ for fixed $1\leq j \leq N$ gives

$$\begin{array}{rcl}0& \le & \mathbb{E}\left[{\varphi }_j\right({(X^j+Y^j)}^{-}\left)\right]\le \sum _{n=1}^N\mathbb{E}\left[{\varphi }_n\right({(X^n+Y^n)}^{-}\left)\right]\\ & =& \sum _{n=1}^N\mathbb{E}[-u_n(-{(X^n+Y^n)}^{-}\left)\right]\\ & =& \sum _{n=1}^N\mathbb{E}[u_n{(X^n+Y^n)}^{+}]-\sum _{n=1}^N\mathbb{E}[u_n(X^n+Y^n)]\\ & \le & \sum _{n=1}^N{u}_n(\mathbb{E}[{(X^n+Y^n)}^{+}])-B<\mathrm{\infty },\end{array}$$

(4.23)

where we used Jensen’s inequality and $\mathbf{X}+\mathbf{Y}\in L^1(\mathbb{P};{\mathbb{R}}^N)$. This yields

$$ (X^{j}+Y^{j})^{-}\in L^{\phi _{j}}\subseteq L^{1}(Q_{\mathbf{X}}^{j}). $$

From $Y^{j}=(X^{j}+Y^{j})^{+}-(X^{j}+Y^{j})^{-}-X^{j}\geq -(X^{j}+Y ^{j})^{-}-X^{j}$, we get $0\leq (Y^{j})^{-}\leq (-(X^{j}+Y^{j})^{-}-X ^{j})^{-}=((X^{j}+Y^{j})^{-}+X^{j})^{+}$. Since by assumption, $X^{j}\in M^{\phi _{j}}\subseteq L^{1}(Q_{\mathbf{X}}^{j})$, then also $((X^{j}+Y^{j})^{-}+X^{j})^{+}\in L^{1}(Q_{\mathbf{X}}^{j})$ and so $(Y^{j})^{-}\in L^{1}(Q_{\mathbf{X}}^{j}), 1\leq j\leq N$. □

Lemma 4.17

The random vector$\mathbf{Y}$in Theorem 4.14satisfies$\mathbf{Y}^{+}\in L^{1}(\mathbf{Q}_{\mathbf{X}})$.

Proof

In Theorem 4.14, we have proved the existence of $\mathbf{Y}\in L^1(\mathbb{P};{\mathbb{R}}^N)$ satisfying ${\rho }_B(\mathbf{X})={\sum }_{n=1}^N{Y}^n\in \mathbb{R}$ with $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]\ge B$ and $\mathbf{Y}$ is the ℙ-a.s. limit of a sequence $( \mathbf{Y}_{k})$ in $\mathcal{C}\subseteq {\mathcal{C}}_{\mathbb{R}}\cap M^{\mathrm{\Phi }}$ such that $\sum _{n=1}^{N}Y_{k}^{n}\rightarrow \rho _{B}(\mathbf{X})$ as $k \to \infty$, ${\sum }_{n=1}^N\mathbb{E}[u_n(X^n+Y_k^n)]\ge B$ and ${\sum }_{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_k^n]\le {\sum }_{n=1}^N{Y}_k^n$. By passing to a subsequence, we may assume that $\sum _{n=1}^{N}Y_{k}^{n}\downarrow {\rho _{B}}(\mathbf{X})$. Let $j\in \{1,\dots ,N\}$. Fatou’s lemma gives

$${\mathbb{E}}_{Q_{\mathbf{X}}^j}[{(Y^j)}^{+}]\le \underset{k\to \mathrm{\infty }}{lim\hspace{0.17em}inf}{\mathbb{E}}_{Q_{\mathbf{X}}^j}[{(Y_k^j)}^{+}]\le \underset{k\in \mathbb{N}}{sup}{\mathbb{E}}_{Q_{\mathbf{X}}^j}[Y_k^j]+\underset{k\in \mathbb{N}}{sup}{\mathbb{E}}_{Q_{\mathbf{X}}^j}[{(Y_k^j)}^{-}].$$

(4.24)

First we show that ${sup}_{k\in \mathbb{N}}{\mathbb{E}}_{Q_{\mathbf{X}}^j}[Y_k^j]<\mathrm{\infty }$. Put $a_k^n={\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_k^n]$. Then we obtain that $\sum _{n=1}^{N}a _{k}^{n}\leq \widetilde{A}:=\sum _{n=1}^{N}Y_{k}^{n}\leq \sum _{n=1} ^{N}Y_{1}^{n}$ and

$$\sum _{n=1}^N{U}_n^{Q_{\mathbf{X}}^n}(a_k^n)\ge \sum _{n=1}^N\mathbb{E}[u_n(X^n+Y_k^n)]\ge B$$

for all $k\in \mathbb{N}$. Thus by Lemma 4.7, ${({\mathbf{a}}_k)}_{k\in \mathbb{N}}$ lies in a bounded set in ${\mathbb{R}}^N$ and thus

$$\underset{k\in \mathbb{N}}{sup}{\mathbb{E}}_{Q_{\mathbf{X}}^j}[Y_k^j]<\mathrm{\infty }.$$

(4.25)

Next we show ${sup}_{k\in \mathbb{N}}{\mathbb{E}}_{Q_{\mathbf{X}}^j}[{(Y_k^j)}^{-}]<\mathrm{\infty }$. As in (4.23), we obtain that for all $k\in \mathbb{N}$

$$0\le \mathbb{E}\left[{\varphi }_j\right({(X^j+Y_k^j)}^{-}\left)\right]\le \sum _{n=1}^N{u}_n(\mathbb{E}[{(X^n+Y_k^n)}^{+}])-B.$$

From the proof of Theorem 4.14, we know that ${(X^n+Y_k^n)}_{k\in \mathbb{N}}$ is $L^1(\mathbb{P})$-bounded for all $n=1,\dots ,N$, and thus

$$0\le \underset{k\in \mathbb{N}}{sup}\mathbb{E}\left[{\varphi }_j\right({(X^j+Y_k^j)}^{-}\left)\right]\le \sum _{n=1}^N{u}_n(\underset{k\in \mathbb{N}}{sup}\mathbb{E}[{(X^n+Y_k^n)}^{+}])-B<\mathrm{\infty }.$$

By Remark 2.1, it then follows that ${(X^j+Y_k^j)}_{k\in \mathbb{N}}^{-}$ is $L^{1}(Q_{\mathbf{X}}^{j})$-bounded. Moreover, $Y_{k}^{j}=(X^{j}+Y_{k}^{j})^{+}-(X^{j}+Y_{k}^{j})^{-}-X^{j}\geq -(X ^{j}+Y_{k}^{j})^{-}-X^{j}$ gives

$$ 0\leq (Y_{k}^{j})^{-}\leq \big(-(X^{j}+Y_{k}^{j})^{-}-X^{j}\big)^{-}= \big((X^{j}+Y_{k}^{j})^{-}+X^{j}\big)^{+}, $$

and thus

$$\underset{k\in \mathbb{N}}{sup}{\mathbb{E}}_{Q_{\mathbf{X}}^j}[{(Y_k^j)}^{-}]\le \underset{k\in \mathbb{N}}{sup}{\mathbb{E}}_{Q_{\mathbf{X}}^j}[{(X^j+Y_k^j)}^{-}]+{\mathbb{E}}_{Q_{\mathbf{X}}^j}[|X^j|]<\mathrm{\infty },$$

(4.26)

where we recall that by assumption, $X^{j}\in M^{\phi _{j}}\subseteq L ^{1}(Q_{\mathbf{X}}^{j})$. From (4.25) and (4.26) together with (4.24), the claim follows. □

4.4.3 The final step

For our final result on existence, we need one more assumption.

Definition 4.18

We say that $\mathcal{C}_{0}$ is closed under truncation if for each $\mathbf{Y}\in \mathcal{C}_{0}$, there exists $m_Y\in \mathbb{N}$ and ${\mathbf{c}}_Y=(c_Y^1,\dots ,c_Y^N)\in {\mathbb{R}}^N$ such that

$$\sum _{n=1}^N{c}_Y^n=\sum _{n=1}^N{Y}^n=:c_Y\in \mathbb{R}$$

and for all $m\geq m_{Y}$, we have

$$ \mathbf{Y}_{m}:=\mathbf{Y}I_{\cap _{n=1}^{N}\{|Y^{n}|< m\}}+\mathbf{c} _{Y}I_{\cup _{n=1}^{N}\{|Y^{n}|\geq m\}}\in \mathcal{C}_{0}. $$

(4.27)

Note that in Definition 2.5, the set $\mathcal{C}_{0}^{( \mathbf{n})}$ is closed under truncation.

Theorem 4.19

Let$\mathcal{C}=\mathcal{C}_{0}\cap M^{{\Phi } }$and suppose that${\mathcal{C}}_0\subseteq {\mathcal{C}}_{\mathbb{R}}$is closed for convergence in probability and closed under truncation. For any$\mathbf{X}\in M^{{\Phi } }$, there exists${\tilde{\mathbf{Y}}}_{\mathbf{X}}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$such that

$$\sum _{n=1}^N{\tilde{Y}}_{\mathbf{X}}^n\in \mathbb{R},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+{\tilde{Y}}_{\mathbf{X}}^n)]\ge B,\sum _{n=1}^N({\mathbb{E}}_{Q_X^n}[{\tilde{Y}}_{\mathbf{X}}^n]-{\tilde{Y}}_{\mathbf{X}}^n)=0$$

and

$$\begin{array}{rl}{\rho }_B(\mathbf{X})& =inf\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in {\mathcal{C}}_0\cap M^{\mathrm{\Phi }},\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}=\sum _{n=1}^N{\tilde{Y}}_{\mathbf{X}}^n\\ & =min\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}\\ & ={\tilde{\rho }}_B(\mathbf{X}),\end{array}$$

so that$\tilde{\mathbf{Y}}_{\mathbf{X}}$is the solution to the extended problem$\widetilde{\rho }_{B}(\mathbf{X})$.

Proof

Take as $\tilde{\mathbf{Y}}_{\mathbf{X}}$ the vector $\mathbf{Y}$ in Theorem 4.14, which belongs to $L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$ by Theorem 4.14 and Lemmas 4.16 and 4.17, and to $\mathcal{C}_{0}$ as $\mathcal{C}_{0}$ is closed for convergence in probability and $\mathbf{Y}=\lim _{m\to \infty } \mathbf{Y}_{m}$ ℙ-a.s. and $(\mathbf{Y}_{m}) \subseteq \mathcal{C}_{0}$. Comparing Theorem 4.19 with Theorem 4.14, we see that it remains to prove $\rho _{B}= \widetilde{\rho }_{B}$ and ${\sum }_{n=1}^N({\mathbb{E}}_{Q_X^n}[{\tilde{Y}}_{\mathbf{X}}^n]-{\tilde{Y}}_{\mathbf{X}}^n)\le 0$; this is done in Propositions 4.22 and 4.20 below and requires the truncation assumption on $\mathcal{C}_{0}$. The opposite inequality

$$\sum _{n=1}^N{\tilde{Y}}_{\mathbf{X}}^n={\rho }_B(\mathbf{X})={\rho }_B^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})\le \sum _{n=1}^N{\mathbb{E}}_{Q_X^n}[{\tilde{Y}}_{\mathbf{X}}^n]$$

holds as $\tilde{\mathbf{Y}}_{\mathbf{X}}$ fulfils the budget constraints of $\rho _{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$. □

Proposition 4.20

Suppose that$\mathcal{C}_{0}$is closed under truncation. Then

$$\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y^n]\le \sum _{n=1}^N{Y}^n\mathit{\text{for all }}\mathbf{Y}\in {\mathcal{C}}_0\cap L^1({\mathbf{Q}}_{\mathbf{X}};{\mathbb{R}}^N).$$

Proof

Fix $\mathbf{Y}\in {\mathcal{C}}_0\cap L^1({\mathbf{Q}}_{\mathbf{X}};{\mathbb{R}}^N)$ and consider $\mathbf{Y}_{m}$ for $m\in \mathbb{N}$ as in (4.27), where without loss of generality, we assume $m_{Y}=1$. Note that $\sum _{n=1}^{N}Y_{m}^{n}=c_{Y}$$(= \sum _{n=1}^{N}Y^{n})$. By boundedness of $\mathbf{Y}_{m}$ and (4.27), we have $\mathbf{Y}_{m}\in \mathcal{C}_{0}\cap M^{{ \Phi } }$ for all $m\in \mathbb{N}$. Further, $\mathbf{Y} _{m}\rightarrow \mathbf{Y}$$\mathbf{Q}_{\mathbf{X}}$-a.s. for $m\rightarrow \infty$ and thus, since $|{\mathbf{Y}}_m|\le max\{|\mathbf{Y}|,|{\mathbf{c}}_Y|\}\in L^1({\mathbf{Q}}_{\mathbf{X}};{\mathbb{R}}^N)$ for all $m\in \mathbb{N}$, also $\mathbf{Y}_{m} \rightarrow \mathbf{Y}$ in $L^1({\mathbf{Q}}_{\mathbf{X}};{\mathbb{R}}^N)$ for $m\rightarrow \infty$ by dominated convergence. We then obtain

$$\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y^n]=\underset{m\to \mathrm{\infty }}{lim}\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_m^n]\le \underset{m\to \mathrm{\infty }}{lim}\sum _{n=1}^N{Y}_m^n=c_Y=\sum _{n=1}^N{Y}^n.$$

 □

The map $\widetilde{\rho }_{B}$ is defined on $M^{{\Phi } }$, but the admissible claims $\mathbf{Y}$ belong to the set ${\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$ not included in $M^{{\Phi } }$. As $L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})\subseteq L^1(\mathbb{P};{\mathbb{R}}^N)$ by the same argument as in the proof of Proposition 2.4, we can show that $\widetilde{\rho }_{B}(\mathbf{X})>-\infty$ for all $\mathbf{X} \in M^{\Phi }$. By the same argument as in the proof of Proposition 2.4 and by (2.1), we also deduce that $\widetilde{\rho }_{B}(\mathbf{X})<+\infty$ for all $\mathbf{X}\in M ^{{\Phi } }$, so that the function ${\tilde{\rho }}_B:M^{\mathrm{\Phi }}\to \mathbb{R}$ is convex and monotone decreasing on its domain ${\mathrm{dom}}(\widetilde{\rho })=M^{{ \Phi } }$. From Theorem A.2, we then know that the penalty functions of $\rho _{B}$ and $\widetilde{\rho }_{B}$ are defined as

$$\begin{array}{rcl}{\alpha }_B(\mathbf{Q})& :& =sup\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-X^n]-{\rho }_B(\mathbf{X}):\mathbf{X}\in M^{\mathrm{\Phi }}\},\\ {\tilde{\alpha }}_B(\mathbf{Q})& :& =sup\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-X^n]-{\tilde{\rho }}_B(\mathbf{X}):\mathbf{X}\in M^{\mathrm{\Phi }}\}.\end{array}$$

Lemma 4.21

If$\mathcal{C}_{0}$is closed under truncation, then$\widetilde{\alpha }_{B}(\mathbf{Q}_{\mathbf{X}})=\alpha _{B}( \mathbf{Q}_{\mathbf{X}})$.

Proof

Recall from (1.3) that $\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Z})]=\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Z^n)]$. We then have that

$$\begin{array}{rl}{\tilde{\alpha }}_B({\mathbf{Q}}_{\mathbf{X}})& =sup\{\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]-{\tilde{\rho }}_B(\mathbf{X}):\mathbf{X}\in M^{\mathrm{\Phi }}\}\\ & =\underset{\mathbf{X}\in M^{\mathrm{\Phi }}}{sup}(\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]\\ & \phantom{=:\underset{\mathbf{X}\in M^{\mathrm{\Phi }}}{sup}\{}+sup\{-\sum _{n=1}^N{Z}^n:\mathbf{Z}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Z})]\ge B\})\\ & =sup\{\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]-\sum _{n=1}^N{Z}^n:\mathbf{Z}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\\ & \mathbf{X}\in M^{\mathrm{\Phi }},\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Z})]\ge B\}\\ & \le sup\{\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]-\sum _{n=1}^N{Z}^n:\mathbf{Z}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\\ & \mathbf{X}\in L^1(\mathbb{P};{\mathbf{Q}}_{\mathbf{X}}),\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Z})]\ge B\}\\ & =sup\{\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-W^n]+\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Z^n]-\sum _{n=1}^N{Z}^n:\mathbf{Z}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\\ & \mathbf{W}\in L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\\ & \mathbb{E}[\mathrm{\Lambda }(\mathbf{W})]\ge B\}\\ & =sup\{\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-W^n]:\mathbf{W}\in L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\mathbb{E}[\mathrm{\Lambda }(\mathbf{W})]\ge B\}\\ & \phantom{=:}+sup\{\sum _{n=1}^N({\mathbb{E}}_{Q_{\mathbf{X}}^n}[Z^n]-Z^n):\mathbf{Z}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})\}\\ & \le sup\{\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-W^n]:\mathbf{W}\in L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),\mathbb{E}[\mathrm{\Lambda }(\mathbf{W})]\ge B\}={\alpha }_B({\mathbf{Q}}_{\mathbf{X}}),\end{array}$$

because ${\sum }_{n=1}^N({\mathbb{E}}_{Q_{\mathbf{X}}^n}[Z^n]-Z^n)\le 0$ for all $\mathbf{Z}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$ as shown in Proposition 4.20. The last equality follows from (4.12). The opposite inequality is trivial as $\widetilde{\rho }_{B}\leq \rho _{B}$ implies that

$$\begin{array}{rl}{\tilde{\alpha }}_B({\mathbf{Q}}_{\mathbf{X}})& =sup\{\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]-{\tilde{\rho }}_B(\mathbf{X}):\mathbf{X}\in M^{\mathrm{\Phi }}\}\\ & \ge sup\{\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]-{\rho }_B(\mathbf{X}):\mathbf{X}\in M^{\mathrm{\Phi }}\}={\alpha }_B({\mathbf{Q}}_{\mathbf{X}}).\end{array}$$

 □

Proposition 4.22

If$\mathcal{C}_{0}$is closed under truncation, then

$${\rho }_B(\mathbf{X})={\tilde{\rho }}_B(\mathbf{X})=\underset{\mathbf{Y}\in L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})}{inf}\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in {\mathcal{C}}_0,\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\}.$$

(4.28)

Proof

We know that ${\tilde{\rho }}_B:M^{\mathrm{\Phi }}\to \mathbb{R}$ is convex and monotone decreasing. By definition, $\widetilde{\rho }_{B}\leq \rho _{B}$. Under the truncation assumption, Lemma 4.21 shows that we have $\widetilde{\alpha } _{B}(\mathbf{Q}_{\mathbf{X}})=\alpha _{B}(\mathbf{Q}_{\mathbf{X}})$. Then by Theorem A.2,

$$\begin{array}{rl}{\tilde{\rho }}_B(\mathbf{X})& =sup\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-X^n]-{\tilde{\alpha }}_B(\mathbf{Q}):\frac{d\mathbf{Q}}{dP}\in L^{{\mathrm{\Phi }}^{\ast }}\}\\ & \ge \sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]-{\tilde{\alpha }}_B({\mathbf{Q}}_{\mathbf{X}})\\ & =\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-X^n]-{\alpha }_B({\mathbf{Q}}_{\mathbf{X}})={\rho }_B(\mathbf{X}).\end{array}$$

 □

Corollary 4.23

Under the assumptions of Theorem 4.19, we have

$$\begin{aligned} \rho _{B}(\mathbf{X}) =&\rho _{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})= \widetilde{\rho }_{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})= \widehat{\rho }_{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})= \widetilde{\rho }_{B}(\mathbf{X}), \end{aligned}$$

(4.29)

$$\begin{aligned} \pi _{A}(\mathbf{X}) =&\pi _{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})= \widetilde{\pi }_{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})= \widehat{\pi }_{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X}), \end{aligned}$$

(4.30)

for$A:=\rho _{B}(\mathbf{X})$, and the unique solutions to the extended problems$\widetilde{\rho }_{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$, $\widehat{\rho }_{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$, $\widetilde{\rho }_{B}(\mathbf{X})$and$\widehat{\pi }_{A}^{ \mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$, $\widetilde{\pi }_{A}^{ \mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$exist and coincide with

$${\tilde{\mathbf{Y}}}_{\mathbf{X}}={\hat{\mathbf{Y}}}_{{\mathbf{Q}}_{\mathbf{X}}}={(-X^n-v_n^{\prime }({\lambda }^{\ast }\frac{d{Q}_{\mathbf{X}}^n}{d\mathbb{P}}\left)\right)}_{n=1,\dots ,N}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}}),$$

and$\mathbf{Q}_{\mathbf{X}}$is the unique solution to the dual problem (3.1).

Proof

From (4.28), (4.9), (4.8), (3.6) and Corollary 4.3, we already know that (4.29) and (4.30) hold true when $A:=\rho _{B}(\mathbf{X})$. By Theorem 4.19, there exists a solution ${\tilde{\mathbf{Y}}}_{\mathbf{X}}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$ to $\widetilde{\rho }_{B}(\mathbf{X})$ and by Proposition 4.11 and Remark 4.12, it coincides with the unique solution $\widehat{\mathbf{Y}}_{\mathbf{Q}_{\mathbf{X}}}$ for $\widehat{\rho } _{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$. By (4.15),

$${\tilde{\rho }}_B^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})={\hat{\rho }}_B^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})=\sum _{n=1}^N{\mathbb{E}}_{Q_X^n}[{\hat{Y}}_{{\mathbf{Q}}_{\mathbf{X}}}^n]$$

and then ${\hat{\mathbf{Y}}}_{{\mathbf{Q}}_{\mathbf{X}}}={\tilde{\mathbf{Y}}}_{\mathbf{X}}\in {\mathcal{C}}_0\cap L^1(\mathbb{P},{\mathbf{Q}}_{\mathbf{X}})$ proves that $\tilde{\mathbf{Y}} _{\mathbf{X}}$ is also the solution for $\widetilde{\rho }_{B}^{ \mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$. From (4.29) and (4.30), we know that $B=\widetilde{\pi }_{A}^{\mathbf{Q}_{ \mathbf{X}}}(\mathbf{X})=\widehat{\pi }_{A}^{\mathbf{Q}_{\mathbf{X}}}( \mathbf{X})$ and $A=\widetilde{\rho }_{B}^{\mathbf{Q}_{\mathbf{X}}}( \mathbf{X})=\widehat{\rho }_{B}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$. Therefore Proposition 4.2 (d) shows that $\tilde{\mathbf{Y}}_{\mathbf{X}}$ is the unique solution to $\widetilde{\pi }_{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$ and $\widehat{\pi }_{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$. □

5 Additional properties of $\mathbf{Q}_{\mathbf{X}}$ and fair risk allocation

In this section, we provide additional properties for the systemic risk measure $\rho (\mathbf{X})$ from (1.5) and for the systemic risk allocations ${\rho }^n(\mathbf{X})={\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]$, $n=1,\dots ,N$, from (1.8). We argue that the choice of $\mathbf{Q}_{\mathbf{X}}$ as systemic vector of probability measures is fair from the point of view of both the system and the individual banks.

5.1 Cash-additivity and marginal risk contribution

In this section, we provide a sensitivity analysis of $\rho ( \mathbf{X})$ with respect to changes in the positions $\mathbf{X}$, which also shows the relevance of the dual optimiser $\mathbf{Q}_{ \mathbf{X}}$. We first show that $\rho (\mathbf{X})$ is cash-additive. Recall $\Lambda$ from (1.3).

Lemma 5.1

Define${\mathcal{W}}_{\mathcal{C}}:=\{\mathbf{Z}\in {\mathcal{C}}_{\mathbb{R}}:\mathbf{Y}\in \mathcal{C}⟺\mathbf{Y}-\mathbf{Z}\in \mathcal{C}\}\cap M^{\mathrm{\Phi }}$. Then the risk measure$\rho$is cash-additive on$\mathcal{W}_{\mathcal{C}}$, i.e.,

$$ \rho (\mathbf{X}+\mathbf{Z})=\rho (\mathbf{X})-\sum _{n=1}^{N}Z^{n} \qquad \textit{for all }\mathbf{Z}\in \mathcal{W}_{\mathcal{C}}\textit{ and } \mathbf{X}\in M^{{\Phi } }, $$

and it satisfies

$$ \left . \frac{d}{d\varepsilon }\rho (\mathbf{X+}\varepsilon \mathbf{V})\right \vert _{\varepsilon =0}=-\sum _{n=1}^{N}V^{n} $$

(5.1)

for all$\mathbf{V}$such that$\varepsilon \mathbf{V}\in \mathcal{W} _{\mathcal{C}}$for all$\varepsilon \in (0,1]$.

Proof

Let $\mathbf{Z}\in \mathcal{W}_{\mathcal{C}}$. Then $\mathbf{W}:=\mathbf{Z}+\mathbf{Y}\in {\mathcal{C}\subseteq \mathcal{C}}_{\mathbb{R}}$ for any $\mathbf{Y}\in \mathcal{C}$. For any $\mathbf{X}\in M^{{ \Phi } }$,

$$\begin{array}{rl}\rho (\mathbf{X}+\mathbf{Z})& =inf\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in \mathcal{C},\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Z}+\mathbf{Y})]\ge B\}\\ & =inf\{\sum _{n=1}^N{W}^n-\sum _{n=1}^N{Z}^n:\mathbf{W}\in \mathcal{C},\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{W})]\ge B\}\\ & =\rho (\mathbf{X})-\sum _{n=1}^N{Z}^n.\end{array}$$

In particular, $\rho ( \mathbf{X+}\varepsilon \mathbf{V})=\rho ( \mathbf{X})-\varepsilon \sum _{n=1}^{N}V^{n}$ for $\varepsilon \mathbf{V}\in \mathcal{W}_{\mathcal{C}}$ and (5.1) follows. □

Example 5.2

For the set $\mathcal{C}^{(\mathbf{n})}$ in Definition 2.5, $\rho$ is cash-additive on $\mathcal{W}_{\mathcal{C}^{( \mathbf{n})}}=\mathcal{C}^{(\mathbf{n})}$. The latter equality holds because we are not imposing any restrictions on the vector $d=(d,\dots ,d_m)\in {\mathbb{R}}^m$ which determines the grouping.

Remark 5.3

Under Assumption 2.2, we have ${\mathbb{R}}^N\subseteq {\mathcal{W}}_{\mathcal{C}}$ and then (5.1) holds for all $\mathbf{V}\in {\mathbb{R}}^N$.

The marginal risk contribution$\frac{d}{d\varepsilon } \rho (\mathbf{X+}\varepsilon \mathbf{V})|_{\varepsilon =0}$ was also considered in [13] and [3] and is an important quantity which describes the sensitivity of the risk of ${\mathbf{X}}$ with respect to the impact $\mathbf{V}\in L^0({\mathbb{R}}^N)$. The property (5.1) cannot be immediately generalised to the case of random vectors $\mathbf{V}$ as ${\sum }_{n=1}^N{V}^n\notin \mathbb{R}$ in general. In the following, we obtain the general local version of cash-additivity, which extends (5.1) to a random setting.

Proposition 5.4

Let$\mathbf{X}$and$\mathbf{V}\in M^{{\Phi } }$. Let$\mathbf{Q}_{\mathbf{X}}$be the solution to the dual problem (3.1) associated to$\rho (\mathbf{X})$and assume that$\rho (\mathbf{X+}\varepsilon \mathbf{V})$is differentiable with respect to$\varepsilon$at$\varepsilon =0$, and that$\frac{d{\mathbf{Q}}_{\mathbf{X}+\epsilon \mathbf{V}}}{d\mathbb{P}}\to \frac{d{\mathbf{Q}}_{\mathbf{X}}}{d\mathbb{P}}$in$\sigma (L^{{ \Phi } ^{\ast }},M^{{\Phi } })$as$\varepsilon \rightarrow 0$. Then

$$\frac{d}{d\epsilon }\rho (\mathbf{X}+\epsilon \mathbf{V}){|}_{\epsilon =0}=-\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[V^n].$$

(5.2)

Proof

As the penalty function $\alpha _{B}$ does not depend on $\mathbf{X}$, (3.4) yields

$$\begin{array}{rl}\frac{d}{d\epsilon }\rho (\mathbf{X}+\epsilon \mathbf{V}){|}_{\epsilon =0}& =\frac{d}{d\epsilon }(\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}+\epsilon \mathbf{V}}^n}[-X^n-\epsilon V^n]-{\alpha }_B({\mathbf{Q}}_{\mathbf{X}+\epsilon \mathbf{V}})){|}_{\epsilon =0}\\ & =\frac{d}{d\epsilon }(\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}+\epsilon \mathbf{V}}^n}[-X^n]-{\alpha }_B({\mathbf{Q}}_{\mathbf{X}+\epsilon \mathbf{V}})){|}_{\epsilon =0}\\ & \phantom{=:}+\sum _{n=1}^N\frac{d}{d\epsilon }(\epsilon {\mathbb{E}}_{Q_{\mathbf{X}+\epsilon \mathbf{V}}^n}[-V^n]){|}_{\epsilon =0}\end{array}$$

(5.3)

$$=0+\sum _{n=1}^N\underset{\epsilon \to 0}{lim}{\mathbb{E}}_{Q_{\mathbf{X}+\epsilon \mathbf{V}}^n}[-V^n]=\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[-V^n],$$

(5.4)

where the equality between (5.3) and (5.4) is justified by the optimality of $\mathbf{Q}_{\mathbf{X}}$ and the differentiability of $\rho (\mathbf{X+}\varepsilon \mathbf{V})$, while the last equality is guaranteed by the convergence of $(\frac{d{\mathbf{Q}}_{\mathbf{X}+\epsilon \mathbf{V}}}{d\mathbb{P}})$. □

Remark 5.5

We emphasise that the generalisation (5.2) of (5.1) holds because we are computing the expectation with respect to the vector $\mathbf{Q}_{\mathbf{X}}$. The assumptions of Proposition 5.4 are satisfied for exponential utility functions, which are considered in Sect. 6.

5.2 Interpretation and implementation of $\rho ( \mathbf{X})$

Going back to the definition (1.5), we see that $\rho ( \mathbf{X})$ represents the minimal total cash amount needed to make the system acceptable at time $T$. For notational simplicity, we write in the sequel $\mathbf{Y}_{\mathbf{X}}$ for the solution of $\rho _{B}( \mathbf{X})$, i.e., do not distinguish $\mathbf{Y}_{\mathbf{X}}$ and $\tilde{\mathbf{Y}}_{\mathbf{X}}$. As already mentioned in Sect. 1 and as a result of Proposition 4.1, one economic justification for $\rho$ is that the optimal allocation $\mathbf{Y}_{\mathbf{X}}$ of $\rho (\mathbf{X})$ maximises the expected system utility among all random allocations of cost less than or equal to $\rho (\mathbf{X})$.

We notice also that the class $\mathcal{C}$ may determine the level of risk sharing (as explained below in (b)) between the banks, ranging from no risk sharing in the case $\mathcal{C}={\mathbb{R}}^N$ of deterministic allocations to the case $\mathcal{C}={\mathcal{C}}_{\mathbb{R}}$ of full risk sharing, and other constraints in between as in the Definition 2.5 of grouping. We now discuss two features of our systemic risk measure.

Implementation of the scenario-dependent allocation

(a) In practice, the scenario-dependent allocation can be described as a default fund as in the case of a CCP (see [3]). The amount $\rho (\mathbf{X})$ is collected at time 0 according to some systemic risk allocation $\rho ^{n}(\mathbf{X})$, $n=1,\dots ,N$, which satisfies $\sum _{n=1}^{N}\rho ^{n}(\mathbf{X})= \rho (\mathbf{X})$. Then at time $T$, this exact same amount is redistributed among the banks according to the optimal scenario-dependent allocations $Y_{\mathbf{X}}^{n}$ satisfying $\sum _{n=1}^{N}Y_{\mathbf{X}}^{n}=\rho (\mathbf{X})$, so that the fund acts as a clearing house, assuming that each bank fulfils its commitment.

(b) An alternative interpretation and implementation of the scenario-dependent allocation more in the spirit of monetary risk measures is in terms of capital requirements together with a risk sharing mechanism. Consider again a given systemic risk allocation $\rho ^{n}(\mathbf{X}) , n=1,\dots ,N$. At time 0, a capital requirement $\rho ^{n}(\mathbf{X})$ is imposed on each bank $n=1, \dots ,N$. Then at time $T$, a risk sharing mechanism takes place: each bank provides (if negative) or collects (if positive) the amount $Y_{\mathbf{X}}^{n}-\rho ^{n}(\mathbf{X})$, assuming as before that each bank fulfils its commitment. Note that in sum, the financial position of bank $n$ at time $T$ is $X^{n}+\rho ^{n}(\mathbf{X})+(Y_{ \mathbf{X}}^{n}-\rho ^{n}(\mathbf{X}))=X^{n}+Y_{\mathbf{X}}^{n}$ as required. This risk sharing mechanism is made possible by the clearing property$\sum _{n=1}^{N}( Y_{\mathbf{X}} ^{n}-\rho ^{n}(\mathbf{X})) =0$, which follows from $\sum _{n=1}^{N}Y _{\mathbf{X}}^{n}=\rho (\mathbf{X})$ and the full risk allocation requirement $\sum _{n=1}^{N}\rho ^{n}(\mathbf{X})=\rho ( \mathbf{X})$. The incentive for a single bank to enter in such a mechanism is made clear below after we introduce the choice of a fair risk allocation in Sect. 5.3.

Total risk reduction and dependence structure of $\mathbf{X}$

From a system-wide point of view, considering the optimal random allocation $\mathbf{Y}_{\mathbf{X}}$ implies a reduction of the total amount needed to secure the system (compared with the optimal deterministic allocation). This reduction is also a consequence of our framework of scenario-dependent allocations that allows taking into account the dependence structure of $\mathbf{X}$. An example showing these features can be found in [7, Example 7.1]. If the aggregation function ${\Lambda }$ is a sum of utility functions as in (1.3), one can see directly that the dependence structure of $\mathbf{X}$ is taken into account from the constraint $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]\ge B$ in (1.5), which depends only on the marginal distributions of $\mathbf{X}$ in the case of deterministic $Y^{n}$.

5.3 Fair systemic risk allocation $\rho ^{n}( \mathbf{X})$

We now address the problem of choosing a systemic risk allocation $(\rho ^{n}(\mathbf{X}))_{n=1,\dots ,N}$ in ${\mathbb{R}}^N$ (or individual contributions at time zero) as introduced in Definition 1.2. Note that in our setting, besides providing a ranking of the institutions in terms of their systemic riskiness, a risk allocation $\rho ^{n}(\mathbf{X})$ can be interpreted as a capital contribution/requirement for institution $n$ in order to secure the system.

From (5.2), we see that ${\mathbb{E}}_{{\mathbf{Q}}_{\mathbf{X}}}[\cdot ]$ defined by ${\mathbb{E}}_{{\mathbf{Q}}_{\mathbf{X}}}[\mathbf{Y}]={\sum }_{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y^n]$ already appeared as a multivariate valuation operator, and on the other hand, we have obtained in (4.20) that the minimiser ${\mathbf{Y}_{\mathbf{X}}}$ and the maximiser ${\mathbf{Q}_{\mathbf{X}}}$ of the dual problem satisfy

$$\rho (\mathbf{X})=\sum _{n=1}^N{Y}_{\mathbf{X}}^n=\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n],$$

which shows that ${\rho }^n(\mathbf{X})={\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]$, $n=1,\dots ,N$, gives a systemic risk allocation.

Any vector $\mathbf{Q}=( {Q}^{n}) _{n=1,\dots ,N}$ of probability measures gives rise to a valuation operator ${\mathbb{E}}_{\mathbf{Q}}[\cdot ]$ and to the systemic risk measure $\rho ^{\mathbf{Q}}$ given by (1.10). Note, however, that in (1.10), the clearing condition $\sum _{n=1}^{N}Y^{n}=\rho (\mathbf{X})$ is not guaranteed since the optimisation is there performed over all $\mathbf{Y}\in M ^{{\Phi } }$. Now, using the valuation ${\mathbb{E}}_{{\mathbf{Q}}_{\mathbf{X}}}[\cdot ]$ given by the dual optimiser, we know by Proposition 4.11 that the optimal allocation in (1.10) fulfils the clearing condition ${\mathbf{Y}}_{\mathbf{X}}\in {\mathcal{C}}_{\mathbb{R}}$, and is in fact the same as the optimal allocation for the original systemic risk measure in (1.5). From (4.19) and (4.20), we obtain

$$\sum _{n=1}^N{Y}_{\mathbf{X}}^n=\rho (\mathbf{X})={\rho }^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})=\sum _{n=1}^N{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n],$$

which shows that the valuation by ${\mathbb{E}}_{{\mathbf{Q}}_{\mathbf{X}}}[\cdot ]$ agrees with the systemic risk measure $\rho (\mathbf{X})$. This supports the introduction of ${\mathbb{E}}_{{\mathbf{Q}}_{\mathbf{X}}}[\cdot ]$ as a suitable systemic valuation operator.

The essential question for a financial institution is now whether its allocated share of the total systemic risk given by the risk allocation $({\mathbb{E}}_{Q_{\mathbf{X}}^1}[Y_{\mathbf{X}}^1],\dots ,({\mathbb{E}}_{Q_{\mathbf{X}}^N}[Y_{\mathbf{X}}^N])$, is fair. With the choice $\mathbf{Q}=\mathbf{Q}_{\mathbf{X}}$, Corollary 4.3, Lemma 4.5 and (4.11) lead to

$${\pi }_A(\mathbf{X})={\pi }_A^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})=\underset{{\sum }_{n=1}^N{a}^n=A}{max}\sum _{n=1}^N\underset{{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y^n]=a^n}{sup}\mathbb{E}[u_n(X^n+Y^n)].$$

(5.5)

Choose $A=\rho _{B}(\mathbf{X})$. Then Proposition 4.2 and the fact that $\mathbf{Y_{\mathbf{X}}}$ is then the solution of $\pi _{A}^{\mathbf{Q}_{\mathbf{X}}}(\mathbf{X})$ yield ${\mathbb{E}}_{Q_{{\mathbf{X}}^n}}[Y_{\mathbf{X}}^n]=a_{\ast }^n$, ${\sum }_{n=1}^N{\mathbb{E}}_{Q_{{\mathbf{X}}^n}}[Y_{\mathbf{X}}^n]=A$, and (5.5) can be rewritten as

$${\pi }_A(\mathbf{X})={\pi }_A^{{\mathbf{Q}}_{\mathbf{X}}}(\mathbf{X})=\sum _{n=1}^N\underset{{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y^n]={\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]}{sup}\mathbb{E}[u_n(X^n+Y^n)].$$

This means that by using $\mathbf{Q}_{\mathbf{X}}$ for valuation, the system utility maximisation in (1.9) reduces to individual utility maximisation for the banks without the “systemic” constraint $\mathbf{Y} \in \mathcal{C}$, i.e., to

$$sup\{\mathbb{E}[u_n(X^n+Y^n)]:Y^n\text{ such that }{\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y^n]={\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]\}\text{for all }n.$$

The optimal allocation $Y_{{\mathbf{X}}}^{n}$ and its value ${\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]$ can thus be considered fair by the $n$th bank as $Y_{{\mathbf{X}}}^{n}$ maximises its individual expected utility among all random allocations (not constrained to be in ${\mathcal{C}}_{\mathbb{R}}$) with value ${\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]$. In particular, it is clear then that for individual banks, it is more advantageous to use random rather than cash-valued allocations as the supremum will be larger, as previously stated in Sect. 5.2 (a) and (b). This finally argues for the fairness of the risk allocation $({\mathbb{E}}_{Q_{\mathbf{X}}^1}[Y_{\mathbf{X}}^1],\dots ,{\mathbb{E}}_{Q_{\mathbf{X}}^N}[Y_{\mathbf{X}}^N])$ as fair valuation of the optimal scenario-dependent allocation $(Y^{1}_{\mathbf{X}}, \dots ,Y^{N}_{\mathbf{X}})$.

6 The exponential case

In this section, we focus on a relevant case under Assumption 2.2, that is, we set $\mathcal{C}=\mathcal{C}^{( \mathbf{n})}$, see Definition 2.5 and Example 3.5, and choose $u_{n}(x)=-e^{-\alpha _{n}x}/\alpha _{n}$, $\alpha _{n}>0$, $n=1,\dots ,N$, as in Example 3.6. Then $v_{n}(y)=\frac{1}{ \alpha _{n}}(y\ln y-y)$ and $v_{n}^{\prime }(y)=\frac{1}{\alpha _{n}}\ln y$. We select $B<\sum _{n=1}^{N}u_{n}(+\infty )=0$. Under these assumptions, $\phi _{n}(x):=-u_{n}(-|x|)+u_{n}(0)=\frac{1}{\alpha _{n}}(e ^{\alpha _{n}|x|}-1)$,

$$M^{{\varphi }_n}=M^{exp}:=\{X\in L^0(\mathbb{R}):\mathbb{E}[e^{c|X|}]<+\mathrm{\infty }\text{ for all }c>0\},$$

the Orlicz hearts $M^{\phi _{n}}$, $n=1,\dots ,N$, coincide with the single Orlicz heart $M^{\exp }$ associated to the exponential Young function $x\mapsto e^{|x|}-1$, and the random variable $\overline{X}:= \sum _{n}X^{n}\in M^{\exp }$ is well defined. The systemic risk measure $\rho :{(M^{exp})}^N\to \mathbb{R}$ from (2.3) becomes

$$\rho (\mathbf{X})=inf\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in {\mathcal{C}}^{(\mathbf{n})},\mathbb{E}[-\sum _{n=1}^N\frac{1}{{\alpha }_n}exp(-{\alpha }_n(X^n+Y^n))]=B\}.$$

(6.1)

Recall that each set $\mathcal{C}^{(\mathbf{n})}$ is closed in probability and closed by truncation. From Proposition 2.4 and Corollary 4.23, we deduce

Proposition 6.1

The map$\rho$in (6.1) is finite-valued, monotone decreasing, convex, continuous and subdifferentiable on the Orlicz heart$M^{{\Phi } }=(M^{\exp })^{N}$, and the problem$\widetilde{\rho }(\mathbf{X})$admits the unique solution$\tilde{\mathbf{Y}}_{\mathbf{X}}$given in Corollary 4.23.

For a given partition $\mathbf{n}$ and allocations $\mathcal{C}^{( \mathbf{n})}$, we can explicitly compute the value $\rho (\mathbf{X})$, the unique optimal allocation of (6.1) and the unique optimiser $\mathbf{Q}_{\mathbf{X}}$ of the corresponding dual problem (3.10). Note that in the present exponential case, the vector $\tilde{\mathbf{Y}}_{\mathbf{X}}=\mathbf{Y}_{\mathbf{X}}\in (M^{ \exp })^{N}$ is the solution for $\rho (\mathbf{X})$ and $\widetilde{\rho }(\mathbf{X})$.

Theorem 6.2

For$m=1,\dots ,h$and$k\in I_{m}$, we have

$$d_m={\beta }_{m}ln(-\frac{\beta }{B}\mathbb{E}[exp(-\frac{{\bar{X}}_m}{{\beta }_m})\left]\right),$$

(6.2)

$$\begin{aligned} Y_{m}^{k} &=-X^{k}+\frac{1}{\beta _{m}\alpha _{k}}\overline{X}_{m}+\frac{1}{ \beta _{m}\alpha _{k}}d_{m}\in M^{\exp }, \end{aligned}$$

(6.3)

where$\overline{X}_{m}=\sum _{k\in I_{m}}X^{k}$, $\beta _{m}= \sum _{k\in I_{m}}\frac{1}{\alpha _{k}}$, $\beta =\sum _{i=1}^{N}\frac{1}{ \alpha _{i}}$and

$$ \rho (\mathbf{X})=\sum _{i=1}^{N}Y^{i}=\sum _{m=1}^{h}d_{m}. $$

The vector$\mathbf{Q}_{\mathbf{X}}$of probability measures with densities

$$\frac{d{Q}_{\mathbf{X}}^m}{d\mathbb{P}}:=\frac{e^{-\frac{1}{{\beta }_m}{\bar{X}}_m}}{\mathbb{E}[e^{-\frac{1}{{\beta }_m}{\bar{X}}_m}]},m=1,\dots ,h,$$

(6.4)

is the solution of the dual problem (3.10), i.e.,

$$\rho (\mathbf{X})=\sum _{m=1}^h{\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{X}}_m]-{\alpha }_B({\mathbf{Q}}_{\mathbf{X}}),$$

(6.5)

and${\mathbb{E}}_{Q_{\mathbf{X}}^m}[Y_{\mathbf{X}}^n]$, $m=1, \dots ,h$, $n\in I_{m}$, is a systemic risk allocation as in Definition 1.2.

Proof

By (3.11), we note that $\mathbf{Q}_{\mathbf{X}}$ defined in (6.4) belongs to $\mathcal{D}$. Using $\mathbf{Q}_{\mathbf{X}}$ and selecting ${\lambda }^{\ast }=-\frac{B}{\beta }$ from Example 3.6, it is easy to verify that the random variable $Y_{\mathbf{X}}^n:=-X^n-v_n^{\prime }({\lambda }^{\ast }\frac{d{Q}_{\mathbf{X}}^n}{d\mathbb{P}})$ from Corollary 4.23 coincides with the expression in (6.3) and $\sum _{n\in I_{m}}Y _{\mathbf{X}}^{n}=d_{m}$.

We prove below that ${\sum }_{m=1}^h{d}_m={\sum }_{m=1}^h{\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{X}}_m]-{\alpha }_B({\mathbf{Q}}_{\mathbf{X}})$. A priori, these equations are not sufficient to prove that $(\mathbf{Y}_{\mathbf{X}},\mathbf{Q}_{\mathbf{X}})$ are indeed the solutions to the primal and dual problems, as one needs to know that one of the two is indeed an optimiser of the corresponding problem. The proof that $\mathbf{Y}_{\mathbf{X}}$ defined in (6.3) is the optimiser of $\rho (\mathbf{X})$ uses the Lagrange method and several estimates of lengthy computations; it is omitted.³

Assuming that $\mathbf{Y}_{\mathbf{X}}$ is the optimiser of the problem associated to $\rho$, so that we have $\rho (\mathbf{X})=\sum Y^{I}= \sum d_{m}$, we now prove (6.5). First notice that

$$H(Q_{\mathbf{X}}^m|\mathbb{P})={\mathbb{E}}_{Q_{\mathbf{X}}^m}[ln\frac{d{Q}_{\mathbf{X}}^m}{d\mathbb{P}}]=\frac{1}{{\beta }_m}{\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{X}}_m]-ln\mathbb{E}[e^{-\frac{1}{{\beta }_m}{\bar{X}}_m}].$$

By (3.13), $\alpha _{B}(\mathbf{Q}_{\mathbf{X}})$ can be rewritten as

$$\begin{array}{rl}{\alpha }_B({\mathbf{Q}}_{\mathbf{X}})& =\sum _{m=1}^h\sum _{i\in I_m}(\frac{1}{{\alpha }_i}H(Q_{\mathbf{X}}^m|\mathbb{P})+\frac{1}{{\alpha }_i}ln(-\frac{B}{\beta }))\\ & =\sum _{m=1}^h({\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{X}}_m]-{\beta }_{m}ln(-\frac{\beta }{B}\mathbb{E}[e^{-\frac{1}{{\beta }_m}{\bar{X}}_m}]\left)\right)\\ & =\sum _{m=1}^h({\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{X}}_m]-d_m)=\sum _{m=1}^h{\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{X}}_m]-\rho (\mathbf{X}),\end{array}$$

as $\rho (\mathbf{X})=\sum _{i=1}^{N}Y^{i}=\sum _{m=1}^{h}d_{m}$. Then (3.12) concludes the proof. □

Remark 6.3

Note that if we arbitrarily change the components of the vector $\mathbf{X}$, but keep fixed the components in one given subgroup, say $I_{m_{0}}$, then the risk measure $\rho (\mathbf{X})$ will of course change, but $d_{m_{0}}$ and $Y_{m_{0}}^{k}$ for $k\in I_{m_{0}}$ remain the same.

6.1 Sensitivity analysis

Let $\mathbf{X} \in (M^{\exp })^{N}$, $\mathbf{V}\in (M^{\exp })^{N}$ and set $\overline{V}_{m}:=\sum _{k\in I_{m}}V_{k}$ for $m=1,\dots ,h$. We consider a perturbation $\varepsilon \mathbf{V}$, $\epsilon \in \mathbb{R}$, and perform a sensitivity analysis. Consider the optimal allocations $Y_{\mathbf{X+}\varepsilon \mathbf{V}}^{i}$ and the solution $\mathbf{Q}_{\mathbf{X}+\varepsilon \mathbf{V}}$ of the dual problem associated to $\rho (\mathbf{X}+\varepsilon \mathbf{V})$; see (6.4). By (6.3) and (6.2), we have

$$ Y_{\mathbf{X+}\varepsilon \mathbf{V}}^{n}=-X^{n}-\varepsilon V^{n}+\frac{1}{ \beta _{m}\alpha _{n}}( \overline{X}_{m}+\varepsilon \overline{V}_{m}) +\frac{1}{ \beta _{m}\alpha _{n}}d_{m}(\mathbf{X}+\varepsilon \mathbf{V}), $$

where

$$d_m(\mathbf{X}+\epsilon \mathbf{V})={\beta }_{m}ln(-\frac{\beta }{B}\mathbb{E}[exp(-\frac{{\bar{X}}_m+\epsilon {\bar{V}}_m}{{\beta }_m})\left]\right).$$

Proposition 6.4

Let$\rho$be the systemic risk measure defined in (6.1). Then we have:

1) The marginal risk contribution of group$m$is

$${\frac{d}{d\epsilon }{d}_m(\mathbf{X}+\epsilon \mathbf{V})|}_{\epsilon =0}={\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{V}}_m],m=1,\dots ,h.$$

2) The local causal responsibility is

$${\frac{d}{d\epsilon }{\mathbb{E}}_{Q_{\mathbf{X}}^m}[Y_{\mathbf{X}+\epsilon \mathbf{V}}^n]|}_{\epsilon =0}={\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^n],n\in I_m.$$

3) $\frac{d}{d\epsilon }{\mathbb{E}}_{Q_{\mathbf{X}+\epsilon \mathbf{V}}^m}[Z]{|}_{\epsilon =0}=-\frac{1}{{\beta }_m}{\mathrm{Cov}}_{Q_{\mathbf{X}}^m}({\bar{V}}_m,Z)$for any$Z\in M^{\exp }$.

4) The marginal risk allocation of institution$n\in I_{m}$is

$${\frac{d}{d\epsilon }{\mathbb{E}}_{Q_{\mathbf{X}+\epsilon \mathbf{V}}^m}[Y_{\mathbf{X}+\epsilon \mathbf{V}}^n]|}_{\epsilon =0}={\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^n]-\frac{1}{{\beta }_m}{\mathrm{Cov}}_{Q_{\mathbf{X}}^m}({\bar{V}}_m,Y_{\mathbf{X}}^n)$$

(6.6)

$$\begin{array}{rl}& ={\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^n]+\frac{1}{{\beta }_m}{\mathrm{Cov}}_{Q_{\mathbf{X}}^m}({\bar{V}}_m,X^n)\\ & \phantom{=:}-\frac{1}{{\alpha }_n}\frac{1}{{\beta }_m^2}{\mathrm{Cov}}_{Q_{\mathbf{X}}^m}({\bar{V}}_m,{\bar{X}}_m).\end{array}$$

(6.7)

5) The sensitivity of the penalty function is

$$ \left . \frac{d}{d\varepsilon }\alpha _{B}(\mathbf{Q}_{\mathbf{X+} \varepsilon \mathbf{V}})\right \vert _{\varepsilon =0}=\sum _{m=1}^{h}\frac{1}{ \beta _{m}}\mathrm{Cov}_{{Q_{\mathbf{X}}^{m}}}(\overline{V}_{m}, \overline{X}_{m}). $$

6) The systemic marginal risk contribution is

$${\frac{d}{d\epsilon }\rho (\mathbf{X}+\epsilon \mathbf{V})|}_{\epsilon =0}=\sum _{m=1}^h\sum _{i\in I_m}{\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^i]=\sum _{m=1}^h{\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{V}}_m].$$

Proof

The proof is the result of lengthy computations and is omitted.⁴ □

The interpretation of the above formulas is not simple because we are dealing with the systemic probability measure$Q_{\mathbf{X}} ^{m}$and not with the “physical” measure ℙ. Think of the difference between the physical measure ℙ and a martingale measure. If we replace $Q_{\mathbf{X}}^{m}$ with ℙ, none of the results of Proposition 6.4 will hold in general.

The first term ${\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^n]$ in (6.6) or (6.7) is easy to interpret: ${\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^n]$ is the contribution to the marginal risk allocation of bank $n$ regardless of any systemic influence. The sign of the increment $V^{n}$ in the first term of (6.6) is here relevant; an increment (positive) corresponds to a risk reduction, regardless of the dependence structure. If $\mathbf{V}$ is deterministic, the marginal risk allocation to bank $n$ is exactly ${\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^n]=-V^n$ and no other terms are present.

To understand the other terms in (6.6) or (6.7), take $\mathbf{V=}V^{j}\mathbf{e}_{j}$ with $j\neq n$. Then the first term in (6.6) disappears ($V ^{n}=0$) and we obtain

$${\frac{d}{d\epsilon }{\mathbb{E}}_{Q_{\mathbf{X}+\epsilon V^j{\mathbf{e}}_j}^m}[Y_{\mathbf{X}+\epsilon V^j{\mathbf{e}}_j}^n]|}_{\epsilon =0}=\frac{1}{{\beta }_m}{\mathrm{Cov}}_{Q_{\mathbf{X}}^m}(V^j,X^n)-\frac{1}{{\alpha }_n}\frac{1}{{\beta }_m^2}{\mathrm{Cov}}_{Q_{\mathbf{X}}^m}(V^j,{\bar{X}}_m).$$

To fix ideas, suppose that $\mathrm{Cov}_{{Q_{\mathbf{X}}^{m}}}(V ^{j},X^{n})<0$ and examine for the moment only the contribution of $\frac{1}{\beta _{m}}\mathrm{Cov}_{{Q_{\mathbf{X}}^{m}}}(V^{j},X^{n})$. This component does not depend on the specific $\alpha _{n}$, but it depends on the dependence structure between $(V^{j},X^{n})$. If the systemic risk probability $Q_{\mathbf{X}}^{m}$ attributes negative correlation to $(V^{j},X^{n})$, then from the systemic perspective, this is good (independently of the sign of $V^{j}$); indeed, a decrement in bank $j$ is balanced by bank $n$, and vice versa. If bank $n$ is negatively correlated (as seen by $Q_{\mathbf{X}}^{m}$) with the increment of bank $j$, then the risk allocation of bank $n$ should decrease. Therefore, bank $n$ takes advantage of this as its risk allocation is reduced ($\frac{1}{\beta _{m}}\mathrm{Cov}_{{Q_{ \mathbf{X}}^{m}}}(V^{j},X^{n})<0$). Since the overall marginal risk allocation of the group $m$ is fixed (and equal to ${\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{V}}_m]={\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^j]$ from 1)), someone else has to pay for this advantage to bank $n$. This is the last term in (6.7), which is discussed next.

For the third component in (6.7), we distinguish between the systemic component $-\frac{1}{\beta _{m}^{2}}\mathrm{Cov}_{{Q_{ \mathbf{X}}^{m}}}(V^{j},\overline{X}_{m})$, which only depends on the aggregate group $\overline{X}_{m}$, and the systemic relevance $\frac{1}{\alpha _{n}}$ of bank $n$. The systemic quantity is therefore distributed among the various banks according to $\frac{1}{\alpha _{n}}$. In addition, this term must compensate for the possible risk reduction (the second term in (6.7)) as the overall risk allocation to group $m$ is determined by ${\mathbb{E}}_{Q_{\mathbf{X}}^m}[-{\bar{V}}_m]={\mathbb{E}}_{Q_{\mathbf{X}}^m}[-V^j]$.

Finally, 1) and 6) express the same property (which holds in general, as shown in Proposition 5.4) for one group or for the entire system, respectively.

6.2 Monotonicity

Another desirable fairness property is monotonicity. If ${\mathcal{C}}_1\subseteq {\mathcal{C}}_2\subseteq {\mathcal{C}}_{\mathbb{R}}$, then we have $\rho _{1}(\mathbf{X})\geq \rho _{2}( \mathbf{X})$ for the corresponding systemic risk measures

$${\rho }_i(\mathbf{X}):=inf\{\sum _{n=1}^N{Y}^n:\mathbf{Y}\in {\mathcal{C}}_i,\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y^n)]\ge B\},i=1,2.$$

The two extreme cases occur for ${\mathcal{C}}_1:={\mathbb{R}}^N$ (the deterministic case) and ${\mathcal{C}}_2:={\mathcal{C}}_{\mathbb{R}}$ (the unconstrained scenario-dependent case). Hence we know that when going from deterministic to scenario-dependent allocations, the total systemic risk decreases. It is then desirable that each institution profits from this decrease in total systemic risk in the sense that also its individual risk allocation should decrease, i.e.,

$$ \rho _{1}^{n}(\mathbf{X})\geq \rho _{2}^{n}(\mathbf{X}) \qquad \text{for each }n=1,\dots ,N. $$

(6.8)

The opposite would clearly be perceived as unfair. In the next result (see in particular (6.11)), we prove that (6.8) holds true in the context of the Definition 2.5 of grouping when the risk allocation ${\rho }^n(\mathbf{X})={\mathbb{E}}_{Q_{\mathbf{X}}^n}[Y_{\mathbf{X}}^n]$ is computed using $\mathbf{Q}_{\mathbf{X}}$. If we were to select a vector of probability measures $\mathbf{R}$ different from $\mathbf{Q}_{\mathbf{X}}$ to compute the risk allocation with the formula ${\mathbb{E}}_{R^n}[Y_{\mathbf{X}}^n]$, the property (6.8) would be lost in general.

For a given partition $\mathbf{n}$ and $\mathcal{C}=\mathcal{C}^{( \mathbf{n})}$, let $Y_{r}^{k}$, $k\in I_{r}$, $r=1,\dots ,h$, be the corresponding optimal allocations of the primal problem (6.1) and $Q_{\mathbf{X}}^{r}$, $r=1,\dots ,h$, the solutions of the corresponding dual problem (3.10) (in this section, we suppress the label $\mathbf{X}$ from the optimal allocation $\mathbf{Y}_{ \mathbf{X}}$ to $\rho (\mathbf{X})$).

Consider for some $m\in \{ 1,\dots ,h\}$ a nonempty subgroup $I_{m}^{\prime }$ of the group $I_{m}$ and set $I_{m}^{\prime \prime }:=I_{m}\backslash I_{m}^{\prime }$. Then the $h+1$ groups $I_{1},I _{2},\dots ,I_{m-1},I_{m}^{\prime },I_{m}^{\prime \prime },I_{m+1}, \dots ,I_{h}$ correspond to a new partition $\mathbf{n}^{\prime }$. The optimal allocations of the primal problem (6.1) with $\mathcal{C}=\mathcal{C}^{(\mathbf{n}^{\prime })}$ coincide with $Y_{r}^{k}$, $k\in I_{r}$, for $r\neq m$. For $r=m$, $i\in I_{m}^{ \prime }$, we have the following.

Proposition 6.5

Denote by$(Y^{i}_{m})^{\prime }$, $i\in I_{m}^{\prime }$, the optimal allocation to the primal problem with$\mathcal{C}=\mathcal{C}^{( \mathbf{n}^{\prime })}$. Then

$${\mathbb{E}}_{Q_{\mathbf{X}}^m}\left[\sum _{i\in I_m^{\prime }}{Y}_m^i\right]\le \sum _{i\in I_m^{\prime }}{(Y_m^i)}^{\prime }:=d_m^{\prime }.$$

(6.9)

In particular, if the group$I_{m}^{\prime }$consists of only one single element$\{ i\}$, then$(Y^{i}_{m})^{\prime }$is deterministic and

$${\mathbb{E}}_{Q_{\mathbf{X}}^m}[Y_m^i]\le {(Y_m^i)}^{\prime }\mathit{\text{for each }}i\in I_m.$$

(6.10)

If we compare the deterministic optimal allocation$\mathbf{Y}^{ \ast }$ (corresponding to$\mathcal{C}={\mathbb{R}}^N$) with the random optimal allocations$\mathbf{Y}$associated to one single group (i.e., with$\mathcal{C}={\mathcal{C}}_{\mathbb{R}}\cap {(M^{exp})}^N$), we conclude that

$${\mathbb{E}}_{Q_{\mathbf{X}}}[Y^n]\le {(Y^{\ast })}^n\mathit{\text{for each }}n=1,\dots ,d,$$

(6.11)

where$Q_{\mathbf{X}}$is the unique solution of the dual problem with$\mathcal{C}={\mathcal{C}}_{\mathbb{R}}\cap {(M^{exp})}^N$.

Proof

Given the subgroup $I_{m}^{\prime }$, define $\beta _{m}^{\prime }:= \sum \limits _{k\in I_{m}^{\prime }}\frac{1}{\alpha _{k}}$. Then the value with respect to $\mathcal{C}^{(\mathbf{n}^{\prime })}$ is given by

$$d_m^{\prime }={\beta }_m^{\prime }ln(-\frac{\beta }{B}\mathbb{E}[exp(-\frac{1}{{\beta }_m^{\prime }}\sum _{k\in I_m^{\prime }}{X}^k)\left]\right).$$

Summing the components of the solutions relative to $\mathcal{C}^{( \mathbf{n})}$ over $k\in I_{m}^{\prime }$, we get

$$\begin{aligned} \sum _{k\in I_{m}^{\prime }}\mathbf{Y}_{m}^{k} &= \sum _{k\in I_{m}^{\prime }}\left ( \frac{1}{\beta _{m}\alpha _{k}} \overline{X}_{m}-X^{k}\right ) +\sum _{k\in I_{m}^{\prime }}\frac{1}{ \beta _{m}\alpha _{k}}d_{m} \\ &=\bigg( \frac{\beta _{m}^{\prime }}{\beta _{m}}\overline{X}_{m}- \sum _{k\in I_{m}^{\prime }}X^{k}\bigg) +\frac{\beta _{m}^{\prime }}{ \beta _{m}} d_{m}. \end{aligned}$$

Using Jensen’s inequality, we obtain

$$\begin{array}{rl}{\mathbb{E}}_{Q_{\mathbf{X}}^m}\left[\sum _{k\in I_m^{\prime }}{\mathbf{Y}}_m^k\right]& ={\beta }_m^{\prime }lnexp\left(\frac{1}{{\beta }_m^{\prime }}{\mathbb{E}}_{Q_{\mathbf{X}}^m}\right[(\frac{{\beta }_m^{\prime }}{{\beta }_m}{\bar{X}}_m-\sum _{k\in I_m^{\prime }}{X}^k)\left]\right)\\ & \phantom{=:}+\frac{{\beta }_m^{\prime }}{{\beta }_m}{\beta }_{m}ln(-\frac{\beta }{B}\mathbb{E}[exp(-\frac{{\bar{X}}_m}{{\beta }_m})\left]\right)\\ & \le {\beta }_m^{\prime }ln\left({\mathbb{E}}_{Q_{\mathbf{X}}^m}\right[exp(\frac{1}{{\beta }_m}{\bar{X}}_m-\frac{1}{{\beta }_m^{\prime }}\sum _{k\in I_m^{\prime }}{X}^k)\left]\right)\\ & \phantom{=:}+{\beta }_m^{\prime }ln(-\frac{\beta }{B}\mathbb{E}[exp(-\frac{{\bar{X}}_m}{{\beta }_m})\left]\right)\\ & ={\beta }_m^{\prime }ln\mathbb{E}\left[\frac{exp(-\frac{{\bar{X}}_m}{{\beta }_m})exp(\frac{1}{{\beta }_m}{\bar{X}}_m)exp(-\frac{1}{{\beta }_m^{\prime }}{\sum }_{k\in I_m^{\prime }}{X}^k)}{\mathbb{E}[e^{-\frac{1}{{\beta }_m}{\bar{X}}_m}]}\right]\\ & \phantom{=:}+{\beta }_m^{\prime }ln(-\frac{\beta }{B}\mathbb{E}[exp(-\frac{{\bar{X}}_m}{{\beta }_m})\left]\right)\\ & ={\beta }_m^{\prime }ln(-\frac{\beta }{B}\mathbb{E}[exp(-\frac{1}{{\beta }_m^{\prime }}\sum _{k\in I_m^{\prime }}{X}^k)\left]\right)=d_m^{\prime }.\end{array}$$

Then (6.10) and (6.11) follow directly by (6.9). □

Appendix A

1.1 A.1 Properties of the utility functions and proof of Proposition 2.4

Lemma A.1

Under Assumption 2.2and if we have$\lim _{x\rightarrow - \infty } \frac{u_{n}(x)}{x} =+\infty$and$\lim _{x\rightarrow +\infty }\frac{u_{n}(x)}{x}=0$, then:

(a) There exist$c\in \mathbb{R}$and$b\in {\mathbb{R}}_{+}$such that

   (i) $u_{n}(x)\leq bx+c$for all$x\geq 0$and all$n$,

   (ii) $u_{n}(x)\leq 2bx+c$for all$x\leq 0$and all$n$.

(b) For all$\varepsilon >0$, there exists$b=b(\varepsilon )>0$such that$u_{n}(x)\leq \varepsilon x+b$for$x\geq 0$and all $n$.

Proof

From 2) in Assumption 2.2, we know that $\mathrm{dom}(u_n)=\mathbb{R}$ for each $n$. Hereafter, the left derivatives of the concave increasing functions $u_{n}$ are denoted by $u_{n}^{\prime }$; they satisfy $u_{n}^{\prime }(x)\geq 0$ for all $x\in \mathbb{R}$.

(a) For (i), the concavity of each $u_{n}$ implies that $u_{n}(x)\leq u_{n}^{\prime }(0)x+c_{n}$ for all $x\in \mathbb{R}$ (for some $c_{n}$), and setting $b:=\max _{n=1,\dots ,N}u_{n}^{\prime }(0) \geq 0$ and $c\geq \max _{n=1,\dots ,N}c_{n}$ therefore gives $u_{n}(x)\leq bx+c$ for all $x\geq 0$.

For (ii), we prove that for every $M>0$, there exists a constant $d>0$ with $u_{n}(x)\leq Mx+d$ for all $n$ and $x\leq 0$. By taking $M=2b$, we obtain (ii). The assumption $\lim _{x\rightarrow -\infty } \frac{u _{n}(x)}{x}=+\infty$ implies that there exists $K>0$ (which depends on $M$) such that $u_{n}(x)\leq Mx$ for $x\leq -K$ and for all $n$. Hence $Mx-u_{n}(x)\geq 0$ for $x\in (-\infty ,-K)$. As the function $Mx-u_{n}(x)$ is continuous on $[-K,0]$, we may add a properly chosen $d>0$ to get $Mx+d-u_{n}(x)\geq 0$ for all $x\in (-\infty ,0]$ and all $n$.

(b) The assumption $\lim _{x\rightarrow +\infty } \frac{u_{n}(x)}{x}=0$ guarantees the existence of a constant $K>0$, which depends on $\varepsilon$, such that $u_{n}(x) \leq \varepsilon x$ for $x\geq K$ and all $n$. Hence

$$ u_{n}(x)\leq \varepsilon x+K\varepsilon +\max _{n=1,\dots ,N} \sup _{[0,K]}u _{n}(s), \qquad \forall \,x\geq 0. $$

 □

Proof of Proposition 2.4

To show $\rho >-\infty$, we suppose by way of contradiction that $\rho (\mathbf{X})=-\infty$ for some $\mathbf{X}\in M^{\mathrm{\Phi }}\subseteq L^1(\mathbb{P};{\mathbb{R}}^N)$. Let $(\mathbf{Y}_{m})\subseteq \mathcal{C}$ satisfy $\sum _{n=1}^{N}Y_{m}^{n}\downarrow -\infty$ as $m\rightarrow \mathbf{\infty }$ and $\mathrm{\Lambda }({\mathbf{X}+\mathbf{Y}}_m)\in \mathbb{A}$ for each $m$ for $\Lambda$ from (1.3). The first condition implies ${\sum }_{n=1}^N\mathbb{E}[Y_m^n]\downarrow -\mathrm{\infty }$ as $m\rightarrow \mathbf{\infty .}$ Note also that by Jensen’s inequality,

$$B\le \mathbb{E}[\mathrm{\Lambda }({\mathbf{X}+\mathbf{Y}}_m)]\le \mathrm{\Lambda }(\mathbb{E}[{\mathbf{X}+\mathbf{Y}}_m])=\sum _{n=1}^N{u}_n(\mathbb{E}[X^n]+\mathbb{E}[Y_m^n]).$$

(A.1)

We now prove that ${\sum }_{n=1}^N{u}_n(\mathbb{E}[X^n]+\mathbb{E}[Y_m^n])\downarrow -\mathrm{\infty }$ as $m\rightarrow \mathbf{\infty }$, which contradicts (A.1). Set $\mathbf{x}_{m}:=(x_{m}^{n})_{n=1}^{N}$, where $x_m^n:=\mathbb{E}[Y_m^n]$. Since $\sum _{n=1} ^{N}x_{m}^{n}\downarrow -\infty$, there must exist $n_{0}\in \{ 1, \dots ,N\}$ and a subsequence $(\mathbf{x}_{h_{m}})$ such that $x_{h_{m}}^{n_{0}}\downarrow -\infty$ as $m\rightarrow \mathbf{\infty .}$ With a slight abuse of notation, denote the subsequence $(\mathbf{x}_{h_{m}})$ again by $(\mathbf{x}_{m})$. Then we have $x_{m}^{n_{0}}\downarrow -\infty$. If there exists another coordinate $n_{1}\in \{ 1,\dots ,N\} \backslash \{n_{0}\}$ such that $\liminf _{m\rightarrow \infty }x_{m}^{n_{1}}=-\infty$, take a subsequence $(\mathbf{x}_{k_{m}})$ such that $x_{k_{m}}^{n_{1}}\downarrow -\infty$. By a diagonal procedure, we obtain one single sequence again denoted by $(\mathbf{x}_{m})$ such that $x_{m}^{n_{0}}\downarrow - \infty$ and $x_{m}^{n_{1}}\downarrow -\infty$ as $m\rightarrow \mathbf{\infty }$. We may adopt this procedure (at most $N$ times) analogously in the case where $\limsup _{m\rightarrow \infty }x_{m} ^{n_{2}}=+\infty$ for some coordinate $n_{2}$. At the end, we obtain one single sequence $(\mathbf{x}_{m})$ and three disjoint sets of coordinate indices $N_{-}$, $N_{+}$, $N^{\ast }$ such that

$$\begin{aligned} x_{m}^{n}\downarrow -\infty &\text{if }n\in N_{-}\subseteq \left \{ 1,\dots ,N\right \} , \\ x_{m}^{n}\uparrow +\infty &\text{if }n\in N_{+}\subseteq \left \{ 1, \dots ,N\right \} , \\ | x_{m}^{n}| \leq K &\text{for all }m\text{ and all }n\in N^{\ast }= \left \{ 1,\dots ,N\right \} \backslash (N_{-}\cup N_{+}), \end{aligned}$$

where $K$ is a constant independent of $m$. We know that $N_{-}\neq \emptyset$ since $n_{0}\in N_{-}$ (but the other two sets $N_{+}$ and $N^{\ast }$ may be empty). Since $\sum _{n=1}^{N}x_{m}^{n}\downarrow - \infty$, we deduce that for large $m$, $\ \sum _{n=1}^{N}x_{m}^{n} \leq 0$ so that for each fixed (large) $m$,

$$ \sum _{n\in N_{+}}x_{m}^{n}\leq -\sum _{n\in N_{-}}x_{m}^{n}- \sum _{n\in N^{\ast }}x_{m}^{n}\leq -\sum _{n\in N_{-}}x_{m}^{n}+NK. $$

(A.2)

Using the inequalities of Lemma A.1 (a) and in (A.2) gives for each fixed large $m$

$$\begin{array}{rl}\sum _{n=1}^N{u}_n(\mathbb{E}[X^n]+\mathbb{E}[Y_m^n])& =\sum _{n\in N_{+}}{u}_n(\mathbb{E}[X^n]+x_m^n)+\sum _{n\in N_{-}}{u}_n(\mathbb{E}[X^n]+x_m^n)\\ & \phantom{=:}+\sum _{n\in N^{\ast }}{u}_n(\mathbb{E}[X^n]+x_m^n)\\ & \le C_1+\sum _{n\in N_{+}}b{x}_m^n+\sum _{n\in N_{-}}2b{x}_m^n+\sum _{n\in N^{\ast }}{u}_n(K)\\ & \le C_2-\sum _{n\in N_{-}}b{x}_m^n+bNK+\sum _{n\in N_{-}}2b{x}_m^n\\ & =C_3+b\sum _{n\in N_{-}}{x}_m^n\end{array}$$

with constants $C_{1},C_{2},C_{3}$ all independent of $m$. Since $x_{m}^{n}\downarrow -\infty$ for each $n\in N_{-}$, we get $b\sum _{n\in N_{-}}x_{m}^{n}\downarrow -\infty$ as $m\rightarrow \infty$. This contradicts (A.1) and hence shows that $\rho (\mathbf{X})>-\infty$ for all $\mathbf{X} \in M^{{ \Phi } }$.

Let $\mathbf{X} \in M^{{\Phi } }$. Then $\mathbb{E}[\mathrm{\Lambda }(\mathbf{X})]>-\mathrm{\infty }$ and $\mathbf{X}+m \mathbf{1\uparrow +\infty }$ ℙ-a.s. if $m\rightarrow \mathbf{\infty }$, $m\in \mathbb{R}$, where $\mathbf{1=(}1 \mathbf{,\dots ,}1\mathbf{).}$ We have $\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+m\mathbf{1})]>-\mathrm{\infty }$ for $m>0$ because of $\mathbb{E}[\mathrm{\Lambda }(\mathbf{X})]>-\mathrm{\infty }$, and monotone convergence implies $\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+m\mathbf{1})]\uparrow \mathrm{\Lambda }(+\mathrm{\infty })>B$. Since ${\mathbb{R}}^N\subseteq \mathcal{C}$, this gives $m\mathbf{1}\in \mathcal{C}$ and $\{\mathbf{Y}\in \mathcal{C}:\mathrm{\Lambda }(\mathbf{X}+\mathbf{Y})\in \mathbb{A}\}\ne \mathrm{\varnothing }$ so that $\rho (\mathbf{X})<+\infty$. Hence $\rho :M^{\mathrm{\Phi }}\to \mathbb{R}$ and then convexity and monotonicity are straightforward. The remaining properties in (a) are a consequence of Theorem A.2 below and the fact that $M^{{\Phi } }$ is a Banach space.

To prove (b), we claim that if $\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Y})]>B$, then $\mathbf{Y}\in \mathcal{C}$ cannot be optimal, i.e.,

$$\mathbf{Y}\in \mathcal{C}\text{ and }\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Y})]>B⟹\sum _{n=1}^N{Y}^n>{\rho }^{=}(\mathbf{X}).$$

(A.3)

Indeed, the continuity of $u_{n}$ and $\mathbb{E}[u_n(Z^n)]>-\mathrm{\infty }$ for all $\mathbf{Z}\in M^{{\Phi } }$ imply the existence of $\delta \in {\mathbb{R}}_{+}^N\setminus \{\mathbf{0}\}$ such that $\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Y}-\delta )]=B$ and so, as $\mathbf{Y-\delta }\in \mathcal{C}$, $\rho ^{=}( \mathbf{X)\leq }\sum _{n=1}^{N}(Y^{n}-\delta ^{n})<\sum _{n=1}^{N}Y^{n}$. This implies $\rho (\mathbf{X})=\rho ^{=}(\mathbf{X})$ because if we had $\rho (\mathbf{X})<\rho ^{=}(\mathbf{X})$, then by definition of $\rho (\mathbf{X})$, there would exist $\varepsilon >0$ and $\mathbf{Y}\in \mathcal{C}$ with $\mathbb{E}[\mathrm{\Lambda }(\mathbf{X}+\mathbf{Y})]>B$ and $\sum _{n=1}^{N}Y^{n}\leq \rho ( \mathbf{X)+}\varepsilon \mathbf{<}\rho ^{=}(\mathbf{X})$, which contradicts (A.3).

We now show uniqueness by way of contradiction. Suppose $\rho ( \mathbf{X})$ is attained by two distinct $\mathbf{Y}_{1}\in \mathcal{C}$ and $\mathbf{Y}_{2}\in \mathcal{C}$ so that $\mathbb{P}[{\mathbf{Y}}_1^j\ne {\mathbf{Y}}_2^j]>0$ for some $j$. Then we have

$$\rho (\mathbf{X})=\sum _{n=1}^N{Y}_k^n\text{and}\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y_k^n)]=B,\text{for }k=1,2.$$

For $\lambda \in \lbrack 0,1]$, set $\mathbf{Y}_{\lambda }:=\lambda \mathbf{Y}_{1}+(1-\lambda )\mathbf{Y}_{2} \in \mathcal{C}$ as $\mathcal{C}$ is convex. This implies

$$ \sum _{n=1}^{N}Y_{\lambda }^{n}=\lambda \sum _{n=1}^{N}Y_{1}^{n}+(1- \lambda )\sum _{n=1}^{N}Y_{2}^{n}=\rho (\mathbf{X}) , \qquad \forall \lambda \in \lbrack 0,1], $$

and for $\lambda \in (0,1)$,

$$\begin{array}{rl}B& =\lambda \mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y_1^n)]+(1-\lambda )\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y_2^n)]\\ & <\mathbb{E}\left[\sum _{n=1}^N{u}_n\right(\lambda X^n+\lambda Y_1^n+(1-\lambda )X^n+(1-\lambda )Y_2^n\left)\right]\\ & =\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Y_{\lambda }^n)],\end{array}$$

where we used that $u_{j}$ is strictly concave and $\mathbb{P}[Y_1^j\ne Y_2^j]>0$. This is a contradiction to $\rho (\mathbf{X})= \rho ^{=}( \mathbf{X})$ and (A.3). □

1.2 A.2 Orlicz setting

We first recall an important result for the characterisation of systemic risk measures of the form (2.3) on an Orlicz heart.

Theorem A.2

(Biagini and Frittelli [10, Theorem 1])

Suppose that ℒ is a Fréchet lattice and$\rho :\mathcal{L}\to \mathbb{R}\cup \{+\mathrm{\infty }\}$is convex and monotone decreasing. Then:

1) $\rho$is continuous in the interior of${\mathrm{dom}}( \rho )$with respect to the topology of ℒ.

2) $\rho$is subdifferentiable in the interior of${\mathrm{dom}}(\rho )$.

3) Denote by${\mathcal{L}}^{\ast }$the dual of ℒ (for the topology for which ℒ is a Fréchet lattice) and set${\mathcal{L}}_{+}^{\ast }=\{ Q\in {\mathcal{L}} ^{\ast }: Q\textit{ is positive}\}$. For all$\mathbf{X}\in {\mathrm{int}}( {\mathrm{dom}}(\rho ))$,

$$ \rho (\mathbf{X})=\max _{Q\in {\mathcal{L}}_{+}^{\ast }}\big( Q(- \mathbf{X})-\alpha (Q)\big) $$

with$\alpha :{\mathcal{L}}^{\ast }\to \mathbb{R}\cup \{+\mathrm{\infty }\}$defined by

$$ \alpha (Q)=\sup _{\mathbf{X}\in {\mathcal{L}}}\big( Q(-\mathbf{X})- \rho (\mathbf{X})\big) $$

is then$\sigma ({\mathcal{L}}^{\ast },{\mathcal{L}})$-lower semicontinuous and convex.

Proof of Proposition 3.4

Consider the convex functional ${\mathrm{\Theta }}_n:M^{{\varphi }_n}(\mathbb{R})\to \mathbb{R}$ defined by ${\mathrm{\Theta }}_n(Z):=\mathbb{E}[-u_n(Z)]$ and let $\Theta _{n}^{\ast }$ be its convex conjugate. Then $\Theta _{n}(Z^{n})>-\infty$ as $M^{{\varphi }_n}(\mathbb{R})\subseteq L^1(\mathbb{P})$ and $\mathbb{E}[u_n(Z^n)]\le u_n(\mathbb{E}[Z^n])<+\mathrm{\infty }$, and $\Theta _{n}(Z ^{n})<+\infty$ as $Z^n\in M^{{\varphi }_n}(\mathbb{R})$ implies $\mathbb{E}[u_n(Z^n)]>-\mathrm{\infty }$. Thus we have ${\mathrm{\Theta }}_n^{\ast }(\xi )=\mathbb{E}[v_n(-\xi )]$ for $\xi \in L^{{\varphi }_n^{\ast }}(\mathbb{R})$ by [10, Sect. 5.2]. Define $f:M^{\mathrm{\Phi }}\to \mathbb{R}$ by

$$f(\mathbf{Z}):=\sum _{n=1}^N\mathbb{E}[-u_n(Z^n)]+B=\sum _{n=1}^N{\mathrm{\Theta }}_n(Z^n)+B$$

and observe that

$$\mathcal{A}:=\{\mathbf{Z}\in M^{\mathrm{\Phi }}:\sum _{n=1}^N\mathbb{E}[u_n(Z^n)]\ge B\}=\{\mathbf{Z}\in M^{\mathrm{\Phi }}:f(\mathbf{Z})\le 0\}.$$

We have that $f$ is convex and decreasing with respect to the componentwise order. Let $f^{\ast }(\mathbf{\xi })$ be its convex conjugate for $\mathbf{\xi }\in L^{{\Phi } ^{\ast }}$. We assume that $\xi \not \equiv \mathbf{0}$. By the Fenchel inequality $\mathbb{E}[\mathbf{Z}\xi ]\le f(\mathbf{Z})+f^{\ast }(\xi )$, we obtain for all $\mathbf{Z}\in \mathcal{A}$ and $\lambda >0$ that

$$\mathbb{E}[-\mathbf{Z}\xi ]=\lambda \mathbb{E}[\mathbf{Z}(-\frac{1}{\lambda }\xi \left)\right]\le \lambda [f(\mathbf{Z})+f^{\ast }(-\frac{1}{\lambda }\xi \left)]\le \lambda f^{\ast }\right(-\frac{1}{\lambda }\xi ).$$

Hence

$${\alpha }_B(\xi ):=\underset{\mathbf{Z}\in \mathcal{A}}{sup}\mathbb{E}[-\mathbf{Z}\xi ]\le \underset{\lambda >0}{inf}\lambda f^{\ast }(-\frac{1}{\lambda }\xi ).$$

(A.4)

By the definition of the convex Fenchel conjugate and the fact that $M^{{\Phi } }$ is a product space, we have

$$\begin{array}{rl}{f}^{\ast }(\xi )& :=\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}(\mathbb{E}[\xi \mathbf{Z}]-f(\mathbf{Z}))=-B+\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}(\sum _{n=1}^N\mathbb{E}[{\xi }_n{Z}^n]-\sum _{n=1}^N{\mathrm{\Theta }}_n(Z^n))\\ & \phantom{:}=-B+\sum _{n=1}^N\left(\underset{Z\in M^{\mathrm{\Phi }}(\mathbb{R})}{sup}\right(\mathbb{E}[{\xi }_{n}Z]-{\mathrm{\Theta }}_n(Z)\left)\right)=-B+\sum _{n=1}^N{\mathrm{\Theta }}_n^{\ast }({\xi }_n),\end{array}$$

where we have used (2.2), and therefore

$$\begin{array}{rl}\underset{\lambda >0}{inf}\lambda f^{\ast }(-\frac{1}{\lambda }\xi )& =\underset{\lambda >0}{inf}(-B\lambda +\lambda \sum _{n=1}^N{\mathrm{\Theta }}_n^{\ast }(-\frac{1}{\lambda }{\xi }_n\left)\right)\\ & =\underset{\lambda >0}{inf}(-B\lambda +\lambda \sum _{n=1}^N\mathbb{E}[v_n\left(\frac{1}{\lambda }{\xi }_n\right)\left]\right).\end{array}$$

To prove (3.7), we only need to show that there is no duality gap in (A.4), i.e., if $\alpha _{B}(\mathbf{\xi })<+\infty$, then

$$ \alpha _{B}(\mathbf{\xi })=\inf _{\lambda >0}\lambda f^{\ast }\bigg(-\frac{1}{ \lambda }\mathbf{\xi }\bigg). $$

(A.5)

Observe that by the definition of $f^{\ast }$, we have for each $\lambda >0$ that

$$\lambda f^{\ast }(-\frac{1}{\lambda }\xi ):=\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}(\mathbb{E}[-\xi \mathbf{Z}]-\lambda f(\mathbf{Z})).$$

As $\xi \not \equiv \mathbf{0}$ and $M^{{\Phi } }$ is a linear space, we have ${sup}_{\mathbf{Z}\in M^{\mathrm{\Phi }}}\mathbb{E}[-\xi \mathbf{Z}]=+\mathrm{\infty }$ and therefore

$$\underset{\lambda >0}{inf}\lambda f^{\ast }(-\frac{1}{\lambda }\xi )=\underset{\lambda >0}{inf}\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}(\mathbb{E}[-\xi \mathbf{Z}]-\lambda f(\mathbf{Z}))=\underset{\lambda \ge 0}{inf}\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}(\mathbb{E}[-\xi \mathbf{Z}]-\lambda f(\mathbf{Z})).$$

We claim that

$$\underset{\lambda \ge 0}{inf}\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}(\mathbb{E}[-\xi \mathbf{Z}]-\lambda f(\mathbf{Z}))=\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}\underset{\lambda \ge 0}{inf}(\mathbb{E}[-\xi \mathbf{Z}]-\lambda f(\mathbf{Z})).$$

(A.6)

Assuming (A.6), we may immediately conclude that

$$\begin{array}{rcl}\underset{\lambda >0}{inf}\lambda f^{\ast }(-\frac{1}{\lambda }\xi )& =& \underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}\underset{\lambda \ge 0}{inf}(\mathbb{E}[-\xi \mathbf{Z}]-\lambda f(\mathbf{Z}))\\ & =& \underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{sup}(\mathbb{E}[-\xi \mathbf{Z}]-\underset{\lambda \ge 0}{sup}\lambda f(\mathbf{Z}))=\underset{\mathbf{Z}\in \mathcal{A}}{sup}\mathbb{E}[-\xi \mathbf{Z}]={\alpha }_B(\xi ).\end{array}$$

We now prove (A.6) by showing the equivalent condition

$$\underset{\lambda \ge 0}{sup}\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{inf}(\mathbb{E}[\xi \mathbf{Z}]+\lambda f(\mathbf{Z}))=\underset{\mathbf{Z}\in M^{\mathrm{\Phi }}}{inf}\underset{\lambda \ge 0}{sup}(\mathbb{E}[\xi \mathbf{Z}]+\lambda f(\mathbf{Z})).$$

(A.7)

In order to make an easy comparison with the results from [42] mentioned below, let $f_0(\mathbf{Z}):=\mathbb{E}[\xi \mathbf{Z}]$. Consider the function $F:M^{\mathrm{\Phi }}\times \mathbb{R}\to \mathbb{R}\cup \{+\mathrm{\infty }\}$ defined by

$$ F(\mathbf{Z},u)=\left \{ \textstyle\begin{array}{ll} f_{0}(\mathbf{Z}) & \qquad \text{if }\mathbf{Z}\in M^{{\Phi } }\text{ and }f(\mathbf{Z}) \leq u, \\ +\infty & \qquad \text{otherwise}, \end{array}\displaystyle \right . $$

(see [42, Eq. (2.8)]) and the associated Lagrangian $K(\mathbf{Z},\lambda )$ (see [42, Eq. (4.4)]). Then (A.7) can be rewritten as

$$ \sup _{\lambda \geq 0}\inf _{\mathbf{Z} \in M^{{\Phi } }}K( \mathbf{Z},\lambda )=\inf _{\mathbf{Z} \in M^{{\Phi } }} \sup _{\lambda \geq 0}K(\mathbf{Z},\lambda ). $$

(A.8)

As $f:M^{\mathrm{\Phi }}\to \mathbb{R}$ is convex decreasing and finite-valued, Theorem A.2 guarantees that it is continuous on $M^{{\Phi } }$ (for the $M^{{\Phi } }$-norm). Therefore (see [42, Example 1, pages 7 and 22], the function $F$ is closed and convex in $(\mathbf{Z},u)$. The absence of a duality gap in (A.5) is now expressed by (A.8) and follows from [42, Theorems 17 and 18], provided that the (convex) value function $\phi (u):={inf}_{\mathbf{Z}\in M^{\mathrm{\Phi }}}F(\mathbf{Z},u),u\in \mathbb{R}$, defined in [42, Eq. (4.7)] is bounded from above in a neighbourhood of 0. This is easily verified by showing the existence of an element $\mathbf{Z}_{0}\in M^{{\Phi } }$ such that $u\mapsto F( \mathbf{Z}_{0},u)$ is bounded from above in a neighbourhood of 0. This concludes the proof of (3.7).

To prove (3.8), we set ${\xi }_n:=\frac{d{Q}^n}{d\mathbb{P}}\ge 0$ a.s. From Lemma A.5 below, $v_{n}$ is strictly convex with $v_{n}(+\infty )=+\infty$, $v_{n}(0+)=u_{n}(+\infty )$, $\lim _{z\rightarrow +\infty } \frac{v_{n}(z)}{z}=+\infty$ because of Assumption 2.2, 2) and $v_{n}$ is continuously differentiable. As $u_{n}^{\prime }(+\infty )=0$ and $u_{n}^{\prime }(-\infty )=+\infty$, we get $v_{n}^{\prime }(0)=- \infty$ and $v_{n}^{\prime }(+\infty )=+\infty$. Set $\eta =\frac{1}{ \lambda }\in (0,+\infty )$ and consider the differentiable function $F:(0,+\mathrm{\infty })\to \mathbb{R}$ defined by

$$F(\eta ):=-B\eta +\eta \sum _{n=1}^N\mathbb{E}\left[v_n\left(\frac{1}{\eta }{\xi }_n\right)\right].$$

Then $\alpha _{B}(\mathbf{\xi })=\inf _{\eta >0}F(\eta )$ and (3.9) can be rewritten as

$$ F^{\prime }(\eta )=0 $$

(A.9)

with

$$F^{\prime }(\eta )=-B+\sum _{n=1}^N\mathbb{E}\left[v_n\left(\frac{1}{\eta }{\xi }_n\right)\right]-\frac{1}{\eta }\sum _{n=1}^N\mathbb{E}\left[{\xi }_n{v}_n^{\prime }\left(\frac{1}{\eta }{\xi }_n\right)\right].$$

Note that if $\eta ^{\ast }>0$ is the (unique, see below) solution to (A.9), then inserting $\eta ^{\ast }$ into $F(\eta )$ immediately gives (3.8).

Next, using the integrability conditions provided by Lemma A.4 below, we show the existence of a solution $\eta ^{\ast }>0$ of (A.9). First we consider $\eta \rightarrow +\infty$. Since $\sum _{n=1}^{N}v_{n}(0+)=\sum _{n=1}^{N}u_{n}(+\infty )>B$ by Assumption 2.2, we have

$$\underset{\eta \to +\mathrm{\infty }}{lim\hspace{0.17em}inf}(-B+\sum _{n=1}^N\mathbb{E}[v_n\left(\frac{1}{\eta }{\xi }_n\right)\left]\right)>0.$$

Moreover, $v_{n}^{\prime }(0)=-\infty$ shows that

$$\underset{\eta \to +\mathrm{\infty }}{lim\hspace{0.17em}inf}-\frac{1}{\eta }\sum _{n=1}^N\mathbb{E}\left[{\xi }_n{v}_n^{\prime }\left(\frac{1}{\eta }{\xi }_n\right)\right]\ge 0.$$

Hence $\liminf _{\eta \rightarrow +\infty }F^{\prime }(\eta )>0$. We now look at $\eta \rightarrow 0$ and find

$$\begin{array}{rcl}\underset{\eta \to 0}{lim}{F}^{\prime }(\eta )& =& -B+\underset{\eta \to 0}{lim}\left(\sum _{n=1}^N\mathbb{E}\right[v_n\left(\frac{1}{\eta }{\xi }_n\right)]-\frac{1}{\eta }\sum _{n=1}^N\mathbb{E}[{\xi }_n{v}_n^{\prime }\left(\frac{1}{\eta }{\xi }_n\right)\left]\right)\\ & =& -B+\underset{t\to +\mathrm{\infty }}{lim}(\sum _{n=1}^N\mathbb{E}[v_n(t{\xi }_n)]-t\sum _{n=1}^N\mathbb{E}[{\xi }_n{v}_n^{\prime }(t{\xi }_n)])\\ & =& -B+\sum _{n=1}^N\underset{t\to +\mathrm{\infty }}{lim}\mathbb{E}[v_n(t{\xi }_n)-t{\xi }_n{v}_n^{\prime }(t{\xi }_n)].\end{array}$$

The convexity of $v_{n}$ implies that for any fixed $z_{0}>0$ and $z>z_{0}$,

$$ v_{n}(z)-v_{n}(z_{0})\leq v_{n}^{\prime }(z)(z-z_{0}). $$

From $\lim _{z\rightarrow +\infty }\frac{v(z)}{z}=+\infty$, $v_{n}^{\prime }(z)\rightarrow +\infty$ as $z\rightarrow +\infty$ and

$$ v_{n}(z)-zv_{n}^{\prime }(z)\leq v_{n}(z_{0})-z_{0}v_{n}^{\prime }(z) \downarrow -\infty \qquad \text{as }z\rightarrow +\infty , $$

we have by monotone convergence that

$$\underset{t\to +\mathrm{\infty }}{lim}\mathbb{E}[v_n(t{\xi }_n)-t{\xi }_n{v}_n^{\prime }(t{\xi }_n)]=-\mathrm{\infty },$$

so that $\liminf _{\eta \rightarrow 0}F^{\prime }(\eta )=-\infty$. By the continuity of $F^{\prime }$, we obtain the existence of a solution $\eta ^{\ast }>0$ for (A.9). Uniqueness follows from the strict convexity of $F$. □

Remark A.3

In [42, Theorem 4.106], (A.5) is deduced by different means for univariate risk measures defined on $L^{\infty }$. In [3], (A.5) is obtained by different means in the multi-dimensional deterministic case, i.e., in ${\mathbb{R}}^N$.

1.3 A.3 Auxiliary results for existence

The following auxiliary result is standard and can be found in many articles on utility maximisation; see for example [8, Lemma 18]. Recall that we are working under Assumption 2.2, 4).

Lemma A.4

Let$\upsilon :{\mathbb{R}}_{+}\to \mathbb{R}$be a strictly convex differentiable function satisfying$\upsilon ^{\prime }(0+)=-\infty$, $\upsilon ^{\prime }(+\infty )=+\infty$and let$Q\ll \mathbb{P}$. Then:

(a) ${\upsilon }^{\prime }(\lambda \frac{dQ}{d\mathbb{P}})\in L^1(Q)$for all$\lambda >0$.

(b) Setting$F(\lambda ):=\mathbb{E}[\frac{dQ}{d\mathbb{P}}{\upsilon }^{\prime }(\lambda \frac{dQ}{d\mathbb{P}})]$defines a bijection between$(0,+\infty )$and$(-\infty ,+\infty )$.

By applying the classical convex duality theory for real-valued functions (see [41, Sects. 12 and 26]), we get

Lemma A.5

The convex conjugate function$v:\mathbb{R}\to (-\mathrm{\infty },+\mathrm{\infty }]$of$u$given by$v(y)={sup}_{x\in \mathbb{R}}(u(x)-xy)$is a proper lower semicontinuous convex function, equal to$+\infty$on$(-\infty ,0)$, bounded from below on ℝ, finite-valued, strictly convex, continuously differentiable on$(0,+\infty )$and satisfying

$$\begin{aligned} v(+\infty ) &=+\infty , \qquad v(0+)=u(+\infty ), \qquad v^{\prime }(0+)=-\infty , \qquad v^{\prime }(+\infty )=+\infty , \\ u^{\prime }(x) &=(v^{\prime })^{-1}(-x), \qquad u\big(-v^{\prime }(y)\big)=-yv^{\prime }(y)+v(y),\quad \forall y \geq 0, \end{aligned}$$

where the usual rule$0\cdot \infty =0$is applied.

Proposition A.6

(Biagini et al. [11, Proposition 3.6])

Let$Q\ll \mathbb{P}$. For all$c\in \mathbb{R}$, the optimiser$\lambda (c;Q)$of

$$\underset{\lambda >0}{min}\left(\mathbb{E}\right[v\left(\lambda \frac{dQ}{d\mathbb{P}}\right)]+\lambda c)$$

is the unique positive solution of the first order condition

$${\mathbb{E}}_Q\left[v^{\prime }\left(\lambda \frac{dQ}{d\mathbb{P}}\right)\right]+c=0.$$

If$sup\{\mathbb{E}[u(g)]:g\in L^1(Q)\mathit{\text{ and }}{\mathbb{E}}_Q[g]\le c\}<u(+\mathrm{\infty })$, then the random variable$\hat{g}:=-v^{\prime }(\lambda (c;Q)\frac{dQ}{d\mathbb{P}})$belongs to the set$\{g\in L^1(Q):{\mathbb{E}}_Q[g]=c\}$and satisfies$u(\hat{g})\in L^1(\mathbb{P})$and

$$\begin{array}{rl}\underset{\lambda >0}{min}\left(\mathbb{E}\right[v\left(\lambda \frac{dQ}{d\mathbb{P}}\right)]+\lambda c)& =sup\{\mathbb{E}[u(g)]:g\in L^1(Q)\mathit{\text{ and }}{\mathbb{E}}_Q[g]\le c\}\\ & =\mathbb{E}[u(\hat{g})]<u(+\mathrm{\infty }).\end{array}$$

1.4 A.4 Proofs for Sect. 4.2

Proof of Proposition 4.4

From $M^{{\varphi }_n}\subseteq L^1(\mathbb{P},Q^n)\subseteq L^1(Q^n)$, we clearly have $U_{n}(a^{n})\leq \widetilde{U}_{n}(a^{n})\leq \widehat{U}_{n}(a^{n}) \leq u_{n}(+\infty )$ so that

$$ \text{if $U_{n}(a^{n})=u(+\infty )$, then $U_{n}(a^{n})=\widetilde{U} _{n}(a^{n})=\widehat{U}_{n}(a^{n})=u_{n}(+\infty )$.} $$

(A.10)

By the Fenchel inequality, we get

$$\mathbb{E}[u_n(X^n+W)]\le \lambda ({\mathbb{E}}_{Q^n}[X^n]+{\mathbb{E}}_{Q^n}[W])+\mathbb{E}\left[v_n\left(\lambda \frac{d{Q}^n}{dP}\right)\right]$$

and hence

$$\begin{array}{rl}{U}_n(a^n)& \le {\tilde{U}}_n(a^n)\le {\hat{U}}_n(a^n)\\ & \le \underset{\lambda >0}{inf}(\lambda ({\mathbb{E}}_{Q^n}[X^n]+a^n)+\mathbb{E}[v_n\left(\lambda \frac{d{Q}^n}{dP}\right)\left]\right)<+\mathrm{\infty }\end{array}$$

(A.11)

as $\mathbb{E}[v_n(\lambda \frac{d{Q}^n}{dP})]<+\mathrm{\infty }$. Therefore (4.4) is a consequence of (A.10) and (4.6).

To show (4.6), we consider the integral functional $I:M^{{\varphi }_n}\to \mathbb{R}$ defined by $I(X^n)=\mathbb{E}[u_n(X^n)]$. It is finite-valued, monotone increasing and concave on $M^{\phi _{n}}$ (as $\mathbb{E}[u_n(X^n)]\le u_n(\mathbb{E}[X^n])<+\mathrm{\infty })$, and therefore by Theorem A.2, it is norm-continuous on $M^{\phi _{n}}$. We can then follow the well-known duality approach (see for example [11]), as follows.

Consider the convex cone $D^0:=\{W\in M^{{\varphi }_n}:{\mathbb{E}}_{Q^n}[W]\le 0\}$ which is the polar cone of the one-dimensional cone $D:=\{ \lambda \frac{dQ^{n}}{dP}: \lambda \geq 0\}$, so that the bipolar $D^{00}$ coincides with $D$. Let ${\delta }_{D^0}:M^{{\varphi }_n}\to \mathbb{R}\cup \{+\mathrm{\infty }\}$ be the support functional of $D^{0}$. By Kozek [38], or directly by hand, the concave conjugate $I^{\ast }:L^{{\varphi }_n^{\ast }}\to \mathbb{R}\cup \{-\mathrm{\infty }\}$ is given by $I^{\ast }({\xi }^n)=\mathbb{E}[-v_n({\xi }^n)]$, and so by the Fenchel duality theorem,

$$\begin{array}{rcl}{U}_n(a^n)& =& \underset{W\in D^0}{sup}\mathbb{E}[u_n(X^n+a^n+W)]=\underset{Z\in D^0+X^n+a^n}{sup}\mathbb{E}[u_n(Z)]\\ & =& \underset{Z\in M^{{\varphi }_n}}{sup}(\mathbb{E}[u_n(Z)]-{\delta }_{D^0+X^n+a^n}(Z))\\ & =& \underset{{\xi }^n\in L^{{\varphi }_n^{\ast }}}{min}({\delta }_{D^0+X^n+a^n}^{\ast }({\xi }^n)-\mathbb{E}[-v_n({\xi }^n)])\\ & =& \underset{{\xi }^n\in L^{{\varphi }_n^{\ast }}}{min}(\mathbb{E}[{\xi }^n(X^n+a^n)]+{\delta }_{D^{00}}({\xi }^n)+\mathbb{E}[v_n({\xi }^n)])\\ & =& \underset{{\xi }^n\in D^{00}}{min}(\mathbb{E}[{\xi }^n(X^n+a^n)]+\mathbb{E}[v_n({\xi }^n)])\\ & =& \underset{\lambda >0}{min}(\lambda ({\mathbb{E}}_{Q^n}[X^n]+a^n)+\mathbb{E}[v_n\left(\lambda \frac{d{Q}^n}{dP}\right)\left]\right),\end{array}$$

where we used $\delta _{D^{0}}^{\ast }=\delta _{D^{00}}$, $D^{00}=D$ and the fact that the minimum is obtained at $\lambda > 0$. The last fact follows because if $\lambda =0$, then $U_n(a^n)=\mathbb{E}[v_n(0)]=u_n(+\mathrm{\infty })$, in contradiction to the assumption. We complete the proof by showing (4.5). From the inequality (A.11), it is clear that $U_{n}(-\infty )=-\infty$. Define

$$V_n(\lambda ):=\mathbb{E}\left[v_n\left(\lambda \frac{d{Q}_n}{d\mathbb{P}}\right)\right]+\lambda {\mathbb{E}}_{Q_n}[X^n].$$

When $U_{n}(a^{n})< u_{n}(+\infty )$, we have $U_{n}(a^{n})= \inf _{\lambda >0}( V_{n}(\lambda )+\lambda a^{n})$ from (4.6), which shows that $U_{n}$ and $V_{n}$ are conjugate to each other, i.e., we have

$$ V_{n}(\lambda )=\sup _{a^{n}>0}\big( U_{n}(a^{n})-\lambda a^{n}\big). $$

From Lemmas A.4 and A.5, we know that the convex function $V_{n}$ is differentiable on $(0,+\infty )$ and so $U_{n}$ is differentiable on $(-\infty ,+\infty )$ and $U_{n}^{\prime }(a)=(V _{n}^{\prime })^{-1}(-a)>0$.

We only need to show that $U_{n}^{\prime }(+\infty )=0$ and $U_{n}^{\prime }(-\infty )=+\infty$. We have $V_{n}(0+)=+\infty$ because $v_{n}(0+)=u_{n}(+\infty )=+\infty$. Since $v_{n}^{\prime }(0+)=- \infty$, we get $V_{n}^{\prime }(0+)=-\infty$ and $U_{n}^{\prime }(+ \infty )=0$. Moreover, by Jensen’s inequality,

$$\begin{array}{rl}{V}_n^{\prime }(+\mathrm{\infty })& =\underset{\lambda \to +\mathrm{\infty }}{lim}\frac{V_n(\lambda )}{\lambda }=\underset{\lambda \to +\mathrm{\infty }}{lim}\frac{1}{\lambda }\mathbb{E}\left[v_n\left(\lambda \frac{d{Q}_n}{d\mathbb{P}}\right)\right]+{\mathbb{E}}_{Q_n}[X^n]\\ & \ge \underset{\lambda \to +\mathrm{\infty }}{lim}\frac{1}{\lambda }{v}_n\left(\lambda \right)+{\mathbb{E}}_{Q_n}[X^n]=v_n^{\prime }(+\mathrm{\infty })+{\mathbb{E}}_{Q_n}[X^n]=+\mathrm{\infty },\end{array}$$

which implies $U_{n}^{\prime }(-\infty )=+\infty$. □

Proof of Lemma 4.7

The set $K$ is clearly closed. We show that it is bounded. For $N=1$, this is true. Let $N>1$. First we prove that for all $j=1,\dots ,N$,

$$ U_{j}(a)\bigg( 1+\frac{\sum _{n\neq j}U_{n}(A-(N-1)a)}{U_{j}(a)}\bigg) \longrightarrow -\infty \qquad \text{as }a\downarrow -\infty . $$

(A.12)

Recall that $U_{n}(-\infty )=-\infty$ and $U_{n}(+\infty )\leq u_{n}(+ \infty )$ for all $n$. Suppose that for some $k\in \{1,\dots ,N\}$, we have $u_{k}(+\infty )<+\infty$. Then $U_{k}(+\infty )<+\infty$ and for all $j=1,\dots ,N$,

$$ \lim _{a\rightarrow -\infty } \frac{U_{k}(A-(N-1)a)}{U_{j}(a)} =0. $$

(A.13)

Now suppose that for some $k\in \{1,\dots ,N\}$, we have $u_{k}(+ \infty )=+\infty$. Then Proposition 4.4 shows that $U_{k}(a^{k})<+\infty =u_{k}(+\infty )$, $U_{k}^{\prime }>0$, $U_{k}^{\prime }(-\infty )=+\infty$ and $U_{k}^{\prime }(+\infty )=0$. By l’Hôpital’s rule, we obtain again for all $j=1,\dots ,N$ that

$$ \lim _{a\rightarrow -\infty } \frac{U_{k}(A-(N-1)a)}{U_{j}(a)} = \lim _{a\rightarrow -\infty }\frac{-(N-1)U_{k}^{\prime }(A-(N-1)a)}{U _{j}^{\prime }(a)}=0. $$

(A.14)

From (A.13) and (A.14), we deduce that (A.12) holds true.

We conclude that for any constant $B$, there exists a constant $R$ such that for all $j=1,\dots ,N$ and $a< R$, we have

$$ U_{j}(a)\bigg( 1+\frac{\sum _{n\neq j}U_{n}(A-(N-1)a)}{U_{j}(a)}\bigg) < B. $$

Let $\mathbf{a}\in K$ and take $i$ with $a^{i}=\min \{a^{1},\dots ,a ^{N}\}$. Note that for all $j=1,\dots ,N$, we have $a^{j}\leq A-(N-1)a^{i}$ because $\sum _{n=1}^{N}a^{n}\leq A$. Assume that $a^{i}< R$. Then

$$ B\leq \sum _{n=1}^{N}U_{n}(a^{n})\leq U_{i}(a^{i})\bigg( 1+\frac{ \sum _{n\neq i}U_{n}(A-(N-1)a^{i})}{U_{i}(a^{i})}\bigg) $$

which is a contradiction. Therefore $a^{j}\geq R$ for all $j=1,\dots ,N$, and then also $a^{j}\leq A-(N-1)R$ for all $j=1,\dots ,N$ because $\sum _{n=1}^{N}a^{n}\leq A$. This proves the claim. □

Let $\mathbf{X}\in M^{{\Phi } }$ and consider the function $F(\delta ):=\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n-\delta )]$ with $\delta \in \mathbb{R}$. If $\mathbf{Y}\in M^{{\Phi } }$, then $F$ is finite-valued and concave on ℝ, hence continuous on ℝ (see the discussion at the beginning of Sect. 4.2). However, when $\mathbf{Y}\in L^{1}(\mathbf{Q})$ satisfies $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n)]>B$ (with the understanding that $u_n(X^n+Y^n)\in L^1(\mathbb{P})$ for each $n$), it is not any more evident if $F$ is continuous on ℝ as one has to guarantee that $\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Y^n-\delta )]>-\mathrm{\infty }$ for $\delta >0$.

Lemma A.7

If$\mathbf{X}\in M^{{\Phi } }$and$\mathbf{Z}\in L^{1}( \mathbf{Q})$satisfy$\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Z^n)]>B$, then there exists$\widetilde{\mathbf{Z}}\in L^{1}(\mathbf{Q})$which satisfies${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[{\tilde{Z}}^n]<{\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Z^n]$and$\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+{\tilde{Z}}^n)]=B$.

Proof

Set $A_{n}:=\{ X^{n}+Z^{n}>k_{n}\}$ and let $k_n\in \mathbb{R}$ satisfy $\mathbb{P}[A_n]>0$ and $Q^{n}[A_{n}]>0$. For any $\delta >0$, consider the random variable $\widetilde{\mathbf{Z}}\in L^{1}( \mathbf{Q})$ with $\widetilde{Z}^{n}:=Z^{n}-\delta 1_{A_{n}}$ and define $G(\delta ):=\mathbb{E}[{\sum }_{n=1}^N{u}_n(X^n+Z^n-\delta 1_{A_n})]$. Then

$$\begin{array}{rl}G(\delta )& =\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Z^n)1_{A_n^c}]+\mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Z^n-\delta )1_{A_n}]\\ & \ge \mathbb{E}[\sum _{n=1}^N{u}_n(X^n+Z^n)1_{A_n^c}]+\mathbb{E}[\sum _{n=1}^N{u}_n(k_n-\delta )1_{A_n}]>-\mathrm{\infty },\end{array}$$

which implies that $G$ is continuous on ${\mathbb{R}}_{+}$ and the result follows. □

Proof of Lemma 4.8

From (3.5) and $\rho _{B}^{ \mathbf{Q}}(\mathbf{X})=\widetilde{\rho }_{B}^{\mathbf{Q}}(\mathbf{X})$, note that the penalty function can also be written as

$$\begin{array}{rcl}{\alpha }_B(\mathbf{Q})& =& -\sum _{n=1}^N{\mathbb{E}}_{Q^n}[X^n]-{\rho }_B^{\mathbf{Q}}(\mathbf{X})=-\sum _{n=1}^N{\mathbb{E}}_{Q^n}[X^n]-{\tilde{\rho }}_B^{\mathbf{Q}}(\mathbf{X})\\ & =& sup\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[-Z^n]:\mathbf{Z}\in L^1(\mathbb{P},\mathbf{Q}),\mathbb{E}[\mathrm{\Lambda }(\mathbf{Z})]\ge B\},\end{array}$$

for $\Lambda$ from (1.3). Set

$$c^{=}(\mathbf{Q}):=inf\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Z^n]:\mathbf{Z}\in L^1(\mathbb{P},\mathbf{Q}),\mathbb{E}[\mathrm{\Lambda }(\mathbf{Z})]=B\}.$$

Similarly to the proof of (A.3), we show that

$$\mathbf{Z}\in L^1(\mathbb{P},\mathbf{Q})\text{ and }\mathbb{E}[\mathrm{\Lambda }(\mathbf{Z})]>B⟹\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Z^n]>c^{=}(\mathbf{Q}).$$

(A.15)

Indeed, Lemma A.7 implies the existence of $\tilde{\mathbf{Z}}\in L^1(\mathbb{P},\mathbf{Q})$ satisfying $\mathbb{E}[\mathrm{\Lambda }(\tilde{\mathbf{Z}})]=B$ and ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[{\tilde{Z}}^n]<{\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Z^n]$, and therefore we have

$$c^{=}(\mathbf{Q})\le \sum _{n=1}^N{\mathbb{E}}_{Q^n}[{\tilde{Z}}^n]<\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Z^n].$$

It follows that

$$c(\mathbf{Q}):=-{\alpha }_B(\mathbf{Q})=inf\{\sum _{n=1}^N{\mathbb{E}}_{Q^n}[Z^n]:\mathbf{Z}\in L^1(\mathbb{P},\mathbf{Q}),\mathbb{E}[\mathrm{\Lambda }(\mathbf{Z})]\ge B\}=c^{=}(\mathbf{Q}).$$

Indeed, $-\infty < c(\mathbf{Q})\leq c^{=}(\mathbf{Q)}$; so assume $c(\mathbf{Q})< c^{=}(\mathbf{Q)}$. By the definition of $c(\mathbf{Q})$, there exist $\varepsilon >0$ and $\mathbf{Z}\in L^1(\mathbb{P},\mathbf{Q})$ with ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Z^n]\le c(\mathbf{Q})+\epsilon <c^{=}(\mathbf{Q})$ and $\mathbb{E}[\mathrm{\Lambda }(\mathbf{Z})]>B$, which contradicts (A.15).

Finally, uniqueness follows from an argument similar to the one applied at the end of the proof of Proposition 2.4, replacing $\sum _{n=1}^{N}Y^{n}$ with ${\sum }_{n=1}^N{\mathbb{E}}_{Q^n}[Y^n]$. □