Trading strategies generated pathwise by functions of market weights

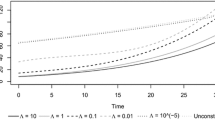
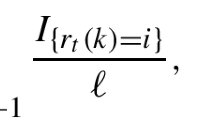Abstract

Twenty years ago, E.R. Fernholz introduced the notion of “functional generation” to construct a variety of portfolios solely in terms of the individual companies’ market weights. I. Karatzas and J. Ruf recently developed another approach to the functional construction of portfolios which leads to very simple conditions for strong relative arbitrage with respect to the market. Here, both of these notions are generalized in a pathwise, probability-free setting; portfolio-generating functions, possibly less smooth than twice differentiable, involve the current market weights as well as additional bounded-variation functionals of past and present market weights. This leads to a wider class of functionally generated portfolios than was heretofore possible to analyze, to novel methods for dealing with the “size” and “momentum” effects, and to improved conditions for outperforming the market portfolio over suitable time horizons.

Appendix: Proofs

Proof of Proposition 3.9

We follow the argument in [14, Proposition 4.8], using the pathwise Itô formula instead of the standard Itô formula for semimartingales. With

$$ K(t) := \exp \bigg(\int _{0}^{t} \frac{d\Gamma ^{G}(s)}{G(\mu (s), A(s))}\bigg) $$

(A.1)

in (3.23), the pathwise Itô formula (Proposition 2.2) yields

$$\begin{aligned} G\big(\mu (t), A(t)\big)K(t) &= G\big(\mu (0), A(0)\big)K(0) +\int _{0}^{t}\sum _{i=1}^{d}\partial _{i}G\big(\mu (s), A(s)\big)K(s)d\mu _{i}(s) \\ & \phantom{=:}+\int _{0}^{t}K(s)d\Gamma ^{G}(s) +\int _{0}^{t}\sum _{i=0} ^{m}D_{i}G\big(\mu (s), A(s)\big)K(s)dA_{i}(s) \\ & \phantom{=:}+\frac{1}{2}\int _{0}^{t}\sum _{i=1}^{d}\sum _{j=1}^{d} \partial _{i, j}^{2}G\big(\mu (s), A(s)\big)K(s)d[\mu _{i}, \mu _{j}](s) \\ &=G\big(\mu (0), A(0)\big)K(0) + \int _{0}^{t}\sum _{i=1}^{d}\partial _{i}G\big(\mu (s), A(s)\big)K(s)d\mu _{i}(s) \\ &=G\big(\mu (0), A(0)\big)K(0) + \int _{0}^{t}\sum _{i=1}^{d}\eta _{i}(s)d \mu _{i}(s) \\ &=G\big(\mu (0), A(0)\big)K(0) + \int _{0}^{t}\sum _{i=1}^{d}\psi _{i}(s)d \mu _{i}(s). \end{aligned}$$

Here, the second equality uses the expression in (3.4) and the last equality relies on [14, Proposition 2.3]. Since (3.23) holds at time zero, it follows that (3.23) holds at any time $t \in [0, T]$. The justification for (3.24) is exactly the same as that of [14, Proposition 4.8]. □

Proof of Theorem 3.10

For any absolutely continuous function $f$ with a right-continuous Radon–Nikodým derivative $f'$ of finite variation and any two real numbers $a$ and $b$, applying integration by parts with the notation (2.3) gives

(A.2)

We then recall (3.5), (3.6), (A.1) and consider the telescoping expansion

$$\begin{aligned} &G\big(\mu (t), A(t)\big)K(t) - G\big(\mu (0), A(0)\big)K(0) \\ &=\sum _{i=1}^{d} \sum _{{\scriptstyle t_{j} \in \mathbb{T}_{n} \atop\scriptstyle t_{j} \leq t}} \Big( f _{i}\big(X_{i}(t_{j+1})\big)K(t_{j+1}) - f_{i}\big(X_{i}(t_{j})\big)K(t _{j}) \Big) \\ &=\sum _{i=1}^{d} \sum _{{\scriptstyle t_{j} \in \mathbb{T}_{n} \atop\scriptstyle t_{j} \leq t}} f_{i} \big(X_{i}(t_{j+1})\big)\big(K(t_{j+1})-K(t_{j})\big) \end{aligned}$$

(A.3)

$$\begin{aligned} & \phantom{=:}+\sum _{i=1}^{d} \sum _{{\scriptstyle t_{j} \in \mathbb{T}_{n} \atop\scriptstyle t_{j} \leq t}} \Big( f _{i}\big(X_{i}(t_{j+1})\big) - f_{i}\big(X_{i}(t_{j})\big) \Big) K(t _{j}) . \end{aligned}$$

(A.4)

Then we further expand the last double sum (A.4) as

(A.5)

$$\begin{aligned} & \phantom{=:} -\sum _{i=1}^{d} \sum _{{\scriptstyle t_{j} \in \mathbb{T}_{n} \atop\scriptstyle t_{j} \leq t}} f'_{i}\big(X_{i}(t_{j})\big)K(t_{j}) \big(A_{i}(t_{j+1}) - A _{i}(t_{j})\big) \end{aligned}$$

(A.6)

$$\begin{aligned} & \phantom{=:} +\sum _{i=1}^{d} \sum _{{\scriptstyle t_{j} \in \mathbb{T}_{n} \atop\scriptstyle t_{j} \leq t}} K(t_{j}) \int _{\mathbb{R}} \big(L^{X_{i}, \mathbb{T}_{n}} _{t_{j+1}}(x)-L^{X_{i}, \mathbb{T}_{n}}_{t_{j}}(x)\big) df'_{i}(x), \end{aligned}$$

(A.7)

where the first equation is from (A.2), and the second follows from (3.5) and (2.4).

Next, we show that the sum of (A.3), (A.6) and (A.7) vanishes as $n \rightarrow \infty$. First, since $\lim _{n \rightarrow \infty } \Vert {\mathbb{T}}_{n}\Vert =0$, the limit of (A.3) is a Lebesgue–Stieltjes integral

$$ \sum _{i=1}^{d} \int _{0}^{t} f_{i}\big(X_{i}(s)\big)dK(s) = \int _{0} ^{t} G\big(\mu (s), A(s)\big)dK(s), $$

because $f_{i}(X_{i}(\cdot ))$ is bounded on the compact interval $[0, T]$ for each $i=1, \dots , d$. From (3.11), the change-of-variable formula for Lebesgue–Stieltjes integrals gives

$$\begin{aligned} \int _{0}^{t} G\big(\mu (s), A(s)\big)dK(s) = \int _{0}^{t} K(s)d\Gamma ^{G}(s) = \int _{0}^{t} K(s) \big( d\Gamma _{1}^{G}(s) - d\Gamma _{2} ^{G}(s) \big), \end{aligned}$$

(A.8)

where

$$ \Gamma ^{G}_{1}(t) := \sum _{i=1}^{d} \int _{0}^{t} \vartheta _{i}(s)dA _{i}(s), \qquad \Gamma ^{G}_{2}(t) := \sum _{i=1}^{d} \int _{\mathbb{R}} L_{t}^{X_{i}}(x)df'_{i}(x). $$

It follows that the limit of (A.6) is $-\sum _{i=1}^{d} \int _{0}^{t} K(s)\vartheta _{i}(s)dA_{i}(s)$. On the other hand, the last integral of (A.8) can be expressed as the limit

$$\begin{aligned} \int _{0}^{t} K(s)d\Gamma _{2}^{G}(s) &= \lim _{n \rightarrow \infty } \sum _{{\scriptstyle t_{j} \in \mathbb{T}_{n} \atop\scriptstyle t_{j} \leq t}} K(t_{j}) \big( \Gamma _{2}^{G}(t_{j+1}) - \Gamma _{2}^{G}(t_{j}) \big) \\ &=\lim _{n \rightarrow \infty } \sum _{i=1}^{d} \sum _{{\scriptstyle t_{j} \in \mathbb{T}_{n} \atop\scriptstyle t_{j} \leq t}} K(t_{j}) \int _{\mathbb{R}} \big(L_{t_{j+1}}^{X_{i}}(x)-L_{t_{j}}^{X_{i}}(x) \big) df'_{i}(x), \end{aligned}$$

which coincides with the limit of (A.7). Therefore, the limits of (A.3), (A.6) and (A.7) are zero, whereas the remaining term of (A.4) is (A.5), whose limit we denote as

$$ \sum _{i=1}^{d} \int _{0}^{t} f'_{i}\big(X_{i}(s)\big)K(s) d\mu _{i}(s) = \sum _{i=1}^{d} \int _{0}^{t} \eta _{i}(s) d\mu _{i}(s), $$

from (3.6) and (3.21). We obtain in this way that

$$\begin{aligned} G\big(\mu (t), A(t)\big)K(t) - G\big(\mu (0), A(0)\big)K(0) &= \sum _{i=1}^{d} \int _{0}^{t} \eta _{i}(s) d\mu _{i}(s) \\ &=\sum _{i=1}^{d} \int _{0}^{t} \psi _{i}(s) d\mu _{i}(s), \end{aligned}$$

where the last equality follows from $\sum _{i=1}^{d} \mu _{i}(\cdot ) \equiv 1$ and (3.22). The result (3.23) then follows from the self-financibility of $\psi$ and the relationship

$$ V^{\psi }(0) = \sum _{i=1}^{d} \psi _{i}(0)\mu _{i}(0) = \sum _{i=1}^{d} \big(\vartheta _{i}(0)-C(0)\big) \mu _{i}(0) = G\big(\mu (0), A(0) \big)K(0). $$

Finally, (3.24) can be justified in the same manner as Proposition 3.9. □