1 Introduction

An increasing number of traditionally qualitative scientific disciplines are becoming quantitative, including systems biology (e.g. Pokhilko et al. 2013), ecology (e.g. Ovaskainen et al. 2016), personalised medicine (e.g. Gao et al. 2017) and the social sciences (e.g. Thai et al. 2017), with models and hypotheses formulated in terms of systems of coupled ordinary differential equations (ODEs). The equations typically depend on parameters that cannot be directly measured, but rather have to be inferred on the basis of observations or measurements at the systems level. This places formidable challenges on statistical inference. Since non-linear ODEs typically do not have closed-form solutions, a numerical integration is required every time the model parameters are changed. This would not be a problem if a closed-form solution of the likelihood equation were available. However, likelihood landscapes of complex non-linear systems are typically multimodal, which calls for an iterative global optimization scheme (in a maximum likelihood context) or a Markov chain Monte Carlo sampling scheme (in a Bayesian context). Since each of these individual adaptation steps is now associated with the computational costs of a numerical integration, the overall computational complexity can be become excessive.

A way to circumvent the high computational complexity of explicitly solving the ODEs is the method of gradient matching; see the Introduction section of Niu et al. (2017) for a comprehensive review. The idea is to interpolate the time series data, then optimize the ODE parameters so as to minimize some metric measuring the difference between the slopes of the tangents to the interpolants, and the parameter-dependent time derivatives from the ODEs. In this way, the ODEs never have to be solved explicitly, and the typically unknown initial conditions are effectively profiled over. A disadvantage of this two-step scheme is that the results of parameter inference may critically hinge on the quality of the initial interpolant, which is particularly a problem if the interpolant is subject to overfitting. A way to address this issue is to regularize the interpolants by the ODEs themselves, as first suggested by Ramsay et al. (2007).

Various methods have subsequently been proposed in the statistics and machine learning literature, based on P-splines (Liang and Wu 2008), parallel tempering (Campbell and Steele 2012), Gaussian processes (Dondelinger et al. 2013; Calderhead et al. 2009; Barber and Wang 2014; Macdonald et al. 2015), and reproducing kernel Hilbert spaces (RKHS, see González et al. 2013, 2014). The latter approach has been implemented in software by Vujacic et al. (2015) in the R package odest. Whilst being computationally efficient, a shortcoming of this method is that it has been designed for linear ODEs, and requires a series of heuristic approximations for extension to nonlinear ODEs. This limitation has been overcome in the more recent methods of Niu et al. (2016) and Niu et al. (2017). Pfister et al. (2018) developed the episode R package that implements an adaptive integral-matching algorithm for learning polynomial or rational ODEs with a sparse network structure. King et al. (2015) developed the pomp R package for statistical inference in partially observed and stochastic systems for which the likelihood is intractable.

The present article describes a recently developed software package for inference in systems described by differential equations, which can have an arbitrarily non-linear structure (addressing the limitation of odest), are not required to be sparse (as opposed to episode), and not of the form of partially observed Markov processes (as opposed to pomp). It implements the gradient matching method proposed in Niu et al. (2016, (2017). This method is based on the framework of reproducing kernel Hilbert spaces (RKHS), which combines nonlinear-model flexibility and robust regularization to prevent overfitting. Three standard regularization methods are included: a standard general-purpose approach from the theory of RKHS, an approach based on nonlinear time-warping, and a method that specifically includes the ODEs in the regularization framework. All the methods are illustrated on a set of sparse and noisy time series generated from standard benchmark ODE models, and their pros and cons in terms of an accuracy versus efficiency trade-off are discussed. The software package, called KGode, is available from the comprehensive R archive network (CRAN).

2 Method

2.1 Dynamical systems

Consider a dynamical system comprising r interacting states \(x_s, 1\le s\le r\), the time evolution of which is governed by coupled non-linear ordinary differential equations (ODEs):

$$\begin{aligned} \dot{{\textit{\textbf{x}}}}=\frac{d {\textit{\textbf{x}}}}{d t}= {\textit{\textbf{f}}}\left( {\textit{\textbf{x}}}(t),{\varvec{\theta }} \right) ', \end{aligned}$$
(1)

where \({\textit{\textbf{x}}}=(x_1,\ldots ,x_r)'\) is a time-dependent vector of state variables, and \({\varvec{\theta }}\) a vector of unknown parameters. Without loss of generality we will assume fixed initial conditions \({\textit{\textbf{x}}}_0\). If these are unknown they can be integrated into the set of parameters \({\varvec{\theta }}\). We assume that we observe time series of n noisy observations \({\textit{\textbf{y}}}_s=(y_{s1},\ldots ,y_{sn})'\) for each of the states \({\textit{\textbf{x}}}_s=(x_{s1},\ldots ,x_{sn})'\), subject to iid additive Gaussian noise \({\varvec{\epsilon }}_{k} \sim N(0, \sigma ^2{\textit{\textbf{I}}})\):

$$\begin{aligned} {\textit{\textbf{y}}}_{s} = {\textit{\textbf{x}}}_{s} + {\varvec{\epsilon }}_{s} \end{aligned}$$
(2)

and the objective of inference is to learn \({\varvec{\theta }}\) from the noisy measurements \({\textit{\textbf{y}}}\).

2.2 Standard gradient matching

Let \({\mathcal {H}}\) be a Hilbert space of real functions g defined on an index set \({\mathbb {D}} \subset {\mathbb {R}}^m\). Then \({\mathcal {H}}\) is called a Reproducing Kernel Hilbert Space (RKHS) endowed with an inner product \(<.,.>\) if and only if there exists a function \(k(\cdot ,\cdot ): {\mathbb {D}} \times {\mathbb {D}} \rightarrow {\mathbb {R}}\) such that for all \(t \in {\mathbb {D}}\) and all \(g \in {\mathcal {H}}\) the inner product \(<g( \cdot ), k(t,\cdot )>\) is equal to g(t) and the kernel function \(k(t,\cdot )\) is in \({\mathcal {H}} \) (Aronszajn 1950). When adopting an RKHS approach for function estimation, functions are expressed as a linear combination of kernel functions evaluated at the data points

$$\begin{aligned} g(t) = \sum _{i=1}^n b_i k(t, t_i) \end{aligned}$$
(3)

with \(b_i \in {\mathbb {R}}\) and \(t_i \in {\mathbb {D}}\). Many standard kernel functions exist including the squared exponential or radial basis function (RBF) kernel, the spline kernel, and the multi-layer perceptron (MLP) kernel (see e.g. Bishop 2006, chapter 6). The kernel parameters can be denoted as \({\varvec{\varphi }}\).

In this framework, the unknown state variables in Eq. (1) for the sth component of the dynamical system at time t can be modelled as

$$\begin{aligned} g_s(t;{\textit{\textbf{b}}}_s) \; =\; \sum _{i=1}^{n}b_{si} k(t,t_i) \end{aligned}$$
(4)

with derivatives

$$\begin{aligned} {\dot{g}}_s(t;{\textit{\textbf{b}}}_s)= & {} \frac{\partial g_s(t;{\textit{\textbf{b}}}_s)}{\partial t} \; = \; \sum _{i=1}^{n} b_{si} \frac{\partial k(t,t_i)}{\partial t} \; = \; \sum _{i=1}^{n} b_{si} {\dot{k}}(t,t_i), \end{aligned}$$
(5)

where \({\textit{\textbf{b}}}_s\) is the vector of kernel regression coefficients \(b_{si}\). We denote by \({\textit{\textbf{B}}}\) the matrix of all regression parameter vectors, for all ODE state variables: \({\textit{\textbf{B}}}= ({\textit{\textbf{b}}}_1,\ldots ,{\textit{\textbf{b}}}_r)\). Following standard kernel ridge regression, smooth interpolants \(g_s(t)\) are obtained by minimizing the following regularized loss function:

$$\begin{aligned} {\mathcal {L}}({\textit{\textbf{b}}}_s,{\varvec{\varphi }}_s;\lambda _s) = \sum _{i=1}^{n} \Big ( g_s( t_{i};{\textit{\textbf{b}}}_s) - y_{s}(t_i) \Big )^2 + \lambda _s||{\textit{\textbf{q}}}_s||^2 \end{aligned}$$
(6)

where \({\varvec{\varphi }}_s\) denotes the vector of hyperparameters of the kernel function (e.g. the length scale(s) of an RBF kernel),Footnote 1\(\lambda _s\ge 0\) is a regularization parameter, and the regularization term \(||{\textit{\textbf{q}}}_s||^2\) is the squared norm of \({\mathcal {H}}_s\):

$$\begin{aligned} ||{\textit{\textbf{q}}}_s||^2 = {\textit{\textbf{b}}}^T_s {\textit{\textbf{K}}}_s {\textit{\textbf{b}}}_s \end{aligned}$$
(7)

where \({\textit{\textbf{K}}}_s\) is the Gram matrix,

$$\begin{aligned} {\textit{\textbf{K}}}_s \; = \; \left( \begin{array}{ccc} k(t_1,t_1) &{} \ldots &{} k(t_1,t_n)\\ \ldots &{} \ldots &{} \ldots \\ k(t_n,t_1) &{} \ldots &{} k(t_n,t_n)\\ \end{array} \right) \end{aligned}$$
(8)

The minimization of \({\mathcal {L}}({\textit{\textbf{b}}}_s,{\varvec{\varphi }}_s;\lambda _s)\) with respect to \({\textit{\textbf{b}}}_s\) for given \({\varvec{\varphi }}_s\) and \(\lambda _s\) is a convex optimization problem with solution

$$\begin{aligned} {\textit{\textbf{b}}}_s = ({\textit{\textbf{K}}}_s+ \lambda _s {\textit{\textbf{I}}} )^{-1} {\textit{\textbf{y}}}_s. \end{aligned}$$
(9)

Given \(\lambda _s\), the kernel hyper-parameters \({\varvec{\varphi }}_s\) are optimized independently by minimizing the loss function in Eq. (6) with a standard optimization routine, such as trust region or quasi-Newton. The regularization parameters \(\lambda _s\) are estimated using 10-fold cross validation.

Finally, the ODE parameters \({\varvec{\theta }}\) can be estimated by minimizing the difference between \(\dot{{\textit{\textbf{g}}}}(t_i)\) and the gradient predicted from the ODEs, \({\textit{\textbf{f}}}( {\textit{\textbf{g}}}(t_i),{\varvec{\theta }})\), using the following loss function:

$$\begin{aligned} L({\varvec{\theta }}) \; = \; \sum _{s=1}^r \sum _{i=1}^{n} \Big [ {\dot{g}}_s(t_i,{\textit{\textbf{b}}}_s) - f_s( {\textit{\textbf{g}}}(t_i),{\varvec{\theta }}) \Big ]^2 \end{aligned}$$
(10)

There could be multiple local minima in the optimization of Eq. (10). A standard way to address this is to repeat the optimization from different initializations, either randomly chosen or (better) from a space-filling design in parameter space, and then to keep the best value. However, the combination of results from different local optima can also be used for uncertainty quantification. Pearce et al. (2020) show that under certain regularity conditions, the parameter distribution obtained from different local optima is a good approximation of the Bayesian posterior distribution. Repeating our optimization procedures from different intializations is a computationally cheaper alternative to Markov chain Monte Carlo simulations for uncertainty quantification, and an example of the distribution one can obtain in this way is provided in Fig. 7. The standard gradient matching (RKG) method is implemented in KGode in the rkg(.) function, which is described in Algorithm 1.

figure a

2.3 Warped gradient matching

The standard gradient matching approach critically depends on the ability of the RKHS interpolant, defined by the linear combination of kernels, to adequately represent the solution of the ODE system. Small ‘wiggles’, which may be hardly discernible at the level of the interpolant itself, can have dramatic effects at the level of the derivatives, which determine the parameter estimation. For noisy data, an adequate smoothing scheme is essential. However, any smoothing scheme is based on intrinsic functional length scales and these length scales may vary in time. Consider, for instance, estimating an oscillating signal with varying frequency. If the length scale is tuned to the high-frequency domain, overfitting will typically result in the low frequency domain; if it is tuned to the low frequency domain, over-smoothing will affect the high frequency domain. In either case, the estimation of the derivatives will be poor, hampering ODE parameter estimation.

To overcome the difficulties imposed by variations in intrinsic functional length scales on smooth function interpolation, we introduce a two-layer approach, illustrated in Fig. 1. The objective of the first layer is to transform, for each of the variables s of the dynamical system, time t via a bijection \({\tilde{t}}=w_s(t)\) such that in warped time \({\tilde{t}}\), the unknown solutions \(x_s\) of the dynamical system show less variation in their intrinsic length scales. More specifically, we target oscillating functions and aim to transform them into a regular sinusoid by exploiting the fact that a sinusoid is closed under second-order differentiation (subject to rescaling). The basic idea is that a regular sinusoid is easy to learn, whereas a quasi-periodic signal with varying frequencies is not. The objective, hence, is to find a warping of the time axis that counter-acts the inhomogeneity in the period. We define the transformation of time as

$$\begin{aligned} {{\tilde{t}}} = w_s(t,{\textit{\textbf{b}}}^w,l^w)= & {} \sum _{j=1}^n \exp {(b_j^w)} {\mathcal {S}}(t - t_j, l^{w} ) \nonumber \\ {\mathcal {S}}(z,l^w)= & {} \frac{1}{1+ \exp (-l^w z)} \end{aligned}$$
(11)

where the strict monotonicity of \({\mathcal {S}}(.)\) and the non-negativity of \(\exp (.)\) guarantee bijectivity. The sigmoidal nature of the transfer function allows for compression and expansion of the time axis, with flat regions corresponding to the former, and steep regions corresponding to the latter. \(l^w\) is the hyper parameter of the basis function of the warping function. In the original time domain, the sth variable of the dynamical system, \(x_s(t)\), is approximated by the smooth interpolant \(g_s(t)\). This function is now transformed, by virtue of the bijection (11), into \(q_s({\tilde{t}})\), where

$$\begin{aligned} g_s(t) = q_s\circ w_s(t) = q_s({{\tilde{t}}}) \end{aligned}$$
(12)

and \(w_s(t)\) is shorthand notation for the bijection defined in (11).

Step 1: Initialization We initialize the system with standard kernel ridge regression, i.e. by solving Eqs. (7)–(9) resulting in smooth interpolants \(g_s(t)\) in the original time domain t. We then initialize \({\tilde{t}}=t\) and \(g_s(t) = q_s({\tilde{t}})\), for each of the variables s of the dynamical system in turn.Footnote 2 The transformation of time is defined in Eqs. (11)–(12). The bijection between the original time domain \(t \in [T_0,T_1]\) and the warped time domain \({\tilde{t}} \in [{\tilde{T}}_0,{\tilde{T}}_1]\) is obtained by minimizing the following objective function with respect to the parameters \(l^{w}, {\textit{\textbf{b}}}^w, {\tilde{T}}_0\) and \({\tilde{T}}_1\):

$$\begin{aligned} L_w(l^{w},{\textit{\textbf{b}}}^w,{\tilde{T}}_0,{\tilde{T}}_1)= & {} \int \Big ( {\ddot{q}}_s({{\tilde{t}}}) + [\lambda ^w]^2 q_s({{\tilde{t}}}) \Big )^2 d{\tilde{t}} \nonumber \\&+ \lambda _t \left( \left( {\tilde{T}}_1 - T_1 \right) ^2 + \left( {\tilde{T}}_0 - T_0 \right) ^2 \right) \end{aligned}$$
(13)

where the dependence on \(l^{w}\) and \({\textit{\textbf{b}}}^w\) is via Eq. (11), and \({\ddot{q}}_s({{\tilde{t}}})\) is shorthand notation for \({\ddot{q}}_s({\tilde{t}})=\frac{d^2 q_s({\tilde{t}})}{d {\tilde{t}}^2}\). The first term in Eq. (13) intends to homogenize the intrinsic functional length scales by encouraging functional invariance with respect to second-order differentiation. The second term in Eq. (13) is a regularization term that penalizes range changes, and \(\lambda ^w\) is the corresponding regularization parameter, which is optimized by cross-validation.

Fig. 1
figure 1

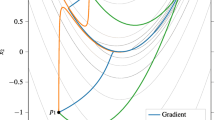
Graphical representation of the proposed method. A dynamical system, depending on the kinetic parameters \(\theta \) (top left), has solutions subject to varying intrinsic length scales (top right). To improve inference, time t is warped into \({\tilde{t}}\) via a bijection (centre) with the objective to homogenize the intrinsic length scales (bottom right). This is achieved by minimizing an objective function that encourages functional invariance with respect to second-order differentiation (far right). The dynamical system in the warped domain can easily be obtained by application of the chain rule from standard calculus (bottom left). The kinetic parameters \(\theta \) are then obtained by minimizing a second objective function based on gradient matching (far left). To avoid obfuscation, the figure does not specifically represent the distinction between the unknown true functions, x(t), and the interpolants used for their approximation, g(t) and \(q({\tilde{t}})\). A mathematically equivalent and more convenient way is to define the gradient matching in the original domain, after mapping the interpolants back into the original time domain. This has also not been shown, again to avoid obfuscation

Full size image

Step 2: Interpolation. The second step deals with function interpolation. The original data points \(y_s(t_i)\) are mapped to the warped time points, \(y_s({{\tilde{t}}}_i)\). We then apply standard kernel ridge regression with an RBF kernel in the warped time domain, as in Eq. (9), which gives us the smooth interpolant \(q_s({{\tilde{t}}})\), for each of the variables s in the dynamical system in turn:

$$\begin{aligned} q_s({{\tilde{t}}};{\varvec{b^q}}_s) \; =\; \sum _{j=1}^{n}b_{sj}^q k({{\tilde{t}}},{{\tilde{t}}}_j) \end{aligned}$$
(14)

In order to perform gradient matching, we need to compute the gradient in the original time domain for each ODE state. By applying the chain rule of standard calculus, as in Eq. (15), the gradient in the original time domain can be calculated as the dot product of the gradient in the warped domain \({\dot{q}}_s({\tilde{t}})\) and the gradient of the warping function \( d {\tilde{t}}/dt = {\dot{w}}_s(t)\), where \(w_s(t)\) is defined in Eq. (11). To control the smoothness of the warping function over the entire time domain, the standard kernel ridge regression with an MLP kernel (Bishop 2006, chapter 6) is applied to the set of warped time points \(\{ t_i,{\tilde{t}}_i\}\) obtained in Step 1. Unwarping \(q_s({{\tilde{t}}})\) back into the original time domain t is straightforward. Since \(w_s(t)\) is bijective, we have \(g_s(t)=q_s({{\tilde{t}}})\), see Eq. (12), and

$$\begin{aligned} \frac{d g_s(t)}{d t}=\frac{d q_s({{\tilde{t}}})}{d t} = \sum _{j=1}^{n}b_{sj}^q \frac{\partial k({{\tilde{t}}},{{\tilde{t}}}_j)}{\partial {{\tilde{t}}}} \frac{d {{\tilde{t}}}}{d t} = \sum _{j=1}^{n}b_{sj}^q \frac{\partial k({{\tilde{t}}},{{\tilde{t}}}_j)}{\partial {{\tilde{t}}}} {\dot{w}}_s(t). \end{aligned}$$
(15)

Step 3: Parameter estimation. Finally, we estimate the ODE parameters (\({\varvec{\theta }}\)) with standard gradient matching, i.e. by minimizing the following objective functionFootnote 3 with respect to \({\varvec{\theta }}\):

$$\begin{aligned} L({\varvec{\theta }}) \; = \sum _{s=1}^r \sum _{i=1}^{n} \Big [ {\dot{g}}_s( t_i) - f_s( {\textit{\textbf{g}}}(t_i),{\varvec{\theta }}) \Big ]^2 \end{aligned}$$
(16)

where \({\dot{g}}_s( t_i)\) is given by Eq. (15). The warped gradient matching (RKGW) method is implemented in KGode in the warpfun(.) function, which is described in Algorithm 2.

figure b

2.4 ODE regularization

The ODE parameter estimation described in the previous two sections is purely based on the observed data without considering the dynamics of the ODE system. We now introduce an approach for estimating the ODE parameters by using the ODEs themselves as a regulariser. The first step follows standard gradient matching. In step 2, a combined loss function is introduced to penalize both the deviation of interpolants from the data and the difference between the gradient obtained from the interpolants and the gradient predicted from the ODEs. The ODE parameters and the coefficients of the kernel basis can be updated simultaneously or iteratively by minimizing the combined loss function.

Step 1—Initialization of regression coefficients and ODE parameters using standard gradient matching. Following standard kernel ridge regression, the interpolants \(g_s(t)\) from Eq. (4) are obtained by minimizing the loss function in Eq. (6). The RKHS regression coefficients are computed from Eq. (9). The ODE parameters are estimated by minimizing the loss function in Eq. (10). The regularizing influence of the ODEs acting back onto the interpolant is incorporated by minimizing the objective function \({\textit{\textbf{E}}}({\varvec{\theta }},{\textit{\textbf{B}}})\) of Eq. (17) in step 2.

Step 2—Minimization of the combined objective function. The subsequent minimization of \({\textit{\textbf{E}}}({\varvec{\theta }},{\textit{\textbf{B}}})\) with respect to both arguments is a complex non-convex optimization problem. We provide two schemes for optimizing \({\textit{\textbf{E}}}({\varvec{\theta }},{\textit{\textbf{B}}})\). The first scheme involves optimizing both \({\textit{\textbf{b}}}\) and \({\varvec{\theta }}\) simultaneously using a standard optimization routine, such as conjugate gradients or quasi-Newton.

$$\begin{aligned} {\textit{\textbf{E}}}({\varvec{\theta }},{\textit{\textbf{B}}})= & {} \sum _{s=1}^r \left( \sum _{i=1}^{n} \Big [ g_s(t_{i};{\textit{\textbf{b}}}_s) - y_{si} \Big ]^2 \right) \nonumber \\&+ \lambda \sum _{s=1}^r \left( \sum _{i=1}^{n} \Big [ {\dot{g}}_s( t_i;{\textit{\textbf{b}}}_s) - f_s( {\textit{\textbf{g}}}(t_i, {\textit{\textbf{ B }}} ),{\varvec{\theta }}) \Big ]^2 \right) \end{aligned}$$
(17)

As this can be computationally expensive, we also present a fast iterative approach as an alternative. Consider Eq. (17). When fixing \({\textit{\textbf{B}}}\) in the argument of \(f_s(.)\), the objective function becomes convex in the remaining parameters \({\textit{\textbf{B}}}\) because of the linearity in Eq. (4). This convexity can be exploited with a modified optimization algorithm. First, we define the following modified objective function:

$$\begin{aligned} {\varvec{\tilde{E}}}({\varvec{\theta }},{\textit{\textbf{B}}},{\varvec{{\tilde{B}}}})= & {} \sum _{s=1}^r \left( \sum _{i=1}^{n} \Big [ g_s(t_{i};{\textit{\textbf{b}}}_s) - y_{si} \Big ]^2 \right) \nonumber \\&+ \lambda \sum _{s=1}^r \left( \sum _{i=1}^{n} \Big [ {\dot{g}}_s( t_i;{\textit{\textbf{b}}}_s) - f_s( {\textit{\textbf{g}}}(t_i, {\varvec{ {\tilde{B}} }} ),{\varvec{\theta }}) \Big ]^2 \right) \end{aligned}$$
(18)

We can now iterate the following steps to optimize \({\textit{\textbf{B}}}\) and \({\varvec{\theta }}\):

  1. 1.

    Given \({\textit{\textbf{B}}}={\varvec{{\tilde{B}}}}\) and \({\varvec{\theta }}\), minimize \({\tilde{E}}({\varvec{\theta }},{\textit{\textbf{B}}},{\varvec{{\tilde{B}}}})\) with respect to \({\textit{\textbf{B}}}\),

    i.e. find \({\textit{\textbf{B}}}_{new} \; = \; \mathrm{argmin}_{{\textit{\textbf{B}}}} {\tilde{E}}({\varvec{\theta }},{\textit{\textbf{B}}},{\varvec{{\tilde{B}}}})\)

  2. 2.

    Set \({\textit{\textbf{B}}} = {\textit{\textbf{B}}}_{new}\) and minimize \({\tilde{E}}({\varvec{\theta }},{\textit{\textbf{B}}}_{new},{\textit{\textbf{B}}}_{new})\) wrt \({\varvec{\theta }}\),

    i.e. find \({\varvec{\theta }}_{new} \; = \; \mathrm{argmin}_{\theta } {\tilde{E}}({\varvec{\theta }},{\textit{\textbf{B}}}_{new},{\textit{\textbf{B}}}_{new})\)

The ODE regularization (RKG3) method is implemented in KGode in the third(.) function, which is described in Algorithm 3.

figure c
figure d

2.5 Warping plus ODE regularization

In this section, we combine the warping scheme with the ODE regularization method. The rationale is to use warping to learn the interpolation of the nonstationary signal and then apply ODE regularization to further improve the ODE parameter estimations. We first apply the standard gradient matching as an initialization. The warping scheme in Sect. 2.3 is applied in the second step. The ODE regularization can then be introduced in the last step to regularize the warped interpolant. Since we are doing gradient matching with the warped interpolant, we need to compute the gradient in the original time domain by multiplying the gradient of the interpolant \(d{q}_s( {{\tilde{t}}}_i;{\textit{\textbf{b}}}_s^q)/ d {{\tilde{t}}}_i\) by the gradient of the warping function \(d {{\tilde{t}}}_i/ dt_i\), following the chain rule of basic calculus. Similar to step 2 of Sect. 2.4, ODE parameters can be estimated by minimizing the combined loss function from Eq. (17), which can be re-written as Eq. (19). As in the previous section, we provide two approaches to optimize this loss function in step 3. In the first approach, we optimize both the ODE parameters \({\varvec{\theta }}\) and \({\textit{\textbf{B}}}^q\) simultaneously. The alternative approach is to follow the fast iterative updating scheme described in Sect. 2.4. The weighting parameter \(\lambda \) can be estimated with cross-validation.

Step 1—Standard gradient matching as in Sect. 2.2.

Step 2—Warped gradient matching as in Sect. 2.3.

Step 3—Minimization of the combined objective function. Replace \(g_s(t)\) with \(q_s({{\tilde{t}}})\) in Eqs. (17) and (18) and apply the chain rule to the derivative of the interpolant. This gives:

$$\begin{aligned} {\textit{\textbf{E}}} ({\varvec{\theta }},{\textit{\textbf{B}}}^q )= & {} \sum _{s=1}^r \sum _{i=1}^{n} \Big [ q_s({\tilde{t}}_{i};{\textit{\textbf{b}}}_s^q) - y_{si} \Big ]^2 \nonumber \\&+ \lambda \sum _{s=1}^r \sum _{i=1}^{n} \Big [ \frac{ d{q}_s( {{\tilde{t}}}_i;{\textit{\textbf{b}}}_s^q)}{d {{\tilde{t}}}_i} \frac{d {{\tilde{t}}}_i}{dt_i} - f_s( {\textit{\textbf{q}}}({{\tilde{t}}}_i, {\varvec{B^q }} ),{\varvec{\theta }}) \Big ]^2 \end{aligned}$$
(19)

or

$$\begin{aligned} {\textit{\textbf{E}}} ({\varvec{\theta }},{\textit{\textbf{B}}}^q,{\varvec{{\tilde{B}}}}^q )= & {} \sum _{s=1}^r \sum _{i=1}^{n} \Big [ q_s({\tilde{t}}_{i};{\textit{\textbf{b}}}_s^q) - y_{si} \Big ]^2 \nonumber \\&+ \lambda \sum _{s=1}^r \sum _{i=1}^{n} \Big [ \frac{ d{q}_s( {{\tilde{t}}}_i;{\textit{\textbf{b}}}_s^q)}{d {{\tilde{t}}}_i} \frac{d {{\tilde{t}}}_i}{dt_i} - f_s( {\textit{\textbf{q}}}({{\tilde{t}}}_i, {\varvec{ {\tilde{B}}^q }} ),{\varvec{\theta }}) \Big ]^2 \end{aligned}$$
(20)

We can now either apply standard optimization algorithms, like conjugate gradients or quasi-Newton, to minimize \({\textit{\textbf{E}}} ({\varvec{\theta }},{\textit{\textbf{B}}}^q )\) in Eq. (20) simultaneously with respect to both \({\varvec{\theta }}\) and \({\textit{\textbf{B}}}^q\), or apply the iterative routine described below Eq. (18) to the objective function of Eq. (20).

The warping plus ODE regularization (RKGW3) method is implemented in KGode in the warpfun(.) and third(.) functions. The warping step has been described in Sect. 2.3. The ODE regularization for the warped signal is implemented in the third(.) function (the same function described in Sect. 2.4). Two additional arguments are used for ODE regularization with the warped signal, more details of which are described in Algorithm 4.

Table 1 Classes and functions for the package KGode and their relation to the mathematical equations
Full size table

2.6 Uncertainty quantification in ODE parameter estimation

For quantifying the uncertainty of the parameter estimates, we use an approach based on residual bootstrapping (Efron and Tibshirani 1994). The basic idea is to generate a set of surrogate data that capture typical expected variations in the data, and then repeat the parameter estimation on these surrogate data to get a distribution of estimates. From this distribution, uncertainty quantification statistics like the standard deviation or median absolute deviation can be computed. In more detail, let \(D=\{{\textit{\textbf{y}}}(t_1),\ldots ,{\textit{\textbf{y}}}(t_N)\}\) denote the original data, i.e. the noisy time series of N measurements or observations. Let \(\{{\textit{\textbf{x}}}(t_1),\ldots ,{\textit{\textbf{x}}}(t_N)\}\) denote the approximation of the unknown true signal, obtained from the RKHS procedure described in Sect. 2. From the original data and the solution of the ODEs we obtain a set of residuals, \(E=\{{\varvec{\varepsilon }}(t_1),\ldots ,{\varvec{\varepsilon }}(t_N)\}\), where \({\varvec{\varepsilon }}(t_i)= {\textit{\textbf{y}}}(t_i)-{\textit{\textbf{x}}}(t_i)\). We now draw N elements with replacement from set E, to obtain a bootstrap residual set \({\tilde{E}}=\{{\varvec{{\tilde{\varepsilon }}}}(t_1),\ldots ,{\varvec{{\tilde{\varepsilon }}}}(t_N)\}\), from which we obtain the bootstrap training set \({\tilde{D}}=\{{\varvec{{\tilde{y}}}}(t_1),\ldots ,{\varvec{{\tilde{y}}}}(t_N)\}\), where \({\varvec{{\tilde{y}}}}(t_i)= {\textit{\textbf{x}}}(t_i)+{\varvec{{\tilde{\varepsilon }}}}(t_i)\). We then apply the same parameter estimation procedure to the bootstrap training data \({\tilde{D}}\) as for the original data D. This procedure is repeated K times, for K separate bootstrap sets \({\tilde{D}}_1,\ldots ,{\tilde{D}}_K\), leading to K parameter estimates \({\varvec{{\tilde{\theta }}}}_1,\ldots ,{\varvec{{\tilde{\theta }}}}_K\). This distribution can be summarized e.g. by the standard deviation or by the median absolute deviation (MAD). The latter is a robust measure of variability that is less susceptible to outliers than the standard deviation (Leys et al. 2013). We multiply the MAD with a constant scale factor of \(k = 1.4826\), henceforth referred to as adjusted MAD, which makes it a consistent estimator for the estimation of the standard deviation of a normally distributed random variable (Ruppert 2010).

3 Library architecture and examples

The KGode package is designed around the R6 class model. R6 classes have reference semantics and so computation is performed by mutating the state of objects. This can be seen in the following subsections, where instances of an ode object are created using the new constructor method. When the solve_ode method is called on this instance, the state internal to the object is modified, which can then be accessed at a later stage. The main classes and functions are shown in Table 1, with ode being the central class in the system, used to store formulas and parameters and to perform ODE solving, with the other functions being used to add extra functionality on top, such as gradient matching, time warping and ODE regularization. Examples of the use of all of these classes and functions to perform parameter inference in dynamical systems is shown below.

3.1 Defining the differential equations and generating data from them

In this section, we provide an example of the code used with the FitzHugh–Nagumo system. The FitzHugh–Nagumo ODEs are defined as a functionFN_fun, where x[1] and x[2] are the two states and a, b and c are the three ODE parameters in Eq. (21). The numerical solver used in our package is the ode23s function of the pracma package. The intermediate time points are selected by the numerical solver.

FitzHugh–Nagumo The FitzHugh–Nagumo system is a two-dimensional dynamical system used for modelling spike generation in axons (FitzHugh 1955). It has two state variables, \(x_1\) and \(x_2\), and three parameters: a, b and c. We numerically solved the ODEs for \(a=0.2, b=0.2, c=3, t\in (0,10)\), and initial conditions \(x_1(0)=0.5\) and \(x_2(0)=1\).

$$\begin{aligned} \begin{aligned} \dot{x_1}= \frac{dx_1}{dt} = c\cdot \left( x_1 - x_1^3/3 + x_2 \right) , \qquad \dot{x_2}= \frac{dx_2}{dt} = -c^{-1} \left( x_1 -a + b \cdot x_2 \right) \end{aligned}\nonumber \\ \end{aligned}$$
(21)
figure e

We start, in lines 1–7, by loading the KGode package and defining a function (FN_fun) that computes the gradients of the states of the model at a particular value of time (t) and the corresponding state (x). The function returns the gradients as an \(N_s\)-by-1 matrix, where \(N_s\) is the number of states. In line 8, the function is passed as an argument to a new ode object; the other argument (sample) determines which time points (as chosen by the solver) to provide output for. The default value (sample=1) returns all of the time points chosen by the solver, whereas sample=n returns each nth time point. As we are generating data, we need to provide the initial state values (xinit), which take the form of a matrix with one column and one row per state (line 9). The final argument required by the numerical ODE solver is the time interval over which to solve the ODEs (tinterv). In this example, the time interval is \([0,10]\). This argument takes the form of a list comprising of two elements, the start and end times. The ODEs are numerically integrated by calling method solve_ode of the ode class, as seen on line 11. The first argument is a list of the ODEs parameters (par_ode) in the order they are expected by the ODE function (FN_fun). In this example, the values are 0.2, 0.2 and 3. The other arguments are as explained above. Finally, in line 12, we extract the number of time points (n_o), and define the noise level in line 13. The simulated data are created by adding independent identically distributed normal noise to the outputs of the numerical integration (line 14). The time points of the numerical solution are extracted in line 15. If the user wants to use a real dataset, the numerical integration (line 11) and the perturbation by noise (line 14) are replaced by reading in the data from an external file.

3.2 Standard gradient matching

We start with an example of ODE parameter estimation for the FitzHugh–Nagumo system, using the standard gradient matching (RKG) method introduced in Sect. 2.2 and defined in Algorithm 1. The RKG method is implemented as function rkg. The input arguments are an ode class object (odem), the noisy observation (y_no) and the kernel type (ktype).

In order to create an ode class object, we need to provide the ODE parameter initialization (init_par), the ODE state initialization (init_yode) and the time points of observation (init_t). The ODE parameter initialization init_par is set as a vector of size 3 (line 1), for the three parameters of the FitzHugh–Nagumo model. In this example, all initial values are set to 0.1. The ODE states are initialized in line 2, with the initialization vector,init_yode, set to the noisy observations, y_no. The time points of observations are defined in line 3, which were obtained from the last line of the code fragment in the previous subsection. The ode class object odem is created in line 4 by taking the FitzHugh–Nagumo ODE function FN_fun as the first argument. The second argument, grfun, is optional and allows the user to provide an analytically derived gradient of the objective function with respect to the ODE parameters. If this gradient is not available, it can be computed numerically by setting grfun=NULL (as is done in this example). The other arguments are as explained above. In line 6, the kernel type (ktype) for the RKHS interpolation scheme is defined. In this example, it is set to ’rbf’, which stands for the RBF kernel. The ODE parameters are estimated using the standard gradient matching method of Sect. 2.2 by calling the rkg function in line 7. The input arguments are as explained above. The rkg function returns a list rkgres containing the RKHS interpolation results for each of the ODE’s states. In line 8, the ode class object odem gets updated and the ODE parameter estimation results can be accessed from its attribute, odem$ode_par. The interpolation for each of the ODE states can be accessed via the rkgres attribute (rkgres$intp[1,]), as in line 10, where the first index of the matrix rkgres$intp[,] indicates the ODE state. Here rkgres$intp[1,] gives us the prediction of the first ODE state.

figure f

The interpolation from the standard gradient matching method is plotted together with the true solution of the ODEs and the noisy observation in panel (a) and (b) in Fig. 2. These plots can be produced by running the code in line 10, and editing the outputs with standard plotting programs. The QQ plots and the residual plots are given in panel (c)–(f) in Fig. 2.

Fig. 2
figure 2

RKG (RBF kernel) interpolation for the FitzHugh–Nagumo model. Panel (a) shows the true signal (solid line), the noisy data (crosses), with signal-to-noise ratio SNR = 20 db, and the interpolant obtained from standard RBF kernel RKHS regression (RKG—dashed line) for the first state variable, \(x_1.{ Thecorrespondingplotsforthesecondstatevariable},\,x_2\), are shown in panel (b). The QQ plots of the residuals are in panels (c) and (d). The residual analysis plots are in panels (e) and (f)

Full size image
Fig. 3
figure 3

RKG (MLP kernel) interpolation for the FitzHugh–Nagumo model. Panel (a) shows the true signal (solid line), the noisy data (crosses), with signal-to-noise ratio SNR = 20 db, and the interpolant obtained from MLP kernel RKHS regression (RKG—dashed line) for the first state variable, \(x_1.{ Thecorrespondingplotsforthesecondstatevariable},\,x_2\), are shown in panel (b). The QQ plots of the residuals are in panels (c) and (d). The residual analysis plots are in panels (e) and (f)

Full size image

The package also offers different kernel options, such as the RBF kernel and the MLP kernel. Switching the kernel can be easily done with the redefinition command, e.g. ktype = ’mlp’. The interpolant obtained from MLP RKHS regression and the corresponding QQ plot of the residuals are given in Fig. 3. The points of the QQ plots in panel (d) of Fig. 3 fall along a line in the middle of the graph, but curve off in the extremities, which indicates a heavy-tailed distribution of the residuals. From a visual inspection of the figure, it is clear that RKHS regression with the RBF kernel achieves a better fit than RKHS regression with the MLP kernel.

figure g

3.3 Warping gradient matching

The warping gradient matching scheme, described in Sect. 2.3 and Algorithm 2, is applied to estimate the parameters of a biopathways ODE system. The biopathways ODEs are defined as a function BP_fun. The variables x[1], x[2],x[3], x[4] and x[5] represent the five states, and k1,k2,k3,k4,k5,k6 are the six ODE parameters, as shown in Eq. (22).

Biopathways The biopathway model describes the interaction of five protein isoforms, \(S, dS,R,RS,Rpp\), in a signal transduction pathway and was previously studied by Vyshemirsky and Girolami (2008). Changes in protein abundance over time are described by a combination of mass action and Michaelis–Menten kinetics:

$$\begin{aligned} {[} {\dot{S}} ]= & {} - k_1 \cdot [S] - k_2 \cdot [S] \cdot [R] + k_3 \cdot [RS] \nonumber \\ {[}{\dot{dS}}]= & {} k_1 \cdot \left[ S\right] \nonumber \\ \dot{[R]}= & {} -k_2 \cdot [S] \cdot [R] + k_3 \cdot [RS] + \frac{k_5 \cdot [Rpp]}{k_6 + [Rpp]} \nonumber \\ \dot{[RS]}= & {} k_2 \cdot [S] \cdot [R] - k_3 \cdot [RS]- k_4 \cdot [RS] \nonumber \\ \dot{[Rpp]}= & {} k_4 \cdot [RS] - \frac{k_5 \cdot [Rpp]}{k_6 + [Rpp]} \end{aligned}$$
(22)

The square brackets, \([\cdot ],\,{ denoteconcentrationsofproteinisoforms}({ thestates}),\,{ and}k_{1:6}{} { representthe}6{ kineticparameterstobeinferred}.{ Itturnsoutthat}k_5{ and}k_6{ areonlyweaklyidentifiable},\,{ andwehavethusassessedtheaccuracyofinferencebasedontheratio}\frac{k_5}{k_6}.{ Inthisexample},\,{ wenumericallysolvetheODEsfor}k_1=0.07, k_2=0.6, k_3=0.05, k_4=0.3, k_5=0.017, k_6=0.3, t\in (0,100),\,{ withinitialconditions}S(0)=1, dS(0)=0, R(0)=1, RS(0)=0{ and}Rpp(0)=0.{ Usingthedefaultstepsizesettingsofthenumericalintegrationscheme},\,{ thisgenerates}n= 14\) data points. Similar to Sect. 3.1, the first 11 lines define the ODE function (BP_fun), which is used to compute the gradients of the states of the Biopathways model at time (t) and state (x). The function returns the gradients as a 5-by-1 matrix, reflecting the fact that the Biopathways model has 5 states. The function is passed as an argument to the ode object in line 12. The other argument is set as sample=2, which is a thinning factor that instructs the numerical integrator to keep every second time point.

figure h

To generate data, we need to specify the initial state values (xinit), which are here given by a 1-by-5 matrix (line 13). The last argument required by the numerical ODE solver is the time interval (tinterv), which is defined as a vector comprising the start and end times. In this example, the times are 0 and 100. The ODEs are then numerically solved by calling method solve_ode of the ode class in line 15. The true values of the ODE parameters are given as the first argument (par_ode); the other arguments are as explained above. Finally, we extract the number of time points (n_o) and emulate real-world data by adding independent and identically distributed (iid) normal noise to the simulated values (line 17).

figure i

Next, we essentially follow the steps described in Sect. 2.3. We begin with the standard gradient matching scheme (RKG) with RBF kernel to estimate the ODE’s parameters. In line 18, the ODE parameter initialization, init_par, is set as a vector of length 6, with all elements equal to 0.1. In the following line, line 19, the ODE states initialization, init_yode, is set to the vector of noisy observations y_no. The vector of selected time points, init_t, is set to the times of the observations (line 20). An ode class object (odem_BP) is created in lines 21–22 by taking the ODE function BP_fun as the first argument, with the other arguments as explained above. In line 23, the kernel type, ktype, is set to ’rbf’, which indicates the use of the RBF kernel for RKHS interpolation. Finally the ODE parameters are estimated by calling the rkg function in line 24. The rkg function returns a list object, rkgres, containing the interpolation results for each of the ODE states. The ODE parameter estimation results can be accessed from the attribute ode_par of the ode class object odem_BP, which in this example code fragment is done in lines 25–26.

figure j

In order to learn the warping function defined in Eq. (11), a list of user-defined target periods of the warped signal needs to be provided for each ODE state. In this example, the target period peod is defined as a vector of size 5 with all elements equal to 200; see line 27. The period of the warped signal is allowed to vary from peod-eps to peod+eps, where in this example eps is set equal to 20, in line 28. With this configuration, the estimated period will be in the range of 180–220. The warping function is modelled as a linear combination of sigmoid functions, as shown in Eq. (11). The initial value of the hyperparameter of the sigmoid basis function is estimated with function warpInitLen, in line 29. The list object rkgs of the standard gradient matching results is used as the input argument of the warpInitLen function. The rest of the arguments are peod and eps, as explained above. The function returns a list object, fixlens, which contains the estimated hyperparameters of the sigmoid basis function for each ODE state.

Steps 1 and 2 of the warping process described in Sect. 2.3 are built into the function warpfun. This requires the standard RKHS interpolation results, inter_rkhs, as one of the input arguments. These standard RKHS interpolation results are given as a list object from the attribute of rkgres in line 30. Here, rkgres is the list object returned by the standard gradient matching function rkg, as in line 24 of the code fragment shown earlier on. The other arguments are the ode class object odem_BP, the user-defined target period peod, the period range parameter eps, the initial value of the hyperparameter for the sigmoid basis function fixlens, the vector of noisy observations y_no and the vector of observation time points init_t. The warping functions are learned by calling the function warpfun in line 31. The function returns a list object warp_BP that contains the warping results.

In this example,the ODE parameters are estimated with gradient matching using the gradient of the interpolant, the gradient of the warping function and the gradient from the ODEs. The ODE parameter estimates are available from the attribute of the returned list object warp_BP$wkkk$ode_par in line 32. The parameter estimation results are displayed in line 33. Notice the large values for the estimates of the last two parameters, k5 and k6, which are orders of magnitudes above the other values. This reflects the weak identifiability inherent in the estimation process, which only allows the reliable estimation of the fraction k5/k6 rather than the values of k5 and k6 themselves. In fact, a comparison of the estimated ratio k5/k6 with the true ratio gives very good agreement, whereas the individual values of k5 and k6 may vary substantially. The gradient of the warping function dtilda_t is given as warp_BP$dtilda, in line 34. The interpolants for the various ODE states have also improved as a consequence of carrying out the RKHS regression in the warped time domain. The improved interpolants are returned as the attribute of the list object warp_BP$bbbw in line 35. In line 36, the warped time points are returned as a vector of size 14, tilda_t, from warp_BP$wtime. In line 37, the warping functions for the ODE states, wfun, are returned as a list of functions from warp_BP$wfun. In the present example, the length of the function list, wfun, is 5, which is the number of ODE states in the biopathways system. Note that these warping functions can be used to project the time points from the original domain into the warped domain. In order to have a better visualization of the warping function, we introduce in line 38 a vector of dense, equidistant grid points, grids, of length 101. The warping function for the first ODE state, wfun[[1]], is used to project the grid points from the original domain into the warped domain, wgrid, by calling method wfun[[1]]$predictT(grids) in line 39. The returned object is a vector of length 101.

Fig. 4
figure 4

Warping example for the Biopathways model. The true signal (dotted line), the noisy data (crosses), the initial interpolation using the standard RBF kernel RKHS regression (RKG) (solid line) and the RKGW interpolation using warping (dashed line) are shown in panel (a). RBF regression is unable to cope with both the rapid drop and the saturated section of the curve. The warping function is shown in panel (b). The interpolation in the warped time domain using the RBF kernel (dashed blue line) and the warped true signal (dotted red line) are shown in panel (c). QQ plots of the residuals for the warping method and the RKG method are shown in panels (d) and (e), respectively

Full size image

A plot of the warping functions over the grid points is shown in Fig. 4b. The interpolation results obtained with time warping are compared with the standard gradient matching approach in Fig. 4a. Figure 4c shows a comparison of the interpolants in the warped time domain and the true solution. Finally, two QQ plots of the residuals obtained with the warping and the RKG methods are shown in Fig. 4d, e. The points in panel (e) form a curve instead of a straight line, which indicates that the distribution of the residuals is skewed and deviates from the assumed Gaussian form. It is clear in this case that the warping method achieves a substantially better fit of the data than the non-warped RKG method.

3.4 ODE regularization

In this section we illustrate how gradient matching with ODE regularization, as discussed in Sect. 2.4 and defined in Algorithm 3, is applied to estimate the parameters of the Lotka–Volterra system.

Lotka–Volterra. The Lotka–Volterra equations describe the dynamics of ecological systems with predator–prey interactions (Lotka 1920):

$$\begin{aligned} \begin{aligned} \dot{x_1}= \alpha \cdot x_1 - \beta \cdot x_1 \cdot x_2, \ \dot{x_2}= -\gamma \cdot x_2 + \delta \cdot x_1 \cdot x_2 \end{aligned} \end{aligned}$$
(23)

where the dot denotes a derivative with respect to time, \(\alpha ,\beta ,\gamma ,\delta \) are four parameters to be inferred, and \(x_1\) and \(x_2\) are the states of the model, indicating the number of prey and predators respectively. We numerically solved the ODEs for \(\alpha =0.2, \beta =0.35, \gamma =0.7, \delta =0.4\) and initial conditions \(x_1(0)=1\) and \(x_2(0)=2\).

The Lotka–Volterra ODEs are defined as a function, LV_fun, in lines 1–8 of the following code fragment, where x[1], x[2] are the two states and alpha,beta,gamma,delta are the four ODE parameters, as defined in Eq. (23):

figure k

Following the procedure in Sect. 3.1, the ODE function (LV_fun) is defined to compute the gradients of the states of the Lotka–Volterra model at time (t) and state (x). The function returns the gradients as a 2 by 1 matrix, reflecting the fact that the Lotka–Volterra model has 2 states. The function is passed as the second argument to object ode in line 9. The first argument of ode is sample, which is here set to sample=1 to indicate that the numerical solutions at all time points chosen by the numerical solver are to be returned. As we generate data, the initial state values (xinit) are provided as a 1 by 2 matrix (line 10). In this example, they are set to \(x_1(0)=1\) and \(x_2(0)=2\), as indicated above. The last argument required by the numerical ODE solver is the time interval defining the start and end times (tinterv). In this example, these times are set to 0 and 30, respectively; see line 11. The ODEs are then solved numerically by calling method solve_ode of the ode class in line 12. The true values of ODE parameters are given as the first argument, par_ode. In this example, these are the parameter values \(\alpha =0.2, \beta =0.35, \gamma =0.7, \delta =0.4\). The other arguments of this method are as explained above. Finally, in line 13, we extract the number of time points (n_o), and in line 14 we simulate realistic data by adding independent and identically distributed normal noise to the numerical solution of the ODEs. In this example, the simulated data, y_no, are a matrix of size 43 by 2, where 43 is the number of time points (chosen by the numerical ODE solverFootnote 4), and 2 is the number of states (prey and predator).

figure l

Following the procedure of step 1 in Sect. 2.4, we first apply standard gradient matching to estimate the ODEs parameters and update the RKHS regression coefficients, i.e. \({\textit{\textbf{b}}}_s\) in Eq. (4). As in Sect. 3.2, the ODE parameter initialization, init_par, is set as a vector of length 4 in line 15. The ODE states are initialized in line 16, where they are set to the noisy observations, y_no. The vector of time points, init_t, would usually be set to include the times points at which measurements or observations were taken. For this example using simulated data, init_t is the vector of time points for which values have been returned by the numerical ODE solver. An ode class object (odem_LV) is created in line 18, which takes the ODE function, LV_fun, and the parameters just explained, init_par, init_yode, init_t, as arguments. The kernel type, ktype, is set to ’rbf’, which indicates the use of the RBF kernel for the RKHS interpolation. Finally the ODE parameters are estimated by calling function rkg in line 21. The rkg function returns a list object, rkgres, which contains the interpolation results for each of the ODE states. The ODE parameter estimation results are recorded as the attribute, ode_par, of the ode class object odem_LV in line 22.

figure m
Fig. 5
figure 5

ODE regularization with iterative updating scheme. The figure shows the true solution (solid line) of the Lotka–Volterra system, noisy observations of sample size \(n=42\) (crosses), the interpolant obtained with the standard gradient matching method (red dashed line), and the interpolant obtained with the ODE regularization method (blue dash-dotted line). It is seen that the ODE regularization interpolant shows better agreement with the true signal. This demonstrates the effectiveness of the regularization inherent in the ODE regularization step by which the ODEs act back as a regulariser on the interpolant

Full size image

In step 2 of Sect. 2.4, we have shown how the ODE parameter estimation can be improved by optimizing the combined loss function in Eq. (17). Step 2 of Sect. 2.4 is implemented in lines 23–27. Here we provide two schemes for the ODE regularization. A scheme indicator crtype is defined in line 23. If crtype==’i’, the fast iterative approach of Eq. (18) is used. If crtype==’3’, we update the ODE parameters and RKHS regression coefficients simultaneously, by optimizing the function in Eq. (17). In this example we employ the iterative approach. The weighting parameter \(\lambda \) of the penalty term in Eq. (18) is estimated using cross validation. A list of potential values of \(\lambda \) are defined in lam, line 24; in this example, there are 4 candidate values, ranging from 0.01 to 10. The optimum value of \(\lambda \) is selected by calling function crossv in line 25. The input arguments are the vector lam, the ode class object odem_LV, a list of rkhs objects rkgres$bbb, which are created in the previous standard gradient matching step, the scheme type crtype, and the observation y_no. The crossv function returns a list object containing the optmized value of \(\lambda \). Next, function third is called in line 26 to re-estimate the ODE parameters and improve the interpolation by using the ODEs for regularization, as described in Algorithm 3. The optimized value of \(\lambda \) is the first argument. The remaining input arguments of function third are the same as for function crossv, which have been explained above. The third function returns a list object containing the improved ODE parameters and ODE state interpolants. The interpolation results of the ODE regularization are compared with the standard gradient matching approach in Fig. 5.

3.5 Warping plus ODE regularization

We have described the combination of time warping and ODE regularization in Sect. 2.5 and Algorithm 4. In the present section, we demonstrate an application of this scheme to the Lotka–Volterra system. The ODE model is the same as in Eq. (23). We assume that the true parameters are \(\alpha =1, \beta =1, \gamma =4, \delta =1\) and the initial conditions are \(x_1(0)=0.5\) and \(x_2(0)=1\). The numerical integration of the ODEs and the generation of the training data is done with the following code fragment, which is similar to the corresponding code in Sect. 3.4:

figure n

Following the steps in Sect. 2.5 (lines 8–11), we next run the standard gradient matching scheme (RKG) with an RBF kernel (specified in line 12) by calling function rkg, in line 13. The RKG estimates of the ODE parameters are listed in odem_LV$ode_par; see line 15.

figure o
Fig. 6
figure 6

Warping plus ODE regularization. The figure shows the true solution (black dotted line) of the Lotka–Volterra system, noisy observations of sample size \(n=28\) (crosses), the interpolant obtained with the standard gradient matching method (green dash-dotted line), the interpolant obtained from the warping scheme (red solid line), and the interpolant obtained with warping plus ODE regularization method (blue dashed line). It is seen that the standard gradient matching interpolant and warping interpolant show clear signs of overfitting. The interpolant obtained from the combined warping plus ODE regularization scheme, on the other hand, shows much better agreement with the true signal. This demonstrates the effectiveness of the regularization inherent in the ODE regularization step, by which the ODEs act back as a regulariser on the interpolant

Full size image

The results of the standard gradient matching scheme are used to initialize the time warping described in Sect. 2.3, invoked as in step 2 of Sect. 2.5. The user-defined period of the warped signal peod is defined as a vector of size 2 in line 16. The target period peod can vary in the range of peod+eps to peod-eps. The slack parameter eps is set equal to 1 in line 17. The hyperparameter of the warping basis function is initialized by calling function warpInitLen in line 18. The warping functions are learned by calling the function warpfun in line 19. The input arguments have been explained in Sect. 2.5. The function returns a list object, warp_LV, which contains the warping results.

figure p

The gradient of the warping function can be accessed as dtilda = warp_LV $dtilda in line 20. The interpolation results after warping are available from Winterp_rkhs = warp_BP$bbbw in line 21. The warped time \({\tilde{t}}{} \) is listed in tilda_t = warp_BP$wtime in line 22. The ODE parameters are estimated with gradient matching by combining the gradient of the interpolant, the gradient of the warping function and the gradient from ODEs. The results are displayed by typing warp_LV$wkkk$ode_par in line 23.

figure q

The ODE regularization step for the warped signal, described in Sect. 2.5, is implemented in function third. The warping indicator, woption = ’w’, switches the warping option on, in line 24. In line 25, the optimization scheme is set to crtype = ’3’, which tells the program that the ODE parameters and kernel regression coefficients are to be updated simultaneously. Following the specification of a discrete set of candidate values (here: \(\{1, 0.1, 0.01, 0.0001\}){ inline}~26,\,{ theweightingparameter}\lambda \) in Eq. (19) is estimated using cross-validation, which is implemented as function crossv in line 27. The input arguments of third, called in line 29, are the weighting parameter \(\lambda \), lambdaw3, which has been extracted in the previous line, line 28, the ode class object odem_LV, the rkhs object after warping Winterp_rkhs, the optmization scheme type cytype, the warping indicator woption and the gradient of the warping function, dtilda. The ODE parameter estimation and interpolation results are returned as a list object in res, in line 29. The parameter estimation is displayed by typing res$oppar in line 30. Various plots of the interpolant obtained with different gradient matching and regularization methods are shown in Fig. 6.

3.6 Uncertainty quantification in ODE parameter estimation

In the following example, we apply the residual bootstrap method described in Sect. 2.6 to the Lotka–Voltera model for estimating the uncertainty of the parameter estimation. We emphasize that the function bootstrap is a function of our own package; it is not the CRAN package with the same name.

figure r

Following the same model settings as in Sect. 3.5, we assume that the standard gradient matching approach in lines 1–15 of the code example in Sect. 3.5 has been applied. A list of rkhs class objects is stored in interp_rkhs in line 1 of the R code above. The length of the list is the same as the number the ODEs states, which is stored in nst in line 2. Recall that the Lotka–Volterra model has two states: prey and predator; hence nst=2. The ODE parameter estimation can be accessed from the attributes of the ode class object odem_LV$ode_par in line 3. An empty list object intp_data is created in line 4 to store the ODE states interpolation. The interpolation results from the RKHS regression are calculated in line 5. The number of bootstrap replicates is set to K=12 in line 6. The bootstrap procedure is performed by calling the function bootstrap in line 7. The inputs to function bootstrap are the ode class object odem_LV, the vector of noisy observations y_no, the kernel type ktype, the number of bootstrap replicates K, the vector of ODE parameter estimates ode_par, and the RKHS interpolation results intp_data. The first three inputs have been defined in Sect. 3.5. The outputs are the adjusted median absolute deviations for the ODEs parameters. The four ODE parameter estimates for the Lotka–Volterra model are shown in line 8 and the corresponding adjusted median absolute deviations in line 9.

Fig. 7
figure 7

Dot plot of parameter estimates for the Lotka–Volterra model introduced in Sect. 3.4for 100 different random initializations. The true values for the parameters are alpha = 0.2, beta = 0.35, gamma = 0.7, delta = 0.4

Full size image
Fig. 8
figure 8

RKG and ODE-regularized (RKG3) interpolation for the Hudson’s Bay Company’s data, using the Lotka–Volterra model. Panel (a) shows the data (crosses) and the interpolant obtained from RKHS regression (RKG—dashed line) and ODE regularization with RKG3 (solid line) for the first state variable, \(x_1\) (hares). The corresponding plots for the second state variable, \(x_2\) (lynxes), are shown in panel (b). The remaining panels show QQ plots of the residuals

Full size image
Fig. 9
figure 9

Model prediction for the Hudson Bay’s Company’s pelt data. The parameter estimates from the RKG and ODE regularization (RKG3) methods were inserted into the Lotka–Volterra model. The numerical solution of the ODEs are plotted. Panel (a) shows the data (crosses) and the numerical solution of the ODEs, whose parameters were estimated from RKHS regression (RKG—dashed line) and ODE regularization (RKG3—solid line) for the first state variable, \(x_1\) (hares). The corresponding plots for the second state variable, \(x_2\) (lynxes), are shown in panel (b)

Full size image

3.7 Effects of the initialization on ODE parameter estimation

Due to the optimization procedure of the KGode algorithm and potential multimodality of the objective function, different initializations may converge to different local optima and may therefore give different parameter estimates. This is illustrated in Fig. 7, where the example of Sect. 3.4 was run 100 times with different random number generator seeds. The variation in the parameter estimates is evident. We emphasize that this is not necessarily a bad thing, as the combination of results from different local optima can be used for uncertainty quantification. The parameter distributions in Fig. 7 have some resemblance with posterior distributions from Bayesian analysis. In fact, a recent study carried out by Pearce et al. (2020) shows that under certain regularity conditions, the parameter distribution obtained from different local optima is a good approximation of the Bayesian posterior distribution. We conjecture that a combination with the bootstrap method discussed in Sect. 3.6 will further improve the uncertainty quantification, but a detailed investigation of this is beyond the remit of the present work. We note that the parameter distributions in Fig. 7 are reassuring. The true parameters are included in the bulk (rather than the tails) of the distributions, which confirms the consistency of our parameter estimation method, while the spreads of the distributions indicate the intrinsic uncertainty of parameter estimation.

3.8 Real data application

In this section, we apply our standard gradient matching (RKG) and ODE regularization (RKG3) methods to a real data set, the lynx and hare pelts collected by the Hudson’s Bay company in Canada at the beginning of the 20th century (Carpenter 2018). The Lotka–Volterra model is fit to Canadian lynx (predator) and snowshoe hare (prey) populations between 1905 and 1920, based on the number of pelts collected annually. The data and interpolation for both predator and prey are plotted in panels (a) and (b) of Fig. 8. By checking the QQ plots in Fig. 8, we observe that the residuals of the RKG method are skewed to the right, whilst the ODE regularization method achieves a better fit. Unlike the simulation examples in the previous section, where we know the true ODE parameters, the true parameters in this case are unknown. The parameter estimates from both methods are therefore fed back into the Lotka–Volterra system, and we compare the numerical solutions of the ODEs with the original data. The results are shown in Fig. 9. Both methods show reasonable agreement between the model prediction and the data. The numerical solutions from the RKG3 method have a better fit for the predator (\(x_1\)) in panel (a), whereas there is not much of a difference between both methods for the prey (\(x_2\)) in panel (b).

4 Summary

We have described the software implementation of a gradient matching method for parameter inference in ODEs, based on reproducing kernel Hilbert spaces (RKHS). The suite of options includes fast schemes based on traditional RKHS regularization, and more advanced approaches, which are based on time warping and a regularization of the interpolant by the ODEs themselves. Parameter estimation uncertainty is quantified with a method based on the residual bootstrap. All methods are illustrated on well-established benchmark ODE models from the literature, and we have shown how the tools can be applied and adapted by the user for parameter inference in their own ODE systems.