On the Degree of Irreversibility of Friction in Sheared Soft Adhesive Contacts

Abstract

A number of authors have experimentally assessed the influence of friction on adhesive contacts, and generally the contact area has been found to decrease due to tangential shear stresses at the interface. The decrease is however generally much smaller than that predicted already by the Savkoor and Briggs 1977 classical theory using “brittle” fracture mechanics mixed mode model extending the JKR (Griffith like) solution to the contact problem. The Savkoor and Briggs theory has two strong assumptions, namely that (i) shear tractions are also singular at the interface, whereas they have been found to follow a rather constant distribution, and that (ii) no dissipation occurs in the contact. While assumption (ii) has been extensively discussed in the Literature the role of assumption (i) remained unclear. We show that assuming entirely reversible slip at the interface with a constant shear stress fracture mechanics model leads to results almost indistinguishable from the Savkoor and Briggs model (and further in disagreement with experiments), hence it is assumption (ii) that critically affects the results. We analyze a large set of experimental data from Literature and show that the degree of irreversibility of friction can vary by orders of magnitude, despite similar materials and geometries, depending on the velocity at which the tangential load is applied.

1 Introduction

The application of fracture mechanics to contact problems starts with the Johnson Kendall & Roberts (JKR) model [1], which studied the contact of two adhesive elastic spheres, essentially extending the Griffith energy balance to the case where contact corresponds to the ligament of an external crack. This energy balance is well described by Maugis [2], including a full thermodynamic treatment, which essentially states that the contact area is defined by an equilibrium between the mode I “energy release rate” $G_{\rm I}$ and the reversible thermodynamic work of adhesion $w_{0}$ in mode I

$$G_{\rm I}=w_{0}.$$

(1)

More recently, a large interest has arisen in adhesion [3], particularly in the problem of the effect of frictional forces on adhesion [4,5,6,7,8,9,10,11,12,13]. The seminal paper of Savkoor and Briggs [14] extended the fracture mechanics model of contact of two adhesive elastic spheres to the case of mixed mode fracture (see Fig. 1ac), by considering both normal and tangential forces. Waters and Guduru [15] reworked Savkoor and Briggs analysis [14] for a sheared rigid sphere adhering to an elastic halfspace (see Fig. 1b) and stated the problem in terms of the two stress intensity factors $K_{\rm I}$ and $K_{\rm II}$ (mode I and mode II, given that mode III is eliminated by averaging along the periphery, see [15]), obtaining the following balance:

$$\frac{1}{2E^{\ast}}\left[ K_{\rm I}^{2}+\frac{(2-\nu )}{2\left( 1-\nu \right) }K_{II}^{2}\right] =w_{0},$$

(2)

where $\nu$ is Poisson’s ratio, E is the Young modulus and $E^{\ast}=E/\left( 1-\nu^{2}\right)$ is the composite elastic modulus of the halfspace. Savkoor and Briggs’ axisymmetric model contains two assumptions essentially:

• (i) that the stress field also in the shear direction is singular and

• (ii) that there is no dissipation due to friction, so that both mode I and mode II are entirely reversible processes.

Savkoor and Briggs model [14] turns out to be equivalent to the JKR model, but with a work of adhesion that is reduced of a quantity proportional to the square of the tangential load, yet in quantitative terms the reduction appeared too large with respect to experimental evidence [4, 9, 14, 15].

Fig. 1

a Fracture mechanics modes: sketch. b Schematic representation of a rigid sphere adhering to an elastic halfspace that is sheared by a tangential force T. c Schematic representation of the combination of modes at the periphery of the contact area in presence of adhesion and friction. (a) from [16] and c from [6]

In the light of obtaining a better agreement with experiments, various authors [5,6,7, 11, 15, 17,18,19,20] have adopted a practical approach which has some tradition in mixed mode fracture of interfaces which generally shows that the toughness strongly depended on the phase angle $\psi =\arctan \left( K_{\rm II}/K_{\rm I}\right),$ namely adopting a phenomenological mode-mixity function $f\left( \psi \right)$ to account for the dissipative effects happening at the interface, by increasing the apparent toughness of the interface [21,22,23,24] as:

$$w_{\rm c}=w_{0}f\left( \psi \right).$$

(3)

This obviously introduces an empirical (although phenomenological) function which permits to fit experiments although does not clarify in detail the relative importance of assumptions (i) and (ii) above.

In McMeeking et al. [10], the general energy balance was recently discussed for a sliding sphere under adhesion and friction, considering constant shear stress in the sliding regions, as supported by various experiments (see [11, 25, 26]). In McMeeking et al. [10], it was remarked that, when considering the effect of dissipation induced by friction slip, one should give up the attempts to use principles of minimum potential energy, which would be only correct if one had only reversible (conservative) forces, but nevertheless fracture mechanics principles can still be used. In short, it was concluded that if surface microstructures associated with frictional slip (such as interface dislocations) are not able to store any elastic strain energy in a reversible manner (that is, friction is entirely irreversible), then the adhesion problem follows exactly the JKR framework. However, in intermediate cases, one should recur to phenomenological models to separate reversible from irreversible contributions to friction in fitting the data points, as we shall attempt in the present note in detail.

While in Literature assumption (ii) has been widely discussed, the aim of this note is to assess the influence of assumption (i) in terms of a proper description of the physical problem, also in view of a quite large set of experimental data from the recent Literature.

2 The Model

Let us consider a rigid sphere adhering to a linear elastic soft halfspace and sheared by a tangential force T (see Fig. 1b). A quite general fracture mechanics energy balance can be written as an equality between the reversible strain energy release rates with the reversible work of adhesion $w_{0}$ [10]

$$\left( G_{\rm I}+G_{\rm II}\right)^{\rm re}=G_{\rm I}+\tau_{0}\overline{\delta_{0}}^{\rm re}=w_{0},$$

(4)

where $G_{\rm II}$ is the standard energy release rate of the mode I problem (which we assume entirely reversible as it is commonly done for JKR), and the second term comes from writing only the reversible part of $G_{\rm II},$ namely $G_{\rm II}^{\rm re}=\tau_{0}\overline{\delta_{0}}^{\rm re},$ using the equivalent of a Dugdale crack in mode II [27], where $\tau_{0}$ is the shear strength at the interface and $\overline{\delta_{0}}^{\rm re}$ is the reversible part of the slip displacement at the contact’s periphery averaged along the perimeter. From Savkoor PhD dissertation [28],¹ the total slip averaged at the contact’s periphery $\overline{\delta_{0}},$ the remote displacement D and the tangential loads T are, respectively,

$$\overline{\delta_{0}}=\frac{2}{\pi }\frac{2-\nu }{1-\nu }\frac{\tau_{0} }{E^{\ast}}a\left( \sqrt{1-\left( \frac{b}{a}\right)^{2}}\cos^{-1}\left( \frac{b}{a}\right) +\frac{b}{a}-1\right),$$

(5)

$$D=\frac{2-\nu }{1-\nu }\frac{\tau_{0}}{E^{\ast}}a\sqrt{1-\left( \frac{b}{a}\right)^{2}},$$

(6)

$$T=2\tau_{0}a^{2}\left( \frac{b}{a}\sqrt{1-\left( \frac{b}{a}\right)^{2}}+\cos^{-1}\left( \frac{b}{a}\right) \right),$$

(7)

where a is the contact radius, b is the radius of the sticking region and Eqs. (5,6,7) are valid in partial slip up to full sliding, i.e., for $D\le \frac{2-\nu }{1-\nu }\frac{\tau_{0}}{E^{\ast}}a.$

Figure 2 shows the shear force ratio $T/T_{\rm full}$ ((a), $T_{\rm full}=\tau_0\pi a^2$) and the total slip averaged on the crack periphery divided by the contact radius ${\overline{\delta }}_0/a$ ((b), $\tau_0/E^{\ast}=0.2$ as common in soft contacts [8]) as a function of b/a. For vanishing tangential load one has $b/a\approx 1,$ then by increasing T slip starts to advance within the contact circle and for $T=T_{\rm full}$ invades all the contact area $b/a=0.$

Fig. 2

a Shear force ratio $T/T_{\rm full}$ versus b/a, with $T_{\rm full}=\tau_0\pi a^2$ and b total slip averaged on the crack periphery divided by the contact radius ${\overline{\delta }}_0/a$ ($\tau_0/E^{\ast}=0.2$ in Eq. (5), which is a typical value in soft contacts) versus b/a

The calculation of mode I energy release rate for the standard JKR problem [2] gives

$$G_{\rm I}=\frac{K_{I}^{2}}{2E^{\ast}}=\frac{1}{2E^{\ast}}\left( \frac{P_{\rm a} }{2a\sqrt{\pi a}}\right)^{2}=\frac{1}{8\pi {E^{\ast}}a^{3}}\left( \frac{4E^{\ast}a^{3}}{\mathrm{3R}}-P\right)^{2},$$

(8)

where we have split the total load $P=P_{\rm H}-P_{\rm a}$ into two contributions: a compressive Hertzian load $P_{\rm H}=\frac{4{E^{\ast}}a^{3}}{\mathrm{3R}}$ and a Boussinesq flat punch solution with total load $P_{\rm a}$ which is responsible of the contact edge singularity.

Writing the condition (4), and moreover, assuming that the reversible part is a constant fraction of the total mode II energy release rate, one can define

$$\lambda =\frac{G_{\rm II}^{\rm re}}{G_{\rm II}}=\frac{\overline{\delta_{0}}^{\rm re}}{\overline{\delta_{0}}},$$

(9)

which also implies that the mode II energy dissipated by irreversible phenomena amount to $G_{\rm II}^{\rm irr} = (1-\lambda )G_{\rm II}.$ Condition (4) gives

$$\frac{1}{8\pi E^{\ast}a^{3}}\left( \frac{4E^{\ast}a^{3}}{3R}-P\right)^{2}+\lambda \tau_{0}\overline{\delta_{0}}=w_{0},$$

(10)

which however cannot be written simply in terms of tangential load.

Equation (10) helps in clarifying the difference between the cohesive model presented here and that in [18]. Johnson (see Eq. (4.4) in [18]) assumed that all mode II energy release rate $G_{\rm II}$ is available for the external crack to advance and introduced a mode-mixity function to account for an increased interface toughness under mode-mixed loading. Here a different assumption is made. It is not the interface toughness that is increased, rather it is the reversible mode II energy release rate $G_{\rm II}^{\rm rev},$ available for the external crack to advance, that is only a small fraction of the total mode II energy release rate $G_{\rm II}.$ The simplest assumption, in the lack of further information, is to assume that $\lambda =G_{\rm II}^{rev}/G_{\rm II}$ is constant (Eq. (9)). For further details and in depth discussion the reader is referred to [10].

As in McMeeking et al. [10], the Linear Elastic Fracture Mechanics LEFM limit can be obtained when slip is limited (i.e., $b/a\approx 1$) as:

$$\overline{\delta_{0}}_{\rm LEFM}=\frac{(2-\nu )}{2(1-\nu )}\frac{T^{2} }{8\pi \tau_{0}E^{\ast}a^{3}}.$$

(11)

Hence, in the LEFM limit, Eq. (10) gives

$$P=\frac{4E^{\ast}a^{3}}{3R}-\sqrt{8\pi a^{3}E^{\ast}w_{0}-\lambda \frac{(2-\nu )}{2(1-\nu )}T^{2}}.$$

(12)

More in general the Dugdale crack cohesive model [27] can be elucidated with respect to the LEFM limit. From Eq. (5,11) the ratio $\overline{\delta_{0}}/\overline{\delta_{0}}_{\rm LEFM}$ can be written as:

$$\frac{\overline{\delta_{0}}}{\overline{\delta_{0}}_{\rm LEFM}} =8 \frac{\left( \sqrt{1-\left( \frac{b}{a}\right)^{2}}\cos^{-1}\left( \frac{b}{a}\right) +\frac{b}{a}-1\right) }{\left( \frac{b}{a}\sqrt{1-\left( \frac{b}{a}\right)^{2}}+\cos^{-1}\left( \frac{b}{a}\right) \right)^2},$$

(13)

where we used Eq. (7), which using $T_{\rm full}=\pi \tau_{0}a^{2},$ can be written as follows:

$$\frac{T}{T_{\rm full}} =\frac{2}{\pi }\left( \frac{b}{a}\sqrt{1-\left( \frac{b}{a}\right)^{2}}+\cos^{-1}\left( \frac{b}{a}\right) \right).$$

(14)

Hence, by varying b/a from 0 to 1, one can derive a parametric corrective function $h(T/T_{\rm full})$ that links the average slip at the contact’s periphery in the Dugdale cohesive model $\overline{\delta_{0}}$ with that in the LEFM limit $\overline{\delta_{0}}_{\rm LEFM}$ (see Fig. 3)

$$\overline{\delta_{0}}=\overline{\delta_{0}}_{\rm LEFM}h\left( \frac{T}{T_{\rm full}}\right) =\frac{(2-\nu )}{2(1-\nu )}\frac{T^{2}}{8\pi \tau_{0}E^{\ast}a^{3}}h\left( \frac{T}{T_{\rm full}}\right).$$

(15)

From Eq. (10), we could write

$$P=\frac{4E^{\ast}a^{3}}{3R}-\sqrt{8\pi a^{3}E^{\ast}w_{0}-\frac{(2-\nu )}{2(1-\nu )} \lambda T^{2}h\left( T\right) }.$$

(16)

Figure 3 shows that the corrective function $h\left( \frac{T}{T_{\rm full}}\right)$ starts from 1 at ${T}/T_{\rm full}=0$ as indeed for vanishing tangential load $a\approx b$ and the cohesive Dugdale model coincides with the LEFM model. By increasing the shearing load $h\left( \frac{T}{T_{\rm full}}\right)$ increases monotonically, hence the average slip at the contact’s periphery in the full Dugdale cohesive model is greater than in the LEFM limit, which means that a fully reversible cohesive model leads to reduction of contact area stronger than the Savkoor and Briggs model.

Fig. 3

Non-dimensional corrective function $h\left( T/T_{\rm full}\right)$ versus the ratio $T/T_{\rm full},$ being $T_{\rm full}=\tau_{0}\pi a^{2}$

The energy balance in Eq. (4) can be equivalently recast in terms of a mode-mixity function (see Appendix 1 for the full derivation) as:

$$\left[ G_{\rm I}+\lambda \tau_{0}\overline{\delta_{0}}\right] =w_{0} \Leftrightarrow \left[ G_{\rm I}+\tau_{0}\overline{\delta_{0}}\right] =w_{0}f\left( \psi \right),$$

(17)

where

$$\begin{aligned}f\left( \psi \right) & = \left[ 1+\left( \lambda -1\right) \sin^{2}\left( \psi \right) \right]^{-1},\\ \psi & = \arctan \left( \sqrt{\frac{\tau_{0}\overline{\delta_{0}}}{G_{\rm I}}}\right) =\arctan \left( \frac{T\sqrt{\frac{(2-\nu )}{2(1-\nu )}h\left( T\right) }}{\frac{4E^{\ast}a^{3}}{3R}-P}\right).\end{aligned}$$

(18)

The equilibrium condition is then written as:

$$P=\frac{4E^{\ast}a^{3}}{3R}-\sqrt{8\pi E^{\ast}a^{3}w_{0}f\left( \psi \right) - \frac{(2-\nu )}{2(1-\nu )}T^{2}h\left( T\right) },$$

(19)

which is mathematically equivalent to Eq. (16). Notice that for a pure LEFM model (singular shear traction distribution) $h\left( T\right) =1$ in both Eqs. (19) and (18), and that the equilibrium condition (19) corresponds to the classical model by Savkoor and Briggs [14] when one poses $f\left( \psi \right) =h\left( T\right) =1.$

3 Fit of Experimental Results

3.1 Detailed Analysis of Experimental Observations

We discuss the proposed cohesive model in light of recent experimental results published by Mergel et al. [8] (see their Fig. 5c). Mergel and coauthors studied the contact of a polydimethylsiloxane (PDMS) hemispherical cap that is in contact with a smooth glass plate (this is equivalent to the model presented in Section 2) and is sheared by a tangential force T. The elastic and adhesive properties of the contact pair are: $w_{0}=27$ mJ/m² $R=9.42$ mm, $\nu =1/2,$$E^{\ast}=2.133$ MPa. To determine the parameter $\lambda$ that best fits the experimental data, it is convenient to use the equilibrium condition as written in Eq. (19). From Mergel et al. [8] experimental data, we calculated the dimensionless interfacial toughness

$$\frac{w_{c}}{w_{0}}=\frac{\left( \frac{4E^{\ast}a^{3}}{3R}-P\right)^{2}+\frac{3}{2}T^{2}h\left( T\right) }{8\pi E^{\ast}a^{3}w_{0}}$$

(20)

and then used Eq. (18) to fit the data. An example on how the data are fitted is shown in Fig. 4 for the experimental data corresponding to the normal loads²$P=\left[ 7.74,1.59,-\,0.06\right]$ mN, respectively, (a, b), (c, d), (e, f). In Fig. 4 we plot the measured $w_{\rm c}/w_{0}$ as a function of $\psi$ (markers) and the fitted curves (red solid curve) using both the LEFM model (a, c, e) and the Dugdale crack cohesive model (b, d, f). As shown in Fig. 4, the experimental data are very well fitted by Eq. (18) ($R^{2}>0.999$) for the three different normal loads and along all the range of variation of the phase angle $\psi.$ The best-fitted $\lambda$ are reported in Table 1 for each normal load and for both the models.

Fig. 4

The ratio $w_{\rm c}/w_{0}$ as a function of $\psi$ as obtained from Mergel et al. [8] experimental results (markers) and fitted by Eq. (18) (red solid curve). The reported data are obtained for $P=\left[ 7.74,1.59,-0.06\right]$ mN, respectively, panels (a, b), (c, d), (e, f). Data are fitted on the left column (a, c, e) with the LEFM model, while on the right column (b, d, f) with the equivalent Dugdale crack cohesive model (Color figure online)

Table 1 Best-fitted $\lambda$ obtained for both the Dugdale and LEFM model

We used the fitting procedure explained above to fit the experimental data in Mergel et al. [8] for the normal $\hbox{loads}^{2}$$P=\left[ 7.74,3.81,2.92,1.59,0.95,0.51,-\,0.06,-\,0.46\right]$ mN. In Fig. 5, the area versus tangential load curves are reported as obtained from experiments (markers) and as fitted by the LEFM model (black dashed line) and the equivalent Dugdale crack cohesive model (red solid line). Notice that a completely reversible mode II energy release rate ($\lambda =1,$ gray dot-dashed lines) leads clearly to a very poor comparison between experiments and theory. This is because, as shown in Table 1, the best-fitted $\lambda$ are very small for this set of experiments, i.e., the degree of irreversibility of friction is extremely high and the contact shrinking cannot be captured by assuming a full reversible slip at the interface. Furthermore, no advantage is gained in using the LEFM or the Dugdale model, as the differences between the two models cannot be appreciated (gray dot-dashed lines). Instead, when using the $\lambda$ obtained from the best-fit procedure applied to each normal load, assuming a singular shear traction distribution does not affect much the quality of the fit as both the LEFM (black dashed lines) and Dugdale (red solid lines) model quite satisfactorily fit the experimental data. In particular, the two models are nearly identical for low shearing loads T and for the lighter normal loads, while small differences between the two models can be appreciated for higher normal loads (say $P>1$ mN) and in the proximity of the point of instability to full sliding.

Fig. 5

Contact area as a function of the tangential load for the normal loads $P=\left[ 7.74,3.81,2.92,1.59,0.95,0.51,-0.06,-0.46\right]$ mN where the gray dot-dashed curves are obtained with $\lambda =1$ (the two models are indistinguishable) while the solid red lines (dashed black lines) are the theoretical predictions for the Dugdale crack (LEFM) model using the best-fitted $\lambda.$ The experimental data from [8] (their Fig. 5(c)) are reported as colored markers. For $P=\left[ 7.74,1.59,-0.06\right]$ mN the best-fitted $\lambda$ are reported in Table 1 (Color figure online)

3.2 Comparison with More Literature data

To allow a broader comparison with experimental data, we used the proposed model to fit a wider set of experimental results on the decay of contact area under shearing loads obtained from Literature results [4, 8, 14, 15]. A summary of the data source, materials used, composite elastic modulus $E^{\ast},$ surface energy $w_{0},$ sphere radius R,  and imposed tangential displacement rate v (i.e., the velocity at which the tangential loading arm is actuated) are reported in Table 2.

All the experimental data have been obtained using similar experimental test rigs, which consist in a hemispherical cap (PDMS or Rubber, see Table 2) that is pressed against a glass flat plate. In a usual experiment, the hemisphere is first loaded in the normal direction up to a specified normal load and then a certain constant velocity v (see Table 2) is applied at the tangential loading arm that transfers the shearing load to the interface. The mentioned procedure has two exceptions. First: in Savkoor and Briggs [14] the tangential load was applied step-wise, with each step approximately equal to $\sim\, 2.5$ mN and with 1 minute pause between one step and the other. We considered this procedure Quasi-STatiC (QSTC in Table 2). Second: in Waters and Guduru [15] the hemisphere was first loaded, then unloaded up to a specified normal load and then sheared tangentially.

Table 2 Summary of the experimental data used to populate Fig. 5

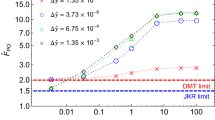
Following the procedure described in the previous subsection, we have determined the best-fitted $\lambda$ for each set of experimental data in Table 2 (within the same data-set, experiments are performed at different normal loads) using both the Dugdale (filled symbols) and the LEFM (open symbols) model. The best fitted $\lambda$ are reported in Fig. 6 (see Fig. 6 caption for the markers) for a range of normal loads between $P\simeq -10$ mN and $P\simeq 2500$ mN. Figure 6 shows that the values of $\lambda$ obtained may vary drastically from one experiment to the other of various orders of magnitude, nevertheless $\lambda$ remains almost constant for a given experiment (same markers are grouped together). Furthermore, all the data obtained at Tribology and System Dynamics Laboratory (LTDS, École Centrale de Lyon) with similar equipment/materials/procedure [data-set (c, d) respectively down-pointing triangle and circles] gave very similar values of $\lambda,$ of the order of $10^{-3},$ with small differences between the Dugdale and the LEFM model that should be ascribed to function $h\left( T\right).$ Waters and Guduru [15] data (set (b), squares) gives a larger but almost constant value of $\lambda ,$ about $10^{-1},$ while [14] data (set (a), triangles) are in the range $0.3<\lambda <1.$ We notice here that these data sets (a, b) are also those with larger hemisphere radius and that Savkoor and Briggs data are showing more scatter compared to the other sets. The authors themselves provide a different value of work of adhesion for each normal load justifying this with the extreme sensitivity of the experimental results to the exact surface conditions.

Fig. 6

Best fitted $\lambda$ as a function of the normal load extracted from the data-set in Table 2 using both the Dugdale (filled symbols) and the LEFM (open symbols) model. Data Source [8] circles, [15] squares, [14] up-pointing triangles, [4] down-pointing triangle

Although it is not possible to draw general conclusions on the effect of all the parameters $\left( E^{\ast},w_{0},R,\;\right)$ on the amount of reversible tangential slip, we emphasize that for PDMS Waters and Guduru [15] showed a strong dependence of $\lambda$ on the rate v at which the tangential load is applied (v is the velocity at which the loading arm is actuated). Figure 7 shows that the values of $\lambda$ obtained for the data-set (b, c, d) scale very well with the velocity v and are in line with Literature results (stars) by Waters and Guduru [15] (data extracted from their Fig. 10b). Notice that the latter values of $\lambda$ (stars in Fig. 7), were obtained by Waters and Guduru [15] using a different mode-mixity function with respect to that used here (18). Nevertheless Waters and Guduru [15] used only the data where circular symmetry of the contact patch was observed, i.e., for low phase angles ($\psi \lesssim \pi /3,$ see their Fig. 9–10). It has been shown in [6] that all the mode-mixity functions introduced in [23, 24] (and used so far in the contact mechanics Literature) start quadratic at low $\psi$ and, for small $\lambda,$ are almost indistinguishable one from the other (see Fig. 7 in [6]), hence it is reasonable to carry out the comparison in Fig. 7.

The physical processes responsible for the observed increase in the degree of irreversibility may be of different nature. Here “irreversible” is associated with all phenomena which degrade energy, transforming it into heat. If there is a slipped region surrounded by an unslipped region, the perimeter will be a “dislocation line” having edge character in some places and screw character elsewhere around the periphery, and its Burger vector can be arbitrary since such interface dislocations are not true lattice dislocations. The reversibility may be associated with patches where the slip is different from the average slip, hence when such heterogeneities are relaxed some of the stored elastic energy can get back reversibly to contribute to the contact shrinking process. The scaling of $\lambda$ with sliding velocity may be consistent with viscoelastic effects, as in classical models for normal unloading of viscoelastic solids [30] and as pointed out by Waters and Guduru in their early work [15]. Notice that for Savkoor and Briggs data [14] the highest values for $\lambda$ ($\ge\,0.3,$ see Fig. 6) were obtained, which agrees well with their quasi-static loading procedure. It is noticed that this seems in contrast with the results of Vorvolakos and Chaudhury [31] who showed that the contact area of a PDMS sphere in full sliding remained constant up to $v_{\rm full}\approx 10^{-3}$ m/s and then decreases at the Hertzian value for larger relative speed, which would imply a more reversible process at higher speed. This discrepancy calls for further investigations. Nevertheless their experiments were performed in the full-sliding regime (while we have considered tests with local micro-slip) with sliding velocity $v_{\rm full}$ up to $\sim\,10^{-1}$ m/s which is three orders of magnitude larger then the highest loading velocity v we have considered here ($10^{-4}$ m/s), hence different physical mechanisms for contact area reduction may be at play.

The model presented here is based on Liner Elastic Fracture Mechanics, as such, its validity should be restricted to the range of low normal loads. Indeed, recent results suggest that adhesion plays an important role for light normal loads (see Fig. 13c in Mergel et al. [13]), while for higher normal loads nonlinear effects should be taken into account [12, 13]. The relative weight of the two effects (adhesion and finite deformations) is still debated in Literature.

Fig. 7

Best fitted $\lambda$ as a function of the rate at which the tangential displacement is applied to the loading arm for the data-set (b–e) in Table 2 using the Dugdale model. Data source [15] squares, [4] down-pointing triangle, [8] circles. The stars represent the results obtained by Waters and Guduru [15] as reported in their Fig. 10b

4 Conclusions

In this work, we have revisited the classical problem of an adhesive sphere under shearing loads, particularly with the aim to highlight what is the relative role of the assumptions which are often made in theoretical models: (i) that shear tractions are singular at the interface (LEFM model), whereas they have been found to follow a rather constant distribution, and that (ii) no dissipation occurs in the contact. We have shown that relaxing assumptions (i) alone does not lead to a better description of the physical problem. Instead, it is of outmost importance to provide a faithful description of the dissipation that occurs in the tangential direction. By analyzing a large set of experimental data from the Literature, we found that generally data from the same experimental set-up group together and show negligible dependence on the normal load, even when it is varied from the order of mN to N. By considering all the available experimental data, we have shown that the reversible fraction of mode II energy release rate “$\lambda$” scales very well (power law) with the velocity at which the tangential load is applied. In particular, we have shown that the process becomes almost completely irreversible $\left( \lambda \rightarrow 0\right)$ at large velocity. It would be interesting to understand more about the dependence of $\lambda$ on the material and geometry of the contact pair, as otherwise the fracture mechanics theory remains rather limited by the need to perform experiments on the actual case study, where the need to measure the contact area limits the possible experiments to transparent materials for example.

Appendix 1

Deriving equations (18) requires some algebra. From the equilibrium condition (4)

$$\left( G_{\rm I}+\lambda \tau_{0}\overline{\delta_{0}}\right)=w_{0} \rightarrow$$

(21)

$$\left( G_{\rm I}+\tau_{0}\overline{\delta_{0}}\right)=w_{0}\frac{\left( 1+\frac{\tau_{0}\overline{\delta_{0}}}{G_{\rm I}}\right) }{\left( 1+\lambda \frac{\tau_{0}\overline{\delta_{0}}}{G_{\rm I}}\right)} \rightarrow$$

(22)

$$\left(G_{\rm I}+\tau_{0}\overline{\delta_{0}}\right)=w_{0}\frac{1+\frac{\tau_{0}\overline{\delta_{0}}}{G_{\rm I}}}{1+\frac{\tau_{0}\overline{\delta_{0}}}{G_{\rm I}}+\left( \lambda -1\right) \frac{\tau_{0}\overline{\delta_{0}}}{G_{\rm I}}} \rightarrow$$

(23)

$$\left(G_{\rm I}+\tau_{0}\overline{\delta_{0}}\right)= w_{0}\frac{1}{1+\left( \lambda -1\right) \frac{\frac{\tau_{0} \overline{\delta_{0}}}{G_{\rm I}}}{1+\frac{\tau_{0}\overline{\delta_{0}}}{G_{\rm I}}} } \rightarrow$$

(24)

$$\left( G_{\rm I}+\tau_{0}\overline{\delta_{0}}\right)=w_{0}\left[ 1+\left( \lambda -1\right) \sin^{2}\left( \psi \right) \right]^{-1},$$

(25)

where we used the identity $\sin \left( \arctan \left( x\right) \right)^{2}=\frac{x^{2}}{1+x^{2}}.$ Hence the mode-mixity function $f(\psi )$ is written as:

$$f\left(\psi \right) =\left[ 1+\left( \lambda -1\right) \sin^{2}\left( \psi \right) \right]^{-1}$$

(26)

and the phase angle

$$\psi =\arctan \left( \sqrt{\frac{\tau_{0}\overline{\delta_{0}}}{G_{\rm II}} }\right) =\arctan \left( \frac{T\sqrt{\frac{(2-\nu )}{2(1-\nu )} h\left( T\right) }}{\frac{4E^{\ast}a^{3}}{3R}-P}\right),$$

(27)

where we used Eq. (8) and (15). Notice that as Eq. (211) is equivalent to Eq. (25) also the equilibrium equations (16) and (19) in the main text are exactly equivalent.