Qubit coherence effects in a RbCl quantum well with asymmetric Gaussian confinement potential and applied electric field

Abstract

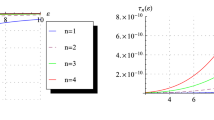
We theoretically investigate the coherent time of a single qubit in a RbCl quantum well (QW) with asymmetric Gaussian confinement potential (AGCP) using the Pekar-type variational method. Additionally, we utilize Fermi’s golden rule to consider strong coupling between electrons and longitudinal optical phonons in the QW with an electric field applied. The results show that the coherence time changes with AGCP QW’s height, height of the QW, polaron radius and electric field. Moreover, we also show that the coherence time is minimized to $\tau = 412.0\;{\text{ps}}$ in a confinement potential range $R = 0.19\;{\text{nm}}$. Thus we conclude that these tunable parameters of the QW are vital for adjusting the coherence time and deciding the stability of the qubit.

Appendix

Acorrding to trial ground and first excited state wavefunctions of electron and phonon system (polaron)

$$ \varphi_{0} = \pi^{{ - \frac{{3}}{4}}} \lambda_{0}^{{\frac{{3}}{2}}} \exp \left[ { - \frac{{\lambda_{0}^{2} r^{2} }}{2}} \right]\left| {0_{ph} } \right\rangle , $$

(A1)

$$ \varphi_{1} = \left( {\frac{{\pi^{3} }}{4}} \right)^{{ - \frac{{1}}{4}}} \lambda_{1}^{{\frac{{5}}{2}}} r\cos \theta \exp \left( { - \frac{{\lambda_{1}^{2} r^{2} }}{2}} \right)\exp \left( { \pm i\phi } \right)\left| {0_{ph} } \right\rangle , $$

(A2)

we can calculate the ground and first-exited energies of polaron. Form (A1) and (A2), we also choose trial ground and first excited state wavefunctions of electron $\left| 0 \right\rangle = \pi^{{ - \frac{{3}}{4}}} \lambda_{0}^{{\frac{{3}}{2}}} \exp \left[ { - \frac{{\lambda_{0}^{2} r^{2} }}{2}} \right]$ and $\left| 1 \right\rangle = \left( {\frac{{\pi^{3} }}{4}} \right)^{{ - \frac{{1}}{4}}} \lambda_{1}^{{\frac{{5}}{2}}} r\cos \theta \exp \left( { - \frac{{\lambda_{1}^{2} r^{2} }}{2}} \right)\exp \left( { \pm i\phi } \right)$ with $\left\langle 0 \right.\left| 0 \right\rangle = 1$, $\left\langle 1 \right.\left| 1 \right\rangle = 1$, $\left\langle 0 \right.\left| 1 \right\rangle = 0$.

For a QW with AGCP, these energies can be expressed as:

$$ \begin{aligned} E_{0} & = \left( {\varphi_{0} ,U^{ - 1} HU\varphi_{0} } \right) \\ & = \frac{{3\hbar^{2} }}{4m}\lambda_{0}^{2} - V_{0} \left( {1 + \frac{{1}}{{2\lambda_{0}^{2} R^{2} }}} \right)^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} - \frac{{\sqrt \pi e^{ * } }}{{2\lambda_{0} }}F - \frac{\sqrt 2 }{\sqrt \pi }\alpha \hbar \omega_{LO} \lambda_{0} r_{0} , \\ \end{aligned} $$

(A3)

$$ \begin{aligned} E_{1} & = \left( {\varphi_{1} ,U^{ - 1} HU\varphi_{1} } \right) \\ & = \frac{{5\hbar^{2} }}{4m}\lambda_{1}^{2} - V_{0} \left( {1 + \frac{{1}}{{2\lambda_{1}^{2} R^{2} }}} \right)^{{ - \frac{{3}}{2}}} - \frac{{\sqrt \pi e^{ * } }}{{2\lambda_{1} }}F - \frac{3\sqrt 2 }{4\sqrt \pi }\alpha \hbar \omega_{LO} \lambda_{1} r_{0} . \\ \end{aligned} $$

(A4)

Therefore, the energy-level separation is written as

$$ \Delta E = E_{1} - E_{0} $$

(A5)

Appling Eqs. (A1), (A2) and (A5), we can obtain the coherence time.

Based on the electric dipole approximation and FGR [21], the coherence time can be expressed by the spontaneous emission rate [22]

$$ \tau^{{{ - }1}} = \frac{{e^{2} \left( {E_{1} - E_{0} } \right)}}{{\varepsilon_{0} \hbar^{2} C^{3} }}\left| {\left( {\varphi_{0} ,e^{{ - i\varvec{k} \cdot \varvec{r}}} \cdot \varvec{p}\varphi_{1} } \right)} \right|^{2} . $$

(A6)

We can now expand the $e^{{ - i\varvec{k} \cdot \varvec{r}}} \approx 1 - i\varvec{k} \cdot \varvec{r} + \ldots$ term to allow us to compute matrix element more easily. Since the $\varvec{k} \cdot \varvec{r} \approx \frac{\alpha }{2}$ and the matrix element is squared, our expansion will be in powers of $\alpha^{2}$ which is a small number. The dominant decays will be those form the zearth order approximation which is $e^{{ - i\varvec{k} \cdot \varvec{r}}} \approx 1$.

Due to the Hamiltonian and $\varvec{r}$ in satisfying relationship of $\left[ {H,\varvec{r}} \right] = \frac{\hbar }{i}\frac{\varvec{p}}{m}$, we can write $\varvec{p} = \frac{im}{\hbar }\left[ {H,\varvec{r}} \right]$ in terms of the commutator.

$$ \begin{aligned} & \left( {\varphi_{0} ,e^{{ - i\varvec{k} \cdot \varvec{r}}} \cdot \varvec{p}\varphi_{1} } \right) \approx \left( {\varphi_{0} ,\varvec{p}\varphi_{1} } \right) \\ & \quad = \frac{im}{\hbar }\left( {\varphi_{0} ,\left[ {H,\varvec{r}} \right]\varphi_{1} } \right) \\ & \quad = \frac{{im\left( {E_{1} - E_{0} } \right)}}{\hbar }\left( {\varphi_{0} ,\varvec{r}\varphi_{1} } \right) \\ & \quad = \frac{{im\left( {E_{1} - E_{0} } \right)}}{\hbar }\left\langle 0 \right|\varvec{r}\left| 1 \right\rangle \\ \end{aligned} $$

(A7)

Thus, the spontaneous emission rate is expressed as

$$ \tau^{{{ - }1}} = \frac{{e^{2} \left( {E_{1} - E_{0} } \right)^{3} }}{{\varepsilon_{0} \hbar^{4} C^{3} }}\left| {\left\langle 0 \right|\varvec{r}\left| 1 \right\rangle } \right|^{2} . $$

(A8)

Here, we put the $\left| 0 \right\rangle$ and $\left| 1 \right\rangle$ into $\left| {\left\langle 0 \right|\varvec{r}\left| 1 \right\rangle } \right|^{2} .$

We first operate the

$$ \left\langle 0 \right|\varvec{r}\left| 1 \right\rangle = 4^{{\frac{{5}}{4}}} \pi^{{ - \frac{{1}}{2}}} \lambda_{0}^{{\frac{{3}}{2}}} \lambda_{0}^{{\frac{{5}}{2}}} \exp \left( { \pm i\phi } \right)\int_{0}^{\infty } {\exp \left( { - \frac{{\lambda_{0}^{2} r^{2} }}{2}} \right)\exp \left( { - \frac{{\lambda_{1}^{2} r^{2} }}{2}} \right)} r^{4} {\text{d}}r $$

(A9)

$$ \int_{0}^{\infty } {\exp \left( { - \frac{{\lambda_{0}^{2} r^{2} }}{2}} \right)\exp \left( { - \frac{{\lambda_{1}^{2} r^{2} }}{2}} \right)} r^{4} {\text{d}}r = \frac{{3}}{8}\frac{\sqrt \pi }{{\left( {\frac{{1}}{2}\left( {\lambda_{0}^{2} + \lambda_{1}^{2} } \right)} \right)^{2} \sqrt {\frac{{1}}{2}\left( {\lambda_{0}^{2} + \lambda_{1}^{2} } \right)} }} $$

(A10)

Substitute formula (A10) into formula (A9), (A9) is changed as

$$ \left\langle 0 \right|\varvec{r}\left| 1 \right\rangle = \frac{{12\lambda_{0}^{{\frac{{3}}{2}}} \lambda_{0}^{{\frac{{5}}{2}}} }}{{\left( {\frac{{1}}{2}\left( {\lambda_{0}^{2} + \lambda_{1}^{2} } \right)} \right)^{2} \sqrt {\frac{{1}}{2}\left( {\lambda_{0}^{2} + \lambda_{1}^{2} } \right)} }} $$

(A11)

$$ \left| {\left\langle 0 \right|\varvec{r}\left| 1 \right\rangle } \right|^{2} = \frac{{144\lambda_{0}^{3} \lambda_{0}^{5} }}{{\left( {\lambda_{0}^{2} + \lambda_{1}^{2} } \right)^{5} }} $$

(A12)

We put formula (A12) into formula (A9)

$$ \tau^{{{ - }1}} = \frac{{e^{2} \left( {E_{1} - E_{0} } \right)^{3} }}{{\varepsilon_{0} \hbar^{4} C^{3} }}\left| {\left\langle 0 \right|\varvec{r}\left| 1 \right\rangle } \right|^{2} = \frac{{e^{2} \left( {E_{1} - E_{0} } \right)^{3} }}{{\varepsilon_{0} \hbar^{4} C^{3} }}\frac{{144\lambda_{0}^{3} \lambda_{0}^{5} }}{{\left( {\lambda_{0}^{2} + \lambda_{1}^{2} } \right)^{5} }} $$

(A13)