Effective boundary conditions at a rough wall: a high-order homogenization approach

Abstract

Effective boundary conditions, correct to third order in a small parameter $\epsilon$, are derived by homogenization theory for the motion of an incompressible fluid over a rough wall with periodic micro-indentations. The length scale of the indentations is l, and $\epsilon = l/L \ll 1$, with L a characteristic length of the macroscopic problem. A multiple scale expansion of the variables allows to recover, at leading order, the usual Navier slip condition. At next order the slip velocity includes a term arising from the streamwise pressure gradient; furthermore, a transpiration velocity ${\mathcal {O}}(\epsilon ^{2})$ appears at the fictitious wall where the effective boundary conditions are enforced. Additional terms appear at third order in both wall-tangent and wall-normal components of the velocity. The application of the effective conditions to a macroscopic problem is carried out for the Hiemenz stagnation point flow over a rough wall, highlighting the differences among the exact results and those obtained using conditions of different asymptotic orders.

1 Introduction

The definition of the boundary conditions at a solid, impermeable wall in contact with an incompressible viscous fluid has occupied researchers even before the Frenchman Henri Navier first derived the equations which now bear his name. In his seminal 1823 paper, Navier [1] argued that the viscous force exerted by the fluid onto a wall is balanced by the resistance opposed by the wall, the latter being proportional to a slip velocity. If the wall-normal direction is denoted by Y and the wall-tangent velocity by U, the slip velocity reads:

$$\begin{aligned} U=\epsilon \lambda ^{x}U_{Y}, \end{aligned}$$

(1)

with the Navier constant, $\lambda ^{x}$, an effective penetration depth, equal to the distance into the wall where the linearly extrapolated velocity component actually vanishes. The small parameter $\epsilon$ is defined later. In the equation above, and in the following ones, an independent variable used as subscript denotes partial differentiation with respect to that variable.

Navier’s condition was challenged and argued upon for one hundred years, until Taylor [2] settled the issue with a series of experiments on the flow between concentric, differentially rotating cylinders, near the onset of the first hydrodynamic instability. Taylor theoretical treatment, which provided results in excellent agreement with the experiments, was based on the idea that the fluid could not slip when in contact with the solid surface. From that moment on, the no-slip condition gained (almost) universal acceptance. Configurations for which a slip condition remained in use included the triple-line flow (for example, to describe the leading edge motion of a liquid drop sliding down an incline), the flow of rarified gases, for example in micro-fluidic devices (in this case Navier’s condition is often associated to Maxwell’s name), or the flow over micro-corrugated surfaces, eventually impregnated with a lubricant fluid (for a recent review the reader is referred to [3]). All of these exceptional cases share the peculiarity that the continuum description of the flow either breaks down or becomes too difficult/expensive to be resolved, e.g. by a computational technique, so that a conjugate, microscopic-macroscopic, view becomes preferable. These are the cases in which a homogenization strategy proves very valuable.

The present paper is dedicated to describing an upscaling approach to derive effective boundary conditions near a rough wall, so that in a practical application the rough wall can be replaced by a smooth, fictitious surface over which the flow can slip and through which transpiration is possible, yielding in the bulk of the domain the same result as the real, rough wall. This strategy permits to capture micro-scale effects avoiding the prohibitively expensive numerical resolution of microscopic flow structures. Like in most of the previous studies, the rough pattern is assumed to repeat itself periodically over a scale much shorter than a characteristic dimension of the macroscopic flow; this renders the problem amenable to a multiple-scale description [4]. As opposed to the literature reviewed below, the effective conditions obtained here are correct to third order in terms of a small parameter, ratio of microscopic to macroscopic length scales. Thus, the present model describes more accurately than previous conditions available in the literature the effect of the asymptotic small scales onto the large-scale flow. As a significant result, it will be shown that all of the parameters entering the boundary conditions at second order arise from the numerical resolution of a unique microscopic Stokes problem; at third order a few additional auxiliary systems must be solved.

The need to have accurate models of the flow near patterned walls is especially felt when the motion is turbulent, as it occurs in multiple applications. Then, it is known that skin friction drag usually increases, when comparing to the smooth-wall case under identical conditions, except for cleverly-designed wall patterns. Examples of the latter include riblets [5,6,7,8] and other nature-inspired wall indentations [9,10,11,12]. Provided the roughness is embedded within the viscous sublayer, the effective rough-wall conditions develop herein will permit to carry out, at a fraction of the time, parametric searches of regular surface patterns apt, for example, at minimizing skin friction.

The most important early publication describing the application of a two-scale expansion to infer effective conditions at a rough wall is due to Achdou et al. [13]. These authors focussed on the two-dimensional, incompressible case and derived conditions to second order in terms of the small parameter $\epsilon$, a measure of the relative roughness size. For later comparison, the (nonlinear) conditions in [13] to be enforced at some effective surface read:

$$\begin{aligned} U= & {} \epsilon \lambda ^{x}U_{Y}-\epsilon ^{2}[\xi P_{X}+\chi U^{2}], \end{aligned}$$

(2)

$$\begin{aligned} V= & {} 0, \end{aligned}$$

(3)

with P the pressure. The constants $\lambda ^{x}$, $\xi$ and $\chi$ arise from the solution of Stokes-like problems in a periodic unit cell built around a single roughness element. For the macroscopic laminar flow configurations tested in their paper, Achdou and colleagues obtained good results when comparing against complete simulations, leading them to state that the first-order condition is already very accurate, and to conclude that it is not sure that it is worth using the second-order condition. We will argue below that the condition (3) is not second-order accurate.

Subsequent developments did not follow the path initiated by Achdou and collaborators, and were mostly limited to examining various aspects of the Navier condition. For example, Jäger and Mikelić [14] gave a rigorous justification of Navier slip for the flow in a plane channel, and conducted asymptotic estimates of the tangential drag force and the effective mass flow rate. Basson and Gérard-Varet [15] used stochastic homogenization to extend the previous analysis to the case of a channel flow with roughness modeled by a spatially homogeneous random field. Kamrin et al. [16], using different scaling variables from those employed here, recovered a tensorial form of Navier slip for the flow over periodic surfaces as a second-order approximation. They introduced a mobility tensor ${\varvec{\Lambda }}$ (or Navier slip tensor) and, after decomposing the wall in Fouries series, provided a formula for ${\varvec{\Lambda }}$, demonstrating its symmetry. Luchini [17] extended the analysis by considering two configurations. In the first, named the shallow-roughness limit, the surface considered was $Y=\epsilon H$(X,  Z), i.e. the roughness becomes smoother as $\varepsilon \rightarrow 0$. The second limit, named the small-roughness limit, was concerned with a family of surfaces defined by $Y=\epsilon H$($X/\epsilon ,$$Z/\epsilon$) i.e. a pattern which remains geometrically similar to itself with varying $\epsilon$. Luchini’s first-order analysis accounted for the effect of the roughness aspect ratio via a protrusion coefficient and for the interference between equal roughness elements placed in a periodic arrangement via a proximity coefficient. Aspects connected to heat transfer and concentration gradients across heterogeneous and rough boundaries were studied by Introïni et al. [18] and Guo et al. [19] by an upscale analysis based on volume-averaging theory. Also in this case, the Navier slip condition was recovered to first order. More recent analyses based on multiscale homogenization were conducted by Jiménez-Bolaños and Vernescu [20], Zampogna et al. [21] and Lācis et al. [22]. The latter study was the only one to push the development to second order, albeit only for V , deriving a transpiration condition at a fictitious wall. The condition was tested successfully for the case of a turbulent channel flow bound by a rough wall, demonstrating the importance of accounting for wall-normal velocity fluctuations in a rough wall model. The present contribution starts from these premises.

In the next section the problem is formulated mathematically, following the approach initiated by Lācis et al. [22]. A related, but different, strategy believed to lead faster to accurate results is described in Sect. 3. The coefficients stemming from the solutions of the microscopic problems are then used in the effective conditions, summarized in Sect. 4. It is important to stress the following two points: (1) simple Navier slip for the wall tangent velocity is modified at higher orders by terms containing the streamwise pressure gradient and the time-derivative of the tangential stress near the wall, and (2) a second-order wall-normal velocity component appears. In Sect. 5 the effective conditions are applied to a laminar boundary layer flow and it is shown that the first-order conditions do not produce a very accurate result, when compared to complete, feature-resolving simulations. The concluding section summarizes the findings of the paper and provides the general three-dimensional form of the effective slip/transpiration conditions capable to model a regularly microstructured wall.

2 Mathematical formulation

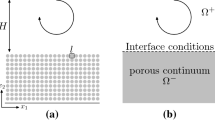
A regularly microstructured surface is considered; for reasons of clarity we limit the present analysis to two-dimensional Cartesian coordinates. The wall has a characteristic microscopic length scale equal to l (say, the periodicity of the pattern); the macroscopic length scale is L (for example, the channel half-thickness, or the length of a flat plate). The presence of two characteristic dimensions renders the problem amenable to a two-scale expansions, in terms of the small parameter $\epsilon = l/L$. The situation is schematized in Fig. 1: two domains can be set up, a macroscopic, outer one (with variables denoted by capital letters) and a microscopic, inner one (small letters). A matching in velocity and traction vectors between the two domains must be enforced and, anticipating the scalings of inner and outer velocities, we formally have

$$\begin{aligned} \lim _{Y \rightarrow 0} {\mathbf{U}} = \lim _{y \rightarrow \infty } \epsilon \,{\mathbf{u}}, \end{aligned}$$

(4)

and similarly for traction. In actual numerical practice the outer, effective boundary conditions will be enforced at some vertical position, denoted ${\mathcal {Y}}$, with the corresponding inner velocity evaluated at ${\bar{y}}={\mathcal {Y}}/\epsilon$, for the condition to read

$$\begin{aligned} {\mathbf{U}}|_{Y={\mathcal {Y}}} = \epsilon \,{\mathbf{u}}|_{y={\bar{y}}}. \end{aligned}$$

(5)

Fig. 1

Sketch of a regularly microstructured surface with close-up of a unit cell

The goal of this section is to formulate the effective boundary conditions for the outer flow, pushing the development beyond the leading order Navier slip term. Such conditions will depend on the inner flow regime and geometry of the roughness elements.

To set up the small-scale problem we need to normalize the equations properly. The flow in the inner domain is driven by a dimensional force, per unit surface area, which we will indicate as ${\hat{\mathbf {S}}}=({\hat{S}}^{{T}},~{\hat{S}}^{{N}}$), applied in ${\bar{y}}$. The superscripts T and N indicate, respectively, the tangential and the normal component of this force. Since the shear component of ${\hat{\mathbf {S}}}$ drives the flow in the roughness layer, the velocity scale there is ${\mathcal {U}} = {\mathcal {O}}({\hat{S}}^{T}l/\mu )$, with $\mu$ the dynamic viscosity of the fluid. Using l as inner length scale, $l/{\mathcal {U}}$ as time scale, and $\mu \, {\mathcal {U}}/l$ as pressure scale, the dimensionless equations in the inner region read:

$$\begin{aligned}&u_{x}+v_{x}=0,\nonumber \\&{\mathcal {R}}(u_{t}+{\mathbf{u }}\cdot \nabla u)=-p_{x}+\nabla ^{2}u,\nonumber \\&{\mathcal {R}}(v_{t}+{\mathbf{u }}\cdot \nabla v)=-p_{y}+\nabla ^{2}v. \end{aligned}$$

(6)

The quantity ${\mathcal {R}}$ is the microscopic Reynolds number, defined by ${\mathcal {R}} = \rho {\mathcal {U}}l/\mu$, $\rho$ being the fluid density, and ${\mathbf{u }}=(u, v)$.

The velocity scale in the outer domain is $U_{out}$ (equal, for example, to the bulk velocity in a macroscopic channel), so that $S^{T}=\displaystyle {\frac{{\hat{S}}^{{T}} L}{\mu U_{out}}}$ and $S^{N}=\displaystyle {\frac{{\hat{S}}^{{N}} L}{\mu U_{out}}}$ are the dimensionless traction components in $Y = {\mathcal {Y}}$. By introducing also the outer time and pressure scales, $L/U_{out}$ and $\rho U^{2}_{out}$, the equations in the macroscopic domain become:

$$\begin{aligned}&U_{X}+V_{Y}=0,\nonumber \\&(U_{T}+{\mathbf{U }}\cdot \nabla ' U)=-P_{X}+Re^{-1}(U_{XX}+U_{YY}),\nonumber \\&(V_{T}+{\mathbf{U }}\cdot \nabla ' V)=-P_{Y}+Re^{-1}(V_{XX}+V_{YY}), \end{aligned}$$

(7)

with U $=$ (U,  V) and $Re = \rho U_{out}L/\mu$, Reynolds number of the outer flow. The operator $\nabla '$ is defined by $\nabla '=$ ($\partial /\partial X,$$\partial /\partial Y$), whereas it is $\nabla =$ ($\partial /\partial x,$$\partial /\partial y$). The ratio between inner and outer length scales yields (X,  Y) $=$$\epsilon$(x,  y) and this suggests to express the variables in the near-wall region as power series expansions in terms of the small parameter $\epsilon$, i.e.

$$\begin{aligned} f=f^{(0)}+\epsilon f^{(1)}+\epsilon ^{2}f^{(2)}..., \end{aligned}$$

(8)

with $f = u, v$ or p. Whereas the outer flow variables (U,  V,  P) depend only on the macroscopic independent variable ${\mathbf {X}}$$= (X, Y)$, plus eventually time T, the inner flow variables, at all orders in $\epsilon$, are assumed to depend on both ${\mathbf {X}}$ and ${\mathbf{x}}$$= (x, y)$, plus time t. Thus, in Eq. (6) we need to pose $\nabla \rightarrow \nabla + \epsilon \nabla '$. Following the approach initiated by Lācis et al. [22] at leading order in $\epsilon$ we have:

${\mathcal {O}}(\epsilon ^{0})$

$$\begin{aligned}&u_{x}^{(0)}+v_{y}^{(0)}=0,\nonumber \\&-p_{x}^{(0)}+u_{xx}^{(0)}+u_{yy}^{(0)}+\delta (y-{\bar{y}})S^{T}=0,\nonumber \\&-p_{y}^{(0)}+v_{xx}^{(0)}+v_{yy}^{(0)}+\delta (y-{\bar{y}})S^{N}=0, \end{aligned}$$

(9)

provided that ${\mathcal {U}}$ is chosen as ${\mathcal {U}} =$$\epsilon U_{out}$ so that ${\mathcal {R}} = \epsilon ^{2} Re$. With the present choice, inner and outer time scales coincide, i.e. $t = T$. The (arbitrary) position ${\bar{y}} = {\mathcal {Y}}/\epsilon$ where the traction force impressed by the outer flow, modeled via a Dirac delta function, is assumed to apply can be taken on the outer edge of the wall micro-structure, i.e. ${\mathcal {Y}} = {\bar{y}} = 0$ (cf. Fig. 1). Any other position different from ${\bar{y}}=0$ is equally acceptable¹ and applying the effective boundary condition in the macroscopic problem at a position ${\mathcal {Y}} \ne 0$ leads to a solution endowed with the same formal accuracy as the choice ${\mathcal {Y}} = 0$. The components of the dimensionless traction vector ${\mathbf {S}}$ are

$$\begin{aligned} S^{T}=U_{Y}+V_{X},\quad S^{N}=-ReP+2V_{Y}. \end{aligned}$$

(10)

The system of equations at first order in $\epsilon$ is:

${\mathcal {O}}(\epsilon ^{1})$

$$\begin{aligned}&u_{x}^{(1)}+v_{y}^{(1)}=-u_{X}^{(0)}-v_{Y}^{(0)},\nonumber \\&-p_{x}^{(1)}+u_{xx}^{(1)}+u_{yy}^{(1)}=p_{X}^{(0)}-2u_{Xx}^{(0)}-2u_{Yy}^{(0)},\nonumber \\&-p_{y}^{(1)}+v_{xx}^{(1)}+v_{yy}^{(1)}=p_{Y}^{(0)}-2v_{Xx}^{(0)}-2v_{Yy}^{(0)}. \end{aligned}$$

(11)

Both microscopic systems must be solved subject to periodic conditions along x, “no-slip” at $y = y_{wall}$, and vanishing “stress” at $y\rightarrow \infty$. The latter reads

$$\begin{aligned}&u_{y}^{(0)}+v_{x}^{(0)}=-p^{(0)}+2v_{y}^{(0)}=0, \end{aligned}$$

(12a)

$$\begin{aligned}&u_{y}^{(1)}+v_{x}^{(1)}=-u_{Y}^{(0)}-v_{X}^{(0)}, \,-p^{(1)}+2v_{y}^{(1)}=-2v_{Y}^{(0)}. \end{aligned}$$

(12b)

Once the solutions of (9) and (11) are found, the macroscopic, effective conditions for the outer flow at the fictitious wall in $Y = 0$ are

$$\begin{aligned} U(X,0,t)= & {} \epsilon \left[ \int _{0}^{1}(u^{(0)}+\epsilon u^{(1)})\Big |_{y=0}dx\right] +{\mathcal {O}}(\epsilon ^{3}), \end{aligned}$$

(13)

$$\begin{aligned} V(X,0,t)= & {} \epsilon \left[ \int _{0}^{1}(v^{(0)}+\epsilon v^{(1)})\Big |_{y=0}dx\right] +{\mathcal {O}}(\epsilon ^{3}). \end{aligned}$$

(14)

2.1 The order zero solution

System (9) is linear and this permits the search of a solution in the form:

$$\begin{aligned} f^{(0)}=f^{\dag }(x,y)S^{T}+f^{\ddag }(x,y)S^{N}, \end{aligned}$$

(15)

for the generic dependent variable $f^{(0)}$. The ansatz for the unknowns yields two decoupled systems.

System 1: Shear stress forcing

$$\begin{aligned}&u_{x}^{\dag }+v_{y}^{\dag }=0,\nonumber \\&-p_{x}^{\dag }+u_{xx}^{\dag }+u_{yy}^{\dag }+\delta (y)=0,\nonumber \\&-p_{y}^{\dag }+v_{xx}^{\dag }+v_{yy}^{\dag }=0. \end{aligned}$$

(16)

System 2: Normal stress forcing

$$\begin{aligned}&u_{x}^{\ddag }+v_{y}^{\ddag }=0,\nonumber \\&-p_{x}^{\ddag }+u_{xx}^{\ddag }+u_{yy}^{\ddag }=0,\nonumber \\&-p_{y}^{\ddag }+v_{xx}^{\ddag }+v_{yy}^{\ddag }+\delta (y)=0. \end{aligned}$$

(17)

These two systems are endowed with “no-slip” and vanishing “stress” conditions at, respectively, $y=y_{wall}$ and $y\rightarrow \infty$.

Considering, for example, a triangular microscopic roughness element, the solutions of (16) and (17) are readily available by a numerical approach, described in Appendix 1. An example of solution of system 1 is displayed in Fig. 2; the numerical domain extends from $y = -0.5$ (roughness troughs) up to $y = 5$; the latter value, denoted $y_{\infty }$ in the following, must be taken sufficiently far away from the roughness crest in $y = 0$ for the solution to be independent of it. For the geometry under consideration we have verified that the solution near the roughness does not change when $y_{\infty }$ is taken larger than about 3. By averaging the streamwise velocity distribution along x in $y = 0$ it is found that $\lambda ^{x}:=\int _{0}^{1}u^{\dag }(x,0)\,\mathrm{d}x=0.0780$, whereas the x-averaged values of $v^{\dag }$ and $p^{\dag }$ at $y = 0$ are equal to zero. It goes without saying that, had we chosen a value of ${{\bar{y}}}$ different from 0, we would have found a different result for $\lambda ^x$.

System 2 has the simple solution $u^{\ddag } = v^{\ddag } = 0$, together with $p^{\ddag }_{x}= 0$ and $p^{\ddag }_{y} = \delta (y)$. From the definition of the Heaviside step function, dH/d$y := \delta (y)$, and the boundary condition $p^{\ddag } = 0$ at $y\rightarrow \infty$ it is simple to find $p^{\ddag } = H(y)-1$, i.e. $p^{\ddag }$ is identically equal to $-1$ when $y < 0$, and it vanishes for $y > 0$. Eventually, we have

$$\begin{aligned}&\int _{0}^{1}u^{(0)}(x,0,t)\,\mathrm{d}x=\lambda ^{x}S^{T}, \end{aligned}$$

(18a)

$$\begin{aligned}&\int _{0}^{1}v^{(0)}(x,0,t)\,\mathrm{d}x=0, \end{aligned}$$

(18b)

$$\begin{aligned}&\int _{0}^{1}p^{(0)}(x,0^{-},t)\,\mathrm{d}x=ReP-2V_{Y}. \end{aligned}$$

(18c)

Fig. 2

Isolines of $u^{\dag }$ (left), $v^{\dag }$ (center) and $p^{\dag }$. The domain has been cut at $y = 2.5$ to focus on the behavior close to the roughness, even if in the actual computation $y_{\infty } = 5$. The small irregularity visible in the isolines of $p^{\dag }$ is related to the presence of the delta function in $y = 0$

2.2 The order one solution

On account of (15), the linear system (11) becomes

$$\begin{aligned}&u_{x}^{(1)}+v_{y}^{(1)}=-u^{\dag }S^{T}_{X}-v^{\dag }S^{T}_{Y},\nonumber \\&-p_{x}^{(1)}+u_{xx}^{(1)}+u_{yy}^{(1)}=p^{\dag }S^{T}_{X} +p^{\ddag }S^{N}_{X}-2u^{\dag }_{x}S^{T}_{X}-2u^{\dag }_{y}S^{T}_{Y},\nonumber \\&-p_{y}^{(1)}+v_{xx}^{(1)}+v_{yy}^{(1)}=p^{\dag }S^{T}_{Y} +p^{\ddag }S^{N}_{Y}-2v^{\dag }_{x}S^{T}_{X}-2v^{\dag }_{y}S^{T}_{Y}, \end{aligned}$$

(19)

subject at $y\rightarrow \infty$ to the conditions:

$$\begin{aligned} u_{y}^{(1)}+v_{x}^{(1)}=-u^{\dag }S^{T}_{Y}-v^{\dag }S^{T}_{X},\,\, \,-p^{(1)}+2v_{y}^{(1)}=-2v^{\dag }S^{T}_{Y}. \end{aligned}$$

(20)

The solution has thus the generic form:

$$\begin{aligned} \begin{aligned} f^{(1)}={\hat{f}}_1(x,y)S^{T}_{X}+\breve{f}_1(x,y)S^{N}_{X} +{\hat{f}}_2(x,y)S^{T}_{Y}+\breve{f}_2(x,y)S^{N}_{Y}. \end{aligned} \end{aligned}$$

(21)

Four separate systems can be set up, equipped with “no-slip” conditions at $y=y_{wall}$ and periodicity in x.

System 3: Forcing by X-gradient of shear stress

$$\begin{aligned}&{\hat{u}}_{1\,x}+{\hat{v}}_{1\,y}=-u^{\dag },\nonumber \\&-{\hat{p}}_{1\,x}+{\hat{u}}_{1\,xx}+{\hat{u}}_{1\,yy} =p^{\dag }-2u^{\dag }_{x},\nonumber \\&-{\hat{p}}_{1\,y}+{\hat{v}}_{1\,xx}+{\hat{v}}_{1\,yy}=-2v^{\dag }_{x},\nonumber \\&\text {subject to} \,\,\,{\hat{u}}_{1\,y}+{\hat{v}}_{1\,x} = -v^{\dag }, \,\, \nonumber \\&\quad -{\hat{p}}_1+2{\hat{v}}_{1\,y}=0, \,\, \text {at} \,\,y \rightarrow \infty . \end{aligned}$$

(22)

System 4: Forcing by X-gradient of normal stress

$$\begin{aligned}&\breve{u}_{1\,x}+\breve{v}_{1\,y}=0,\nonumber \\&\quad -\breve{p}_{1\,x}+\breve{u}_{1\,xx}+\breve{u}_{1\,yy}=H(y)-1,\nonumber \\&\quad -\breve{p}_{1\,y}+\breve{v}_{1\,xx}+\breve{v}_{1\,yy}=0,\nonumber \\&\text {subject to} \,\,\,\breve{u}_{1\,y}+\breve{v}_{1\,x} = 0, \,\, \nonumber \\&\quad -\breve{p}_1+2\breve{v}_{1\,y}=0, \,\, \text {at} \,\,y \rightarrow \infty . \end{aligned}$$

(23)

System 5: Forcing by Y-gradient of shear stress

$$\begin{aligned}&{\hat{u}}_{2\,x}+{\hat{v}}_{2\,y}=-v^{\dag },\nonumber \\&\quad -{\hat{p}}_{2\,x}+{\hat{u}}_{2\,xx}+{\hat{u}}_{2\,yy}=-2u^{\dag }_{y},\nonumber \\&\quad -{\hat{p}}_{2\,y}+{\hat{v}}_{2\,xx}+{\hat{v}}_{2\,yy}=p^{\dag }-2v^{\dag }_{y},\nonumber \\&\quad \text {subject to} \,\,\,{\hat{u}}_{2\,y}+{\hat{v}}_{2\,x} = -u^{\dag }, \,\, \nonumber \\&\quad -{\hat{p}}_2+2{\hat{v}}_{2\,y}=-2{v}^{\dag }, \,\, \text {at} \,\,y \rightarrow \infty . \end{aligned}$$

(24)

System 6: Forcing by Y-gradient of normal stress

$$\begin{aligned}&\breve{u}_{2\,x}+\breve{v}_{2\,y}=0,\nonumber \\&\quad -\breve{p}_{2\,x}+\breve{u}_{2\,xx}+\breve{u}_{2\,yy}=0,\nonumber \\&\quad -\breve{p}_{2\,y}+\breve{v}_{2\,xx}+\breve{v}_{2\,yy}=H(y)-1,\nonumber \\&\quad \text {subject to} \,\,\,\breve{u}_{2\,y}+\breve{v}_{2\,x} = 0, \,\, \nonumber \\&\quad -\breve{p}_2+2\breve{v}_{2\,y}=0, \,\, \text {at} \,\,y \rightarrow \infty . \end{aligned}$$

(25)

Systems 3 to 5 are computed by the same numerical method used so far; the fields are plotted in Figs. 3, 4 to 5. The only results of interest are $m_{21}:=\int _{0}^{1}{\hat{v}}_1(x,0)\,\mathrm{d}x=-0.0058$, and $m_{12} := \int _{0}^{1} \breve{u}_1(x,0) \, \mathrm{d}x=0.0058$. Systems 6 admits the simple analytical solution $\breve{u}_2 = \breve{v}_2 = 0$ and $\breve{p}_2 = y\,H(-y)$.

Fig. 3

Isolines of ${\hat{u}}_1$ (left), ${\hat{v}}_1$ (center) and ${\hat{p}}_1$

Fig. 4

Isolines of $\breve{u}_1$ (left), $\breve{v}_1$ (center) and $\breve{p}_1$

Fig. 5

Isolines of ${\hat{u}}_2$ (left), ${\hat{v}}_2$ (center) and ${\hat{p}}_2$

Using Eqs. (13) and (14) an approximation for the macroscopic slip and transpiration velocity components at $Y = 0$ is now available. To close this section we observe that

• we could easily extend the solution up to next order, including inertial terms, and

• the approach outlined above is not the only one which can be conceived to infer slip and transpiration conditions for the outer flow, to mimic the effect of a rough wall.

An alternative approach, which follows the lines initiated by Luchini et al. [7] for the case of riblets, is described next. In this second approach the concentrated volume force at ${{\bar{y}}}$ in Eq. (9) is absent and, as such, there is no need to approximate a delta or a unit step distribution using an extremely dense mesh around ${{\bar{y}}}$. The results obtained in this section will be reproduced next with this alternative approach, and extended to the subsequent $\epsilon$ order.

3 The (easier) alternative

The same inner and outer scales used in Sect. 2 are employed here. The main difference of this approach with what was done in the previous section is that now there is no source term in the equations, and the flow is assumed to be driven by the horizontal shear traction ${\mathbb {S}}^{T}$ in $y\rightarrow \infty$ [7, 16]. Notice that the traction vector at $y_{\infty }$ is different from ($S^{T}$, $S^{N}$), the latter denoting the force on $y = {{\bar{y}}}$ (with ${\bar{y}}$ set to zero in the previous section). The outer boundary at $y = y_{\infty }$ is taken sufficiently far away from the rough wall to guarantee that at the outer edge of the microscopic domain the results have lost memory of the rough-wall shape, i.e. the solution there becomes x-independent. In the present approach this value of $y_\infty$ can then be taken to coincide with the position ${{\bar{y}}}$ where matching (5) is applied. At the outer edge of the domain the conditions are thus

$$\begin{aligned} u_{y}+v_{x}={\mathbb {S}}^{T},~~~-p+2v_{y}={\mathbb {S}}^{N}. \end{aligned}$$

(26)

The inner system of equations is constituted by system (6), equipped with no-slip conditions at $y = y_{wall}$ and periodicity along x. As before, we assume a series expansion in powers of $\epsilon$ for the dependent variables and plug into the inner flow equations, obtaining the homogeneous Stokes system for the variables at leading order. The traction imposed by the outer flow at $y_{\infty }$ is transferred to the order zero microscopic variables, i.e.

$$\begin{aligned} u_{y}^{(0)}+v_{x}^{(0)}={\mathbb {S}}^{T},~~~-p^{(0)}+2v^{(0)}_{y}={\mathbb {S}}^{N}. \end{aligned}$$

(27)

At higher orders we have:

$$\begin{aligned}&u_{y}^{(i)}+v_{x}^{(i)}=-u_{Y}^{(i-1)}-v_{X}^{(i-1)},~~~-p^{(i)} +2v^{(i)}_{y}\nonumber \\&\quad =-2v_{Y}^{(i-1)}~~~i=1,2,.... \end{aligned}$$

(28)

Employing a result by Jiménez-Bolaños and Vernescu [20], the order zero solution is

$$\begin{aligned} u^{(0)}= & {} u^{\dag }(x,y){\mathbb {S}}^{T}, \end{aligned}$$

(29)

$$\begin{aligned} v^{(0)}= & {} v^{\dag }(x,y){\mathbb {S}}^{T}, \end{aligned}$$

(30)

$$\begin{aligned} p^{(0)}= & {} p^{\dag }(x,y){\mathbb {S}}^{T}-{\mathbb {S}}^{N}. \end{aligned}$$

(31)

It is clear that the $^{\dag }$ variables here are different from those introduced in Sect. 2. We maintain the same notation only for reasons of convenience, and we will do the same also below with the variables denoted by ${\hat{\bullet }}$ and $\breve{\bullet }$. The system in terms of $^{\dag }$ variables is the homogeneous Stokes system, and the boundary conditions at $y_{\infty }$ are:

$$\begin{aligned} u_{y}^{\dag }+v_{x}^{\dag }=1,~~~-p^{\dag }+2v^{\dag }_{y}=0. \end{aligned}$$

(32)

A solution of this system for the triangular roughness geometry is given in Fig. 6. It is found in particular that at the outer edge of the unit cell, taken to be $y_{\infty } = 5$, it is $\gamma ^{x}:=u^{\dag }(x,5)=5.07778$ and $v^{\dag }(x,5)=p^{\dag }(x,5)=0.$ It should also be observed that the isolines of $v^{\dag }$ and $p^{\dag }$ are identical to those displayed in Fig. 2 (central and right frames).

Fig. 6

Isolines of $u^{\dag }$ (left), $v^{\dag }$ (center) and $p^{\dag }$

The system at ${\mathcal {O}}(\epsilon )$ is

$$\begin{aligned}&u^{(1)}_{x}+v^{(1)}_{y}=-u^{\dag }{\mathbb {S}}^{T}_{X}-v^{\dag } {\mathbb {S}}^{T}_{Y},\nonumber \\&-p^{(1)}_{x}+u^{(1)}_{xx}+u^{(1)}_{yy}=p^{\dag }{\mathbb {S}}^{T}_{X} -{\mathbb {S}}^{N}_{X}-2u^{\dag }_{x}{\mathbb {S}}^{T}_{X}\nonumber \\&\quad -2u^{\dag }_{y}{\mathbb {S}}^{T}_{Y},\nonumber \\&-p^{(1)}_{y}+v^{(1)}_{xx}+v^{(1)}_{yy}=p^{\dag }{\mathbb {S}}^{T}_{Y}\nonumber \\&\quad -{\mathbb {S}}^{N}_{Y}-2v^{\dag }_{x}{\mathbb {S}}^{T}_{X}-2v^{\dag }_{y}{\mathbb {S}}^{T}_{Y}, \end{aligned}$$

(33)

and at $y_{\infty }$ we have

$$\begin{aligned} u_{y}^{(1)}+v_{x}^{(1)}=-u^{\dag }{\mathbb {S}}^{T}_{Y}-v^{\dag } {\mathbb {S}}^{T}_{X},~~~-p^{(1)}+2v^{(1)}_{y}=-2v^{\dag }{\mathbb {S}}^{T}_{Y}, \end{aligned}$$

(34)

for the general solution to read (similar to Eq. 21):

$$\begin{aligned} f^{(1)}={\hat{f}}_1(x,y){\mathbb {S}}^{T}_{X}+\breve{f}_1(x,y) {\mathbb {S}}^{N}_{X}+{\hat{f}}_2(x,y){\mathbb {S}}^{T}_{Y}+\breve{f}_2(x,y){\mathbb {S}}^{N}_{Y}, \end{aligned}$$

(35)

and four additional systems can be set up, equipped with the same boundary conditions along x and at the wall as the previous ones. These new systems read exactly like systems 3 to 6, except that now the Heaviside function H(y) disappears from the right-hand-sides of (23) and (25). For example, the new system 4 becomes

$$\begin{aligned}&\breve{u}_{1\,x}+\breve{v}_{1\,y}=0,\nonumber \\&-\breve{p}_{1\,x}+\breve{u}_{1\,xx}+\breve{u}_{1\,yy}=-1,\nonumber \\&-\breve{p}_{1\,y}+\breve{v}_{1\,xx}+\breve{v}_{1\,yy}=0,\nonumber \\&\text {subject to} \,\,\,\breve{u}_{1\,y}+\breve{v}_{1\,x} = 0, \,\, \nonumber \\&\quad -\breve{p}_1+2\breve{v}_{1\,y}=0, \,\, \text {at} \,\,y \rightarrow \infty . \end{aligned}$$

(36)

All the new systems are solved numerically as done previously, except for that relative to $(\breve{u}_2, \breve{v}_2, \breve{p}_2)$ which admits the simple analytical solution $\breve{u}_2 = \breve{v}_2 = 0$, and $\breve{p}_2 =y - y_\infty$. The solution of the system for $({{\hat{u}}}_1, {{\hat{v}}}_1, {{\hat{p}}}_1)$ (Eq. 36) is displayed in Fig. 7 and, as expected, the field of ${\hat{u}}_1$ is the same as that reported in Fig. 3 (left frame.) We find that ${\hat{u}}_1(x,5) = 0$ and $n_{21}:={\hat{v}}_1(x,5)=-12.89469$.

Fig. 7

Isolines of ${\hat{u}}_1$ (left), ${\hat{v}}_1$ (center) and ${\hat{p}}_1$

The fields of $(\breve{u}_1, \breve{v}_1, \breve{p}_1)$ are identical, to graphical accuracy, to those shown in Fig. 4; the coefficients of interest at ${{\bar{y}}} = y_{\infty } = 5$ are $n_{12}:=\breve{u}_1(x, 5)= 12.89469$ and $\breve{v}_1(x,5)=\breve{p}_1(x, 5)=0$. The numerical solution for $({{\hat{u}}}_2, {{\hat{v}}}_2, {{\hat{p}}}_2)$ yields vanishing values of the fields at $y=y_\infty$. The field of ${{\hat{u}}}_2$ does not go to zero monotonically for increasing y, unlike ${{\hat{v}}}_2$ and ${{\hat{p}}}_2$. For y larger than about 1 we observe that ${{\hat{u}}}_2$ becomes uniform in x and follows closely the quadratic behavior ${{\hat{u}}}_2 = (y + \gamma ^x - y_\infty )(y_\infty - y)$.

The coefficients we have found so far are different from those obtained previously and this is due to the fact that now the boundary conditions at the fictitious wall in the macroscopic problem are not enforced at ${\mathcal {Y}} = \epsilon {{{\bar{y}}}} = 0$ (as we did in Sect. 2), but at ${\mathcal {Y}} = \epsilon {{{\bar{y}}}} = \epsilon y_{\infty }$. Equation (5) thus reads

$$\begin{aligned}&U(X,\epsilon y_{\infty },t)\approx \epsilon \gamma ^{x}{\mathbb {S}}^{T}+\epsilon ^{2}n_{12}{\mathbb {S}}^{N}_{X}, \end{aligned}$$

(37)

$$\begin{aligned}&V(X,\epsilon y_{\infty },t)\approx \epsilon ^{2}n_{21}{\mathbb {S}}^{T}_{X}. \end{aligned}$$

(38)

It is, however, simple to reconcile the results found here with those given in Sect. 2. Table 1 shows how the coefficients vary as $y_{\infty }$ is modified. All the data fit very well to either a straight line or a parabola, and the results can thus be easily extrapolated to any desired ${{\bar{y}}}$ position where we choose to match inner and outer solutions. In particular, we have

$$\begin{aligned} n_{12}= & {} -n_{21}=\frac{{{\bar{y}}}^{2}}{2}+\lambda ^{x} {{\bar{y}}} + m_{12}, \end{aligned}$$

(39)

$$\begin{aligned} \gamma ^{x}= & {} \frac{dn_{12}}{d {{\bar{y}}}}={{\bar{y}}} +\lambda ^{x}, \end{aligned}$$

(40)

with $\lambda ^{x} = 0.07778$ and $m_{12} = -m_{21} = 0.00581$. By setting ${{\bar{y}}}=0$ in (39, 40) we recover exactly the coefficients given in Sect. 2, up to an error of ${\mathcal {O}}(10^{-4})$ which we attribute to the approximations made in modelling Dirac and Heaviside distributions.

Table 1 Variation of higher-order coefficients with the choice of $y_{\infty }$

The results embodied by Eqs. (39–40) permit to state that, for two-dimensional roughness elements such as those considered here, it is sufficient to solve system (36) twice, evaluating $n_{12}$ for two different values of ${{\bar{y}}} = y_\infty$, to recover the two coefficients, $\lambda ^x$ and $m_{12}$.

An even better result is however available. We observe, in fact, that

$$\begin{aligned} n_{12} = -n_{21} = \int _0^1 \int _{y_{wall}}^{y_\infty } \, u^\dag \, \mathrm{d}y \, \mathrm{d}x; \end{aligned}$$

(41)

this implies that a single resolution of the homogeneous Stokes system for the $^\dag$ variables, equipped with (32), is sufficient to recover all coefficients necessary to write the matching interface conditions at second order, whether they are enforced at ${{\bar{y}}}=y_\infty$ (cf. Eqs. 37–38) or at ${{\bar{y}}} = 0$. This is confirmed by several other calculations for different roughness patterns, reported in Appendix 2. The advantage of the strategy described in this section is its simplicity, precision and accuracy; all the numerical results here and in Appendix 2 are believed to be correct up to the last reported decimal digit.

Eventually, at $Y = 0$ the effective conditions to second order read:

$$\begin{aligned} U(X,0,t)\approx & {} \epsilon \lambda ^{x}S^{T}+\epsilon ^{2}m_{12}S^{N}_{X}, \end{aligned}$$

(42)

$$\begin{aligned} V(X,0,t)\approx & {} \epsilon ^{2}m_{21}S^{T}_{X}. \end{aligned}$$

(43)

3.1 Going to higher order in $\epsilon$

It is possible, and relatively easy, to obtain the higher-order correction to assess the role of the convective terms on the effective conditions at large scale. The microscopic equations at ${\mathcal {O}}(\epsilon ^{2})$ are

$$\begin{aligned}&u_{x}^{(2)}+v_{y}^{(2)}=F^{mass},\nonumber \\&-p_{x}^{(2)}+u_{xx}^{(2)}+u_{yy}^{(2)}=F^{x-mom},\nonumber \\&-p_{y}^{(2)}+v_{xx}^{(2)}+v_{yy}^{(2)}=F^{y-mom}, \end{aligned}$$

(44)

subject to the usual “no-slip” and x-periodic boundary conditions, plus

$$\begin{aligned} u_{y}^{(2)}+v_{x}^{(2)}=-u^{(1)}_{Y}-v^{(1)}_{X},~~~-p^{(2)} +2v^{(2)}_{y}=-2v^{(1)}_{Y}~~~\text {at}~~~y_{\infty }. \end{aligned}$$

(45)

The source terms present in the system of ${\mathcal {O}}(\epsilon ^{2})$ are

$$\begin{aligned}&F^{mass}\,\,\,\,\,\,=-{\hat{u}}_1\,{\mathbb {S}}^{T}_{XX}-\breve{u}_1\, {\mathbb {S}}^{N}_{XX}-{\hat{u}}_2\,{\mathbb {S}}^{T}_{XY}\nonumber \\&\quad -{\hat{v}}_1\, {\mathbb {S}}^{T}_{XY}-\breve{v}_1\,{\mathbb {S}}^{N}_{XY} -{\hat{v}}_2\,{\mathbb {S}}^{T}_{YY},\nonumber \\&F^{x-mom}=[{\hat{p}}_1-2{\hat{u}}_{1\,x}-u^{\dag }]\,{\mathbb {S}}^{T}_{XX} +[\breve{p}_1-2\breve{u}_{1\,x}]\,{\mathbb {S}}^{N}_{XX}\nonumber \\&\quad +[{\hat{p}}_2-2{\hat{u}}_{2\,x}-2{\hat{u}}_{1\,y}]\,{\mathbb {S}}^{T}_{XY}\nonumber \\&\quad +[\breve{p}_2-2\breve{u}_{1\,y}]\, {\mathbb {S}}^{N}_{XY} -[2{\hat{u}}_{2\,y}+{u}^\dag ]\,{\mathbb {S}}^{T}_{YY}\nonumber \\&\quad +Re\,[u^{\dag }{\mathbb {S}}^{T}_{t}+(u^{\dag }u^{\dag }_{x} +v^{\dag }u^{\dag }_{y})({\mathbb {S}}^{T})^{2}],\nonumber \\&F^{y-mom}=[-2{\hat{v}}_{1\,x}-v^{\dag }]\,{\mathbb {S}}^{T}_{XX} -2\breve{v}_{1\,x}\,{\mathbb {S}}^{N}_{XX}\nonumber \\&\quad +[{\hat{p}}_1-2{\hat{v}}_{2\,x}-2{\hat{v}}_{1\,y}]\,{\mathbb {S}}^{T}_{XY}\nonumber \\&\quad +[\breve{p}_1-2\breve{v}_{1\,y}]\,{\mathbb {S}}^{N}_{XY}\nonumber \\&\quad +[{{\hat{p}}}_2 - 2{\hat{v}}_{2\,y}-{v}^\dag ]\,{\mathbb {S}}^{T}_{YY} +\breve{p}_2\,{\mathbb {S}}^{N}_{YY}\nonumber \\&\quad +Re\,[v^{\dag }{\mathbb {S}}^{T}_{t}+(u^{\dag }v^{\dag }_{x} +v^{\dag }v^{\dag }_{y})({\mathbb {S}}^{T})^{2}], \end{aligned}$$

(46)

so that the unknown vector ${\mathbf{g}}^{(2)} = (u^{(2)},v^{(2)},p^{(2)})$ can be written as

$$\begin{aligned} \begin{aligned} {\mathbf{g}}^{(2)}&=\mathbf{g}_1\,{\mathbb {S}}^{T}_{XX} + {\mathbf{g}}_2\,{\mathbb {S}}^{N}_{XX} + {\mathbf{g}}_3\,{\mathbb {S}}^{T}_{XY} + {\mathbf{g}}_4\,{\mathbb {S}}^{N}_{XY}\\&\quad + {\mathbf{g}}_5\,{\mathbb {S}}^{T}_{YY} + {\mathbf{g}}_6\,{\mathbb {S}}^{N}_{YY}+ {\mathbf{g}}_7\,{\mathbb {S}}^{T}_{t} + {\mathbf{g}}_8\,({\mathbb {S}}^{T})^{2}, \end{aligned} \end{aligned}$$

(47)

with ${\mathbf{g}}_i = (a_{i},b_{i},c_{i}), \,\,i = 1 ... 8$. This leads to eight new auxiliary problems (all equipped with the same boundary conditions along x and at the wall), given in Appendix 3. As it was the case previously, we are interested in the (constant) values of $a_i$ and $b_i$ at $y_\infty$, for $i = 1...8$. The numerical solutions of the systems at ${\mathcal {O}}(\epsilon ^2)$ are easily available and the non-trivial results of interest, obtained employing $y_{\infty } = 5$, are:

$$\begin{aligned} \rho ^{x}:= & {} a_{1}(x,5)=218.21,\\ p_{12}:= & {} \displaystyle \frac{1}{Re}a_{7}(x,5)=-43.64,\\ p_{21}:= & {} b_{2}(x,5)=-43.64. \end{aligned}$$

With the coefficients in our hands, the microscopic second order terms evaluated in $y_{\infty }={{\bar{y}}} = 5$ finally is

$$\begin{aligned} u^{(2)}= & {} \rho ^{x}{\mathbb {S}}^{T}_{XX}+Re\,p_{12}{\mathbb {S}}^{T}_{t}, \end{aligned}$$

(48)

$$\begin{aligned} v^{(2)}= & {} p_{21}{\mathbb {S}}^{N}_{XX}. \end{aligned}$$

(49)

It is possible to compute the coefficients at different values of ${{\bar{y}}}=y_\infty$ to infer trends for the effective conditions to be applied, for example, at the roughness rim. The results we have computed are summarized in Table 2 and we have verified that they fit cubic curves to very good accuracy. In particular, it is

$$\begin{aligned} \rho ^{x}= & {} \frac{5}{3}(\gamma ^{x})^{3}=\frac{5}{3}(\bar{y}+\lambda ^{x})^{3}, \end{aligned}$$

(50)

$$\begin{aligned} p_{12}= & {} p_{21}=-\frac{(\gamma ^{x})^{3}}{3}=-\frac{1}{3}({{\bar{y}}} +\lambda ^{x})^{3}; \end{aligned}$$

(51)

by setting ${{\bar{y}}}=0$, the coefficients to be employed in the macroscopic conditions for U and V at $Y = 0$ are:

$$\begin{aligned} \theta ^{x}= & {} \frac{5}{3}(\lambda ^{x})^{3}=0.00078, \end{aligned}$$

(52)

$$\begin{aligned} q_{12}= & {} q_{21}=-\frac{(\lambda ^{x})^{3}}{3}=-0.00016. \end{aligned}$$

(53)

It is important to stress, again, that the choice ${{\bar{y}}} = 0$ is just one among infinitely many other possibilities. A different choice of the fictitious wall is always possible and, for example, Lācis et al. [22] typically set ${{\bar{y}}}$ slightly above the upper rim of the roughness elements.

Table 2 Variation of higher-order coefficients with $\bar{y}$

4 The effective wall conditions

For the two-dimensional micro-indentations considered, the matching interface conditions read:

$$\begin{aligned} U(X,0,t) &= {} \epsilon \lambda ^{x}S^{T}+\epsilon ^{2}m_{12}S^{N}_{X}\nonumber \\&+\epsilon ^{3}[\theta ^{x}S^{T}_{XX}+Re\,q_{12}S^{T}_{t}]+{\mathcal {O}}(\epsilon ^{4}), \end{aligned}$$

(54)

$$\begin{aligned} V(X,0,t) & = {} \epsilon ^{2}m_{21}S^{T}_{X}+\epsilon ^{3}q_{21}S^{N}_{XX}+{\mathcal {O}}(\epsilon ^{4}), \end{aligned}$$

(55)

i.e., the X-component of the velocity at the fictitious wall in $Y=0$ is ${\mathcal {O}}(\epsilon )$ and the Y-component is ${\mathcal {O}}(\epsilon ^2)$. Observe that $m_{12}=-m_{21}>0$ and $q_{12}=q_{21}<0$.

While preparing this paper for submission we became aware of a very recent work by Sudhakar et al. [23] with the development of conditions to second order for both U and V, obtained as a subset of the dividing-line conditions between a clear fluid and a porous medium. The approach followed by these authors is similar to that described in Sect. 2 and their second-order result coincides with ours. The present contribution is the first to push the development to third order.

By observing that the shear stress at $Y = 0$ is

$$\begin{aligned} S^{T}=\frac{1}{\epsilon \lambda ^{x}}U(X,0,t)+{\mathcal {O}}(\epsilon ), \end{aligned}$$

(56)

and using continuity, we can write the leading term of the transpiration velocity in $Y = 0$ as

$$\begin{aligned} V(X,0,t)\approx -\epsilon \lambda ^{y}U_{X}, \end{aligned}$$

(57)

with $\lambda ^{y} = m_{12}/\lambda ^{x}$ a (positive) transpiration length, as postulated by Gómez-de-Segura et al. [24]. With the geometry considered here it is $\lambda ^{y}\approx 0.0747$. By writing out the components of traction, the effective rough-wall conditions (up to second order) can be written as:

$$\begin{aligned} U(X,0,t)\approx & {} \underbrace{\epsilon \lambda ^{x}U_{Y}} -\epsilon ^{2}m_{12}Re\,P_{X}\nonumber \\&+\epsilon ^{2}(2\,m_{12}+\lambda ^{x}\lambda ^{y})V_{XY}, \end{aligned}$$

(58)

$$\begin{aligned} V(X,0,t)\approx & {} \underbrace{\epsilon \lambda ^{y}V_{Y}}. \end{aligned}$$

(59)

The terms in (58–59) with underbraces correspond to those used previously [3, 22] to assess the effect of wall transpiration for the case of a turbulent flow in a channel with regularly corrugated walls. However, for things to be formally correct, all of the terms ${\mathcal {O}}(\epsilon ^{2})$ in Eq. (58) should be included. Equation (59) states that blowing and suction occur through the fictitious wall in $Y=0$ and that the location where the vertical velocity vanishes is a penetration distance equal to about $\epsilon \lambda ^y$ below $Y=0$. Note also that the integral of V over the whole $Y=0$ plane must vanish if the rough surface is impermeable.

In the following section an example will be shown in which the effective conditions are tested up to order one, two and three.

5 Macroscopic results

To assess the accuracy of the effective wall conditions we have chosen to study a steady boundary layer flow past a rough wall; the configuration considered is the stagnation point flow, an exact solution of the Navier–Stokes equations when the wall is smooth. As it turns out, a similarity solution exists also when the wall is rough and this is addressed first.

5.1 Hiemenz flow over a rough wall: a similarity formulation

The ansatz behind Hiemenz similarity solution [25] consists in writing the velocity components in (7) as

$$\begin{aligned} \begin{aligned} U=Xf'(Y),~~~V=-f(Y), \end{aligned} \end{aligned}$$

(60)

so that the continuity equation is automatically satisfied. The pressure is further expressed as

$$\begin{aligned} \begin{aligned} P=P_{0}-\frac{1}{2}[X^{2}+g(Y)], \end{aligned} \end{aligned}$$

(61)

with $P_{0}$ the stagnation pressure. These assumptions are also applied to the case of a regularly microstructured wall, with boundary conditions (54–55) on $Y = 0$, so that the two momentum equations become

$$\begin{aligned}&\frac{1}{Re}f'''+ff''-f'^{2}+1=0, \end{aligned}$$

(62)

$$\begin{aligned}&\frac{1}{Re}f''+ff''-\frac{g'}{2}=0. \end{aligned}$$

(63)

The first nonlinear ordinary differential equation above can be solved for f(Y) and, once the solution is available, Eq. (63) can be solved for g(Y), upon imposing that $P = P_{0}$ at the stagnation point (which translates into $g(0) = 0.$) The boundary conditions up to ${\mathcal {O}}(\epsilon ^{3})$ to be used with Eq. (62) are

$$\begin{aligned}&\epsilon \lambda ^{x}f''-f'+\epsilon ^{2}m_{12}Re=0,\nonumber \\&\epsilon ^{2}m_{21}f'' +f+\epsilon ^{3}q_{21}Re=0\,\text {at}\,Y=0, \end{aligned}$$

(64)

$$\begin{aligned}&f'=1\,\text {at}\,Y\rightarrow \infty ; \end{aligned}$$

(65)

the second-order conditions are found by setting $q_{21}$ to zero, while for those at first order it is sufficient to also impose $m_{12} = -m_{21} = 0$.

5.2 The numerical approximation

Rather than solving (62–65) we have opted to address, by the same finite elements method used for the microscopic systems, the full Navier–Stokes equations (7), either resolving the flow field within the roughness elements, or modelling it with the effective conditions. We consider a domain of length equal to 10L along $X^{*}$, and focus on the results over the first four units of length past the stagnation point. The outer edge of the domain is set in $Y^{*} = 2L$ ($^{*}$ superscripts are employed to denote dimensional variables.) Symmetry conditions are enforced along the $X^{*} = 0$ axis, and the flow is considered to develop only in the positive $X^{*}$ direction. The external potential flow is $U^{*} = aX^{*}, V^{*} = -aY^{*}$; the constant a is the inverse of a time scale; the characteristic velocity can thus be chosen as aL and the dimensionless outer irrotational motion is thus of the form $(U, V) = (X, -Y)$.

For the viscous near-wall flow we choose a Reynolds number $Re=\displaystyle {{aL^{2}}/{\nu }}$ ($\nu$ the fluid’s kinematic viscosity) equal to 25; to account for the presence of a constant-thickness boundary layer, in enforcing the inflow condition the vertical coordinate must be shifted by a quantity equal to the displacement thickness $\delta _{1}$, i.e. at $Y = 2$, outer edge of the domain, the inflow conditions in dimensionless form must read:

$$\begin{aligned} U=X,\quad V=-Y+\delta _{1}. \end{aligned}$$

(66)

Finally, on the $X = 10$ boundary the usual “do-nothing” condition is employed, which corresponds to zeroing the traction components.

In the no-roughness case the computed solution compares very well with the similarity solution, and it is found $\delta _{1}= 0.64795\, Re^{-{1}/{2}}$. When roughness is present on the lower wall, cf. Fig. 8, the solution changes slightly as shown in Fig. 9, and the displacement thickness decreases to $0.5680\,Re^{-1/2}$.

Fig. 8

Stagnation point flow over a rough wall, visualized via velocity vectors (left.) In the images on the right the flow in the vicinity and within the micro-indentations is visualized by streamlines around $X = 3.4$, highlighting Moffatt eddies in the triangular cavities. Only for comparison purposes, such eddies are shown at two Reynolds numbers, $Re = 25$ (top) and 250 (bottom) (in both cases it is $\epsilon =l/L=0.2$.)

Fig. 9

Comparison between the wall-parallel velocity profiles along Y evaluated at $X =$ 1, 2 and 3 in the case of smooth wall (solid lines) and rough wall (dots) with $\epsilon =0.2$, in correspondence to the roughness peaks. The rough-wall results displayed are those computed with a feature-resolving simulation; results for a microstructured wall simulated by employing effective conditions at order one, two or three are superimposed to the feature-resolving results and cannot be distinguished to graphical accuracy

The case lends itself to being treated with the effective conditions (54–55) even if, on the one hand, the parameter $\epsilon$ is not so much smaller than one and, on the other, the microscopic Reynolds number, ${\mathcal {R}} = \epsilon ^{2}Re$, is equal to one so that the terms on the left-hand-side of the two momentum equations in (6) might appear to be leading order terms. This is thus a strenuous test for the theory.

The wall-normal velocity at the fictitious wall in $Y=0$ is zero, by definition, at first order, but we find that it does not vanish when applying the effective conditions at higher orders. In particular, V(X, 0, t) is approximately constant and equal to $-0.0014$ ($-0.0017$) when second (respectively, third) order effective conditions are used. This means that a net mass flux into the wall occurs and this might be due to two causes. On the one hand, $\epsilon$ is not infinitesimal in the problem considered here ($\epsilon = 0.2$) and thus the terms neglected in the expansion of the conditions at $Y=0$ are not vanishingly small. On the other, when evaluating $S^T_X$ and $S^N_{XX}$ to be used in (55) discretization errors are inevitable. Note, however, that the unphysical mass flux through the wall is less than $0.1\%$ of the total mass flux which enters the domain from the upper boundary. An even more difficult test case for the condition on the vertical velocity at $Y = 0$ would be represented by a three-dimensional turbulent wall flow, because of the presence of violent near-wall events, such as ejections and sweeps. As shown by Bottaro [3], the transpiration condition seems adequate in a turbulent channel flow when $\epsilon = 0.2$ and the friction Reynolds number is 180; however, a better approximation is necessary when $\epsilon = 0.4$ (cf. figures 17 and 20 in the cited reference.)

In Fig. 10 a close-up view of the U velocity component is shown near the surface where the effective conditions are enforced, highlighting the fact that the approximations made do a good job at representing the physics near the roughness. Further away from the wall the disagreement with the “exact” solution cannot be ascertained, to graphical accuracy. The slip and transpiration velocity components at $Y = 0$ for the same cases are displayed in Fig. 11, together with the pressure. Whereas the vertical velocity at the fictitious wall oscillates around zero in the complete simulation, and is very close to zero when Eq. (55) is used, the streamwise velocity displays amplifying oscillations in the resolved case, and grows linearly in X when the effective conditions are employed, consistent with (60). The conditions at second and third orders almost coincide and are very close to the running average of the feature-resolving simulation (displayed with a solid line): the growth of the “exact” solution is more rapid than that found with simple Navier slip and the difference is appreciable.

Fig. 10

Close-up of the streamwise velocity near Y = 0, for X = 1.1, 2.1 and 3.1, i.e. on the troughs of the roughness elements. The solid lines represent the result of the feature-resolving simulation, the white bullets are the results of the Navier condition, the black square symbols correspond to the second-order condition, and the third-order results are shown with white triangles

Fig. 11

Top: slip velocity U at $Y = 0$ for the feature-resolving solution, displaying typical oscillations (dashed line); the results at different asymptotic orders are displayed using the same symbols as in Fig. 10. The second/third order conditions are very close to the running average of the “exact” slip velocity, displayed with a solid line. The “exact” wall-normal velocity V at $Y = 0$ is plotted in the same image, using a dotted line. Bottom: pressure at $Y = 0$, same symbols and line-styles as above. The parabolic behavior of the pressure with X agrees with ansatz (68)

6 Conclusions

Two different approaches have been presented to derive effective boundary conditions which go beyond the usual Navier–slip paradigm, to model regularly microstructured walls without the need to numerically resolve fine-scale near-wall details. The techniques employed, inspired by previous studies [7, 22], differ in the details of the small-scale formulation but produce the same results. They are based on matching the outer flow solution, which only depends on macroscopic spatial variables and time, to the inner flow state, which is assumed to depend on both small- and large-scale variables. Thus, the effect of roughness shape and periodicity is captured by the inner equations and transferred to the outer flow at the matching location (set at $Y={\mathcal {Y}}=\epsilon {{\bar{y}}}$) through a set of coefficients. The inner, microscopic equations are treated via an asymptotic development of the variables and the solution is found at orders zero, one and two. At leading order Navier-slip is recovered for the wall-tangent velocity, together with a no-transpiration condition. At next order the tangential gradient of the normal stress appears in the wall-parallel velocity component(s), whereas the wall-normal velocity displays the appearance of the tangential gradient of the tangential stress. This means that blowing and suction through the inner-outer interface might occur. The position of this interface can be chosen at will, and the convenient choice $Y=0$, coinciding with the rim of the roughness elements, is pursued here. Any other position $Y=\epsilon {\bar{y}}$ would have been acceptable and would have produced results to the same order of accuracy.

One important result obtained here for a two-dimensional configuration is that a single solution of the homogeneous Stokes system of equations in a x-periodic unit cell, equipped with no-slip at the wall and forced at the outer edge by conditions (32), is sufficient to recover the coefficients $\gamma _x$ and $n_{12}$. This is all we need in the effective conditions at order $\epsilon ^2$ (cf. Eqs. 37, 38). The discussion which follows Eq. (38) in the paper addresses the issue of how these coefficients must be modified for the inner-outer matching to be enforced elsewhere, for example, at $Y=0$ (Eqs. 42, 43). Finally, Sect. 3.1 of the paper illustrates the development at the next higher order in $\epsilon$, to account also for convective terms at the microscale, to eventually reach the macroscopic matching Eqs. (54–55), correct to ${\mathcal {O}}(\epsilon ^3)$.

The application of the effective conditions to a steady, laminar flow case, the Hiemenz flow over a rough wall, demonstrates that the nominally higher-order terms can produce sizable effects. In particular, for the problem examined a difference is observed between the macroscopic effective conditions at order one and two, whereas the terms of order three correct the order-two result by very little. The ${\mathcal {O}}(\epsilon ^3)$ terms may become important in more complex flow configurations, possibly three dimensional and unsteady. In this latter case, after naming the two tangential stress components $S^{T_{x}}=U_{Y}+V_{X}$ and $S^{T_{z}}=W_{Y}+V_{Z}$, we argue that the effective slip/transpiration is

$$\begin{aligned}&\begin{bmatrix} U \\ W\end{bmatrix} =\epsilon {\varvec{\Lambda }} \begin{bmatrix} S^{T_{x}} \\ S^{T_{z}} \end{bmatrix} +\epsilon ^{2}{\mathbf{M }} \begin{bmatrix} S^{N}_{X} \\ S^{N}_{Z} \end{bmatrix} +\epsilon ^{3}{\varvec{\Theta }}^{{\mathbf{x }}} \begin{bmatrix} S^{T_{x}}_{XX} \\ S^{T_{x}}_{XZ} \\ S^{T_{x}}_{ZZ} \end{bmatrix}\nonumber \\&\quad +\epsilon ^{3}\mathbf {\Theta ^{z}} \begin{bmatrix} S^{T_{z}}_{XX} \\ S^{T_{z}}_{XZ} \\ S^{T_{z}}_{ZZ} \end{bmatrix} +\epsilon ^{3}\,Re\,{\mathbf {Q}} \begin{bmatrix} S^{T_{x}}_{t} \\ S^{T_{z}}_{t} \end{bmatrix} +{\mathcal {O}}(\epsilon ^{4}), \end{aligned}$$

(67)

$$\begin{aligned}&V=\epsilon ^{2}\mathbf {m_{1}}\begin{bmatrix} S^{T_{x}}_{X} \\ S^{T_{x}}_{Z} \end{bmatrix} +\epsilon ^{2}\mathbf {m_{2}} \begin{bmatrix} S^{T_{z}}_{X} \\ S^{T_{z}}_{Z} \end{bmatrix}\nonumber \\&\quad +\epsilon ^{3}{\mathbf {p}} \begin{bmatrix} S^{N}_{XX} \\ S^{N}_{XZ} \\ S^{N}_{ZZ} \end{bmatrix} +{\mathcal {O}}(\epsilon ^{4}). \end{aligned}$$

(68)

${\varvec{\Lambda }}$, M and Q are $2\times 2$ matrices; ${\varvec{\Theta }}^{{\mathbf{x }}}$ and ${\varvec{\Theta }}^{{\mathbf{z }}}$ are $2\times 3$ matrices; $\mathbf {m_{1}}$ and $\mathbf {m_{2}}$ are $1\times 2$ while $\mathbf {p}$ is $1\times 3$. In principle, obtaining all coefficients of the matrices above would require a large number of numerical resolutions of differently forced three-dimensional Stokes systems. It is expected, however, that the effective number of auxiliary problems to be solved is significantly lower, in analogy to the two-dimensional case. Challenging test cases for the conditions given above are envisaged in future work, including in particular turbulent wall flows. It is indeed a nice and unexpected surprise to observe [3, 22] that a model of the rough surface based on only the leading order, non-trivial terms for the velocity components (i.e. those including only the factors ${\varvec{\Lambda }}$, $\mathbf {m_{1}}$ and $\mathbf {m_{2}}$ in Eqs. 67, 68) produces good results for both mean flows and second order statistics, in a large-Re turbulent channel flow. The issue, related to the effect of the wall normal velocity fluctuations [26], deserves a thorough look. We will also address the cases of elastically deforming microstructures and of rigid roughness elements impregnated by a lubricant fluid (cf., respectively, Zampogna et al. [27] and Alinovi and Bottaro [28] for the theories at first order.)

Appendices

Appendix 1: Numerical approach

The incompressible two-dimensional creeping flow equations for the generic unknown ($\mathbf {u}$, p) are solved with a finite element method using the FreeFEM open source code [29]. The approach is based on a weak formulation of the equations, which means introducing two regular test functions v and q, and solving the integral

$$\begin{aligned} \begin{aligned} \int _{0}^{1}\int _{y_{wall}}^{y_{\infty }}-{\mathbf {v}}\cdot \nabla p-\nabla {\mathbf {v}}\cdot \nabla {\mathbf {u}}+q\nabla \cdot {\mathbf {u}}\,\,\mathrm{d}y\,\mathrm{d}x=\mathrm{r.h.s}, \end{aligned} \end{aligned}$$

(69)

with the variables approximated by triangular $P_{1}-P_{2}$ Taylor-Hood elements. The term denoted as r.h.s. can contain contributions from volume source terms, from boundary conditions, or from both, depending on the system being treated. A similar approach, also based on the FreeFEM code, is used also for solving the Navier–Stokes equations. Particular care is needed when the Dirac delta in $y=0$ or the Heaviside step functions appear in the equations. In these cases, the grid needs to be refined locally (cf. Fig. 12.) We have chosen to model the delta function as a normal distribution of variance $\sigma ^{2}=5\times 10^{-7},$ i.e.

$$\begin{aligned} \begin{aligned} \delta (y)\approx \frac{1}{\sqrt{2\pi \sigma ^{2}}}e^{-y^{2}/2\sigma ^{2}}, \end{aligned} \end{aligned}$$

(70)

and the step function as

$$\begin{aligned} \begin{aligned} H(-y)\approx 0.5[\mathrm{tanh}(\alpha y)-1], \end{aligned} \end{aligned}$$

(71)

with $\alpha = 10^{3}$. All results reported here have been checked for grid-convergence; validation tests have also been carried out using the software COMSOL (www.comsol.com). The results described in Sect. 2, obtained using the approximations (70) and (71), converge towards those presented in Sect. 3 as the grid is refined and the parameters $\alpha$ and $\sigma ^{2}$ are increased. A better way to treat the delta and step functions would be to split the domain into two parts and enforce jump conditions across, as proposed by Lācis et al. [22]. However, it is not necessary to proceed this way, since a simpler and very accurate alternative is available (cf. Sect. 3.)

Fig. 12

Sample grids used in the absence (left) or presence of force singularities in the equations at $y = 0$. When a delta or a step function is present the grid is refined around the tip of the roughness in $y = 0$; conversely, when the fields are smooth the points are chosen to be uniformly distributed along each side of the domain. The grids displayed are composed by 1132 (left) and 1913 (right) triangles, whereas those used in the actual computations have, respectively, 125,720 and 88,419 triangles

Appendix 2: Sample results for other roughness geometries

The coefficient of the effective slip conditions (42–43) to second order are easily available for a variety of wall shapes by any one of the approaches described in the paper. We have considered the indentations shown in Fig. 13 and the relevant coefficients are reported in Table 3. Pattern B, which at $y = 0$ has the largest wetted surface, displays the lowest slip and transpiration coefficients. This is expected since no-slip prevails at the roughness edge over half of the total streamwise distance. By the converse argument, the blade-like indentation A has larger coefficients (which can increase even further by reducing the thickness of the blade). Shapes D and E present values of the coefficients very close to one another, and in case D, where a quasi-cusped tip is present, the slip is largest. This provides an indication also of the geometries to be preferentially tested in cases where the microcavities are filled with an immiscible lubricant fluid (such as air or vapor, when considering superhydrophobic coatings); first order results [28] confirm this indication and feature-resolving direct numerical simulations of turbulence in a channel bound by lubricant-impregnated walls [30] further highlight the significance of wall-normal velocity fluctuations and their strong correlation to the total drag. The high-order approach described here can easily be extended to the case of lubricant-filled micro-cavities, to better capture phenomena which, to date, have only been modelled using the (first-order) Navier condition.

Fig. 13

Microscopic domains with some two-dimensional roughness shapes tested. Shape A is a blade of dimensionless thickness equal to 0.2. The thickness of the square roughness element B is 0.5. Roughness C is a semicircle. Roughness D is defined by a parabolic-linear contour, and roughness E is a 90 degrees triangle (right)

Table 3 Variation of slip and transpiration parameters for different roughness geometries

Appendix 3: The systems at order $\epsilon ^2$

The eight microscopic systems which arise at order $\epsilon ^2$ are given below, together with the boundary conditions which apply at the outer edge of the domain.

Forcing by ${\mathbb {S}}^{T}_{XX}$

$$\begin{aligned}&a_{1x}+b_{1y}=-{\hat{u}}_1,\nonumber \\&-c_{1x}+a_{1xx}+a_{1yy}={\hat{p}}_1-2{\hat{u}}_{1\,x}-u^{\dag },\nonumber \\&-c_{1y}+b_{1xx}+b_{1yy}=-2{\hat{v}}_{1\,x}-v^{\dag }, \end{aligned}$$

(72)

together with $\,\,a_{1y}+b_{1x}=-{\hat{v}}_1~~\text {and}~-c_{1}+2b_{1y}=0~~~ \text {at}~~~y_{\infty }.$

Forcing by ${\mathbb {S}}^{N}_{XX}$

$$\begin{aligned}&a_{2\,x}+b_{2\,y}=-\breve{u}_1,\nonumber \\&-c_{2\,x}+a_{2\,xx}+a_{2\,yy}=\breve{p}_1-2\breve{u}_{1\,x},\nonumber \\&-c_{2\,y}+b_{2\,xx}+b_{2\,yy}=-2\breve{v}_{1\,x}, \end{aligned}$$

(73)

together with $\,\, a_{2\,y}+b_{2\,x}=-\breve{v}_1~~\text {and}~-c_{2}+2b_{2\,y}=0~~~ \text {at}~~~y_{\infty }.$

Forcing by ${\mathbb {S}}^{T}_{XY}$

$$\begin{aligned}&a_{3\,x}+b_{3\,y}=-{\hat{u}}_2-{\hat{v}}_1,\nonumber \\&-c_{3\,x}+a_{3\,xx}+a_{3\,yy}={\hat{p}}_2-2{\hat{u}}_{2\,x}-2{\hat{u}}_{1\,y},\nonumber \\&-c_{3\,y}+b_{3\,xx}+b_{3\,yy}={\hat{p}}_1-2{\hat{v}}_{2\,x}-2{\hat{v}}_{1\,y}, \end{aligned}$$

(74)

together with $\,\, a_{3\,y}+b_{3\,x}=-{\hat{u}}_1-{\hat{v}}_2~~\text {and}~-c_{3} +2b_{3\,y}=-2{\hat{v}}_1~~~\text {at}~~~y_{\infty }$.

Forcing by ${\mathbb {S}}^{N}_{XY}$

$$\begin{aligned}&a_{4\,x}+b_{4\,y}=-\breve{v}_1,\nonumber \\&-c_{4\,x}+a_{4\,xx}+a_{4\,yy}=\breve{p}_2-2\breve{u}_{1\,y},\nonumber \\&-c_{4\,y}+b_{4\,xx}+b_{4\,yy}=\breve{p}_1-2\breve{v}_{1\,y}, \end{aligned}$$

(75)

together with $\,\, a_{4\,y}+b_{4\,x}=-\breve{u}_1~~\text {and}~-c_{4}+2b_{4\,y} =-2\breve{v}_1~~~\text {at}~~~y_{\infty }.$

Forcing by ${\mathbb {S}}^{T}_{YY}$

$$\begin{aligned}&a_{5\,x}+b_{5\,y}=-{\hat{v}}_2,\nonumber \\&-c_{5\,x}+a_{5\,xx}+a_{5\,yy}=-2{\hat{u}}_{2\,y}-u^\dag ,\nonumber \\&-c_{5\,y}+b_{5\,xx}+b_{5\,yy}={\hat{p}}_2-2{\hat{v}}_{2\,y}-v^\dag , \end{aligned}$$

(76)

together with $\,\, a_{5\,y}+b_{5\,x}=-{\hat{u}}_2~~\text {and}~-c_{5} +2b_{5\,y}=-2{\hat{v}}_2~~~\text {at}~~~y_{\infty }$.

Forcing by ${\mathbb {S}}^{N}_{YY}$

$$\begin{aligned}&a_{6\,x}+b_{6\,y}=0,\nonumber \\&-c_{6\,x}+a_{6\,xx}+a_{6\,yy}=0,\nonumber \\&-c_{6\,y}+b_{6\,xx}+b_{6\,yy}=\breve{p}_2, \end{aligned}$$

(77)

together with $\,\, a_{6\,y}+b_{6\,x}=0~~\text {and}~-c_{6}+2b_{6\,y}=0~~~\text {at}~~~y_{\infty }.$ Given that $\breve{p}_2=y-y_\infty$ it is simple to find $a_6=b_6=0$ and $c_6=-\displaystyle \frac{(y-y_\infty )^2}{2}$.

Forcing by ${\mathbb {S}}^{T}_{t}$

$$\begin{aligned}&a_{7\,x}+b_{7\,y}=0,\nonumber \\&-c_{7\,x}+a_{7\,xx}+a_{7\,yy}=Re\,u^{\dag },\nonumber \\&-c_{7\,y}+b_{7\,xx}+b_{7\,yy}=Re\,v^{\dag }, \end{aligned}$$

(78)

together with $\,\,a_{3y}+b_{3x}=0~~\text {and}~-c_{3}+2b_{3y}=0~~~\text {at}~~~y_{\infty }$.

Forcing by $({\mathbb {S}}^{T})^{2}$

$$\begin{aligned}&a_{8\,x}+b_{8\,y}=0,\nonumber \\&-c_{8\,x}+a_{8\,xx}+a_{8\,yy}=Re\,(u^{\dag }u^{\dag }_{x}+v^{\dag }u^{\dag }_{y}),\nonumber \\&-c_{8\,y}+b_{8\,xx}+b_{8\,yy}=Re\,(u^{\dag }v^{\dag }_{x}+v^{\dag }v^{\dag }_{y}), \end{aligned}$$

(79)

together with $\,\,a_{8\,y}+b_{8\,x}=0~~\text {and}~-c_{8} +2b_{8\,y}=0~~~\text {at}~~~y_{\infty }.$