Quadratic algebras arising from Hopf operads generated by a single element

Abstract

The operads of Poisson and Gerstenhaber algebras are generated by a single binary element if we consider them as Hopf operads (i.e. as operads in the category of cocommutative coalgebras). In this note we discuss in detail Hopf operads generated by a single skew-symmetric element of arbitrary arity. We explain why the dual space to the space of n-ary operations in these operads are quadratic and Koszul algebras. We give a detailed description of generators, relations and monomial bases in these algebras.

Combinatorial computations with graphs

1.1 Computing homology of ${\textsf {Graphs}}^{k\downarrow }$

In this section, we prove Theorem 3.20 which states that the operads of graphs ${\textsf {Graphs}}_{d+1}^{k}$ is equivalent to the operad ${\textsf {Pois}}^k_d$.

Proof

It is easy to see that the combinatorial map $\psi :\textsf {ho}{\textsf {Pois}}_d^k \rightarrow {\textsf {Graphs}}_{d+1}^{k\downarrow }$ is a map of operads. Let us define a natural surjective inverse map of complexes of $\mathbb {S}$-modules $\epsilon :{\textsf {Graphs}}_{d+1}^{k\downarrow } \rightarrow \textsf {ho}{\textsf {Pois}}_{d}^{k}$ which sends all graphs that contain a vertex with more than one incoming edge to zero and what remains is uniquely presented as an operadic tree. For example:

The map $\epsilon$ is not a map of operads; however, this is a one-sided inverse to the map of $\mathbb {S}$-modules ${\textsf {ho}{\textsf {Pois}}}_d^{k} \rightarrow {\textsf {Graphs}}_{d+1}^{k\downarrow }$ and in order to finish the proof of Theorem 3.20 it is enough to show that the kernel of $\epsilon$ is an acyclic complex. Let us define a combinatorial filtration on the kernel of $\epsilon$, such that it is easy to show that the corresponding associated graded differential is acyclic.$\square$

Definition A.1

For each oriented graph $\Gamma \in {\textsf {Graphs}}_{d+1}^{k\downarrow }$ containing a vertex with more than one incoming edge we can assign a unique directed path (called the bad path) yielding the following properties:

• the bad path starts in a bad vertex (= a vertex containing more than one incoming edge);

• the bad path ends in an external vertex and this is the lowest possible external vertex with a possible incoming path from a bad vertex;

• the bad path contains a unique bad vertex (the source of a path).

In the example below, we draw the bad path in red and fill the bad vertices in grey:

The vertex splitting differential may either increase the length of the bad path or increase the number of an external vertex in the target of a path. Consider a filtration on $co\ker (\epsilon ^{\checkmark })$ by the number of the bad external vertex and consider a grading by the length of the bad path on the associated graded complex. The associated graded differential preserves the index of the bad external vertex and increases the length of the bad path. Moreover, the associated graded differential does not interact with edges that start not in the bad path. Consequently, the associated graded complex is a direct sum of complexes . Where the summand is spanned by the set of graphs that coincide after contracting the bad path. Let us show that each of these subcomplexes is acyclic. Consider a particular graph . Let v be a vertex in the bad path of $\Gamma$ then v has the following restriction on the set of incoming and outgoing edges outside of a bad path:

• if v is not the source vertex of a bad path then v has even positive number of outgoing edges (outside of a bad path) and no incoming edges;

• if v is the starting vertex of a bad path then v has even number of outgoing (outside of a bad path) edges and at least two incoming edges;

• if v is a target external vertex in a bad path then v has zero number of outgoing edges.

Let us order the set $S(\Gamma )$ of edges starting at vertices in the bad path and ending outside of a bad path. Let $A:=\mathbb {Q}[e_1,\ldots ,e_m]$ be the free commutative (polynomial) algebra generated by the variables indexed by $S(\Gamma )$. Let $A^{(k)}:=\oplus _{n\geqslant 0}A_{kn}\subset A$ be the k-th Segre power consisting of polynomials of degrees divisible by k. The latter is known to be a quadratic Koszul algebra. Consider the Bar resolution:

$$\begin{aligned} B(A^{(k)}):= & {} \bigoplus _{m\geqslant 0} A^{(k)}\otimes \underbrace{A^{(k)}_{+}{\otimes }\ldots \otimes A^{(k)}_{+}}_{m}, \ d(a_0\otimes a_1\otimes \ldots \otimes a_m)\\= & {} \sum _{i=0}^{m-1} (-1)^{i} a_0\otimes \ldots \otimes a_{i} a_{i+1} \otimes \ldots \end{aligned}$$

which is the resolution of a trivial left $A^{(k)}$-module. We notice that the $\mathbb {S}_m$-invariants of the multilinear part of the bar resolution $B(A^{(k)})$ is dual to the subcomplexes spanned by graphs which have the same shape as $\Gamma$ after contracting the bad path. The multilinear part of $B(A^{(k)})$ is acyclic and thanks to Maschke’s theorem the subspace of $\mathbb {S}_m$-invariants form an acyclic subcomplex and consequently, is also acyclic.

The case of an absence of outgoing edges outside of a bad path has to be considered separately, but in this case, the length of a bad path may be either 0 or 1 and it is clear that it has no homology. $\square$

1.2 Computing homology of $\textsf {ICG}^{k\downarrow }$

This section is devoted to giving proof of the key Lemma 3.24. The proof is based on a collection of consecutive spectral sequence arguments such that the associated graded differential for each particular spectral sequence is a vertex splitting (edge contraction) that does not brake certain symmetries defined combinatorially in terms of graphs. Maschke’s theorem is the key argument that helps in this type of computations. One also should have in mind that any given pair of integers $n\geqslant 1$ and $l\geqslant 0$ the number of graphs in $\textsf {ICG}^{k\downarrow }(n)$ with a given loop order l is finite. Consequently, all spectral sequences we are dealing with converge because all complexes split to the direct sums of finite-dimensional ones.

Let us start from certain combinatorial definition that leads to the generalization of Lemma 3.24:

Definition A.2

For each subset $S\subset [1n]$ consider the subspace $\textsf {ICG}_S^{k\downarrow }(n)\subset \textsf {ICG}^{k\downarrow }(n)$ spanned by internally connected graphs $\Gamma$ yielding the two following properties:

• (i) for all $s\in S$ the graph $\Gamma$ has a unique edge ending in the external vertex and the source vertex of this edge has more than one outgoing edges: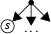

• (ii) we do not allow an internal vertex of valency $k+1$ such that with it has no incoming edges and k (of $k+1$) outgoing edges are connected to the k different external vertices $s_1,\ldots ,s_k\in S$:

  

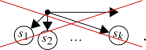  (A.3)

Lemma A.4

All nontrivial cohomology classes in $\textsf {ICG}_S^{k\downarrow }(n)$ can be represented by linear combinations of internally trees whose all inner vertices either have one output and two inputs or have $k+1$ outgoing edges and no incoming edges.

In particular, for each given loop degree the homology is concentrated in a unique homological degree.

Note that Lemma 3.24 is a particular case of Lemma A.4 when $S=\emptyset$.

Proof

The proof is the simultaneous (increasing) induction on the number n of externally connected vertices, (decreasing) induction on the cardinality of the subset S and (increasing) induction on the loop grading of a graph.

For the base of induction ($|S|=n$), we notice that there are no oriented graphs (with no oriented loops) in ${\textsf {ICG}}^{k\downarrow }_{[1n]}(n)$. Indeed, each internal vertex of a graph $\Gamma \in \textsf {ICG}^{k\downarrow }$ has at least one outgoing edge and if, also, each external vertex of $\Gamma$ is connected by a unique edge and the source of this edge has at least one edge ending in an internal vertex then one can construct a directed path of arbitrary length that avoids external vertices. However, the number of vertices is finite and hence this path contains a loop what is not allowed in $\textsf {ICG}^{k\downarrow }$.

(Induction step). Suppose $m\in [1n]{\setminus } S$ and thanks to the induction on n we may suppose that we are dealing with the ideal of graphs connected with . For each graph $\Gamma \in {\textsf {ICG}}^{k\downarrow }_{S}(n)$, we can define the maximal subtree $T_m:=T_m(\Gamma )\subset \Gamma$ whose vertices are defined by the following property:

$w\in T_m$${\mathop {\Leftrightarrow }\limits ^{def}}$ There exists a unique (nondirected) path (with no selfintersections) that starts inw and ends in.

Let $T_m^{\downarrow }$ be the subtree of $T_m$ spanned by those vertices v of $T_m$ yielding the conditions:

(a1):

the unique path starting at v and ending in is a directed path;

(a2):

if the vertex v is internal (differs from ) then it has a unique outgoing edge.

Let $\Gamma _1,\ldots ,\Gamma _k$ be the set of internally connected components of the complementary graph $\Gamma {\setminus } T_m^{\downarrow }$ (internal vertices of $T_m^{\downarrow }$ are considered as external vertices of the complementary graph $\Gamma {\setminus } T_m^{\downarrow }$). Moreover, $\forall 1\leqslant i\leqslant k$ there exists exactly one vertex $v_i\in T_m^{\downarrow }$ such that there exists not less than one edge ending in $v_i$ that belongs to $\Gamma _i$. The uniqueness of $v_i$ is governed by definition of $T_m\supset T_m^{\downarrow }$. In Picture (A.5), we consider an example of a graph $\Gamma$. The complementary graph $\Gamma {\setminus } T_m^{\downarrow }$ has three connected component drawn in different colors (green, yellow and blue). We draw the tree $T_m^{\downarrow }$ together with the incoming edges that correspond to connected components that is designed by corresponding coloring:

(A.5)

Consider the filtration ${\mathcal {F}}^{p}$ of ${\textsf {ICG}}^{k\downarrow }_{S}(n)$ by the number p of internally connected components of the graph $\Gamma {\setminus } T_m^{\downarrow }(\Gamma )$. While ordering the corresponding graded components, we end up with the following isomorphism of symmetric collections:

$$\begin{aligned} \textsf {gr}^{{\mathcal {F}}}\textsf {ICG}_{S}^{k\downarrow } \simeq \textsf {L}_{\infty } \circ \left( {\mathcal {F}}^{1}/{\mathcal {F}}^{>1}(\textsf {ICG}_{S}^{k\downarrow })\right) \end{aligned}$$

Thanks to the Koszulness of the operad $\textsf {Lie}$ it remains to explain that the quotient complex ${\textsf {ICG}}^{k\downarrow }_{S}(n)^1:={\mathcal {F}}^{1}/{\mathcal {F}}^{>1}(\textsf {ICG}_{S}^{k\downarrow })$ spanned by graphs $\Gamma \in {\textsf {ICG}}^{k\downarrow }_{S}(n)$ with unique internally connected component $\Gamma _1$ of $\Gamma {\setminus } T_m^{\downarrow }(\Gamma )$ has appropriate cohomology.

Note that the graph $\Gamma {\setminus } T_m^{\downarrow }(\Gamma )$ may have a unique internally connected component if and only if $T_m^{\downarrow }(\Gamma )$ either is equal to or consists of one edge . Therefore, the complex ${\textsf {ICG}}^{k\downarrow }_{S}(n)^1$ admits a decomposition ${\textsf {ICG}}^{k\downarrow }_{S}(n)^1 = {\textsf {ICG}}^{k\downarrow }_{S}(n)^1_{0} \oplus {\textsf {ICG}}^{k\downarrow }_{S}(n)^1_{1}$ where the additional rightmost lower index corresponds to the number of edges in $T_m^{\downarrow }$. Consider the homotopy $h:{\textsf {ICG}}^{k\downarrow }_{S}(n)^1_{1}\twoheadrightarrow {\textsf {ICG}}^{k\downarrow }_{S}(n)^1_{0}$ to the first differential in the corresponding spectral sequence given by contraction of the edge if allowed. The kernel of the surjective homotopy h is spanned by graphs having more than one outgoing edge from the unique internal vertex $v\in T_m^{\downarrow }$. In particular, the complex ${\textsf {ICG}}^{k\downarrow }_{{S\sqcup \{m\}}}(n)$ is a direct summand of the kernel of h and can be reached by the decreasing induction on the cardinality of S.

Thus, it remains to show that the complement of ${\textsf {ICG}}^{k\downarrow }_{{S\sqcup \{m\}}}(n)$ in the kernel of h (which we denote by K) is acyclic. Note that the complement K consists of graphs that has the forbidden vertex (A.3) connected with certain external vertices $t_1,\ldots ,t_{k-1}\in S$ and m. Consider the filtration by the lexicographical order of the subset T of first $k-1$ external vertices adjacent to m (via exactly one internal vertex v). The associated graded complex $K_T$ admits additional two-step filtration $K_T=K_T^{k+1}\oplus K_T^{>k+1}$, where $K_T^{k+1}$ is spanned by graphs with the vertex v of valency $k+1$. Note that in the latter case the vertex v has only outgoing edges connected with T,m and the remaining part of the graph. Consider the homotopy $h'$ to the associated graded differential given by contraction of the unique edge connecting v and the remaining part of the graph:

The homotopy $h'$ defines a bijection between graphs spanning $K_T^{k+1}$ and $K_T^{>k+1}$ except one particular case when the remaining part of the graph consists of one external vertex and if $S=T$ or $S=T\sqcup \{t\}$ the cohomology of $K_T$ is spanned by the image of the generator $t_{t_1,\ldots ,t_{k-1},t,m}$ with respect to the map $\psi$ defined in (3.23). As promised we finished with the increasing induction on the cardinality of the subset S of external vertices. $\square$