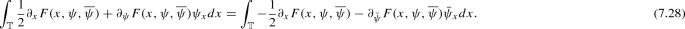Abstract
Consider a class of 1-d Hamiltonian derivative nonlinear Schrödinger equations
where \(V\in \Theta _m\) [\(\Theta _m\) is defined in (1.5)]. The nonlinearity of these equations includes \((\psi _x,\bar{\psi }_x)\) and depends on space variable x periodically, which means that the nonlinearity is unbounded (see Definition 1.1) and the momentum set (see Definition 2.2) of the corresponding Hamiltonian function is unbounded. In this paper, we obtain that for any potential V outside a small measure subset of \( {\Theta }_m \), if the initial value is smaller than \(R\ll 1\) in p-Sobolev norm, then the corresponding solution to this equation is also smaller than 2R during a time interval \((-\,cR^{-r_*},cR^{-r_*})\) (for any given positive \(r_*\)). The main methods are constructing Birkhoff normal forms to unbounded Hamiltonian systems which have unbounded momentum sets and using the special symmetry of the Hamiltonian functions to control p-Sobolev norms of the solutions.
Similar content being viewed by others
Notes
Suppose \(a\in \ell ^p(\mathbb {Z}^*,\mathbb {C})\), \(b\in \ell ^q(\mathbb {Z}^*,\mathbb {C})\) and \(\frac{1}{p}+\frac{1}{q}=\frac{1}{r}+1,\) with \(1\le p,q,r\le \infty \). Then \(\Vert f*g\Vert _{\ell ^r(\mathbb {Z}^*,\mathbb {C})}\le \Vert f\Vert _{\ell ^p(\mathbb {Z}^*,\mathbb {C})}\cdot \Vert g\Vert _{\ell ^q(\mathbb {Z}^*,\mathbb {C})}.\)
Since \(F(x,\psi ,\bar{\psi })\) satisfies assumptions \(\mathbf{B_1}\)–\(\mathbf{B_2}\), the following equation holds true for any \(\psi (\cdot , t)\in H^{p}(\mathbb {T},\mathbb {C}) \) fulfilling \(\psi (x+2\pi ,t)=\psi (x,t)\)
$$\begin{aligned} 0=\int _{\mathbb {T}} \frac{d F}{d x}(x,\psi ,\bar{\psi })d x= \int _{\mathbb {T}} \partial _x F(x,\psi ,{\overline{\psi }}) +\partial _{\psi } F (x,\psi ,{\overline{\psi }}){\psi }_x +\partial _{\bar{\psi }} F (x,\psi ,{\overline{\psi }})\bar{\psi }_x dx, \end{aligned}$$i.e.,
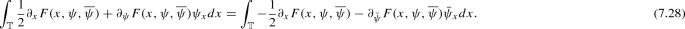
From (7.28) and assumptions \(\mathbf{B_1}\)–\(\mathbf{B_2}\), it follows
$$\begin{aligned} \overline{\int _{\mathbb {T}} \mathbf{i}\frac{1}{2}\partial _x F(x,\psi ,{\overline{\psi }}) + \mathbf{i}\partial _{\psi } F (x,\psi ,{\overline{\psi }})\psi _x dx}= & {} \int _{\mathbb {T}} (-\mathbf{i})\frac{1}{2}\partial _x F(x,\psi ,{\overline{\psi }}) - \mathbf{i}\partial _{\bar{\psi }} F (x,\psi ,{\overline{\psi }})\bar{\psi }_x dx\\= & {} \int _{\mathbb {T}} \mathbf{i}\frac{1}{2}\partial _x F(x,\psi ,{\overline{\psi }}) + \mathbf{i}\partial _{\psi } F (x,\psi ,{\overline{\psi }})\psi _x dx, \end{aligned}$$which means that the Hamiltonian function \(H_{(1.8)}(\psi ,\bar{\psi })\) is real.
References
Asano, K.: On semi-linear parabolic partial differential equations. Publ. Res. Inst. Math. Sci. Ser. A 1, 67–98 (1965)
Baldi, P., Berti, M., Haus, E., Montalto, R.: Time quasi-periodic gravity water waves in finite depth. Invent. Math. 214(2), 739–911 (2018)
Baldi, P., Berti, M., Montalto, R.: KAM for autonomous quasi-linear perturbations of mKdV. Boll. Unione Mat. Ital. 9, 143–188 (2016)
Bambusi, D., A Birkhoff normal form theorem for some semilinear PDEs. In: Hamiltonian Dynamical Systems and Applications, NATO Sci. Peace Secur. Ser. B Phys. Biophys., pp. 213–247. Springer, Dordrecht (2008)
Bambusi, D.: Birkhoff normal form for some nonlinear PDEs. Commun. Math. Phys 234(2), 253–285 (2003)
Bambusi, D., Delort, J.M., Grébert, B., Szeftel, J.: Almost global existence for Hamiltonian semilinear Klein–Gordon equations with small Cauchy data on Zoll manifolds. Commun. Pure Appl. Math. 60, 1665–1690 (2007)
Bambusi, D., Grébert, B.: Birkhoff normal form for partial differential equations with tame modulus. Duke Math. J. 135, 507–567 (2006)
Berti, M., Biasco, L., Procesi, M.: Existence and stability of quasi-periodic solutions for derivative wave equations. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 24(2), 199–214 (2013)
Berti, M., Biasco, L., Procesi, M.: KAM for reversible derivative wave equations. Arch. Ration. Mech. Anal. 212(3), 905–955 (2014)
Berti, M., Delort, J.M.: Almost global solutions of capillary–gravity water waves equations on the circle. In: Lecture Notes of the Unione Matematica Italiana, vol. 24. Springer, Cham; Unione Matematica Italiana (Bologna), 2018. x+268 pp
Bourgain, J.: Construction of quasi-periodic solutions for Hamiltonian perturbations of linear equations and applications to nonlinear PDE. Int. Math. Res. Notices 1994(11), 475–497 (1994)
Bourgain, J.: Construction of approximative and almost-periodic solutions of perturbed linear Schrödinger and wave equations. Geom. Funct. Anal. 6, 201–230 (1996)
Bourgain, J.: On diffusion in high-dimensional Hamiltonian systems and PDE. J. Anal. Math. 80, 1–35 (2000)
Bourgain, J.: Green’s function estimates for lattice Schrödinger operators and applications. In: Annals of Mathematics Studies, vol. 158. Princeton University Press, Princeton, NJ (2005)
Craig, C., Wayne, C.: Newton’s method and periodic solutions of nonlinear wave equations. Commun. Pure Appl. Math. 46(11), 1409–1498 (1993)
Delort, J.M.: On long time existence for small solutions of semi-linear Klein–Gordon equations on the torus. J. Anal. Math. 107, 161–194 (2009)
Delort, J.M.: Quasi-linear perturbations of Hamiltonian Klein–Gordon equations on spheres. Mem. Am. Math. Soc. 234(1103), vi+80 (2015)
Delort, J.M.: A quasi-linear Birkhoff normal forms method. Appliccation to the quasi-linear Klein–Gordon equation on \(\mathbb{S}^1\). Astérisque No. 341, vi+113 pp. (2012). ISBN: 978-2-85629-335-5
Delort, J.M., Szeftel, J.: Long time existence for small data nonlinear Klein–Gordon equations on tori and spheres. Int. Math. Res. Not. 37, 1897–1966 (2004)
Delort, J.M., Szeftel, J.: Long-time existence for semi-linear Klein–Gordon equations with small Cauchy data on Zoll manifolds. Am. J. Math. 128(5), 1187–1218 (2006)
Delort, J.M.: Existence globale et comportement asymptotique pour Ĺéquation de Klein–Gordon quasilinéaire à données petites en dimension 1. Ann. Sci. École Norm. Sup. (4) 34(1), 1–61 (2001). Erratum: Ann. Sci. École Norm. Sup. (4) 39(2), 335–345 (2006)
Delort, J.M.: Long-time Sobolev stability for small solutions of quasi-linear Klein–Gordon equations on the circle. Trans. Am. Math. Soc. 361(8), 4299–4365 (2009)
Eliasson, L., Kuksin, S.B.: KAM for the nonlinear Schrödinger equation. Ann. Math. (2) 172(1), 371–435 (2010)
Faou, E., Grébert, B.: Quasi-invariant modified Sobolev norms for semi linear reversible PDEs. Nonlinearity 23(2), 429–443 (2010)
Feola, R., Iandoli, F.: Long time existence for fully nonlinear NLS with small Cauchy data on the circle. arXiv:1806.03437
Geng, J., Xu, X., You, J.: An infinite dimensional KAM theorem and its application to the two dimensional cubic Schrödinger equation. Adv. Math. 226(6), 5361–5402 (2011)
Grébert, B.: Birkhoff normal form and Hamiltonian PDEs. In: Partial differential equations and applications. Sémin. Congr. Soc. Math. France, Paris, 15, 1–46 (2007)
Kappeler, T., Pöschel, J.: KdV and KAM. Springer, Berlin (2003)
Klainerman, S.: On “almost global” solutions to quasilinear wave equations in three space dimensions. Commun. Pure Appl. Math. 36, 325–344 (1983)
Kuksin, S.B.: Nearly Integrable Infinite-dimensional Hamiltonian Systems, Lecture Notes in Mathematics, vol. 1556. Springer, Berlin (1993)
Kuksin, S.B.: Analysis of Hamiltonian PDEs. In: Oxford Lecture Series in Mathematics and Its Applications, vol. 19. Oxford University Press, Oxford (2000)
Kuksin, S.B.: A KAM theorem for equations of the Korteweg–de Vries type. Rev. Math. Math. Phys. 10(3), 1–64 (1998)
Liu, J., Yuan, X.: A KAM theorem for Hamiltonian partial differential equations with unbounded perturbations. Commu. Math. Phys. 307, 629–673 (2011)
Liu, J., Yuan, X.: KAM for the derivative nonlinear Schrödinger equation with periodic boundary conditions. J. Differ. Equ. 256, 1627–1652 (2014)
Wayne, C.E.: Periodic and quasi-periodic solutions of nonlinear wave equations via KAM theory. Commun. Math. Phys. 127(3), 479–528 (1990)
Yuan, X.P., Zhang, J.: Long time stability of Hamiltonian partial differential equations. SIAM J. Math. Anal. 46(5), 3176–3222 (2014)
Yuan, X.P., Zhang, J.: Averaging principle for the KdV equation with a small initial value. Nonlinearity 29, 603–656 (2016)
Zhang, J., Gao, M., Yuan, X.: KAM tori for reversible partial differential equations. Nonlinearity 24, 1189–1228 (2011)
Acknowledgements
This paper is supported in part by Science and Technology Commission of Shanghai Municipality (No. 18dz2271000). Funding was provided by National Natural Science Foundation of China (Grant No. 11871023).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1
Appendix 1
1.1 Proof of Theorem 3
Proof
Denote
where \(P_r(u,{\bar{u}})\) is an r-degree homogeneous polynomial of \(P(u,{\bar{u}})\). Thus (2.8) can be rewritten as
To start with, the results hold at rank \(r=0\). For any \(R<R_*\) and any N satisfying (4.22), we will look for a bounded Lie-transformation \({{\mathcal {T}}}_0\) to eliminate the non-normalized monomials of \(\Gamma ^N_{\le 2}g^{(-1)}_{3}\). The Lie-transformation \({{\mathcal {T}}}_0\) is constructed from 1-time flow \(\Phi _{S^{(0)}}^t\) of the following equations,
where \(S^{(0)}\) is undetermined. Under transformation \({{\mathcal {T}}}_0\) the new Hamiltonian \(H^{(0)}\) has the following form,
where \( ({\cdot })_{(\nu ,S^{(0)})}\) is defined in (4.25). The auxiliary Hamiltonian function \(S^{(0)}\) is obtained by solving the following homological equation
Using Remark 3.2, \(\Gamma ^N_{>2} P_3\) and \(\Gamma ^N_{\le 2}P_3\) are still of \(\beta \)-type symmetric coefficients semi-bounded by C(r) with \(r=-1\), where C(r) is defined in (4.23). From Lemma 4.2, \(Z_{3}\) is a 3-degree \((\gamma ,\alpha ,N)\)-normal form of \( \Gamma ^N_{\le 2}P_{3}\) and the Hamiltonian vector field of \(S^{(0)}\) satisfies
From (7.4), the following holds true
The Lie-transformation \({{\mathcal {T}}}_0 \) satisfies
Use the bootstrap method to estimate \({{\mathcal {T}}}_0 \). First, assume that
By (7.5)–(7.7), the following inequality holds true
Since R is small enough, from (4.22) and (7.8), the transformation \( {{\mathcal {T}}}_0 \) satisfies
which means
Denote \( {{\mathcal {T}}}^{ (0)}:={{\mathcal {T}}}_0 \). By (4.22), (7.6) and (7.8), it is verified that (4.24) holds for rank \(r=0\):
Set
Since \(Z_3\) and \( {g}^{(-1)}_3\) have \(\beta \)-type symmetric coefficients, by Remark Remark 3.2 and Lemma 3.1, \(Z^{(0)}\) and \({{\mathcal {R}}}^{N(0)}\) are still having \(\beta \)-type symmetric coefficients. Denote the \(r_*+3\)-degree polynomial of power series (7.3) as \(g^{(0)}\) and the remainder as \({{\mathcal {R}}}^{T(0)}\), i.e.,
where for any \(4\le t\le r_*+3\),
and for any \(t> r_*+3\)
From Remark 4.4 and Lemma 3.1, \(g^{(0)}\) and \({{\mathcal {R}}}^{T(0)}\) also have \(\beta \)-type symmetric coefficients. In order to estimate the coefficients of them, one needs to estimate the coefficients of \((H_0)_{(t-2,S^{(0)})}\), \(\sum _{n'=1}^{t-3}(g^{(-1)}_{t-n'})_{(n',S^{(0)})}\) and \(\sum _{n'=1}^{t-3}({{\mathcal {R}}}^{T(-1)}_{t-n'})_{(n',S^{(0)})}\). By Remark 4.4, we get that
and
When N satisfies (4.22), together with (7.11) and (7.12), it follows
Similarly, \({{\mathcal {R}}}^{T(0)}(u,{\bar{u}})\) has still \(\beta \)-type symmetric coefficients semi-bounded by C(0).
Now assume that the results hold for rank \(r< r_*\). By these assumptions, there exist a real number \({\tilde{R}}<R_*\) and a Lie-transformation which changes Hamiltonian (7.1) into the following form
which is defined in \(B_p(R_r)\) (\( R<{\tilde{R}}<R_*\)), where \(R_r:=\frac{2r_*-r}{2r_*}R\). One should construct a bounded Lie-transformation \({{\mathcal {T}}}_r\) to eliminate the non-normalized monomials of \(\Gamma ^N_{\le 2}g^{(r)}_{r+4}\). Because \(g_{r+4}^{(r)}\) has \(\beta \)-type symmetric coefficients, by Remark 3.2, the coefficients of \(\Gamma ^N_{\le 2}g^{(r)}_{r+4}\) and \(\Gamma ^N_{>2}g^{(r)}_{r+4}\) are of \(\beta \)-type symmetric coefficients semi-bounded by C(r). Make use of the 1-time flow of the following equation, for any \(j\in \mathbb {Z}^*\)
to define a Lie-transformation \({{\mathcal {T}}}_r\), under which the new Hamiltonian has the following form formally,
The auxiliary Hamiltonian \(S^{(r)}\) can be obtained by solving the following homological equation
From Lemma 4.2, \(Z_{r+4}\) is an \((r+4)\)-degree \((\gamma ,\alpha ,N)\)-normal form of \(\Gamma ^N_{\le 2}g^{(r)}_{r+4}\) and
The Hamiltonian vector field \(X_{S^{(r)}}\) satisfies
Using (7.16) and bootstrap method, suppose that
for any \(t\in [0,1]\). Then we obtain
By (4.22) and (7.18), the transformation \({{\mathcal {T}}}_r \) satisfies
which verifies (7.17). Denote \( {{\mathcal {T}}}^{ (r+1)}:={{\mathcal {T}}}^{ (r)}\circ {{\mathcal {T}}}_r \). By (7.17) and (7.18), noting that \(R< {\tilde{R}}<R_*<1\), it holds
Because \(C(t)\le C(t+1)\) for any positive integer t, from (7.19), one has that
Denote
By Remark 4.4 and Lemma 3.1, \(Z^{(r+1)}\) and \({{\mathcal {R}}}^{N(r+1)}\) have \(\beta \)-type symmetric coefficients. Denote
where
and
where [a] denotes the integer part of the real number a. Using Lemma 3.1 and Remark 4.4, from the fact that \( g^{(r)}, \ {{\mathcal {R}}}^{T(r)}, \ {{\mathcal {R}}}^{N(r)}\) and \( Z^{(r)}\) have \(\beta \)-type symmetric coefficients semi-bounded by C(r), then \(g^{(r+1)}\) and \({{\mathcal {R}}}^{T(r+1)}\) also have \(\beta \)-type symmetric coefficients.
Using Remark 4.4, the following estimates hold: for any \(|l+k|=t\) with \({{\mathcal {M}}}(l,k)=i\in M_{(g^{(r)}_{r+4})_{(\frac{t-r-4}{r+2},S^{(r)})}}\),
for any \(|l+k|=t\) with \({{\mathcal {M}}}(l,k)=i\in M_{(g^{(r)}_{t-n'(r+2)})_{(n',S^{(r)})}}\),
for any \(|l+k|=t\) with \({{\mathcal {M}}}(l,k)=i\in M_{(Z^{(r)}_{t-n'(r+2)})_{(n',S^{(r)})}},\)
for any \(|l+k|=t\) with \({{\mathcal {M}}}(l,k)= i\in M_{({{\mathcal {R}}}^{N(r)}_{t-n'(r+2)})_{(n',S^{(r)})}}\)
and for any \(|l+k|=t\) with \({{\mathcal {M}}}(l,k)= i\in M_{({{\mathcal {R}}}^{T(r)}_{t-n'(r+2)})_{(n',S^{(r)})}}\)
By (7.21)–(7.25) and assumption (4.22), for any \(r+5\le t\le r_*+3\), \(|l+k|=t\) and \(i\in M_{g^{(r+1)}_{t}}\), the following estimate holds
which means that \(g^{(r+1)}(u,{\bar{u}})\) has \(\beta \)-type symmetric coefficients semi-bounded by \(C(r+1)>0\).
Similarly, \( {{\mathcal {R}}}^{T(r+1)}(u,{\bar{u}})\) and \({{\mathcal {R}}}^{N(r+1)}(u,{\bar{u}}) \) are also of \(\beta \)-type symmetric coefficients semi-bounded by \(C(r+1)>0\). \(\square \)
1.2 The Result to DNLS Eq. (1.8)
Suppose that the function \(F(x,\psi ,\bar{\psi })\) in Eq. (1.8) satisfies the followings.
- \(\mathbf{B}_\mathbf{1}\):
-
\(F(x,\xi , \eta )\) is a polynomial about \((\xi , \eta )\) in a neighborhood of the origin and satisfies
$$\begin{aligned} \overline{F(x,\psi ,\bar{\psi })}=F(x,\psi ,\bar{\psi }), \ F(x,\psi ,\bar{\psi })= F(x+2\pi ,\psi ,\bar{\psi }) \end{aligned}$$(7.27)and \(F(x,\psi ,\bar{\psi })\) vanishes at least at order 2 in \((\psi ,\bar{\psi })\) at the origin.
- \(\mathbf{B}_\mathbf{2}\):
-
For any fixed \((\psi ,\bar{\psi })\) being in a neighborhood of the origin, \(F(\cdot , \psi ,\bar{\psi }) \in H^{\beta +1}(\mathbb {T},\mathbb {C})\) (\(\beta \) is a big enough positive real number) satisfies
$$\begin{aligned} F(x+2\pi ,\psi ,\bar{\psi })=F(x,\psi ,\bar{\psi }). \end{aligned}$$
Then (1.8) becomes a Hamiltonian PDE with a real value Hamiltonian functionFootnote 3
on symplectic space \(({\widetilde{H}}^{p}(\mathbb {T},\mathbb {C}),\)\(w^0)\), where
and
The corresponding Hamiltonian vector of \(H_{(1.8)}(\psi ,\bar{\psi })\) under symplectic form \(w^0\) is
and the Eq. (1.8) can be written as
Theorem 5
Suppose that the Eq. (1.8) satisfies assumptions \(\mathbf{B_1}\)–\(\mathbf{B_2}\). For any integer \(r_*>1\), there exist an almost full measure set \(\widetilde{\Theta }^0_m \subset \Theta ^0_m\) and \(p_*>0\) such that for any fixed \(V \in \widetilde{\Theta }^0_m \) and any p fulfilling \( (\beta -4)/2>p>p_{*}\), if the initial data of the solution to (1.8) satisfies
then one has
The proof of Theorem 5 is similar to Theorem 1. We list the main idea.
-
1.
Under Fourier transformation, constructing small-norm almost global solutions to Eq. (1.8) becomes into studying the long time stability of the solutions around the origin point to the follow Hamiltonian equation
$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} {\dot{u}}_j= -\,\mathbf{i} \partial _{{{\bar{u}}}_j} H_{(2.8)} (u,{\bar{u}}),\\ \dot{{\bar{u}}}_j=\ \ \mathbf{i} \partial _{ u_j} H_{(2.8)}(u,{\bar{u}}), \end{array}\right. \quad j\in \mathbb {Z} \end{aligned}$$(7.32)defined in \(({{\mathcal {H}}}^p (\mathbb {Z},\mathbb {C}),{\tilde{w}}^0)\), with a symplectic form \({\tilde{w}}^0:=\mathbf{i}\sum _{j\in \mathbb {Z}} d u_j \wedge d{\bar{u}}_j\) and a Hamiltonian function
$$\begin{aligned} H_{(7.33)}(u,{\bar{u}})=H_0 + P(u,{\bar{u}}), \end{aligned}$$(7.33)where
$$\begin{aligned} H_0:=\sum _{j\in {\mathbb {Z}}} \omega ^0(V)|u_j|^2,\quad \omega _j^0(V):=-j^2+\frac{v_j}{\langle j \rangle ^m}\in \mathbb {R}, \ \omega ^0_j(V)=\omega ^0_{-j}(V). \end{aligned}$$(7.34)The polynomial
$$\begin{aligned} P (u,{\bar{u}})=\sum _{t= 3}^n P_t(u,{\bar{u}}),\quad P_t(u,{\bar{u}}):= \sum \limits _{|k+l|=t, {{\mathcal {M}}}(l,k)=i\in M_{P_t}\subset \mathbb {Z} } P^i_{t,lk} u^{l}{\bar{u}}^k \end{aligned}$$does not have \(\beta \)-type symmetric coefficients, but its coefficients have the following form
$$\begin{aligned} P^i_{t,lk}:=\sum _{({l}^0,{k}^0,i^0)\subset {{\mathcal {A}}}_{P^i_{t,lk} }}\ {P}^{i({l}^0,{k}^0,i^0)}_{t,lk}\left( {{\mathcal {M}}}({l}^0, {k}^0)-\frac{i^0}{2}\right) , \end{aligned}$$where
$$\begin{aligned} {{\mathcal {A}}}_{P^i_{t,lk}}\subset \{({\tilde{l}},{\tilde{k}},{\tilde{i}}) \ |\ 0\le {\tilde{l}}_j\le l_j,\ 0\le {\tilde{k}}_j\le k_j,\ \text{ for } \text{ any } j\in \mathbb {Z},\ ({\tilde{l}},{\tilde{k}})\in \mathbb {N}^{{{\mathbb {Z}}}}\times \mathbb {N}^{{{\mathbb {Z}}}},\ {\tilde{i}}\in \mathbb {Z}\}, \end{aligned}$$and for any \((l^0,k^0,i^0)\in {{\mathcal {A}}}_{P^i_{t,lk}}\), it holds true
$$\begin{aligned} (k- k^0,l-{l}^0, i^0-2i)\in {{\mathcal {A}}}_{P^{-i}_{t,kl}},\quad \overline{P^{i(l^0,k^0,i^0)}_{t,lk}}=P^{-i(k-k^0, {l}-l^0, i^0-2i)}_{t,kl}. \end{aligned}$$(7.35)Moreover, there exists a constant \(C>0\) such that for any \(l,k\in \mathbb {N}^{{\mathbb {Z}}}\) with \(|l+k|=t \) and \({{\mathcal {M}}}(l,k)=i\), the following inequality holds true
$$\begin{aligned} \sum _{(l^0,k^0,i^0)\in {{\mathcal {A}}}_{P^i_{t,lk}}} |P^{i(l^0,k^0,i^0)}_{t,lk}|\cdot \max \{ \langle i^0\rangle , \langle i^0-2i\rangle \} \le \frac{ C^{t-2}}{\langle i\rangle ^{\beta }}. \end{aligned}$$(7.36)Similar to Proposition 3.1, we get that the Hamiltonian vector field \(X_P:B_p(R)\subset {{\mathcal {H}}}^p(\mathbb {Z},\mathbb {C})\rightarrow {{\mathcal {H}}}^{p-1}(\mathbb {Z},\mathbb {C})\)(\(0<R \ll 1\)).
Fortunately, the condition (7.35) and (7.36) help us to get that the t-degree homogeneous \(P_t(u,{\bar{u}})\) holds the inequalities in Proposition 3.2 and Corollary 1 under symplectic form \({\tilde{w}}^0\).
-
2.
We establish the high order Birkhoff normal form to system (7.32) under a bounded symplectic transformation around the origin point. From the definitions of symplectic structure \({\tilde{w}}^0\) and \(\omega (V):=(\omega _j(V))_{j\in \mathbb {Z}}\), for any \(j\in \mathbb {Z}\) and any (l, k) fulfilling \(\sum _{j\in \mathbb {Z}} |l_j+l_{-j}-k_j-k_{-j}|=0\) we obtain
$$\begin{aligned} \{ u^l{\bar{u}}^k, \Vert u\Vert _p^2\}_{{\tilde{w}}^0}=\sum _{j\in \mathbb {Z}} \mathbf{i}(l_j+l_{-j}-k_j-k_{-j})u^l{\bar{u}}^k=0 \end{aligned}$$(7.37)and for any \(V\in \Theta _m^0\)
$$\begin{aligned} \{ u_j{\bar{u}}_{-j}+{\bar{u}}_ju_{-j}, \ \omega _j(V) |q_j|^2+\omega _{-j}(V)|q_j|^2 \}_{{\tilde{w}}^0}=0. \end{aligned}$$(7.38)From (7.37) and (7.38), although we can not found a symplectic transformation to eliminate the term \(u^l{\bar{u}}^k\) in \(P(u,{\bar{u}})\) which satisfies \(\sum _{j\in \mathbb {Z}} |l_j+l_{-j}-k_j-k_{-j}|=0\), this term will not effect the \({{\mathcal {H}}}^p(\mathbb {Z},\mathbb {C})\)-norm of the solution to (7.32). In this case \((\gamma ,\alpha ,N)\) non resonant condition to \(\omega (V)\) up to r order has some differences with the one (defined in Definition 4.1). Now it should be hold for any (l, k) fulfilling \(\Gamma _{>N}(l+k)\le 2,\)\( \sum _{j\in \mathbb {Z}} |l_j+l_{-j}-k_j-k_{-j}|\ne 0\) and \(3\le |l+k|\le r, \) and satisfies
$$\begin{aligned} |\langle \omega (V), \ (l-k)\rangle |>\frac{\gamma M_{l,k}}{N^{\alpha }}. \end{aligned}$$(7.39)By the \((\gamma ,\alpha ,N)\)-non resonant condition (7.39) to \(\omega (V)\) up to r order, there exists a symplectic transformation under which Hamiltonian system (7.32) is changed into
$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} {\dot{u}}_j= -\,\mathbf{i} \partial _{{{\bar{u}}}_j} H^{(r)} (u,{\bar{u}}),\\ \dot{{\bar{u}}}_j=\ \ \mathbf{i} \partial _{ u_j} H^{(r)} (u,{\bar{u}}), \end{array}\right. \quad j\in \mathbb {Z} \end{aligned}$$(7.40)with
$$\begin{aligned} H^{(r+3)}(u,{\bar{u}})=H_0+\underbrace{Z^{(r+3)}(u,{\bar{u}})+{{\mathcal {R}}}^{N(r+3)}(u,{\bar{u}})+{{\mathcal {R}}}^{T(r+3)}(u,{\bar{u}})}_{P^{(r+3)}(u,{\bar{u}})}, \end{aligned}$$\(P^{(r+3)}(u,{\bar{u}})\) still satisfies (7.35) and (7.36) for a new positive constant \(C_*\) taking place C in (7.36). The \((r+3)\)-degree \((\gamma ,\alpha ,N)\)-normal from \(Z^{(r+3)}(u,{\bar{u}})\) depends on not only \(|u_j|^2\) but also \((u_j{\bar{u}}_{-j}+{\bar{u}}_ju_{-j})_{j\in \mathbb {Z}}\). From (7.38), the normal form \(Z(u,{\bar{u}})\) still satisfies the estimate of Lemma 4.1 under symplectic form \({\tilde{w}}^0\). For any N satisfying (4.22), we have
$$\begin{aligned} \sup _{\Vert (u,{\bar{u}})\Vert _p\le R} |\{Z^{(r+3)}(u,{\bar{u}})+{{\mathcal {R}}}^{N(r+3)}(u,{\bar{u}})+{{\mathcal {R}}}^{T(r+3)}(u,{\bar{u}}),\Vert u\Vert _p^2 \}_{{\tilde{w}}^0}| \prec R^{r+1}. \end{aligned}$$Using the same method, the long time stability result of (7.32) under non-resonant assumption is obtained.
Final, similar to Lemma 6.1, there exists a almost full measure subset \( \widetilde{\Theta }_m^0 \subset {\Theta }_m^0 \), for any \(V\in \widetilde{\Theta }_m^0\), the frequencies \(\omega (V)\) satisfies the non resonant condition (7.39).
1.3 Proof of Theorem 4
Prior to giving the proof of Theorem 4, we list some results.
Consider an equation
Let \(\omega _{\varepsilon }=\text{ diag }\{ \big ((\mathbf{i}+\varepsilon ) \omega _j\big )_{j\in \mathbb {Z}^*}\}\), be an operator with domain \(D(\omega _{\varepsilon })=D(\omega )\), where \(D(\omega )=\ell ^2_{2}(\mathbb {Z}^*,\mathbb {C})\). For any \(\alpha >0\), we define
where \(PV[z^{\alpha }]\) denote the principal value of \(z^{\alpha }\).
Theorem 6
Let \(1/2\le \alpha <1\) and \(u_0\in D(\omega _{\varepsilon }^{\alpha })=\ell ^2_{2\alpha }(\mathbb {Z}^*,\mathbb {C})\). Suppose that there exist two non-negative and non-decreasing functions g, f defined on \([0,\infty )\) such that
and
Then for any \(\varepsilon >0\) there exists \(T_0>0\) such that Eq. (7.41) has a unique local strict solution.
where \(T_0\) is a constant depending only on \(\Vert u_0\Vert _{2\alpha }\).
The proof of Theorem 6 is found in Theorem 2.1 in [1].
Remark 7.1
We call u(t) be a strict solution to (7.41) on [0, T] if
-
1.
u(t) is strongly continuous on [0, T] and strongly continuously differentiable on (0, T],
-
2.
for each \(t\in (0,T]\)u(t) belongs to \(D(\omega _{\varepsilon })\) and \(\omega _{\varepsilon }u(t)\) is strongly continuous in (0, T],
-
3.
u(t) satisfies (7.41).
Theorem 7
If \(u_0\in D(\omega _{\varepsilon }^{\infty })=\cap _{\alpha >0} D(\omega _{\varepsilon }^{\alpha })\), then the solution u to Eq. (7.41) belongs to \( C^{\infty }(0,T_0,D(\omega ^{\infty })).\)
In order to prove Theorem 7, we need the following Lemma.
Lemma 7.1
Let \(y(t)\in D(\omega _{\varepsilon }^{\alpha })\) and \( \omega _{\varepsilon }^{\alpha } y(t)\) be continuous in [0, T] for some \(\alpha >0\). Put
Then for any \(\beta \) with \(0<\beta <1\), \(v(t)\in D(\omega _{\varepsilon }^{\alpha +\beta })\) for \(t\in [0,T]\) and
Moreover, \(\omega _{\varepsilon }^{\alpha +\beta } v(t) \) is Hölder continuous in [0, T] with exponent \((1-\alpha )\).
The proof of Lemma 7.1 see Lemma 2.5 in [1]. Now we prove the Theorem 7.
Proof
From (7.41), we have
Assumptions on \(u_0\) imply that the first term belongs to \(C^{\infty }(0,T_0, D(\omega _{\varepsilon }^{\infty }))\). Because
where \(u_{\theta }=u+\theta (v-u)\), \(u_{\theta '}=u+\theta ' (v-u)\) with \(\theta ,\ \theta '\in (0,1)\). When \(u,v\in D(\omega _{\varepsilon }^{\alpha })\), it follows
Using Lemma 3.2, we get that
and
where g and f are functions defined on \([0,\infty )\) which are non-negative and non-decreasing. Form Theorem 6, note that \(u\in C(0,T_0, D(\omega _{\varepsilon }^{\alpha }))\) for any \(\alpha \) with \(1/2< \alpha <1\).
In much the same way as above we see that
Then applying Lemma 7.1, for any \(\beta '\in (0,1)\), we have \(u\in C(0,T_0, D(\omega ^{\alpha +\beta +\beta '-1}))\). Repeatly, this argument yields
Then in virtue of (7.41) we obtain
Further regularities with respect to t follows immediately from (7.43) and (7.44). \(\square \)
Let us prove Theorem 4.
Proof
Since \(D(\omega ^{\infty })=D(\omega _{\varepsilon }^{\infty })\) is dense in \(D(\omega ^{p/2})\), we find sequence \(\{u_{0\varepsilon }\} \subset D(\omega _{\varepsilon }^{\infty })\) such that
Let \(u_{\varepsilon }(t)\) be a solution of initial value problem.
Then using Theorem 7, there exists \(u_{\varepsilon }(t)\in C^{\infty }(0,T_0; D(\omega ^{\infty }))\). Applying \({\tilde{\omega }}^{p/2}\) (\({\tilde{\omega }}:={\textit{diag}}\{(j^2)_{j\in \mathbb {Z}^*}\}\) commuted with \(\omega \)) to the both sides of Eq. (7.45), and taking the inner product of the resultant equation with \({\tilde{\omega }}^{p/2}{\bar{u}}_{\varepsilon }\), we have
If \(p>3\),
and using Lemma 3.2 we get
Integrating both sides of (7.47) from 0 to t, we get
The solution \(\Vert u_{\varepsilon }(t)\Vert _p\) of (7.48) can be majorized by the solution of
with \(\eta =\Vert u_{\varepsilon }(0)\Vert _p^2\), where h is a non-negative and non-decreasing function. The solution of (7.49) exists only for \(0\le t<T_*:=\frac{\eta }{2c\ h(2\eta )}\). Hence, \(\{u_{\varepsilon }\}\) remains bounded on \(\ell ^{\infty }(0,T_*,\ell ^2_{p}(\mathbb {Z}^*,\mathbb {C}))\) for any \(\varepsilon \in [0,\varepsilon _0]\) provided that we choose \(0<T_1< \min (T_0,T_*)\). Thus, we have
Integration of (7.46) with respect to t yields
and
In view of (7.45), we get
\(u_{\varepsilon }(t)\) is strongly continuous on \(C(0,T_1, \ell ^2_{p-2}(\mathbb {Z}^*,\mathbb {C})).\)
We show the convergence of approximate solutions \(\{u_{\varepsilon }(t)\}\). Set \(v(t)=u_{\varepsilon }(t)-u_{\delta }(t)\). And v(t) satisfies the following equation
Summing the inner product of (7.54) with \({\bar{v}}\) and the inner product of the conjugate of (7.54) with v, we get
where \({\text{ Re }}(z)\) is the real part of z. Calculus the first term in the right side, we get that
where \(u_{\theta }=u_{\varepsilon }+\theta (u_{\delta }-u_{\varepsilon })\), \(u_{\theta '}=u_{\varepsilon }+\theta '(u_{\delta }-u_{\varepsilon })\), \(\theta , \theta '\in (0,1)\). The last equation is holding by the fact that \(\overline{\partial _{u{\bar{u}}}P(u_{\theta }, {\bar{u}}_{\theta })}= \partial _{{\bar{u}}u}P(u_{\theta }, {\bar{u}}_{\theta })\), i.e., \(\langle \sigma \partial _{u{\bar{u}}}P(u_{\theta }, {\bar{u}}_{\theta })v,v\rangle \) is real. So \(\text{ Re }\ \mathbf{i} \langle \sigma \partial _{u{\bar{u}}}P(u_{\theta }, {\bar{u}}_{\theta }){v}, v)=0\). \(\square \)
Lemma 7.2
When \(P(u,{\bar{u}})\) is an r-degree homogeneous polynomial with \(\beta \)-type symmetric coefficients semi-bounded by \(C>0\), then we have that
Proof
We write
where
and
where
and
Let us consider \(D(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\), first. For any \((l,k)\in \alpha [3]\), it holds true that
Take (7.57) into \(D(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\) and get that
The first part of the right side of Eq. (7.58) equals to \(-D(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\). From (7.58), we get that
In the following we will estimate \(A(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\), \(B(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\), \(C(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\) and \(D(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\) in (7.59). In order to do that, we should calculate the boundary of the coefficients of them. The coefficient of \(u^{l-e_j-e_n}{\bar{u}}^{k}{\bar{v}}_j{\bar{v}}_n\) in \(A(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\) is bounded by
The coefficients of the term with \((l,k)\in \alpha [2]\) of \(B(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\) is bounded by
The coefficients of \(C(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\) are bounded by the following fact
The coefficients of \(D(u_{\theta },{\bar{u}}_{\theta },v,{\bar{v}})\) is bounded by
From (7.60)–(7.62), using Lemma 3.2, we get that
\(\square \)
From Eq. (7.55) and (7.56), using Lemma 7.2, it follows that
Then
which implies that \(\{u_{\varepsilon }\}\) is a Cauchy sequence in \(C(0,T_1,\ell ^2(\mathbb {Z}^*,\mathbb {C}))\). Thus, there exists a function u(x, t) such that as \(\varepsilon \rightarrow 0\),
From the estimate of (7.50)–(7.52),
Taking the inner product of (7.45) with \(v\in D(\omega _{\varepsilon }^*)=D(\omega )=\ell ^2_{2}(\mathbb {Z}^*,\mathbb {C})\) and integrating on (0, t), we find
Letting \(\varepsilon \) tend to zero, we get
for any \(v\in D(\omega )\), where \(\langle \cdot , \cdot \rangle \) denote the duality between \(D(\omega )'=\ell ^2_{-2}(\mathbb {Z}^*,\mathbb {C})\) and \(D(\omega )=\ell ^2_{2}(\mathbb {Z}^*,\mathbb {C})\) and \(\bar{\omega }\) is an unique continuous linear extension of \(\omega \) from \(\ell ^2\) to \(D(\omega )\).
Hence we obtain
which implies that u(t) is strongly absolutely continuous in \(D(\omega ^{\alpha -1})\) at almost all \(t\in (0,T_1)\)
\(\square \)
Rights and permissions
About this article
Cite this article
Zhang, J. Almost Global Solutions to Hamiltonian Derivative Nonlinear Schrödinger Equations on the Circle. J Dyn Diff Equat 32, 1401–1455 (2020). https://doi.org/10.1007/s10884-019-09773-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-019-09773-y
Keywords
- Derivative nonlinear Schrödinger (DNLS) equations
- Hamiltonian systems
- Unbounded
- Long time stability
- Momentum
- Birkhoff normal form