Swing-Up Control Design for Spring Attatched Passive Joint Acrobot

Abstract

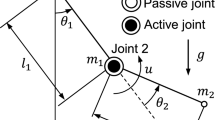
This paper presents the conditions and PD controller to swing-up the Acrobot to which a spring is attached at the passive joint (first joint). Because the motion of the system is in the vertical plane, there are some system parameters associated with gravity. The range of a spring constant and controller gain that allow the PD controller to swing-up the system is defined depending on these parameter values. To prove that the PD controller makes the system approach the equilibrium points, one of which is swing-up state (upright equilibrium point, UEP), the motion of the first link is analyzed according to the motion of the second link and the torque on the active joint (second joint) with an actuator. Among these equilibrium points, the conditions that can only converge to the UEP of the system are found.

Appendix

This section shows that Lyapunov function candidate (25) is positive definite; that is, $V\left( \mathbf{0} \right) =0$ and $V\left( {{\textit{\textbf{q}}}},\ \dot{{{\textit{\textbf{q}}}}}\right) >0$ for all $\left( {{\textit{\textbf{q}}}},\ \dot{{{\textit{\textbf{q}}}}}\right) \ne \mathbf {0}$. Because $\frac{1}{2}{\dot{{{\textit{\textbf{q}}}}}}^T{{\textit{\textbf{M}}}}\left( {{\textit{\textbf{q}}}}\right) \dot{{{\textit{\textbf{q}}}}}$ in Eq. (26) is kinetic energy, it is always greater than or equal to zero. Thus, $\frac{1}{2}{\dot{{{\textit{\textbf{q}}}}}}^T{{\textit{\textbf{M}}}}\left( {{\textit{\textbf{q}}}}\right) \dot{{{\textit{\textbf{q}}}}}$ is assumed to be zero and applied to Eq. (25).

$$\begin{aligned} \begin{aligned} V\left( {{\textit{\textbf{q}}}},\mathbf{0} \right)&=\beta _1\left( \cos {q_1}-1\right) +\beta _2\left( \cos {\left( q_1+q_2\right) }-1\right) \\ {}&\quad +\, \frac{1}{2}\left( k_1q_1^2+K_Pq_2^2\right) \end{aligned} \end{aligned}$$

(50)

The minimum value of Eq. (50) is calculated using Matlab function called fminunc that is suitable to find the minimum of unconstrained multivariable function. The values of $k_1$ and $K_P$ are substituted with constants from 0 to 100 at 0.1 intervals, respectively. When the minimum value of Eq. (50) is zero and both $q_1$ and $q_2$ are zero, $k_1$ and $K_P$ values are presented in the following figures. These are positive V and represented by dots in the graph. But there are so many points, it looks like a plane. At the same time, the boundary of $K_P$ is calculated by substituting $k_1$ satisfying Eq. (46) into Eq. (47). The results are drawn with a solid line. Since the $K_{P}$ boundary is the minimum value of $K_P$, the range of $K_P$ that satisies Eq. (47) is upper the boundary. $\beta _1$ and $\beta _2$ in Eq. (49) are used. To calculate the minimum of Eq. (50), the initial states of $q_1$ and $q_2$ are set to $\left( \pi ,\ \pi \right) ,\ \left( -\pi ,\ -\pi \right) ,\ \left( \pi ,\ -\pi \right) ,\ \left( -\pi ,\ \pi \right) ,\ \left( 0,\ 0\right)$.

As shown from Fig. 6, 7, 8, 9 and Fig. 10, if $k_1$ and $K_P$ satisfying Eqs. (46) and (47) are used, the Lyapunov function candidate (25) has zero at $\left( {{\textit{\textbf{q}}}},\ \dot{{{\textit{\textbf{q}}}}}\right) =\mathbf{0}$, which is the minimum. Therefore, Lyapunov function candidate (25) can be positive definite when $k_1$ and $K_P$ satisfy Eqs. (46) and (47).

Fig. 6

Result of $k_1$ and $K_P$: initial state of $\left( \textit{q}_1,\ \textit{q}_2\right)$ is $(\pi ,\ \pi )$

Fig. 7

Result of $k_1$ and $K_P$: initial state of $\left( \textit{q}_1,\ \textit{q}_2\right)$ is $(-\pi ,\ -\pi )$

Fig. 8

Result of $k_1$ and $K_P$: initial state of $\left( \textit{q}_1,\ \textit{q}_2\right)$ is $(\pi ,\ -\pi )$

Fig. 9

Result of $k_1$ and $K_P$: initial state of $\left( \textit{q}_1,\ \textit{q}_2\right)$ is $(-\pi ,\ \pi )$

Fig. 10

Result of $k_1$ and $K_P$: initial state of $\left( \textit{q}_1,\ \textit{q}_2\right)$ is $(0,\ 0)$