Vibration analysis of coupled straight–curved beam systems with arbitrary discontinuities subjected to various harmonic forces

Abstract

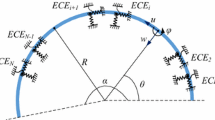
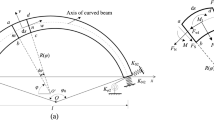
In this paper, a modified variational method is developed to study the free and forced vibration of coupled straight–curved beam systems with an arbitrary number of eccentric discontinuities (EDs). Based on the generalized shell theory, the kinetic and potential functional of the curved beam with arbitrary subtended angles is formulated. Since the shear and inertial (or radial–tangential–rotational coupling) effects are included for the curved beam, the longitudinal vibration is also introduced to the energy functional for a straight Timoshenko beam. Using corresponding coordinate transformations, the Lagrange multiplier method and least-square weighted residual method are employed to impose the continuity constraints on the internal interfaces and boundaries among the straight and curved beams. The proposed method allows a flexible choice of the admissible functions and can be used for various combinations of the straight and curved beams to model corresponding engineering structures. Concentrated forces, uniformly distributed loads and space-dependent loads are considered to demonstrate great efficiency and accuracy of the present approach for the forced as well as the free vibration of the coupled system. Most of the present results are compared with those from finite element program ANSYS, and good agreement is observed. Influences of the EDs on the dynamic responses of the coupled system are also examined.

Appendices

Appendix A: Generalized mass and stiffness matrices of the coupled beam system

The disjoint generalized mass and stiffness matrices of the coupled straight–curved beam system are, respectively, assembled as

$$\begin{aligned} {\mathbf{M}}= & {} \hbox {diag}\left[ {{\begin{array}{*{20}c} {\underbrace{{\mathbf{M}}_{\mathrm{c,1}} ,{\mathbf{M}}_{\mathrm{c,}2} ,\ldots ,{\mathbf{M}}_{\mathrm{c,}N_{c} } }_{N_{c} \hbox { curved beam segments}},} {\underbrace{{\mathbf{M}}_{\mathrm{s,1}} ,{\mathbf{M}}_{\mathrm{s,}2} ,\ldots ,{\mathbf{M}}_{\mathrm{s,}N_{s} } }_{N_{s} \hbox { straight beam segments}},} {\underbrace{{\mathbf{M}}_{\mathrm{c,1}} ,{\mathbf{M}}_{\mathrm{c,}2} ,\ldots ,{\mathbf{M}}_{\mathrm{c,}N_{c} } }_{N_{c} \hbox { curved beam segments}},} {\underbrace{{\mathbf{M}}_{\mathrm{s,1}} ,{\mathbf{M}}_{\mathrm{s,}2} ,\ldots ,{\mathbf{M}}_{\mathrm{s,}N_{s} } }_{N_{s} \hbox { straight beam segments}}} \end{array} }} \right] \nonumber \\ \end{aligned}$$

(A.1)

$$\begin{aligned} {\mathbf{K}}= & {} \hbox {diag}\left[ {{\begin{array}{*{20}c} {\underbrace{{\mathbf{K}}_{\mathrm{c,1}} ,{\mathbf{K}}_{\mathrm{c,}2} ,\ldots ,{\mathbf{K}}_{\mathrm{c,}N_{c} } }_{N_{c} \hbox { curved beam segments}},} {\underbrace{{\mathbf{K}}_{\mathrm{s,1}} ,{\mathbf{K}}_{\mathrm{s,}2} ,\ldots ,{\mathbf{K}}_{\mathrm{s,}N_{s} } }_{N_{s} \hbox { straight beam segments}},} {\underbrace{{\mathbf{K}}_{\mathrm{c,1}} ,{\mathbf{K}}_{\mathrm{c,}2} ,\ldots ,{\mathbf{K}}_{\mathrm{c,}N_{c} } }_{N_{c} \hbox { curved beam segments}},} {\underbrace{{\mathbf{K}}_{\mathrm{s,1}} ,{\mathbf{K}}_{\mathrm{s,}2} ,\ldots ,{\mathbf{K}}_{\mathrm{s,}N_{s} } }_{N_{s} \hbox { straight beam segments}}} \end{array} }} \right] \nonumber \\ \end{aligned}$$

(A.2)

where $\mathbf{M }_{c,i}$ and $\mathbf{K }_{c,i}$ ($i\in \left[ {1,N_{c} } \right] )$ are the disjoint generalized mass and stiffness matrices for the curved beam component, respectively. For more details, the readers may refer to Ref. [23]. The generalized mass and stiffness matrices of the ith straight beam segment can be given by

$$\begin{aligned} {\mathbf{M}}_{s}^{i}= & {} \int _{x_{i} } {\left[ {{\begin{array}{*{20}c} {{\mathbf{M}}_{uu}^{i} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{M}}_{ww}^{i} } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{M}}_{\varphi \varphi }^{i} } \\ \end{array} }} \right] \mathrm{d}x} \end{aligned}$$

(A.3)

$$\begin{aligned} {\mathbf{K}}_{s}^{i}= & {} \int _{x_{i} } {\left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{uu}^{i} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{K}}_{ww}^{i} } &{} {{\mathbf{K}}_{w\varphi }^{i} } \\ {{\mathbf{0}}} &{} {{\mathbf{K}}_{w\varphi }^{i,T} } &{} {{\mathbf{K}}_{\varphi \varphi }^{i} } \\ \end{array} }} \right] \mathrm{d}x} \end{aligned}$$

(A.4)

The elements of the mass matrices are:

$$\begin{aligned} {\mathbf{M}}_{uu}^{i}= & {} \rho _{si} A_{si} {\mathbf{U}}_{i}^{T} {\mathbf{U}}_{i} , \end{aligned}$$

(A.5a)

$$\begin{aligned} {\mathbf{M}}_{ww}^{i}= & {} \rho _{si} A_{si} {\mathbf{W}}_{i}^{T} {\mathbf{W}}_{i} , \end{aligned}$$

(A.5b)

$$\begin{aligned} {\mathbf{M}}_{\varphi \varphi }^{i}= & {} \rho _{si} I_{si} {\varvec{\Phi }}_{i}^{T} {\varvec{\Phi }}_{i} \end{aligned}$$

(A.5c)

The elements of the stiffness matrices are:

$$\begin{aligned} {\mathbf{K}}_{uu}^{i}= & {} E_{si} A_{si} \frac{\partial {\mathbf{U}}_{i}^{T} }{\partial x}\frac{\partial {\mathbf{U}}_{i} }{\partial x}, \end{aligned}$$

(A.6a)

$$\begin{aligned} {\mathbf{K}}_{ww}^{i}= & {} \kappa _{si} G_{si} A_{si} \frac{\partial {\mathbf{W}}_{i}^{T} }{\partial x}\frac{\partial {\mathbf{W}}_{i} }{\partial x} \end{aligned}$$

(A.6b)

$$\begin{aligned} {\mathbf{K}}_{w\varphi }^{i}= & {} -\kappa _{si} G_{si} A_{si} \frac{\partial {\mathbf{W}}_{i}^{T} }{\partial x}{\varvec{\Phi }}_{i} , \end{aligned}$$

(A.6c)

$$\begin{aligned} {\mathbf{K}}_{\varphi \varphi }^{i}= & {} E_{si} I_{si} \frac{\partial {\varvec{\Phi }}_{i}^{T} }{\partial x}\frac{\partial {\varvec{\Phi }}_{i} }{\partial x}+\kappa _{si} G_{si} A_{si} {\varvec{\Phi }}_{i}^{T} {\varvec{\Phi }}_{i} \end{aligned}$$

(A.6d)

According to the organization of the elements in the generalized displacement vector, assembling all interface matrices of the straight beam component leads to the generalized interface matrices ${\mathbf{K}}_{\lambda }^{s}$ and ${\mathbf{K}}_{\kappa }^{s}$ of the straight beam component. The interface matrix ${\mathbf{K}}_{\lambda }^{i}$ of the straight beam at the interface located at $x=x_{i}$ is given by

$$\begin{aligned} {\mathbf{K}}_{\lambda }^{i} =\left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{u_{i} u_{i} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{u_{i} u_{i+1} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{K}}_{w_{i} w_{i} } } &{} {{\mathbf{K}}_{w_{i} \varphi _{i} } } &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{w_{i} w_{i+1} } } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{K}}_{w_{i} \varphi _{i} }^{T} } &{} {{\mathbf{K}}_{\varphi _{i} \varphi _{i} } } &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{\varphi _{i} w_{i+1} } } &{} {{\mathbf{K}}_{\varphi _{i} \varphi _{i+1} } } \\ {{\mathbf{K}}_{u_{i} u_{i+1} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{K}}_{w_{i} w_{i+1} }^{T} } &{} {{\mathbf{K}}_{\varphi _{i} w_{i+1} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{\varphi _{i} \varphi _{i+1} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ \end{array} }} \right] \end{aligned}$$

(A.7)

The detailed elements of the interface matrix ${\mathbf{K}}_{\lambda }^{i}$ are:

$$\begin{aligned} {\mathbf{K}}_{u_{i} u_{i} }= & {} E_{si} A_{si} \left( {\frac{\partial {\mathbf{U}}_{i}^{T} }{\partial x}{\mathbf{U}}_{i} +{\mathbf{U}}_{i}^{T} \frac{\partial {\mathbf{U}}_{i} }{\partial x}} \right) , \end{aligned}$$

(A.8a)

$$\begin{aligned} {\mathbf{K}}_{u_{i} u_{i+1} }= & {} -E_{si} A_{si} \frac{\partial {\mathbf{U}}_{i}^{T} }{\partial x}{\mathbf{U}}_{i+1} \end{aligned}$$

(A.8b)

$$\begin{aligned} {\mathbf{K}}_{w_{i} w_{i} }= & {} \kappa _{si} G_{si} A_{si} \left( {\frac{\partial {\mathbf{W}}_{i}^{T} }{\partial x}{\mathbf{W}}_{i} +{\mathbf{W}}_{i}^{T} \frac{\partial {\mathbf{W}}_{i} }{\partial x}} \right) , \end{aligned}$$

(A.8c)

$$\begin{aligned} {\mathbf{K}}_{w_{i} \varphi _{i} }= & {} -\kappa _{si} G_{si} A_{si} {\mathbf{W}}_{i}^{T} {\varvec{\Phi }}_{i} \end{aligned}$$

(A.8d)

$$\begin{aligned} {\mathbf{K}}_{w_{i} w_{i+1} }= & {} -\kappa _{si} G_{si} A_{si} \frac{\partial {\mathbf{W}}_{i}^{T} }{\partial x}{\mathbf{W}}_{i+1} , \end{aligned}$$

(A.8e)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{i} \varphi _{i} }= & {} E_{si} I_{si} \left( {\frac{\partial {\varvec{\Phi }}_{i}^{T} }{\partial x}{\varvec{\Phi }}_{i} +{\varvec{\Phi }}_{i}^{T} \frac{\partial {\varvec{\Phi }}_{i} }{\partial x}} \right) \end{aligned}$$

(A.8f)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{i} w_{i+1} }= & {} \kappa _{si} G_{si} A_{si} {\varvec{\Phi }}_{i}^{T} {\mathbf{W}}_{i+1} , \end{aligned}$$

(A.8g)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{i} \varphi _{i+1} }= & {} -E_{si} I_{si} \frac{\partial {\varvec{\Phi }}_{i}^{T} }{\partial x}{\varvec{\Phi }}_{i+1} \end{aligned}$$

(A.8h)

The generalized matrix ${\mathbf{K}}_{\kappa }^{i}$ due to the least-square weighted terms at the interface located at $x=x_{i}$ is given below

$$\begin{aligned} {\mathbf{K}}_{\kappa }^{i} =\left[ {{\begin{array}{*{20}c} {{{\bar{\mathbf{K}}}}_{u_{i} u_{i} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{u_{i} u_{i+1} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{w_{i} w_{i} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{w_{i} w_{i+1} } } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{\varphi _{i} \varphi _{i} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{\varphi _{i} \varphi _{i+1} } } \\ {{{\bar{\mathbf{K}}}}_{u_{i} u_{i+1} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{u_{i+1} u_{i+1} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{w_{i} w_{i+1} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{w_{i+1} w_{i+1} } } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{\varphi _{i} \varphi _{i+1} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{\varphi _{i+1} \varphi _{i+1} } } \\ \end{array} }} \right] \end{aligned}$$

(A.9)

where the detailed elements are obtained by

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{u_{i} u_{i} }= & {} \kappa _{su} {\mathbf{U}}_{i}^{T} {\mathbf{U}}_{i} , \end{aligned}$$

(A.10a)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{u_{i} u_{i+1} }= & {} -\kappa _{su} {\mathbf{U}}_{i}^{T} {\mathbf{U}}_{i+1} , \end{aligned}$$

(A.10b)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{u_{i+1} u_{i+1} }= & {} -\kappa _{su} {\mathbf{U}}_{i+1}^{T} {\mathbf{U}}_{i+1} \end{aligned}$$

(A.10c)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{w_{i} w_{i} }= & {} \kappa _{sw} {\mathbf{W}}_{i}^{T} {\mathbf{W}}_{i} , \end{aligned}$$

(A.10d)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{w_{i} w_{i+1} }= & {} -\kappa _{sw} {\mathbf{W}}_{i}^{T} {\mathbf{W}}_{i+1} , \end{aligned}$$

(A.10e)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{w_{i+1} w_{i+1} }= & {} -\kappa _{sw} {\mathbf{W}}_{i+1}^{T} {\mathbf{W}}_{i+1} \end{aligned}$$

(A.10f)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{\varphi _{i} \varphi _{i} }= & {} \kappa _{s\varphi } {\varvec{\Phi }}_{i}^{T} {\varvec{\Phi }}_{i} , \end{aligned}$$

(A.10g)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{i} \varphi _{i+1} }= & {} -\kappa _{s\varphi } {\varvec{\Phi }}_{i}^{T} {\varvec{\Phi }}_{i+1} , \end{aligned}$$

(A.10h)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{i+1} \varphi _{i+1} }= & {} -\kappa _{s\varphi } {\varvec{\Phi }}_{i+1}^{T} {\varvec{\Phi }}_{i+1} \end{aligned}$$

(A.10i)

Appendix B: Generalized interface stiffness matrices at the joints of the straight and curved beam components

The interface matrix ${\mathbf{K}}_{\lambda }^{s,c}$ at the interface between the straight and curved beam is expressed as

$$\begin{aligned} {\mathbf{K}}_{\lambda }^{s,c} =\left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{u_{s} u_{s} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{u_{s} u_{c} } } &{} {{\mathbf{K}}_{u_{s} w_{c} } } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{K}}_{w_{s} w_{s} } } &{} {{\mathbf{K}}_{w_{s} \varphi _{s} } } &{} {{\mathbf{K}}_{w_{s} u_{c} } } &{} {{\mathbf{K}}_{w_{s} w_{c} } } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{K}}_{w_{s} \varphi _{s} }^{T} } &{} {{\mathbf{K}}_{\varphi _{s} \varphi _{s} } } &{} {{\mathbf{K}}_{\varphi _{s} u_{c} } } &{} {{\mathbf{K}}_{\varphi _{s} w_{c} } } &{} {{\mathbf{K}}_{\varphi _{s} \varphi _{c} } } \\ {{\mathbf{K}}_{u_{s} u_{c} }^{T} } &{} {{\mathbf{K}}_{w_{s} u_{c} }^{T} } &{} {{\mathbf{K}}_{\varphi _{s} u_{c} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{K}}_{u_{s} w_{c} }^{T} } &{} {{\mathbf{K}}_{w_{s} w_{c} }^{T} } &{} {{\mathbf{K}}_{\varphi _{s} w_{c} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{\varphi _{s} \varphi _{c} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ \end{array} }} \right] \end{aligned}$$

(B.1)

The detailed elements of the interface matrix ${\mathbf{K}}_{\lambda }^{i}$ are:

$$\begin{aligned} {\mathbf{K}}_{u_{s} u_{s} }= & {} E_{s} A_{s} \left( {\frac{\partial {\mathbf{U}}_{s}^{T} }{\partial x}{\mathbf{U}}_{s} +{\mathbf{U}}_{s}^{T} \frac{\partial {\mathbf{U}}_{s} }{\partial x}} \right) , \end{aligned}$$

(B.2a)

$$\begin{aligned} {\mathbf{K}}_{u_{s} u_{c} }= & {} -a_{11} E_{s} A_{s} \sin \left( {\frac{\alpha }{2}} \right) \frac{\partial {\mathbf{U}}_{s}^{T} }{\partial x}{\mathbf{U}}_{c} \end{aligned}$$

(B.2b)

$$\begin{aligned} {\mathbf{K}}_{u_{s} w_{c} }= & {} -a_{12} E_{s} A_{s} \cos \left( {\frac{\alpha }{2}} \right) \frac{\partial {\mathbf{U}}_{s}^{T} }{\partial x}{\mathbf{W}}_{c} , \end{aligned}$$

(B.2c)

$$\begin{aligned} {\mathbf{K}}_{w_{s} w_{s} }= & {} \kappa _{s} G_{s} A_{s} \left( {\frac{\partial {\mathbf{W}}_{s}^{T} }{\partial x}{\mathbf{W}}_{s} +{\mathbf{W}}_{s}^{T} \frac{\partial {\mathbf{W}}_{s} }{\partial x}} \right) \end{aligned}$$

(B.2d)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{s} u_{c} }= & {} a_{21} \kappa _{s} G_{s} A_{s} \cos \left( {\frac{\alpha }{2}} \right) {\varvec{\Phi }}_{s}^{T} {\mathbf{U}}_{c} , \end{aligned}$$

(B.2e)

$$\begin{aligned} {\mathbf{K}}_{w_{s} u_{c} }= & {} -a_{21} \kappa _{s} G_{s} A_{s} \cos \left( {\frac{\alpha }{2}} \right) \frac{\partial {\mathbf{W}}_{s}^{T} }{\partial x}{\mathbf{U}}_{c} \end{aligned}$$

(B.2f)

$$\begin{aligned} {\mathbf{K}}_{w_{s} w_{c} }= & {} -a_{22} \kappa _{s} G_{s} A_{s} \sin \left( {\frac{\alpha }{2}} \right) \frac{\partial {\mathbf{W}}_{i}^{T} }{\partial x}{\mathbf{W}}_{i+1} \end{aligned}$$

(B.2g)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{s} \varphi _{s} }= & {} E_{s} I_{s} \left( {\frac{\partial {\varvec{\Phi }}_{s}^{T} }{\partial x}{\varvec{\Phi }}_{s} +{\varvec{\Phi }}_{s}^{T} \frac{\partial {\varvec{\Phi }}_{s} }{\partial x}} \right) \end{aligned}$$

(B.2h)

$$\begin{aligned} {\mathbf{K}}_{w_{s} \varphi _{s} }= & {} -\kappa _{s} G_{s} A_{s} {\mathbf{W}}_{s}^{T} {\varvec{\Phi }}_{s} , \end{aligned}$$

(B.2i)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{s} w_{c} }= & {} a_{22} \kappa _{s} G_{s} A_{s} \sin \left( {\frac{\alpha }{2}} \right) {\varvec{\Phi }}_{s}^{T} {\mathbf{W}}_{i+1} , \end{aligned}$$

(B.2j)

$$\begin{aligned} {\mathbf{K}}_{\varphi _{s} \varphi _{c} }= & {} -E_{s} I_{s} \frac{\partial {\varvec{\Phi }}_{s}^{T} }{\partial x}{\varvec{\Phi }}_{c} \end{aligned}$$

(B.2k)

The generalized matrix ${\mathbf{K}}_{\kappa }^{s,c}$ due to the least-square weighted terms at the interface between the straight and curved beam is given below

$$\begin{aligned} {\mathbf{K}}_{\kappa }^{s,c} =\left[ {{\begin{array}{*{20}c} {{{\bar{\mathbf{K}}}}_{u_{s} u_{s} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{u_{s} u_{c} } } &{} {{{\bar{\mathbf{K}}}}_{u_{s} w_{c} } } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{w_{s} w_{s} } } &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{w_{s} u_{c} } } &{} {{{\bar{\mathbf{K}}}}_{w_{s} w_{c} } } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{\varphi _{s} \varphi _{s} } } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{\varphi _{s} \varphi _{c} } } \\ {{{\bar{\mathbf{K}}}}_{u_{s} u_{c} }^{T} } &{} {{{\bar{\mathbf{K}}}}_{w_{s} u_{c} }^{T} } &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{u_{c} u_{c} } } &{} {{{\bar{\mathbf{K}}}}_{u_{c} w_{c} } } &{} {{\mathbf{0}}} \\ {{{\bar{\mathbf{K}}}}_{u_{s} w_{c} }^{T} } &{} {{{\bar{\mathbf{K}}}}_{w_{s} w_{c} }^{T} } &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{u_{c} w_{c} }^{T} } &{} {{{\bar{\mathbf{K}}}}_{w_{c} w_{c} } } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{\varphi _{s} \varphi _{c} }^{T} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{{\bar{\mathbf{K}}}}_{\varphi _{c} \varphi _{c} } } \\ \end{array} }} \right] \end{aligned}$$

(B.3)

where the detailed elements are obtained by

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{u_{s} u_{s} }= & {} \kappa _{u} {\mathbf{U}}_{s}^{T} {\mathbf{U}}_{s} , \end{aligned}$$

(B.4a)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{u_{s} u_{c} }= & {} -\kappa _{u} a_{11} \sin \left( {\frac{\alpha }{2}} \right) {\mathbf{U}}_{s}^{T} {\mathbf{U}}_{c} , \end{aligned}$$

(B.4b)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{u_{s} w_{c} }= & {} -\kappa _{u} a_{12} \cos \left( {\frac{\alpha }{2}} \right) {\mathbf{U}}_{s}^{T} {\mathbf{W}}_{c} \end{aligned}$$

(B.4c)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{w_{s} w_{s} }= & {} \kappa _{w} {\mathbf{W}}_{s}^{T} {\mathbf{W}}_{s} , \end{aligned}$$

(B.4d)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{w_{s} u_{c} }= & {} -\kappa _{w} a_{21} \cos \left( {\frac{\alpha }{2}} \right) {\mathbf{W}}_{s}^{T} {\mathbf{U}}_{c} , \end{aligned}$$

(B.4e)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{w_{s} w_{c} }= & {} -\kappa _{w} a_{ww} \sin \left( {\frac{\alpha }{2}} \right) {\mathbf{W}}_{s}^{T} {\mathbf{W}}_{c} \end{aligned}$$

(B.4f)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{\varphi _{s} \varphi _{s} }= & {} \kappa _{\varphi } {\varvec{\Phi }}_{s}^{T} {\varvec{\Phi }}_{s} , \end{aligned}$$

(B.4g)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{\varphi _{s} \varphi _{c} }= & {} -\kappa _{\varphi } {\varvec{\Phi }}_{s}^{T} {\varvec{\Phi }}_{c} , \end{aligned}$$

(B.4h)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{\varphi _{c} \varphi _{c} }= & {} -\kappa _{\varphi } {\varvec{\Phi }}_{c}^{T} {\varvec{\Phi }}_{c} \end{aligned}$$

(B.4i)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{u_{c} u_{c} }= & {} \left( {\kappa _{u} a_{11}^{2} \sin ^{2}\left( {\frac{\alpha }{2}} \right) +\kappa _{w} a_{21}^{2} \cos ^{2}\left( {\frac{\alpha }{2}} \right) } \right) {\mathbf{U}}_{c}^{T} {\mathbf{U}}_{c} \end{aligned}$$

(B.4j)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{u_{c} w_{c} }= & {} \left( {\kappa _{u} a_{11} a_{12} +\kappa _{w} a_{21} a_{22} } \right) \sin \left( {\frac{\alpha }{2}} \right) \cos \left( {\frac{\alpha }{2}} \right) {\mathbf{U}}_{c}^{T} {\mathbf{W}}_{c} \end{aligned}$$

(B.4k)

$$\begin{aligned} {{\bar{\mathbf{K}}}}_{w_{c} w_{c} }= & {} \left( {\kappa _{w} a_{22}^{2} \sin ^{2}\left( {\frac{\alpha }{2}} \right) +\kappa _{u} a_{12}^{2} \cos ^{2}\left( {\frac{\alpha }{2}} \right) } \right) {\mathbf{W}}_{c}^{T} {\mathbf{W}}_{c} \end{aligned}$$

(B.4l)

For the generalized mass and stiffness matrices of EDs, the readers may refer to Ref. [23]