1 Introduction

In recent years, the Van der Waals phase transition first discovered by Andrew Chamblin et al. [1, 2] has been widely investigated in many literatures. In particular, Van der Waals phase transition of AdS black holes has promoted to the extended phase space where this phase transition was given a clearer picture description [3]. In this framework, Kubiznak and Mann [3] studied the critical behavior of the Reissner–Nordström-AdS black hole using standard thermodynamic methods, and drew the Van der Waals phase transition diagram by using the state equation and Gibbs free energy equation of the black hole. According to these phase transition diagrams, it is obvious that there exists a first-order phase transition from a small black hole to a large black hole when \(T<T_{C}\), and a second-order phase transition when \(T=T_{C}\). Similar to fluid, phase diagrams of \(P-T\) can also be drawn, that is, there exist the coexistence curves of the two phases terminating at the critical point. In recent years, Van der Waals phase transition has been discussed in detail on the \(P-V\) plane in various AdS space-time backgrounds [4,5,6,7,8,9,10,11,12,13,14,15,16]. Furthermore, in the \(T-S\) (or \(\beta -S\)) plane, under the canonical ensemble, the isocharges line also reveal the Van der Waals behavior [5, 17,18,19,20,21,22,23]. Most of the results show that the isotherms on the \(P-V\) plane and the isocharges on the \(T-S\) plane do exhibit the characteristics of van der Waals phase transition: the system undergoes second-order phase transition at critical temperature and first-order phase transition at effective low temperature. Caceres et al. [18] showed the extended phase structures of STU black holes in four different charge configurations on the \(P-V\) plane and \(T-S\) plane. It is found that Van der Waals phase transitions can be observed in two special charge configurations (three and four equal charge cases). In addition, Van der Waals phase transition is also found such as in the \(\Phi -q\) [24] plane, and \(T-\alpha \) plane [25].

It is known that Gauss–Bonnet black hole solutions do only exist in higher dimensions since the Gauss–Bonnet term has no dynamics in four dimensions. However, in 2020, by extending the Gauss–Bonnet term multiplied by a factor \(1/(D-4)\) and rescaling the coupling constant \(\alpha \rightarrow \frac{\alpha }{D-4}\) to Einstein’s gravity, taking the dimension \(D \rightarrow 4\) limit, Glavan and Lin [26] successfully presented a novel 4-dimensional covariant modified theory of gravity, where Gauss–Bonnet invariant makes an important contribution to gravitational dynamics, while keeps the number of graviton degrees of freedom and can be free from Ostrogradsky instability. The novelty of the classical modified theory is that it bypasses Lovelock’s theorem and solves the singularity question of the vacuum static spherically symmetric solutions, leading to some completely different phenomena compared with pure Einstein theory. In particularly, making use of this modified theory, Glavan and Lin [26] firstly obtained a significant four-dimensional Gauss–Bonnet AdS black hole solution, which opens a new window to explore Gauss–Bonnet gravity in low-dimensional space time for theoretical and astronomical observations.

Now, the four-dimensional Gauss–Bonnet Black Holes have aroused great interest. For the first time, for asymptotically flat Gauss–Bonnet Black Holes, Konoplya and Zinhailo [27] investigated quasinormal modes of scalar, electromagnetic and gravitational perturbations, and indicated that the black hole with positive coupling constant becomes gravitationally unstable unless coupling constant is small enough. At the same time they discovered the radius of the black hole shadow, and showed that there is a linear relationship between the radius and the Gauss Bonne coupling constant. For the spherically symmetric Gauss–Bonnet black hole, by studying the geodesic motions of timelike and null particles, the innermost stable circular orbit as well as the photon sphere and shadow were analyzed in detail, and it turned out universal bounds on the size of a spherically symmetric black hole can be broken since the coupling constant can be allowed to be negative in the background of the Gauss–Bonnet black hole [28]. For the rotating Gauss–Bonnet black hole which first constructed by adopting the Newman–Janis algorithm by Wei and Liu [29], the shadow cast were studied via the null geodesics. Furthermore by employing the observation of M87*, they also calculated angular diameter of the shadow, and a first constraint to the Gauss–Bonnet gravity was obtained [29]. For the charged Gauss–Bonnet black hole in AdS spacetime which was generalized by Fernandes [30] in analytical closed form, some properties such as the asymptotics, the horizons, and the general relativity limit were investigated in detail. Moreover, in Ref. [31], the authors discussed on the thermodynamic phase transition in extended phase space by exhibiting \(P-V\) criticality as well as Gibbs free energy and specific heat behaviors, and found that, the Van der Waals like behavior can be observed in both charged and neutral cases. More recently, the effect of the Gauss–Bonnet constant on the shadows and photon sphere was discussed, and it turned out the larger to Gauss–Bonnet constant is, the smaller of the radii of the shadow and photon sphere will be [32].

For the spherically symmetric higher dimensional Gauss–Bonnet AdS black hole, holographic Van der Waals-like phase transition have been discussed by using entanglement entropy, Wilson loop, and two point correlation function [33]. The results showed that, these non-local observables undergo van der Waals-like phase transition for a fixed charge or a fixed Gauss–Bonnet parameter, which is completely similar to the black hole entropy. Furthermore, they also found that the non-charged five dimensional Gauss–Bonnet AdS black hole could still undergo the van der Waals-like phase transition rather than the Hawking-Page phase transition, which is quite different from a neutral spherical symmetric black hole in the pure Einstein gravity. It is interesting to detect whether holographic Van der Waals phase transition exists also for the novel AdS black holes in order to further test the Gauss–Bonnet gravity in low dimensions. The novel spherically symmetric Gauss–Bonnet AdS black holes possesses far richer features since there exist Gauss–Bonnet coupling parameter in the Einstein–Gauss–Bonnet gravity. In the extended phase space, for Gauss–Bonnet AdS black holes, both the Gauss–Bonnet coupling parameter and cosmological parameter can be treated as dynamical variables. So in the new Einstein–Gauss–Bonnet gravity, the thermodynamic phase space become more extensive. In this paper, we present how the Gauss–Bonnet coupling parameter affects thermodynamics phase transition besides charge. Furthermore, for the first time, in the framework of holography, using the two point correlation function, we test the Van der Waals phase transition of the novel four dimensional AdS black holes. As a result, we find that, not only the charged but also neutral cases, one can observe holographic van der Waals phase transition for the novel Gauss–Bonnet AdS black holes by employing the black hole entropy and two point correlation function.

2 Thermodynamic phase transitions in \(T-S\) plane

In this section, using thermal entropy, in the \(T-S\) plane, we will concentrate mainly on detecting phase transitions from the novel spherically symmetric Gauss–Bonnet AdS black holes. Firstly let us start by briefly reviewing the black hole solutions and thermodynamics in four dimensions. Very recently, Glavan and Lin [26] proposed an new Gauss–Bonnet theory in lower dimensions, and derived an novel vacuum spherically symmetric Gauss–Bonnet black hole solution by setting the action \(S=S_{EH}+S_{GB}\), that is

$$\begin{aligned} S[g_{\mu \nu }]=\int \mathrm{d}^{D}x\sqrt{-g} \left[ \frac{M^{2}_{P}}{2} R-\Lambda _{0}+\frac{\alpha }{D-4}{\mathcal {G}}\right] , \end{aligned}$$
(1)

where \(\alpha \) is a dimensionless Gauss–Bonnet coupling constant in \(D =4\), \(\mathcal {G}\) is the Gauss–Bonnet invariant, \(M_{P}\) is the reduced Planck mass. Soon afterwards. Taking into account the Einstein–Maxwell Gauss–Bonnet theory with a negative cosmological constant, Fernandes [30] generalized the Gauss–Bonnet black hole solution to include electric charge AdS spacetime. The metric of the charged AdS black hole in Gauss–Bonnet gravity reads [30, 31]

$$\begin{aligned} \mathrm{d}s^{2}= -f(r)\mathrm{d}t^{2}+\frac{1}{f(r)}\mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^{2}_{D-2} \end{aligned}$$
(2)

with a function

$$\begin{aligned} f(r)=1+\frac{r^{2}}{2\alpha }\left( 1-\sqrt{1+4\alpha \left( -\frac{1}{l^{2}}+\frac{2M}{r^{3}}-\frac{Q^{2}}{r^{4}}\right) }\,\right) , \end{aligned}$$
(3)

where M and Q represent the mass and charge of the black hole, and \(L=\sqrt{3/\Lambda }\) with \(\Lambda \) the cosmological constant (\(\Lambda =-3/l^{2}\)). The Hawking temperature of charged Gauss–Bonnet AdS black hole is

$$\begin{aligned} T=\frac{f'(r)}{4\pi }=\frac{r^{2}_{h}-Q^{2}-\alpha + \frac{3r^{4}_{h}}{l^{2}}}{4\pi r^{3}_{h}+8\pi \alpha r_{h} },\nonumber \\ \end{aligned}$$
(4)

where \(r_{h}\) is the outer event horizon. By solving \(f(r_{h})=0\), we obtain the mass of the black hole with regard to the function of the event horizon

$$\begin{aligned} M=\frac{r^{3}_{h}}{2l^{2}}+\frac{Q^{2}}{2r_{h}}+\frac{\alpha }{2r_{h}}+\frac{r_{h}}{2}. \end{aligned}$$
(5)

For Gauss–Bonnet AdS black hole, the parameter \(\alpha \) can be treated as a thermodynamic variable [34, 35], so the thermodynamic first law of charged Gauss–Bonnet AdS black hole becomes [31]

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+\Phi \mathrm{d}Q+V\mathrm{d}P+\mathcal {A}\mathrm{d}\alpha , \end{aligned}$$
(6)

where \(\Phi \) and \(\mathcal {A}\) are the potentials conjugate to Q and \(\alpha \), respectively. The entropy of the black hole [25] can be given by

$$\begin{aligned} S=\pi r_{h}^{2}+4\pi \alpha \log [r_{h}]. \end{aligned}$$
(7)

From theses expressions above, we obtain the following relationship between the entropy S and temperature T for the charged Gauss–Bonnet AdS black hole

$$\begin{aligned}&T(S,Q,\alpha ,l)\nonumber \\&\quad = \frac{-Q^2-\alpha +2 \alpha \text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] +\frac{12 \alpha ^2 \text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] ^2}{l^2}}{8 \sqrt{2} \pi \alpha ^{\frac{3}{2}} \sqrt{\text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] }+8 \sqrt{2} \pi \alpha ^{\frac{3}{2}} \text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] ^{\frac{3}{2}}},\nonumber \\ \end{aligned}$$
(8)

where ProductLog[z] gives the main solution of \(z=\omega e^{\omega }\) about \(\omega \). From the expression (8), it is obvious that the relationship of temperature and entropy is associated with charge Q, Gauss–Bonnet parameter \(\alpha \) and cosmological parameter l. In Ref. [25], in the \(T-V\) plane the phase transition has been studied in case of cosmological parameter treated as thermodynamic variable in the extended phase space. Here, for different the charge Q and Gauss–Bonnet parameter \(\alpha \) respectively, we focus on discussing the phase transitions for the two cases. In order to detect phase transition in the \(T-S\) plane in the fixed charged ensemble for the charged Gauss–Bonnet AdS black hole, we need to get the critical values by employing the following equations

$$\begin{aligned} \left( \frac{\partial T}{\partial S}\right) _{Q}=\left( \frac{\partial ^{2} T}{\partial ^{2} S}\right) _{Q}=0. \end{aligned}$$
(9)

The critical values of charge, entropy and temperature are

$$\begin{aligned} S_{C}= & {} \pi \alpha \text {Log}\Bigg \{\frac{1}{144} \exp \left[ \frac{l^2-12 \alpha +\sqrt{l^4-40 l^2 \alpha +144 \alpha ^2}}{12 \alpha }\right] {}\nonumber \\ {}&\times \bigg (l^2-12\sqrt{l^4-40 l^2 \alpha +144 \alpha ^2}\,\bigg )^2\Bigg \}, \end{aligned}$$
(10)
$$\begin{aligned} Q_{C}= & {} \frac{1}{6\sqrt{2}l}\bigg [l^4+36 \alpha \left( 12 \alpha -\sqrt{l^4-40 l^2 \alpha +144 \alpha ^2}\,\right) {}\nonumber \\ {}&+l^2 \left( -144 \alpha +\sqrt{l^4-40 l^2 \alpha +144 \alpha ^2}\,\right) \bigg ]^{1/2}, \end{aligned}$$
(11)
$$\begin{aligned} T_{C}= & {} \frac{1}{8 \sqrt{2} \pi \alpha ^{3/2} \sqrt{\text {ProductLog}[b]} (1+\text {ProductLog}[b])}{}\nonumber \\ {}&\times \Bigg \{ -\alpha +2 \alpha \text {ProductLog}[b]+\frac{12 \alpha ^2 \text {ProductLog}[b]^2}{l^2}{}\nonumber \\ {}&-\frac{1}{5184 l^4}\Bigg [l^4+36 \alpha \left( 12 \alpha -\sqrt{l^4-40 l^2 \alpha +144 \alpha ^2}\right) {}\nonumber \\ {}&+l^2 \left( -144 \alpha +\sqrt{l^4-40 l^2 \alpha +144 \alpha ^2}\right) \Bigg ]^{2}\Bigg \}, \end{aligned}$$
(12)

where

$$\begin{aligned} b= & {} \frac{1}{24\alpha }\Bigg \{\exp \left[ \frac{l^2-12 \alpha +\sqrt{l^4-40 l^2 \alpha +144 \alpha ^2}}{12 \alpha }\right] {}\\ {}&\times \left( l^2-12 \alpha +\sqrt{l^4-40 l^2 \alpha +144 \alpha ^2}\right) ^2\Bigg \}^{1/2}. \end{aligned}$$

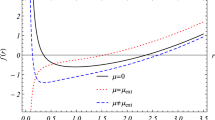
For the neutral Gauss–Bonnet AdS black hole obtained by setting \(Q=0\), we concentrate on studying the phase transitions in different Gauss–Bonnet parameter \(\alpha \). By employing the equations

$$\begin{aligned} \left( \frac{\partial T}{\partial S}\right) _{\alpha }=\left( \frac{\partial ^{2} T}{\partial ^{2} S}\right) _{\alpha }=0, \end{aligned}$$
(13)

the critical values can be given by

$$\begin{aligned}&S_{C}=\frac{11\pi l^2 }{36\left( 15+8\sqrt{3}\right) }\text {Log}\left[ \frac{121(3+2 \sqrt{3})^2 e^{6+4 \sqrt{3}} l^4}{324(15+8\sqrt{3})^{2}}\right] , \end{aligned}$$
(14)
$$\begin{aligned}&\alpha _C=\frac{11l^2}{36\left( 15 +8 \sqrt{3} \right) }, \end{aligned}$$
(15)
$$\begin{aligned}&T _C=\frac{\left[ 22 \left( 15+8 \sqrt{3}\right) \right] ^{-1/2}}{4 \pi l(1+\text {ProductLog}[\epsilon ])\sqrt{\text {ProductLog}[\epsilon ]} }{}\nonumber \\ {}&\quad \quad \times \Bigg \{-3 \left( 15+8 \sqrt{3}\right) +11 l \text {ProductLog}[\epsilon ]^{2}{}\nonumber \\ {}&\quad \quad +6 \left( 15+8 \sqrt{3}\right) \text {ProductLog}[\epsilon ]\Bigg \}, \end{aligned}$$
(16)

where \( \epsilon =\sqrt{3 \left( 7+4 \sqrt{3}\right) } e^{3+2 \sqrt{3}}. \) According to the expression in Eq. (8) and these critical values, we plot the phase transition diagrams in the \(T-S\) plane in Figs. 1 and 2. From Fig. 1, we can see that, for the charged Gauss–Bonnet AdS black hole in the ensemble of fixed charges, Van der Waals phase transition can be presented in the \(T-S\) plane. According to Fig. 2, for the neutral Gauss–Bonnet AdS black hole, the phase structure of Van der Waals can be also observed for the different Gauss–Bonnet parameter \(\alpha \). Therefore, the critical behavior can be detected not only charged but also neutral Gauss–Bonnet AdS black holes, which is completely similar to that of Van der Waals liquid-gas system in general thermodynamics.

Fig. 1
figure 1

The relationship between temperature T versus the entropy S for varying Q for the case \(\alpha =1\) and \(l=20\) for charged Gauss–Bonnet AdS black hole in four dimension

Full size image
Fig. 2
figure 2

The relationship between temperature T versus entropy S for varying \(\alpha \) for the case \(l=20\) for neutral Gauss–Bonnet AdS black hole in four dimension

Full size image

The Van der Waals phase transition can be further confirmed through plot of free energy in this Gauss–Bonnet AdS background. According to the relationship \(F=M-TS\), we can obtain the free energy

$$\begin{aligned} F(r,Q,\alpha )= & {} \frac{-3\left( r^2-Q-\alpha + 3r^4/l^2 \right) \left( r^2+4\alpha \text {Log}[r]\right) }{4\left( r^3+2 \alpha r\right) }{}\nonumber \\ {}&+\frac{r^3}{2l^2}+\frac{Q}{2r}+\frac{r}{2}+\frac{\alpha }{2r}. \end{aligned}$$
(17)

Obviously, as can be seen from Figs. 3 and 4, these phase diagrams of free energy in \(F-T\) plane completely similar to those of the general Van der Waals liquid-gas thermodynamic system. For the cases of \(Q<Q_{C}\) and \(\alpha <\alpha _{C}\), there is always a swallowtail shape in each plot, which corresponds to the unstable phase of the first order phase transition. For the cases of \(Q=Q_{C}\) and \(\alpha =\alpha _{C}\), there is always a an inflection point in each plot, which is the critical point of the second order phase transition. For the cases of \(Q>Q_{C}\) and \(\alpha >\alpha _{C}\), the corresponding curve is always continuous in each plot, which means that there is no phase transition.

Fig. 3
figure 3

The relationship between temperature T versus the free energy F for varying Q for the case \(\alpha =1\) and \(l=20\) for charged Gauss–Bonnet AdS black hole in four dimension

Full size image
Fig. 4
figure 4

The relationship between temperature T versus the free energy F for varying \(\alpha \) for the case \(l=20\) for neutral Gauss–Bonnet AdS black hole in four dimension

Full size image

We have inferred that Gauss–Bonnet AdS black holes possess the characteristics of Van der Waals phase transition by studying free energy above. In addition, phase transition behavior and stability can be also reflected by heat capacity. Next, for Gauss–Bonnet AdS black holes in both cases, we use heat capacity to further discuss criticality and thermodynamic phase transitions in \(C_{Q}-S\) plane. The heat capacity of charged Gauss–Bonnet AdS black hole can be expressed as

$$\begin{aligned} C_{Q}= & {} T\left( \frac{\partial S}{\partial T}\right) _{Q}=\Bigg \{4 \pi \alpha \left( 1+\text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] \right) ^2 {}\nonumber \\ {}&\times \Bigg (-l^2 \left( Q^2+\alpha \right) +2 l^2 \alpha \text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] {}\nonumber \\ {}&+12 \alpha ^2 \text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] ^2\Bigg )\Bigg \}{}\nonumber \\ {}&\times \Bigg \{l^2 \left( Q^2+\alpha \right) +l^2 \left( 3 Q^2+5 \alpha \right) \text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] {}\nonumber \\ {}&-2 \left( l^2-18 \alpha \right) \alpha \text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] ^2{}\nonumber \\ {}&+12 \alpha ^2 \text {ProductLog}\left[ \frac{e^{\frac{S}{2 \pi \alpha }}}{2 \alpha }\right] ^3\Bigg \}^{-1}. \end{aligned}$$
(18)
Fig. 5
figure 5

The figure shows \(C_{Q}\) vs S for different charges Q for the charged Gauss–Bonnet AdS black hole. Here parameters \(\alpha =1\) and \(l=20\)

Full size image
Fig. 6
figure 6

The figure shows \(C_{\alpha }\) vs S for different charges \(\alpha \) for the neutral Gauss–Bonnet AdS black hole. Here parameter \(l=20\)

Full size image

Based on above heat capacity at constant charge Q, we draw the following phase transition curves in Fig. 5. We can see clearly from the diagram that two heat capacity singularities appear when \(Q<Q_{C}\) in Fig. 5a, where two stable black holes (with positive heat capacity) and one unstable black hole (with negative heat capacity) are separated, which corresponds to the first-order phase transition. For the case of \(Q=Q_{C}\), the two divergence points merge into a turning point, which forms critical point of the second-order phase transition. When \(Q>Q_{C}\), the singularity disappears and the curve of heat capacity becomes continuous, which means that the black hole no longer has a phase transition. Thus, it can be seen that the critical behavior of heat capacity in Fig. 5 is consistent with that of free energy in Fig. 3.

The heat capacity of neutral Gauss–Bonnet AdS black hole can be expressed as

$$\begin{aligned} C_{\alpha }= & {} T\left( \frac{\partial S}{\partial T}\right) _{\alpha }=4 \pi \Bigg (1+\text {ProductLog}\left[ \frac{\sqrt{e^{S/\pi }}}{2}\right] \Bigg ) \Bigg (\alpha {}\nonumber \\ {}&+\text {ProductLog}\left[ \frac{\sqrt{e^{S/\pi }}}{2}\right] \Bigg ) \Bigg (-l^2\alpha {}\nonumber \\ {}&+2 l^2 \text {ProductLog}\left[ \frac{\sqrt{e^{S/\pi }}}{2}\right] +12 \text {ProductLog}\left[ \frac{\sqrt{e^{S/\pi }}}{2}\right] ^2\Bigg ){}\nonumber \\ {}&\times \Bigg \{l^2 \alpha ^2 +5l^2 \alpha \text { }\text {ProductLog}\left[ \frac{\sqrt{e^{S/\pi }}}{2}\right] -2 \left( l^2-18 \alpha \right) {}\nonumber \\ {}&\times \text {ProductLog}\left[ \frac{\sqrt{e^{S/\pi }}}{2}\right] ^2+12 \text {ProductLog}\left[ \frac{\sqrt{e^{S/\pi }}}{2}\right] ^3\Bigg \}^{-1}.\nonumber \\ \end{aligned}$$
(19)

Based on above heat capacity at constant \(\alpha \), we can plot phase transition curves of neutral Gauss–Bonnet AdS black hole in Fig. 6. Compared with that in Fig. 5, it turns out they have no difference in quality, only in quantity. In addition, the critical behavior of heat capacity in Fig. 6 is also consistent with that of free energy in Fig. 4.

3 Holographic phase transition from the two-point correlation function

By utilizing the black hole entropy we have detected Van der Waals phase transition behavior. In this section, for the novel Gauss–Bonnet AdS black holes, we continue to study whether the two-point correlation function can exhibit similar phase structure in the frame of holography. From AdS/CFT correspondence, the equal-time two point correlation function is given as follows [36]

$$\begin{aligned} \left\langle \mathcal {O}(t_{0},x_{i})\,\mathcal {O}(t_{0},x_{j})\right\rangle \approx e^{-\triangle L'(x_{i},x_{j})}, \end{aligned}$$
(20)

where \(\triangle \) is the conformal dimension of scalar operator \(\mathcal {O}\), and \(L'(x_{i},x_{j})\) is the smallest geodesic length between \((t_{0},\,x_{i})\) and \((t_{0},\,x_{j})\). According to the symmetry of the novel Gauss–Bonnet AdS black holes, here we order \(x_{i}=\theta \) corresponding the boundary \(\theta _{0}\). With \(\theta \) this trajectory can also be parameterized, and the geodesic length \(L'(x_{i},x_{j})\) can be calculated by

$$\begin{aligned} L'(x_{i},x_{j})=\int _{0}^{\theta _{0}}\sqrt{\frac{r\,'^{\,2}(\theta )}{f(r(\theta ))}+r^{\,2}(\theta )}\,\mathrm{d}\theta , \end{aligned}$$
(21)

where \(r'\equiv \mathrm{d}r/\mathrm{d}\theta \), Thus via Euler–Lagrange variation using Eq. (21), the motion equation of \(r(\theta )\) can be described by

$$\begin{aligned} 0 = \left( {\dot{r}(\theta )} \right) ^2 \dot{f}(r(\theta )) - 2f(r(\theta ))\ddot{r}(\theta ) + 2r(\theta )f(r(\theta ))^2.\nonumber \\ \end{aligned}$$
(22)

Through the above equation, \(r(\theta )\) can be solved numerically by adopting the boundary conditions \(r'(0)=0\), \(r(0)=r_{0}\). Since the smallest geodesic length in Eq. (21) is divergent for a fixed \(\theta _{0}\) we need to regularize \(L'(x_i ,x_j )\) by subtracting the geodesic length of vacuum Gauss–Bonnet AdS \(L_{0}\) (with same boundary \(\theta _{0}\)). In the novel Gauss–Bonnet gravity, the vacuum Gauss–Bonnet AdS is given by

$$\begin{aligned} \mathrm{d}s^2= & {} - (1 + \frac{{r^2 }}{{2\alpha }}(1 - \sqrt{1 - 4\alpha \frac{1}{{l^2 }}} ))\,\mathrm{d}t^2 {} \nonumber \\ {}&+ \frac{1}{{(1 + \frac{{r^2 }}{{2\alpha }}(1 - \sqrt{1 - 4\alpha \frac{1}{{l^2 }}} ))}}\mathrm{d}r^2 + r^2 (\mathrm{d}\theta ^2 + \sin ^2 \,\theta \mathrm{d}\,\varphi ^2 ).\nonumber \\ \end{aligned}$$
(23)

Notice that Gauss–Bonnet parameter \(\alpha \) has an influence on the vacuum Gauss–Bonnet AdS spacetime. It’s hard to get an analytical result, so we calculate numerically \(L_{0}\) by using the same steps as before. Here we order the regularized two point correlation function \(\delta L = L' - L_0\).

Fig. 7
figure 7

\(T-|\delta L|\) diagram for different values Q for the charged Gauss–Bonnet AdS black hole. Here we set parameters \(\alpha =1\), \(l=20\), \(\theta _{0}=0.35\) and \(\theta _{C}=0.349\)

Full size image
Fig. 8
figure 8

\(T-|\delta L|\) diagram for different values \(\alpha \) for the neutral Gauss–Bonnet AdS black hole. Here we set parameters, \(l=20\), \(\theta _{0}=0.50\) and \(\theta _{C}=0.499\)

Full size image

Via the numerical calculation, in Figs. 7 and 8, we plot \(T - \left| {\delta L} \right| \) diagrams for the charged and neutral AdS black holes in Gauss–Bonnet gravity respectively. Compared with black hole entropy in Figs. 1 and 2, we find out the two point correlation function in \(T - \left| {\delta L} \right| \) plane can show a completely similar critical behavior like black hole entropy, and possesses the same critical charge and critical Gauss–Bonnet coupling parameter. As can be seen that, when \(Q<Q_{C}\) for the charged case and when \(\alpha <\alpha _{C}\) for the neutral case, three distinct regions emerge including small black hole and intermediate black hole as well as large black hole. The intermediate black hole with negative slope is unstable due to the analogous heat capacity \(C = T\frac{{\partial \delta L}}{{\partial T}} < 0\) in \(T - \left| {\delta L} \right| \) plane, and there is a first-order phase transition between stable large and small black holes. When \(Q=Q_{C}\) for the charged case and when \(\alpha =\alpha _{C}\) for the neutral case, the unstable region merges into a inflection point which is a critical point, and at this point, the second-order phase transition can occur in this \(T - \left| {\delta L} \right| \) plane. However, no phase transition occurs above the critical point. It is worth noting that not only the charge but also the Gauss–Bonnet coupling parameter play an important role in displaying the phase transition of Gauss–Bonnet AdS black holes, furthermore, the two-point correlation function can exhibit similar phase structure in the frame of holography.

4 Conclusion

This novel Gauss–Bonnet AdS black holes in the Einstein–Gauss–Bonnet gravity is significantly different from static spherically symmetric black holes in pure Einstein’s gravity, and contain more abundant features, which is worthy of further exploration. In this paper, motivated by holography, for the first time we detect the holographic properties of novel four dimensional Gauss–Bonnet AdS black holes. Our results show that, for the charged Gauss–Bonnet AdS black hole, the holographic Van der Waals phase transition can be observed not only in the \(T-S\) plane but also \(T - \left| {\delta L} \right| \) plane in fixed charge ensemble, which is similar to that in \(P-V\) plane in extended phase space [26]. This means that Gauss–Bonnet AdS black holes have holographic features. Furthermore, for the neutral Gauss–Bonnet AdS black hole, using black hole entropy and the two-point correlation function, we can also detect the holographic Van der Waals phase transition. This is different from the spherical symmetric noncharged black hole under Einstein’s gravity, where Van der Waals phase transition does not take place for four dimensional neutral black hole. Therefore this indicates the Gauss–Bonnet coupling parameter has an important effect on holographic Van der Waals phase transition.

The four-dimensional novel Gauss–Bonnet AdS gravity with the equations of motion suggested in Ref. [27] and with only two dynamical degrees of freedom, is not compliance with Lovelock’s theorem. Thus the subtleties of this gravity have arisen. Some problems can be solved by considering the regularization of the four-dimensional Gauss–Bonnet gravity. It is notice that, through breaking the temporal diffeomorphism invariance and remaining the three-dimensional spatial diffeomorphism invariance, a consistent theory of four-dimensional Einstein–Gauss–Bonnet gravity with two dynamical degrees of freedom has been constructed [37], which is in agreement with the Lovelock’s theorem. The results show that the solutions of four dimensional Gauss–Bonnet AdS black holes are also solutions of consistent theory defined by the Hamiltonian suggested in [37]. It still remains to be studied whether rotating black holes and quasi-normal modes conform to the consistent theory. As we know, higher dimensional Gauss–Bonnet AdS gravity is consistent with Lovelock’s theorem, and is a consistent theory. In Ref. [34], authors have indicated that for the spherically symmetric five dimensional Gauss–Bonnet AdS black hole, the non-local observables such as the entanglement entropy, Wilson loop, and two point correlation function, undergo van der Waals-like phase transition in the dual field theory regardless of the dual gravity model. In this paper, by using two point correlation function, we have presented holographic Van der Waals-like phase transition for the four-dimensional Gauss–Bonnet AdS black holes, and our conclusion are identical with literature [33]. We leave the analysis of the entanglement entropy and Wilson loop to future works.