Modelling dendritic spines with the finite element method, investigating the impact of geometry on electric and calcic responses

Abstract

Understanding the relationship between shape and function of dendritic spines is an elusive topic. Several modelling approaches have been used to investigate the interplay between spine geometry, calcium diffusion and electric signalling. We here use a second order finite element method to solve the Poisson–Nernst–Planck equations and describe electrodiffusion in dendritic spines. With this, we obtain relationships between dendritic geometry and calcic as well as electric responses to synaptic events. Our findings support the hypothesis that spine geometry plays a role shaping the electrical responses to synaptic events. Our method was also able to reveal the fine scale distribution of calcium in spines with irregular shapes.

Appendix

1.1 The multicompartmental model used for validation

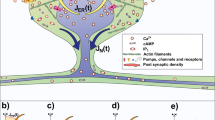
Our multicompartemental model consisted of the sections: the spine head, the spine neck and the dendritic shaft. Membrane electric potential and free calcium concentration were obtained in each compartment by solving ordinary differential equations. Below are the equations solved in each compartment for the membrane potential given a synaptic sodium and calcium currents $\mathrm {I}_{\mathrm {syn,Na}}$ and $\mathrm {I}_{\mathrm {syn,Ca}}$.

$$\begin{aligned} \frac{\mathrm {dV}^{\mathrm {head}}}{\mathrm {d}t}= & {} \frac{\mathrm {I}_{\mathrm {syn,Ca}} +\mathrm {I}_{\mathrm {syn,Na}}}{\mathrm {Cap}^{\mathrm {head}}} +\frac{\mathrm {V}^{\mathrm {head}}-\mathrm {V}^{\mathrm {neck}}}{\mathrm {Res}^{\mathrm {neck}}\mathrm {Cap}^{\mathrm {head}}}, \end{aligned}$$

(37)

$$\begin{aligned} \frac{\mathrm {dV}^{\mathrm {neck}}}{\mathrm {d}t}= & {} {\frac{\mathrm {V}^{\mathrm {neck}}-\mathrm {V}^{\mathrm {head}}}{\mathrm {Res}^{\mathrm {neck}}\mathrm {Cap}^{\mathrm {neck}}}+\frac{\mathrm {V}^{\mathrm {neck}}-\mathrm {V}^{\mathrm {dend}}}{\mathrm {Res}^{\mathrm {neck}}\mathrm {Cap}^{\mathrm {neck}}}}, \end{aligned}$$

(38)

$$\begin{aligned} \frac{\mathrm {dV}^{\mathrm {dend}}}{\mathrm {d}t}= & {} {\frac{\mathrm {V}^{\mathrm {dend}}-\mathrm {V}^{\mathrm {neck}}}{\mathrm {Res}^{\mathrm {neck}}\mathrm {Cap}^{\mathrm {dend}}}+\frac{\mathrm {V}^{\mathrm {dend}} -\mathrm {V}^{\mathrm {end}}}{\mathrm {Cap}^{\mathrm {dend}}\mathrm {Res}^{\mathrm {dend}}}}. \end{aligned}$$

(39)

Meanwhile the concentration of free calcium in each compartment evolves according to

$$\begin{aligned} \frac{\mathrm {dCa}^\mathrm {head}}{\mathrm {d}t}= & {} \frac{\mathrm {I}_{\mathrm {syn,Ca}}}{2\cdot F\cdot \mathrm {Vol}^{\mathrm {head}}}+\frac{2\pi (\mathrm {r}^{\mathrm{neck}})^2D(\mathrm {Ca}^{\mathrm{head}} -\mathrm {Ca}^{\mathrm{neck}})}{\mathrm {L}^{\mathrm{neck}}\mathrm {Vol}^{\mathrm{head}}} +\mathrm {Ca}^{\mathrm{head}}_{\mathrm{st}},\\ \frac{\mathrm {dCa}^\mathrm {neck}}{\mathrm {d}t}= & {} \frac{2\pi (\mathrm {r}^{\mathrm{neck}})^2D(\mathrm {Ca}^{\mathrm{neck}}-Ca^{\mathrm{head}})}{\mathrm {L}^\mathrm{neck} \mathrm{Vol}^{\mathrm{neck}}} +\frac{2\pi D (\mathrm {r}^{\mathrm{neck}})^2(\mathrm {Ca}^{\mathrm{neck}} -\mathrm{Ca}^{\mathrm{dend}})}{\mathrm {L}^{\mathrm{neck}}\mathrm{Vol}^{\mathrm{neck}}},\\ \frac{\mathrm {dCa}^\mathrm {dend}}{\mathrm {d}t}= & {} \frac{2\pi (\mathrm {r}^{\mathrm{neck}})^2D(\mathrm {Ca}^{\mathrm{dend}}-\mathrm{Ca}^{\mathrm{neck}})}{\mathrm {L}^{\mathrm{neck}}\mathrm{Vol}^{\mathrm{dend}}}+\frac{2\pi (\mathrm {r}^{\mathrm{dend}})^2D(\mathrm {Ca}^{\mathrm{dend}}-\mathrm{Ca}^{\mathrm{rest}})}{\mathrm {L}^{\mathrm{dend}}\mathrm{Vol}^{\mathrm{dend}}}+\mathrm {Ca}^{\mathrm{dend}}_{\mathrm{st}}, \end{aligned}$$

where $D=\mathrm {D}^{\mathrm{app}}_{\mathrm {Ca}}\cdot \mathrm {D}_{\mathrm {Ca}}$ is the effective diffusion coefficient of calcium ion. The electrical capacities of the compartments are given by

$$\begin{aligned} \mathrm {Cap}^{\mathrm{head}}= & {} \mathrm {d}_{\mathrm {mem}}\varepsilon _0\varepsilon _\mathrm {m} \mathrm {Surf}^{\mathrm {head}},\end{aligned}$$

(40)

$$\begin{aligned} \mathrm {Cap}^{\mathrm{neck}}= & {} \mathrm {d}_\mathrm {mem}\varepsilon _0\varepsilon _\mathrm {m} \mathrm {Surf}^{\mathrm {neck}},\end{aligned}$$

(41)

$$\begin{aligned} \mathrm {Cap}^{\mathrm{dend}}= & {} \mathrm {d}_\mathrm {mem}\varepsilon _0\varepsilon _\mathrm {m} \mathrm {Surf}^{\mathrm {dend}}, \end{aligned}$$

(42)

with the surfaces of the compartments being respectively given by

$$\begin{aligned} \mathrm {Surf}^{\mathrm{head}}= & {} 4\pi (\mathrm {r}^{\mathrm{head}})^2-(\pi \mathrm {r}^{\mathrm{neck}})^2,\end{aligned}$$

(43)

$$\begin{aligned} \mathrm {Surf}^{\mathrm{neck}}= & {} 2\pi (\mathrm {r}^{\mathrm{neck}}) \mathrm {L}^{\mathrm{neck}},\end{aligned}$$

(44)

$$\begin{aligned} \mathrm {Surf}^{\mathrm{dend}}= & {} 2\pi (\mathrm {r}^{\mathrm{dend}}) \mathrm {L}^{\mathrm{dend}}-\pi (\mathrm {r}^{\mathrm{neck}})^2. \end{aligned}$$

(45)

The electrical resistances of the neck and the dendrites are respectively given by

$$\begin{aligned} \mathrm {Res}^{\mathrm{neck}}= & {} \mathrm {R}^{\mathrm{cyt}} \frac{\mathrm {L}^{\mathrm{neck}}}{\pi (\mathrm {r}^{\mathrm{neck}})^2},\end{aligned}$$

(46)

$$\begin{aligned} \mathrm {Res}^{\mathrm{dend}}= & {} \mathrm { R^{cyt}}\frac{\mathrm {L}^{\mathrm{dend}}}{\pi (\mathrm {r}^{\mathrm{dend}})^2}, \end{aligned}$$

(47)

with the cytosol resistivity given by

$$\begin{aligned} \mathrm {R}^{\mathrm{cyt}}=\left( F\sum _i z_i^2 C_i D_i\right) ^{-1}, \end{aligned}$$

where the sum is taken over all ionic concentrations, $z_i$ is the valence of the ith specie, $D_i$ is the diffusion coefficient and $C_i$ is the resting concentration of the ith specie. The calcium released from store in the head and the dendrite are obtained by

$$\begin{aligned} \mathrm {Ca}^\mathrm {head}_\mathrm {st}= & {} \rho \; \mathrm {X}_\mathrm {head}\left( \mathrm {Ca}^\mathrm {head}_{\mathrm {store}} -\mathrm {Ca}^\mathrm {head}\right) ,\end{aligned}$$

(48)

$$\begin{aligned} \mathrm {Ca}^\mathrm {dend}_\mathrm {st}= & {} \rho \; \mathrm {X}_\mathrm {dend}\left( \mathrm {Ca}^{\mathrm {dend}}_\mathrm {store} -\mathrm {Ca}^{\mathrm {dend}}\right) , \end{aligned}$$

(49)

where the fraction of store calcium concentration and of open channels are given by solving the following ODE’s

$$\begin{aligned} \frac{\mathrm {dX}_{\mathrm{head}}}{\mathrm {dt}}= & {} -\frac{1}{\tau _{\mathrm {store}}}\left( \mathrm {X}_{\mathrm {head}}-(\mathrm {RA}) \mathrm {Re}(\mathrm {Ca}^{\mathrm {head}})\right) ,\end{aligned}$$

(50)

$$\begin{aligned} \frac{\mathrm {dX}_{\mathrm{dend}}}{\mathrm {dt}}= & {} -\frac{1}{\tau _{\mathrm {store}}}\left( \mathrm {X}_{\mathrm {dend}}-(\mathrm {RA}) \mathrm {Re}(\mathrm {Ca}^{\mathrm {dend}})\right) ,\end{aligned}$$

(51)

$$\begin{aligned} \frac{\mathrm {d}\mathrm {Ca}^{\mathrm{head}}_{\mathrm{store}}}{\mathrm {dt}}= & {} -\rho \;\mathrm {X}_{\mathrm {head}}\left( \mathrm {Ca}^{\mathrm {head}}_{\mathrm {store}}\right) ,\end{aligned}$$

(52)

$$\begin{aligned} \frac{\mathrm {d}\mathrm {Ca}^{\mathrm {dend}}_{\mathrm {store}}}{\mathrm {dt}}= & {} -\rho \;\mathrm {X}_{\mathrm {dend}}\left( \mathrm {Ca}^{\mathrm {dend}}_{\mathrm {store}}\right) , \end{aligned}$$

(53)

and

$$\begin{aligned} Re(\mathrm {Ca}^{\mathrm{head}})= & {} \mathrm {R}_0\frac{(\mathrm {Ca}^{\mathrm {head}} -[\mathrm {Ca}^{2+}]_{\theta })}{([\mathrm {Ca}^{2+}]_{\mathrm {max}} -[\mathrm {Ca}^{2+}]_{\theta })}\;\exp \left( -\frac{(\mathrm {Ca}^{\mathrm {head}} -[\mathrm {Ca}^{2+}]_{\theta })}{([\mathrm {Ca}^{2+}]_{\mathrm {max}} -[\mathrm {Ca}^{2+}]_{\theta })}\right) ,\nonumber \\ \end{aligned}$$

(54)

$$\begin{aligned} Re(\mathrm {Ca}^{\mathrm{dend}})= & {} \mathrm {R}_0\frac{(\mathrm {Ca}^{\mathrm {dend}} -[\mathrm {Ca}^{2+}]_{\theta })}{([\mathrm {Ca}^{2+}]_{\mathrm {max}} -[\mathrm {Ca}^{2+}]_{\theta })}\; \exp \left( -\frac{(\mathrm {Ca}^{\mathrm {dend}}-[\mathrm {Ca}^{2+}]_{\theta })}{([\mathrm {Ca}^{2+}]_{\mathrm {max}} -[\mathrm {Ca}^{2+}]_{\theta })}\right) .\nonumber \\ \end{aligned}$$

(55)

1.2 Multicompartment model used to determine the boundary condition of electric potential

As stated in this Appendix, the Dirichlet boundary condition for the electric potential at the open ends of the dendritic section were determined by a coarser multicompartment model. This model is similar to the one described in the previous subsection. However, the present model relies on more neural compartments, namely: one compartment for the spine head, one compartment for the spine neck, six compartments for the dentritic shaft and one compartment for the soma. The dynamic of membrane potential in the ith compartment ($V_i$) is given by

$$\begin{aligned} \frac{\mathrm {d} V_i}{\mathrm {d}t}=\frac{\mathrm {I}_{\mathrm {i,mem}}}{\mathrm {Cap}\cdot \mathrm {Surf}_i}+\frac{\mathrm {I}_{\mathrm {i,long}}}{\mathrm {Cap}\cdot \mathrm {Surf}_i}, \end{aligned}$$

(56)

where $\mathrm {Cap}$ is the membrane electric capacitance per unit area as determined in the previous subsection, $\mathrm {Surf}_\mathrm{i}$ is the surface area of the ith compartment, $\mathrm {I}_{\mathrm{i,mem}}$ is the transmembrane current in the ith compartment and $\mathrm {I}_{\mathrm{i,long}}$ is the longitudinal current between compartment i and adjacent compartments. The transmembrane current is given by

$$\begin{aligned} \mathrm {I}_{\mathrm {i,mem}}=\mathrm {I}_\mathrm {i,mem}^{\mathrm {leak}} +\mathrm {I}_{\mathrm {i,mem}}^{\mathrm {syn}}, \end{aligned}$$

(57)

where the first term describes the current through leak channels while the second describes the synaptic current.

The longitudinal current is given by

$$\begin{aligned} \mathrm {I}_{\mathrm {i,long}}=\sum _{k\ne \mathrm {j}} \frac{\mathrm {CSA}_{\mathrm {i,k}}(\mathrm {V}_\mathrm {k}-\mathrm {V}_\mathrm {i})}{\mathrm {Res}_{\mathrm {i,k}}}, \end{aligned}$$

(58)

where $\mathrm {CSA}_{\mathrm{i,k}}$ is the surface area of the common cross-section between adjacent compartments i and k, if the compartments i and k are not adjacent, then this is set to 0. The value of $\mathrm {Res}_{\mathrm{i,k}}$ is defined only if the compartments i and k are adjacent and stands for the electrical resistance between compartments i and k. If i and k are adjacent dendritic compartments, we have

$$\begin{aligned} \mathrm {Res}_{\mathrm {i,k}}=\frac{\mathrm {R}^{\mathrm {cyt}}\cdot \mathrm {L}^{\mathrm {dend}}}{\pi (\mathrm {r}^{\mathrm {dend}})^2}, \end{aligned}$$

where $\mathrm {R}^{\mathrm{cyt}}$ is the cytoplasmic resistivity defined in the previous subsection, $\mathrm {L}^{\mathrm{dend}}$ is the length of the dendrite compartment and $\mathrm {r}^{\mathrm{dend}}$ is the radius of the dendrite. The resistance between the soma and the adjacent dendritic compartment is given by

$$\begin{aligned} \mathrm {Res}_{1,2}=\frac{\mathrm {R}^{\mathrm {cyt}}\cdot \mathrm {L}^{\mathrm {dend}}}{2\pi (\mathrm{r}^{\mathrm{dend}})^2}. \end{aligned}$$

The resistance between the spine neck compartment and the adjacent dendritic dendrite compartment is given by

$$\begin{aligned} \mathrm {Res}_{\mathrm {i,k}}=\frac{\mathrm {R}^{\mathrm {cyt}}\cdot \mathrm {L}^{\mathrm {neck}}}{2\pi (\mathrm {r}^{\mathrm {neck}})^2}, \end{aligned}$$

where $\mathrm {L}^{\mathrm{neck}}$ is the length of the spine neck and $\mathrm {r}^{\mathrm{neck}}$ is the radius of the spine neck. Finally, the resistance between the spine head and spine neck is also given by

$$\begin{aligned} \mathrm {Res}_{\mathrm {i,k}}=\frac{\mathrm {R}^{\mathrm {cyt}}\cdot \mathrm {L}^{\mathrm {neck}}}{2\pi (\mathrm {r}^{\mathrm{neck}})^2}. \end{aligned}$$

Though not used, we also computed the dynamics of calcium concentration according to

$$\begin{aligned} \frac{\mathrm {d} C_i}{\mathrm {d}t}=\frac{\mathrm {I}_{\mathrm {i}}^{\mathrm {Ca,syn}}}{2\cdot F\cdot \mathrm {Vol}_{i}}+\frac{\mathrm {Surf}_\mathrm {i}\cdot \mathrm {J}^{\mathrm {ext}}_\mathrm {i}}{\mathrm {Vol}_{i}} +\frac{\mathrm {J}_\mathrm {i}^{\mathrm {Ca,long}}}{\mathrm {Vol}_{i}}, \end{aligned}$$

where $\mathrm {C}_\mathrm {i}$ is the calcium concentration in the ith compartment, $\mathrm {I}_\mathrm{i}^{\mathrm {Ca,syn}}$ is the synaptic current in the ith compartment $\mathrm {J}^{\mathrm {ext}}_\mathrm {i}$ is the $\mathrm {Ca}^{2+}$ extrusion flux in the ith compartment and $\mathrm {J}_\mathrm {i}^{\mathrm {Ca,long}}$ describes the longitudinal flux of $\mathrm {Ca}^{2+}$ between adjacent compartments. The latter is given by

$$\begin{aligned} \mathrm {J}_\mathrm{i}^{\mathrm{Ca,long}}=\sum _{\mathrm{k}\ne \mathrm{i}} \mathrm{J}_{\mathrm{i,k}}^{\mathrm{Ca}}, \end{aligned}$$

where $\mathrm {\mathrm{J}_{\mathrm{i,k}}^{\mathrm{Ca}}}$ is the flux of $\mathrm {Ca}^{2+}$ from compartment k to compartment i equal to zero if the compartments i and k are not adjacent and if the compartments are adjacent, this is given by

$$\begin{aligned} \mathrm {J}_{\mathrm{i,k}}^{\mathrm{Ca}}=\frac{\mathrm{D}_{\mathrm{Ca}}^{\mathrm{app}} {\mathrm{CSA}}_{\mathrm{i,k}}}{{\mathrm{dist}}_{\mathrm{i},\mathrm{k}}}, \end{aligned}$$

where $\mathrm {dist}_{\mathrm{i,k}}$ is the distance between the center of the compartments (Table 3).

Table 3 Parameters for the multicompartmental model

1.2.1 Variational formulation, finite element approximation and time discretization

The first two equations of (33) are respectively multiplied by test functions $\phi$ and $\varphi$ and integrated over the domain $\varOmega$:

$$\begin{aligned} \begin{aligned} {\int _\varOmega }\frac{\partial C_k}{\partial t}\,\phi \, dx-{\int _\varOmega }\nabla F_k\, \phi \, dx={\int _\varOmega }Z_k\, \phi \, dx,\\ {\int _{\varOmega }}\nabla \left( \varepsilon \, \nabla V \right) \,\varphi \, dx+F\sum _{k=1}^{4}{\int _\varOmega }z_{k}\,C_{k}\,\varphi \, dx=0. \end{aligned} \end{aligned}$$

(59)

Applying integration by parts, we obtain

$$\begin{aligned} \begin{aligned} {\int _\varOmega }\frac{\partial C_k}{\partial t}\,\phi \, dx-{\int _{\partial \varOmega }}\left( F_k\cdot n\right) \,\phi \, ds+{\int _\varOmega }F_k\,\nabla \phi \, dx={\int _\varOmega }b_{k}\;Z_k\, \phi \, dx,\\ {\int _{\partial \varOmega }}\left( \varepsilon \, \nabla V \cdot n\right) \,\varphi \, ds-{\int _\varOmega }\left( \varepsilon \,\nabla V\right) \cdot \nabla \varphi \, dx+F\sum _{k=1}^{4}{\int _\varOmega }z_{k}\,C_{k}\,\varphi \, dx=0. \end{aligned} \end{aligned}$$

(60)

The functional space of the ionic concentrations and the electric potential is denoted by ${\mathscr {C}}$ which is defined as:

$$\begin{aligned} {{\mathscr {C}}}=\left\{ \varphi ,\;\phi \in H^{1}\left( \varOmega \right) ,\,\varphi =0\;\mathrm {and}\,\phi =0\,\mathrm {on}\,\varGamma _{g}\right\} . \end{aligned}$$

Hence we look for $C_k \in H^1(\varOmega )$ such that $C_k-C^0_k \in \mathrm {{\mathscr {C}}}$ for $k=1,\ldots ,4$ and also $V \in H^1(\varOmega )$ such that $V-V_d \in \mathrm {{\mathscr {C}}}$. So we obtain the weak formulation

$$\begin{aligned}&{\int _\varOmega }\frac{\partial C_k}{\partial t}\,\phi \, dx-{\int _{\varGamma _r}} U_k\, \phi \, ds-{\int _{\varGamma _b}} L_k \,\phi \, ds+{\int _\varOmega } F_k \,\nabla \phi \, dx={\int _\varOmega }b_{k}\;Z_k\, \phi \, dx,\nonumber \\&{\int _{\varGamma _b \cup \varGamma _r}}\left( \varepsilon \, P\right) \,\varphi \, ds-{\int _\varOmega }\left( \varepsilon \,\nabla V\right) \cdot \nabla \varphi \, dx+F\sum _{k=1}^{4}{\int _\varOmega }z_{k}\,C_{k}\,\varphi \, dx=0. \end{aligned}$$

(61)

The domain $(\varOmega )$ is partitioned into a finite mesh ${\mathscr {T}}:\left\{ G\right\}$ of simplicial ${\mathscr {G}}$. We represent the unknown functions $C_k$ and V and the test functions $\phi$ and $\varphi$ by piecewise polynomials on this mesh. Finite dimensional approximation space ${\mathscr {H}}$ of piecewise polynomials of degree n is considered on the generated mesh ${\mathscr {T}}$:

$$\begin{aligned} {{\mathscr {H}}}=\left\{ \varphi ,\; \phi \in H_{n}^1\left( G\right) ,\;\varphi =0\;\mathrm {and}\;\phi =0\;\mathrm {on}\;\varGamma _{g}\right\} . \end{aligned}$$

We therefore look for $C_{k}\in H^1_n$ such that $C_k-C_k^0\in \mathrm {{\mathscr {H}}}$ for all $k=1,\ldots ,4$ and $V \in H_n^1$ such that $V-V_d \in \mathrm {{\mathscr {H}}}$ such that:

$$\begin{aligned}&{\int _\varOmega }\frac{\partial C_k}{\partial t}\,\phi \, dx-{\int _{\varGamma _r}} U_k\, \phi \, ds-{\int _{\varGamma _b}} L_k\, \phi \, ds+{\int _\varOmega }F_k\,\nabla \phi \, dx={\int _\varOmega }b_{k}\;Z_k\, \phi \, dx,\nonumber \\&{\int _{\varGamma _b \cup \varGamma _r}}\left( \varepsilon \, P\right) \varphi \, ds-{\int _\varOmega }\left( \varepsilon \,\nabla V\right) \cdot \nabla \varphi \, dx+F\sum _{k=1}^{4}{\int _\varOmega }z_{k}\,C_{k}\,\varphi \, dx=0. \end{aligned}$$

(62)

To discretize the time derivative in the first equation of equation (62), we employ the second order Backward Difference Formula method (BDF2) also known as the Gear time-stepping scheme.

$$\begin{aligned}&{\int _\varOmega }\frac{1}{\triangle t}\left( \frac{3}{2}\,C_{k}^{r+1}-2\,C_{k}^{r}+\frac{1}{2}\,C_{k}^{r- 1}\right) \,\phi \, dx-{\int _{\varGamma _{r}}}U_{k}\,\phi \, ds-{\int _{\varGamma _{b}}}L_{k}\,\phi \, ds\nonumber \\&\quad +{\int _\varOmega }D_{k}\,\nabla C_{k}^{r+1}\,\nabla \phi \, dx +{\int _\varOmega }\frac{D_{k}}{\alpha _{k}}\,C_{k}^{r+1}\,\nabla V^{r+1}\,\nabla \phi dx={\int _\varOmega }b_{k}\;Z^{r+1}_k\, \phi \, dx, \end{aligned}$$

(63)

$$\begin{aligned}&{\int _{\varGamma _{b}\cup \varGamma _{r}}}\varepsilon P\varphi ds-{\int _\varOmega \varepsilon }\nabla V^{r+1}\cdot \nabla \varphi dx+F\sum _{k=1}^{3}{\int _\varOmega }z_{k}C_{k}^{r+1}\varphi dx=0. \end{aligned}$$

(64)

1.2.2 Elementary variational formulation

The elementary variational formulation is obtained by integrating over an element K. We obtain

$$\begin{aligned}&{\int _K}\frac{1}{\triangle t}\left( \frac{3}{2}\, C_{k}^{r+1}-2\,C_{k}^{r}+\frac{1}{2}\,C_{k}^{r-1}\right) \,\phi \, dx+{\int _K}D_{k}\,\nabla C_{k}^{r+1}\cdot \nabla \phi \, dx\nonumber \\&\quad +{\int _K}\frac{D_{k}}{\alpha _{k}}\, C_{k}^{r+1}\,\nabla V^{r+1}\cdot \nabla \phi \, dx={\int _K}b_{k}\;Z^{r+1}_k\, \phi \, dx\nonumber \\&\quad +{\int _{\partial K\cap \varGamma _{r}}}U_{k}\,\phi \, ds+{\int _{\partial K\cap \varGamma _{b}}}L_{k}\,\phi \, ds, \end{aligned}$$

(65)

$$\begin{aligned}&F\sum _{k=1}^{4}{\int _K}z_{k}\,C_{k}^{r+1}\,\varphi \, dx- {\int _K\varepsilon }\,\nabla V^{r+1}\cdot \nabla \varphi \, dx= -{\int _{\partial K \cap \left( \varGamma _{b} \cup \varGamma _{r} \right) }}\varepsilon \, P\,\varphi \, ds.\nonumber \\ \end{aligned}$$

(66)

Ritz method (Brenner and Scott 2008) is applied on each element K by letting

$$\begin{aligned} C_{k}\mid _{K}\simeq & {} C_{k}^{K}=\sum _{i=1}^{n_{d}^{K}} C_{k,i}^{K}\,N_{i}^{K},\\ V\mid _{K}\simeq & {} V^{K}=\sum _{i=1}^{n_{d}^{K}} V_{i}^{K}\,M_{i}^{K}, \end{aligned}$$

where $N_{i}^{K}$ and $M_{i}^{K}$ are the interpolation functions on the element K for $i=1,2,\ldots n_{d}$. Substituting the two equations above into Equations (65) and (66) and taking successively $\phi =\phi _{i}^{K}$ and $\varphi =\varphi _{i}^{K}$, we obtain

$$\begin{aligned}&\sum _{i=1}^{n_{d}^{K}}\, C_{k,i}^{r+1,K}{\int _K}\left[ \left( \frac{1}{\triangle t}\frac{3}{2}\right) N_{i}^{K}\phi _{i}^{K}+D_{k}\nabla N_{i}^{K}\nabla \phi _{i}^{K}\right] dx\nonumber \\&\quad +\sum _{i=1}^{n_{d}^{K}} V_{i}^{r+1,K}{\int _K}\frac{D_{k}}{\alpha _{k}}\left( C_{k,i}^{r+1}N_{i}^{K}\right) \nabla M_{i}^{K}\nabla \phi _{i}^{K}dx-\sum _{i=1}^{n_{d}^{K}}{\int _K}b_{k}\;Z^{r+1}_{k,i}\, \phi _{i}^{K}\, dx\nonumber \\&\quad -\sum _{i=1}^{n_{d}^{K}} C_{k,i}^{r-1,K} {\int _K}\frac{1}{2}N_{i}^{K}\phi _{i}^{K}dx+\sum _{i=1}^{n_{d}^{K}} C_{k,i}^{r,K}{\int _K}2N_{i}^{K}\,\phi _{i}^{K}\,dx \nonumber \\&\quad +{\int _{\partial K\cap \varGamma _{r}}}U_{k}\,\phi \, ds+{\int _{\partial K\cap \varGamma _{b}}}L_{k}\,\phi \, ds, \end{aligned}$$

(67)

and

$$\begin{aligned}&F\sum _{i=1}^{n_{d}^{K}}\sum _{k=1}^{3} C_{k,i}^{r+1,K}{\int _K}z_{k}N_{i}^{K}\varphi _{i}^{K}dx-\sum _{i=1}^{n_{d}^{K}} V_{i}^{r+1,K}{\int _K\varepsilon }\nabla M_{i}^{K}\cdot \nabla \varphi _{i}^{K}dx\nonumber \\&\quad =-\sum _{i=1}^{n_{d}^{K}}{\int _{\partial K\cap \left( \varGamma _{b}\cup \varGamma _{r}\right) }}\varepsilon P\varphi _{i}^{K}ds, \end{aligned}$$

(68)

where $Z=\mathrm {Ca}^{{2+}}_{\mathrm{store}}$ and it is obtained by solving Eqs. (48) and (50) using an implicit linear multi-step method (backward difference formula). From this, we obtain the elementary system

$$\begin{aligned} \left( \begin{array}{c@{\quad }c} A_{11}^{K} &{} A_{12}^{K}\left( C_{k}^{r+1,K}\right) \\ A_{21}^{K} &{} A_{22}^{K} \end{array}\right) \left( \begin{array}{c} \delta C_{k}^{r+1,K}\\ \delta V^{r+1,K} \end{array}\right) =\left( \begin{array}{c} F_{1}^{K}\\ F_{2}^{K} \end{array}\right) \end{aligned}$$

(69)

from which we finally obtain the following algebraic system

$$\begin{aligned} A\left( U^{r+1,K}\right) U^{r+1,K}=F\left( U^{r+1,K}\right) . \end{aligned}$$

Observe that this system is non linear since there is a coupling term in (69). A Newton–Raphson method is used to solve the problem at time step $r+1$. We solve iteratively the first order linearisation of the system.

$$\begin{aligned} K_{U}\delta _{U}= & {} F\left( U_{p}\right) -A\left( U_{p}\right) U_{p}, \\ U_{p+1}= & {} \delta _{U}+U_{p}, \end{aligned}$$

to obtain $U^{r+1}$ when the correction $\delta _{U}$ is small enough. We resolve the issue with the required two initial values in Eqs. (67) and (67) by introducing $\delta _{C}$, $\delta _{V}$ (Dione et al. 2016) and neglecting the second order terms in the equations as

$$\begin{aligned}&\sum _{i=1}^{n_{d}^{K}} V_{i}^{p+1,K}{\int _K}\frac{D_{k}}{\alpha _{k}} \left( C_{k,i}^{p+1}N_{i}^{K}\right) \nabla M_{i}^{K}\cdot \nabla \phi _{i}^{K}dx\\&\quad \approx \sum _{i=1}^{n_{d}^{K}} V_{i}^{p,K}{\int _K}\frac{D_{k}}{\alpha _{k}}\left( C_{k,i}^{p}N_{i}^{K}\right) \nabla M_{i}^{K}\cdot \nabla \phi _{i}^{K}dx\\&\quad +\sum _{i=1}^{n_{d}^{K}}V_{i}^{p,K}{\int _K}\frac{D_{k}}{\alpha _{k}}\left( \delta _{C}N_{i}^{K}\right) \nabla M_{i}^{K}\cdot \nabla \phi _{i}^{K}dx\\&\quad + \sum _{i=1}^{n_{d}^{K}} \delta _{V}{\int _K}\frac{D_{k}}{\alpha _{k}}\left( C_{k,i}^{p}N_{i}^{K}\right) \nabla M_{i}^{K}\cdot \nabla \phi _{i}^{K}dx. \end{aligned}$$

The numerical computations were implemented using finite element library MEF++ software (Version 5) developed at the laboratory of the Groupe Interdisciplinaire de Recherche en Éléments Finis (GIREF) at the department of mathematics and statistic, Université Laval.

The boundary of the domain consist of points, curves and surfaces which are grouped as a geometric entities on which we define the boundary conditions using iMEF++. iMEF++ is a software developed by GIREF.