Possible New Envelope Types of Hot Jupiters

Abstract—For the case of the sub-Alfvén regime of the stellar wind flyby around the planet, the flow structure in the vicinity of a hot Jupiter have been studied by three-dimensional numerical simulation. As an example, the hot Jupiter HD 209458b was considered. The planet’s magnetic moment was set equal to 10% of the magnetic moment of Jupiter. The average magnetic field at the parent star’s surface was taken to be 0.5 G, corresponding to a relatively strong wind field. Under such conditions, calculations have shown that a quasi-closed ionospheric (gas) envelope with an induced shockless magnetosphere forms around a hot Jupiter. Under the influence of the strong magnetic field of stellar wind, envelope matter outflowing from the inner Lagrange point does not move along the ballistic trajectory, but rather moves along magnetic field lines of the wind toward the star. Therefore, for the sub-Alfvén flow regime, a new ionospheric envelope type of hot Jupiters is considered to be discovered, supplementing the classification suggested earlier based on results of purely gas-dynamic modeling. Possible distinctive features of the observational manifestations of such envelopes are discussed.

THE COMPUTATION METHOD OF THE STELLAR WIND PARAMETERS

Some simple transformations allow the following expressions to be obtained from Eqs. (1)–(5)

$$\begin{gathered} (v_{r}^{2} - u_{S}^{2})(v_{r}^{2} - u_{F}^{2})\frac{{d{{v}_{r}}}}{{dr}} \\ = \frac{{{{v}_{r}}}}{r}\left[ {(v_{r}^{2} - u_{A}^{2})\left( {2c_{s}^{2} + v_{\varphi }^{2} - \frac{{G{{M}_{{\text{s}}}}}}{r}} \right) + 2{{v}_{r}}{{u}_{A}}{{v}_{\varphi }}{{u}_{\varphi }}} \right], \\ \end{gathered} $$

(22)

with notation

$${{u}_{S}} = \mathop {\left\{ {\frac{1}{2}\left[ {c_{s}^{2} + {{a}^{2}} - \sqrt {{{{(c_{s}^{2} + {{a}^{2}})}}^{2}} - 4c_{s}^{2}u_{A}^{2}} } \right]} \right\}}\nolimits^{1/2} ,$$

(23)

$${{u}_{F}} = \mathop {\left\{ {\tfrac{1}{2}\left[ {c_{s}^{2} + {{a}^{2}} + \sqrt {{{{(c_{s}^{2} + {{a}^{2}})}}^{2}} - 4c_{s}^{2}u_{A}^{2}} } \right]} \right\}}\nolimits^{1/2} ,$$

(24)

$${{a}^{2}} = \tfrac{{B_{r}^{2} + B_{\varphi }^{2}}}{{4\pi \rho }},$$

(25)

$${{u}_{\varphi }} = \tfrac{{{{B}_{\varphi }}}}{{\sqrt {4\pi \rho } }}.$$

(26)

The values ${{u}_{S}}$ and ${{u}_{F}}$ determine the values of slow and fast magnetosonic velocities, respectively. From Eq. (22), it can be seen that there are two singular points in the solution: the slow magnetosonic one $r = {{r}_{S}}$, where velocity is ${{v}_{r}} = {{u}_{S}}$, and the fast magnetosonic one, $r = {{r}_{F}}$, where velocity ${{v}_{r}} = {{u}_{F}}$. In these points, the coefficient of the derivative $d{{v}_{r}}{\text{/}}dr$ vanishes. In order for the solution to remain smooth, the right-hand side of Eq. (22) must also vanish at these points. However, as it will be seen below, the Alfvén point $r = {{r}_{A}}$, where wind velocity ${{v}_{r}} = {{u}_{A}}$, is also a singular solution point.

We will set boundary conditions by the values of velocity ${{{v}}_{0}}$, density ${{\rho }_{0}}$, and temperature ${{T}_{0}}$ in a certain point ${{r}_{0}}$. These values allow the computations of the constants

$${{c}_{0}} = \sqrt {\frac{{2{{k}_{{\text{B}}}}{{T}_{0}}}}{{{{m}_{{\text{p}}}}}}} ,$$

(27)

$$\dot {M} = 4\pi r_{0}^{2}{{\rho }_{0}}{{{v}}_{0}}.$$

(28)

The last expression follows from the mass conservation law (8). The value $\dot {M}$ defines mass-loss rate via stellar wind. Let us denote the density and temperature in the Alfvén point as ${{\rho }_{A}}$ and ${{v}_{A}}$, respectively. Then, with account of (28), we obtain

$$\dot {M} = 4\pi r_{A}^{2}{{\rho }_{A}}{{v}_{A}}.$$

(29)

Expression (29) allows one to find

$${{\rho }_{A}} = \frac{1}{{4\pi }}\mathop {\left( {\frac{{\dot {M}}}{{r_{0}^{2}{{B}_{0}}}}} \right)}\nolimits^2 ,$$

(30)

where ${{B}_{0}} = {{B}_{{\text{s}}}}{{({{R}_{{\text{s}}}}{\text{/}}{{r}_{0}})}^{2}}$ is the strength of the radial magnetic field in the point ${{r}_{0}}$.

Let us introduce dimensionless values ${{x}_{A}} = {{r}_{A}}{\text{/}}{{r}_{0}}$ and ${{y}_{A}} = {{{v}}_{A}}{\text{/}}{{{v}}_{0}}$. It is easy to verify that the relation

$${{y}_{A}} = \frac{\beta }{{x_{A}^{2}}},$$

(31)

where

$$\beta = \frac{{{{B}_{0}}}}{{{{v}_{0}}\sqrt {4\pi {{\rho }_{A}}} }}$$

(32)

is correct.

To solve the equations, it is convenient to rewrite them in the dimensionless form. For this, let us introduce dimensionless variables $\xi = r{\text{/}}{{r}_{A}}$ and $\eta = {{{v}}_{r}}{\text{/}}{{{v}}_{A}}$. Then, the Alfvén Mach number (18) is $\lambda = \xi \sqrt \eta$. Additionally, we introduce

$$z = \mathop {\left( {\frac{\rho }{{{{\rho }_{0}}}}} \right)}\nolimits^{0.5(\gamma - 1)} = \mathop {(\beta {{\lambda }^{2}})}\nolimits^{0.5(1 - \gamma )} .$$

(33)

In dimensionless units, Eq. (22) becomes

$$\frac{{d\eta }}{{d\xi }} = \frac{{\eta Y}}{{\xi X}},$$

(34)

where

$$X = {{({{\lambda }^{2}} - 1)}^{3}}(y_{A}^{2}{{\eta }^{2}} - \alpha {{z}^{2}}){{\xi }^{2}} - \omega {{\lambda }^{4}}x_{A}^{2}{{({{\xi }^{2}} - 1)}^{2}},$$

(35)

$$\begin{gathered} Y = {{({{\lambda }^{2}} - 1)}^{3}}\left( {2\alpha \xi {{z}^{2}} - \frac{\mu }{{{{x}_{A}}}}} \right)\xi \\ + \;\omega x_{A}^{2}({{\lambda }^{2}} - {{\xi }^{2}})({{\lambda }^{4}} - 3{{\lambda }^{2}}{{\xi }^{2}} + {{\lambda }^{2}} + {{\xi }^{2}}), \\ \end{gathered} $$

(36)

$$\alpha = \frac{{c_{0}^{2}}}{{v_{0}^{2}}},$$

(37)

$$\mu = \frac{{G{{M}_{{\text{s}}}}}}{{{{r}_{0}}v_{0}^{2}}},$$

(38)

$$\omega = \frac{{{{\Omega }_{{\text{s}}}}r_{0}^{2}}}{{v_{0}^{2}}}.$$

(39)

As noted above, slow magnetosonic ($\xi = {{\xi }_{S}}$, $\eta = {{\eta }_{S}}$) and fast magnetosonic ($\xi = {{\xi }_{F}}$, $\eta = {{\eta }_{F}}$) points are singular. However, obtained expressions show that in the solution Alfvén point ($\xi = 1$, $\eta = 1$) also is singular, since $X$ and $Y$ also simultaneously become equal to zero. Let us write energy integral (9) in the dimensionless form too:

$$\begin{gathered} E = \frac{{y_{A}^{2}{{\eta }^{2}}}}{2} + \frac{{\alpha {{z}^{2}}}}{{\gamma - 1}} - \frac{\mu }{{{{x}_{A}}\xi }} \\ + \;\frac{{\omega x_{A}^{2}}}{{2{{\xi }^{2}}{{{({{\lambda }^{2}} - 1)}}^{2}}}}[{{\lambda }^{4}} + (2{{\lambda }^{2}} - 1)({{\xi }^{2}} - 2){{\xi }^{2}}]. \\ \end{gathered} $$

(40)

Then, in point ${{r}_{0}}$, ${{\xi }_{0}} = 1{\text{/}}{{x}_{A}}$, ${{\eta }_{0}} = 1{\text{/}}{{y}_{A}}$, ${{\lambda }_{0}} = 1{\text{/}}\sqrt \beta$. Therefore, in this point Eq. (40) becomes:

$$\begin{gathered} E = \frac{1}{2} + \frac{\alpha }{{\gamma - 1}} - \mu + \frac{\omega }{{2{{{(\lambda _{0}^{2} - 1)}}^{2}}}} \\ \times \;[\lambda _{0}^{4}x_{A}^{4} + (2\lambda _{0}^{2} - 1)(1 - 2x_{A}^{2})]. \\ \end{gathered} $$

(41)

As unknown values in the solution, we will use ${{\xi }_{S}}$, ${{\eta }_{S}}$, ${{\xi }_{F}}$, ${{\eta }_{F}}$, ${{x}_{A}}$, $E$, and $\gamma$. Altogether, there are 7 unknowns. The system of equations contains four equations $X = 0$, $Y = 0$ in the points ${{\xi }_{S}}$ and ${{\xi }_{F}}$, two equations (40), for the points ${{\xi }_{S}}$ and ${{\xi }_{F}}$, and Eq. (41). This system of nonlinear algebraic equations may be solved by iterations.

As boundary conditions, the values of the solar wind parameters at the point ${{r}_{0}} = 10\,{{R}_{ \odot }}$ [60] are used: velocity ${{v}_{0}} = 100$ km/s, density ${{\rho }_{0}} = 2.34 \times {{10}^{{ - 21}}}$ g/cm³ (corresponding numerical density ${{n}_{0}} = 1400$ cm^–3), temperature ${{T}_{0}} = 7.3 \times {{10}^{5}}$ K. The star HD 209458 has mass ${{M}_{{\text{s}}}} = 1.1\;{{M}_{ \odot }}$ and radius ${{R}_{{\text{s}}}} = 1.2\;{{R}_{ \odot }}$. Angular velocity of stellar rotation is ${{\Omega }_{{\text{s}}}} = 5.05 \times {{10}^{{ - 6}}}$ s^–1, which corresponds to the linear velocity at the equator ${{v}_{{{\text{rot}}}}} = 4.2$ km/s. The magnetic field at the stellar surface was equal to ${{B}_{{\text{s}}}} = 0.5$ G, which corresponds to the magnitude of the average magnetic field at the Sun’s surface in a quiet state.

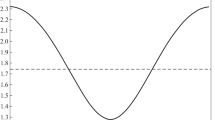
From this, the following parameters values are obtained: outflow rate $\dot {M} = 1.43 \times {{10}^{{11}}}\;{\text{g/s}} = 2.26 \times$${{10}^{{ - 15}}}\,{{M}_{ \odot }}{\text{/yr}}$, the density at the Alfvén point ρ_A = $1.33 \times {{10}^{{ - 22}}}$ g/cm³, dimensionless quantities α = 1.205, $\beta = 17.617$, $\mu = 2.098$, $\omega = 0.123$. It is important to note that the rate of stellar mass loss $\dot {M}$ in our stellar wind model is only one of its parameters. It does not coincide with the real rate of mass loss, since the problem only in the plane of the planetary orbit was solved. Since the real wind is not spherically-symmetric, these values ​​can vary by several factors. The calculation results of the wind structure are presented in Fig. 9. A family of integral curves corresponding to the various types of solutions is shown. Some of these curves pass through the singular points whose positions are indicated by circles. Here, the Alfvén singular point in the plane of variables ($\xi$, $\eta$) has coordinates (1, 1). As a solution corresponding to the stellar wind, it is necessary to use the integral curve passing through all three singular points. The dependence $\eta (\xi )$ for this curve can be obtained solving numerically Eq. (40) for various coordinates $\xi$, substituting the found values ​​of ${{x}_{A}}$ and $E$. The corresponding curve in Fig. 9 is shown in bold.

Fig. 9.

Integral curves corresponding to the various types of solutions for magnetohydrodynamic stellar wind. Singular points are indicated by circles. The Alfvén singular point has coordinates (1, 1). The bold line corresponds to the solution passing through all three singular points. The right panel shows the neighborhood of the Alfvén point.

The system’s numerical solution of nonlinear algebraic equations describing the structure of stellar wind gives the following coordinates of the magnetosonic singular points: ${{\xi }_{S}} = 0.307$, ${{\eta }_{S}} = 0.467$, ${{\xi }_{F}} = 1.065$, ${{\eta }_{F}} = 1.026$. The left panel of Fig. 9 shows that the slow magnetosonic point is a singular point of the “saddle” type (see, for example, [73]). The fast magnetosonic point is located close to the Alfvén point, the vicinity of which is shown enlarged in the right panel of Fig. 9. It can be seen that the fast magnetosonic point is also a singular point of the “saddle” type. The Alfvén singular point has a more complex topology, since it has a higher singularity order. For the Alfvén point, the value ${{x}_{A}} = 2.748$ that corresponds to the radius ${{r}_{A}} = 27.48\,{{R}_{ \odot }}$ was obtained. The adiabatic index turned out to be equal to $\gamma = 1.004$. Thus, the stellar wind in the vicinity of the hot Jupiter can be considered as almost isothermal.