An Edge-Based Model of SEIR Epidemics on Static Random Networks

Abstract

Studies have been done using networks to represent the spread of infectious diseases in populations. For diseases with exposed individuals corresponding to a latent period, an SEIR model is formulated using an edge-based approach described by a probability generating function. The basic reproduction number is computed using the next generation matrix method and the final size of the epidemic is derived analytically. The SEIR model in this study is used to investigate the stochasticity of the SEIR dynamics. The stochastic simulations are performed applying continuous-time Gillespie’s algorithm given Poisson and power law with exponential cut-off degree distributions. The resulting predictions of the SEIR model given the initial conditions match well with the stochastic simulations, validating the accuracy of the SEIR model. We varied the contribution of the disease parameters and the average degree of the network in order to investigate their effects on the spread of disease. We verified that the infection and the recovery rates show significant effects on the dynamics of the disease transmission. While the exposed rate delays the spread of the disease, increasing it towards infinity would lead to almost the same dynamics as that of an SIR case. A network with high average degree results to an early and higher peak of the epidemic compared to a network with low average degree. The results in this paper can be used as an alternative way of explaining the spread of disease and it provides implications on the control strategies applied to mitigate the disease transmission.

Appendices

Appendix A: Summary of the Notations Used in This Study

See the Tables 3 and 4.

Table 3 Parameters and variables for the network SEIR model

Table 4 Edge-based variables for the network SEIR model

Appendix B: Random Network Generation Using Molloy–Reed’s Algorithm

Figures 16 and 17 are examples of networks generated applying Molloy–Reed’s algorithm with Poisson and power-law with exponential cut-off (PLEC) degree distributions, respectively. An adjacency matrix indicating the random pairing of edges is used to store information about the network structure. Both networks consist of 50 nodes with possible edges joined by two distinct nodes. Loops and multiple edges are discarded in the network generation. We visualize both networks positioning the nodes in a circular manner and the degrees of nodes increase in counterclockwise direction.

Fig. 16

A random network with $N=50$ nodes and a Poisson degree distribution with average degree 6, generated following the Molloy–Reed configuration model (1995)

Fig. 17

A random network with $N=50$ nodes and a power-law with exponential cut-off degree distribution with average degree 6, generated following the Molloy–Reed configuration model (1995)

Appendix C: Detailed Derivation of the SEIR Model

At time t, we choose uniformly at random a susceptible base v of degree k in the network corresponding to k edges. Each edge attached to v could either be of type ${{\mathcal {S}}}{{\mathcal {S}}}$, $\mathcal {SE}$, ${{\mathcal {S}}}{{\mathcal {I}}}$, or ${{\mathcal {S}}}{{\mathcal {R}}}$. Suppose that from the susceptible base v, an edge of type ${{\mathcal {S}}}{{\mathcal {I}}}$ has a uniform probability ${\bar{p}}^{\mathcal {I}} = \dfrac{{\bar{N}}^{{{\mathcal {S}}}{{\mathcal {I}}}} }{{\bar{N}}^{{\mathcal {S}}}}$. We note that an edge of type $\mathcal {SI}$ is considered equivalent to an edge of type ${{\mathcal {I}}}{{\mathcal {S}}}$. Thus, ${\bar{N}}^{{{\mathcal {S}}}{{\mathcal {I}}}}={\bar{N}}^{{{\mathcal {I}}}{{\mathcal {S}}}}$. Similarly, ${\bar{N}}^{{{\mathcal {S}}}{{\mathcal {E}}}}={\bar{N}}^{{{\mathcal {E}}}{{\mathcal {S}}}}$ and $\bar{N}^{{{\mathcal {S}}}{{\mathcal {R}}}}={\bar{N}}^{{{\mathcal {R}}}{{\mathcal {S}}}}$.

Consequently, there are $k {\bar{p}}^{\mathcal {I}}$ expected $\mathcal {SI}$ edges attached to v and within a small time interval, $rk {\bar{p}}^{\mathcal {I}}$ of these type ${{\mathcal {S}}}{{\mathcal {I}}}$ edges are expected to transmit infection to the susceptible base v. Thus, the hazard $\lambda (k)$ for a susceptible node v to be infected at time t is

$$\begin{aligned} \lambda (k) = rk\bar{p}^{\mathcal {I}} = rk\dfrac{{\bar{N}}^{\mathcal {SI}} }{{\bar{N}}^{{\mathcal {S}}}}. \end{aligned}$$

(17)

The hazard $\lambda (k)$ tells us that the probability of selecting a newly infected node is proportional to the number of type $\mathcal {SI}$ edges. Similarly, define the following probabilities

$$\begin{aligned} {\bar{p}}^{\mathcal {E}} = \dfrac{{\bar{N}}^{{{\mathcal {S}}}{{\mathcal {E}}}} }{\bar{N}^{{\mathcal {S}}}}, \quad {\bar{p}}^{\mathcal {R}} = \dfrac{{\bar{N}}^{\mathcal {SR}} }{{\bar{N}}^{{\mathcal {S}}}} \quad \text {and} \quad \bar{p}^{\mathcal {S}} = \dfrac{{\bar{N}}^{{\mathcal {S}}}-{\bar{N}}^{\mathcal {SE}}-{\bar{N}}^{{{\mathcal {S}}}{{\mathcal {I}}}}-{\bar{N}}^{{{\mathcal {S}}}{{\mathcal {R}}}} }{\bar{N}^{{\mathcal {S}}}}, \end{aligned}$$

where ${\bar{p}}^{\mathcal {S}} + {\bar{p}}^{\mathcal {E}} + {\bar{p}}^{\mathcal {I}} +{\bar{p}}^{\mathcal {R}} =1$.

Consider a degree-one node which remains susceptible at time t with probability $\theta$. The dynamics of $\theta$ are dependent on the hazard $\lambda$. In particular, with $k = 1$ from Eq. (17), the rate of change in the probability that a degree one node remains susceptible is equal to the rate at which infection is transmitted along the type ${{\mathcal {S}}}{{\mathcal {I}}}$ edge. Thus,

$$\begin{aligned} {\dot{\theta }} = \dfrac{\text {d}\theta }{\text {d} t}=-\lambda (1) \theta = -r {\bar{p}}^{\mathcal {I}}\theta , \end{aligned}$$

(18)

and by integration we get

$$\begin{aligned} \theta = \exp \left( -r \int _{s=0}^{t}{{\bar{p}}^{\mathcal {I}}_s \text {d} s}\right) . \end{aligned}$$

(19)

At time t, if a base node v of degree k is susceptible, then the probability that v is still susceptible is

$$\begin{aligned} \theta ^k = \exp \left( -\int _{s=0}^{t}{rk{\bar{p}}^{\mathcal {I}}_s \text {d} s}\right) = \left[ \exp \left( -r\int _{s=0}^{t}{{\bar{p}}^{\mathcal {I}}_s \ \text {d} s}\right) \right] ^k . \end{aligned}$$

(20)

This probability $\theta ^k$, together with the probability $p_k$ of a node to have degree k, is used to obtain the fraction ${\bar{S}}$ of susceptible nodes at time t using the probability generating function (PGF). The PGF of a given degree distribution $p_k$ is defined as $G(x)=\sum _{k=0}^\infty p_k x^k$. Using this PGF for $x=\theta$, we obtain

$$\begin{aligned} {\bar{S}} =p_0 + p_1\theta + p_2\theta ^2+p_3\theta ^3+\cdots =\sum _{k=0}^\infty p_k \theta ^k = G(\theta ), \end{aligned}$$

(21)

which satisfies the following properties:

• $G(1)= \sum _{k=0}^\infty p_k =1$, and

• $G^{\prime }(\theta )=\sum _{k=1}^\infty kp_k \theta ^{k-1}.$

It follows that $G^{\prime }(1 )=\sum _{k=1}^\infty kp_k =\left\langle K\right\rangle$, which is defined as the mean degree of all nodes in the random network. We use the “dot” $(\,\dot{}\,)$ and the “prime” $(^{\prime }{})$ notations for $\dfrac{d}{dt}$, and $\dfrac{d}{d\theta }$, respectively. Differentiating ${\bar{S}}$ with respect to time t, gives

$$\begin{aligned} \dot{\bar{S}}=G^{\prime }(\theta ){{\dot{\theta }}} = -r {\bar{p}}^\mathcal I\theta G^{\prime }(\theta ), \end{aligned}$$

(22)

the rate at which the fraction of susceptible nodes becomes infected at an instant. Equivalently, the rate at which the fraction of susceptible nodes becomes exposed is

$$\begin{aligned} -\dot{\bar{S}} = r {\bar{p}}^{\mathcal {I}}\theta G^{\prime }(\theta ). \end{aligned}$$

(23)

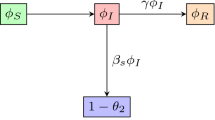
Accordingly, the fraction of exposed nodes ${\bar{E}}$ increases at a rate $-\dot{\bar{S}}$ where the fraction of susceptible nodes becomes infected, and ${\bar{E}}$ also decreases at a rate $\alpha {\bar{E}}$ at which exposed nodes becomes infectious. So, we obtain

$$\begin{aligned} \dot{\bar{E}}=-\dot{\bar{S}}-\alpha {\bar{E}} = r {\bar{p}}^\mathcal I\theta G^{\prime }(\theta )-\alpha {\bar{E}}. \end{aligned}$$

(24)

Consequently, the fraction of infectious nodes ${\bar{I}}$ increases at a rate $\alpha {\bar{E}}$ and decreases at a rate $\beta {\bar{I}}$ at which infectious nodes recover, so that

$$\begin{aligned} \dot{\bar{I}}=\alpha {\bar{E}} - \beta {\bar{I}}. \end{aligned}$$

(25)

After having derived the equations for the node-based variables $\dot{\bar{S}}, \dot{\bar{E}}$, and $\dot{\bar{I}}$, we proceed with the formulation of the model by finding equations for $\dot{\bar{p}}^{{\mathcal {I}}}, \dot{\bar{p}}^{{\mathcal {E}}}$, and $\dot{\bar{p}}^{{\mathcal {S}}}$. It should be noted that the dynamics of both $\theta$ and ${\bar{S}}$ depend on ${\bar{p}}^{\mathcal {I}}$. Differentiating ${\bar{p}}^{\mathcal {I}} = \dfrac{{\bar{N}}^{\mathcal {SI}}}{{\bar{N}}^{{\mathcal {S}}}}$ yields

$$\begin{aligned} \dot{\bar{p}}^{{\mathcal {I}}} = \dfrac{\dot{\bar{N}}^\mathcal {SI}}{{\bar{N}}^{{\mathcal {S}}}}-\dfrac{{\bar{N}}^{\mathcal {SI}}\dot{\bar{N}}^{\mathcal {S}}}{({\bar{N}}^{{\mathcal {S}}})^2}. \end{aligned}$$

(26)

Recall that ${\bar{N}}^{{\mathcal {S}}}$ denotes the fraction of edges with a susceptible base. Thus, ${\bar{N}}^{{\mathcal {S}}}$ can be expressed as

$$\begin{aligned} {\bar{N}}^{\mathcal {S}}= & {} \dfrac{\sum _k k p_k \text {Pr}(\text {deg}\,k\, \text {node being susceptible at time}\,t)}{\sum _k kp_k} \nonumber \\= & {} \dfrac{\sum _k k p_k\theta ^k}{G^{\prime }(1)} =\dfrac{\theta G^{\prime }(\theta )}{G^{\prime }(1)}, \end{aligned}$$

(27)

for $k\in {\mathbb {N}}$. On the other hand,

$$\begin{aligned} {\bar{N}}^{\mathcal {SI}}={\bar{N}}^{\mathcal {S}}\left( \dfrac{\bar{N}^{\mathcal {SI}}}{{\bar{N}}^{\mathcal {S}}} \right) = {\bar{N}}^{\mathcal {S}} \bar{p}^{\mathcal {I}}={\bar{p}}^{\mathcal {I}}\theta \dfrac{ G^{\prime }(\theta )}{G^{\prime }(1)}. \end{aligned}$$

(28)

Differentiating Eq. (27), and using Eq. (1), we have

$$\begin{aligned} \dot{\bar{N}}^{\mathcal {S}} =-r {\bar{p}}^{\mathcal {I}}\theta \left[ \dfrac{ G^{\prime }(\theta )+\theta G^{\prime \prime }(\theta )}{G^{\prime }(1)}\right] . \end{aligned}$$

(29)

The rate of change of ${\bar{N}}^{\mathcal {SI}}$ considers what happens after infection is transmitted from an infectious node to a susceptible node across a type ${{\mathcal {S}}}{{\mathcal {I}}}$ edge. Because infection cannot be transmitted back to its source, we consider the excess degree of the newly exposed node. The excess degree is described as the number of edges incident or attached to a newly exposed node other than the traversed type ${{\mathcal {S}}}{{\mathcal {I}}}$ edge. If we let the degree of the newly exposed node v be $d_v = k$, where k is at least 1, and the excess degree is denoted by $\delta _v$, then $\delta _v = k-1$ with its minimum value equal to zero. In the case of isolated nodes, where $d_v = 0$, the excess degree is still zero since there are no edges we can traverse to arrive at an isolated node.

After the susceptible base becomes infected and moves into the exposed class, the status of the other incident edges (counted by the excess degree) will change. For instance, a type $\mathcal {SS}$ edge changes to a type ${{\mathcal {S}}}{{\mathcal {E}}}$ edge. The processes for computing the degree distribution for susceptible nodes and the excess degree distribution are similar to those used in Volz (2008).

The following notations and definitions will be used henceforth:

• $\delta _{XY}$, the excess degree of a node in set X, selected with probability proportional to the number of type XY edges, not counting one type XY edge, where $X, Y \in \left\{ {\mathcal {S}}, {\mathcal {E}}, {\mathcal {I}}, \mathcal R\right\}$;

• $\delta _{XY}(Z)$, the excess degree $\delta _{XY}$ counting only the edges from the base node of type X to a target node in set Z, where $Z \in \left\{ {\mathcal {S}}, \mathcal E, {\mathcal {I}}, {\mathcal {R}}\right\}$;

• $d_v(Z)$, the random variable which represents the number of edges from a base node, say v, to nodes in the set $Z \in \left\{ {\mathcal {S}}, {\mathcal {E}}, {\mathcal {I}}, \mathcal R\right\}$;

• $x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}}$, dummy variables corresponding to the number of type ${\mathcal {S}}{\mathcal {Y}}$ edges where Y is ${\mathcal {S}}, {\mathcal {E}}, {\mathcal {I}} \ \text {and}\ {\mathcal {R}}$, respectively,

• $G_{\mathcal {S}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right)$, the degree distribution for susceptible nodes; and

• $G_{XY}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right)$, the excess degree distribution for nodes in X selected with probability proportional to the number of type XY edges.

The degree distribution $G_{\mathcal {S}}\left( x_{\mathcal {S}}, x_\mathcal E, x_{\mathcal {I}}, x_{\mathcal {R}} \right)$ keeps track of how frequently a susceptible node is connected to other nodes of different types, taking into consideration the probability of forming the corresponding types of edges. Then, when infection is transmitted to a susceptible node, it changes the distribution of edges connected from the newly infected susceptible node. Thus, finding $\delta _{\mathcal {SI}}$ requires the computation of $G_{\mathcal {S}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right)$.

To proceed with the model derivation, assume that the network is uncorrelated. Suppose we take two edges $(x,y_1)$ and $(x,y_2)$ with base node $x \in {\mathcal {S}}$, and the events that target node $y_1\in X$ and target node $y_2\in Y$, respectively, are independent, where $X, Y \in \left\{ {\mathcal {S}}, {\mathcal {E}}, {\mathcal {I}}, {\mathcal {R}}\right\}$. Then, edges from a susceptible base to target nodes in states ${\mathcal {S}}, {\mathcal {E}}, {\mathcal {I}} \ \text {and}\ {\mathcal {R}}$ are multinomially distributed with probabilities $\bar{p}^{\mathcal {S}}, \bar{p}^{\mathcal {E}}, \bar{p}^{\mathcal {I}} \ \text {and} \ \bar{p}^\mathcal R=1-\bar{p}^{\mathcal {S}}-\bar{p}^{\mathcal {E}}-\bar{p}^{\mathcal {I}}$, respectively. The degree distribution for susceptible nodes is calculated by

$$\begin{aligned} G_{\mathcal {S}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right) = \dfrac{\sum \limits _k p_k\theta ^k\sum \limits _{h,j,l|h+j+l\le k}x_{\mathcal {S}}^h x_\mathcal E^j x_{\mathcal {I}}^l x_{\mathcal {R}}^{k-h-j-l}\text {Pr}\left( {\mathcal {D}} \right) }{\sum \limits _k p_k\theta ^k\sum \limits _{h,j,l|h+j+l \le k}\text {Pr}\left( {\mathcal {D}} \right) }, \end{aligned}$$

where

$$\begin{aligned} \text {Pr}\left( {\mathcal {D}} \right)= & {} \text {Pr}{\left( d_v(\mathcal S)=h, d_v({\mathcal {E}})=j, {d}_v({\mathcal {I}})=l \, | \,\bar{p}^\mathcal S, \bar{p}^{\mathcal {E}}, \bar{p}^{\mathcal {I}} \right) }\qquad \qquad \\= & {} \dfrac{k!}{h!j!l!(k-h-j-l)!}{(\bar{p}^{\mathcal {S}})^h (\bar{p}^{\mathcal {E}})^j(\bar{p}^{\mathcal {I}})^l(1-\bar{p}^\mathcal S-\bar{p}^{\mathcal {E}}-\bar{p}^{\mathcal {I}} )^{k-h-j-l}}. \end{aligned}$$

Applying the multinomial theorem,

$$\begin{aligned} \sum \limits _{h,j,l|h+j+l \le k}\text {Pr}\left( {\mathcal {D}} \right)&= 1,\quad \left[ x_{\mathcal {S}}\bar{p}^{\mathcal {S}}+ x_{\mathcal {E}}\bar{p}^\mathcal E+x_{\mathcal {I}}\bar{p}^{\mathcal {I}}+ x_{\mathcal {R}} (1-\bar{p}^\mathcal S-\bar{p}^{\mathcal {E}}-\bar{p}^{\mathcal {I}} )\right] ^k \\&= \sum \limits _{h,j,l|h+j+l\le k} \left[ \dfrac{k!}{h!j!l!(k\!-\!h\!-\!j\!-\!l)!}(x_{\mathcal {S}}\bar{p}^{\mathcal {S}})^h (x_{\mathcal {E}}\bar{p}^{\mathcal {E}})^j (x_{\mathcal {I}}\bar{p}^\mathcal I)^l \right. \\&\quad \Biggl .\left[ x_{\mathcal {R}} (1-\bar{p}^{\mathcal {S}}-\bar{p}^{\mathcal {E}}-\bar{p}^{\mathcal {I}} )\right] ^{k-h-j-l} \Biggr ] \end{aligned}$$

and the definition of PGF, we therefore have

$$\begin{aligned}&G_{\mathcal {S}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right) \nonumber \\&\quad = \dfrac{G\left( \theta \left[ x_{\mathcal {S}}\bar{p}^\mathcal S+x_{\mathcal {E}}\bar{p}^{\mathcal {E}}+x_{\mathcal {I}}\bar{p}^\mathcal I+x_{\mathcal {R}}\left( 1-\bar{p}^{\mathcal {S}}-\bar{p}^{\mathcal {E}}- \bar{p}^{\mathcal {I}}\right) \right] \right) }{G(\theta )}. \end{aligned}$$

(30)

If we randomly choose a type ${{\mathcal {S}}}{{\mathcal {I}}}$ edge (v, y) , follow it to the susceptible node v,  and count the number of type ${{\mathcal {S}}}{{\mathcal {S}}}, {{\mathcal {S}}}{{\mathcal {E}}}, {{\mathcal {S}}}{{\mathcal {I}}},$ and ${{\mathcal {S}}}{{\mathcal {R}}}$ edges from v other than the traversed ${{\mathcal {S}}}{{\mathcal {I}}}$ edge, then we can determine the excess degree of v and its excess degree distribution. So, for any susceptible node v and using the degree distribution $G_\mathcal S\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right)$ for susceptible nodes selected randomly with probability proportional to the number of type ${{\mathcal {S}}}{{\mathcal {I}}}$ edges, the excess degree distribution can be generated as follows:

$$\begin{aligned}&G_{\mathcal {SI}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right) \nonumber \\&\quad =\dfrac{\sum \limits _k p_k\theta ^k\sum \limits _{h,j,l|h+j+l \le k}l \cdot x_{\mathcal {S}}^h x_{\mathcal {E}}^j x_{\mathcal {I}}^{l-1} x_{\mathcal {R}}^{k-h-j-l}\text {Pr}\left( {\mathcal {D}} \right) }{\sum \limits _k p_k\theta ^k\sum \limits _{h,j,l|h+j+l \le k} l\cdot \text {Pr}\left( {\mathcal {D}} \right) } \nonumber \\&\quad =\dfrac{G^{\prime }\left( \theta \left[ x_{\mathcal {S}}\bar{p}^\mathcal S+x_{\mathcal {E}}\bar{p}^{\mathcal {E}}+x_{\mathcal {I}}\bar{p}^\mathcal I+x_{\mathcal {R}}\left( 1-\bar{p}^{\mathcal {S}}-\bar{p}^{\mathcal {E}}- \bar{p}^{\mathcal {I}}\right) \right] \right) }{G^{\prime }\left( \theta \right) }. \end{aligned}$$

(31)

We apply similar computations for the excess degree distribution for the following cases where the degree distribution $G_\mathcal S\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right)$ for susceptible nodes are selected randomly with probability proportional to the number of type ${{\mathcal {S}}}{{\mathcal {E}}}$ edges, of type ${{\mathcal {S}}}{{\mathcal {S}}}$ edges and of type ${{\mathcal {S}}}{{\mathcal {R}}}$ edges. Because the edges from a susceptible base are multinomially distributed to target nodes in states ${\mathcal {S}}, {\mathcal {E}}, {\mathcal {I}}, \text {and}\ {\mathcal {R}},$

$$\begin{aligned} G_{\mathcal {SI}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right)= & {} G_{\mathcal {SS}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right) \nonumber \\= & {} G_{\mathcal {SE}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right) \\= & {} G_{\mathcal {SR}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right) . \end{aligned}$$

From the excess degree distribution $G_{\mathcal {SI}}\left( x_\mathcal S, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right)$, which is expressed using the derivative of the PGF for the degree distribution among susceptible nodes, we can compute the corresponding excess degree by differentiating $G_{\mathcal {SI}}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_{\mathcal {R}} \right)$ and letting the dummy variables equal one. Hence, from Eq. (31) we have

$$\begin{aligned} \delta _{\mathcal {SI}}&= {\dfrac{\text {d}}{\text {d}x}G_\mathcal {SI}\left( x,x,x,x\right) }\Big |_{x=1} \nonumber \\&= {\dfrac{\text {d}}{\text {d}x}\left[ \dfrac{G^{\prime }\left( \theta \left[ x\bar{p}^{\mathcal {S}} + x\bar{p}^{\mathcal {E}} + x\bar{p}^{\mathcal {I}} + x\left( 1-\bar{p}^{\mathcal {S}}-\bar{p}^{\mathcal {E}}- \bar{p}^\mathcal I\right) \right] \right) }{G^{\prime }\left( \theta \right) }\right] }\Big |_{x=1} \nonumber \\ \delta _{\mathcal {SI}}&= \theta \dfrac{G^{\prime \prime }(\theta )}{G^{\prime }(\theta )}. \end{aligned}$$

(32)

Particularly, the excess degree of a susceptible base linked to an infectious target, other than the one that infects it, is

$$\begin{aligned} \delta _{\mathcal {SI}}({\mathcal {I}})&= {\dfrac{\text {d}}{\text {d}x_{\mathcal {I}}}G_\mathcal {SI}\left( x_{\mathcal {S}}, x_{\mathcal {E}}, x_{\mathcal {I}}, x_\mathcal R\right) }\Big |_{x_{\mathcal {S}}= x_{\mathcal {E}}= x_{\mathcal {I}}= x_{\mathcal {R}}=1} \nonumber \\ \delta _{\mathcal {SI}}({\mathcal {I}})&= \theta \bar{p}^\mathcal I\dfrac{G^{\prime \prime }(\theta )}{G^{\prime }(\theta )}. \end{aligned}$$

(33)

Similarly, for $\delta _{\mathcal {SI}}({\mathcal {E}})$ and $\delta _{\mathcal {SI}}({\mathcal {S}})$, we obtain the following:

$$\begin{aligned} \delta _{\mathcal {SI}}({\mathcal {E}})&= \theta \bar{p}^\mathcal E\dfrac{G^{\prime \prime }(\theta )}{G^{\prime }(\theta )}, \end{aligned}$$

(34)

and

$$\begin{aligned} \delta _{\mathcal {SI}}({\mathcal {S}})&= \theta \bar{p}^\mathcal S\dfrac{G^{\prime \prime }(\theta )}{G^{\prime }(\theta )}. \end{aligned}$$

(35)

When infection is transmitted to a susceptible base, the excess degrees $\delta _{\mathcal {SI}}({\mathcal {I}})$, $\delta _\mathcal {SI}({\mathcal {E}})$, and $\delta _{\mathcal {SI}}({\mathcal {S}})$ are associated with the corresponding rates of increase or decrease of the edges from the susceptible base to the other (infectious, exposed, or susceptible) target nodes. This would lead us to further derive expressions for $\dot{\bar{p}}^{{\mathcal {I}}}, \dot{\bar{p}}^{{\mathcal {E}}}$, and $\dot{\bar{p}}^{{\mathcal {S}}}$.

In a small time interval $\varDelta t \rightarrow 0$, the fraction of type ${{\mathcal {S}}}{{\mathcal {I}}}$ edges decreases either because

• the fraction of newly infected nodes $-\dot{\bar{S}}$ leaves the susceptible class, enters the exposed class, and will have on the average of $\delta _{\mathcal {SI}}({\mathcal {I}})$ at rate $\dfrac{-\dot{\bar{S}}\delta _{\mathcal {SI}}({\mathcal {I}})}{G^{\prime }(1)}$; note that $\delta _{\mathcal {SI}}({\mathcal {I}})$ does not consider the ${{\mathcal {S}}}{{\mathcal {I}}}$ edge where infection is transmitted;

• a susceptible base receives infection from an infectious target at rate $r{\bar{N}}^{\mathcal {SI}}$; or

• an infectious node recovers at rate $\beta {\bar{N}}^{\mathcal {SI}} =\beta \bar{{\mathcal {I}}}\left( \dfrac{\bar{N}^{\mathcal {SI}}}{\bar{{\mathcal {I}}}}\right)$ since $\beta \bar{{\mathcal {I}}}$ nodes become recovered and the average number of type ${{\mathcal {S}}}{{\mathcal {I}}}$ edges per infectious node is proportional to $\dfrac{{\bar{N}}^{\mathcal {SI}}}{\bar{{\mathcal {I}}}}$.

On the other hand, the fraction of type ${{\mathcal {S}}}{{\mathcal {I}}}$ edges increases when exposed nodes become infectious; that is, $\bar{N}^{\mathcal {SI}}$ increases at a rate $\alpha {\bar{N}}^{\mathcal {SE}}$, where

$$\begin{aligned} {\bar{N}}^{\mathcal {SE}} = \bar{p}^{\mathcal {E}}\theta \dfrac{G^{\prime }(\theta )}{G^{\prime }(1)}. \end{aligned}$$

(36)

Thus, we get

$$\begin{aligned} \dot{\bar{N}}^{\mathcal {SI}}&=\alpha \bar{N}^{\mathcal {SE}}-\left[ \dfrac{-\dot{\bar{S}}\delta _\mathcal {SI}({\mathcal {I}})}{G^{\prime }(1)}+(r+\beta ){\bar{N}}^{\mathcal {SI}} \right] \nonumber \\&= \alpha \bar{p}^{\mathcal {E}}\theta \dfrac{G^{\prime }(\theta )}{G^{\prime }(1)}-\left[ \dfrac{r\left( p^{\mathcal {I}}\right) ^2 \theta ^2 G^{\prime \prime }(\theta )}{G^{\prime }(1)}+(r+\beta )\bar{p}^{\mathcal {I}}\theta \dfrac{G^{\prime }(\theta )}{G^{\prime }(1)} \right] \end{aligned}$$

(37)

after using Eqs. (23), (28), (33) and (36).

Substituting Eqs. (27), (28), (29) and (37) into Eq. (26), we then have

$$\begin{aligned} \dot{\bar{p}}^{{\mathcal {I}}} =\alpha {\bar{p}}^{\mathcal {E}}-(r+\beta )\bar{p}^{\mathcal {I}}+ r\left( {\bar{p}}^{\mathcal {I}}\right) ^2. \end{aligned}$$

(38)

Accordingly, since $\dot{\bar{p}}^{{\mathcal {I}}}$ in Eq. (38) involves ${\bar{p}}^{\mathcal {E}}$ that changes over time, we consider the dynamics of ${\bar{p}}^{\mathcal {E}}$. Similar arguments are used in deriving

$$\begin{aligned} \dot{\bar{p}}^{{\mathcal {E}}} = \dfrac{\dot{\bar{N}}^\mathcal {SE}}{{\bar{N}}^{{\mathcal {S}}}}-\dfrac{{\bar{N}}^{\mathcal {SE}}\dot{\bar{N}}^{\mathcal {S}}}{({\bar{N}}^{{\mathcal {S}}})^2} \end{aligned}$$

(39)

expressed in terms of the edge-based dynamic variables. Consider the type ${\mathcal {SE}}$ edges. When either an exposed node becomes infectious or the susceptible node newly infected resulting to an average of $\delta _{\mathcal {SI}}({\mathcal {E}})$ edges from the susceptible node to the exposed node, ${\bar{N}}^{\mathcal {SE}}$ reduces at the rates $\alpha {\bar{N}}^{\mathcal {SE}}$ and $\dfrac{-\dot{\bar{S}}\delta _{\mathcal {SI}}({\mathcal {E}})}{G^{\prime }(1)}$, respectively. Considering the type ${{\mathcal {S}}}{{\mathcal {S}}}$ edges in the excess degree of the susceptible node being infected, the event leads to an increase of ${\bar{N}}^{\mathcal {SE}}$ at the rate $\dfrac{-\dot{\bar{S}}\delta _{\mathcal {SI}}({\mathcal {S}})}{G^{\prime }(1)}$. Thus, we have

$$\begin{aligned} \dot{\bar{N}}^{\mathcal {SE}}&=\dfrac{-\dot{\bar{S}}\delta _\mathcal {SI}({\mathcal {S}})}{G^{\prime }(1)}-\left[ \dfrac{-\dot{\bar{S}}\delta _{\mathcal {SI}}({\mathcal {E}})}{G^{\prime }(1)}+\alpha \bar{N}^{\mathcal {SE}} \right] \nonumber \\ \dot{\bar{N}}^{\mathcal {SE}}&=({\bar{p}}^{\mathcal {S}}-\bar{p}^{\mathcal {E}})r{\bar{p}}^{\mathcal {I}} \theta ^2\dfrac{ G^{\prime \prime }(\theta )}{G^{\prime }(1)}-\alpha \bar{p}^{\mathcal {E}}\theta \dfrac{G^{\prime }(\theta )}{G^{\prime }(1)} \end{aligned}$$

(40)

Therefore, we get

$$\begin{aligned} \dot{\bar{p}}^{{\mathcal {E}}} = r{\bar{p}}^{\mathcal {S}} \bar{p}^{\mathcal {I}} \theta \dfrac{ G^{\prime \prime }(\theta )}{G^{\prime }(\theta )}-\alpha {\bar{p}}^{\mathcal {E}}+r\bar{p}^{\mathcal {E}}{\bar{p}}^{\mathcal {I}}. \end{aligned}$$

(41)

Finally, to complete the model, we consider expressing

$$\begin{aligned} \dot{\bar{p}}^{{\mathcal {S}}} = \dfrac{\dot{\bar{N}}^\mathcal {SS}}{{\bar{N}}^{{\mathcal {S}}}}-\dfrac{{\bar{N}}^{\mathcal {SS}}\dot{\bar{N}}^{\mathcal {S}}}{({\bar{N}}^{{\mathcal {S}}})^2} \end{aligned}$$

(42)

in terms of $\theta , {\bar{p}}^{\mathcal {I}}, {\bar{p}}^{\mathcal {S}}$. With

$$\begin{aligned} \bar{N}^{\mathcal {SS}}={\bar{p}}^{\mathcal {S}}_t\theta \dfrac{G^{\prime }(\theta )}{G^{\prime }(1)}, \end{aligned}$$

(43)

we have

$$\begin{aligned} \dot{\bar{N}}^{{{\mathcal {S}}}{{\mathcal {S}}}} = -2\times \dfrac{-\dot{\bar{S}}\delta _{\mathcal {SI}}({\mathcal {S}})}{G^{\prime }(1)} = -2r\bar{p}^{\mathcal {I}}\bar{p}^{\mathcal {S}}\theta ^2\dfrac{G^{\prime \prime }(\theta )}{G^{\prime }(1)}, \end{aligned}$$

(44)

since one newly infected node in an ${{\mathcal {S}}}{{\mathcal {S}}}$ pairing results in a decrease of $\bar{N}^{\mathcal {SS}}$ at the rate $\dfrac{-\dot{\bar{S}}\delta _{\mathcal {SI}}({\mathcal {S}})}{G^{\prime }(1)}$. Hence,

$$\begin{aligned} \dot{\bar{p}}^{{\mathcal {S}}} = r{\bar{p}}^{\mathcal {I}}\bar{p}^{\mathcal {S}}\left[ 1-\dfrac{\theta G^{\prime \prime }(\theta )}{G^{\prime }(\theta )} \right] . \end{aligned}$$

(45)

Appendix D: SEIR Simulations with Large Number of Initial Infections

We varied the initial number of infecteds to illustrate its effects on the dynamics of the epidemic (Kiss et al. 2017). We generated a single network each of Poisson and scale-free type. We fixed the network population at $N= 10{,}000$ with an average degree of 6, the disease parameters at $r=0.8$, $\alpha =0.5$ and $\mu =1$. The initial number of infecteds is set at $E_0 = I_0 = 20$ and $E_0 = I_0 = 50$ corresponding to Figs. 18 and 19, respectively.

Fig. 18

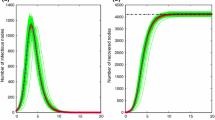
Comparison of the ensemble average of 100 runs of stochastic simulations of the SEIR dynamics and the solution of the SEIR model (5) with the final epidemic size with $E_0 = I_0 = 20$ in a (a) Poisson network, and a (b) scale-free network for a fraction of each population class

Fig. 19

Comparison of the ensemble average of 100 runs of stochastic simulations of the SEIR dynamics and the solution of the SEIR model (5) with the final epidemic size with $E_0 = I_0 = 50$ in a (a) Poisson network, and a (b) scale-free network for a fraction of each population class