Modelling the Effect of Incubation and Latent Periods on the Dynamics of Vector-Borne Plant Viral Diseases

Abstract

Most of the plant viral diseases spread through vectors. In case of the persistently transmitted disease, there is a latent time of infection inside the vector after acquisition of the virus from the infected plant. Again, the plant after getting infectious agent shows an incubation time after the interaction with an infected vector before it becomes diseased. The goal of this work is to study the effect of both incubation delay and latent time on the dynamics of plant disease, and accordingly a delayed model has been proposed. The existence of the equilibria, basic reproductive number ($\mathcal {R}_0$) and stability of equilibria have been studied. This study shows the relevance of the presence of two time delays, which may lead to system stabilization.

Appendices

Appendix A

We follow the method established in the paper by Heffernan et al. (2005) for calculating $\mathcal {R}_0$.

We consider the next-generation matrix G which comprises two parts, namely F and V, where

$$\begin{aligned} {F}= & {} \left[ \frac{\partial {F}_i(E_0)}{\partial x_j}\right] =\left[ \begin{array}{ll} 0 &{} ~~ \lambda K \\ \frac{\beta \Pi }{d} &{}~~0 \\ \end{array} \right] \\ {V}= & {} \left[ \frac{\partial {V}_i(E_0)}{\partial x_j}\right] =\left[ \begin{array}{ll} m~ &{}~~ 0\\ \\ 0 ~&{} ~~ d \\ \end{array}\right] \end{aligned}$$

where ${F}_i$ are the new infections, while the ${V}_i$ transfers of infections from one compartment to another. $E_0$ is the disease-free equilibrium. We get $\mathcal {R}_0=\frac{\Pi k\lambda \beta }{md^2}$, and it is the dominant eigenvalue of the matrix ${G} = {F}{V}^{-1}$.

Appendix B

We rewrite the model (1), without delay, as follows:

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}= & {} rS\left( 1-\frac{S+I}{K}\right) -\lambda SV\,\equiv \,f_1(S,I,U,V),\end{aligned}$$

(22a)

$$\begin{aligned} \frac{\mathrm{d}I}{\mathrm{d}t}= & {} \lambda SV-mI\,\equiv \,f_2(S,I,U,V),\end{aligned}$$

(22b)

$$\begin{aligned} \frac{\mathrm{d}U}{\mathrm{d}t}= & {} \Pi -\beta UI-dU\,\equiv \,f_3(S,I,U,V),\end{aligned}$$

(22c)

$$\begin{aligned} \frac{\mathrm{d}V}{\mathrm{d}t}= & {} \beta UI-dV\,\equiv \,f_4(S,I,U,V), \end{aligned}$$

(22d)

and consider $\lambda$ as bifurcation parameter to check the change in stability of the disease-free equilibrium point $E_2(K,0,\frac{\Pi }{d},0)$. Jacobian matrix for (22) evaluated at $E_2$ is given by

$$\begin{aligned} J\left( E_2\right) \,=\,\left[ \begin{array}{llll} -r &{} -r &{} 0 &{} -\lambda K\\ 0 &{} -m &{} 0 &{} \lambda K\\ 0 &{} -\frac{\beta \Pi }{d} &{} -d &{} 0\\ 0 &{} \frac{\beta \Pi }{d} &{} 0 &{} -d\\ \end{array}\right] . \end{aligned}$$

(23)

This matrix has a zero eigenvalue when $\lambda \,\equiv \,\lambda _*\,=\,\frac{d^2m}{K\Pi \beta }$. The system undergoes a transcritical bifurcation as $\lambda$ crosses $\lambda _*$. To prove the transversality condition of transcritical bifurcation, we use standard notations in Perko (1996). The system (22) can be written in compact form as

$$\begin{aligned} \frac{\mathrm{d}{X}}{\mathrm{d}t}=\mathbf{f}({X}), \end{aligned}$$

(24)

and the Jacobian matrix in (23) is denoted as $A\,=\,J\left( E_2\right)$. For $\lambda \,=\,\lambda _*$, the matrix A has a zero eigenvalue, eigenvectors corresponding to zero eigenvalue for the matrices A and $A^t$ are given by

$$\begin{aligned} W_1= & {} \left[ \begin{array}{l} -\frac{r+m}{r} \\ 1 \\ -\frac{\Pi \beta }{d^2} \\ \frac{\Pi \beta }{d^2} \\ \end{array}\right] ,\nonumber \\ W_2= & {} \left[ \begin{array}{l} 0 \\ \frac{\Pi \beta }{md} \\ 0 \\ 1 \\ \end{array}\right] . \end{aligned}$$

(25)

Partial differentiation of $\mathbf{f}$ with respect to $\lambda$ gives

$$\begin{aligned} {\mathbf {f}}_\lambda \,=\,\left[ \begin{array}{l} -SV \\ SV \\ 0 \\ 0 \\ \end{array}\right] , \end{aligned}$$

(26)

and the Jacobian of $\mathbf{f}_\lambda$ can be calculated as follows:

$$\begin{aligned} D\mathbf{f}_\lambda \,=\, \left[ \begin{array}{llll} -V &{}\quad 0 &{}\quad 0 &{}\quad -S \\ V &{}\quad 0 &{}\quad 0 &{}\quad S \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array}\right] . \end{aligned}$$

(27)

Hence, we can verify the transversality conditions for transcritical bifurcation as follows:

$$\begin{aligned} W_2^t\left[ \mathbf{f}_\lambda (E_2,\lambda _*)\right]= & {} 0, \end{aligned}$$

(28a)

$$\begin{aligned} W_2^t\left[ D\mathbf{f}_\lambda (E_2,\lambda _*)\,W_1\right]= & {} \frac{\Pi ^2\beta ^2K}{md^3}\,\,\ne \,\,0, \end{aligned}$$

(28b)

$$\begin{aligned} W_2^t\left[ D^2\mathbf{f}(E_2,\lambda _*)\,(W_1,W_1)\right]= & {} -\frac{2\beta ^2\Pi }{d^2}\left( 1+\frac{\Pi d(r+m)}{rK\beta }\right) \,\,\ne \,\,0. \end{aligned}$$

(28c)

These ensure that the boundary equilibrium point $E_2$ loses stability through transcritical bifurcation.

Appendix C

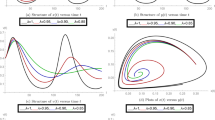
For the values in Table 1, we get the four roots of Eq. (15) as: $- \,0.0664$, 0.0360 and $- \,0.0108 \pm 0.0430i$. We get one pair of complex root and the positive root as 0.0360. Here, $\omega _4 = - 4.6897\times 10^{-6}<0$. According to Lemma 1, Eq. (15) will have at least one positive root.

Equation (16) has three roots: $- 0.0374$ and $- 0.0008 \pm 0.0073i$. We have got $\delta = 2.6996 \times 10^{-11}>0,$$H(l)<0$. According to Lemma 2, Eq. (15) has one positive root. Then, Eq. (11) has a pair of purely imaginary root. Finally, we have obtained $\theta _0= 0.1897$ from (19), as well as the critical value of $\tau _1$, namely $\tau _1^*=15.38$, from relation (18).