Nanobeam Theory Taking Into Account Physical Nonlinearity

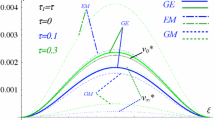
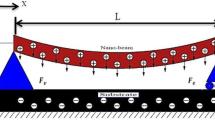
In this paper, we construct a new theory of nanobeams taking into account the dependence of the material properties on the stress state. The theory is based on the Euler–Bernoulli kinematic model in the first approximation. The beam material is isotropic but heterogeneous. For the first time, the physical nonlinearity and the dependence of the material properties on the temperature are taken into account in the study of nanobeams, and the theory is developed for arbitrary materials. It is based on the theory of small elasticplastic strains and on the the modified torque theory of elasticity. The stationary temperature field is determined by solving the three-dimensional Poisson equation with boundary conditions of orders 1–3. The initial equations are derived from the Hamilton–Ostrogradskii principle. The desired system of partial differential equations is reduced to the Cauchy problem by the finite difference method of the second order of accuracy, and the Cauchy problem is solved by the Runge–Kutta or Newmark method. At each time step, an iterative procedure is developed by the Birger method of variable elasticity parameters. The stationary solution follows from the dynamic solution of the problem obtained by the method of determination (the method of the parameter position). The convergence of the solution is investigated depending on the number of points of partition along the length and thickness of the beam in the finite difference method as well as on the method of solving the Cauchy problem and the size-dependent parameter, i.e., the solution of the problem is considered to have almost infinite number of degrees of freedom. Numerical examples are given for a beam rigidly clamped at the ends with the stress-strain diagram for aluminum. Accounting for the size-dependent parameter in the nanobeam theory significantly affects the load-carrying capacity of nanobeams.