Abstract
In this paper, we formulate necessary and sufficient conditions for relative compactness in the space \(BG({\mathbb {R}}_+,E)\) of regulated and bounded functions defined on \({\mathbb R}_+\) with values in the Banach space E. Moreover, we construct four new measures of noncompactness in the space \(BG({\mathbb {R}}_+,E)\). We investigate their properties and we describe relations between these measures. We provide necessary and sufficient conditions so that the superposition operator (Niemytskii) maps \(BG({\mathbb {R}}_+,E)\) into \(BG({\mathbb {R}}_+,E)\) and, additionally, be compact.
Similar content being viewed by others
1 Introduction
The measures of noncompactness and fixed point theorems are often chosen to investigate solvability of the nonlinear equations. Using a suitable function space together with convenient measures of noncompactness we can obtain elegant existence theorems. In recent years, there have appeared a lot of papers concerning the space G(J, E) of regular functions defined on a bounded interval J and with values in the Banach space E [2, 4,5,6,7,8,9,10,11, 14]. On the other hand, there have not been any papers focused on the space of regular functions on an unbounded interval \({\mathbb R}_+\). Throughout this paper we are going to fill this gap. We will investigate the space \(BG({\mathbb {R}}_+,E)\) of regular and bounded functions defined on \({\mathbb R}_+\) and with values in the Banach space E.
In Sect. 3 we formulate necessary and sufficient relative compactness conditions in the space \(BG({\mathbb {R}}_+,E)\). In the sequel we construct four new and convenient measures of noncompactness in \(BG({\mathbb {R}}_+,E)\) and investigate their properties.
In Sect. 4 we present necessary and sufficient conditions for superposition operator so that it maps \(BG({\mathbb {R}}_+,E)\) into \(BG({\mathbb {R}}_+,E)\). Moreover, we formulate necessary and sufficient conditions so that the superposition operator \(F_f:BG({\mathbb {R}}_+,E) \rightarrow BG({\mathbb {R}}_+,E) \) is compact.
Finally, Sect. 5 shows the applicability one of the mentioned measures of noncompactness to the existence result for some nonlinear integral equation.
2 Notation, definitions and auxiliary facts
This section is devoted to recalling some facts which will be used in our further investigations.
Assume that E is a real Banach space with the norm \(\Vert \cdot \Vert \) and the zero element \(\theta \). Denote by \(B_E(x,r)\) the closed ball centered at x and with radius r. The symbol \(B_E(r)\) stands for the ball \(B_E(\theta , r)\). We write \(\overline{X}, \mathrm{conv} X, \mathrm{Conv} X\) to denote the closure, convex hull and the convex closure of a set X, respectively. Further, let  denote the family of all nonempty and bounded subsets of E and
denote the family of all nonempty and bounded subsets of E and  its subfamily consisting of all relatively compact sets. The characteristic function of the set A is denoted by \(\mathbf{1}_A\).
its subfamily consisting of all relatively compact sets. The characteristic function of the set A is denoted by \(\mathbf{1}_A\).
We accept the following definition of the notion of a measure of noncompactness [3].
Definition 2.1
A mapping  is said to be a measure of noncompactness in a Banach space E if it satisfies the following conditions:
is said to be a measure of noncompactness in a Banach space E if it satisfies the following conditions:
- \(1^{\circ }\):
-
The family
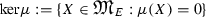 is nonempty and
is nonempty and 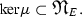
- \(2^{\circ }\):
-
\(X\subset Y\Rightarrow \mu (X)\le \mu (Y).\)
- \(3^{\circ }\):
-
\(\mu (\mathrm{Conv} X)=\mu (X).\)
- \(4^{\circ }\):
-
\(\mu (\lambda X+(1-\lambda )Y)\le \lambda \mu (X)+(1-\lambda ) \mu (Y)\) for \(\lambda \in [0,1].\)
- \(5^{\circ }\):
-
If \(\{X_n\}\) is a sequence of closed sets from
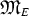 such that \(X_{n+1}\subset X_n\) for \(n=1,2,\ldots \) and if \(\lim \nolimits _{n\rightarrow \infty } \mu (X_n)=0\), then the intersection \(X_\infty :=\bigcap \nolimits ^\infty _{n=1}X_n\) is nonempty.
such that \(X_{n+1}\subset X_n\) for \(n=1,2,\ldots \) and if \(\lim \nolimits _{n\rightarrow \infty } \mu (X_n)=0\), then the intersection \(X_\infty :=\bigcap \nolimits ^\infty _{n=1}X_n\) is nonempty.
In the sequel we will use measures of noncompactness having some additional properties. Namely, a measure \(\mu \) is said to be sublinear if it satisfies the following two conditions:
- \(6^{\circ }\):
-
\(\mu (\lambda X) = |\lambda |\mu (X),\quad \lambda \in {\mathbb {R}}.\)
- \(7^{\circ }\):
-
\(\mu (X+Y)\le \mu (X)+\mu (Y).\)
A sublinear measure of noncompactness \(\mu \) satisfying the condition (maximum property)
- \(8^{\circ }\):
-
\(\mu (X \cup Y) = \max \{\mu (X), \mu (Y)\} \)
and such that  is said to be regular.
is said to be regular.
For a given nonempty bounded subset X of E we denote by \(\beta _E(X)\) the so-called Hausdorff measure of noncompactness of X. This quantity is defined by the formula
The function \(\beta _E\) is an example of the regular measure of noncompactness in E.
Let J denote the interval, bounded \(J=[0,T]\) or unbounded \(J={\mathbb R}_+:=[0,\infty )\). We use the following notation which will be needed further on: if \(J=[0,T]\), then we put \(J^+:=[0,T)\) and \(J^-:=(0,T]\), but if we take \(J={\mathbb R}_+\), then \(J^+:=[0,\infty )\) and \(J^-:=(0,\infty )\).
Now we recall some facts concerning regulated functions.
Definition 2.2
A function \(x:J\rightarrow E\), where E is a topological vector space, is said to be a regulated function if for every \(t\in J^+\) the right-sided limit \(x(t^+) := \lim \nolimits _{s\rightarrow t^+}x(s)\) exists and for every \(t \in J^-\) the left-sided limit \(x(t^-) := \lim \nolimits _{s\rightarrow t^-}x(s) \) exists.
From now on, E denotes a real Banach space.
Denote by G(J, E) the space consisting of all regulated functions defined on the interval J with values in a Banach space E. Obviously, G(J, E) is a linear space.
In the case of \(J=[0,T]\), every function \(x \in G([0,T],E)\) is bounded. Hence, G([0, T], E) can be equipped with the classical supremum norm \(\Vert x\Vert _T := \sup \{\Vert x(t)\Vert : t \in J\}\). It is easy to show that G([0, T], E) is a Banach space.
Compactness criteria and measures of noncompactness in the space G([0, T], E) were investigated in several research papers (see [4,5,6, 11]). First, we recall the concept of a equiregulated subset of the space G([0, T], E).
Definition 2.3
We will say that the set \(X \subset G([0,T],E)\) is equiregulated on the interval \(J=[0,T]\) if the following two conditions are satisfied:
Let us recall the compactness criterion in G([0, T], E). This result was formulated by Fraňková [11], (see also [4,5,6]).
Theorem 2.4
A nonempty subset \(X\subset G([0,T],E)\) is relatively compact in G([0, T], E) if and only if X is equiregulated on the interval [0, T] and the sets X(t) are relatively compact in E for \(t\in [0,T]\).
Now we are going to recall the construction of regular measure of noncompactness in the space G([0, T], E). To this end, let us take a set  . For \(x\in X\) and \(\varepsilon > 0\) let us denote the following quantities:
. For \(x\in X\) and \(\varepsilon > 0\) let us denote the following quantities:
The quantities \(\omega ^-(x,t, \varepsilon )\) and \(\omega ^+(x,t, \varepsilon )\) can be interpreted as left-hand and right-hand sided moduli of convergence of the function x at the point t. Further, let us put:
Finally, let us define quantity
Theorem 2.5
[14] The function \(\mu _T\) given by formula (1) satisfies conditions \(1^{\circ }\)–\(7^{\circ }\) in the space G([0, T], E).
Further, we define the space mentioned in the title of this paper. Denote by \(BG({\mathbb R}_+,E)\) the space consisting of all bounded and regulated functions defined on the interval \({\mathbb R}_+\) with values in a Banach space E, equipped with the norm \(\Vert x\Vert _\infty := \sup \{\Vert x(t)\Vert : t \in {\mathbb R}_+\}\). It is easy to show that \(BG({\mathbb R}_+,E)\) is a Banach space. In the next section we are going to introduce a simple criterion of compactness in \(BG({\mathbb R}_+,E)\) and a few measures of noncompactness in this space.
3 Measures of noncompactness in \(BG({\mathbb R}_+,E)\)
For fixed \(x\in BG({\mathbb R}_+,E)\) and \(T>0\) we put
Further, we give the following compactness criterion based on ideas from [16].
Theorem 3.1
Let E be a real Banach space. Then a nonempty subset \(X\subset BG({\mathbb R}_+,E)\) is relatively compact iff the following three conditions are satisfied:
-
(a)
The set X(t) is relatively compact in E for each \(t\in {\mathbb R}_+\).
-
(b)
For each \(T>0\) the set \(X|_{[0,T]}\) is equiregulated.
-
(c)
For each \(\varepsilon >0\) there are \(\delta >0\) and \(T>0\) such that, for any \(x_1, x_2\in X\), if \(\Vert x_1-x_2\Vert _T < \delta \) then \(\Vert x_1-x_2\Vert _\infty < \varepsilon \).
Proof
\((\Rightarrow )\) In view of the fact that X is a totally bounded set, we obtain that the sets X(t) for arbitrary \(t\in {\mathbb R}_+\) and \(X|_{[0,T]}\) for arbitrary \(T>0\) have this property as well. Therefore, we obtain (a) and, in virtue of Theorem, 2.4 we have (b). Let us assume that (c) is not fulfilled. Then, there exist \(\varepsilon _0>0\) and two sequences \(\{x_n\}, \{y_n\} \subset X\) such that
and
Relative compactness of the set X implies the existence of convergent subsequences \(\{x_{k_n}\}\), \(\{y_{k_n}\}\) of the sequences \(\{x_n\}\) and \(\{y_n\}\), i.e. \(x_{k_n} \rightarrow x \in BG({\mathbb R}_+,E)\) and \(y_{k_n} \rightarrow y\in BG({\mathbb R}_+,E)\). However, we obtain a contradiction. Namely, taking \(n\rightarrow \infty \) we obtain from (2) inequality \(\Vert x-y\Vert _{\infty } \ge \varepsilon _0\). On the other hand, in view of (3) we get \(\Vert x-y\Vert _{\infty }=0.\)
\((\Leftarrow )\) Let us consider an arbitrary sequence \(\{x_n\} \subset X\). Conditions (a) and (b) connected with Theorem 2.4 imply that the sequence \(\{x_n\}\) has a subsequence \(\{x_{1,n}\}\) converging on [0, 1] with respect to the pseudonorm \(\Vert \cdot \Vert _1\) to some regulated function defined on [0, 1]. Similarly, the sequence \(\{x_{1,n}\}\) has a subsequence \(\{x_{2,n}\}\) converging on [0, 2] with respect to the pseudonorm \(\Vert \cdot \Vert _2\) to some regulated function defined on [0, 2]. Therefore, we obtain the sequence of subsequences \(\{x_{i,n}\},\ i=1,2,\ldots \) converging on the interval [0, i] with respect to the pseudonorm \(\Vert \cdot \Vert _i\) to some regulated function defined on \({\mathbb R}_+\). Next, putting \(z_n:=x_{n,n},\ n=1,2,\ldots \) we obtain the sequence \(\{z_n\}\), uniformly convergent on bounded intervals to some regulated function \(z:{\mathbb R}_+ \rightarrow E\). Let us fix \(\varepsilon >0\). Further, if \(T>0\) and \(\delta >0\) are like in (c), then for sufficiently big n we have \(\Vert z-z_n\Vert _T \le \delta \) and in virtue of (c) we obtain \(\Vert z-z_n\Vert _\infty \le \varepsilon \) for sufficiently big n. This yields that \(z\in BG({\mathbb R}_+,E)\) and \(z_n\rightarrow z\) with respect to the norm \(\Vert \cdot \Vert _\infty \) which implies relative compactness of the set X in \(BG({\mathbb R}_+,E)\). \(\square \)
Using this theorem we introduce the first measure of noncompactness in the space \(BG({\mathbb R}_+,E)\). For this purpose we define several symbols. For a given set  and \({\delta }>0\) let us denote
and \({\delta }>0\) let us denote
Using the above quantities we define the mapping  given by the formula
given by the formula
Remark 3.2
In the definition of the quantity \(\varphi ^T(X,\delta )\) in the formula (4) the convex hull \(conv X\) appears. It is caused by the fact that without it the function \(\mu \) would not fulfil the condition \(3^\circ \) of Definition 2.1. This condition, in turn, is necessary to use many fixed point theorems.
The main properties of the function \(\mu \) are contained in the below given theorem.
Theorem 3.3
The function  given by the formula (5) satisfies the conditions \(2^\circ , 3^\circ , 5^\circ , 6^\circ \) and the equality \(\mathrm{ker} \mu = \mathfrak {N}_{BG({\mathbb R}_+,E)}\) holds.
given by the formula (5) satisfies the conditions \(2^\circ , 3^\circ , 5^\circ , 6^\circ \) and the equality \(\mathrm{ker} \mu = \mathfrak {N}_{BG({\mathbb R}_+,E)}\) holds.
Proof
The equality \(\mathrm{ker} \mu = \mathfrak {N}_{BG({\mathbb R}_+,E)}\) is a simple consequence of Theorem 3.1.
We gather several facts concerning the function \(\varphi ^{\infty }_0\). First, let us notice that the properties
are obvious.
Now we will show that
Let us fix \(X\in \mathfrak {M}_{BG({\mathbb R}_+,E)}, T>0, \delta >0\) and take \(x,y\in conv \overline{X}\) such that \(\Vert x-y\Vert _T <\delta \). Then there exist \(\{x_n\},\{y_n\}\subset conv X\) such that \(x_n\rightarrow x\), \(y_n\rightarrow y\). This means that for arbitrary \({\varepsilon }>0\) there exists \(n_0\in {\mathbb N}\) such that for each \(n\ge n_0\) we have
Hence
Since \(x_n-y_n\rightarrow x-y\), then we may choose sufficiently big \(n\in {\mathbb N}\) such that \(\Vert x_n-y_n\Vert _{T}<{\delta }\). Therefore, in virtue of inequality (10) we obtain
and hence
Letting \({\delta }\rightarrow 0\) and \(T\rightarrow \infty \) we obtain (in view of arbitrariness of \({\varepsilon }\))
which together with (6) confirms (9). Further, the property (7) in connection with (9) give us
Keeping in mind Theorem 2.5 we have that the mapping \(\mu _T\) given by the formula (1) satisfies conditions \(1^\circ \)–\(7^\circ \). Hence, to obtain the properties \(2^\circ \), \(6^\circ \), \(3^\circ \) for the measure \(\mu \), it is sufficient to join (6), (8), (11) to the conditions \(2^\circ \), \(6^\circ \), \(3^\circ \) for the measure \(\mu _T\) and to take limit \(T\rightarrow \infty \).
Further, the property \(5^\circ \) will be proved. Let us assume that \(\{X_n\}\) is a decreasing sequence of closed and bounded subsets of the space \(BG({\mathbb R}_+,E)\) and \(\lim \nolimits _{n\rightarrow \infty }\mu (X_n)=0\). Let us take arbitrarily \(x_n \in X_n\). In particular, it follows that \(\lim \nolimits _{n\rightarrow \infty } \mu _T(\{x_i:i\ge n\})=0\) for each \(T>0\). Since the measure \(\mu _T\) satisfies the condition \(5^\circ \) in the space G([0, T], E), putting \(T=1,2,\ldots \) and applying the diagonal method we ensure the existence of subsequence \(\{u_n\}\) of the sequence \(\{x_n\}\), which is uniformly convergent on bounded intervals to the function \(u \in BG({\mathbb R}_+,E)\). In view of \(\lim \nolimits _{n\rightarrow \infty } \varphi _0^{\infty }(\{u_i:i\ge n\})=0\) we conclude that \(\{u_n\}\) is also convergent in the norm \(\Vert \cdot \Vert _\infty \) to u. This means that
\(\square \)
In what follows we provide two examples illustrating that the mapping \(\mu \) does not fulfil the conditions \(4^\circ , 7^\circ \) and \(8^\circ \).
Example 3.4
Let us fix arbitrarily \(e\in E, \Vert e\Vert =1\) and put \(\lambda := \frac{1}{2}\),
Then we get
Let us notice that if \(T>1, \alpha _i\ge 0, i=1,\ldots ,N, \gamma _j \ge 0, j=1,\ldots ,M, \sum \nolimits _{i=1}^N \alpha _i=1 \) and \(\sum \nolimits _{j=1}^M \gamma _j=1\), then
Thus, if \(\Vert x-y\Vert _T<\delta \) for some \(x,y \in \mathrm{conv}X\), then \(\Vert x-y\Vert _\infty <\delta \) and finally \(\varphi ^{\infty }_0(X)=0\). Reasoning similarly, we infer that \(\varphi ^{\infty }_0(Y)=0\). Now, combining it with (12) and (13) we obtain
Further, we have
Moreover,
Hence, we obtain \(\mu (\frac{1}{2}X+\frac{1}{2}Y)\ge 2\) which together with (14) proves that the property \(4^\circ \) is not fulfilled for \(\lambda = \frac{1}{2}\) .
The above mentioned sets X and Y show that the property \(7^\circ \) does not hold either.
Now, let us consider the set \(X\cup Y\). We have
The above properties yields \(\mu (X\cup Y) \ge 2\) which together with (14) gives a contradiction to \(8^\circ \).
Open question
It is not known if the measure \(\mu \) satisfies the weak maximum property. In other words, whether the condition
holds for \(X\in \mathfrak {M}_{BG({\mathbb R}_+,E)},\ x\in E\)?
Remark 3.5
Although the mapping \(\mu \) given by the formula (5) does not fulfil some conditions from Definition 2.1, the conditions which are satisfied are sufficient to apply basic fixed point theorems (i.e. Darbo, Sadovskii). Moreover, the fact \(\mathrm{ker} \mu = \mathfrak {N}_{BG({\mathbb R}_+,E)}\) is undoubtedly an advantage of the function \(\mu \). Indeed, this means that \(\mu \) “catches” every relative compact subset of \(BG({\mathbb R}_+,E)\).
The below given result presents a relationship between the function \(\mu \) and the Hausdorff measure of noncompactness in \(BG({\mathbb R}_+,E)\). As it turns out, in spite of having identical kernels, they are not equivalent.
Theorem 3.6
For each nonempty and bounded set \(X\subset BG({\mathbb R}_+,E)\) we have the inequality
The above estimation is optimal (see Example 3.7).
However, there does not exist a constant \(k>0\) such that
for bounded \(X\subset BG({\mathbb R}_+,E)\).
Proof
Let us denote \(R:=\beta _{BG({\mathbb R}_+,E)}(X)\) and fix \(\varepsilon > 0\). Then there exists a cover \(X \subset \cup _{i=1}^n B_{BG({\mathbb R}_+,E)}(a_i, R+\varepsilon )\), where \(a_i\in BG({\mathbb R}_+,E)\).
Since \(X(t) \subset \cup _{i=1}^n B_{BG({\mathbb R}_+,E)}(a_i(t), R+\varepsilon )\), we obtain
Further, we will show that
Let us fix \(t\in {\mathbb R}_+\). Since \(\{a_i:i=1,\ldots ,n\}\) is a compact set, Theorem 2.4 yields that there exists \(\delta >0\) such that
Let us take \(x\in X\). There exists i such that \(x\in B_{BG({\mathbb R}_+,E)}(a_i, R+\varepsilon )\). Using these considerations we have
which confirms (16). Similarly, we can show that \(\omega _\infty ^-(X) \le 2R+3\varepsilon \), hence we obtain
In the sequel we show that
Since \(\beta _{BG({\mathbb R}_+,E)}(\mathrm{conv} X) = \beta _{BG({\mathbb R}_+,E)}(X)\) there exist vectors \(b_1,\ldots ,b_m \in BG({\mathbb R}_+,E)\) such that
Let us denote the left side of the inequality (18) by g. Hence, there exist sequences \(\{x_n\}, \{y_n\} \subset \mathrm{conv} X\) such that
and
We may further choose an increasing subsequence of natural numbers \(\{k_n\}\) such that there exist indexes i and j which give us
We will show that
Suppose, on the contrary, that \(\Vert b_i - b_j\Vert _\infty > 2R + 3\varepsilon \). Then, for some \(t\in {\mathbb R}_+\) we would have
Thus
In connection with (20) we have (for \(n\in {\mathbb {N}}\) such that \(k_n \ge t\))
which under \(n\rightarrow \infty \) is a contradiction and confirms (22). Combining (21) and (22) we conclude that
Letting \(n\rightarrow \infty \) and applying (19) we have (18).
Summing the inequalities (15), (17) and (18), in view of arbitrariness of \(\varepsilon >0\) we obtain the first part of thesis.
For further purposes let us assume that there exists \(k>0\) such that
Without loss of generality we may assume that \(k\le 1\). Let us fix arbitrarily \(e\in E\), \(\Vert e\Vert =1\) and put
Hence
Let us notice that if \(T>1, \alpha _i\ge 0, i=1,\ldots ,N, \gamma _j \ge 0, j=1,\ldots ,M, \sum \nolimits _{i=1}^N \alpha _i=1 \) and \(\sum \nolimits _{j=1}^M \gamma _j=1\), then
Thus, if \(\Vert x-y\Vert _T<\delta \) for \(x,y \in \mathrm{conv}X\), then \(\Vert x-y\Vert _\infty <\frac{3}{k}\delta \) and this implies \(\varphi ^{\infty }_0(X)=0\). Combining this fact with (24) we get \(\mu (X)=\frac{k}{3}\). Hence, in virtue of (23) and (24) we have \(\frac{k}{2} \le \frac{k}{3}\), which yields a contradiction. \(\square \)
Now, we show that upper estimation from Theorem 3.6 is attained.
Example 3.7
Let \(e\in E\) is such that \(\Vert e\Vert =1\) and let us denote by \({\widehat{e}}\) the function \({\widehat{e}} : {\mathbb R}_+ \rightarrow E\) given by the formula \({\widehat{e}}(t) := e, \ t\in {\mathbb R}_+\). Next, let us put
Then we get \(\beta _{BG({\mathbb R}_+,E)}(X) = 1,\ \max \{\omega _\infty ^-(X), \omega _\infty ^+(X) \}=2,\ \sup \nolimits _{t\in {\mathbb R}_+} \beta _E(X(t)) = 1.\)
Further, for arbitrarily fixed \(T>0\) we define two functions of a real variable \(t\in {\mathbb R}_+\), i.e.
Since \(x,y \in X, \Vert x-y\Vert _T=0, \Vert x-y\Vert _\infty = 4\), we get
and then \(\mu (X) = 7.\) \(\square \)
Inspired by some measures in the space \(BC({\mathbb R}_+,E)\) of bounded and continuous functions (see
[3]), we will introduce several new measures of noncompactness in \(BG({\mathbb R}_+,E)\). For this purpose we will define a few new set functions. Let us take arbitrarily  . So, for a fixed \(T>0\) let us define
. So, for a fixed \(T>0\) let us define
Next, notice that there exists the limit
Moreover we put
where
and we can also define
where diam X(t) is understood as
And now let us consider the functions \(\gamma _a\), \(\gamma _b\), \(\gamma _c\) defined on the family \(\mathfrak {M}_{BG({\mathbb {R}}_+, E)}\) as follows
The main properties of the above mentioned mappings are contained in the below given theorem.
Theorem 3.8
The mappings \(\gamma _a, \gamma _b, \gamma _c\) satisfy axioms \(1^\circ - 7^\circ \) of Definition 2.1.
Proof
First, let us assume that \(\gamma (X)=0\), where  and \(\gamma \) is one of the measures \(\gamma _a, \gamma _b, \gamma _c\). Since equalities \(\max \{\omega _\infty ^-(X), \omega _\infty ^+(X) \} = 0\) and \({{\overline{\beta }}}_{\infty }(X)=0\) are equivalent to conditions (a) and (b) from Theorem 3.1 respectively and each of the conditions \(a_\infty (X)=0,\ b_\infty (X)=0,\) \(c(X)=0\) implies (c) from Theorem 3.1, we have
and \(\gamma \) is one of the measures \(\gamma _a, \gamma _b, \gamma _c\). Since equalities \(\max \{\omega _\infty ^-(X), \omega _\infty ^+(X) \} = 0\) and \({{\overline{\beta }}}_{\infty }(X)=0\) are equivalent to conditions (a) and (b) from Theorem 3.1 respectively and each of the conditions \(a_\infty (X)=0,\ b_\infty (X)=0,\) \(c(X)=0\) implies (c) from Theorem 3.1, we have  . Moreover, let us notice that each of the functions \(a_\infty , b_\infty \) and c satisfies axioms \(2^\circ - 7^\circ \). The proof of this fact is simple and will be omitted. Since, in view of Theorem 2.5 the component \(\mu _T = \max \{\omega _T^-, \omega _T^+ \} + {\overline{\beta }}_T\) satisfies axioms \(2^\circ - 7^\circ \), it is sufficient to add the appropriate conditions for components \(a_\infty , b_\infty , c\) and to take limit \(T\rightarrow \infty \).
. Moreover, let us notice that each of the functions \(a_\infty , b_\infty \) and c satisfies axioms \(2^\circ - 7^\circ \). The proof of this fact is simple and will be omitted. Since, in view of Theorem 2.5 the component \(\mu _T = \max \{\omega _T^-, \omega _T^+ \} + {\overline{\beta }}_T\) satisfies axioms \(2^\circ - 7^\circ \), it is sufficient to add the appropriate conditions for components \(a_\infty , b_\infty , c\) and to take limit \(T\rightarrow \infty \).
Now, we prove \(5^\circ \). Let us assume that \(\{X_n\}\) is a decreasing sequence of closed and bounded subsets of the space \(BG({\mathbb R}_+,E)\) and \(\lim \nolimits _{n\rightarrow \infty }\gamma (X_n)=0\), where \(\gamma \) is one of the measures \(\gamma _a, \gamma _b, \gamma _c\). Let us take arbitrarily \(x_n \in X_n\). Reasoning similarly as in the proof of Theorem 3.3, we can state that the sequence \(\{x_n\}\) contains subsequence which is convergent in the norm \(\Vert \cdot \Vert _\infty \) to some element \(u\in BG({\mathbb R}_+,E)\), and it implies that \(u\in \bigcap \nolimits ^\infty _{n=1}X_n \ne \emptyset .\) \(\square \)
Remark 3.9
The above mentioned measures \(\gamma _a, \gamma _b, \gamma _c\) satisfy several additional conditions (for example \(4^\circ , 7^\circ \)) that are not fulfilled by the measure \(\mu \). However, the measure \(\mu \) “catches” relative compact subsets in a better way than \(\gamma _a, \gamma _b\) and \(\gamma _c\), namely  . We omit the simple examples showing that there is no equality.
. We omit the simple examples showing that there is no equality.
The mutual relations between these five measures \(\beta _{BG({\mathbb R}_+,E)}, \mu , \gamma _a, \gamma _b\) and \(\gamma _c\) are presented in the following theorem.
Theorem 3.10
For arbitrary  the following inequalities are satisfied
the following inequalities are satisfied
Proof
To obtain the inequalities (34), it is sufficient to show that \(\varphi ^{\infty }_0(X)\le 2a_{\infty }(X),\) \(\varphi ^{\infty }_0(X)\le 2b_{\infty }(X)\) and \(\varphi ^{\infty }_0(X)\le c(X).\) As an example we will prove only the second inequality. Namely, let us fix arbitrarily \(\varepsilon >0\) and let \(T>0\) be such that \(b_T(X)\le b_\infty (X)+\varepsilon \). Next, let \(x,y\in conv X\) and \(\Vert x-y\Vert _T \le \varepsilon \). Then we obtain
since \(b_T(conv X) = b_T(X)\). Hence \(\varphi ^T(X,\varepsilon ) \le 4\varepsilon + 2b_\infty (X)\). Letting \(\varepsilon \rightarrow 0\) and \(T\rightarrow \infty \) we derive \(\varphi ^{\infty }_0(X)\le 2b_{\infty }(X)\).
It is sufficient to show that \(b_{\infty }(X)\le 2a_{\infty }(X), c(X)\le 2a_{\infty }(X)\) to obtain the inequalities (35). We omit the simple calculations. \(\square \)
Now, let us fix \(\varepsilon >0\) and choose \(T>0\) such that
It has been shown (see [14]) that \(\beta _{G([0,T],E)}(X|_{[0,T]}) \le \mu _T(X|_{[0,T]})\). Thus there exist functions \(u_1,\ldots ,u_n\in G([0,T],E)\) such that
Now, let \(u_i^a\) be a function belonging to the space \(BG({\mathbb R}_+,E)\) formed by the function \(u_i\) by extension on the interval \((T,\infty )\) using vector \(\theta \). Then the functions \(\{u_i^a:i=1,\ldots ,n\}\) form \(\mu _T(X)+a_\infty (X)+2\varepsilon \)-net of the set X in the space \(BG({\mathbb R}_+,E)\). Indeed, let us fix arbitrarily \(x\in X\) and let i be such that
Then, for \(t>T\) we get
Combining this fact with (38) we obtain \(\Vert x-u_i^a\Vert _\infty \le \mu _T(X|_{[0,T]})+a_\infty (X)+2\varepsilon \), and hence \(\beta _{BG({\mathbb R}_+,E)}(X) \le \mu _T(X|_{[0,T]})+a_\infty (X)+2\varepsilon \). Letting \(T\rightarrow \infty \) and \(\varepsilon \rightarrow 0\) we get the first of inequalities (36).
Now, we prove the second of the inequalities (36). Let us extend each function \(u_i\) on the interval \((T,\infty )\) using vector \(u_i(T)\). We denote such a function by \(u_i^b,\) \(i=1,\ldots ,n\). We show that \(\{u_i^b: i=1,\ldots ,n\}\) forms \(\mu _T(X|_{[0,T]})+b_\infty (X)+2\varepsilon \)-net of the set X in the space \(BG({\mathbb R}_+,E)\). To do this let us take an arbitrary \(x\in X\) and let i be such that (38) holds. Since \(u_i^b(t)=u_i(T)\) for \(t>T\), we get
for \(t>T\). Hence \(\beta _{BG({\mathbb R}_+,E)}(X) \le \mu _T(X|_{[0,T]})+b_\infty (X)+2\varepsilon \) and letting \(T\rightarrow \infty \) and \(\varepsilon \rightarrow 0\) we obtain \(\beta _{BG({\mathbb R}_+,E)}(X) \le \gamma _b(X)\). We omit similar proof of the last inequality from (36). \(\square \)
Remark 3.11
Below is given an example showing that the estimations from Theorem 3.10 are optimal. Moreover, let us notice that it is not possible to majorize any of the measures \(\gamma _a, \gamma _b, \gamma _c\) by \(\beta _{BG({\mathbb R}_+,E)}\) or \(\mu \). The lack of such an estimation is a consequence of the sharp inclusions  .
.
Example 3.12
Let us put \(E:= {\mathbb R}\). We define two sets \(X, Y \subset BG({\mathbb R}_+,{\mathbb R})\) as follows
It is not difficult to show that
Now let \(\dim E = \infty \) and we put
We can easily show that
Applying (39), (40) and (41) we obtain
4 Superposition operator in \(BG({\mathbb R}_+,E)\)
The properties of the superposition operator in the space G([0, T], E) of regulated functions on bounded interval have been studied by several authors (for instance [2, 5,6,7, 13, 15]). However, there are not any results concerning this operator acting in the space of regulated functions on unbounded interval. The results obtained in this section fill the gap. Let us consider a function \(f: {\mathbb R}_+\times E \rightarrow E\). Then, for every function \(x: {\mathbb R}_+ \rightarrow E\), we can define the function \((F_fx)(t) := f(t, x(t)), \ t \in {\mathbb R}_+\). Operator \(F_f\) defined in such a way is called the superposition (or Nemytskii) operator generated by the function f (see [1]).
In connection with the space \(BG({\mathbb R}_+,E)\), the natural question appears: what properties must the function f satisfy so that operator \(F_f\) maps the space \(BG({\mathbb R}_+,E)\) into itself?
A further part of this section is based on the concepts contained in the paper [15]. Inspired by the result obtained in the paper [13], concerning the space G([0, T], E), we have the following theorem.
Theorem 4.1
The superposition operator \(F_f\) maps \(BG({\mathbb R}_+,E)\) into itself if and only if the function f has the following properties:
-
(a)
the limit \(\lim \nolimits _{[0,t)\times E \ni (s,v)\rightarrow (t,x) }f(s,v)\) exists for every \((t,x)\in (0,\infty )\times E,\)
-
(b)
the limit \(\lim \nolimits _{(t,\infty )\times E \ni (s,v)\rightarrow (t,x) }f(s,v)\) exists for every \((t,x)\in {\mathbb R}_+\times E,\)
-
(c)
\(\forall _{r>0} \ \limsup \nolimits _{t\rightarrow \infty } \Vert f(t,B_E(r)) \Vert < \infty .\)
Proof
As it has been shown in [13], the conditions (a) and (b) are equivalent to the fact that for each regulated function \(x:{\mathbb R}_+\rightarrow E\) (unnecessarily bounded) the function \(F_fx\) is regulated on \({\mathbb R}_+\), but unnecessarily bounded. If the operator \(F_f\) maps \(BG({\mathbb R}_+,E)\) into itself, then the condition (c) has to be satisfied, since in the opposite case the function \(x\in BG({\mathbb R}_+,E)\) such that \(F_fx\notin BG({\mathbb R}_+,E)\) could be constructed. Conversely, if the conditions (a)-(c) hold, then for \(x\in BG({\mathbb R}_+,E)\) the function \(F_fx\) is regulated on \({\mathbb R}_+\) and consequently bounded on bounded intervals. Using this fact together with (c) we infer that \(F_fx\) is bounded on \({\mathbb R}_+\). \(\square \)
Using the notation
the condition (b) from Theorem 4.1 can be described as follows
Similarly, we can describe the condition (a) of Theorem 4.1—we omit the details.
Let us denote by \(E^E\) the linear space consisted of all, not necessarily continuous functions \(h:E \rightarrow E\). In this space we introduce uniform compact convergence, i.e. for a given family \(\{h_s\}_{s\in {\mathbb R}_+} \subset E^E\), the uniform compact convergence \(\{h_s\}\) to \(h\in E^E\) with \(s\rightarrow t\in {\mathbb R}_+\) means uniform convergence \(h_s\) to h on all compact subsets in E when \(s\rightarrow t\).
Furthermore, for a fixed function \(f:{\mathbb R}_+\times E \rightarrow E\) and for each \(t\in {\mathbb R}_+\) we shall denote
Hence, we have \(\overline{f}_t \in E^E\) for \(t\in {\mathbb R}_+\).
Now we can formulate a theorem that gives (in terms of the function \(\overline{f}_t\)) necessary conditions for any Banach space E and the sufficient ones, when \(\dim E <\infty \) such that the superposition operator \(F_f\) maps \(BG({\mathbb R}_+,E)\) into itself.
Theorem 4.2
Let the superposition operator \(F_f\) maps \(BG({\mathbb R}_+,E)\) into itself, where E is a Banach space. Then the family of functions \(\{\overline{f}_t\}_{t\in {\mathbb R}_+}\subset E^E\) satisfies the following conditions:
-
(a)
The mapping \({\mathbb R}_+\ni t \mapsto \overline{f}_t \in E^E\) is a regulated function.
-
(b)
The following limits of pointwise convergence exist and
-
(b1)
\(\lim \nolimits _{s\rightarrow t^+} \overline{f}_s\) is continuous in E for \(t\in {\mathbb R}_+\),
-
(b2)
\(\lim \nolimits _{s\rightarrow t^-} \overline{f}_s\) is continuous in E for \(t\in (0,\infty )\),
-
(b1)
-
(c)
\(\forall _{r>0} \ \limsup \nolimits _{t\rightarrow \infty } \Vert \overline{f}_t(B_E(r)) \Vert < \infty .\)
Conversely, if additionally E is a finitely dimensional Banach space and conditions (a), (b) and (c) are satisfied, then the superposition operator \(F_f\) maps \(BG({\mathbb R}_+,E)\) into itself.
Proof
(\(\Rightarrow \)) Let us fix \(t\in {\mathbb R}_+\). Using condition (b) of Theorem 4.1 and based on notation (42) we have the following equality
In the sequel we will prove (b1). To do this, let us take an arbitrary \(x\in E\) and \(\varepsilon >0\). Keeping in mind (43) we infer that there are \(\delta >0\) and \(\tau > 0\) such that
Now, letting \(s\rightarrow t^+\) we have \(\Vert g_t(x) - g_t(v)\Vert \le \varepsilon \) which proves continuity of \(g_t\) in x and thereby on E. Reasoning similarly, we can prove (b2).
Now, we will prove (a), i.e. that \(\overline{f}_s\) tends to \(g_t\) in the compact convergence topology on E when \(s\rightarrow t^+\). Let us fix a non-empty and compact set \(K\subset E\) and \(\varepsilon >0\). Then, in view of (43) and already proven continuity of \(g_t\), we have that for each \(x\in K\) there exist \(\delta _x>0,\ \tau _x>0\) such that concurrently
and
From the family \(\{B_E(x,\delta _x)\}_{x\in K}\) covering compact set K we choose a finite subcover \(\{B_E(x_i,\delta _{x_i})\}_{i=1}^n\). Let us denote \({\overline{\tau }}:= \min \{\tau _{x_i}: i=1,\ldots ,n\}\) and fix arbitrary \(v\in K\). Then there exists i such that \(v\in B_E(x_i, \delta _{x_i})\). Hence, for \(s\in (t, t+{\overline{\tau }})\) taking into account (44) and (45) we infer that the following estimation
holds for any \(v\in K\). In other words, we have uniformly convergence on K. Similarly, we can prove the existence of the limit \(\lim \nolimits _{s\rightarrow t^-} \overline{f}_s\) in the topology of compact convergence.
The condition (c) is a consequence of the Theorem 4.1. Indeed, the condition (c) from Theorem 4.2 is equivalent to (c) from Theorem 4.1.
(\(\Leftarrow \)) Let us assume that \(\dim E<\infty \) and fix \(t\in {\mathbb R}_+\). Condition (a) implies the existence of the limit \(g_t:= \lim \nolimits _{s\rightarrow t^+} \overline{f}_s\) which, based on (b) is continuous on E. Let us fix \(x\in E\) and \(\varepsilon >0\). Continuity of \(g_t\) means that for some \(r>0\) we get
Moreover, (a) implies that for a given compact set \({B}_E(x,r)\) there is a number \(\tau > 0\) such that
Combining it with (46), for \(v \in B_E(x,r),\ s\in (t, t+\tau )\) we derive the following estimate
i.e. condition (43) is satisfied and thereby (b) in Theorem 4.1 holds. Similarly, we can prove (a) in Theorem 4.1, so actually \(F_f\) maps \(BG({\mathbb R}_+,E)\) into \(BG({\mathbb R}_+,E)\). \(\square \)
Corollary 4.3
If a Banach space E is finitely dimensional then the superposition operator \(F_f\) maps \(BG({\mathbb R}_+,E)\) into \(BG({\mathbb R}_+,E)\) if and only if three conditions (a), (b) and (c) in Theorem 4.2 are satisfied.
Now, we give the compactness criterion for the superposition operator \(F_f\).
Theorem 4.4
Let \(f:{\mathbb R}\times E \rightarrow E\). Assume that E is a separable Banach space and the superposition operator \(F_f:BG({\mathbb R}_+,E)\rightarrow BG({\mathbb R}_+,E)\) is continuous and compact (i.e. \(F_f\) transforms bounded sets in relatively compact sets). Then
-
(H1)
there exists a function \(g \in BG({\mathbb R}_+,E)\),
-
(H2)
there exists a sequence \(\{t_n\}\subset {\mathbb R}_+\),
-
(H3)
there exist functions \(h_n:E\rightarrow E, n=1,2,\ldots \) that are continuous, compact and
$$\begin{aligned} \forall _{r>0}\ \ \lim \limits _{n\rightarrow \infty }\Vert h_n(B_E(r))\Vert = 0 \end{aligned}$$(47)
such that
Conversely, if the conditions (H1)–(H3) are satisfied and E is a Banach space then the formula (48) gives such a function f(t, x), that operator \(F_f:BG({\mathbb R}_+,E)\rightarrow BG({\mathbb R}_+,E)\) and it is continuous and compact.
Remark 4.5
Obviously the case when all \(h_n\) functions in the previous theorem are equal to \(\theta \), that is when \(f(t,x) = g(t)\), or only a finite number of them is not equal to \(\theta \) is also allowed.
The proof of Theorem 4.4 will be preceded by two lemmas. However, in order to make our considerations more transparent, we will give a useful notation. For fixed \(x \in BG({\mathbb R}_+,E)\) we will put
In contrast to standard definition of a support we do not require the closure.
Lemma 4.6
If E is a Banach space and \(F_f:BG({\mathbb R}_+,E)\rightarrow BG({\mathbb R}_+,E)\) is compact, then for each \(x,y \in BG({\mathbb R}_+,E)\) the set \(\mathrm{supp} (F_fx-F_fy)\) is at most countable and for each injective sequence \(\{t_n\}\subset {\mathbb R}_+\) we have
Proof
If the set \(\mathrm{supp} (F_fx-F_fy)\) was uncountable or if (49) was not satisfied, then there would exist an injective sequence \(\{s_n\} \subset {\mathbb R}_+\) and a number \(\varepsilon _0 > 0\) such that
Let us introduce the sequence of functions \(u_n:{\mathbb R}_+\rightarrow E,\ n=1,2,\ldots \) defined by the formula
Obviously \(u_n\in BG({\mathbb R}_+,E)\). For \(n\ne m\) we have
This means that the sequence \(\{F_fu_n\}\) is \(\varepsilon _0\)-separable, hence \(F_f\) is not compact, which ends the proof. \(\square \)
We remind that for arbitrary \(u\in E\), the symbol \(\widehat{u}\) denotes the function \(\widehat{u}:{\mathbb R}_+ \rightarrow E\) given by \(\widehat{u}(t)\equiv u, t\in {\mathbb R}_+\).
Lemma 4.7
If E is a separable Banach space and \(F_f:BG({\mathbb R}_+,E)\rightarrow BG({\mathbb R}_+,E)\) is compact and continuous, then there exists a sequence \(T=\{t_n\} \subset {\mathbb R}_+\) such that
Proof
Let \(A=\{a_n: n\in {\mathbb {N}}\}\subset E\) be a countable dense subset of E. Let us put \(T:= \cup _{n=1}^\infty \mathrm{supp} (F_f\widehat{a_n}-F_f\widehat{\theta })\). Keeping in mind Lemma 4.6 we conclude that the set T is countable or finite. If there existed \(x\in E\) such that (50) did not hold, then there would exist \(s\in {\mathbb R}_+\) such that \(s\in \mathrm{supp} (F_f\widehat{x}-F_f\widehat{\theta }) \setminus T\). Thus \(\Vert (F_f\widehat{x}-F_f\widehat{\theta })(s) \Vert = \varepsilon _0\) for some \(\varepsilon _0 >0\) and additionally \((F_f\widehat{a_n}-F_f\widehat{\theta })(s) = \theta \) for \(n\in {\mathbb {N}}\). If we took such a subsequence \(\{a_{k_n}\}\) that \(a_{k_n}\rightarrow x\) in E, we would have
which is in contradiction to the continuity of \(F_f\). \(\square \)
Proof of Theorem 4.4
\((\Rightarrow )\) First let us assume that E is a separable Banach space and \(F_f:BG({\mathbb R}_+,E)\rightarrow BG({\mathbb R}_+,E)\) is compact and continuous. Let \(T=\{t_n\}\) be the sequence such as in Lemma 4.7. We define the function \(g:{\mathbb R}_+\rightarrow E\) and the sequence of functions \(h_n:E\rightarrow E,\ n=1,2,\ldots \) by the following formulas
By Lemma 4.7, for each \(x\in E\) the mapping \({\mathbb R}_+\ni t \rightarrow f(t,x)-f(t,\theta )\) can be non-zero only on the set T and its formula is given by \(\sum \nolimits _{n=1}^\infty \mathbf{1}_{t_n}(t) h_n(x)\). Therefore
Since \(F_f\) is continuous, the functions \(h_n\) must be also continuous. Moreover, since \(F_f\) is compact, the functions \(h_n\) must also be compact. Further, in virtue of Lemma 4.6 we infer that \(\lim \nolimits _{n\rightarrow \infty } (f(t_n,x)-f(t_n,\theta )) = \theta \) for \(x\in E\), i.e.
We have only (47) left to be proved. Suppose the contrary. Then there would exist \(r>0\), a number \(\varepsilon _0 > 0\) and such a subsequence of the sequence \(\{h_n\}\), (also denoted by \(\{h_n\}\)), that
Let \(k_1=1\). We choose \(x_1 \in B_E(r)\) such that \(\Vert h_{k_1}(x_1)\Vert \ge \frac{\varepsilon _0}{2}\). In view of (52) we obtain that there exists \(k_2\in {\mathbb {N}}\) such that \(k_2 > k_1\) and \(\Vert h_i(x_1)\Vert \le \frac{\varepsilon _0}{4}\) for \(i \ge k_2\). Invoking (53) we conclude that there exists \(x_2 \in B_E(r)\) such that \(\Vert h_{k_2}(x_2)\Vert \ge \frac{\varepsilon _0}{2}\). Further, by (52) we know that there exists \(k_3\in {\mathbb {N}}\) such that \(k_3 > k_2\) and \(\Vert h_i(x_2)\Vert \le \frac{\varepsilon _0}{4}\) for \(i \ge k_3\). Continuing this reasoning we obtain a strictly increasing sequence \(\{k_n\} \subset {\mathbb {N}}\) and the sequence \(\{x_n\} \subset B_E(r)\) such that
Let \(n > m\). Then we have
i.e. \(\{F_f\widehat{x_n}\}\) is positively separated and \(F_f\) is not relatively compact which contradicts the assumptions.
\((\Leftarrow )\) Now, let us assume that the conditions (H1)-(H3) hold, E is a Banach space and the function f(t, x) is given by the formula (48). First, we are going to show that \(F_f:BG({\mathbb R}_+,E)\rightarrow BG({\mathbb R}_+,E)\). To do this, let us fix \(x\in BG({\mathbb R}_+,E),\ t\in {\mathbb R}_+\) and the sequence \(\{t'_j\}\) convergent to t from one side, e.g. \(t'_j \rightarrow t^+\). Since the sequence \(\{x(t'_j)\}\) is bounded, then using (47) we get \(\lim \nolimits _{j\rightarrow \infty } \sum \nolimits _{n=1}^\infty \mathbf{1}_{t_n}(t'_j) h_n(x(t'_j)) = \theta \) and in view of (48) we have \((F_fx)(t^+)= \lim \nolimits _{n\rightarrow \infty }(F_fx)(t'_n) = \lim \nolimits _{n\rightarrow \infty }g(t'_n) = g(t^+)\). Similarly we prove that \((F_fx)(t^-) = g(t^-)\) i.e. \(F_fx\) is regulated on \({\mathbb R}_+\). Moreover, in virtue of (H1) and (H3) \(F_fx\) is bounded and therefore \(F_fx \in BG({\mathbb R}_+,E)\).
In the next step we prove that the operator \(F_f\) is compact. Let us fix a bounded sequence \(\{x_n\} \subset B_{BG({\mathbb R}_+,E)}(r)\), where \(r>0\) is a number. Since the operator \(h_1\) is compact, we are able to choose such a subsequence \(\{x_{n,1}\}\) of a sequence \(\{x_{n}\}\) that the sequence \(\{h_1(x_{n,1}(t_1))\}\) is convergent. Further, the operator \(h_2\) is also compact so we are able to choose a subsequence \(\{x_{n,2}\}\) such that the sequence \(\{h_2(x_{n,2}(t_2))\}\) is convergent. Moreover, \(\{h_1(x_{n,2}(t_1))\}\) is also convergent. Continuing this procedure we have a sequence of sequences \(\{x_{n,i}\}_{n=1}^\infty , \ i=1,2,\ldots \) for which \(\{x_{n,i+1}\}_{n=1}^\infty \) is a subsequence of the sequence \(\{x_{n,i }\}_{n=1}^\infty \) and there exists a limit \(\lim \nolimits _{n\rightarrow \infty } h_j(x_{n,i}(t_j))\) for \(i=1,2,\ldots ,\) \(j=1,2,\ldots ,i\). Next, using a diagonal method we define the sequence \(\{y_n\}\) by \(y_n:=x_{n,n},\ n=1,2,\ldots \). Obviously \(\{y_n\}\) is a subsequence of \(\{x_n\}\). Moreover, the limit \(\lim \nolimits _{n\rightarrow \infty } h_i(y_n(t_i))\) exists for each \(i=1,2,\ldots \). This fact together with \((F_fy_n)(t) = g(t)\) for \(t\notin T\) implies that the limit \(\lim \nolimits _{n\rightarrow \infty } (F_fy_n)(t)\) exists for each \(t\in {\mathbb R}_+\). We are able now to introduce the function \(z:{\mathbb R}_+\rightarrow E\) defined by the formula \(z(t) := \lim \nolimits _{n\rightarrow \infty } (F_fy_n)(t)\), i.e.
Keeping in mind (47) we get
This implies that z is regulated on \({\mathbb R}_+\), Moreover, in view of (H1) and (H3) the function z belongs to the space \(BG({\mathbb R}_+,E)\). Using (48) we obtain
Let us fix \(\varepsilon >0\). In virtue of (47) we conclude that there exists \(m\in {\mathbb {N}}\) such that for \(i > m\) we have \(\Vert h_i(B_E(r))\Vert \le \varepsilon \) and therefore \(\sup \nolimits _{i>m}\Vert \lim \nolimits _{n\rightarrow \infty } h_i(y_n(t_i)) - h_i(y_k(t_i))\Vert \le 2\varepsilon \). Since there exists a limit \(\lim \nolimits _{n\rightarrow \infty } h_i(y_n(t_i)), \ i=1,2,\ldots \), there is \(k_0 \in {\mathbb {N}}\) such that for \(k\ge k_0\) and for \(i=1,2,\ldots ,m\) we have
Combining the above obtained estimation and (54) we get for \(k \ge k_0\) the inequality \(\Vert z-F_fy_k\Vert _\infty \le 2\varepsilon \) which proves that \(F_fy_k \rightarrow z\) in \(BG({\mathbb R}_+,E)\) for \(k\rightarrow \infty \).
Continuity of the operator \(F_f\) is a consequence of condition (H3) and the equalities (47) and (48)—we omit a simple proof of this fact. \(\square \)
Corollary 4.8
Let Banach space E be separable. Then \(F_f( BG({\mathbb R}_+,E)) \subset BG({\mathbb R}_+,E)\) and the superposition operator \(F_f: BG({\mathbb R}_+,E)\rightarrow BG({\mathbb R}_+,E)\) is continuous and compact if and only if the conditions (H1)-(H3) of Theorem 4.4 are satisfied and
for some function \(g\in BG({\mathbb R}_+,E)\).
5 An application
As an example of application we consider equation
We will assume that the functions involved in Eq. (55) satisfy the following conditions:
-
(i)
the function \(f:{\mathbb R}_+\times E\rightarrow E\) has the following properties:
-
(i1)
f is bounded on \({\mathbb R}_+ \times B_E(r)\) for \(r>0\),
-
(i2)
there is a constant \(q\ge 0\) such that
$$\begin{aligned} \Vert f(t,x_1) - f(t,x_2)\Vert \le q \Vert x_1 - x_2\Vert \end{aligned}$$for \(t\in {\mathbb R}_+, x_1, x_2 \in E\),
-
(i3)
the family of functions \(\{f(\cdot , x): x\in B_E(r)\}\) is equiregulated on \({\mathbb R}_+\) for all \(r>0\),
-
(i1)
-
(ii)
the mapping \(u:{\mathbb R}_+\times {\mathbb R}_+\times E \rightarrow E\) has the following properties:
-
(ii1)
the function \(u(t,\cdot ,x(\cdot ))\) is integrable on \({\mathbb R}_+\) for any \(t\in {\mathbb R}_+\) and for all \(x\in BG({\mathbb R}_+,E)\),
-
(ii2)
u is bounded on \({\mathbb R}_+\times {\mathbb R}_+\times B_E(r)\) for all \(r>0\),
-
(ii3)
the mapping u(t, s, x) is continuous with respect to the variable x,
-
(ii4)
there exist functions: \(\phi \in BG({\mathbb R}_+,{\mathbb R}_+)\), \(g\in L^1({\mathbb R}_+,{\mathbb R}_+)\) and nondecreasing function \(h:{\mathbb R}_+ \rightarrow {\mathbb R}_+\) such that
$$\begin{aligned} \Vert u(t_2,s,x)-u(t_1,s,x)\Vert \le |\phi (t_2)-\phi (t_1)| g(s) h(\Vert x\Vert ) \end{aligned}$$for all \(t_1, t_2, s \in {\mathbb R}_+, x\in E\),
-
(ii5)
the family of functions \(\{u(t,\cdot ,x): t\in {\mathbb R}_+, x\in B_E(r)\}\) is equiregulated on \({\mathbb R}_+\) for all \(r>0\),
-
(ii6)
there is a function \(k:{\mathbb R}_+\times {\mathbb R}_+ \rightarrow {\mathbb R}_+\), integrable with respect to s on \({\mathbb R}_+\) for all \(t\in {\mathbb R}_+\), such that
$$\begin{aligned} \beta _E\bigl (u(t,s,A)\bigr ) \le k(t,s) \beta _{E}(A) \end{aligned}$$for all \(t,s \ge 0, A\subset E, A\) is bounded,
-
(ii7)
there are functions: \(k_1:{\mathbb R}_+\times {\mathbb R}_+\rightarrow {\mathbb R}_+\), integrable with respect to s on \({\mathbb R}_+\) for all \(t\in {\mathbb R}_+\), and nondecreasing \(\psi :{\mathbb R}_+ \rightarrow {\mathbb R}_+\) such that
$$\begin{aligned} \Vert u(t,s,x)\Vert \le k_1(t,s)\psi (\Vert x\Vert ) \end{aligned}$$for all \(t,s \in {\mathbb R}_+, x\in E\), and moreover
$$\begin{aligned} \lim \limits _{t\rightarrow \infty } \int \limits _0^\infty k_1(t,s)ds = 0, \end{aligned}$$
-
(ii1)
-
(iii)
there is a constant \(r>0\) such that
$$\begin{aligned} \sup \left\{ \bigl \Vert f(t,x(t)) + \int \limits _0^\infty u(t,s,x(s))ds \bigr \Vert :x\in B_{BG({\mathbb R}_+,E)}(r), t\in {\mathbb R}_+ \right\} \le r \end{aligned}$$and
$$\begin{aligned} q+\sup _{t\in {\mathbb R}_+} \int \limits _0^\infty k(t,s)ds < 1. \end{aligned}$$
For our further purposes we will need following fixed point theorem [3].
Theorem 5.1
Let Q be a nonempty bounded closed convex subset of the Banach space E and let \(S:Q\rightarrow Q\) be continuous and such that \(\mu (SX) \le q \mu (X)\) for any nonempty subset X of Q, where q is a constant, \(q\in [0,1)\) and \(\mu \) is a measure of noncompactness. Then S has a fixed point in the set Q.
Now we formulate our theorem as:
Theorem 5.2
Under the conditions (i)–(iii), Eq. (55) has at least one solution in \(BG({\mathbb R}_+,E)\).
Proof
Let \(r>0\) be as in (iii) and denote \(B_r:= B_{BG({\mathbb R}_+,E)}(r)\). For our further purposes we denote by \(\overline{U}\) the constant
Keeping in mind the assumptions (ii2), we have \(\overline{U} < \infty .\)
Now we define three operators \(F_f, U\) and S for \(x\in B_r\):
Firstly we show that \(F_fx, Ux \in BG({\mathbb R}_+,E)\). To do this fix \(t\in {\mathbb R}_+\). Next assume that \(t_1, t_2 \in {\mathbb R}_+\) are such that \(t< t_1 <t_2\). Then, in view of (i2) we have
Using condition (i3) we have that there is limit \(\lim \nolimits _{s\rightarrow t^+}(F_fx)(s)\). Similarly we obtain the existence of \(\lim \nolimits _{s\rightarrow t^-}(F_fx)(s)\), so \(F_fx\) is regulated on \({\mathbb R}_+\). Moreover, in view of (i1), \(F_fx\) is bounded and therefore \(F_fx \in BG({\mathbb R}_+,E)\).
By virtue of (ii4) we get
The condition (ii4) implies that there exists \(\lim \nolimits _{s\rightarrow t^+}(Ux)(s)\) (and similarly for \(\lim \nolimits _{s\rightarrow t^-}(Ux)(s)\)). Then, in view of (ii2), we get \(Ux \in BG({\mathbb R}_+,E)\), and thus by (iii), \(S:B_r\rightarrow B_r\). From the assumption (i2), (ii3) and Lebesgue’s dominated convergence theorem we conclude that the operators \(F_f\) and U are continuous, and therefore \(S:B_r\rightarrow B_r\) is also continuous.
Now we are going to use Theorem 5.1 with the measure \(\gamma _c\) given in (33). Let us take a nonempty set \(X\subset B_r\). From (i2), after standard calculation we get
Next, fix arbitrarily \(T>0, \varepsilon >0\) and \(t\in [0, T)\). Applying (56) we get
Then, using (i3) we derive \(\omega _T^+(F_fX,t) \le q \omega _T^+(X,t)\) as \(\varepsilon \rightarrow 0\), and therefore \(\omega _\infty ^+(F_fX) \le q \omega _\infty ^+(X)\). Similarly we derive \(\omega _\infty ^-(F_fX) \le q \omega _\infty ^-(X)\). Thus
This inequality, together with (58) and (59), imply
Let \(X \subset B_r, T>0, \varepsilon >0, t\in [0,T), t<t_1<t_2\le T, |t_2-t_1| \le \varepsilon .\) Using (57) we have
Keeping in mind that \(\phi \in BG({\mathbb R}_+,{\mathbb R}_+)\) and tending with \(\varepsilon \rightarrow 0\) we get \(\omega _T^+(UX,t)=0\) and therefore \(\omega _\infty ^+(UX)=0\). In similar way we get \(\omega _\infty ^-(UX)=0\). Thus
Now let \(t\in {\mathbb R}_+\) and \(x,y\in X\). From (ii7) we have
Hence \(\limsup \nolimits _{t\rightarrow \infty } {\text {diam}} (UX)(t) = 0\), i.e.
We now introduce an auxiliary operator \(U_T:B_r \rightarrow BG({\mathbb R}_+,E)\) for \(T>0\) by formula
Let us fix \(X\subset B_r, t\in [0,T]\). Keeping in mind (ii5), Theorem 3.1 [15], (ii6) we have
Next, using (ii7) we get for \(x\in X, t\in [0,T]\)
Hence we derive
where \(d_H\bigl ((UX)(t),(U_TX)(t)\bigr )\) is the Hausdorff distance between the sets (UX)(t) and \((U_TX)(t) \subset E\). This implies
Now, taking into account this equality, from (63) we obtain
Linking this estimation with (61) and (62) we get
Thus, joining the above inequality with (60) we infer that
and taking into account Theorem 5.1 we derive that S has at least one fixed point in the ball \(B_r \subset BG({\mathbb R}_+,E)\). \(\square \)
References
Appel, J., Zabrejko, P.P.: Nonlinear Superposition Operators, Cambridge Tracts in Mathematics, vol. 95. Cambridge University Press, Cambridge (1990)
Aziz, W., Merentes, N., Sanchez, J.L.: A note on the composition of regular functions. Z. Anal. Anwend. 33, 119–123 (2014)
Banaś, J., Goebel, K.: Measure of Noncompactness in Banach Spaces. Lecture Notes in Pure and Applied Mathematics, vol. 60. Marcel Dekker, New York (1980)
Banaś, J., Zając, T.: On a measure of noncompactness in the space of regulated functions and its applications. Adv. Nonlinear Anal. 8, 1099–1111 (2019). https://doi.org/10.1515/anona-2018-0024
Cichoń, K., Cichoń, M., Metwali, M.M.A.: On some parameters in the space of regulated functions and their applications. Carpathian J. Math. 34(1), 17–30 (2018)
Cichoń, K., Cichoń, M., Satco, B.: On regulated functions. Fasc. Math. 60, 37–57 (2018). https://doi.org/10.1515/fasmath-2018-0003
Cichoń, K., Cichoń, M., Satco, B.: Measure differential inclusions through selection principles in the space of regulated functions. Mediterr. J. Math. 15, 148 (2018). https://doi.org/10.1007/s00009-018-1192-y
Dieudonné, J.: Foundations of Modern Analysis. Academic Press, New York (1969)
Drewnowski, L.: On Banach spaces of regulated functions. Comment. Math. 57(2), 153–169 (2017)
Fernandes, L.A.O., Arbach, R.: Integral functionals on C-algebra of vector-valued regulated functions. Ann. Funct. Anal. 3, 21–31 (2012)
Fraňková, D.: Regulated functions. Math. Bohemica 116, 20–59 (1991)
Goffman, C., Moran, G., Waterman, D.: The structure of regulated functions. Proc. Am. Math. Soc. 57, 61–65 (1976)
Michalak, A.: On superposition operators in spaces of regular and of bounded variation functions. Z. Anal. Anwend. 35, 285–308 (2016)
Olszowy, L.: Measures of noncompactness in the space of regulated functions. J. Math. Anal. Appl. 476, 860–874 (2019)
Olszowy, L., Zając, T.: Some inequalities and superposition operator in the space of regulated functions. Adv. Nonlinear Anal. 9, 1278–1290 (2020)
Stańczy, R.: Hammerstein equations with an integral over a noncompact domain. Ann. Polonici Math. LXIX.1, 49–60 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dudek, S., Olszowy, L. Measures of noncompactness and superposition operator in the space of regulated functions on an unbounded interval. RACSAM 114, 168 (2020). https://doi.org/10.1007/s13398-020-00900-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13398-020-00900-9
Keywords
- Space of regulated functions
- Criterion of relative compactness
- Measure of noncompactness
- Nemytskii operator



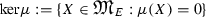 is nonempty and
is nonempty and 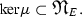
 such that
such that