1 Introduction

In this work, the nonlinear response of an autoparametric system of three degrees of freedom with a spherical pendulum and a damper of the fractional type is investigated. In previous works, the authors studied autoparametric systems containing a spherical pendulum with viscous and magnetorheological damping. Sado and Bobrowska [1] investigated the dynamic properties of the three degrees of freedom autoparametric system with a spherical pendulum in the vicinity of internal and external resonances. The investigated system comprised a spherical pendulum suspended from a mass block which was suspended from a vertical linear spring and a viscous dashpot. In that paper, the energy transfer between vibration modes was studied. Sado et al. [2] investigated the impact of initial conditions on the energy transfer between vibration modes and the occurrence of chaotic motion in the system. Sado and Freundlich [3] examined a three degree of freedom system with a spherical pendulum which was controlled by a magnetorheological damper. The examined system comprised a spherical pendulum suspended from a mass block which was suspended from a vertical linear spring and a magnetorheological damper. They studied the impact of magnetorheological damper properties on the system vibration in the neighborhood of internal and external resonances. The authors showed that apart from the regular behavior of the spherical pendulum, chaotic vibrations for all coordinates can occur near the internal and external resonance areas.

In this paper, the damping described by the fractional derivatives is analyzed. In the engineering practice, the systems containing a spherical pendulum can be used to model the dynamics of certain types of structures, such as cranes [4,5,6,7,8,9], seismic isolators [10], vibration absorbers [11,12,13], energy harvesters [14], inertial sensors [15]. Thus the dynamics of systems with a spherical pendulum is an interesting subject of scientific research and have been analyzed in a number of studies [7,8,9, 11, 13,14,15,16,17,18,19,20,21,22,23,24,25,26].

A brief overview of publications on pendulum research can be found in the paper by Han et al. [16]. Various types of studies on spherical pendulum have been conducted. The first type of studies concerns the dynamics of the spherical pendulum subjected to motion of the suspension point. Miles is probably the first who studied stability of forced oscillations of a spherical pendulum [17, 18]. He studied nonlinear response of a lightly damped spherical pendulum subjected to harmonic excitation in a horizontal plane. Miles assumed linear damping of the pendulum. He found that for sufficiently small damping the planar harmonic motion is unstable over a major portion of the resonant peak. Moreover, non-planar harmonic motion is stable in a spectral neighborhood that overlaps neighborhoods of both stable and unstable planar motions. Furthermore, no stable, harmonic motion is possible in a finite neighborhood of the natural frequency. Miles [19], Miles and Zou [20] studied internal resonance of a slightly detuned spherical pendulum.

Tritton [21], Kana and Douglas [22] experimentally investigated system with a spherical pendulum. They confirmed some theoretical results presented by Miles. Gottlieb and Habib [24] studied experimentally non-linear damping mechanisms that govern the dynamics of the chaotic motion of a spherical pendulum. These authors deduced that consistent modeling and validation of non-linear damping mechanisms are essential for prediction of the spherical pendulum dynamics and bounds for a chaotic response.

Náprstek and Fisher [11], Pospíšil et al [25] studied the pendulum vibration damper modeled as a spherical pendulum. The pendulum was excited kinematically by horizontal motion of the suspension point. Náprstek and Fisher [11] performed analytical and numerical analysis of the damping pendulum, whereas Pospíšil et al. [25] conducted experimental and numerical investigations of such a pendulum.

Markeyev [23] studied the dynamics of an undamped spherical pendulum subjected to the high-frequency vertical harmonic oscillations of the suspension point. He showed existence of two types of motion when the pendulum performs high-frequency oscillations close to conical motions. Leung and Kuang [8] presented an analytical and numerical analysis of a lightly damped spherical pendulum, whose suspension point was harmonically excited in both vertical and horizontal directions. They studied the bifurcation behavior of the pendulum taking into account third order terms in the amplitude in the vicinity of the resonance.

Witkowski et al. [26] studied the dynamics of three coupled conservative spherical pendulums, and showed that linear modes allow us to compute the nonlinear normal modes for increasing energy in the system. They observed a pitchfork bifurcation in the first mode, which causes the appearance of symmetry broken periodic solution and destabilization of the initial one. Additionally, they determined regions of the energy transfer for the system analyzed.

The second type of studies concerns the dynamics of structures with a spherical pendulum [4,5,6,7,8,9,10,11, 13,14,15]. Abdel-Rahman et al. [4] presented a survey of crane models published in the literature, their classification and discussion of their applications and limitations. These authors analyzed the most widely used crane model using the multiple scale method. They proposed appropriate models and control criteria for various cranes applications. Chin et al. [5, 6] studied the dynamics of ship-mounted cranes modeled as an elastic spherical pendulum. The authors studied stability of the solutions and dynamical behavior of the pendulum in the region of one-to-one internal resonance. In the paper by Ghigliazza and Holmes [7] the study of the dynamics of a tower crane was presented. A spherical pendulum in a non-inertial reference frame was used as the crane model. The authors analyzed two cases of motion: the linearly accelerating support, and the support describing a circle at constant speed. They determined integrability of the system and regions of stability and bifurcations. Perig et al. [9] proposed a three degree of freedom mathematical model of a spherical pendulum attached to a crane boom tip for uniform slewing motion of the crane. They presented nonlinear and linearized mathematical models of the considered system. Next, they examined the motion trajectories of the spherical pendulum using numerical and experimental methods.

Tatemichi and Kawaguchi [10] described application of a system of spherical pendulums as a seismic isolator. They presented full-scale tests of a floor isolated by a pendulum system and carried out analytical studies of pendulum isolators used in high buildings and space structures. Ikeda et al. [13] investigated the vibration control of a towerlike structure using a single spherical pendulum vibration absorber. The structure was modeled as a spherical pendulum suspended from a mass block with a horizontal perpendicular system of springs and dampers. The pendulum suspension point was harmonically excited in horizontal plane. The authors implemented coordinates enabled them to avoid the non-integrability of the equations of motion due to a singularity. They made analytical and experimental analysis of the investigated system.

Xu and Tang [14] investigated dynamic behaviour of a piezoelectric cantilever beam with a spherical pendulum for multi-directional energy harvesting. Allan and Townsend [15] studied an automatic seatbelt inertial sensor comprised of a spherical pendulum. They studied the motions of a spherical pendulum to determine possible unintentional release of the sensor during vehicle emergency maneuvers.

In recent years, fractional derivatives have been increasingly used for modeling viscous damping properties [27,28,29,30,31,32,33,34,35,36,37,38]. These derivatives have also begun to be used to model damping in systems having pendulums [39,40,41]. The use of fractional derivatives is caused by the fact that they enable more accurate modeling of the damping properties of materials whose viscoelastic properties are weakly dependent on frequency, therefore the use of the fractional order derivatives makes it possible to model viscoelastic material properties more accurately across a wide frequency range [28,29,30,31,32]. A historical overview of the development of fractional calculus in the mechanics of solids was presented by Rossikhin [36], while a review of publications devoted to the application of fractional calculus in the dynamics of structure elements can be found in a paper by Rossikhin and Shitikova [37]. However, the number of publications considering damping described by a fractional derivative in the systems with pendulums is limited. Rossikhin and Shitikova [38] analyzed vibrations of two degree of freedom system consisting of a plane pendulum suspended from an element mass which was suspended from a linear spring. The authors assumed that the system vibrates in a viscous medium whose damping properties were described by fractional derivatives. Moreover, they assumed small finite value amplitudes of vibrations and they used multiple scales method to solve the problem. They examined impact of damping modeled by a fractional derivative on free damped vibrations and energy exchange in the system.

Seredyńska and Hanyga [40] examined the effects of fractional damping on vibrations of a planar, inextensible and extensible pendulum. This analysis was an illustration of the proposed theory for solving nonlinear differential equations with fractional damping. They established the conditions of existence, uniqueness and dissipativity for a certain class of nonlinear dynamical systems including systems with fractional damping.

Hedrih [41] analyzed multi-pendulum systems with fractional order creep elements. Parallel pendulums were connected with creep elements described by fractional order derivatives. The governing equations of the system and its analytical solution for special cases of the pendulum system were presented. The vibration modes of the systems with one and two pendulums having creep fractional elements were studied. It was concluded that there is a mathematical analogy in descriptions between multi-pendulum systems and chain dynamical systems.

There are no publications devoted to systems with spherical pendulums in which the damping is described by a fractional derivative. The presented model can be used to model the dynamics of cranes with damping described using fractional derivatives. The use of fractional derivatives allows for a more accurate description of the damping properties and dynamic behavior of the analyzed system in a wide range of frequency, which is important in an engineering practice. Therefore, in the authors’ opinion, the impact of damping described by a fractional derivative on the dynamic behavior of the system with a spherical pendulum should be analyzed, which is the purpose of this research.

2 Formulation of the problem

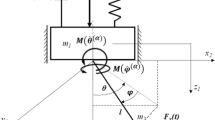
In this study, an impact of fractional damping on dynamic properties of a coupled mechanical system with a spherical pendulum is investigated. It is assumed that the spherical pendulum is suspended from the oscillator excited harmonically in the vertical direction (Fig. 1). The oscillator consists a linear spring and a damper of a fractional type. The position of the oscillator of mass \(m_1\) is described by the coordinate \(z_1\) and position of the pendulum of mass \(m_2\) and length l is described by the coordinates: \(z_2, \theta , \phi\). The coordinate z is the vertical displacement of the body of mass \(m_1\) measured from the static position of equilibrium. The angle \(\theta\) is the angle between the vertical axis and the deflection of the pendulum on the plane xz. The angle \(\phi\) is the angle between the deflections of the pendulum in the plane xz and the pendulum. The body of mass \(m_1\) is subjected to the harmonic vertical excitation assumed as \(F(t) = P \cdot cos(\nu t)\), where: P is the force amplitude, \(\nu\) is the excitation frequency and t is time. The force produced by the fractional damper is

$$\begin{aligned} C(t)=c_\alpha \frac{d^\alpha z(t)}{dt^\alpha } \end{aligned}$$
(1)

where C(t) is the force produced by a fractional damper, z(t) is the displacement, \(c_\alpha\) is a damping coefficient, \(\frac{d^\alpha }{dt^\alpha }\) is the Caputo fractional derivative of the order \(\alpha\) defined as [29, 35]

$$\begin{aligned}&\frac{d^\alpha }{dt^\alpha }f(t)\equiv D_t^\alpha (f(t))\equiv {\dot{f}}^{(\alpha )}(t) \\&\equiv \frac{1}{\varGamma (m-\alpha )}\int \limits _0^t\frac{\frac{d^m f(\tau )}{d\tau ^m }}{(t-\tau )^{\alpha +1-m}}d\tau \end{aligned}$$
(2)

where \({\varGamma (m-\alpha )}\) is the Euler gamma function [35], m is a positive integer number satisfying inequality \({m-1< \alpha < m}\), and \(t > 0\).

Fig. 1
figure 1

Schema of the system analyzed

Full size image

The fractional derivative order is commonly assumed to be in a range of \(0 < \alpha \le 1\) for many real materials [30, 31], and \(\alpha = 1.0\) corresponds to integer order derivative [35]. The Cartesian coordinates of the mass \(m_2\) are

$$\begin{aligned}&x_2=lcos\phi sin\theta \\&y_2=lsin\phi \\&z_2=lcos\phi cos\theta +z_1 \\&z_1=z+z_{st} \end{aligned}$$
(3)

where \(z_{st}\) is the static deflection expressed as

$$\begin{aligned} z_{st}=\frac{(m_1+m_2)g}{k} \end{aligned}$$
(4)

where g is gravitational acceleration.

Calculating derivatives with respect to time of the expressions in Eq. (3), the kinetic energy T of the system is expressed as

$$\begin{aligned} T &=\frac{1}{2}{\dot{z}}_1^2(m_1+m_2 )+\frac{1}{2}m_2 l^2{\dot{\phi }}^2+\frac{1}{2}m_2 l^2{\dot{\theta }}^2cos^2\phi \\&-m_2 l{\dot{z}}_1 {\dot{\phi }} sin\phi cos\theta -m_2 l{\dot{z}}_1 {\dot{\theta }} cos\phi cos\theta \end{aligned}$$
(5)

The potential energy is expressed as

$$\begin{aligned} V=-(m_1+m_2 )z_{1}g-m_2 glcos\phi cos\theta +\frac{1}{2} k(z_{1})^2 \end{aligned}$$
(6)

Assuming fractional dissipation function as \(D = \frac{1}{2}c_\alpha (D_t^\alpha (z))^2\) [38], the equations of motion of the system are as follows

$$\begin{aligned}&\ddot{z}(m_1+m_2)-m_2l\ddot{\theta }cos\phi sin\theta -m_2l\ddot{\phi }sin\phi cos\theta \\&\quad + 2m_2 l {\dot{\phi }} {\dot{\theta }}sin\phi sin\theta -m_l{\dot{\theta }}^2cos\phi cos\theta \\&\quad +c_\alpha {\dot{z}}^{(\alpha )}+k z =F_0 cos\nu t \\&\quad -m_2 l\ddot{z} cos\phi sin\theta +m_2l^2\ddot{\theta }cos^2 \phi - 2m_2 l {\dot{\phi }} {\dot{\theta }}cos\phi sin\phi \\&\quad + m_2 glcos\phi sin\theta =0 \\&\quad -m_2 l\ddot{z} sin\phi cos\theta +m_2l^2\ddot{\phi }+m_2 l^2 {\dot{\theta }}^2 cos\phi sin\phi \\&\quad +m_2 g l sin\phi cos\phi = 0 \end{aligned}$$
(7)

Next, introducing dimensionless time \(\tau = \omega _1 t\) and defining the following parameters

$$\begin{aligned} \omega _1^2&=\frac{k}{m_1+m_2}, \ \omega _2^2=\frac{g}{l},\ \beta =\frac{\omega _2}{\omega _1},\ {\bar{z}}=\frac{z}{l}, \ \mu _1=\frac{\nu }{\omega _1} \\ \gamma&=\frac{c_\alpha \omega _1^\alpha }{(m_1+m_2 ) \omega _1^{2}},\ a=\frac{m_2}{m_1+m_2 }, \ A_1=\frac{F_0}{(m_1+m_2 ) \omega _1^2 l} \end{aligned}$$
(8)

the Eq. (7) can be transformed into a dimensionless form (where the overbars are omitted for convenience)

$$\begin{aligned}&\ddot{z}-a\ddot{\phi }sin\phi cos\theta -a{\dot{\phi }}^2 cos\phi cos\theta +2a{\dot{\phi }} {\dot{\theta }}sin\phi sin\theta \\&\qquad -a\ddot{\theta }cos\phi sin\theta -a{\dot{\theta }}^2 cos\phi cos\theta +\gamma {\dot{z}}^{(\alpha )}+z \\&\quad = A_1 cos(\mu _1 \tau )\\&\qquad \ddot{\theta } cos^2\phi -\ddot{z}cos\phi sin\theta = 2{\dot{\theta }} {\dot{\phi }}cos\phi sin\phi -\beta ^2 cos\phi sin\theta \\&\qquad \ddot{\phi }-\ddot{z}sin\phi cos\cos \theta =-{\dot{\theta }}^2 cos\phi sin\phi -\beta ^2 sin\phi cos\theta \end{aligned}$$
(9)

The equations above can be rewritten in the matrix form

$$\begin{aligned}&\mathbf{A }\ddot{\mathbf{q }}=\mathbf{d } \quad \text {where}\\&\mathbf{A }=\begin{bmatrix} 1 &{} -a cos\phi sin\theta &{} -a sin\phi cos\theta \\ -cos\phi sin\theta &{} cos^2 \phi &{} 0 \\ -sin\phi cos\theta &{} 0 &{} 1 \end{bmatrix} \\&\ddot{\mathbf{q }}= \begin{bmatrix} \ddot{z} \\ \ddot{\theta }\\ \ddot{\phi }\end{bmatrix} \quad \text {and} \quad \mathbf{d }= \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix} \\ \end{aligned}$$
(10)

and the elements of vector d are

$$\begin{aligned} d_1&= A_1 cos(\mu _1 \tau )+a({\dot{\phi }}^2 cos\phi cos\theta -2{\dot{\phi }} {\dot{\theta }} sin\phi sin\theta \\&\quad + {\dot{\theta }}^2 cos\phi cos\theta )-\gamma {\dot{z}}^{(\alpha )}-z \\ d_2&= 2{\dot{\theta }} {\dot{\phi }} cos\phi sin\phi -\beta ^2 cos\phi sin\theta \\ d_3&=-{\dot{\theta }}^2 cos\phi sin\phi -\beta ^2 sin\phi cos\theta \end{aligned}$$
(11)

3 Numerical calculations and discussion

The derived equations of motion can be solved numerically using well-known procedures [42,43,44]. The Adams–Bashforth–Moulton predictor–corrector method [42, 43] is used to solve the Eqs (10). The term on the right side of Eqs (10) with Caputo fractional derivative is calculated numerically using the trapezoidal rule worked out by Diethelm et al [44] in a form

$$\begin{aligned} D_t^{\alpha } z_N= \frac{h^{-\alpha }}{\varGamma (2-\alpha )}\left[ \sum _{j=1}^N a_{j,N} \left( z_{N-j+1}-z_1 \right) \right] \end{aligned}$$
(12)

where h is a time step and

$$\begin{aligned} a_{j,N}={\left\{ \begin{array}{ll} 1 , &{} \text {if }j=1\\ j^{1-\alpha }-2(j-1)^{1-\alpha }+(j-2)^{1-\alpha } , &{} \text {if } 1< j < N-1 \\ (1-\alpha )N^{-\alpha }-N^{1-\alpha }+(N-1)^{1-\alpha } , &{} \text {if } j = N \end{array}\right. } \end{aligned}$$
(13)

The numerical calculations are performed using the “Matlab” package. Firstly, the effects of the order of the fractional derivative \(\alpha\) on the time histories of the system are analyzed. The calculations are performed for free and forced vibrations. Time histories of free vibrations of coordinates z, \(\theta\), \(\phi\), are calculated for the orders of the fractional derivative \(\alpha = 0.25, 0.5, 0.75 ,1.0\). The calculations are performed for the system parameters \(A_1 = 0.0\), \(\gamma = 0.001\), \(a = 0.5\), \(\beta =0.5\), and for the initial conditions \(z(0) = 0.1\), \(\theta (0) = \phi (0)=0.005 ^{\circ }\), \({\dot{z}}(0)={\dot{\theta }}(0)= {\dot{\phi }}(0)=0\). Exemplary time histories for the order of the fractional derivative \(\alpha = 0.25\) are shown in Fig. 2. It can be seen from the time histories that the energy transfer occurs between the modes of vibration in a closed cycle (see Fig. 2).

Fig. 2
figure 2

Time histories of free vibrations, \(z(0) = 0.1\), \(\gamma = 0.001\), \(a = 0.5\), \(\beta =0.5\), \(A_1= 0\), \(\alpha = 0.25\)

Full size image
Fig. 3
figure 3

Comparison of time histories of free vibrations for coordinate \(\theta\), different values of \(\alpha\) and for: \(z(0)= 0.1\), \(\gamma = 0.002\), \(a = 0.5\), \(\beta =0.5\), \(A_1= 0\)

Full size image
Fig. 4
figure 4

Comparison of time histories of free vibrations for coordinate \(\theta\), different values of \(\alpha\) and for: \(z(0)= 0.1\), \(\gamma = 0.004\), \(a = 0.5\), \(\beta =0.5\), \(A_1= 0\)

Full size image
Fig. 5
figure 5

Internal resonance, coordinate \(\theta\), \(A_1 = 0\), \(a=0.5\), and for \(z(0) = 0.1\), a \(\gamma =0.001\), b \(\gamma =0.004\)

Full size image

The influence of the order of the fractional derivative \(\alpha\) on damping coefficient \(\gamma = 0.001\) is small. The influence can be observed for higher values of the damping parameter \(\gamma\). The comparison of time histories of free vibrations for the orders of the fractional derivative \(\alpha = 0.25, 0.5, 0.75, 1.0\), for coordinate \(\theta\) and for the damping coefficients, \(\gamma = 0.002\) and \(\gamma = 0.004\) are presented in Figs. 3 and 4.

As can be seen from Figs. 3 and 4, the influence of the order of the fractional derivative \(\alpha\) on vibration is more noticeable for higher values of the damping coefficient \(\gamma\) . It can be observed that an increase in the order of the fractional derivative causes a decrease in the vibration amplitudes and a faster decrease of vibration amplitudes in time.

Fig. 6
figure 6

Time histories of forced vibrations for coordinates \(z, \theta , \phi\), and for \(A_1 = 0.001\), \(\gamma = 0.001\), \(a = 0.5\), \(\beta =0.5\), \(\mu _1 = 1.0\), \(\alpha = 0.25\)

Full size image

In the next stage, the impact of the order of the fractional derivative \(\alpha\) on the internal resonance is studied. The internal resonance is calculated for the system parameters \(A_1 = 0\), \(a = 0.5\), and for the initial conditions \(z(0) = 0.1\), \(\theta (0) = \phi (0)=0.005 \, ^{\circ }\), \({\dot{z}}(0)={\dot{\theta }}(0)={\dot{\phi }}(0)=0\). The exemplary results for the coordinate \(\theta\) and damping coefficient \(\gamma =0.001\) are shown in Fig. 5a, whereas for damping coefficient \(\gamma =0.004\) are shown in Fig. 5b.

From the graphs shown in Fig. 5a, b, we can see that the decrease in the derivative order increases the maximum amplitude of the internal resonance. As can be seen from Fig. 5a for small value of the damping coefficient (\(\gamma = 0.001\)), the effect of the order of the fractional derivative on the internal resonance is small. For higher values of damping coefficient (\(\gamma = 0.004\)), the effect of the order of the fractional derivative on the internal resonance is significant.

In the case of the damping coefficient \(\gamma =0.001\) and the derivative order \(\alpha = 0.25\), the maximum amplitude occurs for \(\beta =0.492\), while for the other of the order of the fractional derivative the maximum amplitude occurs for \(\alpha =0.496\) (see Fig. 5a). In the case of the damping coefficient \(\gamma =0.004\) and the derivative order \(\alpha = 0.25\), the maximum amplitudes occur for \(\beta = 0.498\), while for the other of the orders of the fractional derivative the maximum amplitude occur for \(\beta = 0.5\) (see Fig. 5b).

Next, the impact of the order of the fractional derivative \(\alpha\) on the forced vibrations is studied. The time histories for various vales of the damping coefficient \(\gamma\) are calculated. The time history for coordinates \(z, \theta , \phi\), and for \(A_1 = 0.001\), \(\gamma = 0.001\), \(a = 0.5\), \(\beta =0.5\), \(\mu _1 = 1.0\), \(\alpha = 0.25\) are shown in Fig. 6.

Fig. 7
figure 7

Comparison of time histories of forced vibrations for coordinate \(\theta\), different values of \(\alpha\) and for: \(A_1= 0.001\), \(\gamma = 0.004\), \(a = 0.5\), \(\beta =0.5\)

Full size image

The comparison of time histories of forced vibrations for the orders of the fractional derivative \(\alpha = 0.25, 0.5, 0.75, 1.0\) for coordinate \(\theta\) and for the damping coefficient \(\gamma = 0.004\) are presented in Fig. 7. It can be observed that an increase in the order of the fractional derivative causes a decrease in the vibration amplitudes and the time of the energy transfer is changed.

Fig. 8
figure 8

External resonance for coordinates \(z, \theta , \phi\), and for \(A_1 = 0.001\), \(\gamma =0.008\), \(a = 0.5\), \(\beta = 0.5\)

Full size image

In the vicinity of the internal resonance (\(\beta = 0.5\)), and for the same values of the derivative orders as previously, the calculations of the external resonance are performed. The calculations are made for the system parameters \(A_1 = 0.001\), \(\gamma = 0.008\), \(a = 0.5\), \(\beta = 0.5\), and the results are presented in Fig. 8. The effect of the order of the fractional derivative on external resonance is small for small damping coefficients \(\gamma\). As can be seen in Fig. 8, an increase in the order of fractional derivative causes a decrease in the amplitude of the external resonance.

Fig. 9
figure 9

Bifurcation diagrams versus excitation frequency \(\mu _1\) for coordinates \(z, \theta , \phi\), and for \(\alpha = 0.25\), \(A_1 = 0.00292\), \(\gamma = 0.00015\), \(\beta =0.5\)

Full size image

Next, the bifurcation diagrams are calculated for selected orders of fractional derivative. The calculations are performed in the vicinity of the internal and external resonances.The diagrams are calculated for coordinates \(z, \theta , \phi\) and the system parameters \(A_1 = 0.00292\), \(\gamma = 0.00015\), \(\beta =0.5\), where the bifurcation parameter is an excitation frequency \(\mu _1\). These diagrams were calculated for the order of the fractional derivative \(\alpha = 0.25, 0.5, 0.75 ,1.0\). The bifurcation diagrams for the order of the fractional derivative \(\alpha = 0.25\) are shown in Fig. 9. It can be seen that irregular vibrations occur for \(\mu _1\) between 0.95 and 1.05. These diagrams show many sudden qualitative changes, that is, many bifurcations in the chaotic attractor as well as in the periodic orbits. Bifurcation diagrams for \(\gamma = 0.00015\) and other values of the order of the fractional derivative are very similar to the bifurcation diagrams in the case of the order of the fractional derivative \(\alpha\) = 0.25. Therefore for small values of the damping coefficient, the effect of the order of the fractional derivative on bifurcations diagrams is minor.

Fig. 10
figure 10

Bifurcation diagrams versus excitation frequency \(\mu _1\) for coordinate z, and \(A_1 = 0.00292\), \(\gamma = 0.004\), \(\beta =0.5\), a \(\alpha = 0.25\), b \(\alpha = 1.0\)

Full size image
Fig. 11
figure 11

Bifurcation diagrams versus excitation frequency \(\mu _1\) for coordinate \(\theta\), and \(A_1 = 0.00292\), \(\gamma = 0.004\), \(\beta =0.5\), a \(\alpha = 0.25\), b \(\alpha = 1.0\)

Full size image
Fig. 12
figure 12

Bifurcation diagrams versus excitation frequency \(\mu _1\) for coordinate \(\phi\), and \(A_1 = 0.00292\), \(\gamma = 0.004\), \(\beta =0.5\), a \(\alpha = 0.25\), b \(\alpha = 1.0\)

Full size image

Then, in order to examine the effect of the order of the fractional derivative on dynamics behavior of the analyzed system, bifurcation diagrams were prepared for larger damping coefficients (\(\gamma = 0.004\)). Bifurcation diagrams for coordinates \(z, \theta , \phi\) and the system parameters \(A_1 = 0.00292\), \(\beta = 0.5\), orders of the fractional derivative \(\alpha = 0.25\) and \(\alpha = 1.0\) (integer order) are presented: in Fig. 10. for coordinate z, in Fig. 11 for coordinate \(\theta\), and in Fig. 12 for coordinate \(\phi\). Comparing bifurcation diagrams shown in Figs. 10,  11 and 12, the effect of the order of the fractional derivative on bifurcations diagrams can be observed. As can be seen, the amplitudes of vibration for \(\alpha = 0.25\) are significantly larger than for \(\alpha = 1.0\).

Moreover, the range of occurrence of the irregular vibration for coordinates \(\theta\) and \(\phi\) is between \(\mu _1\) = 0.995 and 1.009 for \(\alpha = 0.25\), whereas for \(\alpha = 1.0\), the irregular vibrations occur in the range of \(\mu _1\) between 0.961 and 1.04. In addition to various types of regular vibrations, we can also see irregular vibrations in the bifurcation diagrams.

At every point of a bifurcation diagram, vibrations should be analyzed in the phase space. In the presented work, Poincaré maps and the largest Lyapunov exponents for different orders of the fractional derivative \(\alpha\) are calculated. Exemplary Poincaré maps for the system parameters \(A_1 = 0.00292\), \(\gamma = 0.00015\), \(a = 0.5\), \(\beta =0.5\), \(\mu _1 = 1.0\), and orders of the fractional derivative \(\alpha = 0.25\) are presented in Fig. 13 for coordinate z, in Fig. 14 for coordinate \(\theta\) and in Fig. 15 for coordinate \(\phi\).

Fig. 13
figure 13

a Poincaré map, b largest exponents of Lyapunov for coordinate z, and for \(\alpha =0.25\), \(A_1 = 0.00292\), \(\gamma = 0.00015\), \(a = 0.5\), \(\beta =0.5\), \(mu_1 = 1.0\)

Full size image
Fig. 14
figure 14

a Poincaré map, b largest exponents of Lyapunov for coordinate \(\theta\), and for \(\alpha =0.25\), \(A_1 = 0.00292\), \(\gamma = 0.00015\), \(a = 0.5\), \(\beta =0.5\), \(mu_1 = 1.0\)

Full size image
Fig. 15
figure 15

a Poincaré map, b largest exponents of Lyapunov for coordinate \(\phi\), and for \(\alpha =0.25\), \(A_1 = 0.00292\), \(\gamma = 0.00015\), \(a = 0.5\), \(\beta =0.5\), \(mu_1 = 1.0\)

Full size image

As can be seen form Figs. 13, 14 and 15, the Poincaré maps for coordinates \(z, \theta ,\phi\) trace the “strange attractors” and the largest Lyapunov exponents are positive, therefore in this case, the response is chaotic.

4 Conclusions

In this paper, the dynamic behavior of the system with a spherical pendulum and a damper whose viscous properties are described by a fractional derivative is analyzed. The derived equations of motion of the system are solved numerically. The impact of the order of the fractional derivative on time histories, bifurcation diagrams and Poincaré maps is analyzed for selected system parameters. Autoparametric systems are very sensitive to nonlinearities and damping. The performed calculations show that use of the fractional damping has an impact on the time histories of the system. The influence of the order of the fractional derivative \(\alpha\) on vibrations is more considerable for higher values of the damping coefficient \(\gamma\). For some system parameters, when the order of the fractional derivative increases, the vibration amplitudes of the system response decrease. Additionally, chaotic motion is found for some system parameters. In the case of higher damping coefficients, the calculations show qualitative differences between the responses obtained for the system with damping described by fractional and integer order derivatives. Modeling of damping using fractional derivatives allows for a more accurate description of the damping properties of the analyzed system in a wider range of frequency, which is important in an engineering practice.