Suboptimal Comparison of Partitions

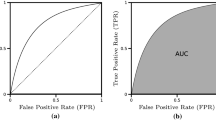
Abstract

The distinction between classification and clustering is often based on a priori knowledge of classification labels. However, in the purely theoretical situation where a data-generating model is known, the optimal solutions for clustering do not necessarily correspond to optimal solutions for classification. Exploring this divergence leads us to conclude that no standard measures of either internal or external validation can guarantee a correspondence with optimal clustering performance. We provide recommendations for the suboptimal evaluation of clustering performance. Such suboptimal approaches can provide valuable insight to researchers hoping to add a post hoc interpretation to their clusters. Indices based on pairwise linkage provide the clearest probabilistic interpretation, while a triplet-based index yields information on higher level structures in the data. Finally, a graphical examination of receiver operating characteristics generated from hierarchical clustering dendrograms can convey information that would be lost in any one number summary.

Appendix

1.1 A.1 Proofs

Here, we present the proof from Section 2.2 that when G = 2 the clustering induced by the optimal classifier is equivalent to the optimal clustering.

We identify the two classes with the symbols 0 and 1. Any partition of the set N := {1,…,n} into two (or fewer) subsets corresponds to exactly two classifications which are mirror images of each other. The term “mirror-image” refers to flipping 0’s to 1’s and 1’s to 0’s. The optimal classifier is based on the posterior probabilities p_i := P(Y_i = 1|x_i),i = 1,…,n. Observation i is classified as a “1” if p_i > 0.5 and to “0” if p_i < 0.5. The case p_i = 0.5 is ignored since the x_i’s are continuous (by assumption) and that event has probability 0. For a given data set X, we refer to this as the optimal classification. This optimal classification induces a partition of N. Our task is to show that the posterior probability of that partition exceeds that of any other partition (into two or fewer subsets).

Define a_i = max(p_i, 1 − p_i) and b_i = 1 − a_i. The posterior probability of the optimal classification is $A = {\prod }_{i=1}^{n} a_{i}$. The mirror-image classification has posterior probability $B = {\prod }_{i=1}^{n} b_{i}$. Both the optimal classifier and its mirror image induce the same unique partition induced by no other classification. The posterior probability of that partition is then Q = A + B. Now we wish to prove that Q is larger than the the posterior probability of any other partition. Any alternative partition can be viewed as one induced by a modification of the optimal classification in which the classification of observation i is flipped for each i ∈ S, where S is some proper subset of N. We do not allow S = N since that leads to the same partition. We use S^c to denote the complement of S in N. Define

$$ A_{1} = \prod\limits_{i \in S^{c}} a_{i}, \quad A_{2} = \prod\limits_{i \in S} a_{i}, \quad B_{1} = \prod\limits_{i \in S^{c}} b_{i}, \quad B_{2} = \prod\limits_{i \in S} b_{i}. $$

Note that A₁ > B₁ and A₂ > B₂ because a_i > b_i for each i. Now, clearly, A = A₁A₂,B = B₁B₂,Q = A₁A₂ + B₁B₂, and the posterior probability of the alternative partition is Q^∗ = A₁B₂ + B₁A₂. Our aim is to prove that Q > Q^∗.

Define λ = A₂/(A₂ + B₂) and note that 1 > λ > 0.5 since A₂ > B₂ > 0. Since A₁ > B₁, we obtain the following obvious statement about convex combinations of A₁ and B₁,

$$ \lambda A_{1} + (1 - \lambda) B_{1} > (A_{1} + B_{1} ) / 2 > (1 - \lambda) A_{1} + \lambda B_{1}. $$

Multiplying the leftmost and rightmost terms in the above inequality by (A₂ + B₂), and using the relationships λ(A₂ + B₂) = A₂ and (1 − λ)(A₂ + B₂) = B₂, we obtain

$$ A_{1} A_{2} + B_{1} B_{2} > A_{1} B_{2} + B_{1} A_{2}, $$

which is simply Q > Q^∗, the desired result.

1.2 A.2 Surprising Examples

In this section, we show two examples that provide informative lessons regarding optimal criteria. Using the notation defined in Section 2, we consider a mixture of two normals; a N(0, 1) with probability π₁ and a N(μ,σ²) with probability π₂ = 1 − π₁. The parameters are: (π₁,μ,σ²). Since a linear transformation leaves the problem essentially unchanged, it suffices to consider μ > 0,σ² ≥ 1 and π₁ ∈ (0, 1).

Now we will derive optimal classifiers for two special cases, i.e., the ones that assign $\hat {g}_{i} = \hat {g}(x_{i}) = 1$ if π₁f₁(x_i) > π₂f₂(x_i), and $\hat {g}_{i} = 2$ otherwise. We will use ϕ(.,a,b) to denote the pdf of the normal distribution with mean a and variance b, and Φ() to denote the cdf of the standard normal distribution.

1.2.1 A.2.1 The Relationship Between K and G

One surprising result from our exploration is that optimal classification can occur when the number of true groups has been misspecified. Here, we show how this can occur.

Suppose σ² > 1. The ratio

$$ \frac{f_{1}(x)}{f_{2}(x)} = \sigma \exp\left( \frac{\mu^{2}}{2(\sigma^{2}-1)} \right) \sqrt{2 \pi \tau^{2}} \phi\left( x, \theta, \tau^{2} \right) $$

has a maximum of

$$ M := {\sigma} \exp\left( \frac{\mu^{2}}{2(\sigma^{2}-1)} \right). $$

In the above,

$$ \theta := \frac{-\mu}{\sigma^{2} - 1}, \quad \tau^{2} := \frac{\sigma^{2}}{\sigma^{2} - 1}. $$

Note that M > 1 since σ² > 1. So if M < π₂/π₁ then π₁f₁(x) < π₂f₂(x) and $\hat {g}(x) = 2$ for all x.

This can arise only if π₂ > 1/2. An example: π₂ = 0.75,μ = 1.5,σ² = 4,M = 2.91 < π₂/π₁ = 3. In this case, the optimal classifier assigns all observations to a single class, even though the model with two classes and all its parameters are completely known. It shows that accurate estimation of the number of classes is not a requirement for optimal classification.

The fact that optimal solutions can occur with the number of classes misspecified might cause some concern for researchers who design algorithms for selecting the number of classes. Popular methods for achieving this objective include the Gap Statistic (Tibshirani et al. 2001) and the Silhouette Score (Kaufman and Rousseeuw 2005).

1.2.2 A.2.2 Compactness

The above example also demonstrates that optimally assigned classes need not be compact. If M ≥ π₂/π₁ then $\hat {g}(x) = 1$ if

$$ |x - \theta| < \sqrt{ 2 \tau^{2} \log \frac{M \pi_{1}}{\pi_{2}} }. $$

Otherwise, we assign $\hat {g}(x) = 2$. That is, x values within $\sqrt { 2 \tau ^{2} \log \frac {M \pi _{1}}{\pi _{2}} }$ from 𝜃 are assigned to class 1. More extreme values, above and below 𝜃 are assigned to class 2. Hence, the region assigned to class 2 is a union of two disjoint sets. This shows that the notion that observations close together should be placed in the same class is generally false.

1.3 A.3 Theoretical Derivation of the Pairwise Indices

Now we give general expressions for the indices and the probabilities of relevant events. Let π_g = P(A_i = g),g = 1,⋯ ,G, and let π denote the column vector (π₁,⋯ ,π_G)^⊤. Of course, ${\sum }_{g=1}^{G} \pi _{g} = 1$.

For two independent observations, say observations 1 and 2, $P(A_{1} = A_{2} ) = {\sum }_{g=1}^{G} {\pi _{g}^{2}} = \pi ^{\top } \pi = ssq(\pi )$, ssq denotes the sum of squares.

Define $b_{gj} = P(\hat {g}_{i} = j | A_{i} = g)$ for g = 1,⋯ ,G; j = 1,⋯ ,K. The b_gj’s are collected into the G × K matrix B.

The marginal distribution of $\hat {g}_{i}$ is given by

$$ \begin{array}{@{}rcl@{}} P(\hat{g}_{1} = j ) &=& \sum\limits_{g=1}^{G} P(A_{1} = g) P(\hat{g}_{1} = j | A_{1} = g) \\ &=& \sum\limits_{g=1}^{G} \pi_{g} b_{gj} = (B^{\top} \pi)_{j}. \end{array} $$

That is, the K-vector B^⊤π is the pmf of $\hat {g}_{i}$, and

$$ P(\hat{g}_{1} = \hat{g}_{2}) = \pi^{\top} B B^{\top} \pi = ssq(B^{\top} \pi). $$

The joint probability of true linkage and its detection in a sample is

$$ \begin{array}{@{}rcl@{}} P(\hat{g}_{1} = \hat{g}_{2} , A_{1} = A_{2}) &=& \sum\limits_{g=1}^{G} \sum\limits_{j=1}^{K} P(\hat{g}_{1} = \hat{g}_{2} =j, A_{1} = A_{2} = g) \\ &=& \sum\limits_{g=1}^{G} \sum\limits_{j=1}^{K} P(A_{1} = A_{2} = g) P(\hat{g}_{1} = \hat{g}_{2} =j | A_{1} = A_{2} = g) \\ &=& \sum\limits_{g=1}^{G} \pi_{g} \sum\limits_{j=1}^{K} b_{gj}^{2} \\ &=& trace(B^{\top} diag({\pi_{g}^{2}}) B) \\ &=& trace(C^{\top} C ), \end{array} $$

where C = diag(π_g)B.

The relevant probabilities can be displayed in a 2 × 2 table as shown in Table 2. Now we easily obtain

$$ \begin{array}{@{}rcl@{}} \gamma_{2} &=& ssq(B^{\top} \pi) - trace(C^{\top} C ), \\ \gamma_{3} &=& ssq(\pi) - trace(C^{\top} C ), \\ \gamma_{1} &=& 1 - ssq(\pi) - ssq(B^{\top} \pi) + trace(C^{\top} C ), \\ CSENS &=& \gamma_{4} / (\gamma_{3} + \gamma_{4}), \\ CSPEC &=& \gamma_{1} / (\gamma_{1} + \gamma_{2}), \\ CPPV &=& \gamma_{4} / (\gamma_{2} + \gamma_{4}), \\ CNPV &=& \gamma_{1} / (\gamma_{1} + \gamma_{3}). \\ \end{array} $$

Rand’s paremeter is γ₂ + γ₄. The kappa parameter is

$$ \kappa = \frac{2 \delta} {1 - \gamma_{1} - \gamma_{4} + 2 \delta}, $$

where δ = γ₁γ₄ − γ₂γ₃.

Table 2 The 2 × 2 table of probabilities used to compute the clustering indices

1.4 A.4 Tables

1.4.1 A.4.1 Mixed Tumor Data

Below are the full index values for the mixed tumor example studied in Appendix. Indices are computed across clustering algorithms and the number of assumed subgroups.

	CSENS
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	0.98	0.943	0.802	0.749	0.724	0.646	0.625
Average linkage HC	0.98	0.959	0.874	0.835	0.817	0.785	0.785
Single linkage HC	0.98	0.959	0.941	0.884	0.85	0.85	0.834
Complete linkage HC	0.946	0.843	0.826	0.756	0.752	0.653	0.653

	CSPEC
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	0.51	0.813	0.873	0.951	0.963	0.977	0.988
Average linkage HC	0.019	0.038	0.131	0.166	0.184	0.715	0.872
Single linkage HC	0.019	0.038	0.057	0.112	0.149	0.601	0.613
Complete linkage HC	0.65	0.685	0.691	0.727	0.727	0.808	0.947

	CSENS + CSPEC
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	1.49	1.76	1.68	1.7	1.69	1.62	1.61
Average linkage HC	1	0.997	1	1	1	1.5	1.66
Single linkage HC	1	0.997	0.998	0.997	0.999	1.45	1.45
Complete linkage HC	1.6	1.53	1.52	1.48	1.48	1.46	1.6

	CPPV
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	0.402	0.628	0.68	0.837	0.867	0.903	0.947
Average linkage HC	0.251	0.251	0.252	0.252	0.251	0.48	0.673
Single linkage HC	0.251	0.251	0.251	0.251	0.251	0.417	0.419
Complete linkage HC	0.476	0.473	0.472	0.482	0.48	0.533	0.806

	CNPV
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	0.987	0.977	0.929	0.919	0.912	0.892	0.887
Average linkage HC	0.748	0.736	0.756	0.75	0.75	0.908	0.923
Single linkage HC	0.748	0.736	0.742	0.743	0.748	0.923	0.917
Complete linkage HC	0.973	0.929	0.922	0.899	0.897	0.874	0.891

	CPPV + CNPV
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	1.39	1.61	1.61	1.76	1.78	1.8	1.83
Average linkage HC	0.999	0.987	1.01	1	1	1.39	1.6
Single linkage HC	0.999	0.987	0.992	0.994	0.999	1.34	1.34
Complete linkage HC	1.45	1.4	1.39	1.38	1.38	1.41	1.7

1.4.2 A.4.2 Lung Cancer Subtype Data

Below are the full index values for the lung cancer example studied in Appendix. Indices are computed across clustering algorithms and the number of assumed subgroups. We also show the pairwise kappa index for both datasets in Fig. 7. Notice that these plots are almost identical to the sensitivity plus specificity plots but have clear differences when compared with the triplet kappa.

Fig. 7

Pairwise kappa for the mixed tumor dataset (Hoshida et al. 2007) (top panel) and lung cancer dataset (Bhattacharjee et al. 2001) (bottom panel). There are noticeable differences between this plot and the one presented in the paper for triplet kappa. This is highly suggestive that the triplet based index is capable of picking up information from higher order structures in the data

	CSENS
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	0.998	0.511	0.425	0.365	0.379	0.37	0.263
Average linkage HC	1	0.986	0.984	0.975	0.962	0.948	0.947
Single linkage HC	0.998	0.996	0.983	0.969	0.968	0.96	0.96
Complete linkage HC	0.93	0.651	0.424	0.414	0.264	0.264	0.259

	CSPEC
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	0.351	0.682	0.81	0.876	0.94	0.941	0.957
Average linkage HC	0.368	0.373	0.373	0.373	0.378	0.382	0.382
Single linkage HC	0.018	0.035	0.041	0.047	0.065	0.205	0.362
Complete linkage HC	0.404	0.688	0.839	0.845	0.87	0.878	0.92

	CSENS + CSPEC
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	1.35	1.19	1.23	1.24	1.32	1.31	1.22
Average linkage HC	1.37	1.36	1.36	1.35	1.34	1.33	1.33
Single linkage HC	1.02	1.03	1.02	1.02	1.03	1.16	1.32
Complete linkage HC	1.33	1.34	1.26	1.26	1.13	1.14	1.18

	CPPV
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	0.603	0.614	0.688	0.744	0.862	0.862	0.858
Average linkage HC	0.61	0.608	0.608	0.606	0.604	0.603	0.602
Single linkage HC	0.501	0.505	0.503	0.501	0.506	0.544	0.598
Complete linkage HC	0.607	0.673	0.722	0.726	0.667	0.682	0.761

	CNPV
	K = 2	K = 3	K = 4	K = 5	K = 6	K = 7	k = 8
K-Means	0.993	0.585	0.587	0.582	0.605	0.602	0.568
Average linkage HC	0.999	0.964	0.959	0.939	0.909	0.882	0.879
Single linkage HC	0.905	0.907	0.708	0.609	0.669	0.84	0.902
Complete linkage HC	0.853	0.666	0.595	0.593	0.544	0.547	0.557

	CPPV+CNPV
	K = 2	K = 3	K = 4	K = 5	K = 6	K 7	k = 8
K-Means	1.6	1.2	1.28	1.33	1.47	1.46	1.43
Average linkage HC	1.61	1.57	1.57	1.54	1.51	1.48	1.48
Single linkage HC	1.41	1.41	1.21	1.11	1.17	1.38	1.5
Complete linkage HC	1.46	1.34	1.32	1.32	1.21	1.23	1.32

1.5 6.5 Distribution of Hierarchical Clustering Assignments

The below contingency tables show distribution of subtypes in each cluster. Hierarchical clustering has a tendency to put outliers into separate clusters. Consequently, we see all of the subgroups being placed into the same cluster when K = 6. As more clusters are allowed we start to see some separation among the subtypes. This corresponds to the improved performance indices discussed in the paper.

Contingency table of cluster assignments for the mixed tumor data when K = 6

Pathology/cluster	1	2	3	4	5	6
Breast	23	1	1	1	0	0
Colon	23	0	0	0	0	0
Lung	22	0	0	0	1	5
Prostate	25	1	0	0	0	0

Contingency table of cluster assignments for the mixed tumor data when K = 7

Pathology/cluster	1	2	3	4	5	6	7
Breast	21	1	1	2	1	0	0
Colon	0	0	0	23	0	0	0
Lung	22	0	0	0	0	1	5
Prostate	0	1	0	25	0	0	0

Contingency table of cluster assignments for the Mixed Tumor Data when K = 8

Pathology/cluster	1	2	3	4	5	6	7	8
Breast	21	1	1	2	1	0	0	0
Colon	0	0	0	23	0	0	0	0
Lung	22	0	0	0	0	0	1	5
Prostate	0	1	0	0	0	25	0	0