Statistical analysis of clustered mixed recurrent-event data with application to a cancer survivor study

Abstract

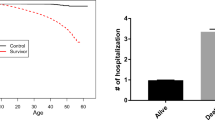
In long-term follow-up studies on recurrent events, the observation patterns may not be consistent over time. During some observation periods, subjects may be monitored continuously so that each event occurence time is known. While during the other observation periods, subjects may be monitored discretely so that only the number of events in each period is known. This results in mixed recurrent-event and panel-count data. In these data, there is dependence among within-subject events. Furthermore, if the data are collected from multiple centers, then there is another level of dependence among within-center subjects. Literature exists for clustered recurrent-event data, but not for clustered mixed recurrent-event and panel-count data. Ignoring the cluster effect may lead to less efficient analysis. In this paper, we present a marginal modeling approach to take into account the cluster effect and provide asymptotic distributions of the resulting regression parameters. Our simulation study demonstrates that this approach works well for practical situations. It was applied to a study comparing the hospitalization rates between childhood cancer survivors and healthy controls, with data collected from 26 medical institutions across North America during more than 20 years of follow-up.

Supplementary Material

In the Supplementary Material, we will sketch the proof for the asymptotic properties of the proposed estimator $\widehat{\varvec{\beta }}$. For this, we need the following regularity conditions.

(C1) The samples $\{ \, N_{i} (\cdot ) , O_{i} (\cdot ) , C_i , \mathbf{Z}_i ; i = 1 , \ldots , n\}$ are independent and identically distributed.

(C2) The $N_{i}(\tau )$’s are bounded almost surely.

(C3) Each component of $\mathbf{Z}_i$ is bounded and $P(C_i\ge \tau |\mathbf{Z}_i)>0$.

(C4) The data type random process $r_i (t)$ ($t \in [0,\tau ]$) is conditionally independent of $N^*_{ik}(t)$, $H_i(t)$, and $C_i$ given $\mathbf{Z}_i$, and $0<\inf _{z,\,0\le t\le \tau } P(r_i(t)=1|\mathbf{Z}_i )<\sup _{z,\,0\le t\le \tau } P(r_i(t)=1|\mathbf{Z}_i )<1$.

(C5) The matrix

$$\begin{aligned} {{\varvec{\Omega }}} = E\left\{ \sum _{k=1}^K \bigg [\int _0^{\tau }r_i(t) \big \{ \mathbf{Z}_i-\bar{\mathbf{z}}_{rk}(\beta , t)\big \}^{\otimes 2}dN_{ik}(t) +\{1-r_i(t)\} \big \{\mathbf{Z}_i-\bar{\mathbf{z}}_{pk}(\beta , t)\big \}^{\otimes 2}d\tilde{N}_{ik}(t)\bigg ] \right\} \end{aligned}$$

is positive definite, where $\overline{\mathbf{z}}_{rk}(t)$ and $\overline{\mathbf{z}}_{pk}(t)$ denote the limits of $\overline{\mathbf{Z}}_{rk}(t)$ and $\overline{\mathbf{Z}}_{pk}(t)$, respectively.

First we will show that $\hat{\varvec{\beta }}$ is consistent and for large n there is unique solution $\hat{{\varvec{\beta }}}$ to the equation $U ({\varvec{\beta }})=0$. For this, consider

$$\begin{aligned} D({\varvec{\beta }})= & {} \frac{1}{n} \sum _{i=1}^n \sum _{k=1}^K \displaystyle \int _0^\tau \bigg \{ r_i(t) Y_{ik}(t) \bigg [( {\varvec{\beta }}-{\varvec{\beta }}_0)^{T}{} \mathbf{Z}_i(t) -\log \bigg \{\frac{\mathbf{S}_{rk}^{(0)} ({\varvec{\beta }};t)}{\mathbf{S}_{rk}^{(0)} ({\varvec{\beta }}_0;t)}\bigg \} \bigg ] d N_{ik}(t)\\&\quad +\,(1- r_i(t)) \varDelta _{ik}(t) \bigg [( {\varvec{\beta }}-{\varvec{\beta }}_0)^{T}{} \mathbf{Z}_i(t) -\log \bigg \{\frac{\mathbf{S}_{pk}^{(0)} ({\varvec{\beta }};t)}{\mathbf{S}_{pk}^{(0)} ({\varvec{\beta }}_0;t)}\bigg \} \bigg ] d\tilde{N}_{ik}(t)\bigg \}\,. \end{aligned}$$

Note that we have that $\partial D({\varvec{\beta }})/\partial {\varvec{\beta }} = n^{-1}U({\varvec{\beta }})$ and $D({\varvec{\beta }})$ converge to a concave function $d({\varvec{\beta }})$. By the similar argument as in Lin et al. (2000) and Cheng and Wei (2000), one can easily show that $\hat{{\varvec{\beta }}}$ converges to ${\varvec{\beta }}_0$ almost surely.

For the asymptotic normality, note that under the assumption that $N_{ik}^*$, $O_{ik}$ and $C_{i}$ are mutually independent given $\mathbf{Z}_i$, we have that

$$\begin{aligned}&E\{dN_{ik}(t)|\mathbf{Z}_i\} = E\{Y_{ik}(t)|\mathbf{Z}_i\}E\{d N^*_{ik}(t)|\mathbf{Z}_i\}\\&\quad = E\{Y_{ik}(t)|\mathbf{Z}_i\}\{e^{{{\varvec{\beta }}}_0^T \mathbf{Z}_{i}}d \mu _{0k} (t) \} = E\{Y_{ik}(t) e^{ {{\varvec{\beta }}}_0^T \mathbf{Z}_{i}} d \mu _{0k} (t)|\mathbf{Z}_i\} \, ,\\&E\{d\tilde{N}_{ik}(t)|\mathbf{Z}_i\} = E\{\varDelta _{ik}(t)|\mathbf{Z}_i\}E\{N^*_{ik}(t)|\mathbf{Z}_i\}E\{dO_{ik}(t)|\mathbf{Z}_i\}\\&\quad = E\{\varDelta _{ik}(t)|\mathbf{Z}_i\}\{e^{{{\varvec{\beta }}}_0^T \mathbf{Z}_{i}} \mu _{0k} (t) \} E\{d O_{ik}(t)|\mathbf{Z}_i\} \\&\quad = E\big \{\varDelta _{ik}(t) e^{{{\varvec{\beta }}}_0^T \mathbf{Z}_{i}} \mu _{0k} (t)\,d E \{ O_{ik}(t)\}|\mathbf{Z}_i\big \} \, . \end{aligned}$$

It follows that $dM_{ik}^r(t)=dN_{ik}(t)-Y_{ik}(t)e^{{{\varvec{\beta }}}_0^T \mathbf{Z}_{i}}\ d \mu _{0k} (t)$ and

$$\begin{aligned} dM_{ik}^p(t)= & {} d\tilde{N}_{ik}(t)-\varDelta _{ik}(t)e^{{{\varvec{\beta }}}_0^T \mathbf{Z}_{i}}\mu _{0k} (t)d E \{ O_{ik}(t)\}\\= & {} d \tilde{N}_{ik}(t) \, - \, \varDelta _{ik} (t) \, e^{{\varvec{\beta }}_0^T \mathbf{Z}_{i} } \, d \varGamma _{0k} (t) \end{aligned}$$

are all mean-zero processes.

By the Taylor series expansion, we have that

$$\begin{aligned}&\sqrt{n}\{\widehat{{\varvec{\beta }}}-{{\varvec{\beta }}}_0\}=\widehat{\varvec{\Omega }}^{-1}({\varvec{\beta }}^{*})\frac{1}{\sqrt{n}} U({\varvec{\beta }}_0)\\&\quad =\widehat{\varvec{\Omega }}^{-1}({\varvec{\beta }}^{*})\displaystyle \frac{1}{\sqrt{n}} \displaystyle \sum _{i=1}^n \sum _{k=1}^K \displaystyle \int _0^\tau \bigg [r_i(t)\Big \{\mathbf{Z}_i-\overline{\mathbf{Z}}_{rk}(t)\Big \}dM^r_{ik}(t)\\&\qquad +\,\{1-r_i(t)\}\Big \{\mathbf{Z}_i-\overline{\mathbf{Z}}_{pk}(t)\Big \}dM^p_{ik}(t) \bigg ], \end{aligned}$$

where ${{\varvec{\beta }}}^*$ is on the line segment between $\widehat{{\varvec{\beta }}}$ and ${\varvec{\beta }}_0$. It is clear that $M_{ik}^r(t)$ and $M_{ik}^p(t)$ are all the differences of two monotone functions in t. Thus based on the results of Lin et al. (2000) (Appendix A.2) or the empirical processes (Pollard 1990, page 15) and the multivariate central limit theorem, one can prove the tightness and weak convergency of $\sqrt{n}\{\widehat{{\varvec{\beta }}}-{{\varvec{\beta }}}_0\}$ by the consistency of $\widehat{{\varvec{\beta }}}$ and $\hat{ \varOmega }({\varvec{\beta }}_0)$ for ${\varvec{\beta }}_0$ and $\varvec{\Omega }$, the nonnegativeness of $r_i(t)$, and the boundedness of $\mathbf{Z}_i$. The asymptotic normality thus follows.