Nonlinear multiscale simulation of instabilities due to growth of an elastic film on a microstructured substrate

Abstract

The objective of this contribution is the numerical investigation of growth-induced instabilities of an elastic film on a microstructured soft substrate. A nonlinear multiscale simulation framework is developed based on the FE² method, and numerical results are compared against simplified analytical approaches, which are also derived. Living tissues like brain, skin, and airways are often bilayered structures, consisting of a growing film on a substrate. Their modeling is of particular interest in understanding biological phenomena such as brain development and dysfunction. While in similar studies the substrate is assumed as a homogeneous material, this contribution considers the heterogeneity of the substrate and studies the effect of microstructure on the instabilities of a growing film. The computational approach is based on the mechanical modeling of finite deformation growth using a multiplicative decomposition of the deformation gradient into elastic and growth parts. Within the nonlinear, concurrent multiscale finite element framework, on the macroscale a nonlinear eigenvalue analysis is utilized to capture the occurrence of instabilities and corresponding folding patterns. The microstructure of the substrate is considered within the large deformation regime, and various unit cell topologies and parameters are studied to investigate the influence of the microstructure of the substrate on the macroscopic instabilities. Furthermore, an analytical approach is developed based on Airy’s stress function and Hashin–Shtrikman bounds. The wavelengths and critical growth factors from the analytical solution are compared with numerical results. In addition, the folding patterns are examined for two-phase microstructures and the influence of the parameters of the unit cell on the folding pattern is studied.

1 Introduction

Biological tissues are an important class of soft materials. Due to their low stiffness, they are subjected to large deformations, and in particular to morphological instabilities, which can be induced due to mechanical forces, changes in temperature, tissue growth, etc. As a result of having a low elastic modulus, soft materials are especially prone to surface instabilities, for example, induced by buckling. These instabilities mostly occur in the form of wrinkling and folding. The evolution of structural instabilities plays a vital role, which appropriates the biological function of a living system [1]. For instance, in brain development of mammals, the brain surface morphology is often connected with intelligence and closely correlated with neurological dysfunction, [2]. Other examples are villi formation in the intestine [3], folding of a developing brain [2, 4, 5], wrinkling of skin [6], and morphogenesis of various fruits [7].

The mathematical modeling of folding in tubular organs and the folding of mucous membranes has been studied and was an interesting subject for scientists [8,9,10,11]. In general, the problem of instabilities in soft materials has also been studied extensively using computational methods in recent years [12,13,14,15,16,17,18,19]. In particular, instabilities of bilayered structures consisting of a stiff film adhered to a soft substrate are important due to their applications in modeling of biological tissues.

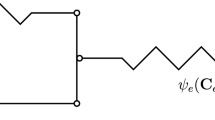
Such a bilayered structure is illustrated in Fig. 1. The film may grow isotropically or anisotropically, and due to the boundary conditions the stress in the film increases while the body tends to relax. By getting close to a critical value of growth in the film, the structure becomes unstable and the stored energy in the film is released, hereby buckling/wrinkling. Recently, these instabilities in form of wrinkling [2, 12, 20], folding [13, 21], and creasing [14, 22, 23] have been studied.

Fig. 1

Growth-induced instability of an elastic growing film on a microstructured elastic non-growing substrate

Growth has already been modeled frequently within the concept of open system thermodynamics, where the body is allowed to exchange mass, momentum, and entropy with its environment across its boundary through corresponding fluxes [24,25,26,27,28]. The concept of finite growth in continuum approaches is used in modeling of growth-induced instabilities [29]. Hence, the modeling of growth is based on the finite deformation theory in nonlinear continuum mechanics and the concept of multiplicative decomposition of the deformation gradient has been used to study and to model growth by continuum approaches. In this theory, the deformation gradient is decomposed into elastic and growth parts, which connect the growth to the kinematic relations [29, 30]. The artificial intermediate configuration has been considered and is necessary in modeling of growth [31]. More details on continuum theory of growth can be found in [24, 31,32,33,34,35,36,37,38,39].

For investigation of instabilities within continuum mechanics and the finite element (FE) framework, two common numerical approaches are perturbation and eigenvalue analysis [40]. Eigenvalue analysis is the more precise method, though computationally more expensive, and in this work we utilize it to capture critical growth factors and corresponding folding patterns.

The influence of different geometrical and mechanical properties of substrates on growth-induced instabilities has already been subjected to extensive studies of film–substrate structures: the effect of curved substrates on instabilities of the film [7, 41], nonuniform stiffness distributions [5, 42,43,44,45], or material properties of the substrate [46], among others. In most of the contributions on the subject, the substrate is considered as a homogeneous material. However, in particular in biomedical applications, the substrate often has a heterogeneous microstructure, which may have a great impact on the growth-induced behavior and instabilities of film–substrate structures. A multiscale framework is proposed to investigate spatial pattern formation and buckling of a thin film on a soft substrate, which is essentially different [19]. Here, we consider the heterogeneity of the substrate through a homogenization procedure of a periodic microstructure in the framework of concurrent multiscale finite element analysis using the FE² method, see [47,48,49]. Within the FE² framework, the effective stiffness in every quadrature point of the numerical integration of the macroscale solution is calculated from the behavior of a respective microstructure, which is homogenized from a nonlinear finite element analysis (FEA) of the representative unit cell (RUC) with applied macroscopic deformation gradient as the boundary condition. Since both, the macro- and microscopic problems are nonlinear and instabilities are of main interest, the concurrent multiscale approach is pursued in this work.

Using this numerical framework, we assume a microstructured substrate and study the effects of microstructural parameters, showing that the heterogeneity of the substrate has a considerable impact on the critical growth of the film and folding patterns. In particular, a representative volume element or unit cell (RVE/RUC) with two material phases in the form of a spherical inclusion is investigated. Furthermore, also an analytical approach based on Airy’s stress function is derived and used to show the reliability of the numerical solutions. Therefore, Hashin–Shtrikman bounds are utilized to determine the effective stiffness of the substrate through an analytical homogenization approach.

The key contributions of this work are:

• 1. The development of a nonlinear concurrent multiscale simulation framework for the analysis of instabilities of growing films on microstructured substrates with periodic microstructure.

• 2. The derivation of a simplified analytical model for critical growth based on Airy’s stress function and Hashin–Shtrikman bounds.

• 3. The verification of the numerical method through convergence and parameters studies and assessment of numerical against analytical results.

• 4. The numerical investigation of the effects of microstructural parameters of the substrate on critical growth and folding patterns of the film.

This manuscript is organized as follows: The computational modeling and simulation method is explained in detail in Sect. 2, and the analytical approach is introduced in Sect. 3. Both methods are applied to compute critical growth of bilayered structures with a thin, growing film on a microstructured substrate in Sect. 4, and the results for varying microstructural parameters are discussed. Finally, a summary and concluding remarks are given in Sect. 5.

2 Computational approach

The numerical approach is based on the theory of finite deformation continuum mechanics (Sect. 2.1). The film is modeled as a nonlinear hyperelastic solid, and its growth is modeled by a multiplicative decomposition of the deformation gradient into elastic and growth parts (Sect. 2.2). The substrate is heterogeneous and possesses a periodic microstructure. On the macroscale, it is also modeled as a nonlinear hyperelastic continuum, but its constitutive behavior is homogenized from the microscale. For this purpose, representative volume elements of the substrate microstructure are analyzed using asymptotic homogenization with the macroscopic deformation gradients as boundary conditions, where their constituents, the two different material phases, are again modeled as nonlinear hyperelastic continua (Sect. 2.3). Both, the macroscopic problem consisting of the growing film attached to the substrate and the microscopic problem consisting of the RVE microstructure of the substrate, are discretized by the finite element method (FEM). The growth-driven, quasi-static deformation of the structure is analyzed by concurrent multiscale simulation (FE² method), and instabilities are determined by solving an accompanying eigenvalue problem for the macroscopic tangent stiffness matrix (Sect. 2.4).

2.1 Continuum mechanics preliminaries

Consider a continuum body $\mathcal {B}_0\subset {\mathbb {R}}^d$, where $d=2,3$, in its material configuration at time $t=0$, in Fig. 2. The body $\mathcal {B}_0$ is deformed from its material configuration into a spatial configuration $\mathcal {B}_t\subset {\mathbb {R}}^d$ at time $t>0$ by a deformation map ${\varvec{\varphi }}:\mathcal {B}_0\rightarrow \mathcal {B}_t$ . The deformation gradient ${\textit{\textbf{F}}} := \text{ Grad }{\varvec{\varphi }}$ transforms a line element $d{\textit{\textbf{X}}}$ from the material configuration to in the spatial configuration via $d{\textit{\textbf{x}}}= {\textit{\textbf{F}}}\, d{\textit{\textbf{X}}}$. Volume transformations due to deformation are denoted with $J =\det {{\textit{\textbf{F}}}}$, which is the determinant of the Jacobian of the deformation map and relates a volume element dV in the material configuration to the volume element dv in the spatial configuration as $dv=J\,dV$.

Fig. 2

Kinematics of growth with multiplicative decomposition of deformation gradient into elastic ${\textit{\textbf{F}}}_e$ and growth ${\textit{\textbf{F}}}_g$ parts. The growth part ${\textit{\textbf{F}}}_g$ maps the body $\mathcal {B}_0$ into an intermediate configuration $\mathcal {B}_g$, which is in general incompatible, and the elastic part of the deformation gradient maps the body $\mathcal {B}_g$ into a stressed spatial configuration $\mathcal {B}_t$. The deformation map or motion ${\varvec{\varphi }}$ maps the body $\mathcal {B}_0$ from the material configuration at time $t=0$ into the spatial configuration $\mathcal {B}_t$ at time $t>0$. The linear tangent map ${{\textit{\textbf{F}}}} := \text{ Grad }{\varvec{\varphi }}$ maps the line element $\text {d}{\textit{\textbf{X}}}$ from the material configuration in $\text {d}{\textit{\textbf{x}}}$ to the spatial configuration

2.2 Growing elastic film

As mentioned previously, a multiplicative decomposition of the deformation gradient into elastic and growth parts is used to model growth kinematics in finite deformation theory. Therefore, the deformation gradient ${\textit{\textbf{F}}}$ reads:

$$\begin{aligned} \begin{aligned} {\textit{\textbf{F}}}= {\textit{\textbf{F}}}_e\ \cdot \ {\textit{\textbf{F}}}_g \ \ \Rightarrow \ \ {\textit{\textbf{F}}}_e\ =\ {\textit{\textbf{F}}}\ \cdot \ {\textit{\textbf{F}}}_{g}^{-1}, \end{aligned} \end{aligned}$$

(1)

where ${\textit{\textbf{F}}}_e$ and ${\textit{\textbf{F}}}_g$ are the elastic and growth parts of the deformation gradient ${\textit{\textbf{F}}}$, respectively. The determinants of the elastic and growth parts of the deformation gradient are interpreted as $J_e =\det {{\textit{\textbf{F}}}_e}$ and $J_g=\det {{\textit{\textbf{F}}}_g}$, respectively. The growth part of the deformation gradient maps the body $\mathcal {B}_0$ from the material configuration, which is stress-free, into an intermediate configuration $\mathcal {B}_g$, which is in general incompatible. The elastic part of the deformation gradient maps the intermediate configuration into a compatible spatial configuration $\mathcal {B}_t$, see Fig. 2.

The growth part of the deformation gradient tensor ${\textit{\textbf{F}}}_g$ does not necessarily correspond to a compatible displacement field, which implies that the change in the zero-stress state does not need to be continuous during growth. Thus, to maintain continuity of the body during the growth process, the elastic deformations are required [29]. Figure 2 illustrates these kinematic relations of growth. For more details on modeling of growth, see [29, 40, 50].

Growth of the film can be considered either as isotropic, which means that the volume changes equally in all directions, or it can be anisotropic, which means unequal growth in different spatial directions. For isotropic growth, the growth part of the deformation gradient can be described as:

$$\begin{aligned} {\textit{\textbf{F}}}_g = {\textit{\textbf{I}}} + g \ {\textit{\textbf{I}}} = (1 + g) \ {\textit{\textbf{I}}}\, , \end{aligned}$$

(2)

with ${\textit{\textbf{I}}}$ being the identity tensor and g a growth parameter. In the absence of growth, $g=0$, the growth tensor is equal to the identity tensor and the deformation gradient is equal to its elastic part ${\textit{\textbf{F}}}_e$. Anisotropic growth along the in-plane directions of the film, without growth in the lateral direction, is defined as:

$$\begin{aligned} {\textit{\textbf{F}}}_g = {\textit{\textbf{I}}} + g \ {\textit{\textbf{I}}}_{\text {ani}}\, , \end{aligned}$$

(3)

where ${\textit{\textbf{I}}}_{\text {ani}}={\textit{\textbf{I}}}-{\textit{\textbf{N}}} \otimes {\textit{\textbf{N}}}$, and ${\textit{\textbf{N}}}$ is the unit normal vector to the film. The free energy function for constitutive modeling of hyperelastic materials is interpreted in terms of ${\textit{\textbf{F}}}$ and ${\textit{\textbf{F}}}_g$ as $\psi ({\textit{\textbf{F}}},{\textit{\textbf{F}}}_g)$ and renders the same value as the elastic free energy. Therefore, the energy function in terms of deformation gradient reads:

$$\begin{aligned} \begin{aligned} \psi = \psi ({\textit{\textbf{F}}},{\textit{\textbf{F}}}_g) = \psi _e({\textit{\textbf{F}}}_e). \end{aligned} \end{aligned}$$

(4)

Due to the balance of linear momentum in finite deformation theory, the governing balance equation for the continuum body $\mathcal {B}_0$ at time $t=0$ in a quasistatic process holds:

(5)

in which ${\textit{\textbf{b}}}_0$ is the body force density in material configuration and ${\textit{\textbf{P}}}$ is the Piola–Kirchhoff stress. Due to the second law of thermodynamics and Coleman–Noll procedure, the Piola–Kirchhoff stress for a hyperelastic material can be determined as [40]:

$$\begin{aligned} \begin{aligned} {\textit{\textbf{P}}}&= \frac{\partial \psi }{\partial {\textit{\textbf{F}}}} = \frac{\partial \psi _e}{\partial {\textit{\textbf{F}}}_e}: \frac{\partial {\textit{\textbf{F}}}_e}{\partial {\textit{\textbf{F}}}} = \frac{\partial \psi _e}{\partial {\textit{\textbf{F}}}_e}:\left( {\textit{\textbf{I}}}\ \overline{\otimes } \ {\textit{\textbf{F}}}_g^{-\top }\right) \\&= {\textit{\textbf{P}}}_e \cdot {\textit{\textbf{F}}}_g^{-\top } \quad \text {with} \quad {\textit{\textbf{P}}}_e := \frac{\partial \psi _e}{\partial {\textit{\textbf{F}}}_e}\, , \end{aligned} \end{aligned}$$

(6)

where the operator $\overline{\otimes }$ denotes a non-standard dyadic product with the index notation property $({\textit{\textbf{A}}}\ \overline{\otimes }\ {\textit{\textbf{B}}})_{ijkl} = {\textit{\textbf{A}}}_{ik}\ {\textit{\textbf{B}}}_{jl}$ for two second-order tensors ${\textit{\textbf{A}}}$ and ${\textit{\textbf{B}}}$. In derivation (6), the following relation is utilized:

$$\begin{aligned} \begin{aligned} \frac{\partial {\textit{\textbf{F}}}_e}{\partial {\textit{\textbf{F}}}} = \frac{\partial ({\textit{\textbf{F}}}\cdot {\textit{\textbf{F}}}_g)}{\partial {\textit{\textbf{F}}}} = {\textit{\textbf{I}}}\ \overline{\otimes }\ {\textit{\textbf{F}}}_g^{-\top }. \end{aligned} \end{aligned}$$

(7)

To compute the tangent stiffness in a nonlinear finite element method, the tangent moduli ${\mathbb {C}}$ needs to be derived. The fourth-order tensor ${\mathbb {C}}$ is the second derivative of the free energy density (4) with respect to the deformation gradient:

$$\begin{aligned} \begin{aligned} {\mathbb {C}}&=\displaystyle \frac{\partial }{\partial {\textit{\textbf{F}}}} \left( \frac{\partial \psi }{\partial {\textit{\textbf{F}}}}\right) = \frac{\partial {\textit{\textbf{P}}}}{\partial {\textit{\textbf{F}}}} = \frac{\text {d}\left( {\textit{\textbf{P}}}_e \cdot {\textit{\textbf{F}}}_g^{-\top }\right) }{\text {d} {\textit{\textbf{F}}}_e} : \frac{\text {d} {\textit{\textbf{F}}}_e}{\text {d} {\textit{\textbf{F}}}} \\&= \left( {\textit{\textbf{I}}}\ \overline{\otimes } \ {\textit{\textbf{F}}}_g^{-1}\right) : {\mathbb {C}}_e : \left( {\textit{\textbf{I}}}\ \overline{\otimes } \ {\textit{\textbf{F}}}_g^{-\top }\right) \\&\text {with} \quad {\mathbb {C}}_e = \frac{\partial {\textit{\textbf{P}}}_e}{\partial {\textit{\textbf{F}}}_e} \, . \end{aligned} \end{aligned}$$

(8)

For the problem at hand, a compressible Neo–Hookean constitutive model is used to compute the hyperelastic response of the material:

$$\begin{aligned} \begin{aligned} \psi _e =&\ \displaystyle \frac{1}{2} \mu \left( {\textit{\textbf{F}}}_e : {\textit{\textbf{F}}}_e - 3 - 2 \ln J_e\right) + \displaystyle \frac{1}{2} \lambda \left( \displaystyle \frac{1}{2} \left( J_e^2 - 1\right) \right. \\&-\ln J_e\Bigr ) \, , \end{aligned} \end{aligned}$$

(9)

where $\mu$ and $\lambda$ are material constants known as Lamé parameters. By considering given free energy function given in (9), the Piola–Kirchhoff stress in (6) and the tangent moduli in (8) read

$$\begin{aligned}&{\textit{\textbf{P}}} = \mu ({\textit{\textbf{F}}}_e-{\textit{\textbf{F}}}_e^{-\top }) \cdot {\textit{\textbf{F}}}_g^{-\top } + \frac{1}{2}\lambda (J_e^2-1)\ {\textit{\textbf{F}}}_e^{-\top }\cdot {\textit{\textbf{F}}}_g^{-\top } \, , \end{aligned}$$

(10)

$$\begin{aligned}&\begin{aligned} {\mathbb {C}} =&\left( {\textit{\textbf{I}}}\ \overline{\otimes } \ {\textit{\textbf{F}}}_g^{-1}\right) : \biggl ( \mu \ \left( {\textit{\textbf{I}}} \ \overline{\otimes } \ {\textit{\textbf{I}}} +{\textit{\textbf{F}}}_e^{-\top } \ \underline{\otimes }\ {\textit{\textbf{F}}}_e^{-1} \right) \\&- \frac{1}{2}\lambda \ (J_e^2-1)\ {\textit{\textbf{F}}}_e^{-\top }\ \underline{\otimes } \ {\textit{\textbf{F}}}_e^{-1} \\&+ \lambda \ J_e^2\ {\textit{\textbf{F}}}_e^{-\top }\otimes {\textit{\textbf{F}}}_e^{-\top }\biggr ) : \left( {\textit{\textbf{I}}}\ \overline{\otimes } \ {\textit{\textbf{F}}}_g^{-\top }\right) \, , \end{aligned} \end{aligned}$$

(11)

where the operator $\underline{\otimes }$ denotes another non-standard dyadic product with the index notation property $({\textit{\textbf{A}}} \ \underline{\otimes } \ {\textit{\textbf{B}}})_{ijkl} = {\textit{\textbf{A}}}_{il}\ {\textit{\textbf{B}}}_{jk}$ for two second-order tensors ${\textit{\textbf{A}}}$ and ${\textit{\textbf{B}}}$.

2.3 Microstructured substrate

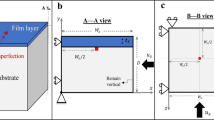
Consider the bilayered film–substrate structure in Fig. 3, which possesses a microstructure in the substrate. The representative volume element $\varOmega$ describes the microstructure of the elastic substrate. It is composed of two different phases $\varOmega _1$ and $\varOmega _2$ with $\varOmega _1\cap \varOmega _2=\emptyset ,\, {\bar{\varOmega }}={\bar{\varOmega }}_1\cup {\bar{\varOmega }}_2$, where $\varOmega _1$ represents a matrix material and $\varOmega _2$ is an inclusion, which could be void or from a different (softer) material.

As the two material phases $\varOmega _1$ and $\varOmega _2$ possess different properties, they lead to unequal stiffness and highly oscillating stress distributions within the body. Since the characteristic size of the microstructure, i.e., the size of the inclusions, is assumed to be much smaller than the overall dimensions of the substrate, it is not feasible to simulate the substrate at full resolution of the microstructure, and instead, it is modeled with a homogenization process, see [48, 49].

Fig. 3

Microstructure of continuum body $\mathcal {B}_t$ in the spatial configuration. Through micro-to-macrotransition, the deformation gradient at every quadrature point in macroscopic solution ${\textit{\textbf{F}}}^{*}$ is applied on boundaries of the RVE domain. The equivalent tangent moduli ${\mathbb {C}}^{*}$ are calculated in the homogenization process of microstructure

The equivalent stiffness of a heterogeneous material is calculated through a homogenization process, which is based on a micro-to-macrotransition. Within the finite element framework, the calculated deformation gradient ${\textit{\textbf{F}}}^{*}$ in the macroscopic domain is assumed to be equal to the averaged deformation gradient of the microscopic domain:

$$\begin{aligned} {\textit{\textbf{F}}}^{*} = \langle {\textit{\textbf{F}}}\rangle = \frac{1}{|\varOmega |}\int _{\varOmega }{\textit{\textbf{F}}} \ \text {d}\varOmega \, . \end{aligned}$$

(12)

For the homogenization, ${\textit{\textbf{F}}}^{*}$ is applied to the microscopic RVE domain as a boundary condition in every iteration of the solution for each numerical integration point of the macroscopic problem. The microscopic problem is solved with the applied deformation gradient on its boundaries, and the resulting averaged stresses ${\textit{\textbf{P}}}^*$ and tangent moduli ${\mathbb {C}}^{*}$ are computed based on the solution:

$$\begin{aligned} {\textit{\textbf{P}}}^{*} = \langle {\textit{\textbf{P}}}\rangle = \frac{1}{|\varOmega |}\int _{\varOmega }{\textit{\textbf{P}}} \ \text {d}\varOmega \, , \qquad {\mathbb {C}}^{*}= \frac{\partial {\textit{\textbf{P}}}^{*} }{\partial {\textit{\textbf{F}}}^{*} } \, . \end{aligned}$$

(13)

These averaged quantities are then transferred back to the macroscopic problem as the equivalent stress and tangent moduli at the quadrature point. Obviously, the material properties and morphological structure of the RVE affect the equivalent stresses ${\textit{\textbf{P}}}^*$ and tangent moduli ${\mathbb {C}}^{*}$ and consequently the macroscopic response of the continuum body.

The RVE domain in Fig. 3 consists of two different material phases $\varOmega _1$ and $\varOmega _2$, as mentioned previously. Their material properties are given in terms of the elastic moduli $E_1$ and $E_2$, respectively. Obviously, if $E_2 = E_1$, the microstructure is homogeneous and the substrate can be assumed as continuous. For $0 \le E_2 < E_1$, the effective stiffness of the microstructure decreases. Similarly, the stiffness decreases with increasing diameter of the circular domain of $\varOmega _2$.

2.4 Numerical framework for instability analysis

For modeling of growth within the nonlinear finite element framework, the growth parameter g, see (2), is usually incrementally increased from $g=0$ at $t=0$ to a final value $g>0$ at $t>0$. This increment of growth raises the value of the deformation gradient ${\textit{\textbf{F}}}$, which causes stress in the elastic film. In the $\text {FE}^2$ procedure, the deformation gradient at every quadrature point in the macrodomain is applied to the microdomain as a displacement boundary condition. Therefore, by dividing spatial nodal positions in the microdomain into boundary nodes of the RVE ${\textit{\textbf{x}}}_c\in \partial \varOmega$ and nodes within the domain ${\textit{\textbf{x}}}_f\in \varOmega$, we have:

$$\begin{aligned} \begin{aligned} {\textit{\textbf{x}}}_c = {\mathbb {D}} \cdot {\textit{\textbf{F}}}^* \, , \end{aligned} \end{aligned}$$

(14)

where ${\mathbb {D}}$ is a matrix containing boundary nodal coordinates of the microcell, see [48]. By partitioning force vector ${\textit{\textbf{f}}}$ and tangent stiffness matrix ${\textit{\textbf{K}}}$ into free degrees of freedom (free DOFs, f index) and constrained DOFs (c index), we get:

$$\begin{aligned} \begin{aligned} {\textit{\textbf{f}}} = \begin{pmatrix} {\textit{\textbf{f}}}_{f} \\ {\textit{\textbf{f}}}_{c} \end{pmatrix} , \quad \quad {\textit{\textbf{K}}}= \begin{pmatrix} {\textit{\textbf{K}}}_{ff} &{} {\textit{\textbf{K}}}_{fc} \\ {\textit{\textbf{K}}}_{cf} &{} {\textit{\textbf{K}}}_{cc} \end{pmatrix} \, . \end{aligned} \end{aligned}$$

(15)

After obtaining a converged finite element solution for a given residuum of the force vector at free DOFs in the micro-RVE, $\Vert {\textit{\textbf{f}}}_f\Vert <\text {tol}$, the condensed stiffness matrix is determined as:

$$\begin{aligned} \begin{aligned} \overline{{\textit{\textbf{K}}}}_{cc}={\textit{\textbf{K}}}_{cc}-{\textit{\textbf{K}}}_{cf}{\textit{\textbf{K}}}_{ff}^{-1}{\textit{\textbf{K}}}_{fc} \, , \end{aligned} \end{aligned}$$

(16)

and then, the effective, homogenized Piola–Kirchhoff stress ${\textit{\textbf{P}}}^*$ and tangent moduli ${\mathbb {C}}^*$ at the macroquadrature point can be computed as:

$$\begin{aligned} \begin{aligned} {\textit{\textbf{P}}}^*=\frac{1}{|{\varOmega }|}\ {\mathbb {D}}\ {\textit{\textbf{f}}}_c\, , \quad {\mathbb {C}}^*= \frac{1}{|{\varOmega }|}\ {\mathbb {D}}\ \overline{{\textit{\textbf{K}}}}_{cc}\ {\mathbb {D}}^\text {T} \, , \end{aligned} \end{aligned}$$

(17)

in which $|{\varOmega }|$ is the volume of the microscopic RVE $\varOmega$. More details on this micro-to-macrotransition can be found in [47,48,49].

Once the computed equivalent Piola–Kirchhoff stress ${\textit{\textbf{P}}}^*$ and the equivalent tangent moduli ${\mathbb {C}}^*$ are transferred to macroscopic quadrature point, the finite element analysis proceeds to determine the solution of the macroscopic problem using a Newton–Raphson scheme. The Newton–Raphson scheme determines the spatial coordinates by vanishing the residuum of the weak form, ${\textit{\textbf{r}}}( {\textit{\textbf{x}}}_{m+1} ) = {\textit{\textbf{r}}}( {\textit{\textbf{x}}}_{m} ) \ + \frac{\partial {\textit{\textbf{r}}}}{\partial {\textit{\textbf{x}}}} \varDelta {\textit{\textbf{x}}}$, where m is the current Newton iteration step, $\varDelta {\textit{\textbf{x}}}={\textit{\textbf{x}}}_{m+1}-{\textit{\textbf{x}}}_{m}$, and the derivative of the residual with respect to ${\textit{\textbf{x}}}$ represents the tangent stiffness matrix as $\mathbf{K } = \partial {\textit{\textbf{r}}} / \partial {\textit{\textbf{x}}}$. More details on the Newton–Raphson scheme in nonlinear finite element method can be found in [51]. The eigenvalue representation for a diagonalizable stiffness matrix $\mathbf{K }\in {\mathbb {R}}^{n \times n}$ for a system with n degrees of freedom can be written as, see [40]:

$$\begin{aligned} \begin{aligned} \mathbf{K }&= \lambda _1 \ {\varvec{\phi }}_1 \otimes {\varvec{\phi }}_1 + \lambda _2 \ {\varvec{\phi }}_2 \otimes {\varvec{\phi }}_2 + ... + \lambda _i \ {\varvec{\phi }}_i \otimes {\varvec{\phi }}_i \\&+ ... + \lambda _n \ {\varvec{\phi }}_n \otimes {\varvec{\phi }}_n = \sum _{i = 1}^{n} \lambda _i \ {\varvec{\phi }}_i \otimes {\varvec{\phi }}_i \, , \end{aligned} \end{aligned}$$

(18)

in which $\lambda _i$ represents the eigenvalues of the stiffness matrix and ${\varvec{\phi }}_i$ the associated unit eigenvectors for $i = 1, ...,n$.

In this work, the eigenvalue analysis of the tangent stiffness matrix is used to determine the instabilities of the structure. The stiffness matrix is initially symmetric and positive definite, i.e., its eigenvalues are all positive, $\lambda _i>0 \, \forall i=1,\ldots ,n$, and becomes indefinite when an instability occurs, i.e., one or more eigenvalues become zero or negative. To determine the critical growth factor $g_\text {cr}$ at which the instability occurs, g is incremented as:

$$\begin{aligned} \begin{aligned} g_{n+1}\ = \ g_n\ +\ \varDelta g \, , \end{aligned} \end{aligned}$$

(19)

where n is the step number. In every step, the eigenvalues of the stiffness matrix are computed and if all eigenvalues are positive, the growth factor is increased for the next step, until one of the eigenvalues becomes zero or negative. To adjust the step size $\varDelta g$, a bisection or secant method can be used. After reaching the critical growth factor $g_\text {cr}$, the associated eigenvector of the negative eigenvalue describes the folding pattern, see [40].

3 Analytical approach

The computational approach introduced in the previous section is based on the large deformation theory to capture geometrical nonlinearities. However, we are interested in instabilities that occur when buckling of the film on the substrate starts, and therefore, a simplified analytical approach is derived based on small strain theory. Geometrical instabilities are implicitly assumed with a buckling analysis of the film.

Consider a two-dimensional structure which consists of a film on a substrate in plane strain scenario, as shown in Fig. 4. The aim is to calculate the critical growth factor of the film, at which the geometrical instabilities occur under growth-induced compression, via buckling analysis of the structure. The film and substrate are assumed as linear elastic materials. The governing equation of the film in Fig. 4, adhered to an infinite half-space, reads [52]:

$$\begin{aligned} \begin{aligned} E_f\frac{bh^3}{12} \ \frac{d^4 w}{d x^4} + h\ \sigma \frac{d^2 w}{d x^2} = f_s \, , \end{aligned} \end{aligned}$$

(20)

where $w=w_0 \cos (nx)$ is the sinusoidal deflection of the film, $E_f$ is the elastic modulus of the film, $\sigma$ is the stress in the film, h is the film thickness, b is the width of the structure, and $f_s$ is the transverse force on the film from the substrate, which depends on the material properties of the substrate. The stress in the film is related to the lateral force P via $P = \sigma h b$. Based on theory of the sandwich members [52], the transverse force reads:

$$\begin{aligned} \begin{aligned} f_s = \ -\frac{2 E_s}{(3 -\nu _s)(1 + \nu _s)} \ n \ w \, , \end{aligned} \end{aligned}$$

(21)

in which $n=2\pi /\lambda$, is the wavenumber on the surface, $E_s$ is the Young’s modulus, $\nu _s$ the Poisson’s ratio of the substrate, and $\lambda$ is the wavelength.

Fig. 4

Analytical model of growing elastic film on a substrate. h is the film thickness; $\lambda$ is the wavelength. $w_0$ represents transverse amplitude, and b is the width of the structure

By regarding $b=1$, substituting (21) in (20), and solving for $\sigma$, we have:

$$\begin{aligned} \begin{aligned} \sigma = E_f\frac{h^2}{12} n^2 + \frac{2 E_s}{(3 - \nu _s)(1 + \nu _s)\ h\ n} \, . \end{aligned} \end{aligned}$$

(22)

The critical wavenumber $n_\text {cr}$ is calculated by minimizing $\sigma$ in (22) as a function of n:

$$\begin{aligned} \begin{aligned} n_\text {cr} = \root 3 \of {\frac{12 E_s}{E_f (3 - \nu _s)(1 + \nu _s) h^3}} \, . \end{aligned} \end{aligned}$$

(23)

Then, the critical stress $\sigma _\text {cr}$ is then obtained by substituting (23) in (22). The critical growth factor at which the film buckles is obtained as:

$$\begin{aligned} \begin{aligned} g_\text {cr}= \frac{\varepsilon _\text {cr}}{1-\varepsilon _\text {cr}} \, \qquad \text {with} \quad \varepsilon _\text {cr}= \frac{\sigma _\text {cr}}{E_f} \, , \end{aligned} \end{aligned}$$

(24)

where $\varepsilon _\text {cr}$ is the critical strain calculated from $\sigma _\text {cr}$.

The right-hand side of (20) represents the contribution of the substrate on the instabilities of the film. This term depends on the material properties of the substrate, $E_s$ and $\nu _s$, which affect the critical growth of the film implicitly. Here, we assume the growing film and substrate as elastic materials; similar work has been done also for viscoelastic materials [46]. As mentioned previously in Sect. 2.3, substrates with heterogeneous microstructure are considered. The material response to external forces can be obtained analytically through a homogenization process of the microstructure, which determines the effective elastic modulus $E_s$.

Analytical bounds such as the ones introduced by Hill, Voigt and Reuss or Hashin and Shtrikman can be utilized to determine the effective material parameters of a RVE consisting of material phases $\varOmega _1$ and $\varOmega _2$, such as the one shown previously in Fig. 3, with Young’s moduli $E_1$ and $E_2$ and Poisson’s ratios $\nu _1$ and $\nu _2$, respectively, or equivalently with bulk moduli $\kappa _1,\kappa _2$ and shear moduli $\mu _1,\mu _2$. The Hill–Reuss–Voigt bounds for the effective Young’s modulus $E^*$ are given as:

$$\begin{aligned} \begin{aligned} \underbrace{\frac{E_1E_2}{\eta _1 E_2+\eta _1 E_2}}_{\begin{array}{c} \text {elastic modulus -}\\ \text {lower bound} \end{array}}\leqslant E^* \leqslant \underbrace{\eta _1 E_1 + \eta _2 E_2}_{\begin{array}{c} \text {elastic modulus-} \\ \text {upper bound} \end{array}} \, , \end{aligned} \end{aligned}$$

(25)

where $\eta _1$ and $\eta _2$ represent the volume fractions of $\varOmega _1$ and $\varOmega _2$, respectively, and are defined as $\eta _1 = |\varOmega _1|/|\varOmega |$ and $\eta _2 = |\varOmega _2|/|\varOmega |= 1-\eta _1$.

However, here we utilize the tighter Hashin–Shtrikman lower and upper bounds for the effective bulk modulus $\kappa ^*$ and shear modulus $\mu ^*$, which are given for a two-phase microstructure as, see [47]:

$$\begin{aligned}&\begin{aligned} \underbrace{ {\kappa }_2 + \frac{\eta _1}{\frac{1}{{\kappa }_1-{\kappa }_2}+\frac{3(1-\eta _1)}{3{\kappa }_2+4{\mu }_2}}}_{\begin{array}{c} \text {bulk modulus -}\\ \text { lower bound} \end{array}} \, \leqslant \, {\kappa }^{*} \leqslant \underbrace{{\kappa }_1 + \frac{1-\eta _1}{\frac{1}{{\kappa }_2-{\kappa }_1}+\frac{3\eta _1}{3{\kappa }_1+4{\mu }_1}}}_{\begin{array}{c} \text {bulk modulus -}\\ \text { upper bound} \end{array}} \, , \end{aligned} \end{aligned}$$

(26)

$$\begin{aligned}&\begin{aligned} \underbrace{{\mu }_2 + \frac{\eta _1}{\frac{1}{{\mu }_1-{\mu }_2}+\frac{6(1-\eta _1)({\kappa }_2+2{\mu }_2)}{5{\mu }_2(3{\kappa }_2+4{\mu }_2)}}}_{\begin{array}{c} \text {shear modulus -}\\ \text { lower bound} \end{array}} \, \leqslant \, {\mu }^{*} \leqslant \\ \underbrace{{\mu }_1 +\frac{1-\eta _1}{\frac{1}{{\mu }_2-{\mu }_1}+\frac{6\eta _1({\kappa }_1+2{\mu }_1)}{5{\mu }_1(3{\kappa }_1+4{\mu }_1)}} }_{\begin{array}{c} \text {shear modulus -}\\ \text { upper bound} \end{array}} \, . \end{aligned} \end{aligned}$$

(27)

Once bulk modulus and shear modulus are computed through (26) and (27), the effective elastic modulus of the substrate is calculated by means of the Lamé conversion formula as:

$$\begin{aligned} \begin{aligned} E_s = \frac{9{\kappa }^*{\mu }^*}{3{\kappa }^*+{\mu }^*} \,. \end{aligned} \end{aligned}$$

(28)

Figure 5 shows that the Hashin–Shtrikman bounds provide a tigher constraint of the effective modulus than the more commonly used Hill–Reuss–Voigt bounds. Since displacement boundary conditions are used for the numerical homogenization, we use the upper Hashin–Shtrikman bound as approximation of the elastic modulus of the substrate $E_s$ in (28).

Fig. 5

Hashin–Shtrikman and Hill–Reuss–Voigt bounds for $E_s$ with $E_1 = 10$ and $E_2=1$ belonging to domains $\varOmega _1$ and $\varOmega _2$, respectively

4 Results and discussion

The numerical and analytical approaches presented above are now applied to investigate the influence of the heterogeneity of the substrate on instabilities due to growth of an elastic film adhered to it, as shown in a typical bilayered structure in Fig. 1. The geometry and problem description under investigation are discussed in Sect. 4.1. Then, details on the numerical implementation and its convergence are provided in Sect. 4.2. Finally, the critical growth parameters for a family of two-phase microstructures are investigated in Sect. 4.3. Results from the numerical nonlinear multiscale analysis are compared with the proposed analytical approach, and the numerically obtained buckling patterns are assessed.

4.1 Description of problem and microstructures under investigation

The problem studied here consists of an elastic, homogeneous film that grows with parameter g, see Sect. 2.2, and is adhered on a heterogeneous, microstructured, elastic substrate, which does not grow at all.

The geometry and boundary conditions of the macroscopic domain are shown in Fig. 6. The length and width of the structure are $L=60$ and $b=1$, respectively. The height of the film is $H_f=1$, and the height of the substrate is $H_s=19$. This geometrical data are taken from a representative example provided in [40, 46]. The displacement of the film and substrate is constrained in x-direction at the left and right side, and at the bottom the substrate is constrained in y-direction. Besides these essential boundary conditions, no natural boundary conditions or volume loads are applied and the deformation of the structure is only caused by the growth of the film.

Fig. 6

Geometry, boundary conditions, and dimensions of elastic growing film on a microstructured substrate. Representative volume element consists of two material phases $\varOmega _1$ and $\varOmega _2$. The geometrical data are taken from a representative example on this topic given in [40, 46]

As mentioned previously in Sect. 2.3, in this contribution, the substrate is represented by a two-phase microstructure with an RVE $\varOmega$, which consists of a matrix with a circular inclusion with material domains $\varOmega _1$ and $\varOmega _2$, possessing elastic moduli $E_1$ and $E_2$, respectively, see Fig. 6. The effective elastic modulus $E_s$ of the substrate results from the homogenization of the microstructure and thus depends on $E_1,E_2$ and the geometry of the microstructure. Hence, we fix the stiffness ratio between the film and the matrix material of the substrate as $E_f/E_1=4$. The Poisson’s ratios of film, substrate matrix, and inclusion are $\nu _f= \nu _1 = \nu _2 = 0.49$. In this study, two critical parameters of the microstructure of the substrate are investigated, which affect the effective stiffness $E_s$ of the substrate and thus the grow-induced instabilities of the overall structure.

The first one is the ratio of the two elastic moduli belonging to phases $\varOmega _1$ and $\varOmega _2$, namely

$$\begin{aligned} \gamma =E_2/E_1\, . \end{aligned}$$

(29)

In Fig. 7, the elastic modulus $E_1$ is fixed to 10 and the stiffness ratio varies from left to right from $\gamma =0.01$ to $\gamma =1$, i.e., from $E_2=0.01 E_1$ to $E_2=E_1$, while the stiffness ratio is constant, $E_f/E_1=4$. The case $\gamma =1$ refers to a homogeneous material, i.e., no microstructure, while $\gamma =0$ would refer to a void inclusion without material, i.e., a matrix with holes. The lower limit is restricted here to $\gamma =0.01$, since $\gamma =0$ would lead to singular finite elements.

The second critical matter under investigation is the relative volume of the two materials, or rather the volume fraction of the matrix domain $\varOmega _1$ to the total volume of the representative volume element $\varOmega$:

$$\begin{aligned} \eta = \frac{|\varOmega _1|}{|\varOmega |} = 1 - \pi \left( \frac{r}{L} \right) ^2 \, , \end{aligned}$$

(30)

where L is the width and height of the square RVE and r the radius of the circular inclusion, for which $0\le r \le 0.5 L$ holds. For $r=0$, the inclusion vanishes, referring again to a homogeneous material, while for $r=0.5 L$ the circular inclusion is fully inscribed into the square RVE. In Fig. 7, the volume fraction is varied from top to bottom from $\eta \approx 0.96$ to $\eta \approx 0.21$, corresponding to the radius varying from $r=0.1 L$ to $r=0.5 L$. Obviously, the volume fraction $\eta$ cannot be 1 and 0, because the circle in microstructure is enclosed by the rectangle. However, $\eta =1$ leads to same results as $\gamma =1$.

In the following, the effect of microstructural parameters on the critical growth factor and associated folding patterns of the film is studied by variation in $\eta$ and $\gamma$ in 30 cases as shown in Fig. 7.

Fig. 7

30 different microstructures representing the heterogeneity of the substrate. These microstructures are constructed by varying stiffness ratio $\gamma$ and volume fraction $\eta$

4.2 Details on the numerical implementation and convergence study

The macroscopic domain is discretized in 2D using 840 bi-quadratic plane strain elements, consisting of 40 elements along x-direction, 19 elements along y-direction for the substrate and 2 elements in y-direction for the film, which is sufficient to accurately capture folding of the film [40]. A nonlinear instability analysis is carried out to capture the critical growth that initiates the instabilities of the structure. As the parameter of the anisotropic growth g is incremented and the film grows in the anisotropically horizontal direction, the eigenvalues of the macroscopic tangent stiffness matrix ${\textit{\textbf{K}}}$ are analyzed. The first negative eigenvalue indicated an instability in structure, and the corresponding unit eigenvector describes the folding pattern of the structure in the form of wrinkling or folding.

As mentioned in Sect. 2.4, within the micro–macrotransition process of the FE² method, the deformation gradient ${\textit{\textbf{F}}}^*$ at every quadrature point in the macrodomain is applied at boundaries of a micro-RVE, the microproblem is solved, and the effective, homogenized stress ${\textit{\textbf{P}}}^*$ is returned to the macroproblem. This procedure is computationally relatively expensive and bears the issue that two FE discretizations are required, one of the macrostructures and another of the micro-RVE. In this work, the significance of the microdomain discretization is studied by observing how much the element size influences critical growth. To this aim, the RVE is discretized by six refined meshes containing 25, 100, 225, 400, 625 and 900 elements in a domain with dimension $L=1$ and parameters $\eta =0.72$ and $\gamma =0.5$, as shown in Fig. 8.

Fig. 8

Convergence study for microdiscretizations with 25, 100, 225, 400, 625 and 900 elements. Computed critical growth $g_\text {cr}$ and required calculation time in hours are plotted for each discretization

The critical growth parameter $g_\text {cr}$ resulting from the FE² nonlinear instability analysis and the overall computation time taken (in hours) are both visualized over the number of elements in the micro-RVE discretization in Fig. 8. The critical growth increases from $g_\text {cr}\approx 0.231$ at 25 elements to $g_\text {cr}\approx 0.239$ at 400 elements and then oscillates with less than 0.2% deviation. However, the calculation time increases from 400 to 900 elements by approximately 20 hours, which is a $55 \%$ increment. By comparing the discretizations with 100 and 400 elements, it can be seen that critical growth at 100 elements only posses around $1.2\%$ deviation with $80\%$ less calculation time, which is still an acceptable approximation. At this point, it should be noted that the bisection method is used to increment the growth factor and determine critical growth $g_\text {cr}$, and thus, the defined error tolerance in the bisection method influences the accuracy of the calculated $g_\text {cr}$. In this study, the critical growth is calculated with three decimal points accuracy. Additionally, the calculation time of course varies for different types of computers and implementations, but the trend should be similar for refined discretizations, anyway.

4.3 Study of critical growth

Having assessed and verified the convergence of the numerical method for determining the critical growth value that initiates an instability in the structure consisting of a growing film on a microstructured substrate, it is now utilized to investigate the influence of the two microstructural parameters, i.e., the relative stiffness ratio $\gamma =E_2/E_1$ and the volume fraction of the matrix domain $\eta = {|\varOmega _1|}/{|\varOmega |}$.

Figure 9 shows the critical growth $g_\text {cr}$ obtained for the 30 cases with varying $\gamma$ and $\eta$, which are introduced in Fig. 7. For fixed values $\gamma =0.01,0.1,$ 0.25, 0.5, 0.75, 1.0, $g_\text {cr}$ is plotted over $\eta$, which is varying from 0 to 1. Both, the numerical solution obtained from the FE² method and the one from the simplified analytical approach are shown. The dashed line between evaluated points of numerical calculation is drawn through the interpolation of these points. Furthermore, the insets show selected buckling modes, i.e, the eigenmodes corresponding to the slightly negative eigenvalue at critical growth, obtained by the numerical multiscale approach.

It can be seen that by increasing $\eta$, or rather the volume fraction of $E_1$, the critical growth increases and the number of folds decreases. Obviously, larger $\eta$ leads to more base material, i.e., a larger area occupied by the larger $E_1$, and consequently stiffer substrate. Therefore, the film needs to grow more to overcome the stiffness of the substrate and to buckle. Furthermore, the critical growth $g_{cr}$ and number of folds increase by increasing $\gamma$, or rather the stiffness ratio of the two material phases $E_1$ and $E_2$. It shows that by increasing $\gamma$ the effective stiffness of the microstructure increases, and consequently, it enhances the stiffness of the substrate. Apparently, for $\gamma = 1$, where $E_1=E_2$, $\eta$ does not affect the stiffness of the film, and therefore, the effective stiffness of the substrate remains constant for all values of $\eta$. For higher values of $\eta$, namely $\eta =0.96$, the critical growth $g_{cr}$ changes slightly with varying stiffness ratio of material phases $\gamma$. These changes are slight, because for higher values of $\eta$ the influence of the material phases $E_2$ is small anyway. Otherwise, for lower values of $\eta$, the critical growth $g_{cr}$ is more sensitive to the changes of material phases $\gamma$, because of the larger proportion of material phase $\varOmega _2$ in the RVE and consequently more effective $E_2$ in the microstructure.

Fig. 9

Instability analysis of an elastic growing film on an heterogeneous microstructured substrate using various representative volume elements. The stiffness ratio between the film and matrix material of the substrate is $E_f/E_1=4$, and the Poisson’s ratios are $\nu _f=\nu _1=\nu _2=0.49$. The insets show selected folding patterns, i.e., buckling modes obtained by the numerical multiscale approach

Overall, the qualitative and quantitative agreement of the results obtained from the analytical and numerical methods is good. In general, a larger deviation of analytical and numerical values for the critical growth $g_{cr}$ can be observed for smaller values of $\gamma$, which can be explained by the larger contrast of the moduli of the two material phases, which makes the analytical bounds for $E_s$ less accurate. Furthermore, the deviation is typically largest for $\eta \approx 0.5-0.7$, i.e., where the inhomogeneity of the microstructure is largest (for $\eta =0$ and $\eta =1$ the microstructure corresponds to homogeneous material), which can also be explained with the analytical bounds probably being wider and less accurate in that range, see Fig. 5.

In summary, the good agreement between the simplified analytical and the numerical FE² methods used for the instability analysis provides a verification for the analysis of critical growth of thin films on microstructured substrates. Moreover, the results clearly show that there is a strong dependence of both critical growth values and buckling patterns on the microstructure of the substrate and its parameters.

4.4 Post-buckling deformation

As mentioned above, the insets in Fig. 9 show selected buckling modes, which are, however, arbitrarily scaled. Thus, the influence of $\gamma$ and $\eta$ on the folding patterns of the film can be investigated, but not the actual post-buckling deformations and their magnitude. Nevertheless, these buckling modes can be the starting point for a nonlinear post-buckling analysis of the film–substrate structure, where they are prescribed as perturbations.

Though the detailed modeling of post-buckling behavior is beyond the scope of this work, an example of the post-buckling deformation for $\gamma =0.1$ and $\eta =0.21$ at the growth of $g\approx 0.14$ is shown in Fig. 10. Here, the deformation can be drawn up to scale and the elements are colored by the Green–Lagrange strain values $E_{11}$ (evaluated at the element centers). As can be seen, the film–substrate structure experiences large deformations of both, the film and the microstructure, and large strains of around $48\%$ in the post-buckling state. This highlights the necessity of the finite strain multiscale simulation framework proposed in this work.

Fig. 10

Post-buckling deformation of an elastic growing film on a microstructured substrate with $\gamma =0.1$ and $\eta =0.21$. The buckled structure shows large deformations and strains, e.g., a maximum Green–Lagrange strain of $E_{11}=0.48$

5 Conclusion

Growth in biological systems and living tissues leads to geometrical instabilities in the form of folding and wrinkling. Investigation of buckling during the growth of living tissues helps to understand such growth-induced folding phenomena, which is a critical matter. Here, a bilayered structure consisting of an elastic, growing film on an elastic, heterogeneous, microstructured substrate is used to study growth-induced instabilities. For this purpose, a concurrent multiscale method has been developed, which utilizes eigenvalue analysis on the tangent stiffness matrix of the macroscopic finite element problem to determine critical growth factors and buckling patterns, and finite element-based homogenization of the microstructure to take into account the material heterogeneity. To verify the numerical results, also a simplified analytical method has been developed, which uses the Hashin–Shtrikman bounds to estimate the effective stiffness of the microstructure. Both methods have been applied to determine the instabilities of bilayers with a two-phase, circular inclusion microstructure, where a good agreement of the results could be observed. The influences of the parameters of the microstructure on critical growth and folding patterns were investigated, and the effect of microstructure material phases on the geometrical instabilities was studied. It could be observed that the morphological pattern and stiffness of the microstructure have a considerable impact on the geometrical instabilities.

In future works, this numerical framework could be utilized for the investigation of growth of living structures to better understand the growth-induced instabilities, especially where the microstructure varies point to point or the microstructure evolves during growth. However, challenges with respect to modeling complex biological applications like brain tissue or airway walls could be highly varying microstructural properties, a lack of scale separation, or instabilities within the RVEs. In those cases, the applicability of the presented framework would have to be verified, since it is based on the assumption of periodicity of microstructural deformations.