Some Remarks About Virtual Annihilation Interactions in Relativistic n-Body Wave Equations in QED

Abstract

The existence of entities consisting of electrons and positrons was predicted in 1946 by J. A. Wheeler and he called them polyelectrons. The simplest bound-state is called positronium (Ps, e⁻e⁺). Wheeler speculated that two Ps atoms may combine to form the di-positronium molecule (Ps₂, e⁻e⁺e⁻e⁺) which was finally observed in 2007. He also conjectured the existence of larger systems such as (Ps₃, e⁻e⁺e⁻e⁺e⁻e⁺). In a previous work the author has formulated the relativistic wave equations in quantum electrodynamics (QED) for a system consisting of n fermions and antifermions of equal masses where n can be any natural number and the equations contain relativistic effects up to the order of O(α⁴), α is the coupling. The kernels of the n-body wave equations in QED include one-photon exchange and virtual annihilation interactions. The latter interactions occur among pairs of fermions and antifermions. The equations have the Schrödinger non relativistic limit. In this manuscript, some points have been provided with respect to the virtual annihilation interactions for the few-body systems in addition to the particular cases of five- (e⁻e⁺e⁻e⁺e⁻) and six-body (e⁻e⁺e⁻e⁺e⁻e⁺) QED systems.

Appendix

It is quite instructive to explicitly write the relativistic wave equations and their non-relativistic limits both in momentum and coordinate space for the few-body systems (two-, three-, and four-body), in addition to more difficult cases, such as the five-body (e⁻e⁺e⁻e⁺e⁻) or six-body systems (Ps₃,e⁻e⁺e⁻e⁺e⁻e⁺), in order to better understand how to apply the general formula for the relativistic n-fermion wave equations, namely (25), and its non relativistic limit (see (31)).

a) :

The two-body systems (such as positronium, e⁻e⁺):

We can choose the following trial state for the two-body problem (e⁻e⁺) as the following expression based on the eq. (16)

$$ |\psi_{2}\rangle =\underset{s_{1}s_{2}}{\sum }\int d^{3}p_{1}d^{3}p_{2}~F_{s_{1}s_{2}}(\mathbf{p}_{1},\mathbf{p}_{2})~b^{\dagger }(\mathbf{p}_{1},s_{1})d^{\dagger }(\mathbf{p} _{2},s_{2})|0\rangle , $$

(75)

Therefore, we obtain the following wave equation (n = 2 in (25)):

$$ \begin{array}{@{}rcl@{}} F_{s_{1}s_{2}}(\mathbf{p}_{1},\mathbf{p}_{2})~[\omega_{p_{1}}+\omega_{p_{2}} -E]\!&=&\!\frac{m^{2}e^{2}}{2(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }~F_{s_{1}^{\prime }s_{2}^{\prime }}(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime })\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p} _{2}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{2})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{2}^{\prime }}\omega_{p_{1}}\omega_{p2}}} \\ &&\!\times\! \left[ \mathcal{M}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{ \text{\textit{Attractive} }}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p} _{1}^{\prime },\mathbf{p}_{2}^{\prime }) - \mathcal{M}_{s_{1}s_{2}s_{1}^{ \prime }s_{2}^{\prime }}^{Annihilation}(\mathbf{p}_{1}, \mathbf{p}_{2},\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime })\right] ,\\ \end{array} $$

(76)

$$ \begin{array}{@{}rcl@{}} {}\mathcal{M}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Attractive}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{1}^{\prime }, \mathbf{p}_{2}^{\prime }) \!&=&\!\overline{u}(\mathbf{p}_{1}^{\prime },s_{1}^{\prime })\gamma^{\mu }u(\mathbf{p}_{1},s_{1})~[D_{\mu \nu }(\omega_{p_{1}^{\prime }}-\omega_{p_{1}},\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1}) \\ &&\!+D_{\mu \nu }(\omega_{p_{2}^{\prime }}-\omega_{p_{2}},\mathbf{p}_{2}^{\prime } - \mathbf{p}_{2})]~\overline{v}\left( \mathbf{p}_{2},s_{2}\right) \gamma^{\nu }v\left( \mathbf{p}_{2}^{\prime },s_{2}^{\prime }\right) , \end{array} $$

(77)

$$ \begin{array}{@{}rcl@{}} \mathcal{M}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Annihilation}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{1}^{\prime }, \mathbf{p}_{2}^{\prime }) &=&\overline{u}(\mathbf{p}_{1}^{\prime },s_{1}^{\prime })\gamma^{\mu }v\left( \mathbf{p}_{2}^{\prime },s_{2}^{\prime }\right) ~[D_{\mu \nu }(\omega_{p_{1}^{\prime }}+\omega _{p_{2}^{\prime }},\mathbf{p}_{1}^{\prime }+\mathbf{p}_{2}^{\prime }) \\ &&+D_{\mu \nu }(-\omega_{p_{1}}-\omega_{p_{2}},-\mathbf{p}_{1}-\mathbf{p}_{2})]\\ &&\times \overline{v}\left( \mathbf{p}_{2},s_{2}\right) \gamma^{\nu }u(\mathbf{p}_{1},s_{1}). \end{array} $$

(78)

For the positronium case the above equations were derived previously by Terekidi and Darewych [19]. One should note that there is no repulsive term for the (Ps: e⁻e⁺) system. They demonstrated [19] that the results for the bound state energies (including virtual annihilation) agree with earlier calculation of positronium (Ps) to the order of O(α⁴) for all states.

For the non-relativistic limit of the wave (76) of (e⁻e⁺) we have

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}}(\mathbf{p}_{1},\mathbf{p}_{2})~\left[ \frac{\mathbf{p} _{1}^{2}}{2m}+\frac{\mathbf{p}_{2}^{2}}{2m}-\epsilon \right] \\ &=&\frac{e^{2}}{(2\pi )^{3}} \underset{s_{1}^{\prime }s_{2}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }~F_{s_{1}^{\prime }s_{2}^{\prime }}(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime })~\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{2}^{\prime }-\mathbf{p}_{1}- \mathbf{p}_{2})\\&&\times\left[ \frac{\delta_{s_{1}s_{1}^{\prime }}\delta _{s_{2}s_{2}^{\prime }}}{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}}{4m^{2}}\right] , \end{array} $$

(79)

where 𝜖 = E − 2m.

By using the Fourier transformation (30), in the coordinate-space, the above equation, namely (79), becomes as the following expression:

$$ \begin{array}{@{}rcl@{}} &&\left[ -\frac{1}{2m}{{\sum}_{i=1}^{2}{\nabla_{i}^{2}}}-\frac{\alpha }{|\mathbf{x }_{1}-\mathbf{x}_{2}|}-\epsilon \right] {\Psi}_{s_{1}s_{2}}(\mathbf{x}_{1}, \mathbf{x}_{2})\\ && +\frac{\pi \alpha }{m^{2}} \delta (\mathbf{x}_{1}-\mathbf{x} _{2}){\sum}_{{s_{1}}^{\prime }{s_{2}}^{\prime }}A_{{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}}{\Psi}_{{s_{1}^{\prime }s_{2}^{\prime }}}(\mathbf{x}_{1}, \mathbf{x}_{2}) =0, \end{array} $$

(80)

where the coupling α = e²/4π defines the fine-structure constant. In the above equation the term that contains the factor δ(x₁ −x₂) describes the virtual annihilation interaction between the fermion (such as e⁻) and antifermion (such as e⁺).

b) :

The three-body systems (such as positronium negative ion, Ps⁻,e⁻e⁺e⁻):

For the positronium negative ion, namely (Ps⁻: e⁻e⁺e⁻), using the trial state (17) we can write

$$ |\psi_{3}\rangle =\underset{s_{1}s_{2}s_{3}}{\sum }\int d^{3}p_{1}d^{3}p_{2}d^{3}p_{3}~F_{s_{1}s_{2}s_{3}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3})b^{\dagger }(\mathbf{p}_{1},s_{1})d^{\dagger }(\mathbf{p}_{2},s_{2})b^{\dagger }(\mathbf{p}_{3},s_{3})|0\rangle , $$

(81)

thereupon, the Ps⁻ wave equation can be written as the following expression (n = 3 in (25):

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}s_{3}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3})[\omega_{p_{1}}+\omega_{p_{2}}+\omega_{p_{3}}-E] \\ &=&\frac{m^{2}e^{2}}{2(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }d^{3}p_{3}^{\prime }~F_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }}(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime },\mathbf{p}_{3}^{\prime }) \\ &&\times\left\{\left[ \mathcal{M}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Attractive}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p} _{1}^{\prime },\mathbf{p}_{2}^{\prime })-\mathcal{M}_{s_{1}s_{2}s_{1}^{ \prime }s_{2}^{\prime }}^{Annihilation}(\mathbf{p}_{1}, \mathbf{p}_{2},\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime })\right] \delta_{s_{3}^{\prime }s_{3}}\right.\\ &&\times\delta^{3}(\mathbf{p}_{3}^{\prime }-\mathbf{p} _{3})\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{2}^{\prime }- \mathbf{p}_{1}-\mathbf{p}_{2})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{2}^{\prime }}\omega_{p_{1}}\omega_{p_{2}}}} \\ &&+\left[ \mathcal{M}_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}^{Attractive}(\mathbf{p}_{2},\mathbf{p}_{3},\mathbf{p}_{2}^{\prime },\mathbf{p}_{3}^{\prime })-\mathcal{M}_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}^{Annihilation}(\mathbf{p}_{2},\mathbf{p}_{3},\mathbf{p}_{2}^{\prime },\mathbf{p}_{3}^{\prime })\right] \delta_{s_{1}^{\prime }s_{1}}\\ &&\times \delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1}) \frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p }_{2}-\mathbf{p}_{3})}{\sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{2}}\omega_{p_{3}}}} \\ && \left. -\mathcal{M}_{s_{1}s_{3}s_{1}^{\prime }s_{3}^{\prime }}^{Repulsive}(\mathbf{p}_{1},\mathbf{p}_{3},\mathbf{p}_{1}^{\prime },\mathbf{ p}_{3}^{\prime })~\delta_{s_{2}^{\prime }s_{2}}~\delta^{3}(\mathbf{p}_{2}^{\prime }-\mathbf{p}_{2})\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+ \mathbf{p}_{3}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{3})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{1}}\omega_{p_{3}}}} \right\}. \end{array} $$

(82)

The expressions for ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Attractive}$, ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Repulsive}$, and ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Annihilation}$ have been provided before in (22), (23) and (24 ), respectively.

In the non-relativistic limit, in the momentum space the (82) becomes as the following expression:

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}s_{3}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3})\left[ \frac{\mathbf{p}_{1}^{2}}{2m}+\frac{\mathbf{p}_{2}^{2}}{2m}+\frac{\mathbf{p} _{3}^{2}}{2m}-\epsilon_{3}\right] \\ &=&\frac{e^{2}}{(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }d^{3}p_{3}^{\prime }~F_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }}(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime },\mathbf{p}_{3}^{\prime }) \\ &&\times\left[\left( \frac{\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}}{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{1}{4m^{2}} ~A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}\right) ~\delta^{3}(\mathbf{p}_{3}^{\prime }-\mathbf{p}_{3})\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{2}^{\prime }-\mathbf{p}_{1}- \mathbf{p}_{2})\right. \\ &&+\left( \frac{\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}}{\mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2} \mathbf{|}^{2}}-\frac{1}{4m^{2}}~A_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\right) ~\delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{3}) \\ &&\left. -\frac{1}{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}~\delta^{3}(\mathbf{p}_{2}^{\prime }-\mathbf{p}_{2})\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{3})\right], \end{array} $$

(83)

where we let 𝜖₃ = E − 3m. In the coordinate space, this becomes the following equation:

$$ \begin{array}{@{}rcl@{}} &&\left\{-\frac{1}{2m}\left( {{\sum}_{i=1}^{3}{\nabla_{i}^{2}}}\right) -\epsilon_{3}-\frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x}_{2}|}-\frac{\alpha }{|\mathbf{x}_{2}-\mathbf{x}_{3}|}+\frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x} _{3}|}\right\}{\Psi}_{s_{1}s_{2}s_{3}}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x} _{3})= \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{1}-\mathbf{x}_{2})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }}{\sum }A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x} _{3}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{2}-\mathbf{x}_{3})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }}{\sum }A_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3}), \end{array} $$

(84)

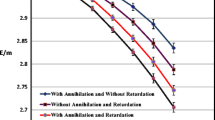
where we have the coupling α = e²/4π. On the right hand side of the (84), the virtual annihilation terms for the Ps⁻ system can be noted (the terms that contain δ(x₁ −x₂) and δ(x₂ −x₃)). As said before, they are really relativistic effects that contribute in the order of O(α)⁴.

• c) The four-body systems (such as positronium molecule, Ps₂, e⁻e⁺e⁻e⁺):

For the positronium molecule (e⁻e⁺e⁻e⁺), by choosing the following trial state (n = 4, cf. 16) we have the following

$$ |\psi_{4}\rangle =\underset{s_{1}...s_{4}}{\sum }\int d^{3}p_{1}...d^{3}p_{4}~F_{s_{1}...s_{4}}(\mathbf{p}_{1},...,\mathbf{p}_{4})b^{\dagger }(\mathbf{p}_{1},s_{1})d^{\dagger }(\mathbf{p}_{2},s_{2})b^{\dagger }(\mathbf{p}_{3},s_{3})d^{\dagger }(\mathbf{p}_{4},s_{4})|0\rangle , $$

(85)

The resulting relativistic wave equation is as below (n = 4 in (25)):

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}s_{3}s_{4}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3}, \mathbf{p}_{4})[\omega_{p_{1}}+\omega_{p_{2}}+\omega_{p_{3}}+\omega_{p_{4}}-E] \\ &=&\frac{m^{2}e^{2}}{2(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }d^{3}p_{3}^{\prime }d^{3}p_{4}^{\prime }~F_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}({\mathbf{p}} _{1}^{\prime },{\mathbf{p}}_{2}^{\prime },{\mathbf{p}}_{3}^{\prime },{\mathbf{p}} _{4}^{\prime }) \\ &&\times\left\{\mathcal{M}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{A}(\mathbf{p}_{1},\mathbf{p}_{2},{\mathbf{p}}_{1}^{\prime },{\mathbf{p}}_{2}^{\prime })~\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}({\mathbf{p}}_{3}^{\prime }-\mathbf{p}_{3})\delta^{3}({\mathbf{p}}_{4}^{\prime }-\mathbf{p}_{4})\frac{\delta^{3}({\mathbf{p}}_{1}^{\prime }+{\mathbf{p}}_{2}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{2})}{ \sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{2}^{\prime }}\omega_{p_{1}}\omega_{p_{2}}}}\right. \\ &&+\mathcal{M}_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}^{A}(\mathbf{p}_{2},\mathbf{p}_{3},{\mathbf{p}}_{2}^{\prime },{\mathbf{p}}_{3}^{\prime })~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}(\mathbf{p}_{4}^{\prime }-\mathbf{p}_{4})\frac{\delta^{3}({\mathbf{p}} _{2}^{\prime }+{\mathbf{p}}_{3}^{\prime }-{\mathbf{p}}_{2}-\mathbf{p}_{3})}{ \sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{2}}\omega_{p_{3}}}} \\ &&+\mathcal{M}_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}^{A}(\mathbf{p}_{3},\mathbf{p}_{4},{\mathbf{p}}_{3}^{\prime },{\mathbf{p}} _{4}^{\prime })~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}~\delta^{3}({\mathbf{p}}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}({\mathbf{p}}_{2}^{\prime }-\mathbf{p}_{2})\frac{\delta^{3}({\mathbf{p}} _{3}^{\prime }+\mathbf{p}_{4}^{\prime }-\mathbf{p}_{3}-\mathbf{p}_{4})}{ \sqrt{\omega_{p_{3}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{3}}\omega_{p_{4}}}} \\ &&+\mathcal{M}_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}^{A}(\mathbf{p}_{1},\mathbf{p}_{4},{\mathbf{p}}_{1}^{\prime },{\mathbf{p}} _{4}^{\prime })~\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}~\delta^{3}(\mathbf{p}_{2}^{\prime }-\mathbf{p}_{2})\delta^{3}(\mathbf{p}_{3}^{\prime }-\mathbf{p}_{3})\frac{\delta^{3}(\mathbf{p} _{1}^{\prime }+\mathbf{p}_{4}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{4})}{ \sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{1}}\omega_{p_{4}}}} \\ &&-\mathcal{M}_{s_{1}s_{3}s_{1}^{\prime }s_{3}^{\prime }}^{Repulsive}(\mathbf{p}_{1},\mathbf{p}_{3},{\mathbf{p}}_{1}^{\prime },{\mathbf{ p}}_{3}^{\prime })~\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}({\mathbf{p}}_{2}^{\prime }-\mathbf{p}_{2})\delta^{3}({\mathbf{p}}_{4}^{\prime }-\mathbf{p}_{4})\frac{\delta^{3}({\mathbf{p}}_{1}^{\prime }+{\mathbf{p}}_{3}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{3})}{ \sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{1}}\omega_{p_{3}}}} \\ && \left. -\mathcal{M}_{s_{2}s_{4}s_{2}^{\prime }s_{4}^{\prime }}^{Repulsive}(\mathbf{p}_{2},\mathbf{p}_{4},{\mathbf{p}}_{2}^{\prime },{\mathbf{ p}}_{4}^{\prime })~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}~\delta^{3}({\mathbf{p}}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}({\mathbf{p}_{3}}^{\prime }-\mathbf{p}_{3})\frac{\delta^{3}({\mathbf{p}}_{2}^{\prime }+{\mathbf{p}}_{4}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{4})}{ \sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{2}}\omega_{p_{4}}}}\right\},\\&& \end{array} $$

(86)

where we let ${\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{A}(\mathbf {p}_{1},\mathbf {p}_{2},{\mathbf {p}}_{1}^{\prime },{\mathbf { p}}_{2}^{\prime })={\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Attractive}(\mathbf {p}_{1},\mathbf {p}_{2},{\mathbf {p}}_{1}^{\prime },{\mathbf {p}_{2}}^{\prime })-{\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Annihilation}$$(\mathbf {p}_{1}, \mathbf {p}_{2},{\mathbf {p}}_{1}^{\prime },{\mathbf {p}}_{2}^{\prime })$, and etc. The expressions for ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Attractive}$, ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Repulsive}$, and ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Annihilation}$ have been provided in the main text in (22), (23) and (24).

For the system (Ps₂ : e⁻e⁺e⁻e⁺), in the non-relativistic limit, we obtain the following expression:

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}s_{3}s_{4}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3}, \mathbf{p}_{4})\left[ \frac{\mathbf{p}_{1}^{2}}{2m}+\frac{\mathbf{p}_{2}^{2} }{2m}+\frac{\mathbf{p}_{3}^{2}}{2m}+\frac{\mathbf{p}_{4}^{2}}{2m}-\epsilon_{4}\right] \\ &=&\frac{e^{2}}{(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}{\sum }\int d^{3}{{p}_{1}^{\prime }}d^{3}{p_{2}^{\prime }}d^{3}{{p}_{3}^{\prime }}d^{3}{{p}_{4}^{\prime }}~F_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}({\mathbf{p}} _{1}^{\prime },{\mathbf{p}}_{2}^{\prime },{\mathbf{p}}_{3}^{\prime },{\mathbf{p}} _{4}^{\prime })\times \\ &&\left[\left( \frac{\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}s_{2}^{\prime }}}{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}}{4m^{2}}\right) \delta_{s_{3}^{\prime }s_{3}} \delta_{s_{4}^{\prime }s_{4}} \delta^{3}({\mathbf{p}}_{3}^{\prime }-\mathbf{p}_{3})\delta^{3}({\mathbf{p}}_{4}^{\prime }- \mathbf{p}_{4})\delta^{3}({\mathbf{p}}_{1}^{\prime }+{\mathbf{p}}_{2}^{\prime }- \mathbf{p}_{1}-\mathbf{p}_{2})\right. \\ &&+\left( \frac{\delta_{s_{2}s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}} }{\mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2}\mathbf{|}^{2}}-\frac{ A_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}s_{1}^{\prime }}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}(\mathbf{p}_{4}^{\prime }-\mathbf{p} _{4})\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p} _{2}-\mathbf{p}_{3}) \\ &&+\left( \frac{\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}} }{\mathbf{|p}_{3}^{\prime }\mathbf{-p}_{3}\mathbf{|}^{2}}-\frac{ A_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}~\delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}({\mathbf{p}}_{2}^{\prime }-\mathbf{p} _{2})\delta^{3}({\mathbf{p}}_{3}^{\prime }+{\mathbf{p}}_{4}^{\prime }-\mathbf{p} _{3}-\mathbf{p}_{4}) \\ &&+\left( \frac{\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{4}^{\prime }s_{4}} }{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{ A_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}}{4m^{2}}\right) \delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}~\delta^{3}({\mathbf{p}}_{2}^{\prime }-\mathbf{p}_{2})\delta^{3}({\mathbf{p}}_{3}^{\prime }-\mathbf{p} _{3})\delta^{3}(\mathbf{p}_{1}^{\prime }+{\mathbf{p}}_{4}^{\prime }-\mathbf{p} _{1}-\mathbf{p}_{4}) \\ &&-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}(\mathbf{p}_{2}^{\prime }-\mathbf{p}_{2})\delta^{3}({\mathbf{p}}_{4}^{\prime }-\mathbf{p}_{4})\frac{\delta^{3}({\mathbf{p}}_{1}^{\prime }+{\mathbf{p}}_{3}^{\prime }- \mathbf{p}_{1}-\mathbf{p}_{3})}{{\mathbf{|p}}_{1}^{\prime }\mathbf{-p}_{1} \mathbf{|}^{2}} \\ &&\left.-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}(\mathbf{p}_{3}^{\prime }-\mathbf{p}_{3})\frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+{\mathbf{p}}_{4}^{\prime }- \mathbf{p}_{2}-\mathbf{p}_{4})}{\mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2} \mathbf{|}^{2}}\right], \end{array} $$

(87)

where we let 𝜖₄ = E − 4m. Its coordinate-space version is the four-body Schrödinger equation, (see (31) with n = 4). In the coordinate space, the four-body equation becomes as the following:

$$ \begin{array}{@{}rcl@{}} &&\left\{-\frac{1}{2m}\left( {\sum\limits_{i=1}^{4}{\nabla_{i}^{2}}}\right) -\epsilon_{4}-\frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x}_{2}|}-\frac{\alpha }{|\mathbf{x}_{2}-\mathbf{x}_{3}|}-\frac{\alpha }{|\mathbf{x}_{3}-\mathbf{x} _{4}|}-\frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x}_{4}|}\right. \\ && \left.+\frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x}_{3}|}+\frac{\alpha }{|\mathbf{x} _{2}-\mathbf{x}_{4}|}\right\}{\Psi}_{s_{1}s_{2}s_{3}s_{4}}(\mathbf{x}_{1}, \mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4}) \\ &=&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{1}-\mathbf{x}_{2})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}{\sum } A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x} _{3},\mathbf{x}_{4}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{2}-\mathbf{x}_{3})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}{\sum } A_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{4}^{\prime }s_{4}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x} _{3},\mathbf{x}_{4}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{3}-\mathbf{x}_{4})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}{\sum } A_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x} _{3},\mathbf{x}_{4}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{1}-\mathbf{x}_{4})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}{\sum } A_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x} _{3},\mathbf{x}_{4}). \end{array} $$

(88)

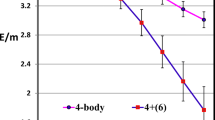
The interactions are expressed by attractive or repulsive Coulomb potentials in the left hand side of the equation and the repulsive contact virtual annihilation interactions (various delta functions in the right hand side of the above equation). For example, for a system such as positronium molecule (e⁻e⁺e⁻e⁺) we have four attractive terms, two repulsive terms, and four virtual annihilation interaction terms (the four terms of the right hand side of the above equation).

d) :

The five-body systems (such as e⁻e⁺e⁻e⁺e⁻):

For the five-body systems such as (e⁻e⁺e⁻e⁺e⁻) we use the trial state (17) in the manuscript. Hence, we have

$$ \begin{array}{@{}rcl@{}} |\psi_{5}\rangle &=&\underset{s_{1}...s_{5}}{\sum }\int d^{3}p_{1}...d^{3}p_{5}~F_{s_{1}...s_{5}}(\mathbf{p}_{1},...,\mathbf{p}_{5})b^{\dagger }(\mathbf{p}_{1},s_{1})d^{\dagger }(\mathbf{p}_{2},s_{2})b^{\dagger }(\mathbf{p}_{3},s_{3})\\ &&d^{\dagger }(\mathbf{p}_{4},s_{4})b^{\dagger }(\mathbf{p}_{5},s_{5})|0\rangle \end{array} $$

(89)

By choosing the above trial state we have the following relativistic wave equation (n = 5 in (25)):

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}s_{3}s_{4}s_{5}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3}, \mathbf{p}_{4},\mathbf{p}_{5})[\omega_{p_{1}}+\omega_{p_{2}}+\omega_{p_{3}}+\omega_{p_{4}}+\omega_{p_{5}}-E] \\ &\!=&\!\frac{m^{2}e^{2}}{2(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }d^{3}p_{3}^{\prime }d^{3}p_{4}^{\prime }d^{3}p_{5}^{\prime }F_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}(\mathbf{p}_{1}^{\prime }, \mathbf{p}_{2}^{\prime },\mathbf{p}_{3}^{\prime },\mathbf{p}_{4}^{\prime }, \mathbf{p}_{5}^{\prime }) \\ &&\!\times\left\{\mathcal{M}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{A}(\mathbf{p}_{1},\mathbf{p}_{2},{\mathbf{p}_{1}^{\prime }},{\mathbf{ p}_{2}^{\prime }})~\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}~\delta_{s_{5}^{\prime }s_{5}}\delta^{3}({\mathbf{p}_{3}^{\prime }} - \mathbf{p}_{3})\delta^{3}({\mathbf{p}_{4}^{\prime }}-\mathbf{p}_{4})\delta^{3}({\mathbf{p}_{5}^{\prime }} - \mathbf{p}_{5})\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+{\mathbf{p}_{2}^{\prime }}-\mathbf{p}_{1}-\mathbf{p}_{2})}{ \sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{2}^{\prime }}\omega_{p_{1}}\omega_{p_{2}}}}\right. \\ &&\!+\mathcal{M}_{s_{2}s_{3}{s_{2}^{\prime }}{s_{3}^{\prime }}}^{A }(\mathbf{p}_{2},\mathbf{p}_{3},{\mathbf{p}_{2}^{\prime }},{\mathbf{p}_{3}^{\prime }})~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}~\delta^{3}({\mathbf{p}_{1}^{\prime }}- \mathbf{p}_{1})\delta^{3}(\mathbf{p}_{4}^{\prime }-\mathbf{p}_{4})\delta ^{3}({\mathbf{p}_{5}^{\prime }}-\mathbf{p}_{5})\frac{\delta^{3}({\mathbf{p}_{2}^{\prime }}+{\mathbf{p}_{3}^{\prime }}-\mathbf{p}_{2}-\mathbf{p}_{3})}{ \sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{2}}\omega_{p_{3}}}} \\ &&\!+\mathcal{M}_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}^{A }(\mathbf{p}_{3},\mathbf{p}_{4},\mathbf{p}_{3}^{\prime },\mathbf{p}_{4}^{\prime })~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}~\delta_{s_{5}^{\prime }s_{5}}\delta^{3}(\mathbf{p}_{1}^{\prime }- \mathbf{p}_{1})\delta^{3}(\mathbf{p}_{2}^{\prime }-\mathbf{p}_{2})\delta ^{3}({\mathbf{p}_{5}^{\prime }}-\mathbf{p}_{5})\frac{\delta^{3}({\mathbf{p}_{3}^{\prime }}+{\mathbf{p}_{4}^{\prime }}-\mathbf{p}_{3}-\mathbf{p}_{4})}{ \sqrt{\omega_{p_{3}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{3}}\omega_{p_{4}}}} \\ &&\!+\mathcal{M}_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}^{A }(\mathbf{p}_{1},\mathbf{p}_{4},{\mathbf{p}_{1}^{\prime }},{\mathbf{p}_{4}^{\prime }})~\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}~\delta^{3}(\mathbf{p}_{2}^{\prime }- \mathbf{p}_{2})\delta^{3}({\mathbf{p}_{3}^{\prime }}-\mathbf{p}_{3})\delta ^{3}({\mathbf{p}_{5}^{\prime }}-\mathbf{p}_{5})\frac{\delta^{3}({\mathbf{p}_{1}^{\prime }}+{\mathbf{p}_{4}^{\prime }}-\mathbf{p}_{1}-\mathbf{p}_{4})}{ \sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{1}}\omega_{p_{4}}}} \\ &&\!+\mathcal{M}_{s_{2}s_{5}s_{2}^{\prime }s_{5}^{\prime }}^{A}(\mathbf{p}_{2},\mathbf{p}_{5},{\mathbf{p}_{2}^{\prime }},{\mathbf{p}_{5}^{\prime }})~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}(\mathbf{p}_{1}^{\prime }- \mathbf{p}_{1})\delta^{3}(\mathbf{p}_{3}^{\prime }-\mathbf{p}_{3})\delta ^{3}(\mathbf{p}_{4}^{\prime }-\mathbf{p}_{4})\frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{5}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{5})}{ \sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{5}^{\prime }}\omega_{p_{2}}\omega_{p_{5}}}} \\ &&\!+\mathcal{M}_{s_{4}s_{5}s_{4}^{\prime }s_{5}^{\prime }}^{A }(\mathbf{p}_{4},\mathbf{p}_{5},\mathbf{p}_{4}^{\prime },\mathbf{p}_{5}^{\prime })~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}~\delta^{3}(\mathbf{p}_{1}^{\prime }- \mathbf{p}_{1})\delta^{3}(\mathbf{p}_{2}^{\prime }-\mathbf{p}_{2})\delta ^{3}(\mathbf{p}_{3}^{\prime }-\mathbf{p}_{3})\frac{\delta^{3}(\mathbf{p}_{4}^{\prime }+\mathbf{p}_{5}^{\prime }-\mathbf{p}_{4}-\mathbf{p}_{5})}{ \sqrt{\omega_{p_{4}^{\prime }}\omega_{p_{5}^{\prime }}\omega_{p_{4}}\omega_{p_{5}}}} \\ &&\!-\mathcal{M}_{s_{1}s_{3}s_{1}^{\prime }s_{3}^{\prime }}^{Repulsive}(\mathbf{p}_{1},\mathbf{p}_{3},{\mathbf{p}_{1}^{\prime }},{\mathbf{ p}_{3}^{\prime }})~\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{4}^{\prime }s_{4}}~\delta_{s_{5}^{\prime }s_{5}}\delta^{3}(\mathbf{p}_{2}^{\prime }- \mathbf{p}_{2})\delta^{3}(\mathbf{p}_{4}^{\prime }-\mathbf{p}_{4})\delta^{3}(\mathbf{p}_{5}^{\prime } - \mathbf{p}_{5})\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{3})}{ \sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{1}}\omega_{p_{3}}}} \\ &&\!-\mathcal{M}_{s_{2}s_{4}s_{2}^{\prime }s_{4}^{\prime }}^{Repulsive}(\mathbf{p}_{2},\mathbf{p}_{4},{\mathbf{p}_{2}^{\prime }},{\mathbf{ p}_{4}^{\prime }})~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}~\delta^{3}({\mathbf{p}_{1}^{\prime }}- \mathbf{p}_{1})\delta^{3}({\mathbf{p}_{3}^{\prime }}-\mathbf{p}_{3})\delta^{3}({\mathbf{p}_{5}^{\prime }} - \mathbf{p}_{5})\frac{\delta^{3}({\mathbf{p}_{2}^{\prime }}+{\mathbf{p}_{4}^{\prime }}-\mathbf{p}_{2}-\mathbf{p}_{4})}{ \sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{2}}\omega_{p_{4}}}} \\ &&\!-\mathcal{M}_{s_{1}s_{5}s_{1}^{\prime }s_{5}^{\prime }}^{Repulsive}(\mathbf{p}_{1},\mathbf{p}_{5},{\mathbf{p}_{1}^{\prime }},{\mathbf{ p}_{5}^{\prime }})~\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}({\mathbf{p}_{2}^{\prime }}- \mathbf{p}_{2})\delta^{3}({\mathbf{p}_{3}^{\prime }}-\mathbf{p}_{3})\delta^{3}({\mathbf{p}_{4}^{\prime }} - \mathbf{p}_{4})\frac{\delta^{3}({\mathbf{p}_{1}^{\prime }}+{\mathbf{p}_{5}^{\prime }}-\mathbf{p}_{1}-\mathbf{p}_{5})}{ \sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{5}^{\prime }}\omega_{p_{1}}\omega_{p_{5}}}} \\ &&\left.\!-\mathcal{M}_{s_{3}s_{5}s_{3}^{\prime }s_{5}^{\prime }}^{Repulsive}(\mathbf{p}_{3},\mathbf{p}_{5},{\mathbf{p}_{3}^{\prime }},{\mathbf{ p}_{5}^{\prime }})\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{4}^{\prime }s_{4}}~\delta^{3}({\mathbf{p}_{1}^{\prime }} - \mathbf{p}_{1})\delta^{3}({\mathbf{p}_{2}^{\prime }} - \mathbf{p}_{2})\delta^{3}({\mathbf{p}_{4}^{\prime }} - \mathbf{p}_{4})\frac{\delta^{3}({\mathbf{p}_{3}^{\prime }} + {\mathbf{p}_{5}^{\prime }}-\mathbf{p}_{3}-\mathbf{p}_{5})}{ \sqrt{\omega_{p_{3}^{\prime }}\omega_{p_{5}^{\prime }}\omega_{p_{3}}\omega_{p_{5}}}}\right\}, \\ \end{array} $$

(90)

where we let ${\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{A}(\mathbf {p}_{1},\mathbf {p}_{2},\mathbf {p}_{1}^{\prime },\mathbf { p}_{2}^{\prime })={\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Attractive}(\mathbf {p}_{1},\mathbf {p}_{2},\mathbf {p}_{1}^{\prime },\mathbf {p}_{2}^{\prime })-{\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Annihilation}$$(\mathbf {p}_{1}, \mathbf {p}_{2},\mathbf {p}_{1}^{\prime },\mathbf {p}_{2}^{\prime })$, and etc. The expressions for ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Attractive}$, ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Repulsive}$, and ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Annihilation}$ have been provide in the main text in (22), (23) and (24).

For the non relativistic equation of the five-body system (e⁻e⁺e⁻e⁺e⁻) in the momentum space we have the following expression:

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}s_{3}s_{4}s_{5}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3}, \mathbf{p}_{4},\mathbf{p}_{5})\left[ \frac{\mathbf{p}_{1}^{2}}{2m}+\frac{ \mathbf{p}_{2}^{2}}{2m}+\frac{\mathbf{p}_{3}^{2}}{2m}+\frac{\mathbf{p} _{4}^{2}}{2m}+\frac{\mathbf{p}_{5}^{2}}{2m}-\epsilon_{5}\right] \\ &=&\frac{e^{2}}{(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }d^{3}p_{3}^{\prime }d^{3}p_{4}^{\prime }~d^{3}p_{5}^{\prime }F_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}(\mathbf{p}_{1}^{\prime }, {\mathbf{p}_{2}^{\prime }},{\mathbf{p}_{3}^{\prime }},{\mathbf{p}_{4}^{\prime }}, {\mathbf{p}_{5}^{\prime }})\times \\ &&\left[\left( \frac{\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}s_{2}^{\prime }}}{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}}{4m^{2}}\right) \delta_{s_{3}^{\prime }s_{3}} \delta_{s_{4}^{\prime }s_{4}} \delta_{s_{5}^{\prime }s_{5}}\delta^{3}({\mathbf{p}_{3}^{\prime }}-\mathbf{p} _{3})\delta^{3}({\mathbf{p}_{4}^{\prime }}-\mathbf{p}_{4})\delta^{3}({\mathbf{ p}_{5}^{\prime }}-\mathbf{p}_{5})\right.\\ &&\times\delta^{3}({\mathbf{p}_{1}^{\prime }}+{\mathbf{ p}_{2}^{\prime }}-\mathbf{p}_{1}-\mathbf{p}_{2}) \\ &&+\left( \frac{\delta_{s_{2}s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}} }{\mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2}\mathbf{|}^{2}}-\frac{ A_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}s_{1}^{\prime }}\delta_{s_{4}^{\prime }s_{4}}~\delta_{s_{5}^{\prime }s_{5}}\delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}({\mathbf{p}_{4}^{\prime }}-\mathbf{p}_{4})\delta^{3}({\mathbf{p}_{5}^{\prime }}- \mathbf{p}_{5})\\ &&\times\delta^{3}({\mathbf{p}_{2}^{\prime }}+{\mathbf{p}_{3}^{\prime }}- \mathbf{p}_{2}-\mathbf{p}_{3}) \\ &&+\left( \frac{\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}} }{\mathbf{|p}_{3}^{\prime }\mathbf{-p}_{3}\mathbf{|}^{2}}-\frac{ A_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{5}^{\prime }s_{5}}\delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}(\mathbf{p}_{2}^{\prime }-\mathbf{p}_{2})\delta^{3}({\mathbf{p}_{5}^{\prime }}- \mathbf{p}_{5})\\ &&\times\delta^{3}({\mathbf{p}_{3}^{\prime }}+{\mathbf{p}_{4}^{\prime }}- \mathbf{p}_{3}-\mathbf{p}_{4}) \\ &&+\left( \frac{\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{4}^{\prime }s_{4}} }{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{ A_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}}{4m^{2}}\right) \delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}\delta^{3}({\mathbf{p}_{2}^{\prime }}-\mathbf{p}_{2})\delta^{3}({\mathbf{p}_{3}^{\prime }}-\mathbf{p}_{3})\delta^{3}({\mathbf{p}_{5}^{\prime }}- \mathbf{p}_{5})\\ &&\times \delta^{3}({\mathbf{p}_{1}^{\prime }}+{\mathbf{p}_{4}^{\prime }}- \mathbf{p}_{1}-\mathbf{p}_{4}) \\ &&+\left( \frac{\delta_{s_{2}s_{2}^{\prime }}\delta_{s_{5}^{\prime }s_{5}} }{\mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2}\mathbf{|}^{2}}-\frac{ A_{s_{2}s_{5}s_{2}^{\prime }s_{5}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}s_{1}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta^{3}({\mathbf{p}_{1}^{\prime }}-\mathbf{p}_{1})\delta^{3}({\mathbf{p}_{3}^{\prime}}-\mathbf{p}_{3})\delta^{3}({\mathbf{p}_{4}^{\prime }}- \mathbf{p}_{4})\\ &&\times\delta^{3}({\mathbf{p}_{2}^{\prime }}+{\mathbf{p}_{5}^{\prime }}- \mathbf{p}_{2}-\mathbf{p}_{5}) \\ &&+\left( \frac{\delta_{s_{4}s_{4}^{\prime }}\delta_{s_{5}^{\prime }s_{5}} }{\mathbf{|p}_{4}^{\prime }\mathbf{-p}_{4}\mathbf{|}^{2}}-\frac{ A_{s_{4}s_{5}s_{4}^{\prime }s_{5}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta^{3}({\mathbf{p}_{1}^{\prime }}-\mathbf{p}_{1})\delta^{3}({\mathbf{p}_{2}^{\prime }}-\mathbf{p}_{2})\delta^{3}({\mathbf{p}_{3}^{\prime }}- \mathbf{p}_{3})\\ &&\times\delta^{3}({\mathbf{p}_{4}^{\prime }}+{\mathbf{p}_{5}^{\prime }}- \mathbf{p}_{4}-\mathbf{p}_{5}) \\ &&-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta^{3}(\mathbf{p}_{2}^{\prime }-\mathbf{p}_{2})\delta^{3}({\mathbf{p}_{4}^{\prime }}-\mathbf{p}_{4})\delta^{3}({\mathbf{p}_{5}^{\prime }}- \mathbf{p}_{5})\frac{\delta^{3}({\mathbf{p}_{1}^{\prime }}+\mathbf{p} _{3}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{3})}{\mathbf{|p}_{1}^{\prime } \mathbf{-p}_{1}\mathbf{|}^{2}} \\ &&-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta^{3}(\mathbf{p}_{1}^{\prime }-\mathbf{p}_{1})\delta^{3}(\mathbf{p}_{3}^{\prime }-\mathbf{p}_{3})\delta^{3}(\mathbf{p}_{5}^{\prime }- \mathbf{p}_{5})\frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p} _{4}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{4})}{\mathbf{|p}_{2}^{\prime } \mathbf{-p}_{2}\mathbf{|}^{2}} \\ &&-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta^{3}({\mathbf{p}_{2}^{\prime }}-\mathbf{p}_{2})\delta^{3}({\mathbf{p}_{3}^{\prime }}-\mathbf{p}_{3})\delta^{3}({\mathbf{p}_{4}^{\prime }}- \mathbf{p}_{4})\frac{\delta^{3}({\mathbf{p}_{1}^{\prime }}+\mathbf{p} _{5}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{5})}{\mathbf{|p}_{1}^{\prime } \mathbf{-p}_{1}\mathbf{|}^{2}} \\ && \left. -\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta^{3}(\mathbf{p}_{2}^{\prime } - \mathbf{p}_{2})\delta^{3}(\mathbf{p}_{4}^{\prime}-\mathbf{p}_{4})\delta^{3}(\mathbf{p}_{5}^{\prime }- \mathbf{p}_{5})\frac{\delta^{3}(\mathbf{p}_{3}^{\prime }+\mathbf{p} _{5}^{\prime }-\mathbf{p}_{3} - \mathbf{p}_{5})}{\mathbf{|p}_{3}^{\prime } \mathbf{-p}_{3}\mathbf{|}^{2}}\right] ,\\ \end{array} $$

(91)

where we let 𝜖₅ = E − 5m. Its coordinate-space version is the five-body Schrödinger , (see (31) with n = 5). In the coordinate space, the five-body equation becomes as the following:

$$ \begin{array}{@{}rcl@{}} &&\left\{-\frac{1}{2m}\left( {\sum\limits_{i=1}^{5}{\nabla_{i}^{2}}}\right) -\epsilon_{5}-\frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x}_{2}|} - \frac{\alpha }{|\mathbf{x}_{2}-\mathbf{x}_{3}|}-\frac{\alpha }{|\mathbf{x}_{3}-\mathbf{x} _{4}|}-\frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x}_{4}|} - \frac{\alpha }{| \mathbf{x}_{2}-\mathbf{x}_{5}|}\right. \\ && -\frac{\alpha }{|\mathbf{x}_{4}-\mathbf{x}_{5}|}+\frac{\alpha }{|\mathbf{x} _{1}-\mathbf{x}_{3}|}+\frac{\alpha }{|\mathbf{x}_{2}-\mathbf{x}_{4}|}+\frac{ \alpha }{|\mathbf{x}_{1}-\mathbf{x}_{5}|}\\&&\left.+\frac{\alpha }{|\mathbf{x}_{3}- \mathbf{x}_{5}|}\vphantom{\sum\limits_{i=1}^{5}}\right\}{\Psi}_{s_{1}s_{2}s_{3}s_{4}s_{5}}(\mathbf{x}_{1}, \mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5}) \\ &=&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{1}-\mathbf{x}_{2})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}{ \sum }A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x} _{5}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{2}-\mathbf{x}_{3})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}{ \sum }A_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x} _{5}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{3}-\mathbf{x}_{4})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}{ \sum }A_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{5}^{\prime }s_{5}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x} _{5}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{1}-\mathbf{x}_{4})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}{ \sum }A_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x} _{5}). \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{2}-\mathbf{x}_{5})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}{ \sum }A_{s_{2}s_{5}s_{2}^{\prime }s_{5}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x} _{5}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{4}-\mathbf{x}_{5})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}{ \sum }A_{s_{4}s_{5}s_{4}^{\prime }s_{5}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x} _{5}) \end{array} $$

(92)

The interactions are expressed by attractive or repulsive Coulomb potentials in the left hand side of the equation and the repulsive contact virtual annihilation interactions (various delta functions in the right hand side of the above equation). For example, for a system such as five body (e⁻e⁺e⁻e⁺e⁻) we have six attractive terms, four repulsive terms, and six virtual annihilation interaction terms (the six terms of the right hand side of the above equation).

• e) The six-body systems (such as Ps₃, e⁻e⁺e⁻e⁺e⁻e⁺):

For the six-body systems such as (Ps₃, e⁻e⁺e⁻e⁺e⁻e⁺) we use the trial state (16) in the manuscript. Hence, we have

$$ \begin{array}{@{}rcl@{}} |\psi_{6}\rangle &=&\underset{s_{1}...s_{6}}{\sum }\int d^{3}p_{1}...d^{3}p_{6}~F_{s_{1}...s_{6}}(\mathbf{p}_{1},...,\mathbf{p}_{6})b^{\dagger }(\mathbf{p}_{1},s_{1})d^{\dagger }(\mathbf{p}_{2},s_{2})b^{\dagger }(\mathbf{p}_{3},s_{3})\\ &&\times d^{\dagger}(\mathbf{p}_{4},s_{4})b^{\dagger }(\mathbf{p}_{5},s_{5})d^{\dagger }(\mathbf{p} _{6},s_{6})|0\rangle \end{array} $$

(93)

By choosing the above trial state we have the following relativistic wave equation (n = 6 in (25)):

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}s_{3}s_{4}s_{5}s_{6}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3},\mathbf{p}_{4},\mathbf{p}_{5},\mathbf{p}_{6})[\omega_{p_{1}}+\omega _{p_{2}}+\omega_{p_{3}}+\omega_{p_{4}}+\omega_{p_{5}}+\omega_{p_{6}}-E] \\ &=&\frac{m^{2}e^{2}}{2(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }d^{3}p_{3}^{\prime }d^{3}p_{4}^{\prime }d^{3}p_{5}^{\prime}d^{3}p_{6}^{\prime }F_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}({\mathbf{p}_{1}^{\prime }},{\mathbf{p}_{2}^{\prime }},{\mathbf{p}_{3}^{\prime }},{\mathbf{p}_{4}^{\prime }},{\mathbf{p} _{5}^{\prime }},{\mathbf{p}_{6}^{\prime }})\times \\ &&\left\{\mathcal{M}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{A}(\mathbf{p}_{1},\mathbf{p}_{2},{\mathbf{p}_{1}^{\prime }},{\mathbf{ p}_{2}^{\prime }})~\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}~\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta_{{\mathbf{p}_{4}},\mathbf{p}_{4}^{\prime }}^{3}\delta^{3}_{{\mathbf{p}_{5}},{\mathbf{p}_{5}^{\prime }}}\delta^{3}_{{\mathbf{p}_{6}},{\mathbf{p}_{6}^{\prime }}}\frac{\delta^{3}({\mathbf{p}_{1}^{\prime }}+{\mathbf{p}_{2}^{\prime}}-\mathbf{p}_{1}- \mathbf{p}_{2})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{2}^{\prime }}\omega_{p_{1}}\omega_{p_{2}}}}\right. \\ &&+\mathcal{M}_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}^{A }(\mathbf{p}_{2},\mathbf{p}_{3},{\mathbf{p}_{2}^{\prime }},{\mathbf{p}_{3}^{\prime }})\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta^{3}_{{ \mathbf{p}_{1}},{\mathbf{p}_{1}^{\prime}}}\delta^{3}_{{\mathbf{p}_{4}},{\mathbf{p}_{4}^{\prime }}}\delta_{\mathbf{p}_{5},\mathbf{p}_{5}^{\prime }}^{3}\delta_{\mathbf{p}_{6},\mathbf{p}_{6}^{\prime}}^{3}\frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p}_{2}- \mathbf{p}_{3})}{\sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{2}}\omega_{p_{3}}}} \\ &&+\mathcal{M}_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}^{A }(\mathbf{p}_{3},\mathbf{p}_{4},{\mathbf{p}_{3}^{\prime }},{\mathbf{p}_{4}^{\prime }})\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}~\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{ \mathbf{p}_{1},\mathbf{p}_{1}^{\prime}}^{3}\delta_{\mathbf{p}_{2},\mathbf{p}_{2}^{\prime }}^{3}\delta^{3}_{{\mathbf{p}_{5}},{\mathbf{p}_{5}^{\prime }}}\delta_{{\mathbf{p}_{6}},\mathbf{p}_{6}^{\prime }}^{3}\frac{\delta^{3}(\mathbf{p}_{3}^{\prime }+\mathbf{p}_{4}^{\prime }-\mathbf{p}_{3}- \mathbf{p}_{4})}{\sqrt{\omega_{p_{3}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{3}}\omega_{p_{4}}}} \\ &&+\mathcal{M}_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}^{A }(\mathbf{p}_{1},\mathbf{p}_{4},{\mathbf{p}_{1}^{\prime }},{\mathbf{p}_{4}^{\prime }})\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{2},\mathbf{p}_{2}^{\prime }}^{3}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta^{3}_{\mathbf{p}_{5},{\mathbf{p}_{5}^{\prime }}}\delta^{3}_{\mathbf{p}_{6},{\mathbf{p}_{6}^{\prime }}}\frac{\delta^{3}({\mathbf{p}_{1}^{\prime }}+\mathbf{p}_{4}^{\prime }-\mathbf{p}_{1}- \mathbf{p}_{4})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{1}}\omega_{p_{4}}}} \\ &&+\mathcal{M}_{s_{2}s_{5}s_{2}^{\prime }s_{5}^{\prime }}^{A }(\mathbf{p}_{2},\mathbf{p}_{5},\mathbf{p}_{2}^{\prime },\mathbf{p}_{5}^{\prime })\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{6}^{\prime }s_{6}}\delta^{3}_{\mathbf{p}_{1},{\mathbf{p}_{1}^{\prime }}}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta^{3}_{\mathbf{p}_{4},{\mathbf{p}_{4}^{\prime }}}\delta^{3}_{\mathbf{p}_{6},{\mathbf{p}_{6}^{\prime }}}\frac{\delta^{3}({\mathbf{p}_{2}^{\prime }}+{\mathbf{p}_{5}^{\prime }}-\mathbf{p}_{2}- \mathbf{p}_{5})}{\sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{5}^{\prime }}\omega_{p_{2}}\omega_{p_{5}}}} \\ &&+\mathcal{M}_{s_{4}s_{5}s_{4}^{\prime }s_{5}^{\prime }}^{A }(\mathbf{p}_{4},\mathbf{p}_{5},{\mathbf{p}_{4}^{\prime }},{\mathbf{p}_{5}^{\prime }})\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{6}^{\prime }s_{6}}\delta^{3}_{\mathbf{p}_{1},{\mathbf{p}_{1}^{\prime }}}\delta_{\mathbf{p}_{2},\mathbf{p}_{2}^{\prime }}^{3}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta_{\mathbf{p}_{6},\mathbf{p}_{6}^{\prime }}^{3}\frac{\delta^{3}(\mathbf{p}_{4}^{\prime }+\mathbf{p}_{5}^{\prime }-\mathbf{p}_{4}- \mathbf{p}_{5})}{\sqrt{\omega_{p_{4}^{\prime }}\omega_{p_{5}^{\prime }}\omega_{p_{4}}\omega_{p_{5}}}} \\ &&+\mathcal{M}_{s_{1}s_{6}s_{1}^{\prime }s_{6}^{\prime }}^{A }(\mathbf{p}_{1},\mathbf{p}_{6},\mathbf{p}_{1}^{\prime },\mathbf{p}_{6}^{\prime })\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{\mathbf{p}_{2},\mathbf{p}_{2}^{\prime }}^{3}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta_{\mathbf{p}_{4},\mathbf{p}_{4}^{\prime }}^{3}\delta_{\mathbf{p}_{5},\mathbf{p}_{5}^{\prime }}^{3}\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{6}^{\prime }-\mathbf{p}_{1}- \mathbf{p}_{6})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{6}^{\prime }}\omega_{p_{1}}\omega_{p_{6}}}} \\ &&+\mathcal{M}_{s_{3}s_{6}s_{3}^{\prime }s_{6}^{\prime }}^{A }(\mathbf{p}_{3},\mathbf{p}_{6},\mathbf{p}_{3}^{\prime },\mathbf{p}_{6}^{\prime })\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{\mathbf{p}_{1},\mathbf{p}_{1}^{\prime }}^{3}\delta_{\mathbf{p}_{2},\mathbf{p}_{2}^{\prime }}^{3}\delta_{\mathbf{p}_{4},\mathbf{p}_{4}^{\prime }}^{3}\delta_{\mathbf{p}_{5},\mathbf{p}_{5}^{\prime }}^{3}\frac{\delta^{3}(\mathbf{p}_{3}^{\prime }+\mathbf{p}_{6}^{\prime }-\mathbf{p}_{3}- \mathbf{p}_{6})}{\sqrt{\omega_{p_{3}^{\prime }}\omega_{p_{6}^{\prime }}\omega_{p_{3}}\omega_{p_{6}}}} \\ &&+\mathcal{M}_{s_{5}s_{6}s_{5}^{\prime }s_{6}^{\prime }}^{A }(\mathbf{p}_{5},\mathbf{p}_{6},\mathbf{p}_{5}^{\prime },\mathbf{p}_{6}^{\prime })\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{\mathbf{p}_{1},\mathbf{p}_{1}^{\prime }}^{3}\delta_{\mathbf{p}_{2},\mathbf{p}_{2}^{\prime }}^{3}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta_{\mathbf{p}_{4},\mathbf{p}_{4}^{\prime }}^{3}\frac{\delta^{3}(\mathbf{p}_{5}^{\prime }+\mathbf{p}_{6}^{\prime }-\mathbf{p}_{5}- \mathbf{p}_{6})}{\sqrt{\omega_{p_{5}^{\prime }}\omega_{p_{6}^{\prime }}\omega_{p_{5}}\omega_{p_{6}}}} \\ &&-\mathcal{M}_{s_{1}s_{3}s_{1}^{\prime }s_{3}^{\prime }}^{Repulsive}(\mathbf{p}_{1},\mathbf{p}_{3},\mathbf{p}_{1}^{\prime },\mathbf{ p}_{3}^{\prime })~\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{4}^{\prime }s_{4}}~\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{2},\mathbf{p}_{2}^{\prime }}^{3}\delta_{\mathbf{p}_{4},\mathbf{p}_{4}^{\prime }}^{3}\delta_{\mathbf{p}_{5},\mathbf{p}_{5}^{\prime }}^{3}\delta_{\mathbf{p}_{6},\mathbf{p}_{6}^{\prime }}^{3}\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p}_{1}- \mathbf{p}_{3})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{1}}\omega_{p_{3}}}} \\ &&-\mathcal{M}_{s_{2}s_{4}s_{2}^{\prime }s_{4}^{\prime }}^{Repulsive}(\mathbf{p}_{2},\mathbf{p}_{4},\mathbf{p}_{2}^{\prime },\mathbf{ p}_{4}^{\prime })~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1},\mathbf{p}_{1}^{\prime }}^{3}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta_{\mathbf{p}_{5},\mathbf{p}_{5}^{\prime }}^{3}\delta_{\mathbf{p}_{6},\mathbf{p}_{6}^{\prime }}^{3}\frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{4}^{\prime }-\mathbf{p}_{2}- \mathbf{p}_{4})}{\sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{4}^{\prime }}\omega_{p_{2}}\omega_{p_{4}}}} \\ &&-\mathcal{M}_{s_{1}s_{5}s_{1}^{\prime }s_{5}^{\prime }}^{Repulsive}(\mathbf{p}_{1},\mathbf{p}_{5},\mathbf{p}_{1}^{\prime },\mathbf{ p}_{5}^{\prime })~\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{2},\mathbf{p}_{2}^{\prime }}^{3}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta_{\mathbf{p}_{4},\mathbf{p}_{4}^{\prime }}^{3}\delta_{\mathbf{p}_{6},\mathbf{p}_{6}^{\prime }}^{3}\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{5}^{\prime }-\mathbf{p}_{1}- \mathbf{p}_{5})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{5}^{\prime }}\omega_{p_{1}}\omega_{p_{5}}}} \\ &&-\mathcal{M}_{s_{3}s_{5}s_{3}^{\prime }s_{5}^{\prime }}^{Repulsive}(\mathbf{p}_{3},\mathbf{p}_{5},\mathbf{p}_{3}^{\prime },\mathbf{ p}_{5}^{\prime })\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{6}^{\prime }s_{6}}\delta^{3}_{\mathbf{p}_{1},{\mathbf{p}_{1}^{\prime }}}\delta^{3}_{{\mathbf{p}_{2}},{\mathbf{p}_{2}^{\prime }}}\delta_{{\mathbf{p}_{4}},\mathbf{p}_{4}^{\prime }}^{3}\delta^{3}_{\mathbf{p}_{6},{\mathbf{p}_{6}^{\prime }}}\frac{\delta^{3}({\mathbf{p}_{3}^{\prime }}+{\mathbf{p}_{5}^{\prime }}-\mathbf{p}_{3}- \mathbf{p}_{5})}{\sqrt{\omega_{p_{3}^{\prime }}\omega_{p_{5}^{\prime }}\omega_{p_{3}}\omega_{p_{5}}}} \\ &&-\mathcal{M}_{s_{2}s_{4}s_{2}^{\prime }s_{4}^{\prime }}^{Repulsive}(\mathbf{p}_{2},\mathbf{p}_{6},\mathbf{p}_{2}^{\prime },\mathbf{ p}_{6}^{\prime })~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{\mathbf{p}_{1},\mathbf{p}_{1}^{\prime }}^{3}\delta_{\mathbf{p}_{3},\mathbf{p}_{3}^{\prime }}^{3}\delta^{3}_{{\mathbf{p}_{4}},{\mathbf{p}_{4}^{\prime }}}\delta^{3}_{\mathbf{p}_{5},{\mathbf{p}_{5}^{\prime }}}\frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+{\mathbf{p}_{6}^{\prime }}-\mathbf{p}_{2}- \mathbf{p}_{6})}{\sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{6}^{\prime }}\omega_{p_{2}}\omega_{p_{6}}}} \\ &&\left.-\mathcal{M}_{s_{4}s_{6}s_{4}^{\prime }s_{6}^{\prime }}^{Repulsive}(\mathbf{p}_{4},\mathbf{p}_{6},{\mathbf{p}_{4}^{\prime }},{\mathbf{ p}_{6}^{\prime }})~\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}\delta_{\mathbf{p}_{1},\mathbf{p}_{1}^{\prime }}^{3}\delta_{{\mathbf{p}_{2}},\mathbf{p}_{2}^{\prime }}^{3}\delta_{{\mathbf{p}_{3}},\mathbf{p}_{3}^{\prime }}^{3}\delta_{{\mathbf{p}_{5}},\mathbf{p}_{5}^{\prime }}^{3}\frac{\delta^{3}({\mathbf{p}_{4}^{\prime }}+{\mathbf{p}_{6}^{\prime }} - \mathbf{p}_{4} - \mathbf{p}_{6})}{\sqrt{\omega_{p_{4}^{\prime }}\omega_{p_{6}^{\prime }}\omega_{p_{4}}\omega_{p_{6}}}}\right\}, \\&& \end{array} $$

(94)

where we let ${\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{A}(\mathbf {p}_{1},\mathbf {p}_{2},\mathbf {p}_{1}^{\prime },\mathbf { p}_{2}^{\prime })={\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Attractive}(\mathbf {p}_{1},\mathbf {p}_{2},\mathbf {p}_{1}^{\prime },{\mathbf {p}_{2}^{\prime }})-{\mathscr{M}}_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}^{Annihilation}$$(\mathbf {p}_{1}, \mathbf {p}_{2},{\mathbf {p}_{1}^{\prime }},{\mathbf {p}_{2}^{\prime }})$, and etc. The expressions for ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Attractive}$, ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Repulsive}$, and ${\mathscr{M}}_{s_{j}s_{k}s_{j}^{\prime }s_{k}^{\prime }}^{Annihilation}$ have been provide in the main text in (22), (23) and (24). Also, the notation, for example, $\delta ^{3}_{{\mathbf {p}_{1}},{\mathbf {p}_{1}^{\prime }}}$ (and similar delta functions) in the above equation means the following: ($\delta ^{3}_{\mathbf {p}_{1},{\mathbf {p}_{1}^{\prime }}}$$=\delta ^{3}({\mathbf {p}_{1}^{\prime }}-\mathbf {p}_{1})$).

For the non relativistic equation of the six-body system, for example (Ps₃, e⁻e⁺e⁻e⁺e⁻e⁺), in the momentum space we have the following expression:

$$ \begin{array}{@{}rcl@{}} &&F_{s_{1}s_{2}s_{3}s_{4}s_{5}s_{6}}(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p} _{3},\mathbf{p}_{4},\mathbf{p}_{5},\mathbf{p}_{6})\left[ \frac{\mathbf{p} _{1}^{2}}{2m}+\frac{\mathbf{p}_{2}^{2}}{2m}+\frac{\mathbf{p}_{3}^{2}}{2m}+ \frac{\mathbf{p}_{4}^{2}}{2m}+\frac{\mathbf{p}_{5}^{2}}{2m}+\frac{\mathbf{p} _{6}^{2}}{2m}-\epsilon_{6}\right] \\ &=&\frac{e^{2}}{(2\pi )^{3}}\underset{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }\int d^{3}p_{1}^{\prime }d^{3}p_{2}^{\prime }d^{3}p_{3}^{\prime }d^{3}p_{4}^{\prime }d^{3}p_{5}^{\prime }d^{3}p_{6}F_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime },\mathbf{p}_{3}^{\prime },\mathbf{p}_{4}^{\prime },\mathbf{p}_{5}^{\prime },\mathbf{p}_{6}^{\prime })\times \\ &&\left[\left( \frac{\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}s_{2}^{\prime }}}{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}}{4m^{2}}\right) \delta_{s_{3}^{\prime }s_{3}} \delta_{s_{4}^{\prime }s_{4}} \delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p} _{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p }_{4}}^{3}\delta_{\mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\delta_{\mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{2}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{2})\right. \\ &&+\left( \frac{\delta_{s_{2}s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}} }{\mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2}\mathbf{|}^{2}}-\frac{ A_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}^{\prime }s_{1}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta_{\mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\delta_{\mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{3}) \\ &&+\left( \frac{\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}} }{\mathbf{|p}_{3}^{\prime }\mathbf{-p}_{3}\mathbf{|}^{2}}-\frac{ A_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}~\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{2}^{\prime },\mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\delta_{\mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\delta^{3}(\mathbf{p}_{3}^{\prime }+\mathbf{p}_{4}^{\prime }-\mathbf{p}_{3}-\mathbf{p}_{4}) \\ &&+\left( \frac{\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{4}^{\prime }s_{4}} }{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{ A_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}}{4m^{2}}\right) \delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{2}^{\prime }, \mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\delta_{\mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{4}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{4}) \\ &&+\left( \frac{\delta_{s_{2}s_{2}^{\prime }}\delta_{s_{5}^{\prime }s_{5}} }{\mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2}\mathbf{|}^{2}}-\frac{ A_{s_{2}s_{5}s_{2}^{\prime }s_{5}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta_{\mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{5}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{5}) \\ &&+\left( \frac{\delta_{s_{4}s_{4}^{\prime }}\delta_{s_{5}^{\prime }s_{5}} }{\mathbf{|p}_{4}^{\prime }\mathbf{-p}_{4}\mathbf{|}^{2}}-\frac{ A_{s_{4}s_{5}s_{4}^{\prime }s_{5}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{2}^{\prime },\mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\delta^{3}(\mathbf{p}_{4}^{\prime }+\mathbf{p}_{5}^{\prime }-\mathbf{p}_{4}-\mathbf{p}_{5}) \\ &&+\left( \frac{\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{6}^{\prime }s_{6}} }{\mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}}-\frac{ A_{s_{1}s_{6}s_{1}^{\prime }s_{6}^{\prime }}}{4m^{2}}\right) \delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{\mathbf{p}_{2}^{\prime }, \mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta_{\mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{6}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{6}) \\&&+\left( \frac{\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{6}^{\prime }s_{6}} }{\mathbf{|p}_{3}^{\prime }\mathbf{-p}_{3}\mathbf{|}^{2}}-\frac{ A_{s_{3}s_{6}s_{3}^{\prime }s_{6}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{2}^{\prime },\mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta_{\mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\delta^{3}(\mathbf{p}_{3}^{\prime }+\mathbf{p}_{6}^{\prime }-\mathbf{p}_{3}-\mathbf{p}_{6}) \\ &&+\left( \frac{\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}} }{\mathbf{|p}_{5}^{\prime }\mathbf{-p}_{5}\mathbf{|}^{2}}-\frac{ A_{s_{3}s_{6}s_{3}^{\prime }s_{6}^{\prime }}}{4m^{2}}\right) \delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{2}^{\prime },\mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta^{3}(\mathbf{p}_{5}^{\prime }+\mathbf{p}_{6}^{\prime }-\mathbf{p}_{5}-\mathbf{p}_{6}) \\ &&-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{2}^{\prime }, \mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta_{\mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\delta_{ \mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{3})}{ \mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}} \\ &&-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\delta_{ \mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{4}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{4})}{ \mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2}\mathbf{|}^{2}} \\ &&-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{2}^{\prime }, \mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta_{ \mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\frac{\delta^{3}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{5}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{5})}{ \mathbf{|p}_{1}^{\prime }\mathbf{-p}_{1}\mathbf{|}^{2}} \\ &&-\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{2}^{\prime },\mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta_{ \mathbf{p}_{6}^{\prime },\mathbf{p}_{6}}^{3}\frac{\delta^{3}(\mathbf{p}_{3}^{\prime }+\mathbf{p}_{5}^{\prime }-\mathbf{p}_{3}-\mathbf{p}_{5})}{ \mathbf{|p}_{3}^{\prime }\mathbf{-p}_{3}\mathbf{|}^{2}} \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&{}-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{\mathbf{p}_{4}^{\prime },\mathbf{p}_{4}}^{3}\delta_{ \mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\frac{\delta^{3}(\mathbf{p}_{2}^{\prime }+\mathbf{p}_{6}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{6})}{ \mathbf{|p}_{2}^{\prime }\mathbf{-p}_{2}\mathbf{|}^{2}} \\ &&{}\left.-\delta_{s_{1}s_{1}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}\delta_{\mathbf{p}_{1}^{\prime }, \mathbf{p}_{1}}^{3}\delta_{\mathbf{p}_{2}^{\prime },\mathbf{p}_{2}}^{3}\delta_{\mathbf{p}_{3}^{\prime },\mathbf{p}_{3}}^{3}\delta_{ \mathbf{p}_{5}^{\prime },\mathbf{p}_{5}}^{3}\frac{\delta^{3}(\mathbf{p}_{4}^{\prime }+\mathbf{p}_{6}^{\prime }-\mathbf{p}_{4}-\mathbf{p}_{6})}{ \mathbf{|p}_{4}^{\prime }\mathbf{-p}_{4}\mathbf{|}^{2}}\right] \end{array} $$

(95)

where we let 𝜖₆ = E − 6m. Its coordinate-space version is the six-body Schrödinger equation, (see (31) with n = 6). In the coordinate space, the six-body equation becomes as the following:

$$ \begin{array}{@{}rcl@{}} &&\left\{-\frac{1}{2m}\left( {{\sum}_{i=1}^{6}{\nabla_{i}^{2}}}\right) -\epsilon_{6}-\frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x}_{2}|}-\frac{\alpha }{|\mathbf{x}_{2}-\mathbf{x}_{3}|} - \frac{\alpha }{|\mathbf{x}_{3}-\mathbf{x} _{4}|} - \frac{\alpha }{|\mathbf{x}_{1}-\mathbf{x}_{4}|} - \frac{\alpha }{| \mathbf{x}_{2}-\mathbf{x}_{5}|}\right.\\ &&-\frac{\alpha }{|\mathbf{x}_{4}-\mathbf{x}_{5}|}-\frac{\alpha }{|\mathbf{x} _{1}-\mathbf{x}_{6}|}-\frac{\alpha }{|\mathbf{x}_{3}-\mathbf{x}_{6}|}-\frac{ \alpha }{|\mathbf{x}_{5}-\mathbf{x}_{6}|} + \frac{\alpha }{|\mathbf{x}_{1}- \mathbf{x}_{3}|} + \frac{\alpha }{|\mathbf{x}_{2}-\mathbf{x}_{4}|} + \frac{ \alpha }{|\mathbf{x}_{1}-\mathbf{x}_{5}|} \\ && \left. +\frac{\alpha }{|\mathbf{x}_{3}-\mathbf{x}_{5}|}+\frac{\alpha }{|\mathbf{x} _{2}-\mathbf{x}_{6}|}+\frac{\alpha }{|\mathbf{x}_{4}-\mathbf{x}_{6}|}\right\} {\Psi}_{s_{1}s_{2}s_{3}s_{4}s_{5}s_{6}}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{ x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x}_{6}) \\ &=&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{1}-\mathbf{x}_{2})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{1}s_{2}s_{1}^{\prime }s_{2}^{\prime }}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{2}-\mathbf{x}_{3})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{2}s_{3}s_{2}^{\prime }s_{3}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{3}-\mathbf{x}_{4})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{3}s_{4}s_{3}^{\prime }s_{4}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{1}-\mathbf{x}_{4})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{1}s_{4}s_{1}^{\prime }s_{4}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{5}^{\prime }s_{5}}\delta_{s_{6}^{\prime }s_{6}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{2}-\mathbf{x}_{5})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{2}s_{5}s_{2}^{\prime }s_{5}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{6}^{\prime }s_{6}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{4}-\mathbf{x}_{5})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{4}s_{5}s_{4}^{\prime }s_{5}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{6}^{\prime }s_{6}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{1}-\mathbf{x}_{6})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{1}s_{6}s_{1}^{\prime }s_{6}^{\prime }}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{3}-\mathbf{x}_{6})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{3}s_{6}s_{3}^{\prime }s_{6}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{4}^{\prime }s_{4}}\delta_{s_{5}^{\prime }s_{5}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6}) \\ &&-\frac{\alpha \pi }{m^{2}}\delta (\mathbf{x}_{5}-\mathbf{x}_{6})\underset{ s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}{\sum }A_{s_{5}s_{6}s_{5}^{\prime }s_{6}^{\prime }}\delta_{s_{1}^{\prime }s_{1}}\delta_{s_{2}^{\prime }s_{2}}\delta_{s_{3}^{\prime }s_{3}}\delta_{s_{4}^{\prime }s_{4}}{\Psi}_{s_{1}^{\prime }s_{2}^{\prime }s_{3}^{\prime }s_{4}^{\prime }s_{5}^{\prime }s_{6}^{\prime }}(\mathbf{x}_{1},\mathbf{x}_{2},\mathbf{x}_{3},\mathbf{x}_{4},\mathbf{x}_{5},\mathbf{x} _{6})\\ \end{array} $$

(96)

The interactions are expressed by attractive or repulsive Coulomb potentials in the left hand side of the equation and the repulsive contact virtual annihilation interactions (various delta functions in the right hand side of the above equation). For a system such as (Ps₃, e⁻e⁺e⁻e⁺e⁻e⁺) we have nine attractive terms, six repulsive terms,and nine virtual annihilation interactions, namely the terms that contain some delta functions [ex: δ(x₁ −x₂) factor in the first term of the right hand side expressions of the (96) describes the virtual annihilation interaction between the first particle (e⁻) and the second particle (e⁺) in Ps₃].