Performance improvement of plug-and-play dual-phase-modulated continuous-variable quantum key distribution with quantum catalysis

Abstract

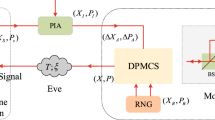
Continuous-variable quantum key distribution based on plug-and-play dual-phase-modulated coherent-states (DPMCS) protocol has been proved to be equivalent to the one-way Gaussian-modulated coherent-states protocol, but it is not just limited to this. This protocol can effectively against the LO-aimed attacks and maintain the system robust. However, the maximum transmission distance of the protocol is restricted due to its large excess noise. In this paper, we enhance the plug-and-play DPMCS protocol using quantum catalysis operation, which can be implemented by the existing technologies. To further highlight the advantage of the implementation of quantum catalysis operation, we make performance comparison not only between the proposed protocol and the original scheme but also the single-photon subtraction-based (SPS) plug-and-play DPMCS protocol. Security analysis shows that the proposed protocol can extend the maximum transmission distance up to hundreds of kilometers even under the effect of the imperfect source noise and show more excellent performance than the SPS-based plug-and-play DPMCS protocol. Furthermore, we also take the finite-size effect into consideration and thus achieve more practical results than those obtained in the asymptotic limit.

Appendices

Appendix A: Calculation of asymptotic secret key rate

Now let us calculate the asymptotic secret key rate. Without loss of generality, we suppose Bob performs homodyne detection. Taking the reverse reconciliation into consideration, the asymptotic secret key rate is given by

$$\begin{aligned} K_{\mathrm{asy}}=P_{t}[\beta I(A:B)-\chi (A:E)], \end{aligned}$$

(8)

where I(A : B) represents the Shannon mutual information between Alice and Bob, $\chi (A:E)$ represents the Holevo bound between Alice and Eve, $\beta$ stands for the reconciliation efficiency for reverse reconciliation, and $P_{t}$ stands for the success probability of implementing SSQC operation.

After passing through the untrusted quantum channel and Alice’s detection, the covariance matrix of $\rho _{\mathrm{FBA}_{2}}$ reads

$$\begin{aligned} \varXi _{\mathrm{FBA}_{2}}=\left( \begin{array}{cc} \vartheta I_{2} &{} \kappa \sigma _{z} \\ \kappa \sigma _{z}&{} \lambda I_{2}\\ \end{array} \right) =\left( \begin{array}{cc} \mathrm{WI}_{2} &{} \sqrt{T}H\sigma _{z} \\ \sqrt{T}H\sigma _{z}&{} T(U+\chi _{\mathrm{line}})I_{2}\\ \end{array} \right) . \end{aligned}$$

(9)

The Shannon mutual information shared by Alice and Bob $I_{AB}$ is given by

$$\begin{aligned} I_{AB}=\frac{1}{2}\log _{2}\frac{V_{B}}{V_{B|A}}, \end{aligned}$$

(10)

with $V_{B}=(\vartheta +1)/2$, $V_{A}=\lambda$, and

$$\begin{aligned} V_{B|A}=V_{B}-\frac{TH^{2}}{2V_{A}}. \end{aligned}$$

(11)

Since Eve can purify the system $\mathrm{FBA}_{2}$ and Alice can employ her measurement to purify the system FBE, thus we have

$$\begin{aligned} \chi _{AE}=G[(\nu _{1}-1)/2]+G[(\nu _{2}-1)/2]-G[(\nu _{3}-1)/2], \end{aligned}$$

(12)

where $G(x)=(x+1)\log _{2}(x+1)-x\log _{2}x$, and the symplectic eigenvalues $\nu _{1,2}$ is given by

$$\begin{aligned} \nu ^{2}_{1,2}=\frac{1}{2}(\varDelta \pm \sqrt{\varDelta ^{2}-4D^{2}}), \end{aligned}$$

(13)

with

$$\begin{aligned} \varDelta= & {} \vartheta ^{2}+\lambda ^{2}-2\kappa ^{2}, \nonumber \\ D= & {} \vartheta \lambda -\kappa ^{2}. \end{aligned}$$

(14)

The symplectic eigenvalue $\nu _{3}$ is expressed as $\nu _{3}=\sqrt{\vartheta ^{2}-\vartheta \kappa ^{2}/\lambda }$. According to above analysis, we can calculate the asymptotic secret key rate in Eq. (8).

Appendix B: Finite-size secret key rate

For the proposed protocol, the finite-size secret key rate is given by [9]

$$\begin{aligned} K_{\mathrm{fin}}=\frac{nP_{t}}{N}[\beta I (A:B)-\chi _{\epsilon _{\mathrm{PE}}}(A:E)-\varDelta (n)], \end{aligned}$$

(15)

where $\beta$ and I(A : B) are as the same as the aforementioned definitions. N stands for the total exchanged signals, and n stands for the number of signals which is taken advantage of for derivation of QKD. Note that the remained signals $f=N-n$ are utilized to perform parameter estimation. $\epsilon _{\mathrm{PE}}$ stands for the failure probability of parameter estimation and $\chi _{\epsilon _{\mathrm{PE}}}(A:E)$ stands for the maximal value of the Holevo information in finite-size scenario. $\varDelta (n)$ is related to the security of the privacy amplification, which is given by

$$\begin{aligned} \varDelta (n)=(2\mathrm{dim} H_{A}+3)\sqrt{\frac{\log _{2}(2/\bar{\epsilon })}{n}}+\frac{2}{n}\log _{2}(1/\epsilon _{\mathrm{PB}}), \end{aligned}$$

(16)

where $\bar{\epsilon }$ and $\epsilon _{\mathrm{PB}}$ stand for, respectively, the smoothing parameter and the failure probability of privacy amplification, and the Hilbert space dim $H_{A}=2$.

To determine $\chi _{\epsilon _{\mathrm{PE}}}(A:E)$, we need to construct the covariance matrix $\varXi _{\epsilon _{\mathrm{PE}}}$ in parameter estimation procedure. Therefore, f couples of correlated variables $(x_{i},y_{i})_{i=1...f}$ are sampled and a normal model is taken advantage of for these correlated variables to link Alice and Bob’s data, which is given by

$$\begin{aligned} y=\tau x+z, \end{aligned}$$

(17)

where $\tau =\sqrt{T}$ and z follows a centered normal distribution with variance $\delta ^{2}=1+T\zeta$. Then, the covariance matrix $\varXi _{\epsilon _{\mathrm{PE}}}$ is given by

$$\begin{aligned} \varXi _{\epsilon _{\mathrm{PE}}}=\left( \begin{array}{cc} \mathrm{WI}_{2} &{} \tau _{\mathrm{min}}H\sigma _{z} \\ \tau _{\mathrm{min}}H\sigma _{z}&{} (\tau ^{2}_{\mathrm{min}}U+\delta ^{2}_{\mathrm{max}})I_{2}\\ \end{array} \right) , \end{aligned}$$

(18)

where $\tau _{\mathrm{min}}$ and $\delta ^{2}_{\mathrm{max}}$ represent minimum of $\tau$ and maximum of $\delta ^{2}$, respectively. It is remarkable that the maximum-likelihood estimators $\hat{\tau }$ and $\hat{\delta }^{2}$, respectively, can be calculated by

$$\begin{aligned} \hat{\tau }=\frac{\sum ^{f}_{i=1}x_{i}y_{i}}{\sum ^{f}_{i=1}x^{2}_{i}} \quad and \quad \hat{\delta }^{2}=\frac{1}{f}\sum ^{f}_{i=1}(y_{i}-\hat{\tau }x_{i})^{2}. \end{aligned}$$

(19)

Besides, the following distributions

$$\begin{aligned} \hat{\tau }\sim N(\tau ,\frac{\delta ^{2}}{\sum ^{f}_{i=1}x^{2}_{i}}) \quad and \quad \frac{f\hat{\delta }^{2}}{\delta ^{2}}\sim \chi ^{2}(f-1) \end{aligned}$$

(20)

mean that the estimators $\hat{\tau }$ and $\hat{\delta }^{2}$ are independent for each other. Since parameters $\tau$ and $\delta ^{2}$ shown in Eq. (20) are true values, we can calculate $\tau _{\mathrm{min}}$ (the lower bound of $\tau$) and $\delta ^{2}_{\mathrm{max}}$ (the upper bound of $\delta ^{2}$), which is expressed as

$$\begin{aligned} \tau _{\mathrm{min}}\approx & {} \hat{\tau }-z_{\epsilon _{\mathrm{PE}}/2}\sqrt{\frac{\hat{\delta }^{2}}{fU}}, \nonumber \\ \delta ^{2}_{\mathrm{max}}\approx & {} \hat{\delta }^{2}+z_{\epsilon _{\mathrm{PE}}/2} \frac{\sqrt{2} \hat{\delta }^{2}}{\sqrt{f}}, \end{aligned}$$

(21)

where $z_{\epsilon _{\mathrm{PE}}/2}$ is such that $1-erf(z_{\epsilon _{\mathrm{PE}}/2}/\sqrt{2})/2=\epsilon _{\mathrm{PE}}/2$, and $erf(x)=\frac{2}{\sqrt{\pi }}\int ^{x}_{0}e^{-t^{2}}dt$ is error function. Theoretically, the expected values of $\hat{\tau }$ and $\hat{\delta }^{2}$ read

$$\begin{aligned} E[\hat{\tau }]= & {} \sqrt{T}, \nonumber \\ E[\hat{\delta }^{2}]= & {} 1+T\zeta . \end{aligned}$$

(22)

Consequently, $\tau _{\mathrm{min}}$ and $\delta ^{2}_{\mathrm{max}}$ can be given by

$$\begin{aligned} \tau _{\mathrm{min}}\approx & {} \sqrt{T}-z_{\epsilon _{\mathrm{PE}}/2}\sqrt{\frac{1+T\zeta }{fU}}, \nonumber \\ \delta ^{2}_{\mathrm{max}}\approx & {} 1+T\zeta +z_{\epsilon _{\mathrm{PE}}/2} \frac{\sqrt{2}(1+T\zeta )}{\sqrt{f}}. \end{aligned}$$

(23)

It is worth mentioning that we can take the optimal value of the error probabilities as [9]

$$\begin{aligned} \bar{\epsilon }=\epsilon _{\mathrm{PE}}=\epsilon _{\mathrm{PB}}=10^{-10}. \end{aligned}$$

(24)

After that, the finite-size secret key rate can be calculated through utilizing the derived bounds $\tau _{\mathrm{min}}$ and $\delta ^{2}_{\mathrm{max}}$.