Structure of negative parity states at ${\mathbf {6}\,\lesssim \, \mathbf {E}_\mathbf {x} <{\mathbf {7.0}} }$ MeV in $\mathbf {^{208}}{} \mathbf{Pb}$

Abstract

In the doubly magic nucleus $^{208}\mathrm{Pb}$ states at excitation energies $6\,\lesssim \, E_x <7.0$ MeV populated by the inelastic proton scattering via the doublet isobaric analog resonances g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ in $^{209}\mathrm{Bi}$ are studied. Sixteen states containing dominant strengths of the configurations g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ are newly assigned spins from $2^-$ to $6^-$, among them ten states are newly identified. Amplitudes with relative signs of up to four one-particle one-hole configurations with strengths down to 0.05% are determined in 40 states with spins from 1$^-$ to $6^-$. Amplitudes of configurations d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ for fourteen states and amplitudes of g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ for twenty-seven states are determined. Total strengths up to the full strength are found for configurations d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ with spins from $1^-$ to $3^-$ and for g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ with spins from 1$^-$ to $6^-$.

1 Introduction

The heaviest doubly magic nucleus $^{208}\mathrm{Pb}$ is fascinating as it offers the opportunity to study different classes of nuclear excitations. Most states in $^{208}\mathrm{Pb}$ are described in the shell model (SM) by one-particle one-hole (1p1h) configurations. More than two dozen states below the neutron and proton threshold ($S(n)=7368$ keV, $S(p)=8004$ keV [1]) are recognized to be not described as 1p1h configurations.

At $E_x \approx 6.0$ MeV configurations built by the coupling of the $3^-$ yrast state with 1p1h configurations were identified in eighteen states [2]. Ten states at $2< E_x<8$ MeV were recognized as tetrahedral configurations [3, 4]. Four states at $E_x< 5.9$ MeV are pairing vibrations [5,6,7]. Four states at $E_x< 6.2$ MeV are suggested to be icosahedral configurations [8].

Negative parity states below $E_x = 7.0$ MeV are almost completely identified by this work. It allows to find positive parity states and non-1p1h states [9] by comparison to SM calculations [10,11,12,13].

The surface delta interaction (SDI) was introduced by Green and Moszkowski [14] and extensively discussed by Talmi [15]. It provides a simple method to understand the interaction among two particles in a complex nucleus [2, 15,16,17,18].

The essential tool to determine amplitudes of 1p1h configurations in states of $^{208}\mathrm{Pb}$ derives from the study of isobaric analog resonances (IAR) [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. It allows to obtain information about the residual interaction among one-particle one-hole configurations [31,32,33,34].

IARs in $^{209}\mathrm{Bi}$ strongly excite only negative parity states. Early data were obtained in 1965–1970 in the USA [21,22,23,24,25,26,27,28,29,30] and in 1968–1969 at Heidelberg (Germany) [35,36,37,38,39,40,41,42]. In 2003–2019 more data were obtained at the Maier-Leibnitz-Laboratorium (MLL) at Garching (Germany) [43,44,45,46,47,48,49,50,51,52,53].

The weak cross sections on the intruder j $_{{15}/{2}}$ IAR could be measured [45] because of the high sensitivity of the Q3D magnetic spectrograph at the MLL with the final detector [54]. Results from the study of the $^{207}\mathrm{Pb}$$({ d, p})$ reaction [55,56,57,58] help much to decide ambuigities. Similarly studying $^{208}\mathrm{Pb}$$({ d, d' })$ [57,58,59] and $^{209}\mathrm{Bi}$$( d,\mathrm{^3 He})$ [60, 61] helps.

The proton decay of IARs allows to determine amplitudes of 1p1h configurations including the sign from the interference pattern in the angular distributions of $({ p, p' })$ [32, 33, 43, 45, 47, 48]. The orthogonality and sum rule relations allow to determine amplitudes of unobserable configurations (either because of vanishing cross sections or because of the absence of a target state) [9, 43, 49].

Table 1 Resonance energy $E^{res}$ and total width $\varGamma ^{tot}$ for IARs LJ in $^{209}\mathrm{Bi}$

The rather firm completeness of the sequence of states for most spins at $E_x< 6.2$ MeV allowed to study the chaoticity among bound states in a heavy nucleus [62,63,64]. The rather complete orthonormal transformation matrices from one-particle one-hole configurations to states [34, 49, 50] for $E_x< 6.2$ MeV allowed to recognize two dozen non-1p1h states, among them the 4140 $2^-$ yrast state newly interpreted as a tetrahedral rotation and vibration [3, 4]. It was first observed by Glöckner [39, 40] who provided a first analysis of the data discussed in this paper.

In Sect. 2 a reminder to the application of the theory of IARs to nuclear spectroscopy is given. In Sect. 3 available experimental data for the description of states at $6.20<E_x<7.0$ MeV in $^{208}\mathrm{Pb}$ are presented. In Sect. 4 results on states at $6.20<E_x<7.0$ MeV in $^{208}\mathrm{Pb}$ are discussed.

Amplitudes of up to four one-particle one-hole configurations with strengths down to 0.05% and relative signs are determined in 40 states at $5.8<E_x< 7.0$ MeV with spins from $1^-$ to $6^-$ and major configurations d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, and g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$.

Because of the large amount of information an appendix separated from the main text shows more figures, excitation functions from 1968 [28], spectra taken in 1969 with semiconductor detectors [41, 42], and spectra taken in 2003–2016 with the Q3D magnetic spectrograph [51, 52, 57, 58]. Finally the appendix includes a survey of the excitation energies of states at $6.20< E_x< 7.15$ MeV with spin and parity assignments complementing Table VI in [50].

2 Isobaric analog resonances

IARs in heavy nuclei were discovered in 1963 [19]. Accelerators with the capability to excite IARs in the lead region with proton energies of 14–20 MeV became available shortly later. The Max-Planck-Institut für Kernphysik (MPIK) at Heidelberg (Germany) bought a MP Van-de-Graaf accelerator for this purpose in 1967.

The high potential of the investigation of IARs in heavy nuclei was recognized by Robson as he wrote at the end of the discussion during the conference on “Isospin in Nuclear Physics” [65] (p. 507): On the experimental side it is safe to predict that there is a gold mine of information still to be dug out. It is becoming clear that more accurate data as well as sophisticated measurements will be what we need. ... Nevertheless, there appears to be a tremendous amount of work still to be done before we will have a reasonable complete set of data and a satisfying understanding of it.

2.1 IARs in $\mathbf {^{209}}\mathrm{Bi}$

Experiments with $^{208}\mathrm{Pb}$$({ p, p' })$ at the MPIK were performed in 1968–1969 [35,36,37,38,39,40,41,42]. In 1970 the construction of the Q3D magnetic spectrograph began and was finished in 1973 [66] except for a useful detector. Several such Q3D magnetic spectrographs were built at different institutes. Only after thirty years of development at the MLL [67,68,69,70] the final detector was finished in 1999 [54]. It was used until end of 2019.

The IARs in $^{209}\mathrm{Bi}$ with parent states g $_{{ 9}/{2}}$, i $_{{11}/{2}}$, j $_{{15}/{2}}$, d $_{{ 5}/{2}}$, s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$ in $^{209}\mathrm{Pb}$ (Table 1) were investigated from 1965 to 1971 in the USA [20,21,22,23,24,25,26,27,28,29,30] and in 1968–1969 at the MPIK [35,36,37,38,39,40,41,42]. The study of the proton decay of IARs in $^{209}\mathrm{Bi}$ was resumed in 2003 after finishing the Q3D detector at the MLL [6, 43,44,45,46,47,48,49,50,51,52, 54].

In 2015 nearly all (about 150) states below $E_x=6.2$ MeV were identified [50]. Almost all negative parity states at $E_x<6.2$ MeV and almost all positive parity states at $E_x<5.9$ MeV were described as 1p1h configurations. Two dozen positive parity states below $E_x=6.5$ MeV were described as non-1p1h configurations [2,3,4,5,6,7, 9]. The $1^-$, $2^-$, $2^+$, $3^-$, $4^+$ yrast states, the third 0$^+$ and another $2^+$ state were recognized as tetrahedral configurations [3, 4, 9]. Four states are interpreted as pairing vibrations [5,6,7]. Another four states are suggested as icosahedral configurations [8].

The doublet IARs g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$, however, were not studied carefully before. The data shown in [39] was not yet further evaluated. The main reason is the four times minor resolution in comparison to data taken with the Q3D magnetic spectrograph at the MLL [6, 43,44,45,46,47,48,49,50,51].

This paper is the first one to identify three dozen states with the structure g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ and d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, and spins from $1^-$ to $6^-$. The excitation energies are in the range $6 \lesssim E_x<7$ MeV. Fourteen states with spins from $3^-$ to $6^-$ are newly identified. Admixtures of other 1p1h configurations to states near $E_x=5.9$ MeV with dominant d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strength and spins $1^-$, $2^-$ and with dominant g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength and spins $3^-$, $4^-$ are determined with high precision from angular distributions [39] and excitation functions [28]. Essential $^{207}\mathrm{Pb}$$({ d, p})$ data were obtained with the Q3D magnetic spectrograph at the MLL in the 1990s using polarized deuterons [55, 56] and in 2004–2018 with unpolarized deuterons [57, 58]. The $^{208}\mathrm{Pb}$$({ d, d' })$ reaction [57, 58] exciting all states without any preference for spin, parity, and structure helped to resolve ambuigities in the interpretation of angular distributions for $^{208}\mathrm{Pb}$$({ p, p' })$.

The $^{209}\mathrm{Bi}$$( d,\mathrm{^3 He})$ reaction [60, 61] does not excite states at $E_x>6$ MeV with measurable cross sections. No data from the reaction $^{208}\mathrm{Pb}$$({\alpha , \alpha '} )$ exciting preferentially natural parity states exist for $E_x>6$ MeV [71].

2.2 Description of the proton decay of IARs

Inelastic proton scattering via an IAR is described in detail in [32, 33]. Complementary descriptions are given in [43, 45, 47, 48]. Computer codes to calculate angular distributions are provided [72, 73]. Here a short summary is given.

2.2.1 Description of 1p1h states

Most states in $^{208}\mathrm{Pb}$ are described by a superposition of 1p1h configurations $LJ^{+1} lj^{-1}$ (shortly $LJ\,lj$) where LJ describes the particle with orbital angular momentum L and spin J and lj the hole accordingly,

$$\begin{aligned} \left| {\tilde{E}}_x, I^\pi \right\rangle= & {} \sum _{LJ} \sum _{lj} c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi } \left| LJ\,lj, I^\pi \right\rangle \nonumber \\&+\sum _{non-1p1h} \left| c_{non-1p1h} ^{{\tilde{E}}_x, I^\pi } \right\rangle . \end{aligned}$$

(1)

${\tilde{E}}_x$ defines an energy label by the excitation energy with four digits rounded to units of keV. Unique energy labels demand deviations of the four digit unit from the value of the excitation energy up to 2 in case of close doublets.

The sequence of configurations and states is enumerated with

$$\begin{aligned}&\mathrm{order \ number}\, {\mathbf {m}} \,\mathrm{for \ configurations}\ \left| E_x^{SDI}, I^\pi _m \right\rangle \nonumber \\&\quad m=1,2,\ldots ,\quad \mathrm{and} \nonumber \\&\mathrm{order \ number} \,{\mathbf {M}} \,\mathrm{for \ states}\ \left| \tilde{E}_x, I^\pi _M \right\rangle , \nonumber \\&\quad M=1,2,\ldots \end{aligned}$$

(2)

The amplitudes c obey the orthonormality and sum-rule conditions

$$\begin{aligned} \sum _{LJ\, lj} \sum _{L'J'\, l'j'} c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi } c_{L'J'\, l'j'} ^{{\tilde{E}}_x, I^\pi } = 0 ,&\quad \sum _{LJ\, lj} \left| c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi } \right| ^2 = 1 , \nonumber \\ \sum _{{\tilde{E}}_x} \sum _{{\tilde{E}}'_x} c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi } c_{LJ\, lj } ^{{\tilde{E}}'_x, I^\pi } = 0 ,&\quad \sum _{{\tilde{E}}_x} \left| c_{LJ\, lj} ^{{\tilde{E}}_x, I^\pi } \right| ^2 = 1 \end{aligned}$$

(3)

for each spin $I^\pi$. The mixing with non-1p1h configurations is negligible,

$$\begin{aligned} \sum _{non-1p1h} \left| c_{non-1p1h} ^{\tilde{E}_x, I^\pi } \right| ^2 \approx 0 . \end{aligned}$$

(4)

For the 2615 $3^-$ yrast state interpreted as a pure tetrahedral rotor [3, 4], however, weak admixtures of 1p1h configurations are observed (Table 4 in [3]). They produce interference patterns with the non-resonant $({ p, p' })$ excitation across all IARs in $^{209}\mathrm{Bi}$ at $14<E_p<22$ MeV (Fig. 1 in [21], Fig. 3 in [22], and Fig. 1 in [74]). A first excited state with spin $3^-$ is a rarity among all nuclei. Besides the $3^-$ yrast state in $^{208}\mathrm{Pb}$ the only other known example is in the doubly magic $^{146}_{64}\hbox {Gd}_{82}$ [75].

For all positive parity states resonantly excited by the j $_{{15}/{2}}$ IAR [45] and for all known negative parity states except for the $3^-$ yrast state, the interference for the $^{208}\mathrm{Pb}$$({ p, p' })$ reaction via an isolated IAR with the non-resonant excitation is negligible. The asymmetry of the excitation functions is explained by the logarithmic dependence of the single particle (s.p.) widths on the proton energy [76] (Sect. 3.3.6). The asymmetry leads to a rather constant cross section continuing beyond the IAR for several hundred keV [20,21,22,23, 45].

In the schematic shell model (SSM) the particle LJ and the hole lj couple to 1p1h configurations $LJ\, lj$ without residual interaction [45]. By including the SDI the multiplet splitting of the 1p1h configurations $LJ\, lj$ is explained [17, 18]. It varies with $-0.73< E_x^ {SDI} - E_x^ {SSM} < +0.38$ MeV. SM calculations with the M3Y interaction [11,12,13] do not yield much differing excitation energies up to $E_x\approx 7.0$ MeV, but the number of states differs (Sect. 4.3.3).

The proton decay of IARs in $^{209}\mathrm{Bi}$ excites all neutron 1p1h configurations in $^{208}\mathrm{Pb}$. The $^{207}\mathrm{Pb}$$({ d, p})$ reaction [1, 55, 56] excites the 1p1h configurations with all particles LJ in $^{209}\mathrm{Pb}$ coupled to the p $_{{ 1}/{2}}$ hole.

The $^{209}\mathrm{Bi}$$( d,\mathrm{^3 He})$ reaction [60, 61] and the $^{209}\mathrm{Bi}$$({ t}, \alpha )$ reaction [77] excite the proton 1p1h configurations with the h $_{{ 9}/{2}}$ particle coupled to some hole lj.

Table 2 S.P. width $\varGamma ^{s.p.}$ for IARs LJ in $^{209}\mathrm{Bi}$ at the reference energy $E_{LJ}$ and for hole orbits lj in $^{208}\mathrm{Pb}$ at the reference energy $E_{lj}$

2.2.2 Mean cross section and centroid energy

Mean cross section. The mean (angle integrated) cross section for the reaction $^{208}\mathrm{Pb}$$({ p, p' })$ on a certain IAR LJ for a state with pure configuration $LJ\,lj$ and spin $I^\pi$ is

$$\begin{aligned} \sigma ^{calc} (LJ\,lj, I^\pi ) = (2 I +1) \varGamma ^{s.p.}_{LJ} \varGamma ^{s.p.}_{lj} a_{LJ\, lj} . \end{aligned}$$

(5)

The formalism [32, 33] derives the factor $a_{LJ\, lj}$. Table 3 shows relevant values for pure configurations [72, 73].

The s.p. widths depend on the energy of the incoming and outgoing protons in a logarithmic manner [76] (Fig. 8 in [40], Fig. 14 in [78]). At a certain proton energy in the range $7< E_p< 14$ MeV the ratio of some s.p. width $\varGamma ^{s.p.}_{LJ}$ to $\varGamma ^{s.p.}_{L'J'}$ for $L'=L+2$ is roughly a factor four for $L=0,\cdots ,7$ and similarly for lj (Table 2).

Figure 1 shows the strength distribution for all neutron 1p1h configurations at $3<E_x <7$ MeV in a schematic manner. The excitation energies and the cross sections are not to scale. Only the ratios of the cross section within a certain multiplet are to scale.

Fig. 1

Schematic view of the 1p1h states at $3< E_x < 7$ MeV excited by the seven IARs g $_{{ 9}/{2}}$, i $_{{11}/{2}}$, j $_{{15}/{2}}$, d $_{{ 5}/{2}}$, s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, and d $_{{ 3}/{2}}$. (The figure is adapted from Fig. 5 in [25].) The number of states with different spins and their strengths are shown in rough relations, the excitation energies are only approximately to scale. The cross section of the configurations with an i $_{{13}/{2}}$ hole is unobservable small. The parity of the states is negative except if the one-particle one-hole configuration contains one intruder, either j $_{{15}/{2}}$ or i $_{{13}/{2}}$

Centroid energy. The centroid energy is calculated as

$$\begin{aligned} \overline{E_x} (LJ\,lj, I^\pi )= & {} \frac{ \sum _{m} E_{x} (I^\pi , m) \left| c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi , m} \right| ^2 }{ \sum _{m} \left| c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi , m} \right| ^2 } , \end{aligned}$$

(6)

where states with order number m are selected to contain major fractions of the configuration $LJ\,lj$. Because of the strong dependence of the s.p. widths on the angular momentum l, weak admixtures of configurations $LJ{ p}{_{{ 1}/{2}}}$ and $LJ{ p}{_{{ 3}/{2}}}$ to states with dominant configuration $LJ{ f}{_{{ 5}/{2}}}$ change the value $\overline{E_x}$ considerably.

2.2.3 Description of angular distributions

The angular distributions near a single IAR are described by a series of even order Legendre polynomials $P_K$ [32, 33],

$$\begin{aligned}&\frac{d \sigma }{d \varOmega } ( \varTheta , {\tilde{E}}_x, I^\pi , LJ, E_p ) \nonumber \\&\quad =\varLambda ( LJ, E_p ) \ (2 I + 1) \nonumber \\&\qquad \sum _{K} P_K (\cos \varTheta ) \sum _{lj} \sum _{l'j'} a_K(I, LJ, lj, l'j') \ \phi (lj, l'j') \nonumber \\&\qquad \times \sqrt{ \varGamma ^{s.p.}_{lj} } \sqrt{ \varGamma ^{s.p.}_{l'j'} } \ c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi } \ c_{LJ\,l'j'} ^{{\tilde{E}}_x, I^\pi } . \ \ \ \ \end{aligned}$$

(7)

Here $\varLambda$ describes the excitation function (Sect. 2.2.4), $a_K$ the geometry of the recoupling, $\varGamma ^{s.p.}_{lj}$ the s.p. widths [40], and $\phi$ a phase difference. Computer codes doing the calculation of the coefficients $a_K$ together with tables and figures are available [72, 73].

The mean cross section is obtained from the fit of angular distributions as

$$\begin{aligned} {\bar{\sigma }} ({\tilde{E}}_x, I^\pi , LJ, E_p )= & {} \varLambda ( LJ, E_p ) (2 I + 1) \nonumber \\&\sum _{lj} a_0 (I, LJ, lj, lj) \varGamma ^{s.p.}_{lj} \left| c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi } \right| ^2 .\nonumber \\ \end{aligned}$$

(8)

An important remark is the maximum value of the summation index K [Eq. (4e) in [32]]

$$\begin{aligned} K \le \min (2L, 2J, \max (2l), \max (2j)) . \end{aligned}$$

(9)

Table 1 shows the resonance energies $E^{res}$ and total widths $\varGamma ^{tot}$ for all known IARs in $^{209}\mathrm{Bi}$. Table 2 shows the s.p. widths $\varGamma ^{s.p.}$ for the particle orbits LJ in $^{209}\mathrm{Pb}$ and the hole orbits lj in $^{207}\mathrm{Pb}$.

2.2.4 Description of excitation functions

The excitation function for the reaction $^{208}\mathrm{Pb}$$({ p, p' })$ via the IAR LJ exciting the state $\left| {\tilde{E}}_x, I^\pi _M \right\rangle$ [Eq. (1)] is described by a Lorentzian [Eq. (4a) in [32]]

$$\begin{aligned} \varLambda ( LJ, E_p )= & {} \frac{ {\varGamma ^{tot}_{LJ} }^{\,2}}{4(E_p - E_{LJ} ^{res})^2 + {\varGamma ^{tot}_{LJ}} ^{\,2} } . \end{aligned}$$

(10)

Figure 2 shows calculated excitation functions covering the s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, and d $_{{ 3}/{2}}$ IARs for a range of proton energies within about ten total widths $\varGamma ^{tot}$.

Fig. 2

Excitation functions for the s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$ IARs in $^{209}\mathrm{Bi}$ calculated with parameters from [28, 40] (Tables 1, 2). Three proton energies chosen during the experiments done in 1969 at Heidelberg [39, 41] are marked at bottom

In reality the shape of the excitation function is highly asymmetric [21, 22]. The asymmetry is explained by the logarithmic energy dependence of the s.p. widths [76] (Fig. 8 in [40]).

2.2.5 Shape of angular distributions

Equation (7) describes the angular distribution for the proton decay of an IAR LJ into the state $|{\tilde{E}}_x, I^\pi \rangle$. The shape is isotropic for orbital angular momentum $L=0$ (the s $_{{ 1}/{2}}$ IAR) or the p $_{{ 1}/{2}}$ hole in case no other configuration admixes [Eq. (9)].

The s.p. width for $l=2$ is roughly four times stronger than for $l=4$ (Sect. 2.2.2). Hence weak admixtures of configurations with a p $_{{ 1}/{2}}$ or f $_{{ 5}/{2}}$ hole to a state ${\tilde{E}}_x, I^\pi$ with dominant configuration $LJ{ p}{_{{ 3}/{2}}}$ creates an angular distribution with a strong $P_2$ component.

In order to enhance the appearance of a dominant $P_2$ shape, $P_2$ is chosen as the abscissa thus leading to an almost linear function in most cases. Figure 3 shows examples with the distributions

$$\begin{aligned} \begin{array}{ll ll l r} \sigma (\varTheta ) = \\ &{} 1\ - &{} P_2(\cos \varTheta ) /3,\ &{} &{}&{} (a) \\ &{} 1\ - &{} \ &{} P_4(\cos \varTheta ) /3, &{}&{} (b) \\ &{} 1\ - &{} P_2(\cos \varTheta ) /3 \ - &{} P_4(\cos \varTheta ) /3, &{}&{} (c) \\ &{} 1\ + &{} P_2(\cos \varTheta ) /3,\ &{} &{}&{} (d) \\ &{} 1\ + &{} \ &{} P_4(\cos \varTheta ) /3, &{}&{} (e) \\ &{} 1\ + &{} P_2(\cos \varTheta ) /3 \ - &{}&{} P_6(\cos \varTheta ) /3 . &{} (f) \\ \end{array} \end{aligned}$$

Fig. 3

Calculated angular distributions shown for $90^\circ \le \varTheta \le 180^\circ$ in steps of $10^\circ$ [Eq. (11)]. The abscissa is chosen as the Legendre polynomial $P_2(\cos \varTheta )$. Hence the values for scattering angles in steps of $\varTheta =10^\circ$ are not equidistant; at bottom $\varTheta =120^\circ$ and $140^\circ$ are marked. Four distributions are shown, $f(\varTheta )= 1$ for the isotropic distribution with a drawn line and without symbols, and a at left with a dash-double-dotted line and diamonds [Eq. (11a)], with a dash-dotted line and squares [Eq. (11b)], with a drawn line and crosses [Eq. (11c)], and b at right with a dash-double-dotted line and diamonds [Eq. (11d)], with a dash-dotted line and squares [Eq. (11e)]. with a drawn line and crosses [Eq. (11f)]

2.3 Configurations excited by IARs in $\mathbf {^{209}}\mathrm{Bi}$

IARs in $^{209}\mathrm{Bi}$ excite neutron 1p1h configurations in each state in $^{208}\mathrm{Pb}$ (Fig. 1). The coupling of a particle LJ to a hole lj creates multiplets with 2–14 members. The cross sections are proportional to the spin factor $2I+1$ [Eq. (7)].

All neutron 1p1h configurations have negative parity except for those built with one intruder, j $_{{15}/{2}}$ or i $_{{13}/{2}}$ for neutron configurations, i $_{{13}/{2}}$ and h $_{{11}/{2}}$ for proton configurations. The configuration j $_{{15}/{2}}$i $_{{13}/{2}}$ has negative parity.

2.3.1 Configurations at ${6\,\lesssim \, E_x <7.0}$ MeV

SM calculations using the SDI [15] predict the multiplet splitting of 1p1h configurations. It also explains the ground state of even-even nuclei to have spin 0$^+$ because of the large down shift in the multiplet splitting with two nucleons in the same orbit [15, 16].

The interaction among two nucleons to be strongly localized is verified by the calculation of the wave functions for neutrons in orbits $82\le N \le 184$ and protons in orbits $50\le N \le 126$ shown in Figures 3, 4 in [79].

Excitation energies for 1p1 configurations in $^{208}\mathrm{Pb}$ were calculated using the SDI for g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, and d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, and other configurations [17, 18] (Tables 3, 6, 7, 8, 9, 10, 11).

The coupling of the $3^-$ yrast state to 1p1h configurations produces states at $E_x\gtrsim 6.0$ MeV [2]. A few more non-1p1h states are suggested at $E_x < 7.2$ MeV [8]. Because most of these states have positive parity, they are of little interest in this paper.

2.3.2 Angular distributions on the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ doublet IARs

Figure 4 shows the shape of the angular distributions for pure configurations with a d $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$ particle and a p $_{{ 3}/{2}}$, f $_{{ 5}/{2}}$ hole and spins from 0$^-$ to $6^-$. The angular distributions for pure configurations with a p $_{{ 1}/{2}}$ hole are isotropic. Note the similarity of the shapes for d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ with corresponding spins $I=L-l$, $I=L-l+1$, $I=L-l+3$ with the exception of $I=L-l+2$ for d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$. The shape for g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ with $I=L-l+5$ is much steeper than the shapes for d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ with $I=L-l+3$.

The interference between the different IARs cannot be calculated. (An attempt was made [80].) However, for spins 0$^-$, 5$^-$, and $6^-$ no interference between the two close IARs g $_{{ 7}/{2}}$ and d $_{{ 3}/{2}}$ and configurations with p $_{{ 3}/{2}}$ or f $_{{ 5}/{2}}$ holes is possible. For spin $1^-$ the shape of the angular distribution for the configurations, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ is similar and hence a distortion of the angular distribution is expected to be weak.

Table 3 States with spins from 0$^-$ to $6^-$ and prominent strengths of the configurations s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$, s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ at $5.8<E_x^{SDI}< 7.2$ MeV. Mean cross sections ${\bar{\sigma }}^{calc}$ are calculated with s.p. widths from [40]. Detected strengths $\sum \left| c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi } \right| ^2$, centroid excitation energies $\overline{E_x}$ derive from Table 4. Total mean cross sections $\sum {\bar{\sigma }}^{exp}$ are estimated from the fit of angular distributions at $E_p=17.40$ MeV for $LJ={ g}{_{{ 7}/{2}}}$ and at $E_p=17.47$ MeV for $LJ={ d}{_{{ 3}/{2}}}$ (Figs. 25, 26, 27, 28, 29, 30, 31)

Table 4 Amplitudes for states in $^{208}\mathrm{Pb}$ with spins 0$^-$-6$^-$ at $5.8<E_x<7.2$ MeV (left) $c_{LJ\, { p}{_{{ 1}/{2}}}} ^{{\tilde{E}}_x, I^\pi }$ determined from $^{207}\mathrm{Pb}$$({ d, p})$ [55] and (right) $c_{LJ\,lj} ^{\tilde{E}_x, I^\pi }$, $LJ={ g}{_{{ 7}/{2}}}, { d}{_{{ 3}/{2}}}$, $lj={ p}{_{{ 1}/{2}}}$, p $_{{ 3}/{2}}$, f $_{{ 5}/{2}}$, f $_{{ 7}/{2}}$, h $_{{ 9}/{2}}$ determined from $^{208}\mathrm{Pb}$$({ p, p' })$ via the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ doublet IARs in $^{209}\mathrm{Bi}$. The sign in parentheses is excluded by the different interference pattern in the angular distribution (Figs. 24, 25, 26, 27, 28, 29, 30, 31)

For spins $2^-$ and $3^-$ the three angular distributions for d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ are dissimilar and hence a distortion by the interference between different IARs is expected to be large. For spin $4^-$ the ratio of the s.p. widths $\varGamma ^{s.p.}_{{ p}{_{{ 3}/{2}}}}$ and $\varGamma ^{s.p.}_{{ f}{_{{ 5}/{2}}}}$ (Table 2) leads to the expectation that a dominant contribution of g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ should yield a rather undistorted shape of the angular distribution.

The shape of angular distributions for spin $3^-$ with a strong g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ component does not differ much from the shape for spin $4^-$ (Fig. 4). Here the SDI calculation of the multiplet splitting helps (Table 3, Sect. 3.4.1).

2.3.3 Excitation functions near the $\mathbf { { g}{_{{ 7}/{2}}}+{ d}{_{{ 3}/{2}}}}$ doublet IARs

The g $_{{ 7}/{2}}$ and d $_{{ 3}/{2}}$ IARs build a strongly overlapping doublet of IARs (Fig. 2, Tables 1, 2). No theoretical description of overlapping doublets of IARs exists (Sect. 2.3.2). By three well chosen proton energies states with dominant 1p1h configurations with either particle may be found.

The ratios of the mean cross section at $E_p=17.47$ MeV and $E_p=17.75$ MeV in relation to that at $E_p=17.40$ MeV,

$$\begin{aligned} R_{47/40}= & {} \frac{ {\bar{\sigma }} ({\tilde{E}}_x, I^\pi , E_p=17.47\,\mathrm{MeV}) }{ {\bar{\sigma }} ({\tilde{E}}_x, I^\pi , E_p=17.40\,\mathrm{MeV}) } \end{aligned}$$

(11)

$$\begin{aligned} R_{75/40}= & {} \frac{ {\bar{\sigma }} ({\tilde{E}}_x, I^\pi , E_p=17.75\,\mathrm{MeV}) }{ {\bar{\sigma }} ({\tilde{E}}_x, I^\pi , E_p=17.40\,\mathrm{MeV}) } \end{aligned}$$

(12)

for pure configurations $LJ\,lj$ (Fig. 2) are expected to be

$$\begin{aligned} R_{47/40}= & {} 0.85 \quad \mathrm{for}\ LJ={ g}{_{{ 7}/{2}}}, \nonumber \\ R_{47/40}= & {} 1.20 \quad \mathrm{for}\ LJ={ d}{_{{ 3}/{2}}}, \nonumber \\ R_{75/40}= & {} 0.15 \quad \mathrm{for}\ LJ={ g}{_{{ 7}/{2}}}, \nonumber \\ R_{75/40}= & {} 0.20 \quad \mathrm{for}\ LJ={ d}{_{{ 3}/{2}}}. \end{aligned}$$

(13)

The ratios $R_{47/40}$, $R_{75/40}$ determined from the fit of angular distributions can be estimated from Table 4 for 40 states. For $LJ={ d}{_{{ 3}/{2}}}$ mean values $R_{47/40}=1.0$ and $R_{75/40}=0.2$ are derived, for $LJ={ g}{_{{ 7}/{2}}}$ mean values $R_{47/40}=0.92$ and $R_{75/40}=0.14$. In most cases it justifies the assumption of the IAR to be either the isolated g $_{{ 7}/{2}}$ or the isolated d $_{{ 3}/{2}}$ resonance. With the 6264 1$^-$ state one exception is found (Sect. 4.1.4).

Fig. 4

Angular distributions for pure configurations (left) d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ and d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ and (right) g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ [Eq. (7)]. The ordinate shows the differential cross section $\sigma ^{calc}$ [Eq. (5)] in relative units running from 0 to 1.5; the value $\sigma ^{calc}=1$ is shown by the horizontal line. The abscissa is chosen as the Legendre polynomial $P_2(\cos \varTheta )$ (Fig. 3). Scattering angles range from 90$^\circ$ to 180$^\circ$ (left to right); the values $P_2(\cos 120^\circ )$ and $P_2(\cos 140^\circ )$ are marked. The angular distributions for the configuration LJ p $_{{ 3}/{2}}$ appear as a linear function for $LJ={ d}{_{{ 3}/{2}}}, { g}{_{{ 7}/{2}}}$ (see Fig. 3). Some configurations g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ have a pronounced extremum at $\varTheta =120^\circ$ or $\varTheta =140^\circ$

3 Experimental data

3.1 Data taking

This paper is based on experiments performed in 1965–1969 in the USA, in 1968–1969 at the MPIK (Heidelberg, Germany), and in 1990–2019 at the MLL (Garching, Germany).

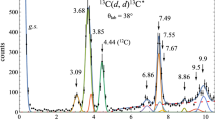
• In 1965–1969 experiments on $^{208}\mathrm{Pb}$$({ p, p' })$ were performed using semiconductor detectors at Austin (USA) and Seattle (USA) [22,23,24, 27,28,29,30]. Angular distributions and excitation functions were taken for levels at $2.6< E_x< 6.9$ MeV near all IARs (Table 1). Figures 16, 17 reproduce excitation functions taken at Seattle [28].

• In 1966 $^{208}\mathrm{Pb}$$({ p, p' })$ spectra were taken with the Elbeck magnetic spectrograph at Los Alamos (USA) with a resolution of about 8 keV [25, 26]. 48 levels at $2.6< E_x< 6.1$ MeV were detected at 12 proton energies $14.95< E_x<17.50$ MeV covering the g $_{{ 9}/{2}}$ IAR with three proton energies, the d $_{{ 5}/{2}}$ IAR with four proton energies, the s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$ IARs with five proton energies. (More original spectra taken at Los Alamos are still available [26].) Cross sections at the single scattering angle $\varTheta = 90^\circ$ were measured.

  Twelve spins of states at $E_x <5.5$ MeV were shown. All spin assignments are still valid. The assignment of spin $3^-$ to the first excited state [81] is valid since seventy years. The identity of the $3^-$ yrast and three higher excited states is known since hundred years [82, 83].

  The excitation energies $E_x^{Ek}$ obtained from $^{208}\mathrm{Pb}$$({ p, p' })$ data taken with the Elbeck magnetic spectrograph were used in subsequent papers [23, 24, 27,28,29,30]. They have to be recalibrated because of the choice of the excitation energy of the 3$^-$ yrast state incorrect by 8 keV (see Eq. (6) in [47]).

  $$\begin{aligned} E_x^{Ek,rec} (E_x)= & {} E_x^{Ek} (E_x) + 6.0 + 0.8 (E_x - 2615)\, [\mathrm{\, keV}].\nonumber \\ \end{aligned}$$

  (14)

  M. Martin noted that the discrepancy stems from the problematic calibration of the excitation energy for the 2615 $3^-$ yrast state before 1960. The extremely high excitation energy was already observed by Rutherford in 1899 [84].

• In 1968–1969 experiments on $^{208}\mathrm{Pb}$$({ p, p' })$ were performed at the MPIK using semiconductor detectors with a mean resolution of 12 keV [39,40,41,42]. Annual reports were produced in 1968–1970 [35,36,37,38]. Spectra were taken near the g $_{{ 9}/{2}}$, j $_{{15}/{2}}$, d $_{{ 5}/{2}}$, and the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ doublet IARs at six proton energies [39]. Scattering angles from $\varTheta =60^\circ$ to $170^\circ$ in steps of $5^\circ$ were covered. The original data are lost but could be reconstructed (Sect. 3.2.1).

  Relative cross sections at different scattering angles were measured with a precision of 2% [40]. Yet absolute cross sections were not determined [39].

  Figures  22, 23 show spectra covering the region $6.0<E_x <7.0$ MeV. Figures 24, 25, 26, 27, 28, 29, 30 and 31 show angular distributions for states with spins from $1^-$ to $6^-$ and excitation energies $5.8<E_x< 7.0$ MeV. The evaluated experimental data shown in the angular distributions are presented in [41, 42]. The data taking was described in [40]. In Sects. 3.2 some details are remembered.

• In the 1990s experiments on $^{207}\mathrm{Pb}$$({ d, p})$ with polarized deuterons and on $^{208}\mathrm{Pb}$$({ p, p' })$ were performed at the MLL (Garching, Germany) using the Q3D magnetic spectrograph and evaluated by Valnion [55, 56].

• In 1992 experiments on $^{208}\mathrm{Pb}$$({\alpha , \alpha '} )$ were performed at the MLL (Garching, Germany) [71]. In this paper the data were not used but for inspecting the 4140 $2^-$ state [3].

• In 2003 experiments on $^{208}\mathrm{Pb}$$({ p, p' })$ were resumed after finishing the final detector for the Q3D magnetic spectrograph at the MLL [54]. The MLL was closed at the end of 2019. Raw data are available [51, 52]. The reactions $^{207}\mathrm{Pb}$$({ d, p})$ and $^{208}\mathrm{Pb}$$({ d, d' })$ were studied in addition [57, 58]. Figures 18, 19, 20, 21 show spectra for $^{208}\mathrm{Pb}$$({ p, p' })$, $^{207}\mathrm{Pb}$$({ d, p})$, and $^{208}\mathrm{Pb}$$({ d, d' })$ in the region $6.0<E_x< 7.3$ MeV.

• In 2019 experiments on $^{208}\mathrm{Pb}$$({ p, p' })$ covering the s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$ IARs were performed but not yet evaluated [53].

3.2 Reconstruction and evaluation

3.2.1 Reconstruction

As described in [40] data for $^{208}\mathrm{Pb}$$({ p, p' })$ were taken with the newly installed MP Van-de-Graaf accelerator at the MPIK in 1968–1969. In total about 6 months of beam time were used to cover the g $_{{ 9}/{2}}$, d $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$, and d $_{{ 3}/{2}}$ IARs. A group of around twenty students and more than twenty technicians were involved in preparing the experiments and performing the data taking. The evaluation was done by Glöckner [39]. Fotographic reproductions of the computer plots for 77 $^{208}\mathrm{Pb}$$({ p, p' })$ spectra both original and fitted by the triangle method [40] are still available [41].

By help of the Engauge Digitizer code [85] scans of the fotographic reproductions were digitized. Using another computer code spectra were reconstructed as input for GASPAN [86]. Details for the description of GASPAN spectra can be found in e.g. [45] or [50]. The resolution of about 12 keV was used as a guide for the reconstruction.

The spectrum analysis code GASPAN [86] was used in the usual manner to fit the spectra. However the level energies were not fitted but had fixed values shown in Table 15. Figures  22, 23 show some spectra. In contrast to the simple triangle method [40] the advanced features of GASPAN were used to fit the contamination peaks from $^{ 12}C$$({ p, p' })$, $^{ 16}O$$({ p, p' })$, $^{208}\mathrm{Pb}$$({ p, d})$, and $^{208}\mathrm{Pb}$$({ p, t})$ with different peak widths. By this manner more levels of $^{208}\mathrm{Pb}$ could be resolved in the neighborhood of the contaminations than found by Glöckner [39].

In general $^{208}\mathrm{Pb}$$({ d, d' })$ spectra show more states than $^{208}\mathrm{Pb}$$({ p, p' })$ because of the presence of positive parity states (Fig. 20), $^{207}\mathrm{Pb}$$({ d, p})$ show markedly different spectra (Fig. 21) because of the selective excitation of configurations with a p $_{{ 1}/{2}}$ hole. Even very weak admixtures can be measured [55, 56].

3.3 Evaluation

3.3.1 Definition of peaks, levels, and states

Spectra with different resolutions were evaluated. Therefore the number of resolved nuclear states differs in different experimental data.

States are distinguished from levels and peaks. We further define a doublet as an ensemble of close lying (mostly two) states. Sometimes a member is known from other experiments only and is not excited at all.

A state is defined by its qualities in some nucleus. A peak is defined as some hump in a spectrum more or less resolved from neighboring humps. A level is defined as the result of a fit by some spectrum analysis tool resolved from its neighboring levels. We are using GASPAN [86].

In the fit of the data obtained in 1968–1969 [41, 42] by GASPAN the option of fixed energies [45] was used. By this means a doublet with two or more states in a distance smaller than the resolution is separated into two levels.

For each enumerated level shown in Table 15 the excitation energy corresponding to the shown energy label ${\tilde{E}}_x$ was selected, preferably from [1], otherwise the mean value obtained from the $^{208}\mathrm{Pb}$$({ p, p' })$, $^{207}\mathrm{Pb}$$({ d, p})$, and $^{208}\mathrm{Pb}$$({ d, d' })$ data obtained with the Q3D magnetic spectrograph was used [51, 52, 57, 58].

Because the separation in spectra taken at similar scattering angles is affected by statistical fluctations, up and down jumps are produced in the angular distribution when comparing cross sections at consecutive scattering angles (see examples discussed in Sect. A.5). In a few evident cases the arithmetic mean for two neighboring levels is used instead the values given by the fit.

The evaluation is not yet finished. Only the most prominent levels are considered in this paper, about half of the resolved levels (Table  15). Angular distributions for 40 states in 37 levels were evaluated (Tables 3, 4, Figs. 24, 25, 26, 27, 28, 29, 30, 31).

3.3.2 Calibration

By combining results from all experiments described in Sect. 3.1 both the excitation energies and the cross sections were calibrated.

• Calibration of excitation energies. Calibration of excitation energies. Excitation energies at $6.2<E_x< 7.2$ MeV were derived from existing Q3D data taken in 2003–2017 at the MLL [51, 52, 57, 58]. Table 15 shows all known levels. The levels recognized in the 1969 Heidelberg data [39] are enumerated. The high resolution data for $^{208}\mathrm{Pb}$$({ p, p' })$ with $E_p=35$ MeV [87] obtained with the Enge split-pole magnetic spectrograph at Michigan (USA) well correlate with the data (Sect. 4.2, Table 15). Some levels not listed in [1] are strongly excited by $^{208}\mathrm{Pb}$$({ p, p' })$ via the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ doublet IARs.

  The calibration of the excitation energies for the MPIK data was done in two steps. Glöckner [39] assumed a linear response of the semiconductor detectors and used the then available information on $^{208}\mathrm{Pb}$ for strong peaks [88]. All contamination peaks from $^{ 12}C$$({ p, p' })$, $^{ 16}O$$({ p, p' })$, $^{208}\mathrm{Pb}$$({ p, d})$, and $^{208}\mathrm{Pb}$$({ p, t})$ were identified. In a second step the excitation energies of states listed in [1, 89, 90] with known spins of $1^-$, $2^-$, and $3^-$ were used. Table 15 shows all states identified at $E_x< 7.15$ MeV.

• Calibration of cross sections. The spectra reconstructed from the data taken with semiconductor detectors in 1969 at the MPIK were fitted by GASPAN by using the feature of fixed energies in [45]. Contamination peaks from $^{ 12}C$$({ p, p' })$, $^{ 16}O$$({ p, p' })$, $^{208}\mathrm{Pb}$$({ p, d})$, and $^{208}\mathrm{Pb}$$({ p, t})$ [39] were fitted with broader widths and a free fit of the position.

  The ordinates of the spectra in the fotographic reproductions show only relative values, scales with 4, 6, 10, or 20 steps without any notations are drawn as ordinate [39]. Excitation functions of $^{208}\mathrm{Pb}$$({ p, p' })$ [28] and spectroscopic factors from $^{207}\mathrm{Pb}$$({ d, p})$ [55, 56] assisted in finding the calibration of the cross section within a factor 0.8 (Sect. 3.4.3).

  The calibration of the relative cross sections across all scattering angles was done with an uncertainty of 2% [40]. The small uncertainty of the relative solid angles derives from the use of a scattering chamber with up to ten solid state detectors in 10$^\circ$ distance. By turning the scattering chamber different detectors were positioned at the same angle.

  The angular distributions taken near the g $_{{ 9}/{2}}$ IAR discussed in [40] were well reproduced. By help of the reconstructed data [41] the 4140 $2^-$ state [3, 4] first stated by Glöckner [39] was observed in $^{208}\mathrm{Pb}$$({ p, p' })$ spectra [57, 58]. $^{208}\mathrm{Pb}$$({ d, d' })$ spectra taken with the Q3D magnetic spectrograph at the MLL confirmed the 4140 $2^-$ state interpreted as a tetrahedral rotation and vibration [59].

  The final results indicate the correctness of the calibration also for the data not discussed in [40], namely all other IARs than g $_{{ 9}/{2}}$ and all off-resonance proton energies. The cross section at $E_p=17.40$ MeV for states with dominant configurations g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ is close to that at $E_p=17.47$ MeV (Eq. (11), Table 4). The g$_{7/2}$ resonance has a maximum at $E_p= 17.43$ MeV and a width of $\varGamma ^{tot}=288$ keV (Table 1, Fig. 2).

  The measured cross sections yield angular distributions where often gaps appear at certain scattering angles because of contamination lines or because the correspondence to known levels is unclear. Figures 24, 25, 26, 27, 28, 29, 30 and 31 show angular distributions. Details are given in the appendix (Sect. A.5). They are selected because of rather firm spin assignments, either previously known or new (Sects. 4.1, 4.2, Tables  3, 4).

A systematic uncertainty of the cross sections in the order of 10% is estimated because of the problematic calibration. The systematic uncertainty of the amplitudes, however, is much lower because of the strong correlations.

3.3.3 Fit of angular distributions by superposition of three 1p1h configurations

The mean distance between any two states in $^{208}\mathrm{Pb}$ is 9 keV. The distance between two states with the same spin and parity is larger than 30 keV. It is explained by the chaoticity [62,63,64]. The state contributing dominantly to a certain level in the MPIK data could be identified by the high resolution Q3D data (Table 15). Mostly a single state corresponds to the level determined in the 12 keV data. However there are two notable exceptions (Sects. 4.1.7, 4.1.8).

Fig. 5

Dependence of the ratio of the Legendre coefficients $a_K/a_0$ on the amplitudes $c_i, i=1,2,3,4$, in the $5^-_{17}$ 6389 state [Eq. (18)]. The drawn lines show the ratio $a_2/a_0\pm \varDelta a_2/a_0$, the dotted lines $a_4/a_0\pm \varDelta a_4/a_0$ (increasing values are indicated), the dash-dotted lines $a_6/a_0\pm \varDelta a_6/a_0$ (increasing values are indicated). The best fit yields the amplitudes $c_{{ g}{_{{ 7}/{2}}}{ f}{_{{ 5}/{2}}}}=+0.97$ and (left frame) $c_{{ g}{_{{ 7}/{2}}}{ f}{_{{ 7}/{2}}}}=+0.11$, $c_{{ g}{_{{ 7}/{2}}}{ h}{_{{ 9}/{2}}}}=+0.15$, $c_{{ g}{_{{ 7}/{2}}}{ p}{_{{ 3}/{2}}}}=-0.01$, (middle and right frames) $c_{{ g}{_{{ 7}/{2}}}{ f}{_{{ 7}/{2}}}}=+0.09$, $c_{{ g}{_{{ 7}/{2}}}{ h}{_{{ 9}/{2}}}}=-0.15$, $c_{{ g}{_{{ 7}/{2}}}{ p}{_{{ 3}/{2}}}}=+0.00$ given by Eq. (18). For details see Sect. 3.3.4

Some states $6.2<E_x< 7.0$ MeV have known spins, new spin assignments are derived for a dozen states (Tables 3, 4, 5, 6, 7, 8, 9, 10, 11). For all states mostly three configurations are sufficient to describe the measured angular distribution. The sensitivity is extremely high, amplitudes corresponding down to 0.1% strength can often be reliably determined together with the relative sign.

The shape of the angular distribution should not vary much with the proton energy $E_p$. In this work three energies are considered, $E_p=17.40$, 17.47, and 17.75 MeV. The shape is determined either for $E_p=17.40$ or 17.47 MeV and not varied for the two other proton energies. The excitation energies calculated by SDI [17] (Fig. 4) and the cross sections for pure configurations (Tables 6, 7, 8, 9, 10, 11) are used as a guide to assign spins.

Assuming a weak mixing of the 1p1h configurations the shape should be given by the dominant component (Fig. 4, Sect. 3.4.4). For states with negligible admixtures of configurations with a p $_{{ 1}/{2}}$ or p $_{{ 3}/{2}}$ hole, configurations with a f $_{{ 7}/{2}}$ hole are included as the third configuration. These amplitudes from distant configurations are assumed to contribute less than 1% of the total strength. If because of the spin the p $_{{ 1}/{2}}$ or p $_{{ 3}/{2}}$ hole is absent configurations with a h $_{{ 9}/{2}}$ hole are included.

There are results where amplitudes $LJ\, lj$ with holes of orbital angular momenta $l=1,3,5$ contribute simultaneously. They could be determined because the $l=1$ hole adds no more than 1% to the total strength (Figs. 27, 28, Table 4).

3.3.4 Sign of amplitudes

The $({ p, p' })$ reaction via IAR is highly sensitive to the relative signs of the amplitudes in the state. An example is given in [9]. Up to four amplitudes may be determined in each state if statistics are sufficient. Two methods are used for the analysis of angular distributions, the method used in this paper is described Sect. 3.3.6.

The high sensitivity in determining the sign of amplitudes is better explained by the method used earlier [32]. This other method starts with the fit of the angular distribution by a series of Legendre polynomials,

$$\begin{aligned}&\frac{d \sigma }{d \varOmega } ( \varTheta , {\tilde{E}}_x, I^\pi , LJ, E_p ) \nonumber \\&\quad =a_0 ({\tilde{E}}_x, I^\pi , LJ, E_p ) \sigma _0 (LJ, E_p, I^{\pi }) \nonumber \\&\qquad \times \sum _{K=even} {\displaystyle \frac{ a_K ({\tilde{E}}_x, I^\pi , LJ, E_p ) P_K (\cos \varTheta ) }{ a_0 ({\tilde{E}}_x, I^\pi , LJ, E_p ) P_K (\cos \varTheta ) } } \end{aligned}$$

(15)

where $a_0 \sigma _0$ is the mean cross section (Sect. 2.2.2). The uncertainty of the cross section is given by

$$\begin{aligned}&\varDelta \frac{d \sigma }{d \varOmega } (\varTheta , {\tilde{E}}_x, I^\pi , LJ, E_p ) \sigma _0(LJ, E_p, I^\pi ) \nonumber \\&\quad =\delta a_0 + \delta a_2 P_2(\cos \varTheta ) + \delta a_4 P_4(\cos \varTheta ) + \delta a_6 P_6(\cos \varTheta ).\nonumber \\ \end{aligned}$$

(16)

Fig. 6

Angular distributions for a the 6389 $5^-_{17}$ with dominant configuration g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ and b the 6688 $5^-_{21}$ state with dominant configuration g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$

Fig. 7

Similar to Fig. 5 for the 6688 state

The relative sign of three amplitudes $c_1, c_2, c_3$ can be determined by observing how the ratio of the Legendre coefficients $a_K / a_0$ depends on the size of the amplitudes. The amplitudes vary in the range $-1 \le c_i \le +1$, $i=1,2$, and

$$\begin{aligned} c_3 = + \sqrt{1 - c_1^2 - c_2^2} . \end{aligned}$$

(17)

A weak fourth amplitude changes the shape slightly,

$$\begin{aligned} c_3 = + \sqrt{1 - c_1^2 - c_2^2 - c_4^2}, \quad |c_4| \ll 1. \end{aligned}$$

(18)

The uncertainty of the coefficients $a_K$ increases with K; for $a_6$ it is very large and hence the value $a_6$ is mostly useless. We discuss two examples.

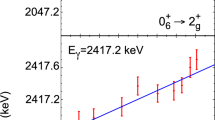
The 6389 state. Figure 5 shows the dependence of the amplitudes on the ratios $a_K/ a_0$ of the Legendre coefficients. Fig. 6a shows the fit of the angular distribution with Legendre polynomials.

On a sphere two circles cross at two points at angles between $0^\circ$ and $90^\circ$. Hence the band $(a_2 \pm \delta a_2) / a_0$ intersects the band with $(a_4 \pm \delta a_4) / a_0$ near two regions. Often they are far apart as shown in the middle of Fig. 5. The valid intersection is chosen by considering the configuration mixing expected from the shell model. In the example presented by Fig. 5 the amplitude g $_{{ 7}/{2}}$f $_{{ 7}/{2}}$ is expected to nearly vanish because of the large distance of the s.p. energies from f $_{{ 5}/{2}}$ to f $_{{ 7}/{2}}$, namely 1.777 MeV. The fit yields the amplitudes of three configurations, $+0.97$ for the dominant configuration g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ and $+0.10$ for g $_{{ 7}/{2}}$f $_{{ 7}/{2}}$. Admixtures of g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$h $_{{ 9}/{2}}$ are weak. The left and right frame of Fig. 5 shows the change of all amplitudes by using the fixed values $\pm 0.15$ for g $_{{ 7}/{2}}$h $_{{ 9}/{2}}$ yielding values $\pm 0.01$ for g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$.

In a second step the mean cross section $\sigma _0 a_0$ is determined by adjusting the common factor $a_0$ in Eq. (15). The final result yields

$$\begin{aligned} c_{{ g}{_{{ 7}/{2}}}{ p}{_{{ 3}/{2}}}} ^{6389, 5^-}= & {} 0.00 \pm 0.02, \nonumber \\ c_{{ g}{_{{ 7}/{2}}}{ f}{_{{ 5}/{2}}}} ^{6389, 5^-}= & {} +0.59 \pm 0.01, \nonumber \\ c_{{ g}{_{{ 7}/{2}}}{ f}{_{{ 7}/{2}}}} ^{6389, 5^-}= & {} +0.06 \pm 0.02, \nonumber \\ c_{{ g}{_{{ 7}/{2}}}{ h}{_{{ 9}/{2}}}} ^{6389, 5^-}= & {} \pm 0.10 \pm 0.10. \end{aligned}$$

(19)

The 6688 state. Figure 6b shows the fit of the angular distribution with Legendre polynomials. Figure 7 shows the dependence of the amplitudes from the ratios $a_K/ a_0$ of the Legendre coefficients.

Similarly as shown for the 6389 state the final result yields

$$\begin{aligned} c_{{ g}{_{{ 7}/{2}}}{ p}{_{{ 3}/{2}}}} ^{6688, 5^-}= & {} +0.78 \pm 0.01, \nonumber \\ c_{{ g}{_{{ 7}/{2}}}{ f}{_{{ 5}/{2}}}} ^{6688, 5^-}= & {} -0.17 \pm 0.10, \nonumber \\ c_{{ g}{_{{ 7}/{2}}}{ f}{_{{ 7}/{2}}}} ^{6688, 5^-}= & {} +0.04 \pm 0.05 . \end{aligned}$$

(20)

The results given by Eq. (19), Eq. (20) differ from the amplitudes shown in Table 4 because of different choices of the s.p. widths thus exhibiting the systematic uncertainty (Sect. 3.3.5). The relative amplitudes are similar and especially the signs are the same, however.

The method presented here is more tedious than the method used by this work. It needs two separate steps. Hence iterations need more effort. The method is advantageous as it demonstrates the uncertainty of the amplitudes more clearly in many cases.

3.3.5 Parameter dependence

The fit of the angular distributions by Eq. (7) needs the total width $\varGamma ^{tot}$ for the IAR, the s.p. widths $\varGamma ^{s.p.}$ for the particle and hole orbits, and the phase differences $\phi$ (which all depend at the proton energy) and at the resonance energy $E^{res}$.

The sensitivity of the fit on the resonance energy $E^{res}$, the total width $\varGamma ^{tot}$, and phase differences $\phi$ is weak. It affects the variation of the mean cross section with the energy. Values for the resonance energy $E^{res}$ were slightly changed within the uncertainties derived by Wharton et al.  [28], see Table 1. The improvement of the fits shown in Figs.  24, 25, 26, 27, 28, 29, 30 and 31 change the relative cross sections on the g $_{{ 7}/{2}}$ and d $_{{ 3}/{2}}$ IARs by about 10%, however the improvement is within the systematic uncertainty of the mean cross section. The resulting amplitudes shown in Table 4 are little affected.

In the fit, the s.p. width $\varGamma ^{s.p.}$ for the particle affects only the absolute cross section and hence a common factor to the size of all amplitudes. In contrast, the s.p. widths $\varGamma ^{s.p.}$ for the holes change all amplitudes in a complicated manner in the fit of the angular distributions.

We did not attempt to construct an orthonormal matrix of the amplitudes [Eq. (3)], but we tried to verify the predictions of the excitation energies calculated by the SDI and the calculations of the total cross sections with the known parameters (Tables 1, 2, 3). The results shown in the left frames of Figs.  8, 9, 10, 11, 12, 13 and Table 3 show the success (Sect. 4).

In the fit, the s.p. widths $\varGamma ^{s.p.}$ for the holes change all amplitudes in a complicated manner. The uncertainty of the value of the dominant amplitude is related to the uncertainty of the corresponding s.p. width; however because of the interference with the other configurations the correspondence is not linear. The logarithmic dependence of the s.p. width for the holes was calculated by Clarkson as described in [76] and shown in [78], see also [72]. In the fit, the phase differences $\phi$ [Eq. (7)] affect the results only weakly. Phase differences calculated by Harney [33, 72] were used.

In this paper we tried to optimize the parameters $\varGamma ^{s.p.}(LJ)$, and $E^{res}(LJ)$. The values $\varGamma ^{s.p.}(lj)$, $\varGamma ^{tot}(LJ)$ and $\phi (lj,l'j')$ were not varied.

The precise spectroscopic factors from $^{207}\mathrm{Pb}$$({ d, p})$ [55, 56] were verified by a fit of the angular distributions for $^{208}\mathrm{Pb}$$({ p, p' })$ with configurations s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 9}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ for almost all states (Table 4). Yet for the 5947 $1^-$ state with dominant d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strength a large discrepancy was found. A correlated problem is the calibration of the cross section (Sect. 3.3.2). Wharton et al. [28] measured excitation functions for the 5947 $1^-$ and 5924 $2^-$ states (Fig. 17); the cross section near $\varTheta =90^\circ$ suggested from Figs.  24, 25 is higher. Calculations using $\varGamma ^{s.p.}_{{ d}{_{{ 3}/{2}}}}=28$ keV [28] especially fail to explain the amplitude $c_{{ d}{_{{ 3}/{2}}}{ p}{_{{ 1}/{2}}}} ^{5947 , 1^-}=0.98$ from $^{207}\mathrm{Pb}$$({ d, p})$ [55, 56] (Table 3). Therefore the s.p. width is estimated as $\varGamma ^{s.p.}_{{ d}{_{{ 3}/{2}}}}=60$ keV (Table 2). A comparison to calculations [76, 78] favors the s.p. widths $\varGamma ^{s.p.}_{{ d}{_{{ 3}/{2}}}}$ and $\varGamma ^{s.p.}_{{ d}{_{{ 5}/{2}}}}$ to be similar. Hence the new value given in Table 2 may be overestimated.

The ratio of the cross sections from $E_p=17.40$ to 17.47 MeV predicted by Eqs. (11)–(13) was verified in first order. A change by 40 keV of the resonance energies (Table 1) improved the results (Eqs. (12), (13), Figs. 24, 25, 26, 27, 28, 29, 30, 31). The change is explained by the unknown procedure to calibrate the proton energy of the accelerators involved [28, 40].

Each amplitude shown in Table 4 has unknown systematic uncertainties in the order of several percent, relatively. The relative signs of the amplitudes, however, are rather firm as discussed in Sect. 3.3.4.

The number of particle-hole configurations included in the fit (2–4) was adjusted until the sign of the weakest configuration could be reliably discriminated. The relative signs of the amplitudes shown in Table 4 are firm; the reverse sign given in parentheses changes the fit by more than 2$\sigma$ in most cases (Figs. 24, 25, 26, 27, 28, 29).

3.3.6 Iterative fitting process

The iterative fitting process is explained in more detail. Spin assignment and fit of the angular distributions are highly interrelated.

The shape is assumed to not depend on the proton energy. This fact was verified in many cases by comparison of angular distributions taken at proton energies $E_p=16.30$, 16.45, 16.60 MeV [41].

The constancy of the shape across an isolated IAR explains the absence of non-resonant contributions in all states. An exception is the $3^-$ yrast state [21, 22, 74] where all amplitudes are weak because of its dominant tetrahedral structure (Sect. 2.2.1). Together with the logarithmic dependence of the s.p. widths from the proton energy [76] the constant shape explains the evident asymmetry of the excitation functions (Fig. 10 in [45]) already observed in the very first experiments on $^{208}\mathrm{Pb}$$({ p, p' })$ via the g $_{{ 9}/{2}}$ IAR for the 3192 $5^-$ and 3475 $4^-$ yrast states [21] and more states [22].

The change of the mean cross section from $E_p=17.40$ to 17.47 MeV predicted by Eqs. (11)–(13) served as a guide to select the particle LJ. Only one major choice of the amplitudes for $LJ\, lj$ was done; the amplitudes were not varied for different proton energies $E_p$ except for the Lorentz factor [Eq. (10)]. For configurations ${ g}{_{{ 7}/{2}}}lj$ the best fit at proton energy $E_p=17.40$ MeV is chosen and for ${ d}{_{{ 3}/{2}}}lj$ at $E_p=17.47$ MeV. The cross section for $E_p=17.75$ MeV is predicted to be reduced by about a factor 5 in all amplitudes (a factor 25 in cross section) (Fig. 2, Eqs. (11), (12)).

The fit of an angular distribution consists of several steps. A major problem is the fact that no states with spins $4^-$, $5^-$, $6^-$ were known before.

Only the 6688 state was strongly suggested to have spin $5^-$ [40]. Indeed the first step in the iterative fitting process was the verification of this assumption by a fit of the shape at all three proton energies $E_p=17.40$, 17.47, 17.75 MeV (Figs.  12, 28, Tables 3, 4). The configuration mixing is determined with $+0.80$g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, $-0.21$g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$, $+0.15$g $_{{ 7}/{2}}$f $_{{ 7}/{2}}$ (Table 4, Eq. (1)). The difference to the values in Eq. (20) and similarly from the values $-0.03$g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, $+0.77$g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, $+0.13$g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$, $-0.20$g $_{{ 7}/{2}}$f $_{{ 7}/{2}}$ for the 6389 $5^-$ state (Table 4) to the values in Eq. (19) exhibit the systematic uncertainties of determining amplitudes.

• 1. In first approximation a single configuration is chosen.

• 2. For states with known spins $1^-$, $2^-$, $3^-$ the shape leads to rather good discrimination between the configurations $LJ\,{ p}{_{{ 3}/{2}}}$ and $LJ\,{ f}{_{{ 5}/{2}}}$ (Figs. 24, 25, 26).

• 3. The shape for states with unknown spin often approaches predictions for pure configurations reasonable (Fig. 4) thus giving an important hint to the spin assignment.

• 4. The mean cross section excludes lower spins in case the values are exceeding the prediction given in Table 3. By this means states with spin 4$^-$, $5^-$, and $6^-$ were rather soon identified.

• 5. As an underlying assumption the major configuration $LJ\, lj$ should correspond to the prediction for the excitation energy by the SDI (Table 3) within less than 200 keV.

• 6. Especially the major strength $LJ\, { p}{_{{ 3}/{2}}}$ should lie 0.33 MeV higher than $LJ\, { f}{_{{ 5}/{2}}}$ but more precisely as predicted by including the multiplet splitting calculated with SDI (Table 3).

• 7. Clearly the orthonormality and sum-rule conditions [Eq. (3)] must be observed.

• 8. After several iterations the distribution of the configuration strengths should verify the assumptions. Figures 8, 9, 10, 11, 12 and 13 yield a final prove.

  This step is most important in the iteration process of the determination of both the spin assignment and the configuration mixing.

• 9. In case of $LJ{ p}{_{{ 1}/{2}}}$ values known from the $^{207}\mathrm{Pb}$$({ d, p})$ study [55] the given particle $LJ={ g}{_{{ 7}/{2}}}$ or d $_{{ 3}/{2}}$ is prefered. The d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ amplitude in the 6088 $3^-$, 6264 $1^-$, 6969 $2^-$ states is weak, but the dominant configurations are ${ g}{_{{ 7}/{2}}}\, lj$.

• 10. In a second approximation the amplitude of another configuration $LJ\, lj$ is chosen and the sign determined.

• 11. In case the relative sign of the two amplitudes could be clearly determined, a third configuration $LJ\, lj$ is included. The change of the sign for the third configuration often leads to different fits.

  In Figs. 24, 25, 26, 27, 28, 29, 30 and 31 both fits with the different choice of the signs are plotted (drawn line for the best fit, dotted line for the excluded reverse sign). Only in some cases a third configuration does not change the shape significantly.

• 12. In a few cases a fourth configuration exhibits significant changes of the shape (Table 4) [9].

Table 5 Strength distribution for the configurations g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, and d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ derived from Table 4

Figures 24, 25, 26, 27, 28, 29, 30 and 31 show the fitted angular distributions discussed in this paper. Table 4 shows the amplitudes $c_{LJ\,lj}$ obtained by the fit, Table 5 the strengths $c^2_{LJ\,lj}$. Figures 8, 9, 10, 11, 12 and 13 show the distribution of the detected strengths.

3.3.7 Criterions for a reasonable fit

The fit is optimized to reproduce the values at backward scattering angles $\varTheta \gtrsim 130^\circ$ because here the contributions from the Legendre polynomials differ most (Fig. 3). Cross sections at scattering angles $\varTheta \lesssim 130^\circ$ were allowed to deviate more.

For two doublets the fit was done for $\varTheta \lesssim 130^\circ$ and $\varTheta \gtrsim 130^\circ$ separately, see Sects. 3.3.8, 4.1.7, 4.1.8.

A common set of amplitudes was used to optimize the fit of the angular distributions taken with the proton energies $E_p=17.40, 17.47, 17.75$ MeV. The square root of the Lorentzian factor defined by Eq. (10) was applied to reduce the amplitudes in the fit of the angular distribution taken near the off-resonance energies (especially $E_p=17.75$ MeV). However the optimal fit was mainly searched near the top of the IAR, near $E_p=17.40$ MeV for configurations with the g $_{{ 7}/{2}}$ particle and near $E_p=17.47$ MeV for configurations with the d $_{{ 3}/{2}}$ particle, see Sect. 3.3.4 and Table 1.

As an effect of the fit with fixed energies (Sect. 3.2.1) fluctuations in the shape of the angular distributions show up. Fluctuations at some scattering angles could be removed by averaging values obtained from neighboring levels [42].

3.3.8 Fit of the two states in known doublets

Angular distributions of the two states in known doublets were fitted by regarding the backward angles for one state as being more important and by regarding forward scattering angles for the other state (Sects. 4.1.7, 4.1.8).

The differential cross section for the doublet is described by the sum of the two components [Eq. (7)]

$$\begin{aligned} \frac{d \sigma }{d \varOmega } ( \varTheta , pair, LJ, E_p )= & {} \frac{d \sigma _1 }{d \varOmega } ( \varTheta , {\tilde{E}}_x ^1, I^\pi _1, LJ _1, E_p ) \nonumber \\&+ \frac{d \sigma _2 }{d \varOmega } ( \varTheta , {\tilde{E}}_x ^2, I^\pi _2, LJ _2, E_p ) . \nonumber \\ \end{aligned}$$

(21)

The differential cross section for the two states is described with the factor $0<\alpha ^2<1$ by

$$\begin{aligned} \frac{d \sigma }{d \varOmega } ( \varTheta , {\tilde{E}}_x ^i, I^\pi _i, L_i J_i, E_p )= & {} \frac{ fak_i (E_p) }{ fak_1 (E_p) + fak_2 (E_p) } \nonumber \\&\times \frac{d \sigma }{d \varOmega } ( \varTheta , pair, L_i J_i, E_p ) , \nonumber \\&\quad i=1,2 , \nonumber \\ \mathrm{with \quad } fak_1 (E_p)= & {} \varLambda ( L_1 J_1, E_p ) (2 I_1 + 1) (1 -\alpha ^2) , \nonumber \\ fak_2 (E_p)= & {} \varLambda ( L_2 J_2, E_p ) (2 I_2 + 1) \alpha ^2. \end{aligned}$$

(22)

The factors $\alpha$ and $\sqrt{1 -\alpha ^2}$ are displayed in Fig. 24 for the 6264 $1^-$ state and in Figs. 30, 31.

3.4 Identification of states with dominant 1p1h strengths and spin assignment

The fit of the angular distribution by three 1p1h constituents often allows for disparate choices, see Sect. 3.3.4 and Fig. 5. The SSM acts as an important guide to determine the dominant 1p1h configuration and to decide the spin assignment. The calculation of the excitation energies by SDI together with estimates of the cross section (Table 3) refines the expectation (Tables 6, 7, 8, 9, 10, 11).

In the end the distribution of the sum of the 1p1h strengths and the centroid energies should reproduce this expectation.

3.4.1 The SM as a guide

Figure 1 serves as an important guide to identify states. The distribution of the 1p1h strength across states in a typical range of less than 150 keV should yield a centroid energy close to the excitation energies calculated by the SDI (Table 6, 7, 8, 9, 10, 11). Figures 8, 9, 10, 11, 12 and 13 show the SDI energies in the left frames for spins from $1^-$ to $6^-$.

3.4.2 Spin assignments

Several states with spins $1^-$, $2^-$, and $3^-$ are known at $6.2<E_x <7.0$ MeV [1, 46, 89,90,91,92,93,94]. Two states with spins $4^-$ and $5^-$ were suggested by the big cross sections [40].

The shape of the angular distribution for a state with one dominant configuration with a d $_{{ 3}/{2}}$ or g $_{{ 7}/{2}}$ particle is close to the shape shown in Fig. 4. (A complete list for all one-particle one-hole configurations built with particles and holes in the orbits $50\le N \le 184$ is found in [72].) This often allows to decide the spin and configuration assignment unambigously.

Considerations from Sect. 3.4.1 together with the orthonormality and sum-rule relations refine the spin assignments in an iterative manner, see Tables 6, 7, 8, 9, 10, 11, 13, 14.

3.4.3 Dominant particle in the 1p1h configurations

The excitation functions of Wharton et al.  [28] served as an important guide for the choice of the dominant particle in the 1p1h configurations. The excitation energies were recalibrated by Eq. (14).

For each level all contributing states could be uniquely determined. Mostly one state is dominant but several close doublets were recognized (5280 0$^-$ and 5292 $1^-$, 5874 $3^-$ and 5886 $4^-$, 5812 $2^-$ and 5813 $2^-$, 6010 $3^-$ and 6012 $4^-$, 6086 $2^-$ and 6088 $3^-$). More details are given in Sect. A.2.

3.4.4 Dominant hole in the 1p1h configurations

Strongly excited states must have components of configurations with either a p $_{{ 1}/{2}}$ or p $_{{ 3}/{2}}$ hole because of the about four times stronger s.p. widths in relation to configurations with a f $_{{ 5}/{2}}$ hole [40]. The shape of the angular distribution should be close to the shape of the dominant configuration (Fig. 4).

Configurations with a dominant f $_{{ 5}/{2}}$ hole produce angular distributions with large coefficients of Legendre polynomial $P_4$ [Eq. (9)] thus deviating from the linearity introduced by the choice of $P_2$ as abscissa.

3.4.5 Presence of 1p1h configurations with a p $_{{ 1}/{2}}$ hole

An important guide to fit the angular distributions taken near the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ IARs derives from the results for $^{207}\mathrm{Pb}$$({ d, p})$ with polarized deuterons by Valnion [55, 56]. For many states one or two values of the amplitudes $c_{LJ\,{ p}{_{{ 1}/{2}}}} ^{{\tilde{E}}_x, I^\pi }$ [Eq. (1)] are determined for $J=L\pm {\frac{ 1}{2}}$ and $L=0,2,4,6$.

The $^{207}\mathrm{Pb}$$({ d, p})$ results allow to give a good first guess of the configurations d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ or g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$. However for some states the dominant configuration does not have the d $_{{ 3}/{2}}$ or g $_{{ 7}/{2}}$ particle (Table 4).

The 5947 $1^-$ and 5924 $2^-$ are known to bear the dominant d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strengths, and the 5874 $3^-$ and 5969 $4^-$ the dominant g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strengths. The angular distributions confirm the values from [55] for all four states. The 6088 state in the 6.09 MeV doublet level is identified to bear the missing g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength for spin $3^-$. The high sensitivity of the angular distributions reveals weak admixtures of d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ in these five states.

The $^{207}\mathrm{Pb}$$({ d, p})$ results also allow to fit doublets unresolved in the 1969 data with the 6010 $3^-$, 6012 $4^-$ states (Sect. 4.1.7) and the 6086 $2^-$, 6088 $3^-$ states (Sect. 4.1.8).

4 Discussion

Among more than hundred known states in the region $6.2<E_x< 7.0$ MeV this paper discusses half of them. The spin assignments should be taken with precaution; some of them are not entirely firm, however the parity assignments are firm because of the resonant excitation on IARs with known parity.

The spin assignment is based on the selective excitation on the g $_{{ 7}/{2}}$ and d $_{{ 3}/{2}}$ IARs in $^{209}\mathrm{Bi}$. Carefully measured angular distributions for $^{208}\mathrm{Pb}$$({ p, p' })$ at three proton energies close to the g $_{{ 7}/{2}}$ and d $_{{ 3}/{2}}$ doublet IAR provide the basis. Both the shape of the angular distribution and the mean cross section were investigated. The high sensitivity of the resonance reaction allows to determine up to four amplitudes of 1p1h configurations for each state. The good knowledge of the s.p. widths [40] is essential. The procedure to fit an angular distribution is described in Sects. 3.3.6, 3.4. An alternative method is described in Sect. 3.3.4.

Data taken with the Q3D magnetic spectrograph at the MLL in 2003–2019 for various reactions with a resolution of 3 keV (Table 15) allowed to find the dominant state for most levels observed with semiconductor detectors at the MPIK in 1969 with a resolution of 12 keV [39].

Data taken for $^{207}\mathrm{Pb}$$({ d, p})$ with polarized deuterons provided precise amplitudes for two dozen states [55]. They were important to calibrate the absolute cross sections (Sect. 3.3.2).

The purpose of the paper is to present a first survey of the strongest excited negative parity states in $^{208}\mathrm{Pb}$ at $6.2<E_x< 7.0$ MeV. No attempt is made to discriminate the parity for all states. In principle it is possible because negative parity states exhibit a change of the cross section across the IARs and the positive parity states tend to have low cross sections.

SM calculations [11,12,13, 17, 18] provide a guide to identify new states (Sect. 3.4, Tables 3, 4). The dominant configuration is suggested by the excitation energy being close to the predicted energy $E_x^{SDI}$. The shape of states with weak admixtures should be close to the shape for the pure configuration (Fig. 4). The resulting strength distribution is expected to not deviate much from the predictions (Figs. 8, 9, 10, 11, 12, 13). The final result confirms the expectation. The results explain the excitation functions measured by Wharton et al. [28] and reproduced in Figs. 16, 17 (Sect. 3).

We discuss only states where good results were obtained. A future analysis of available data [53] on $^{208}\mathrm{Pb}$$({ p, p' })$ will yield more results.

The fits of angular distributions with alternate signs given in parentheses in Table 4 are shown with dashed lines in Figs. 24, 25, 26, 27, 28, 29, 30 and 31. These solutions are not realistic (Sect. 3.3.4).

In addition to states at $6.2<E_x< 7.0$ MeV, states at $5.7<E_x< 6.2$ MeV with dominant configurations involving the p $_{{ 1}/{2}}$ hole are discussed (Sect. 4.1.1).

Table 6 Configurations with spin $1^-$ at $5.8<E_x^{SDI}< 7.2$ MeV (Sect. 2.3.1). States with known spin and parity (order number M) are correlated with model configurations (order number m). Number of figure with a fitted angular distribution and with an excitation function are shown. Yrast states are included. Configuration strengths derived from Table 4

Table 7 Same as Table 6 for spin 2$^-$

Table 8 Same as Table 6 for spin 3$^-$

Table 9 Same as Table 6 for spin 4$^-$

Table 10 Same as Table 6 for spin 5$^-$

Table 11 Same as Table 6 for spin 6$^-$

4.1 Known states

4.1.1 States with dominant g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ and d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strengths

The comparison with $^{207}\mathrm{Pb}$$({ d, p})$ [55, 56] confirms the distribution of the strength of g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ for spins $3^-,4^-$ and of d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ for spins $1^-,2^-$.

Admixtures from d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ and d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ to the 5947 $1^-$, 5924 $2^-$, 6086 $2^-$, states and from g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ to the 5874 $3^-$, 6010 $3^-$, 5969 $4^-$ states are less than 4%, 4%, 15%, 3%, 4% in strength, respectively (Tables 3, 4, 5).

The calibration of the absolute cross sections which was not provided [39] is discussed in Sect. 3.3.2. It introduces systematic uncertainties in the size of the amplitudes but not in the relative signs.

4.1.2 0$^-$ states

The two lowest 0$^-$ states are a perfect example of a two-levels system [91, 92]. Less than 3% strength of other configurations admix.

A search for levels with the unique shape of the angular distribution for d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ (Fig. 4) was not successful. The excitation energy $E_x^{SDI} = 7108$ keV calculated with the SDI [17, 18] is however above the threshold $E_x=7.0$ MeV chosen in the data taking of 1969 [41, 42].

4.1.3 $1^-$ states

At least nineteen states with spin $1^-$ below $E_x=7.5$ MeV are known [1, 89,90,91,92,93,94] (Tables 3, 4, 5, 6). The contribution of the configurations d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ is determined for six states (Tables 4, 5). Below $E_x=7.2$ MeV one state is still missing [93] (Table 6).

The 6264 state was first observed in 1968 by $^{208}\mathrm{Pb}$$({ p, p'\,\gamma })$ [95]. Nearly equal transition strengths from the d $_{{ 5}/{2}}$, s $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$ IARs were observed thus assigning spin $1^-$. The 6264 state is discussed in detail in the following (Sect. 4.1.4).

4.1.4 The 6264 $1^-$ state

The 6264 $1^-_{ 8}$ state is excited on the d $_{{ 5}/{2}}$, s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, and d $_{{ 3}/{2}}$ IARs (Fig. 2 in [46]). An excitation by $^{208}\mathrm{Pb}$$({ d, d' })$ is very weak (Fig. 20). Weak amplitudes of s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$ and d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ are determined from $^{207}\mathrm{Pb}$$({ d, p})$ [55] (Table 4).

The fit of the angular distribution assuming configurations with the g $_{{ 7}/{2}}$ particle (Fig. 24) needs a strength of g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ close to unity which is unlikely. The data points at $\varTheta \approx 120^\circ$ are not fitted. The decrease of the mean cross section from $E_p=17.40$ to 17.47 MeV ($R_{47/40}$ [Eq. (13)]) is however well approximated.

A fit with d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ and d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ does not allow to fit a curved shape because of the limiting degree $K=2$ [Eq. (9)]. Yet the increase of the mean cross section from $E_p=17.40$ to 17.47 MeV ($R_{47/40}$ [Eq. (13)]) is better fitted.

We assume nearly equal cross sections on both IARs ($\alpha = \sqrt{1/2}$ [Eq. (22)]). The amplitudes tabulated in Table 4 derive from the fit curves shown in Fig. 24. Apparently the interference between the two IARs changes the shape of the angular distribution at the three proton energies only slightly.

4.1.5 $2^-$ states

Nineteen $2^-$ states with excitation energies $E_x< 7.0$ MeV are identified [1, 46] (Tables 3, 4, 5, 7). The possible assignment of spin 2$^-$ to the 5993 state (Sect. 4.4) has to be investigated.

The contribution of the configurations d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ is determined for six states and of g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ in four states at $6.2<E_x< 7.0$ MeV (Tables 4, 5, Fig. 9).

The excitation energy $E_x^{SDI} = 7015$ keV for g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ calculated with the SDI [17, 18] is above the threshold $E_x=7.0$ MeV chosen in the data taking of 1969 [41, 42]. Nevertheless half of the g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength was found (Table 5, Fig. 25), see especially Sect. 4.2.1.

4.1.6 $3^-$ states

Twenty-nine states with spin $3^-$ below $E_x=7.5$ MeV are known (Tables 3, 4, 5, 8). The distribution of the configurations g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ is determined for nine states [1, 50] (Tables 4, 5, Fig. 10).

The 6444 $3^-$ state contains weak admixtures of d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ and g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ [55, 56]. The fit of the angular distributions near the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ IAR doublet can be done with either d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ or g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$. The ratio of the cross sections at $E_p=17.40, 17.47$ MeV favors the fit with the g $_{{ 7}/{2}}$ particle (Tables 4, 5).

No angular distribution could be analyzed for $3^-$ states at $6.2<E_x< 7.0$ MeV with order numbers $M=25,$ 27 because of lack of data. The 7020 $3^-$ state with order number $M=29$ [Eq. (2)] is recognized as tetrahedral configuration [3, 4]. It is assumed to differ from the SM states with $m=28,30$.

4.1.7 The 6010 $3^-$, 6012 $4^-$ doublet

The doublet with the 6010 $3^-$ and 6012 $4^-$ states was resolved only late [50]. With the resolution of 12 keV the two states build an unresolved doublet in the 1969 data. Nevertheless the doublet could be fitted (Eqs. (21), (22), Fig. 30).

Both states have about equal mean cross sections. Only the 6010 $3^-$ state is excited by $^{207}\mathrm{Pb}$$({ d, p})$ [50]; the 6012 $4^-$ state with unnatural parity is not excited. Valnion [55] determined the g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength for the 6.01 MeV doublet. It is entirely assigned to the 6010 $3^-$ state with the larger cross section. The amplitude $c_{{ g}{_{{ 7}/{2}}}{ p}{_{{ 1}/{2}}}} ^{6010 3^-} = 0.53$ allows to fix the ratio within about 10% [55, 56]. The fit for the 6010 $3^-$ state clearly yields the relative sign of the two amplitudes of g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ and g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$. The fit for the 6012 4$^-$ state yields the three amplitudes g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ with low uncertainties (Fig. 30).

Kulleck et al.  [30] deduced a large coefficient $A_4$ from the fit of the angular distribution. It can be explained by a considerable admixture of g $_{{ 7}/{2}}$f $_{{ 7}/{2}}$ and a negligible g $_{{ 9}/{2}}$p $_{{ 1}/{2}}$ admixture to the 6012 $4^-$ state [Eq. (9)]. A fit with four amplitudes (i.e. including g $_{{ 7}/{2}}$f $_{{ 7}/{2}}$) was not possible because the 6.01 MeV doublet was not resolved in the 1969 data.

The ratio of the mean cross sections for the 6010 $3^-$ and the 6012 $4^-$ states is determined with $0.57\pm 0.05 : 0.43\mp 0.05$ in agreement with the estimate [50]. Tables 4, 5 show the results, Fig. 30 the fits.

The measured cross sections exhibit a steep decline from $\varTheta = 90^\circ$ towards $\varTheta =170^\circ$. The cross sections observed by Wharton et al.  [28] near $\varTheta = 90^\circ$ and $158^\circ$ (Fig. 17) are well reproduced; this fact was useful in calibrating the cross sections (Sect. 3.3.2).

4.1.8 The 6086 $2^-$, 6088 $3^-$ doublet

The doublet with the 6086 $2^-$, 6088 $3^-$ states was resolved only late [50, 93]. With the resolution of 12 keV they build an unresolved doublet in the 1969 data. Nevertheless the doublet could be fitted (Eqs. (21), (22), Fig. 31, Table 4). The ratio of the mean cross sections is about 1:3.

By neglecting the existence of a doublet the fit of the 6.09 MeV level yields a fit with a d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ component with an amplitude of $|c|=0.3$ for the 6086 $2^-$ state in stark disagreement with the value 0.48 measured by Valnion [55]; the mean cross section is a factor two too low.

The existence of the 6086 $2^-$, 6088 $3^-$ states in the doublet was recently shown [93]. The steep decline at $90^\circ<\varTheta < 120^\circ$ is explained by a strong d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ component in the 6088 $3^-$ state and the negative sign of a d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ admixture yielding a mean cross section slightly higher than for the 6086 $2^-$ state whereas the smooth increase of th cross section at $\varTheta< 140^\circ < 170^\circ$ is well fitted by a strong d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ component and a d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ admixture with negative sign. In both cases the sign of the d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ admixture is clearly determined (Fig. 31, Tables 4, 5).

Table 12 Comparison of excitation energies determined in 1966 [25] and fifty years later

4.2 New spin assignments

Fourteen states are newly identified or newly assigned a spin.

The progress in the evaluation of states in $^{208}\mathrm{Pb}$ over hundred years is impressive [25, 81,82,83,84]. In the region $6.2<E_x< 7.0$ MeV twenty states were observed in 1967 and no spin was known (Table 12). Now about 150 states are discerned (Table 15). Spins from $1^-$ to $6^-$ for 42 states are determined, among them 14 new assignments by this work (Tables 4, 5, 6, 7, 8, 9, 10, 11). It took 50 years with a dormant period of nearly 30 years (about 1970–2005 with few $^{208}\mathrm{Pb}$$({ p, p' })$ data during this time) to obtain these results.

4.2.1 States with spin $2^-$

Ten states with spin $2^-$ at $6.2< E_x< 7.0$ MeV are predicted by the SDI (Table 7), seven states were known previously [1, 46] (Tables 3, 4, 5, Sect. 4.1.5). The 6789 state is newly assigned spin 2$^-$. The unique shape of the angular distribution clearly assigns a strong g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ component, the shape for g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ is similarly steep towards backward scattering angles (Figs.  4, 25). The relative signs of the two amplitudes are firmly determined (Table 4).

4.2.2 States with spin $3^-$

Nine states with spin $3^-$ at $6.2< E_x< 7.0$ MeV are predicted by the SDI (Table 8), seven states were known previously (Tables 3, 4, 5, Sect. 4.1.6). Two more states are newly assigned spin $3^-$.

The 6337 state is newly identified and assigned spin $3^-$ (Fig. 26). It is clearly distinct from the 6340 state suggested with spins $1^-$, $2^-$, or $3^-$ and an uncertainty in excitation energy of 5 keV [1].

The 6243 state is tentatively assigned spin $3^-$ because of the considerable cross section near the g $_{{ 7}/{2}}$ IAR (Fig. 26). Other spins in the range from $1^-$ to 6$^-$ are excluded by the shape of the angular distribution (Fig. 4).

4.2.3 A rather complete system of $4^-$ states

Twenty states with spin $4^-$ below $E_x=7.0$ MeV are known (Tables 3, 4, 5, 9). States with spin $4^-$ and dominant g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ or g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strength were found by the pronounced shape of the angular distribution near the g $_{{ 7}/{2}}$ IAR if a weak d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ admixture can be expected (Fig. 4).

The 6452 state contains a major g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ fraction, the 6529, 6739, 6801, 6944 states contain nearly the complete g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength. The ratio $R_{47/40}$ [Eq. (13)] indicates weak d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ admixtures (Table 4).

The 6739 state was suggested to have spin $4^-$ because of the large cross section [40] (Fig. 27, Tables 4, 5). The angular distributions of the 6739 state indicate an interference between the two IARs g $_{{ 7}/{2}}$ and d $_{{ 3}/{2}}$. The fit at $E_p=17.47$ MeV reproduces the data at $\varTheta > 140^\circ$ but the mean cross section at $E_p=17.40$ MeV is larger. Also the cross section is enhanced in the region at $\varTheta \approx 120^\circ$.

The poor fit of the angular distributions of the 6739 and 6801 states explains the summed strength for g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ to be larger than unity.

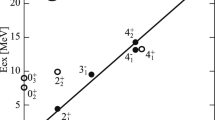
The angular distributions of the 6452 state are well fitted by assuming a strong g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ contribution (Fig. 27). The g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength is weak, indeed the 6452 state is not observed in $^{207}\mathrm{Pb}$$({ d, p})$. The $4^-$ state with order number $M=23$ [Eq. (2)] is identified as a member of the tetrahedral rotation-vibration band (010) (Table 9), the excitation energy agrees perfectly with the prediction [3, 4]. The next SM configuration is predicted 100 keV higher (proton f $_{{ 5}/{2}}$d $_{{ 5}/{2}}$ configuration).

Still three more $4^-$ states with order numbers $M=17,18,21$ are expected at $6.2<E_x< 6.6$ MeV (Fig.  11).

Table 13 A rather complete system of $4^-$ states. Configuration strengths derived from Table 4

4.2.4 States with spin $5^-$

Nineteen states with spin $5^-$ below $E_x=7.0$ MeV are known (Tables 3, 4, 5, 10). States with spins $5^-$ and $6^-$ at $6.2<E_x< 7.0$ MeV are excited by the proton decay of the g $_{{ 7}/{2}}$ IAR only, configurations d $_{{ 3}/{2}}$f $_{{ 7}/{2}}$ and d $_{{ 3}/{2}}$h $_{{ 9}/{2}}$ are far away and their contribution is negligible. The shape of the angular distributions is pronounced near the g $_{{ 7}/{2}}$ IAR (Fig. 4), the cross section of the $5^-$ states is expected to be large.

The 6688 state was tentatively assigned spin $5^-$ [40] because of the large cross section; it was assigned spin $5^-$ [1] in view of the excitation function measured by Wharton et al. [28], see reproduction in Fig. 17. The unique shape of the angular distribution confirms the assignment of the dominant g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ configuration (Fig. 28). The g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength is determined with 64% (Tables 4, 5, Fig. 12).

Three other $5^-$ states are identified by the rather unique shape of the angular distributions and the large cross sections (Table 5, Fig. 28). The 6878 state with 25% g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength thus complements the g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength to near completeness. Similarly the 6354 and 6389 states together contain nearly the full g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strength. Still three more $5^-$ states are expected at $6.2<E_x< 7.0$ MeV (Table 10, Fig. 12). Apparently their cross sections are weak.

Table 14 A rather complete system of $6^-$ states. Configuration strengths derived from Table 4

4.2.5 A rather isolated system of $6^-$ states

Twelve states with spin $6^-$ below $E_x=7.0$ MeV are known (Tables 3, 4, 5, 11). States with spin $6^-$ and dominant g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strength were found by the pronounced shape of the angular distribution near the g $_{{ 7}/{2}}$ IAR (Fig. 4); the cross sections should be rather large because of the spin factor [Eq. (5)]. The SDI predicts $6^-$ states at $6.2<E_x< 7.0$ MeV with order numbers $M=9$–14 [Eq. (2)]; the 10th $6^-$ state is not yet identified.

Indeed the 6462, 6541, 6631, 6777 states are identified to contain the complete g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strength (Tables 4, 5, 11). Admixtures from g $_{{ 7}/{2}}$f $_{{ 7}/{2}}$ and g $_{{ 7}/{2}}$h $_{{ 9}/{2}}$ are less than 4% (Fig. 29). The centroid energy $\overline{E_x}=6.63$ MeV [Eq. (6)] is close to the predicted energy $E_x^{SDI}= 6655$ keV (Tables 3, 14).

The SDI predicts the configuration g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ for spin $6^-$ to be shifted by 160 keV in relation to the SSM due to the Nordheim number $N_h=+1$ similar as for i $_{{11}/{2}}$f $_{{ 5}/{2}}$ and spin $8^-$ [17]. The shift in excitation energy is verified (Table 11).

Eight $6^-$ states are known at much lower excitation energies, there is a gap of 778 keV between the state with order number $M=8$ and 9 (Table 11, Fig. 12). The 14th $6^-$ state is predicted 279 keV higher in excitation energy [17, 18]. Hence the $6^-$ states with order number $M=8$-14 excepting the still missing 10th state may be considered as a complete system isolated from the rest (Fig.  13). Admixtures of configurations with order numbers $m\le 8$ and $m\ge 14$ are expected to be small.

The poor fit of the angular distributions of the 6462 and 6631 states explains the summed strength for g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ to be larger than unity.

Fig. 8

Distribution of strengths $0<|c_{LJ\,lj} ^{{\tilde{E}}_x, I^\pi }|^2 <1$ [Eq. (3)] for configurations with particles $LJ={ s}{_{{ 1}/{2}}}$, d $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$ and holes $lj={ p}{_{{ 1}/{2}}},{ p}{_{{ 3}/{2}}},{ f}{_{{ 5}/{2}}}$ in states at $5.8< E_x < 7.0$  MeV with spin $1^-$ in b–f. Relevant values $L\ 2J$ and $l\ 2j$ are shown at left. The abscissa shows the range of excitation energies $5.8< E_x< 7.0$ MeV. The ordinate is given in relative untis $0<1$ shown at right. (Left frame) Distribution calculated by SDI with unity strength (dens dotted and marked by a diamond), observed centroid energies and summed strength (thick triangle), other configurations listed in Table 6 denoted as “other” in a; the excitation energy $E_x^{SDI} ({ g}{_{{ 9}/{2}}}{ f}{_{{ 7}/{2}}})$ is shown, too, because of its importance in the region $5.5< E_x< 6.2$ MeV (and the position for $E_x^{SDI}>5.8$ MeV marked by a square for spins $2^-$, $4^-$, $6^-$). (Right frame) Distribution determined from experiment. Sum of unobserved strengths shown denoted as “unobs” in a. In each state only either g $_{{ 7}/{2}}$-strength or d $_{{ 3}/{2}}$-strength is determined; an interference between components with different particles LJ cannot be obtained (Sect. 2). The distribution of the s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$ and s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$ strengths is also known [46, 49]

Fig. 9

Similar to Fig. 8 for spin 2$^-$. The distribution of the s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ and s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$ strengths [46, 49] is also known

Fig. 10

Similar to Figs. 8 and 9 for spin $3^-$

Fig. 11

Similar to Fig. 8 and 9 for spin $4^-$

Fig. 12

Similar to Fig. 8 and 9 for spin $5^-$

Fig. 13

Similar to Fig. 8 and 9 for spin $6^-$

4.3 Comparison to shell model calculations

4.3.1 Identified 1p1h strengths

The left parts in Figs. 8, 9, 10, 11, 12 and 13 display the excitation energies in the region $5.8<E_x <7.0$ MeV calculated by the SDI for spins 1$^-$, $2^-$, $3^-$, $4^-$, $5^-$, and $6^-$ and the configurations s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$, s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$, s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$. In the bottom line other SM configurations are shown.

The right parts display the excitation energies and the measured particle-hole strength of all states with spins $1^-$, $2^-$, $3^-$, $4^-$, $5^-$, and $6^-$ in the region $5.8<E_x <7.0$ MeV. For states with identified strengths the complement of the strengths (for a configuration not shown in the figure or an unobserved configuration) is shown in the bottom line as “unobs”. The sum of the identified strengths are shown with thick triangles in the left parts. Table  3 tabulates identified strengths and centroid energies both calculated and derived from experiment.

The $1^ -$states. The strengths for s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$ and d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, and g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ is nearly completely located. Only much g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strength is still missing. The reason is the weakness of the cross section and the interference among the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ doublet IARs.

The $2^ -$states. The strengths for s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ and also for g $_{{ 9}/{2}}$f $_{{ 7}/{2}}$ are nearly completely located; Some s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strength is missing. The g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength is overestimated. For s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$ the reason is the lack of data near the s $_{{ 1}/{2}}$ IAR and the interference with other IARs leading to non-isotropic angular distributions. For d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ the reason is the weakness of the cross section and the interference among the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ doublet IARs. For g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ the reason is the distribution across five states leading to statistical fluctuations.

The $3^ -$states. The strengths for d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ are nearly completely located. For the missing s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ strength the reason is the lack of data near the s $_{{ 1}/{2}}$ IAR and the interference with other IARs leading to non-isotropic angular distributions. Most d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ and some g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strengths are still missing. Again the reason is the weakness of the cross sections and the interference among the IARs.

The $4^ -$states. The g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength was completely found by Valnion [55, 56], note footnotes in Table 4 and Sect. A.2.1. It was crucial in doing calibration of the cross sections (Sect. 3.3.2) and the adjustment of the parameters for the IARs (Tables 1, 2).

The strength for g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ is located within a few percent, see Sect. 4.2.3. No d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ strength could be found. Again the reason is the weakness of the cross sections and the interference among the IARs. The overestimated g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength has the distribution across all states as the reason leading to statistical fluctuations.

The $5^ -$states. The strengths for g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ are located within a few percent. The finding proves the good calibration of the cross sections (Sect. 3.3.2) and the adjustment of the parameters for the IARs (Tables 1, 2).

The $6^ -$states. The strength for g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ is located within a few percent, see Sect. 4.2.5. Again, the finding proves the good calibration of the cross sections (Sect. 3.3.2) and the adjustment of the parameters for the IARs (Tables 1, 2).

4.3.2 Centroid energies

A large amount of one-particle one-hole strengths has been identified (Tables 3, 4, 5). The sum of the configuration strengths $\sum _m \left| c_{LJ\,lj} ^{\tilde{E}_x, I^\pi , m} \right| ^2$ found in the identified states is often close to unity. It allows to compare the centroid energies $\overline{E_x}$ [Eq. (6)] of various configurations to the excitation energies $E_x^{SDI}$ calculated by the SDI [17, 18], refer to Cols. 1 and 5 in Table 3. The good agreement verifies the spin assignments (Tables 6, 7, 8, 9, 10, 11, Figs. 8, 9, 10, 11, 12, 13).

In Figs. 8, 9, 10, 11, 12 and 13 the left part shows the centroid energies for the configurations s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ for the spins from $1^-$ to $6^-$ and indicates the sum of strength determined by a thick triangle. In general the agreement of the centroid energy $\overline{E_x}$ with the energy $E_x^{SDI}$ is good.

The $1^ -$states. The right part of Fig. 8 shows the distribution of the strengths, the left part the values $E_x^{SDI}$ by a dotted line with a diamond at bottom. The centroid energy agrees with $E_x^{SDI}$ within 50 keV (about 100 keV) for (s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$), (d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$), d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$. It deviates by more than 100 keV from $E_x^{SDI}$ for d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$. The reason is simply the limiting choice $E_x<7.0$ MeV in the experimental data. Obviously much d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ strength will be found in the well known $1^-$ states above $E_x=7.0$ MeV in future.

The $2^ -$states. The right part of Fig. 9 shows the distribution of the strengths, the left part the values $E_x^{SDI}$ by a dotted line with a diamond at bottom. The centroid energy agrees with $E_x^{SDI}$ within 50 keV (about 100 keV) for s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$, s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, (d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$), and also for g $_{{ 9}/{2}}$f $_{{ 7}/{2}}$; the left panel shows the position marked by square and the value $E_x^{SDI}$.

It deviates by more than 100 keV from $E_x^{SDI}$ for d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$. For d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ the reason is the limiting choice $E_x<7.0$ MeV in the experimental data as already mentioned. For g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ the distinction from d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ is hindered by the interference among the IARs.

The $3^ -$states. The right part of Fig. 10 shows the distribution of the strengths, the left part the values $E_x^{SDI}$ by a dotted line with a diamond at bottom. The centroid energy agrees with $E_x^{SDI}$ within 50 keV for d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ and within about 100 keV for s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$. It deviates by more than 100 keV from $E_x^{SDI}$ for d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, and g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$. The distinction between g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ and d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ is hindered by the weak cross sections and the interference among the IARs. For d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ and d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ the reason is the limiting choice $E_x<7.0$ MeV in the experimental data as already mentioned.

The $4^ -$states. The right part of Fig. 11 shows the distribution of the strengths, the left part the values $E_x^{SDI}$ by a dotted line with a diamond at bottom. The centroid energy agrees with $E_x^{SDI}$ within 20 keV for g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$. It also agrees for g $_{{ 9}/{2}}$f $_{{ 7}/{2}}$; the left panel shows the position marked by square and the value $E_x^{SDI}$.

The large deviation for g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ is caused by the limiting choice $E_x<7.0$ MeV in the experimental data. Section 4.2.5 discusses more details. No d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ strength could be found, see Sect. 4.3.1.

The $5^-$states. The right part of Fig. 12 shows the distribution of the strengths, the left part the values $E_x^{SDI}$ by a dotted line with a diamond at bottom. The centroid energy agrees with $E_x^{SDI}$ within 50 keV for g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$.

The $6^-$states. The right part of Figs. 13 shows the distribution of the strengths, the left part the value $E_x^{SDI}$ by a dotted line with a diamond at bottom. The centroid energy agrees with $E_x^{SDI}$ within 30 keV for the single configuration g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ resonantly excited near $E_p=17.4$ MeV. Section 4.2.5 discusses more details. It also agrees for g $_{{ 9}/{2}}$f $_{{ 7}/{2}}$ [44]; the left panel shows the position marked by square and the value $E_x^{SDI}$.

4.3.3 Number of states at $6.2<E_x< 7.2$ MeV

Tables  4 and 5 list the results for 40 states with spins from $1^-$ to $6^-$. All states with spins $1^-$, $2^-$, $3^-$ were known before except for two $3^-$ states. The 6243 $3^-$ state is identified because of the considerable cross section near the g $_{{ 7}/{2}}$ IAR, the 6337 $3^-$ state is distinguished from the close lying 6340 state (Table 15).

The assignment of spin $5^-$ to the 6688 state [1, 40] is confirmed. Six $4^-$ states, four $5^-$ states and five $6^-$ states are newly identified. No $4^-$ state with a large d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ component could be identified. The reason is discussed in Sect. 2.3.2. Figure 14 compares the distribution of states with spins from $1^-$ to $6^-$ with calculations.

At $6.2<E_x< 7.2$ MeV the SDI predicts eleven $1^-$ states, ten 2$^-$ states, twelve $3^-$ states, eight $4^-$ states, seven $5^-$ states, six $6^-$ states (Tables 4, 5, 6, 7, 8, 9, 10, 11). As discussed in Sect. 2.3.2, states with spin 1$^-$, $2^-$, $3^-$, and $4^-$ are difficult to differentiate by $^{208}\mathrm{Pb}$$({ p, p' })$ via the g $_{{ 7}/{2}}$+d $_{{ 3}/{2}}$ doublet IARs. Hence the determination of major 1p1h components in five out of ten predicted $1^-$ states (Sect. 4.1.3), in eight out of ten predicted $2^-$ states (Sects. 4.1.5, 4.2.1), in eleven out of twelve predicted $3^-$ states (Sects. 4.1.6, 4.2.2), and in five out of eight predicted $4^-$ states (Sect. 4.2.3) is a good achievement. Four out of seven $5^-$ predicted states (Sect. 4.2.4) and four out of six predicted $6^-$ states are identified (Sect. 4.2.5).

At $6.2<E_x< 7.0$ MeV 103 levels and 126 states are recognized (Table 15). The levels cover states within about 4.0 keV. The SDI predicts 59 states with spins from $1^-$ to 6$^-$ (Tables 6, 7, 8, 9, 10, 11), 40 such states are identified. In addition the 12$^-$, 13$^-$, 14$^-$ yrast and the 12$^-$ yrare states are known [1]. The 6831 8$^-$ and 6879 $7^-$ states are suggested as the coupling of j $_{{15}/{2}}$p $_{{ 1}/{2}}$ to the $3^-$ yrast state [2]. Certainly most of the remaining half of the observed states with unknown spin (about sixty) have positive parity. The SDI predicts only 11 states with spins from $1^+$ to 9$^+$, the coupling of g $_{{ 9}/{2}}$f $_{{ 5}/{2}}$ to the $3^-$ yrast state another two hundred states [2] (Fig. 15).

In the region $6.2<E_x< 7.0$ MeV in total the number of observed states agrees with calculations by the SM for 1p1h configurations [12, 13, 17, 18] and with the coupling of 1p1h configurations to the $3^-$ yrast state [2] rather well, at least for the negative parity states. However several disagreements with the SM are obvious.

We do not discuss the disagreements in this paper because part of them occur with the yrast or yrare states and at $E_x\approx 5.5$ MeV [9]. Tables 6, 7, 8, 9, 10 and 11 show the differences of the order numbers m for the pure SM configurations from M for the states [Eq. (2)].

Fig. 14

Number of states at $5.2< E_x< 7.2$ MeV with negative parity for spins $1^-$, $2^-$, $3^-$, $4^-$, $5^-$, and $6^-$. The number of known states (drawn lines) is compared to calculations with SDI [17, 18] (dotted lines) and with M3Y [12] (dashed lines). Data for $5.80<E_x<6.20$ MeV are taken from Table VI in [50], data for $6.20<E_x<7.15$ MeV from Table 15. The number of known states includes those predicted but not yet observed (Tables 6, 7, 8, 9, 10, 11). The dot at left indicates the zero level of the ordinate. The number of known states at $E_x<7.2$ MeV is (a) 16, (b) 20, (c) 30, (d) 23, (e) 19, (f) 14, with spin $1^-$, $2^-$, $3^-$, $4^-$, $5^-$, $6^-$, respectively, see ordinate at right

Fig. 15

Number of states at $2.5< E_x< 7.2$ MeV compared to calculations for 1p1h configurations a with negative parity, b with any parity and [lowest curve] for non-1p1h configurations. Lines marked with dots show experimental values, dotted lines calculated with SDI [17, 18], drawn curves calculated with M3Y [12]. The lowest curve shows the number of non-1p1h configurations known from experiment and calculated by the SDI for the weak coupling of the $3^-$ yrast state to 1p1h configurations [2]. Larger gaps in the distribution of excitation energies are predicted at $E_x\approx 4.5, 5.5, 6.1, 6.9$ MeV. They are visible in the experimental distributions except for the last one where the knowledge diminishes. The gaps enabled the study of rather isolated systems of states [34] (Sect. 4.3.4)

4.3.4 Comparison of the number of states to calculations

Figure 15 compares the distribution of states with negative and any parity to calculations. The SM predicts gaps in the distribution of excitation energies at $E_x\approx 4.5$, 5.5, 6.1, 6.9 MeV. The gap at $E_x\approx 4.5$ MeV enabled the study of an almost complete system of one $2^-$, one $7^-$, three $3^-$, four $6^-$, five $4^-$, and six $5^-$ states in $^{208}\mathrm{Pb}$ [34]. The spins were finally settled in 1982, the results are shown in Table 4 of [3].

The gap at $E_x\approx 6.1$ MeV enabled the study of the nearly complete ensemble of states below $E_x= 6.2$ MeV [50]. It thus provided data to study the chaoticity among bound states in a heavy nucleus [62,63,64]. By chance the gap at $E_x\approx 6.9$ MeV is close to the arbitrary limit $E_x =7.0$ MeV chosen for the data taken in 1969 (Sect. 2.1).

The mean observed cross section of negative parity states is in the order of 10 $\upmu$b/sr but approaches 500 $\upmu$b/sr for a few states (Table 6, 7, 8, 9, 10 and 11, Fig. 17). Positive parity states are generally weaker excited [45].

At $6.2< E_x < 7.0$ MeV 126 states are observed (Table 15). About 59 states with spins from 1$^-$ to $6^-$ are observed (Tables 4, 5, Sect. 4.4) and about 20 states with spins from $7^-$ to 14$^-$ [1, 50]. Most of the other observed states have unknown parity.

Nearly 200 positive parity states are predicted, among them the majority by the coupling of the $3^-$ yrast state to g $_{{ 9}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 9}/{2}}$p $_{{ 3}/{2}}$, i $_{{11}/{2}}$p $_{{ 1}/{2}}$, and i $_{{11}/{2}}$f $_{{ 5}/{2}}$. The number of observed states which do not have negative parity is much lower. It agrees roughly with the SM calculations with M3Y (Fig.  15). Apparently the majority of positive parity states predicted by the coupling of the $3^-$ yrast state to 1p1h configurations is not yet identified except for 14 states with the coupling to g $_{{ 9}/{2}}$p $_{{ 1}/{2}}$ and four other states [2].

4.4 Discovery of non-1p1h states

Complete spectroscopy of 1p1h configurations allows to find non-1p1h configurations [9]. A discrepancy between the order numbers predicted by SDI and the observed order assists in resolving the correlation. For $5.8<E_x <7.0$ MeV Fig. 14 and Tables 6, 7, 8, 9, 10 and 11 compare the distribution of states for spins from $1^-$ to $6^-$ separately to calculations. The number of observed states with negative parity is rather certain up to $E_x\approx 7.0$ MeV. For some energy regions the order numbers M, m are exchanged but in general the difference $M-m$ [Eq. (2)] is constant for most spins and most regions.

The $1^-$, $2^-$, $3^-$ yrast states were recognized as tetrahedral configurations [3, 4]. Therefore the order number M of the observed states is one higher than calculated by SDI. At $E_x\approx 5.5$ MeV three more $3^-$ states and at $E_x\approx 5.8$ MeV three more $5^-$ states are observed than predicted by the SDI [9]. The 7020 $3^-$ and 7134 $4^-$ states are recognized as tetrahedral configurations [3, 4]. Details are discussed in the following.

The $1^ -$states. Higher excited states are known for spin $1^-$ [1, 89, 90, 92,93,94]. The number of identified states agrees with the expectations by the SDI calculation [17, 18] up to $E_x=7.2$ MeV except for the additional yrast state ($M=1$). The 4842 $1^-$ state is identified as a tetrahedral configuration [3].

In contrast SM calculations with realistic forces underestimate the number of $1^-$ states (Fig. 14a). However such calculations have a general problem to predict $1^-$ states because of handling the center of gravity motion [10,11,12,13]. The problem is solved by introducing one artificial state in addition (see e.g. [10, 13]).

Because the $1^-$ yrast state is described by a dominant non-1p1h configuration the order numbers M of the states are one higher than the order numbers m of the configurations counted by the SDI, $M=m+1$ [Eq. (2)] (Fig. 14a, Table 6). One more $1^ -$ state is predicted at 7.1 MeV but not found [93] (Sect. 4.1.3).

The $2^ -$states. The number of identified states for spin $2^-$ agrees with the expectation by the SM up to $E_x=7.0$ MeV except for the additional yrast state ($M=1$) (Fig. 14b). Hence the order numbers M of the states are one higher than the order numbers m of the configurations counted by the SDI, $M=m+1$ [Eq. (2)] (Table 7). The 4140 $2^-$ yrast state is identified as a tetrahedral configuration; it is not predicted by any SM calculation.

The $3^ -$states. The number of states assigned spin $3^-$ is much larger than predicted by SM calculations (Fig. 14c, Table 8). In addition to the yrast state recognized as tetrahedral configuration [3] disagreements are found at $E_x\approx 5.5$ MeV [9]. For the states at $E_x\approx 5.5$ MeV the identification and the spin assignments are rather firm [50], but final doubts cannot be excluded.

The $4^ -$states. The number of states assigned spin $4^-$ agrees with the SDI calculations (Sect. 4.2.3, Fig. 14d, Tables 9, 14). In contrast SM calculations with the M3Y interaction [12] underestimate the number of states slightly.

Just above the limit $E_x=7.0$ MeV chosen in the data taking of 1969 [41, 42] the 7134 $4^-$ state was recognized as tetrahedral configuration [3, 4].

The $5^ -$states. For spin $5^-$ the number of identified states agrees with expectation by the SM up to $E_x=5.7$ MeV (Fig. 14e). However the large gap of 0.65 MeV between the two configurations g $_{{ 9}/{2}}$f $_{{ 7}/{2}}$j $_{{15}/{2}}$i $_{{13}/{2}}$ predicted by SM calculations is not present. The 5705 5$^-_{13}$ and 5993 $5^-_{14}$ states do not have a SDI equivalent. In Fig. 14 in [50] one more state at $E_x\approx 5.5$ MeV is unexplained. This explains the discrepancy of the order numbers by three ($M=m+3$) [Eq. (2)] for $E_x>6.0$ MeV [9] (Table 10).

The spin assignment to the 5993 state is doubted. An essay indicates that an assignment of spin $2^-$ would be possible, too. Yet this would mean that the discrepancy with the number of one-particle one-hole configurations would lead to $M=m+2$ [Eq. (2)] for the $2^-$ states at $E_x>6.0$ MeV (Table 7). The changed mean spacing between the $2^-$ states would affect the chaoticity only little [62,63,64].

The $6^ -$states. For spin $6^-$ the number of identified states agrees with the SM expectation [Sect. 4.2.5, Fig. 14f, Tables 11, 14]. The knowledge of states ceases above $E_x= 6.7$ MeV.

At $6.2< E_x 7.0$ MeV there are sixteen states with negative parity not yet identified in total, one 0$^-$ state, (no $1^-$ state), one 2$^-$ state, (no $3^-$ state), three $4^-$ states, three $5^-$ states, and two $6^-$ states. In addition two 9$^-$ states, two 10$^-$ states, two 11$^-$ states and another 12$^-$ state are missing.

As Table 15 shows there are about 90 states without a spin assignment at $6.2<E_x<7.0$ MeV. Currently available experimental data do not allow further discussion.

Calculations by [2] predict a large number of positive parity states in the region. The lowest curve in Fig. 15b displays the number of non-1p1h configurations known from experiment and calculated by the weak coupling of the $3^-$ yrast state to 1p1h configurations using the SDI [2].

According to [2] about five dozen states are predicted which nearly agrees with the number of states with unknown spin. The difference between the SDI and the M3Y calculations is thus partly explained.

5 Summary

Precisely measured angular distributions of $^{208}\mathrm{Pb}$$({ p, p' })$ at the MPIK (Heidelberg, Germany) for states $6.2<E_x<7.0$ MeV taken 50 years ago are evaluated. In the last fifteen years new data were gathered for the same region of excitation energies and beyond with four times better resolution and with the additional reactions $^{207}\mathrm{Pb}$$({ d, p})$ and $^{208}\mathrm{Pb}$$({ d, d' })$ at the MLL (Garching, Germany).

Sixteen states are assigned new spins from $2^-$ to $6^-$. Spins with $1^-$, $2^-$, $3^-$, and $5^-$ are additionally verified in twenty-four states. Four $2^-$, one $3^-$, four $4^-$, and one 6$^-$ states are newly identified. Amplitudes for up to four 1p1h configurations are determined with relative signs in thirty-four states at $6.2<E_x< 7.0$ MeV and in addition in six states at $5.7<E_x<6.2$ MeV strongly excited by the $^{207}\mathrm{Pb}$$({ d, p})$ reaction.

The centroid excitation energies and the sum of the strengths for the 1p1h configurations g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ is determined for most spins. The deviation of the centroid excitation energies from SM calculations is less then 50 keV at average. The sum of the strengths amounts up to the full strength in most cases.

The purpose of the paper is to find positive parity states and non-1p1h states in the heavy nucleus $^{208}\mathrm{Pb}$ by studying negative parity 1p1h states at $6.2<E_x< 7.0$ MeV. Obviously some of the sixteen new spin assignments in the chosen region are not yet firm. About half of the 90 levels comprising about 120 states observed in 1969 at $6.2<E_x< 7.0$ MeV are weaker excited and not thoroughly investigated.

Appendices

Figures

1.1 Figures 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15

• Figure 1 shows calculated 1p1h states at $3< E_x < 7$ MeV excited by the seven IARs g $_{{ 9}/{2}}$, i $_{{11}/{2}}$, j $_{{15}/{2}}$, d $_{{ 5}/{2}}$, s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, and d $_{{ 3}/{2}}$ in a schematic manner.

• Figure 2 shows calculated excitation functions for the s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$ IARs in $^{209}\mathrm{Bi}$. Ratios of cross sections given by Eqs. (11) and (12) are derived with unity s.p. widths.

• Figure 3 shows angular distributions calculated by Eq. (11). They enhance the appearance of a dominant $P_2$ shape by choosing the abscissa as $P_2$.

• Figure 4 shows calculated angular distributions for pure configurations with a g $_{{ 7}/{2}}$ or d $_{{ 3}/{2}}$ particle and a p $_{{ 3}/{2}}$ or f $_{{ 5}/{2}}$ hole. The linearity of angular distributions for pure configurations with a d $_{{ 3}/{2}}$ particle or p $_{{ 3}/{2}}$ hole is given by the choice of $P_2$ as abscissa.

• Figures 8, 9, 10, 11, 12 and 13 show in the left panel excitation energies calculated by the SDI for spins $1^-$, 2$^-$, $3^-$, $4^-$, $5^-$, and $6^-$ and the configurations s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$, s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$, s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$. Other 1p1h configurations are shown in the bottom frame. The observed centroid energies and summed strength are shown with thick triangular lines. In the right panel experimental observations of excitation energies and strengths are shown. Strengths of unobserved configurations are displayed at bottom.

• Figure 14 compares the number of states at $5.2< E_x< 7.2$ MeV for spins $1^-$, $2^-$, $3^-$, $4^-$, 5$^-$, $6^-$ to calculations. The dot at left shows the number of states up to $E_x=5.2$ MeV.

• Figure 15 compares the number of states at $2.5< E_x< 7.2$ MeV (a) with any parity and (b) with negative parity to calculations. The lowest curve in panel (b) displays known and calculated non-1p1h states with positive parity.

Fig. 16

Excitation functions for $^{208}\mathrm{Pb}$$({ p, p' })$ reproduced from (top) Fig. 7 and (bottom) Fig. 10 in [28]. For details see Sect.A.2.1

1.2 Figures 16 and 17

Figure 16 shows reproductions of Figs. 7, 8 in [28] (Sect. A.2.1), Fig. 17 reproductions of Figs.  10, 11 in [28] (Sect. A.2.2). The excitation energies have to be recalibrated by Eq. (14). Table 12 confirms the recalibration.

Open (close) circles are values taken at $\varTheta =90^\circ (100^\circ )$, triangles at $\varTheta =158^\circ$; the proton energies of the d $_{{ 5}/{2}}$, s $_{{ 1}/{2}}$, g $_{{ 7}/{2}}$, d $_{{ 3}/{2}}$ IARs are marked by an arrow [28].

In the following the states related to the original levels are described. In most cases a single state describes the essential cross section. The 6.232 + 6.255 doublet was already recognized, however the doublet contains four states resolved by the Q3D measurements (Table 15). Five more doublets were resolved after 2007 [47, 50]; in ten levels other states do not contribute significantly to the cross section; they mostly have positive parity (Table 15).

1.2.1 Figure 16

The top frame of Fig. 16 reproduces Fig. 7 in [28].

• (4.967) The 4974 $3^-_{6}$ state contains 31% d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ strength [55]. The admixture observed on the s $_{{ 1}/{2}}$ IAR is explained by a weak s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ component. Within the resolution of about 30 keV the 4953 $3^+$, 4962 $5^+$, 4996 $7^+$ states are unresolved [50]; they contribute little to the observed excitation function.

• (5.030) The 5038 $2^-_{3}$ state contains 59% d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ strength [55], see also Table 4 in [3]. The admixture observed on the s $_{{ 1}/{2}}$ IAR is explained by a weak s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ component. Within the resolution of about 30 keV neighboring 5010 9$^+$, 5040 $2^+$, 5069 10$^+$ states are unresolved [50]; they contribute little to the observed excitation function.

• (5.121) The 5127 $2^-_{4}$ state contains 33% d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ strength [55]. The admixture observed on the s $_{{ 1}/{2}}$ IAR is explained by a weak s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ component. Within the resolution of 30 keV the neighboring 5093 $8^+$ state is unresolved [50]; it contributes little to the observed excitation function.

• (5.804) Even with MLL Q3D magnetic spectrograph the doublet with the 5812 2$^-_{9}$ and 5813 $3^-_{15}$ states is unresolved. It was resolved by a sophisticated analysis of neighboring states [48].

  The 5813 $3^-$ state contains 12% g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength [55]. It explains the enhancement remarked as being due to the d $_{{ 3}/{2}}$ IAR in 40 keV distance. However a weak admixture with a weak d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ component in both states is certainly also present. Therefore the shape of excitation function deviates significantly from a Lorentzian near $E_p=17.4$ MeV.

  The very weak enhancement on the s $_{{ 1}/{2}}$ IAR may be explained by a small amplitude s $_{{ 1}/{2}}$p $_{{ 3}/{2}}$ in the 5812 $2^-_{9}$ state and s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ in the 5813 $3^-_{15}$ state.

  Within the resolution of about 30 keV the neighboring 5789 $3^+$, 5805 $1^-$, 5819 $2^+$, 5825 $8^+$, 5835 $8^-$, 5844 $1^+$ states are unresolved [50]; they contribute little to the observed excitation function.

• (5.869) The 5874 $3^-_{16}$ state contains 57% d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ strength [55]. Within the resolution of about 30 keV the neighboring states 5864 12$^+$ [12] and the unresolved 5901 9$^+$ state [50] contribute little to the observed excitation function. However the unresolved 5886 $4^-_{12}$ state contributes significantly.

  The admixture observed on the s $_{{ 1}/{2}}$ IAR is explained by a weak s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ component in the 5874 $3^-_{16}$ state. The admixture observed on the g $_{{ 7}/{2}}$ IAR is explained by a g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ component in both states (5874 $3^-_{16}$ and the 5886 $4^-_{12}$).

• (6.000) The 6010 $3^-_{17}$, 6012 $4^-_{14}$ doublet contains 29% d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ strength [55]. It was recently resolved [50]. The analysis of the angular distributions in the Heidelberg data from 1969 yields three amplitudes for each state (Sect. 4.1.7, Table 4). The large amplitudes with a g $_{{ 7}/{2}}$ particle in both states explains the strong enhancement of the excitation function on the g $_{{ 7}/{2}}$ IAR.

  The admixture observed on the s $_{{ 1}/{2}}$ IAR is explained by a weak s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ component in the 6010 $3^-_{17}$ state. Within the resolution of about 30 keV the neighboring 5989 $6^+$, 5993 $5^-$, 6023 $7^+$, 6026 $8^+$, 6037 $6^+$ states are unresolved [50]; they contribute little to the observed excitation function.

The bottom frame of Fig. 16 reproduces Fig. 10 in [28].

• (5.958) The 5969 $4^-_{13}$ state contains 85% g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength¹ Within the resolution of about 30 keV the neighboring 5937 $1^+$, 5947 $1^-$, 5957 $8^+$, 5973 $2^+$, 5981 $7^+$, 5989 $6^+$, 5993 5$^-$ states are unresolved [50]; they contribute little to the observed excitation function.

• (6.232+6.255) The doublet unresolved within the resolution of about 30 keV contains the 6243 $3^-_{20}$, 6275 3$^-_{21}$ and 6264 $1^-_{8}$ states (Tables 6, 8). The 6243 3$^-_{20}$ state contains no LJ p $_{{ 1}/{2}}$ strength; the 6264 $1^-_{8}$ state contains 4% s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$ and 5% d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strength [55]. The considerable enhancement on the g $_{{ 7}/{2}}$ IAR is explained by the strong g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ component in the 6264 $1^-_{8}$ state as well as in the 6275 $3^-_{21}$ state (Table 4).

  The admixture observed on the d $_{{ 5}/{2}}$ IAR is explained by weak d $_{{ 5}/{2}}$f $_{{ 5}/{2}}$ components in the three states.

  The 6256 $2^+$ and the 6217, 6220, 6223, 6234, 6250, 6277 states with unknown spin and unknown parity and the 6283 10$^-$ state contribute little to observed excitation function.

• (6.605) The strong enhancement on the g $_{{ 7}/{2}}$ IAR is explained by two states. The 6617 $3^-_{26}$ state contains a weak g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength [55] and a large g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ component, the 6631 $6^-_{12}$ a significant g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength. The s $_{{ 1}/{2}}$ IAR excites the 6617 $3^-_{26}$ state thus proving a s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ admixture.

  Within the resolution of about 30 keV the 6589 $2^-_{14}$ contributes insignificantly (less than 10 $\upmu$b/sr, see Table 4). The neighboring 6615 12$^-$ and 6597, 6603, 6609, 6619, 6633, 6637 unresolved states with unknown spin and unknown parity [50] contribute little to the observed excitation function.

• (6.681) The 6688 state is excited on the g $_{{ 7}/{2}}$ with the most extreme cross section. It does contain a very weak g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ component. A significant g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ component is concluded. Spin 4$^-$ is excluded by the large cross section (Table 3). It leads to the assignment as the $5^-_{18}$ state (Table 10). The angular distributions near the g $_{{ 7}/{2}}$ IAR exhibit weak admixtures of g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 7}/{2}}$ (Fig.  28, Table 4).

  Within the resolution of about 30 keV the unresolved 6682 $2^-$, 6699 $3^-$, 6708 $2^-$ states and the neighboring 6670, 6673, 6683, 6695 states with unknown spin and unknown parity (Table 15) contribute little to the observed excitation function.

Fig. 17

Excitation functions $^{208}\mathrm{Pb}$$({ p, p' })$ reproduced from (top) Fig. 8 and (bottom) Fig. 11 in [28]. For details see Sect. A.2.2

1.2.2 Figure 17

The top frame of Fig. 17 reproduces Fig. 8 in [28].

• (5.284) The 5.284 level contains the 5280 0$^-_{1}$ and 5292 $1^-_{2}$ states. They contain 65% and 108% d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ (i.e. almost the complete) strength [55], respectively. The admixture observed on the d $_{{ 5}/{2}}$ IAR is explained by a weak d $_{{ 5}/{2}}$f $_{{ 5}/{2}}$ component. Within the resolution of about 30 keV the unresolved neighboring 5286 $2^+$, 5317 $3^+$, 5318 $3^-$, 5327 9$^+$, 5339 8$^+$ states [50] contribute little to the observed excitation function.

• (6.304) The 6.304 level is a doublet with the 6314 1$^-_{9}$ state and the 6317 state with unknown spin. The 6314 $1^-$ state contains 7% s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$ strength [55]. The angular distributions near the d $_{{ 3}/{2}}$ IAR exhibit a strong admixture of d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ (Fig.  24, Table 4) explaining the admixture on the d $_{{ 3}/{2}}$ IAR. Within the resolution of about 30 keV the unresolved neighboring 6293 $3^-$, 6317, 6327, 6332, 6337 $3^-$ states (Table 15) contribute little to the observed excitation function.

The bottom frame of Fig. 17 reproduces Fig. 11 in [28].

• (5.914) The 5924 $2^-$ state contains 68% d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ strength [55]. Although the resolution was about 30 keV it was resolved from the 5947 $1^-$ state. The admixture observed on the s $_{{ 1}/{2}}$ IAR may be plained by a weak s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ component. Unresolved neighboring 5901 9$^+$, 5918 $4^+$, 5928 10$^+$, 5937 $1^+$ states [50] contribute little to the observed excitation function.

• (5.936) The 5947 $1^-$ state contains no s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$ admixture to 93% d $_{{ 5}/{2}}$p $_{{ 1}/{2}}$ strength [55]. Although the resolution was about 30 keV it was resolved from the 5924 $2^-$ state. Unresolved neighboring 5928 10$^+$, 5937 $1^+$ states [50] contribute little to the observed excitation function.

• (6.078) The level contains two states, the 6086 $2^-_{9}$ and the 6088 $3^-_{18}$ states [93] (Sect. 4.1.8). The observed $^{207}\mathrm{Pb}$$({ d, p})$ strength [50, 55] corresponds to 23% d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strength in the 6086 $2^-_{9}$ state or to 16% d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strength in the 6088 $3^-_{18}$ state (Sect. 4.1.8). The excitation observed on the s $_{{ 1}/{2}}$ IAR is explained by weak s $_{{ 1}/{2}}$f $_{{ 5}/{2}}$ components in both states. Within the resolution of about 30 keV the unresolved neighboring 6068 $5^+$, 6076 $1^-$, 6099 $4^+$ states [50] contribute little to the observed excitation function.

1.3 Figures 18, 19, 20 and  21

Spectra for $^{208}\mathrm{Pb}$$({ p, p' })$, $^{208}\mathrm{Pb}$$({ d, d' })$, $^{207}\mathrm{Pb}$$({ d, p})$ shown in Figs. 1819, 20 and 21 were fitted by GASPAN [86] with a Gaussian and an exponential tail [45]. The background is mostly described by a polynomial of first degree; it is displayed by a blue line. Each peak is fitted by a Gaussian of individual width with an exponential tail of common shape; it is displayed by a green curve.

Fig. 18

$^{208}\mathrm{Pb}$$({ p, p' })$ spectra taken for $6.3< E_x <7.3$ MeV on the s $_{{ 1}/{2}}$ IAR with the Q3D magnetic spectrograph at the MLL and fitted by GASPAN. Known negative parity states are identified (Table 15)

Fig. 19

$^{208}\mathrm{Pb}$$({ p, p' })$ spectra taken for $6.3< E_x7.2$ MeV near the g $_{{ 7}/{2}}$ IAR with the Q3D magnetic spectrograph at the MLL and fitted by GASPAN. Known negative parity states are identified (Table 15)

Fig. 20

$^{208}\mathrm{Pb}$$({ d, d' })$ spectra taken for $6.3< E_x7.1$ MeV with the Q3D magnetic spectrograph at the MLL and fitted by GASPAN. Known negative parity states are identified (Table 15)

The width is chosen as a linear function for peaks describing nuclear levels in lead isotopes because of the quadratic dependence on the magnetic field and the limited size of the spectrum. The widths for contamination peaks are varied freely. The fit of the total spectrum is shown by a red line.

For the fits shown in Figs. 22, 23 the option of fixed energies [45] was used (Sect. 3.3.1). Original data displaying spectra for $^{208}\mathrm{Pb}$$({ p, p' })$, $^{208}\mathrm{Pb}$$({ d, d' })$, $^{207}\mathrm{Pb}$$({ d, p})$ are available [57, 58].

• Figure 18 shows spectra taken with the MLL Q3D magnetic spectrograph for $^{208}\mathrm{Pb}$$({ p, p' })$ on the s $_{{ 1}/{2}}$ IAR with $E_p=16.96$ MeV at $6.3<E_x <7.3$ MeV.

• Figure 19 shows spectra taken with the MLL Q3D magnetic spectrograph for $^{208}\mathrm{Pb}$$({ p, p' })$ near the g $_{{ 7}/{2}}$ IAR with $E_p=17.30$ MeV at $6.3<E_x <7.2$ MeV.

• Figure 20 shows spectra taken with the MLL Q3D magnetic spectrograph for $^{208}\mathrm{Pb}$$({ d, d' })$ with $E_d=22$ MeV at $6.3<E_x <7.1$ MeV.

• Figure 21 shows spectra taken with the MLL Q3D magnetic spectrograph for $^{207}\mathrm{Pb}$$({ d, p})$ with $E_d=22$ MeV at $6.3<E_x <7.0$ MeV.

1.4 Figures 22 and 23

Original data displaying reconstructed spectra for $^{208}\mathrm{Pb}$$({ p, p' })$ fitted by GASPAN [86] are available [41, 42].

Figures 22 and 23 show reconstructed spectra taken in 1969 at the MPIK for $^{208}\mathrm{Pb}$$({ p, p' })$ on the d $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$ IARs at $6.0<E_x< 6.5$ and $6.5<E_x< 7.0$ MeV, respectively. The legend in the middle assists to find the levels corresponding to the states with spins from $1^-$ to $6^-$.

• Figure 22 shows reconstructed spectra taken for $^{208}\mathrm{Pb}$$({ p, p' })$ at $6.0<E_x< 6.5$ MeV (top) on the d $_{{ 5}/{2}}$ IAR, and (bottom) on the g $_{{ 7}/{2}}$ IAR. Contaminations from $({ p, t})$ and $({ p, d})$ are identified with the 6128.2, 6136.4 levels. Both the 6010 $3^-_{17}$, 6012 $4^-_{14}$ doublet (Sect. 4.1.7) and the 6086 $2^-$, 6088 $3^-$ doublet (Sect. 4.1.8) are not resolved. The 6264 $1^-_{ 8}$, 6275 $3^-_{21}$, 6314 $1^-_{ 9}$, 6337 3$^-_{23}$, 6354 $5^-_{17}$, 6362 $1^-_{10}$ states are distinguished by the different excitation near the d $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$ IARs. The 6389 $5^-_{18}$ is well isolated. The 6420 $2^-_{12}$, 6452 $4^-_{15}$, 6462 $6^-_{ 9}$ states are distinguished by the different excitation near the d $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$ IARs. The 6486 $1^-_{11}$ is well isolated. The 6529 $4^-_{16}$, 6541 $6^-_{11}$, 6552 $2^-_{13}$ states are distinguished by the different excitation near the d $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$ IARs.

• Figure 23 shows reconstructed spectra taken for $^{208}\mathrm{Pb}$$({ p, p' })$ at $6.5<E_x< 7.0$ MeV (top) on the d $_{{ 5}/{2}}$ IAR, and (bottom) on the g $_{{ 7}/{2}}$ IAR. Contaminations from $({ p, t})$ and $({ p, d})$ are identified in the top frame with the 6592.4, 6868.0 levels. The 6589 $2^-_{14}$, 6617 $3^-_{27}$, 6631 $6^-_{12}$ states are distinguished by the different excitation near the d $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$ IARs. The contamination from $^{208}\mathrm{Pb}$$({ p, d})$ near the d $_{{ 5}/{2}}$ IAR could be discriminated (Sect. 3.2.1). The 6657 $2^-_{15}$ and 6688 $5^-_{20}$ states are well isolated. The 6720 $1^-_{13}$ and 6739 $4^-_{19}$ states are well resolved. The 6777 $6^-_{13}$, 6789 $2^-_{17}$, 6801 $4^-_{16}$, 6820 3$^-_{29}$ states states are distinguished by the different excitation near the d $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$ IARs. The 6868 $2^-_{18}$, 6878 $5^-_{21}$, 6878 $5^-_{21}$ states are distinguished by the different excitation near the d $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$ IARs. The contamination from $^{208}\mathrm{Pb}$$({ p, d})$ near the d $_{{ 5}/{2}}$ IAR could be discriminated (Sect. 3.2.1). The 6929 $2^-_{18}$, 6944 $4^-_{17}$, 6969 $2^-_{20}$ states are distinguished by the different excitation near the d $_{{ 5}/{2}}$ and g $_{{ 7}/{2}}$ IARs.

1.5 Figures 24, 25, 26, 27, 28, 29, 30 and 31

Figures 24 , 25, 26, 27, 28, 29, 30 and 31 show angular distributions for $^{208}\mathrm{Pb}$$({ p, p' })$ reconstructed (Sect. 3.2.1) from data taken with semiconductor detectors in 1969 at the MPIK. The evaluated experimental data are presented in [42].

The ordinate is chosen in units of the mean cross section $\bar{\sigma }$ [Eq. (8)], mostly from 0 to 1.5 $\bar{\sigma }$, otherwise from 0 to 3 ${\bar{\sigma }}$; the value 1 $\bar{\sigma }$ [Eq. (5)] is shown by the dotted line.

Some cross sections are exceeding the scale for various reasons, either the level contains another state not well discriminated or the level is close to a contamination line not well separated. Two doublets are discussed separately (Sects. 4.1.7, 4.1.8).

Instead of the scattering angle $\varTheta$ the Legendre polynomial $P_2(\cos \varTheta )$ is chosen as abscissa (Sect. 2.2.5). The legend for the abscissa is omitted but the values $P_2(\cos \varTheta )$ are marked for $\varTheta =120^\circ$ and $140^\circ$ similar to Fig. 3.

For each state $\left| {\tilde{E}}_x, I^\pi \right\rangle$ [Eq. (1)] amplitudes $c_{LJ\,lj} ^{{\tilde{E}}_x,I^\pi }$ are determined where the particle is either $LJ={ g}{_{{ 7}/{2}}}$ (“gS”) or $LJ={ d}{_{{ 3}/{2}}}$ (“dT”) and the holes $lj={ p}{_{{ 1}/{2}}}$, p $_{{ 3}/{2}}$, f $_{{ 5}/{2}}$, f $_{{ 7}/{2}}$, h $_{{ 9}/{2}}$ described as “pO, pT, fF, fS, hN”.

For each angular distribution two calculations of $^{208}\mathrm{Pb}$$({ p, p' })$ via either the g $_{{ 7}/{2}}$ or the d $_{{ 3}/{2}}$ IAR were chosen to yield reasonable fits tabulated in Table 4. The result from the drawn curve with up to four amplitudes is considered as the best approximation. The result from the dotted curve with the reversed (excluded) sign for one amplitude tabulated within brackets is excluded; it explains the high sensitivity of the method (Sect. 3.3.4).

In Figs. 24 , 25, 26, 27, 28, 29, 30 and 31 the value LJ of the particle (the IAR) and the chosen proton energy $E_p$, the energy label ${\tilde{E}}_x$ and the spin $I^\pi$ [Eq. (1)], the mean cross section $\sigma$ [Eq. (5)] for the proton energies $E_p=17.40,$ 17.47, 17.75 MeV in units of $\upmu$b/sr, the values lj of the considered holes, and the amplitudes of the configurations $LJ \,lj$ multiplied by a factor 100 are written down. Table 4 additionally displays the deselected set of amplitudes with one reverse sign in parentheses.

In Figs. 24, 30, 31 the factors $\alpha$ and $\sqrt{1 -\alpha ^2}$ [Eq. (22)] are indicated, see Sects. 4.1.4, 4.1.7 and 4.1.8, respectively.

• Figure 24 shows angular distributions for states assigned spin $1^-$. Relatively good fits succeeded for all five known states. For the 6264 state an equal excitation on both the g $_{{ 7}/{2}}$ and d $_{{ 3}/{2}}$ IARs is determined (Sect. 4.1.4). Admixtures to the 5947 $1^-_{ 6}$ state with dominant d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strength are determined with 1% d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ and 4% d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ (Tables 4, 5).

• Figure 25 shows angular distributions for states assigned spin $2^-$. Among the nine known $2^-$ states at $E_x>6.2$ MeV relatively good fits of the angular distributions succeeded for eight states. The fits for the 6589 and 6868 states are poor and not shown, the results are included in Table 4. For the 6682 state data are insufficient. Admixtures to the 5924 $2^-_{13}$ state with dominant d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ strength are determined with less than 4% d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$ and d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$ (Tables 4, 5).

• Figure 26 shows angular distributions for states assigned spin $3^-$. Among the nine known $3^-$ states at $E_x<6.2$ MeV the angular distributions for two states succeeded in relatively good fits. The 6243, 6739 states are newly assigned spin $3^-$ (Sect. 4.2.3). Admixtures to the 5874 $3^-_{13}$ with dominant g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength are determined with about 15% g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ (Table 4).

• Figure 27 shows angular distributions for states newly assigned spin $4^-$. Admixtures to the 5969 $4^-_{13}$ with dominant g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ strength are determined with less than 4% g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ (Tables 4, 5).

• Figure 28 shows angular distributions for states newly assigned assigned spin $5^-$; the 6688 state with dominant g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ strength was already identified [28, 40], see Fig. 17; admixtures of g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ are determined (Tables 4, 5). Even four amplitudes may be determined in the 6389 $5^-$ state with $E_p=17.47$ MeV, $-0.00\pm 0.02, +0.59\pm 0.01, +0.06\pm 0.02, +0.20\pm 0.10$ [Eq. (19)], $-0.03, +0.77, +0.13, -0.20$ (Table 4, Fig. 28), ${<}0.05, +0.60, +0.20, -20$ [9] for $g_{7/2} p_{3/2} g_{7/2} f_{5/2}, g_{7/2}f_{7/2}, g_{7/2} h_{9/2}$. The weak amplitude for g$_{7/2} p_{3/2}$ and the relative signs are relevant, the amplitude for g$_{7/2} h_{9/2}$ is uncertain but weak.

• Figure 30 shows angular distributions for the unresolved doublet at $E_x=6.01$ MeV (at left) with spin $3^-$ and (at right) with spin $4^-$. The 6010 $3^-_{17}$ and 6012 $4^-_{14}$ states are discussed in Sect. 4.1.7.

• Figure 31 shows angular distributions for the unresolved doublet at $E_x=6.09$ MeV with the 6086 2$^-_{9 }$ and 6088 $3^-_{18}$ states in Sect. 4.1.8.

Tables

The experimental uncertainties in Tables 1 and 2 are shown in the given references. They are not relevant for this work because of much larger systematic uncertainties which are not discussed in detail.

The strengths in Tables 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14 derive from Table 4. Systematic uncertainties are estimated in the order of several percent.

Fig. 21

$^{207}\mathrm{Pb}$$({ d, p})$ spectra taken for $6.3< E_x7.0$ MeV with the Q3D magnetic spectrograph at the MLL and fitted by GASPAN. Known negative parity states are identified (Table 15)

Fig. 22

Spectra for $^{208}\mathrm{Pb}$$({ p, p' })$ taken in 1969 at the MPIK at $6.0<E_x< 6.6$ MeV (top) on d $_{{ 5}/{2}}$ IAR, (bottom) near g $_{{ 7}/{2}}$ IAR. The spectra are fitted by GASPAN. For details see Sect. A.4

Fig. 23

Figure 22 continued for $6.5<E_x< 7.0$ MeV

Fig. 24

Angular distribution of $^{208}\mathrm{Pb}$$({ p, p' })$ for states assigned spin $1^-$. The description of the x- and y-axes is omitted for clarity. The x-axis is given by the Legendre polynomial of second degree running from $P_2(\cos (90^ \circ ))$ to $P_2(\cos (180^ \circ ))$, see Fig. 3; the values $P_2(\cos (120^ \circ ))$ and $P_2(\cos (140^ \circ ))$ are indicated at bottom. The y-axis is in relative units; the scale from 0 to 1.5 relative units is shown by a thick line at left. The value with relative units of 1.0 is shown by the dotted line, a scale is drawn at the right side. The values LJ, lj for the particles and holes are shown as dT for d $_{{ 3}/{2}}$, gS for g $_{{ 7}/{2}}$, pT for p $_{{ 1}/{2}}$, pT for p $_{{ 3}/{2}}$, fF for f $_{{ 5}/{2}}$, fS for f $_{{ 7}/{2}}$, hN for h $_{{ 9}/{2}}$. The amplitudes are multiplied by a factor 100. The mean cross section $\sigma$ [Eq. (8)] is shown with $\sigma$ in units of $\upmu$b/sr. In the fit of the 6264 state the factors $\alpha$ and $\sqrt{1 -\alpha ^2}$ [Eq. (22)] indicated with “)*” are applied to the amplitudes (Sect. 4.1.4). For more details see Sects. 4.1, A.5

Fig. 25

Angular distribution of $^{208}\mathrm{Pb}$$({ p, p' })$ for states assigned spin $2^-$. For details see Sect. A.5

Fig. 26

Angular distribution of $^{208}\mathrm{Pb}$$({ p, p' })$ for states assigned spin $3^-$. For details see Sect. A.5

Fig. 27

Angular distribution of $^{208}\mathrm{Pb}$$({ p, p' })$ for states assigned spin $4^-$. For details see Sect. A.5

Fig. 28

Angular distribution of $^{208}\mathrm{Pb}$$({ p, p' })$ for states assigned spin $5^-$. For details see Sect. A.5

Fig. 29

Angular distribution of $^{208}\mathrm{Pb}$$({ p, p' })$ for states assigned spin $6^-$. For details see Sect. A.5

Fig. 30

Angular distributions of $^{208}\mathrm{Pb}$$({ p, p' })$ for the doublet with the 6010 3$^-$/6012 $4^-$ states. For details see Sects. 4.1.7, A.5

Fig. 31

Angular distributions of $^{208}\mathrm{Pb}$$({ p, p' })$ for the doublet with the 6086 2$^-$/6088 $3^-$ states. For details see Sects. 4.1.8, A.5

Table 15 Levels in $^{208}\mathrm{Pb}$ at $6.20<E_x<7.00$ MeV observed in spectra taken in 1969 (Sect. 3.1) and reconstructed (Sect. 3.2.1) for $^{208}\mathrm{Pb}$$({ p, p' })$ at $E_p=17.40, 17.47, 17.75$ MeV. Most enumerated levels are unresolved doublets in the original data [39] (marked by a vertical bar). The favored identification with a certain state observed after 2003 for $^{208}\mathrm{Pb}$$({ p, p' })$, $^{208}\mathrm{Pb}$$({ d, d' })$, and $^{207}\mathrm{Pb}$$({ d, p})$ (Sect. 3.1) is based on spin and parity either known (Sect. 4.1) or deduced by this work (Sect. 4.2). Levels observed by Wagner et al. [87] and Valnion [55] are included. Levels at $7.00<E_x<7.15$ MeV are included because they were used for the calibration (Sect. 3.2.1)

• Table 1 shows parameters for IARs in $^{209}\mathrm{Bi}$  (Sects. 2.2.1, 3.3.5).

• Table 2 shows s.p. widths (Sects. 2.2.1, 3.3.5).

• Table 3 compares the predictions of excitation energies calculated by the SDI to results from the fit of the angular distributions for 40 states (Figs.  24, 25, 26, 27, 28, 29, 30 and 31).

• Table 4 shows excitation energies and amplitudes of 1p1h configurations for states discussed in this paper. For 40 states mostly three amplitudes are determined. The relative signs of the amplitudes are neatly determined in most cases; the alternate (excluded) sign shown in Figs.  29, 30 and 31 is given in parentheses, see Sect. 3.3.4.

  Spin assignments of $1^-$, $2^-$, and $3^-$ were done previously (Sect. 4.1) except for the new assignments of spin 3$^-$ to the 6243, 6337 states (Sect. 4.2). New spins are assigned to the 6452 $4^-$, 6529 $4^-$, 6739 $4^-$, 6801 $4^-$, 6944 $4^-$, 6354 $5^-$, 6389 $5^-$, 6878 $5^-$, 6462 $6^-$, 6541 6$^-$, 6631 $6^-$, 6777 $6^-$ states, the early recognized 6688 5$^-$ state is verified (Sect. 4.2).

  The amplitudes from the $^{207}\mathrm{Pb}$$({ d, p})$ analysis [55] with the s $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$ particle and a p $_{{ 1}/{2}}$ hole are weak, states at $5.8<E_x< 6.2$ MeV with major strength of s $_{{ 1}/{2}}$p $_{{ 1}/{2}}$, d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$, and g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ are included (Cols. 6-9). In most cases the fit of the angular distributions for $^{208}\mathrm{Pb}$$({ p, p' })$ yielded similar amplitudes for g $_{{ 7}/{2}}$p $_{{ 1}/{2}}$ and d $_{{ 3}/{2}}$p $_{{ 1}/{2}}$ (Cols. 10 and 15, respectively).

• Table 5 shows the strengths $c^2$ for the states tabulated in Table 4.

• Tables 6, 7, 8, 9, 10 and 11 show calculated excitation energies and cross sections for states with pure configurations d $_{{ 3}/{2}}$p $_{{ 3}/{2}}$, g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$. g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$, and d $_{{ 3}/{2}}$f $_{{ 5}/{2}}$. The detected sum of the strengths of states with these configurations are shown and illustrated in Figs. 8, 9, 10, 11, 12 and 13.

• Table 12 compares results obtained fifty years ago to recent results.

• Table 13 shows the distribution of the g $_{{ 7}/{2}}$p $_{{ 3}/{2}}$ and g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strengths for the $4^-$ states at $6.0<E_x< 7.0$ MeV.

• Table 14 shows the distribution of the g $_{{ 7}/{2}}$f $_{{ 5}/{2}}$ strength for the $6^-$ states at $5.6<E_x< 7.0$ MeV.

• Table 15 shows the excitation energies of states observed by various experiments in the range $6.20<E_x< 7.15$ MeV. The levels used for the calibration at $6.20<E_x<7.0$ MeV are enumerated assuming one level to cover about 4.0 keV in excitation energy. The resolution in the $^{208}\mathrm{Pb}$$({ p, p' })$ reaction studied in 1969 [39] is about 12 keV. In the fit of the 1969 spectra by GASPAN the option of fixed energies was used [45] (Sect. 3.2.1).

  The resolution of about 12 keV is insufficient to clarify the identity of states completely. For this reason it does not make sense to show the uncertainties of the experimental values derived from the $^{208}\mathrm{Pb}$$({ p, p' })$, $^{207}\mathrm{Pb}$$({ d, p})$, $^{208}\mathrm{Pb}$$({ d, d' })$ reactions by [55, 56, 87] and by this work. The mean magnitude of the uncertainties is given as footnotes. This table continues Table VI in [50] for $0\le E_x<6.2$ MeV to $6.2< E_x<7.15$ MeV. Below $E_x<7.15$ MeV in total about 300 states are now identified in $^{208}\mathrm{Pb}$.