Charge Conjugation Symmetry in the Finite Basis Approximation of the Dirac Equation

Abstract

Four-component relativistic atomic and molecular calculations are typically performed within the no-pair approximation where negative-energy solutions are discarded. These states are, however, needed in QED calculations, wherein, furthermore, charge conjugation symmetry, which connects electronic and positronic solutions, becomes an issue. In this work, we shall discuss the realization of charge conjugation symmetry of the Dirac equation in a central field within the finite basis approximation. Three schemes for basis set construction are considered: restricted, inverse, and dual kinetic balance. We find that charge conjugation symmetry can be realized within the restricted and inverse kinetic balance prescriptions, but only with a special form of basis functions that does not obey the right boundary conditions of the radial wavefunctions. The dual kinetic balance prescription is, on the other hand, compatible with charge conjugation symmetry without restricting the form of the radial basis functions. However, since charge conjugation relates solutions of opposite value of the quantum number $\kappa$, this requires the use of basis sets chosen according to total angular momentum j rather than orbital angular momentum ℓ. As a special case, we consider the free-particle Dirac equation, where opposite energy solutions are related by charge conjugation symmetry. We show that there is additional symmetry in that solutions of the same value of $\kappa$ come in pairs of opposite energy.

1. Introduction

Consider an electron of charge $q=-e$ and mass $m_e$, placed in an attractive Coulomb potential $\varphi (r)$. Upon solving the time-independent Dirac equation, one gets a set of solutions ${\psi }_i$ associated with energy levels $E_i$ which forms the spectrum that is shown in a pictorial way in Figure 1a. The charge conjugation operation [1] (C-operation) relates a particle to its anti-particle. The C-conjugated solution $C{\psi }_i$, describes the solution of the same equation but with opposite charge (a positron), flipping the spectrum, as shown in Figure 1c. In the free-particle case, $\varphi (r)=0$, the two spectra, left and right, coalesce into the spectrum in Figure 1b, that contains no bound solutions, and where the C-operation relates positive and negative-energy solutions of the same equation; i.e., $C{\psi }_{\pm E_i}={\psi }_{\mp E_i}$. Note that since the free-particle equation does not require the specification of the charge, it describes, equally well, electrons and positrons.

The Dirac equation is the starting point for four-component relativistic atomic and molecular calculations. In the former case, the high symmetry of the problem allows the use of finite difference methods, whereas molecular applications generally call for the use of finite-basis expansions. Early calculations using finite bases were flawed, since the coupling of the large and small components was not respected. Spurious solutions appeared, and the calculations were converging to energy levels lower than they were meant to. It was observed by Schwarz and Wallmeier [2] and Grant [3] that in such calculations, the matrix representation of the kinetic energy operator obtained in the non-relativistic limit of the Dirac equation did not match the Schrödinger one. It was realized that if the small components’ basis functions are generated from the large component ones by ${\phi }_i^S\propto \sigma ·\mathit{p}{\phi }_i^L$, where $\sigma$ are the Pauli spin matrices, then the non-relativistic limit of the kinetic energy operator goes directly into the Schrödinger one, and the spurious states disappear. This was further analyzed and formalized under the name of kinetic balance by Stanton and Havriliak [4] (see also [5]). Calculations using this prescription were first done by Lee and McLean [6] (using unrestricted kinetic balance; see Section 2.3.3) and Ishikawa et al. [7].

Present-day four-component relativistic atomic and molecular calculations are typically carried out within the no-pair approximation [8,9], where the electronic Hamiltonian is embedded by operators projecting out negative-energy orbitals, hence treating them as an orthogonal complement. However, going beyond the no-pair approximation and considering the effects of quantum electrodynamics (QED)—notably, vacuum polarization and the self-energy of the electron—the negative-energy solutions take on physical reality and require a proper description. Charge conjugation symmetry also becomes an issue [10,11] and has to be considered when designing basis sets.

In the present work, we investigate the realization of charge conjugation symmetry, in short, C-symmetry, of the one-electron Dirac equation within the finite basis approximation. Since basis functions are typically located at nuclear positions, we limit attention to the central field (spherically symmetric) problem. We shall consider three schemes for basis set construction: restricted kinetic balance [4,12], inverse kinetic balance [13], and dual kinetic balance [14]. As such, our work bears some resemblance to the study of Sun et al. [13], who carried out a formal comparison and numerical assessment of these schemes in the framework of conventional relativistic electronic structure calculations. Our focus will be on whether these schemes allow the realization of charge conjugation symmetry for possible use beyond the no-pair approximation. We shall also analyze more specifically the basis set requirements, with particular attention paid to Gaussian-type functions.

2. Theory

2.1. The Dirac Equation and C-Symmetry

The relativistic behavior of an electron placed in an electromagnetic potential ($\varphi ,\mathit{A}$) is described by the Dirac equation:

$$({\widehat{h}}_{-e}-i\hslash {\partial }_t)\psi (\mathit{r},t)=0;{\widehat{h}}_q=\beta m_e{c}^2+c\mathit{\alpha }·[\mathit{p}-q\mathit{A}]+q\varphi (r)$$

(1)

where

$${\alpha }_i=\left[\begin{array}{cc}0& {\sigma }_i\\ {\sigma }_i& 0\end{array}\right]and\beta =\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$$

(2)

are the Dirac matrices, anti-commuting amongst themselves.

Dirac himself noted that if matrices ${\alpha }_y$ and $\beta$ are swapped, then the complex conjugate of a solution to Equation (1) will be the solution of the same equation, but with opposite charge [15]. Kramers coined the term charge conjugation for this symmetry linking particles and their anti-particles [1], and it has later been elevated to one of the three fundamental symmetries of nature through the CPT theorem [10,16,17,18].

In the Dirac representation, the $\mathcal{C}$-operator is given by

$$\mathcal{C}=i\beta {\alpha }_y{\mathcal{K}}_0=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& -1& 0\\ 0& -1& 0& 0\\ 1& 0& 0& 0\end{array}\right]{\mathcal{K}}_0,$$

(3)

where ${\mathcal{K}}_0$ is the complex conjugation operator. The general form was investigated by Pauli [19]. For static potentials, the solution of Equation (1) has the form $\psi (\mathit{r},t)=\psi (\mathit{r})exp\left[-iEt/\hslash \right]$, where $\psi (\mathit{r})$ satisfies the time-independent Dirac equation

$${\widehat{h}}_{-e}\psi (\mathit{r})=E\psi (\mathit{r}).$$

(4)

Since the action of the charge conjugation operation is $\mathcal{C}{\widehat{h}}_{-e}{\mathcal{C}}^{-1}=-{\widehat{h}}_{+e}$, we get the time-independent positronic equation as

$$\begin{array}{cc}\hfill {\widehat{h}}_{+e}\mathcal{C}\psi (\mathit{r})& =-E\mathcal{C}\psi (\mathit{r}),\hfill \end{array}$$

(5)

with the opposite sign of the energy. In passing, we note that the charge conjugation operator can be expressed as $\mathcal{C}={\gamma }_5\beta \mathcal{K}$, where $\mathcal{K}$ is the time-reversal operator.

2.2. Radial Problem

We shall limit attention to the central-field case, with the vector potential $\mathit{A}=\mathit{0}$, and a radial scalar potential $\varphi (r)$. Solutions then have the general form

$${\psi }_{\kappa ,m_j}(\mathit{r})=\frac{1}{r}\left[\begin{array}{c}{P}_{\kappa }(r){\Omega }_{\kappa ,m_j}(\theta ,\varphi )\\ i{Q}_{\kappa }(r){\Omega }_{-\kappa ,m_j}(\theta ,\varphi )\end{array}\right],$$

(6)

where the imaginary number i is introduced to make both radial functions $P_{\kappa }$ and $Q_{\kappa }$ real. The ${\Omega }_{\kappa ,m}$ are two-component complex eigenfunctions of the $\widehat{\kappa }=-\hslash -\sigma ·\widehat{\ell }$ operator [20], and $\kappa$ represents the corresponding eigenvalue. After separation of radial and angular variables, we obtain the radial Dirac equation

$${\widehat{h}}_{-e,\kappa }{\phi }_{\kappa }(r)=E{\phi }_{\kappa }(r);{\widehat{h}}_{-e,\kappa }=\left[\begin{array}{cc}{m}_e{c}^2-e\varphi (r)& -c\hslash [\frac{d}{dr}-\frac{\kappa }{r}]\\ c\hslash [\frac{d}{dr}+\frac{\kappa }{r}]& -m_e{c}^2-e\varphi (r)\end{array}\right],{\phi }_{\kappa }(r)=\left[\begin{array}{c}{P}_{\kappa }\\ Q_{\kappa }\end{array}\right].$$

(7)

The $\mathcal{C}$-operation shown in Equation (3), when applied to the spherical solution, Equation (6), gives [21]

$$\mathcal{C}{\psi }_{\kappa ,m_j}=i{S}_{\kappa }{(-1)}^{m_j+\frac{1}{2}}\frac{1}{r}\left[\begin{array}{c}{Q}_{\kappa }{\Omega }_{-\kappa ,-m_j}\\ i{P}_{\kappa }{\Omega }_{\kappa ,-m_j}\end{array}\right],\mathrm{with}{S}_{\kappa }=\frac{\kappa }{\left|\kappa \right|}.$$

(8)

We observe that the $\kappa$ and $m_j$ quantum numbers in the angular parts have switched sign, and that the radial components are swapped; that is, $P_{\kappa }\rightleftarrows Q_{\kappa }$.

Free-Particle Radial Problem

Usually, the free-particle Dirac equation solutions are presented in the form of plane waves. However, we are interested in atomic (and molecular) calculations where we use spherical basis functions centered at the nuclear positions. It is, therefore, more appropriate to consider the free-particle solutions in spherical symmetry. By setting $\varphi (r)=0$ in the radial Dirac equation (Equation (7)), the solution of this problem is found to be [21,22]

$$\begin{array}{cc}\hfill {\psi }_{\kappa m_j}(r,E)& =\sqrt{\frac{1}{c^3{\hslash }^3\pi }}\left[\begin{array}{c}{\psi }_{\kappa m_j}^L(r,E)\\ {\psi }_{\kappa m_j}^S(r,E)\end{array}\right],\hfill \end{array}$$

(9)

where the large and the small components (upper and lower) are respectively given by

$$\begin{array}{cc}\hfill {\psi }_{\kappa m_j}^L(r,E)& =|E-m_e{c}^2{|}^{\frac{1}{4}}{|E+m_e{c}^2|}^{\frac{3}{4}}{j}_{|\kappa +\frac{1}{2}|-\frac{1}{2}}(kr){\Omega }_{\kappa ,m_j},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\psi }_{\kappa m_j}^S(r,E)& =i{S}_{\kappa }{S}_E|E+m_e{c}^2{|}^{\frac{1}{4}}{|E-m_e{c}^2|}^{\frac{3}{4}}{j}_{|\kappa -\frac{1}{2}|-\frac{1}{2}}(kr){\Omega }_{-\kappa ,m_j},\hfill \end{array}$$

(11)

where $j_{\ell }$ are the spherical Bessel functions of the first kind, $S_x=\frac{x}{\left|x\right|}$ is the sign function, and $k(E)=\sqrt{E^2-m_e^2{c}^4}/c\hslash$ represents the wavenumber. These solutions are normalized to the delta function

$$\int {\psi }_{\kappa ,m_j}^{†}(\mathit{r},E){\psi }_{{\kappa }^{\prime },m_j^{\prime }}(\mathit{r},E^{\prime })d^3\mathit{r}={\delta }_{\kappa {\kappa }^{\prime }}{\delta }_{m_j{m}_j^{\prime }}\delta (E-E^{\prime })$$

(12)

as they describe a continuum of solutions.

By next applying the $\mathcal{C}$-operator to the free-particle solution, we get the C-conjugated partner

$$\mathcal{C}{\psi }_{\kappa m_j}(r,E)=i{(-1)}^{m_j+\frac{1}{2}}{S}_E\sqrt{\frac{1}{c^3{\hslash }^3\pi }}\left[\begin{array}{c}|E+m_e{c}^2{|}^{\frac{1}{4}}{|E-m_e{c}^2|}^{\frac{3}{4}}{j}_{|\kappa -\frac{1}{2}|-\frac{1}{2}}(kr){\Omega }_{-\kappa ,-m_j}\\ S_E{S}_{\kappa }i|E-m_e{c}^2{|}^{\frac{1}{4}}{|E+m_e{c}^2|}^{\frac{3}{4}}{j}_{|\kappa +\frac{1}{2}|-\frac{1}{2}}(kr){\Omega }_{\kappa ,-m_j}\end{array}\right].$$

(13)

We thereby see that it is possible to connect opposite energy solutions, in spherical symmetry, by the C-operation (as we expect from the trivial Dirac plane wave case)

$$\mathcal{C}{\psi }_{\kappa ,m_j}(r,E)=i{(-1)}^{m_j+\frac{1}{2}}{S}_E{\psi }_{-\kappa ,-m_j}(r,-E).$$

(14)

Details about the C-symmetry and the free electron in the spherical case can be found in [21,22,23].

2.3. Finite Basis Approximation

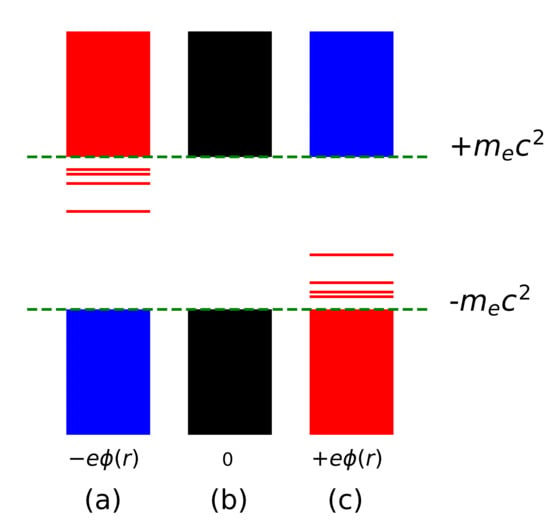
Generally, the plan is to specify a finite number of basis functions, construct the matrix representation of the Dirac equation, and then diagonalize it to get the set of eigenfunctions and eigenvectors. We start by introducing radial basis sets for the large and the small components, ${\{{\pi }_i^{L_{\kappa }}\}}_{i=1}^{n_L}$ and ${\{{\pi }_i^{S_{\kappa }}\}}_{i=1}^{n_S}$ (for each $\kappa$), which means that the radial functions $P_{\kappa }$ and $Q_{\kappa }$ are expanded as

$$P_{\kappa }(r)=\sum _i^{n_L}{c}_{\kappa ,i}^L{\pi }_i^{L_{\kappa }}(r);Q_{\kappa }(r)=\sum _i^{n_S}{c}_{\kappa ,i}^S{\pi }_i^{S_{\kappa }}(r),$$

(15)

giving the matrix representation of the Dirac equation as

$$H_{-e,\kappa }{c}_{\kappa }=S_{\kappa }{c}_{-e,\kappa }{ϵ}_{-e,\kappa },$$

(16)

with

$$\begin{array}{cc}\hfill H_{-e,\kappa }& =\left[\begin{array}{cc}{m}_e{c}^2{S}^{L_{\kappa }{L}_{\kappa }}-e{\varphi }^{L_{\kappa }{L}_{\kappa }}& c\hslash {\Pi }_{\kappa }^{L_{\kappa }{S}_{\kappa }}\\ -c\hslash {\Pi }_{-\kappa }^{S_{\kappa }{L}_{\kappa }}& -m_e{c}^2{S}^{S_{\kappa }{S}_{\kappa }}-e{\varphi }^{S_{\kappa }{S}_{\kappa }}\end{array}\right],\hfill \\ \hfill S_{\kappa }& =\left[\begin{array}{cc}{S}^{L_{\kappa }{L}_{\kappa }}& 0\\ 0& S^{S_{\kappa }{S}_{\kappa }}\end{array}\right],{\mathit{c}}_{-e,\kappa }={\left[\begin{array}{c}{\mathit{c}}^L\\ {\mathit{c}}^S\end{array}\right]}_{-e,\kappa }.\hfill \end{array}$$

(17)

The matrix elements of the above submatrices are given by

$$\begin{array}{cc}\hfill {[S^{X_{\kappa }{X}_{\kappa }}]}_{ij}& ={\int }_0^{\infty }{\pi }_i^{X_{\kappa }}(r){\pi }_j^{X_{\kappa }}(r)dr,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {[{\varphi }^{X_{\kappa }{X}_{\kappa }}]}_{ij}& ={\int }_0^{\infty }{\pi }_i^{X_{\kappa }}(r)\varphi (r){\pi }_j^{X_{\kappa }}(r)dr,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {[{\Pi }_{{\kappa }^{\prime }}^{X_{\kappa }{Y}_{\kappa }}]}_{ij}& =-{\int }_0^{\infty }{\pi }_i^{X_{\kappa }}(r)[\frac{d}{dr}-\frac{{\kappa }^{\prime }}{r}]{\pi }_j^{X_{\kappa }}(r)dr.\hfill \end{array}$$

(20)

We note that the $\kappa$ appearing in superscripts refers to the radial basis functions, whereas the ${\kappa }^{\prime }$ appearing as a subscript is associated with the operator. We also note that the $-e$ term appearing in the subscripts denotes the charge that appears in front of the scalar potential. Since we expect a (real) Hermitian matrix representation, the off-diagonal matrices should be related by the transpose operation; ${\Pi }_{\kappa }^{L_{\kappa }{S}_{\kappa }}=-{[{\Pi }_{-\kappa }^{S_{\kappa }{L}_{\kappa }}]}^T$. Using integration by parts, this implies that that the basis functions should vanish at the boundaries; $r=0$ and $r\to \infty$.

2.3.1. Gaussian-Type Functions

We shall work with Gaussian-type functions, since they play a central role in quantum chemical calculations. The large and the small component radial Gaussian functions are given by

$$\begin{array}{cc}\hfill {\pi }_i^{L_{\kappa }}& ={\mathcal{N}}_i^{L_{\kappa }}{r}^{{\gamma }_p}{e}^{-{\zeta }_i^{\kappa }{r}^2}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\pi }_i^{S_{\kappa }}& ={\mathcal{N}}_i^{S_{\kappa }}{r}^{{\gamma }_q}{e}^{-{\zeta }_i^{\kappa }{r}^2},\hfill \end{array}$$

(22)

with ${\mathcal{N}}_i^{X_{\kappa }}$ the normalization constants. We choose the exponents ${\gamma }_p$ and ${\gamma }_q$ to reproduce the small r behavior of the radial functions in the case of a finite nucleus [21]; that is,

$${\gamma }_p=|\kappa +\frac{1}{2}|+\frac{1}{2};{\gamma }_q=|\kappa -\frac{1}{2}|+\frac{1}{2}.$$

(23)

This also corresponds to the small r behavior of the free-particle radial solutions (Equations (10) and (11)). Furthermore, Sun et al., in calculations on $R{n}^{85+}$ using the dual kinetic balance prescription (discussed later in Section 2.3.4), investigated the use of different integer powers ${\gamma }_p$ and ${\gamma }_q$ of r for large and small Gaussian-type functions [13] and concluded that optimal results, in particular, avoiding variational collapse and divergent integrals, were obtained using the powers given in Equation (23).

2.3.2. C-Symmetry in The Finite Basis Approximation

We say that a basis set respects C-symmetry, thereby leading to a C-symmetric matrix representation, if the C-conjugation of all the elements of the basis set belongs to the basis set itself

$$\forall \phi \in {\left\{{\phi }_i\right\}}_{i=1}^n,\mathcal{C}\phi \in {\left\{{\phi }_i\right\}}_{i=1}^n.$$

(24)

For simplicity’s sake, we shall set the phase factor in Equation (8) to 1, since it does not contribute to expectation values. $\mathcal{C}$ is a map of ${\mathbb{C}}^4\to {\mathbb{C}}^4$; the last condition is equivalent to say that the subspace $\Phi$ of ${\mathbb{C}}^4$ consisting of basis functions $\{{\phi }_1,{\phi }_2,\dots ,{\phi }_n\}$, is preserved by the $\mathcal{C}$-map. We have seen before that in the spherically symmetric case, the C-operation replaces $\kappa \to -\kappa$, ${\pi }^L\rightleftarrows {\pi }^S$ and $m_j\to -m_j$, which means that the realization of the C-symmetry at the basis set level implies

$${\pi }_i^{S_{-\kappa }}={\pi }_i^{L_{\kappa }}\mathrm{and}{\pi }_i^{L_{-\kappa }}={\pi }_i^{S_{\kappa }}.$$

(25)

Under these conditions, we find that

$$\begin{array}{cc}\hfill H_{+e,-\kappa }& =-{\sigma }_x{H}_{-e,+\kappa }{\sigma }_x\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill S_{-\kappa }& =+{\sigma }_x{S}_{+\kappa }{\sigma }_x,\hfill \end{array}$$

(27)

and using the last equations, we get the connection between eigenvalues and eigenvectors

$${ϵ}_{+e,-\kappa }=-{ϵ}_{-e,+\kappa },{\left[\begin{array}{c}{\mathit{c}}^L\\ {\mathit{c}}^S\end{array}\right]}_{+e,-\kappa }={\left[\begin{array}{c}{\mathit{c}}^S\\ {\mathit{c}}^L\end{array}\right]}_{-e,+\kappa }.$$

(28)

2.3.3. Kinetic Balance

Starting from the radial equation (Equation (7)), we get two coupled equations that relate the large and small radial components of the Dirac equation.

$$\begin{array}{cc}\hfill Q_{\kappa }& =\frac{\hslash }{m_{e}c}{\left[1+\frac{E+e\varphi \left(r\right)}{m_e{c}^2}\right]}^{-1}[\frac{d}{dr}+\frac{\kappa }{r}]P_{\kappa }\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill P_{\kappa }& =\frac{\hslash }{m_{e}c}{\left[1-\frac{E+e\varphi \left(r\right)}{m_e{c}^2}\right]}^{-1}[\frac{d}{dr}-\frac{\kappa }{r}]Q_{\kappa }.\hfill \end{array}$$

(30)

The exact couplings are energy and potential-dependent, and therefore not appropriate for the construction of basis sets prior to the calculation of the energy. The energy-dependence can be eliminated by taking non-relativistic limit $c\to \infty$. It is sometimes stated that the expressions in square brackets go to one provided $E\pm e\varphi \left(r\right)<<m_e{c}^2$. However, the correct statement is rather that $E\pm e\varphi \left(r\right)$ should have a finite value as the limit is taken. For a point nucleus, the scalar potential $\varphi \left(r\right)$ is singular at $r=0$, and so this condition is not satisfied. It can be restored by rather considering nuclei of finite charge distributions [24,25]. As it stands, the energy depends quadratically on the speed of light. This dependence can be eliminated by constant shifts, but implies taking different limits for the positive and negative energy branches.

For the positive energy branch, we introduce the shifted energy $E_{+}=E-m_e{c}^2$, and from Equation (29) obtain

$$\underset{c\to \infty }{lim}c{Q}_{\kappa }=\underset{c\to \infty }{lim}\frac{\hslash }{2m_e}{\left[1+\frac{E_{+}+e\varphi \left(r\right)}{2m_e{c}^2}\right]}^{-1}[\frac{d}{dr}+\frac{\kappa }{r}]P_{\kappa }=\frac{\hslash }{2m_e}[\frac{d}{dr}+\frac{\kappa }{r}]P_{\kappa }.$$

(31)

For the negative energy branch, we introduce the shifted energy $E_{-}=E+m_e{c}^2$, and from Equation (30) obtain

$$\underset{c\to \infty }{lim}c{P}_{\kappa }=\underset{c\to \infty }{lim}\frac{\hslash }{2m_e}{\left[1-\frac{E_{-}+e\varphi \left(r\right)}{2m_e{c}^2}\right]}^{-1}[\frac{d}{dr}-\frac{\kappa }{r}]Q_{\kappa }=\frac{\hslash }{2m_e}[\frac{d}{dr}-\frac{\kappa }{r}]Q_{\kappa }.$$

(32)

Conventional atomic and molecular relativistic calculations in a finite basis focus on positive-energy solutions, and so bases are constructed according to the prescription of kinetic balance which imposes the non-relativistic coupling Equation (31) at the level of individual basis functions; that is,

$${\pi }_i^{S_{\kappa }}=a_i^{S_{\kappa }}[\frac{d}{dr}+\frac{\kappa }{r}]{\pi }_i^{L_{\kappa }},\mathrm{with}{a}_i^{S_{\kappa }}=\frac{\hslash }{2m_{e}c}.$$

(33)

The numerical factor $a_i^{S_{\kappa }}$, here set to half the reduced Compton wavelength in accordance with Equation (31), is arbitrary. For instance, if one did not introduce an imaginary i in the atomic spinor, Equation (6), our present choice would be multiplied with this factor. This particular choice of basis functions provides a proper representation of the kinetic energy operator in the non-relativistic limit [4], and therefore prevents the appearance of spurious states in the calculation. For calculations at finite values of the speed of light, it is necessary that the basis is sufficiently flexible so that the relativistic coupling can be realized through adjustment of basis expansion coefficients [26].

The one-to-one correspondence between large and small component basis functions can only be realized in a two-component basis and is denoted restricted kinetic balance (RKB). The terminology was introduced by Dyall and Fægri [12] to contrast with the use of scalar basis functions, where the small component basis functions are taken as derivatives of the large component ones, in no particular linear combinations. This latter scheme is denoted unrestricted kinetic balance (UKB).

Restricted kinetic balance (Equation (33)) leads to the matrix eigenvalue equation (Equation (16)) with elements given in (Equations (A1) and (A2)) of the Appendix A. The matrix representation of the Dirac equation in an RKB basis is that of the modified Dirac equation [27] (see also [28]). From this, Sun et al. [13] conclude that there is no "modified" Dirac equation. However, this is formally incorrect, since the modified Dirac equation has an independent existence at the operator level.

A corresponding prescription

$${\pi }_i^{L_{\kappa }}=a_i^{L_{\kappa }}[\frac{d}{dr}-\frac{\kappa }{r}]{\pi }_i^{S_{\kappa }},\mathrm{with}{a}_i^{L_{\kappa }}=\frac{\hslash }{2m_{e}c}.$$

(34)

that favors negative-energy solutions has been termed inverse kinetic balance [13] (IKB) and is based on Equation (32). In this prescription, the small component basis functions are introduced first; then, the large ones are generated using the last equation. This prescription leads to the eigenvalue equation, whose elements are given in the Appendix A (Equations (A3) and (A4)).

In order to respect the C-symmetry, we impose the conditions of Equation (25) on the RKB prescription, Equation (33), which leads the following equation for large component basis functions

$$[r^2\frac{d^2}{d{r}^2}-\kappa (1+\kappa )-\frac{1}{a_i^{S_{-\kappa }}{a}_i^{S_{\kappa }}}{r}^2]{\pi }_i^{L_{\kappa }}(r)=0.$$

(35)

Its general solution is

$${\pi }_i^{L_{\kappa }}(r)=c_{1}r{j}_{\kappa }(kr)+c_{2}r{y}_{\kappa }(kr),\mathrm{with}{k}^2=-{\left(a_i^{S_{-\kappa }}{a}_i^{S_{\kappa }}\right)}^{-1},$$

(36)

and the small components are then ${\pi }_i^{S_{\kappa }}={\pi }_i^{L_{-\kappa }}$. The $c_i$ are arbitrary coefficients; $j_{\alpha }(z)$ and $y_{\alpha }(z)$ are spherical Bessel functions of the first and second kind respectively. If, on the other hand, we impose C-symmetry on the IKB prescription, Equation (34), we obtain the same general solution, now with $k^2=-{\left(a_i^{L_{-\kappa }}{a}_i^{L_{\kappa }}\right)}^{-1}$. We also note that if we combine the RKB and IKB prescriptions, to describe both positive and negative energy solutions on the same footing, we again get the same general solution, with $k^2=-{\left(a_i^{L_{\kappa }}{a}_i^{S_{\kappa }}\right)}^{-1}$. The problem with this specific choice of functions is that the boundary conditions ${\pi }_i^{L_{\kappa }/S_{\kappa }}(0)=0$ and ${\pi }_i^{L_{\kappa }/S_{\kappa }}(\infty )=0$, are not obeyed simultaneously. Therefore, they are not useful for atomic and molecular calculations.

2.3.4. Dual Kinetic Balance

The kinetic balance prescription is widely employed in atomic and molecular calculations, but favors the positive-energy solutions. The dual kinetic balance prescription (DKB) ensures the right coupling between the large and the small components (in the non-relativistic limit) for both positive and negative energy solutions. It was introduced by Shabaev et al. [14] with the use of B-splines and tested by calculating the one-loop self-energy correction for a hydrogen-like ion. The radial function is expanded as

$$\left[\begin{array}{c}{P}_{\kappa }\\ Q_{\kappa }\end{array}\right]=\sum _i^{n_L}{c}_{\kappa ,i}^{[+]}\left[\begin{array}{c}{\pi }_i^{L_{\kappa }}\\ \frac{\hslash }{2m_{e}c}[\frac{d}{dr}+\frac{\kappa }{r}]{\pi }_i^{L_{\kappa }}\end{array}\right]+\sum _i^{n_S}{c}_{\kappa ,i}^{[-]}\left[\begin{array}{c}\frac{\hslash }{2m_{e}c}[\frac{d}{dr}-\frac{\kappa }{r}]{\pi }_i^{S_{\kappa }}\\ {\pi }_i^{S_{\kappa }}\end{array}\right],$$

(37)

where the first and second set of basis functions have the non-relativistic coupling of positive and negative-energy solutions, respectively, as indicated by the $[\pm ]$ symbol on the coefficients. This particular expansion leads to a generalized eigenvalue problem whose elements are defined in Equations (A9)–(A11) of the Appendix A. Contrary to the case of RKB/IKB the conditions for C-symmetry, Equation (25) can now be imposed without putting constraints on the choice of basis functions. The two matrix representations associated with $(+e,-\kappa )$ and $(-e,+\kappa )$, become related by

$$\begin{array}{cc}\hfill H_{+e,-\kappa }=& -{\sigma }_x{H}_{-e,\kappa }{\sigma }_x,S_{-\kappa }={\sigma }_x{S}_{\kappa }{\sigma }_x,\hfill \end{array}$$

(38)

leading to the C-connection between the eigenvalues and the eigenvectors

$$\begin{array}{c}\hfill {ϵ}_{+e,-\kappa }=-{ϵ}_{-e,+\kappa },{\left[\begin{array}{c}{\mathit{c}}^{[+]}\\ {\mathit{c}}^{[-]}\end{array}\right]}_{+e,-\kappa }={\left[\begin{array}{c}{\mathit{c}}^{[-]}\\ {\mathit{c}}^{[+]}\end{array}\right]}_{-e,+\kappa }.\end{array}$$

(39)

Note, however, that the condition in Equation (25) that ensures the C-symmetry, implies that one has to use the same exponents for both $\pm \kappa$ Gaussian type functions, as has also been pointed out by Dyall [29]. This corresponds, in the terminology of Dyall to j bases, where exponents are optimized for the total angular momentum j quantum number [30], contrary to conventional basis sets where functions are optimized for orbital angular momentum ℓ.

3. Computational Details

To illustrate our findings, we have written numerical codes using the Wolfram Mathematica program [31]. We built the matrix representations of the Dirac equation in the RKB, IKB, and DKB schemes, using spherical Gaussian functions—Equations (21) and (22)—and a point nucleus.

4. Results and Discussion

4.1. Kinetic Balance

We started by doing a simple free-particle calculation, $\varphi (r)=0$, within the RKB scheme. Using spherical Gaussian functions, we specify ${\zeta }^{\kappa }=\{1,2\}$, with $\kappa =\pm 1$ ($s_{\frac{1}{2}}$- and $p_{\frac{1}{2}}$-type functions). By solving the generalized eigenvalue problem for each $\kappa$-block, we get the eigenvalues ${ϵ}_{\kappa }$ reported in

Table 1. Eigenvalues of the free-particle restricted kinetic balance (RKB) calculation (in $E_h$).

Eigenvalue No.		1	2	3	4
$\kappa$	$-1$	18,784.744	−18,784.744	18,780.067	−18,780.067
	$+1$	18,786.676	−18,786.676	18,780.981	18,780.981

. At first glance, one gets the impression that C-symmetry is respected, since eigenvalues come in pairs of opposite signs. However, the pairs occur for the same $\kappa$ and not opposite$\kappa$, as predicted by the C-symmetry. This is confirmed by inspection of the eigenvectors, as exemplified by showing the first two normalized eigenvectors of each $\kappa$ block in

Table 2. Eigenvectors of the free-particle RKB calculation.

			Coefficients
$\mathit{\kappa }$	No.	$\mathit{ϵ}({\mathit{E}}_{\mathit{h}})$	${\mathit{c}}_{\mathit{1}}^{\mathit{L}}$	${\mathit{c}}_{\mathit{2}}^{\mathit{L}}$	${\mathit{c}}_{\mathit{1}}^{\mathit{S}}$	${\mathit{c}}_{\mathit{2}}^{\mathit{S}}$
$-1$	1	+18,784.744	4.9279	−10.2190	4.9271	−10.2174
	2	−18,784.744	0.0616	−0.1278	−393.7590	816.5380
$+1$	1	+18,786.676	−4.0603	13.2692	−4.0594	13.2665
	2	−18,786.676	0.0585	−0.1913	−281.4726	919.8612

.

We see clearly that the expected connection (C-conjugation) between positive and negative energy solutions does not hold here.

In order to understand the reason, we set $\varphi (r)$ to zero in the RKB matrix equation, whose elements are given Equations (A1) and (A2) of the Appendix A. We then get the following equation

$$\left[\begin{array}{cc}{m}_e{c}^2{S}_{\kappa }& T_{\kappa }^{\kappa }\\ T_{\kappa }^{\kappa }& -\frac{1}{2}{T}_{\kappa }^{\kappa }\end{array}\right]\left[\begin{array}{c}{\mathit{c}}^L\\ {\mathit{c}}^S\end{array}\right]=\left[\begin{array}{cc}{S}_{\kappa }& 0\\ 0& \frac{1}{2m_e{c}^2}{T}_{\kappa }^{\kappa }\end{array}\right]\left[\begin{array}{c}{\mathit{c}}^L\\ {\mathit{c}}^S\end{array}\right]{ϵ}_{\kappa }.$$

(40)

The first and second lines of the last equation give

$$\begin{array}{cc}\hfill T_{\kappa }^{\kappa }{\mathit{c}}^S& =[{ϵ}_{\kappa }-m_e{c}^2]S_{\kappa }{\mathit{c}}^L\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill T_{\kappa }^{\kappa }{\mathit{c}}^L& =\frac{[{ϵ}_{\kappa }+m_e{c}^2]}{2m_e{c}^2}{T}_{\kappa }^{\kappa }{\mathit{c}}^S,\hfill \end{array}$$

(42)

and by combining these equations, we get

$$T_{\kappa }^{\kappa }{\mathit{c}}^L={\lambda }_{\kappa }{S}_{\kappa }{\mathit{c}}^L,\mathrm{with}{\lambda }_{\kappa }=\frac{{ϵ}_{\kappa }^2-m_e^2{c}^4}{2m_e{c}^2}.$$

(43)

We see that each eigenvalue ${\lambda }_{\kappa }$ corresponds to two values ${ϵ}_{\kappa }=\pm \sqrt{2m_e{c}^2{\lambda }_{\kappa }+m_e^2{c}^4}$. The corresponding eigenvectors are

$$\psi (\pm {ϵ}_{\kappa })={\mathcal{N}}_{\pm }\left[\begin{array}{c}{\mathit{c}}^L\\ \frac{2m_e{c}^2}{\pm {ϵ}_{\kappa }+m_e{c}^2}{\mathit{c}}^L\end{array}\right]$$

(44)

Although the eigenvalues exist in pairs, it is clear that the upper and lower components of two opposite energy solutions are not related by C-symmetry. In fact, as shown in Section 2.3.3, the RKB prescription does not generally respect C-symmetry.

Note that this pairing of energies can already be seen from the exact spherical free-particle solutions in Equation (9). Upon substitution $E\to -E$ and keeping in mind that $E\in \mathbb{R}\backslash [-m_e{c}^2,+m_e{c}^2]$ we see that the solution of flipped energy sign can be expressed in terms of the original one

$${\psi }_{\kappa m_j}(r,-E)\propto \left[\begin{array}{c}{\psi }_{\kappa m_j}^L(r,E)\\ \frac{E+m_e{c}^2}{-E+m_e{c}^2}{\psi }_{\kappa m_j}^S(r,E)\end{array}\right].$$

(45)

Doing the same calculation using the IBK prescription, we get the sets of eigenvalues shown in

Table 3. Eigenvalues of the free-particle IKB calculation (in $E_h$).

Eigenvalue No.		1	2	3	4
$\kappa$	$-1$	−18,786.676	18,786.676	−18,780.981	18,780.981
	$+1$	−18,784.744	18,784.744	−18,780.067	18,780.067

. The first two eigenvectors of each spectrum are shown in

Table 4. Eigenvectors of the free-particle IKB calculation.

			Coefficients
$\mathit{\kappa }$	No.	$\mathit{ϵ}({\mathit{E}}_{\mathit{h}})$	${\mathit{c}}_{\mathit{1}}^{\mathit{L}}$	${\mathit{c}}_{\mathit{2}}^{\mathit{L}}$	${\mathit{c}}_{\mathit{1}}^{\mathit{S}}$	${\mathit{c}}_{\mathit{2}}^{\mathit{S}}$
$-1$	1	−18,786.676	−4.0594	13.2665	−4.0603	13.2692
	2	18,786.676	−281.4726	919.8612	0.0585	−0.1913
$+1$	1	−18,784.744	4.9271	−10.2174	4.9279	−10.2190
	2	18,784.744	−393.7590	816.5380	0.0616	−0.1278

.

By comparing the eight eigenvectors we have chosen in Table 2 and Table 4, we see that positive and negative-energy solutions that belong to opposite $\kappa$-sign blocks are related by C-symmetry. Indeed, taking into account the condition in Equation (25), we see that RKB and IKB matrices (Equations (A1)–(A4) in the Appendix A) are connected by C-symmetry; that is,

$$\begin{array}{cc}\hfill {\sigma }_x{H}_{-e,+\kappa }^{RKB}{\sigma }_x& =-H_{+e,-\kappa }^{IKB}\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\sigma }_x{S}_{+\kappa }^{RKB}{\sigma }_x& =S_{-\kappa }^{IKB},\hfill \end{array}$$

(47)

leading to the symmetry between RKB and IKB eigensystems

$${ϵ}_{+e,-\kappa }^{IKB}=-{ϵ}_{-e,+\kappa }^{RKB},{\left[\begin{array}{c}{\mathit{c}}^L\\ {\mathit{c}}^S\end{array}\right]}_{+e,-\kappa }^{IKB}={\left[\begin{array}{c}{\mathit{c}}^S\\ {\mathit{c}}^L\end{array}\right]}_{-e,+\kappa }^{RKB}.$$

(48)

This is in line with the observation by Sun et al. [13]. Since RKB and IKB are related by C-symmetry, a combination of the two prescriptions would conserve the C-symmetry. And this is exactly what the DKB is about (Equation (37)).

4.2. Dual Kinetic Balance

We present two simple atomic calculations within the DKB prescription, where we used $s_{\frac{1}{2}}$ and $p_{\frac{1}{2}}$-type spherical Gaussian functions (Equations (21) and (22)) with the same exponents $\zeta =\{1,2\}$, and a point nucleus of charge $Z=1$:

• Calculation 1: with $-e$; electronic charge.
• Calculation 2: with $+e$; positronic charge.

For each calculation, we get two sets of eigenvalues coming from each $\kappa$-block, shown in

Table 5. Eigenvalues of the DKB calculation (in $E_h$).

Charge	$\mathit{\kappa }$	Eigenvalues
		1	2	3	4
$-e$	$-1$	−18,788.264	18,782.511	−18,781.851	18,778.739
	$+1$	−18,787.149	18,785.113	−18,781.223	18,780.084
$+e$	$-1$	18,787.149	−18,785.113	18,781.223	−18,780.084
	$+1$	18,788.264	−18,782.511	18,781.851	−18,778.739

. We then pick the first eigenvalues of each set and show their corresponding eigenvectors in

Table 6. Eigenvectors of the DKB calculation.

			Coefficients
Charge	$\mathit{\kappa }$	$\mathit{ϵ}({\mathit{E}}_{\mathit{h}})$	${\mathit{c}}_{\mathit{1}}^{[+]}$	${\mathit{c}}_{\mathit{2}}^{[+]}$	${\mathit{c}}_{\mathit{1}}^{[-]}$	${\mathit{c}}_{\mathit{2}}^{[-]}$
$-e$	$-1$	−18,788.264	$1.235\times {10}^{-5}$	$-2.295\times {10}^{-5}$	$-3.882$	$13.106$
	$+1$	−18,787.149	$1.069\times {10}^{-5}$	$-3.745\times {10}^{-5}$	$4.489$	$-9.881$
$+e$	$-1$	18,787.149	$4.489$	$-9.881$	$1.069\times {10}^{-5}$	$-3.745\times {10}^{-5}$
	$+1$	18,788.264	$-3.882$	$13.106$	$1.235\times {10}^{-5}$	$-2.295\times {10}^{-5}$

.

We see that the spectra in Table 5 do respect the C-symmetry; i.e., ${ϵ}_{-e,+\kappa }=-{ϵ}_{+e,-\kappa }$. Furthermore, we see that the eigenvectors associated with $(-e,+\kappa )$ and $(+e,-\kappa )$ are related according to Equation (39).

5. Conclusions

We have investigated three basis set schemes for solving the Dirac equation in a central field—restricted, inverse, and dual kinetic balance—and their compatibility with charge conjugation symmetry, which connects solutions of opposite $\kappa$ of the electronic and positronic problem. An interesting observation is that in the free-particle case, where the electronic and positronic problems coalesce, there is further symmetry such that pairs of eigenvalues of opposite sign also occur for the same $\kappa$. We are not aware of any discussion of this feature in the literature.

Charge conjugation symmetry can be realized within restricted and inverse kinetic balance, but only using special functions which do not respect the boundary conditions of the radial Dirac solutions and which are not useful for atomic and molecular calculations. Dual kinetic balance, on the other hand, is compatible with charge conjugation symmetry for any type of radial basis function, provided j bases are used.

An alternative to dual kinetic balance, denoted dual atomic balance, has been proposed by Dyall [29]: In this scheme restricted and inverse kinetic balance is used separately for positive and negative-energy solutions. This requires in principle two separate diagonalizations, followed by a final diagonalization in the dual basis. If one seeks to generate orbitals for use in QED calculations, then a possible simple alternative to the latter scheme is to first carry out a standard four-component relativistic calculation within restricted kinetic balance and electronic charge $q=-e$ and only retain the positive-energy solutions. Then a second calculation is carried out, again within restricted kinetic balance, retaining only positive-energy solutions and with the same potential, but now using the positronic charge $q=+e$. This scheme then has the intriguing property that the final set of orbitals is restricted to observable, positive-energy solutions only. We plan to study these schemes in future work.