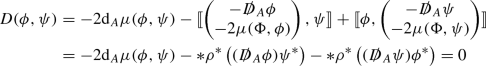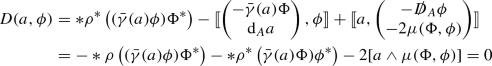Deformation theory of the blown-up Seiberg–Witten equation in dimension three

Abstract

Associated with every quaternionic representation of a compact, connected Lie group there is a Seiberg–Witten equation in dimension three. The moduli spaces of solutions to these equations are typically non-compact. We construct Kuranishi models around boundary points of a partially compactified moduli space. The Haydys correspondence identifies such boundary points with Fueter sections—solutions of a non-linear Dirac equation—of the bundle of hyperkähler quotients associated with the quaternionic representation. We discuss when such a Fueter section can be deformed to a solution of the Seiberg–Witten equation.

Appendices

A Examples of Seiberg–Witten equations

Example A.1

Let $G = \mathrm {U}(n)$ and $S = \mathbf {H}\otimes _{\mathbf {C}}{\mathbf {C}}^n$, where the complex structure on $\mathbf {H}$ is given by right-multiplication by i. Let $\rho : \mathrm {U}(n) \rightarrow \mathrm {Sp}(\mathbf {H}\otimes _{\mathbf {C}}{\mathbf {C}}^n)$ be induced from the standard representation of $\mathrm {U}(n)$. The corresponding Seiberg–Witten equation is the $\mathrm {U}(n)$–monopole equation in dimension three. The closely related ${\mathbf {P}\mathrm {U}}(2)$–monopole equation on 4–manifolds plays a crucial role in Pidstrigach and Tyurin’s approach to proving Witten’s conjecture relating Donaldson and Seiberg–Witten invariants; see, e.g., [8, 20, 27].

In this example as well as in Example 2.15, we have $\mu ^{-1}(0) = \lbrace 0 \rbrace$.

Example A.2

Let G be a compact Lie group, ${\mathfrak g}= {{\,\mathrm{Lie}\,}}(G)$, and fix an ${{\,\mathrm{Ad}\,}}$–invariant inner product on ${\mathfrak g}$. $S :=\mathbf {H}\otimes _\mathbf {R}{\mathfrak g}$ is a quaternionic Hermitian vector space, and $\rho : G \rightarrow \mathrm {Sp}(S)$ induced by the adjoint action is a quaternionic representation. The moment map $\mu : \mathbf {H}\otimes _\mathbf {R}{\mathfrak g}\rightarrow ({\text {Im}}\mathbf {H}\otimes {\mathfrak g})^*$ is given by

$$\begin{aligned} \mu (\xi )&= \frac{1}{2}[\xi ,\xi ] \\&= ([\xi _2,\xi _3]+[\xi _0,\xi _1])\otimes i + ([\xi _3,\xi _1]+[\xi _0,\xi _2])\otimes j + ([\xi _1,\xi _2]+[\xi _0,\xi _3])\otimes k \end{aligned}$$

for $\xi = \xi _0\otimes 1 + \xi _1\otimes i + \xi _2\otimes j + \xi _3\otimes k \in \mathbf {H}\otimes _\mathbf {R}{\mathfrak g}$. Set $H :=\mathrm {Sp}(1) \times G$ and extend the above quaternionic representation of G to H by declaring that $q \in \mathrm {Sp}(1)$ acts by right-multiplication with $q^*$.

Taking Q to be the product of the chosen spin structure ${\mathfrak s}$ with a principal G–bundle, and choosing B such that it induces the spin connection on ${\mathfrak s}$, (2.14) becomes

$$\begin{aligned} \mathrm{d}_A^*a&= 0, \\ *\mathrm{d}_Aa + \mathrm{d}_A\xi&= 0, \quad \text {and}\\ F_A&= \tfrac{1}{2}[a\wedge a] + *[\xi ,a]. \end{aligned}$$

for $\xi \in \Gamma ({\mathfrak g}_P)$, $a \in \Omega ^1(M,{\mathfrak g}_P)$ and $A \in \mathscr {A}(P)$. If M is closed, then integration by parts shows that every solution of this equation satisfies $\mathrm{d}_A\xi =0$ and $[\xi ,a]=0$; hence, $A + ia$ defines a flat $G^{\mathbf {C}}$–connection. Here $G^{\mathbf {C}}$ denotes the complexification of G.

In the above situation, we have $\mu ^{-1}(0)/G \cong (\mathbf {H}\otimes {\mathfrak t})/W$ where ${\mathfrak t}$ is a the Lie algebra of a maximal torus $T \subset G$ and $W = N_G(T)/T$ is the Weyl group of G. However, since each $\xi \in \mu ^{-1}(0)$ has stabilizer conjugate to T, we have $\mu ^{-1}(0)\cap S^\mathrm {reg}= \varnothing$, and the hyperkähler quotient $S^\mathrm {reg}{/\!\! /\!\! /}G$ is empty.

Example A.3

The motivating example for us is the (r, k) ADHM Seiberg–Witten equation, which we expect to play in important role in gauge theory on $G_2$–manifolds,⁸ and which arises from

$$\begin{aligned} S = {{\,\mathrm{Hom}\,}}_{\mathbf {C}}({\mathbf {C}}^r,\mathbf {H}\otimes _{\mathbf {C}}{\mathbf {C}}^k) \oplus \mathbf {H}^*\otimes _\mathbf {R}{\mathfrak u}(k) \end{aligned}$$

with

$$\begin{aligned} G = \mathrm {U}(k) \triangleleft H = \mathrm {SU}(r) \times \mathrm {Sp}(1) \times \mathrm {U}(k) \end{aligned}$$

where $\mathrm {SU}(r)$ acts on ${\mathbf {C}}^r$ in the obvious way, $\mathrm {U}(k)$ acts on ${\mathbf {C}}^k$ in the obvious way and on ${\mathfrak u}(k)$ by the adjoint representation, and $\mathrm {Sp}(1)$ acts on the first copy of $\mathbf {H}$ trivially and on the second copy by right-multiplication with the conjugate. Accoding to Atiyah, Drinfeld, Hitchin, and Manin [1], if $r \geqslant 2$, then $S^\mathrm {reg}{/\!\! /\!\! /}G$ is the moduli space of framed $\mathrm {SU}(r)$ ASD instantons of charge k on $\mathbf {R}^4$, and $\mu ^{-1}(0)/G$ is its Uhlenbeck compactification, If $r = 1$, then $\mu ^{-1}(0)\cap S^\mathrm {reg}= \varnothing$, and $\mu ^{-1}(0)/G = {{\,\mathrm{Sym}\,}}^k\mathbf {H}:=\mathbf {H}^k/S_k$ by [19, Example 3.14].

B Useful identities involving $\mu$

This appendix summarizes and proves a few useful identities regarding $\mu$, some of which are used in this article.

Proposition B.1

For $\xi \in \Omega ^0(M,{\mathfrak g}_P)$, $a \in \Omega ^1(M,{\mathfrak g}_P)$, and $\phi ,\psi \in \Gamma ({\mathfrak S})$, we have

$$\begin{aligned}{}[\xi ,\mu (\phi ,\psi )] = \mu (\phi ,\rho (\xi )\psi ) + \mu (\psi ,\rho (\xi )\phi ), \end{aligned}$$

(B.2)

and for $a \in \Omega ^1(M,{\mathfrak g}_P)$ and $\phi ,\psi \in \Gamma ({\mathfrak S})$, we have

$$\begin{aligned} 2[a \wedge \mu (\phi ,\psi )] = - * \rho ^*\left( ({\bar{\gamma }}(a)\phi )\psi ^*\right) - * \rho ^*\left( ({\bar{\gamma }}(a)\psi )\phi ^*\right) . \end{aligned}$$

(B.3)

Proof

For all $a \in \Omega ^1(M,{\mathfrak g}_P)$, we have

$$\begin{aligned} 2\langle [\xi ,\mu (\phi ,\psi ))], *a \rangle&= \langle \mu (\phi ,\psi ), -*[\xi ,a] \rangle \\&= \langle \phi , -{\bar{\gamma }}([\xi ,a])\psi \rangle \\&= -\langle \phi , \rho (\xi ){\bar{\gamma }}(a)\psi \rangle +\langle \phi , {\bar{\gamma }}(a)\rho (\xi )\psi \rangle \\&= \langle \rho (\xi )\phi , {\bar{\gamma }}(a)\psi \rangle +\langle \phi , {\bar{\gamma }}(a)\rho (\xi )\psi \rangle \\&= 2\langle \mu (\phi ,\rho (\xi )\psi ), *a \rangle +2\langle \mu (\psi ,\rho (\xi )\phi ), *a \rangle . \end{aligned}$$

This proves the first identity. To prove the second identity, note that, for all $\eta \in \Omega ^0(M,{\mathfrak g}_P)$, we have

$$\begin{aligned} 2\langle [a\wedge \mu (\phi ,\psi )], *\eta \rangle&= \langle 2\mu (\phi ), *[\eta ,a] \rangle \\&= \langle \phi , {\bar{\gamma }}([\eta ,a])\psi \rangle \\&= \langle \phi , \rho (\xi ){\bar{\gamma }}(a)\psi \rangle -\langle \phi , {\bar{\gamma }}(a)\rho (\xi )\psi \rangle \\&= -\langle \xi , \rho ^*\left( ({\bar{\gamma }}(a)\psi )\phi ^*\right) \rangle -\langle \xi , \rho ^*\left( ({\bar{\gamma }}(a)\phi )\psi ^*\right) \rangle . \end{aligned}$$

$\square$

Proposition B.4

For all $A \in \mathscr {A}(Q)$ and $\phi , \psi \in \Gamma ({\mathfrak S})$ we have

(B.5)

and

(B.6)

Proof

Fix a point $x \in M$, a positive local orthonormal frame $(e_i)$ around x with $(\nabla e_i)(x) = 0$, and let $\xi$ be a local section of ${\mathfrak g}_P$ defined in a neighborhood of x satisfying $(\nabla \xi )(x) = 0$. We set $\nabla ^A_i :=\nabla ^A_{e_i}$.

At the point $x \in M$, we compute with

This proves the first identity. To prove the second identity, we compute

$\square$

Proposition B.7

If $(\varepsilon ,\Phi ,A) \in (0,\infty )\times \Gamma ({\mathfrak S})\times \mathscr {A}_B(Q)$ is a solution of (2.21) and $R_\Phi (\xi ) = \rho (\xi )\Phi$, then

Here $(e_1,e_2,e_3)$ is local orthonormal frame, $(e^1,e^2,e^3)$ is the dual coframe, $F^B_{ij} :=F_B(e_i,e_j)$, $F^{\mathfrak s}_{ij} :=F_{\mathfrak s}(e_i,e_j)$ with $F_{\mathfrak s}$ denoting the curvature of the spin connection on ${\mathfrak s}$, and $e^{ij} :=e^i \wedge e^j$.

Proof

We compute

$$\begin{aligned} \mathrm{d}_A \rho ^*[(\nabla _A\Phi )\Phi ^*]&= \sum _{i,j=1}^3 \rho ^*[(\nabla ^A_i\nabla ^A_j\Phi )\Phi ^*] e^{ij} + \rho ^*[(\nabla ^A_j\Phi )(\nabla ^A_i\Phi )^*] e^{ij} \\&= \sum _{i,j=1}^3 \frac{1}{2}\rho ^*[(F^A_{ij} \cdot \Phi )\Phi ^*] e^{ij} + \rho ^*[(\nabla ^A_j\Phi )(\nabla ^A_i\Phi )^*] e^{ij}. \end{aligned}$$

Since

$$\begin{aligned} \sum _{i,j=1}^3 \rho ^*[\rho (\mu (\Phi )_{ij})\Phi )\Phi ] e^{ij} = R_\Phi ^*R_\Phi \mu (\Phi ), \end{aligned}$$

the result now follows from Proposition B.4. $\square$

C Proof of Proposition 3.2

For the reader’s convenience, we recall the definitions of the graded vector space $L^\bullet$,

$$\begin{aligned} L^0&:=\Omega ^0(M,{\mathfrak g}_P), \\ L^1&:=\Gamma ({\mathfrak S})\oplus \Omega ^1(M,{\mathfrak g}_P), \\ L^2&:=\Gamma ({\mathfrak S})\oplus \Omega ^2(M,{\mathfrak g}_P), \quad \text {and}\\ L^3&:=\Omega ^3(M,{\mathfrak g}_P), \end{aligned}$$

the graded Lie bracket $\llbracket \cdot ,\cdot \rrbracket$,

$$\begin{aligned} \llbracket a,b \rrbracket&:={[a\wedge b]}&\text {for } a,b \in \Omega ^\bullet (M,{\mathfrak g}_P), \\ \llbracket \xi ,\phi \rrbracket&:=\rho (\xi )\phi&\text {for } \xi \in \Omega ^0(M,{\mathfrak g}_P) \text { and } \phi \in \Gamma ({\mathfrak S}) \text { in degree }1\text { or }2, \\ \llbracket a,\phi \rrbracket&:=-{\bar{\gamma }}(a)\phi&\text {for } a \in \Omega ^1(M,{\mathfrak g}_P) \text { and } \phi \in \Gamma ({\mathfrak S}) \text { in degree }1, \\ \llbracket \phi ,\psi \rrbracket&:=-2\mu (\phi ,\psi )&\text {for } \phi , \psi \in \Gamma ({\mathfrak S}) \text { in degree }1,\text { and} \\ \llbracket \phi ,\psi \rrbracket&:=-*\rho ^*(\phi \psi ^*)&\text {for } \phi \in \Gamma ({\mathfrak S}) \text { in degree }1\text { and } \psi \in \Gamma ({\mathfrak S}) \text { in degree 2}, \end{aligned}$$

and the graded differential $\delta _{{\mathfrak c}}$,

We proceed in four steps.

Step 1$(L^\bullet ,\llbracket \cdot ,\cdot \rrbracket )$ is a graded Lie algebra.

We need to verify the graded Jacobi identity, that is, for every three homogeneous elements $x,y,z \in L^\bullet$ we need to show that

$$\begin{aligned} J(x,y,z) :=(-1)^{\deg {x}\cdot \deg {z}}\llbracket x,\llbracket y,z \rrbracket \rrbracket + (-1)^{\deg {y}\cdot \deg {x}}\llbracket y,\llbracket z,x \rrbracket \rrbracket + (-1)^{\deg {z}\cdot \deg {y}}\llbracket z,\llbracket x,y \rrbracket \rrbracket \end{aligned}$$

vanishes. Here $\deg {x}$ denotes the degree of x.

For degree reasons $J(x,y,z) = 0$, unless $\deg x + \deg y + \deg z \leqslant 3$. $(\Omega ^\bullet (M,{\mathfrak g}_P),{[\cdot \wedge \cdot ]})$ is a graded Lie algebra. Since J(x, y, z) is invariant under permutations of x, y, and z, we can assume that $z \in \Gamma ({\mathfrak S})$ in degree 1 or 2. Hence, only the following five cases remain:

• For $\xi ,\eta \in \Omega ^0(M,{\mathfrak g}_P)$, and $\phi \in \Gamma ({\mathfrak S})$ in degree 1 or 2, we have

  $$\begin{aligned} J(\xi ,\eta ,\phi )&= \llbracket \xi ,\llbracket \eta ,\phi \rrbracket \rrbracket + \llbracket \eta ,\llbracket \phi ,\xi \rrbracket \rrbracket + \llbracket \phi ,\llbracket \xi ,\eta \rrbracket \rrbracket \\&= \rho (\xi )\rho (\eta )\phi - \rho (\eta )\rho (\xi )\phi - \rho ([\xi ,\eta ])\phi = 0. \end{aligned}$$

• For $\xi \in \Omega ^0(M,{\mathfrak g}_P)$, and $\phi ,\psi \in \Gamma ({\mathfrak S})$ in degree 1, we have

  $$\begin{aligned} J(\xi ,\phi ,\psi )&= \llbracket \xi ,\llbracket \phi ,\psi \rrbracket \rrbracket + \llbracket \phi ,\llbracket \psi ,\xi \rrbracket \rrbracket - \llbracket \psi ,\llbracket \xi ,\phi \rrbracket \rrbracket \\&= -2[\xi ,\mu (\phi ,\psi )] + 2\mu (\phi ,\rho (\xi )\psi ) + 2\mu (\psi ,\rho (\xi )\phi ) = 0 \end{aligned}$$

  by Proposition B.1.

• For $\xi \in \Omega ^0(M,{\mathfrak g}_P)$, $\phi \in \Gamma ({\mathfrak S})$ in degree 1 and $\psi \in \Gamma ({\mathfrak S})$ in degree 2, we have

  $$\begin{aligned} J(\xi ,\phi ,\psi )&= \llbracket \xi ,\llbracket \phi ,\psi \rrbracket \rrbracket + \llbracket \phi ,\llbracket \psi ,\xi \rrbracket \rrbracket + \llbracket \psi ,\llbracket \xi ,\phi \rrbracket \rrbracket \\&= -([\xi ,*\rho ^*\left( \phi \psi ^*\right) ] - *\rho ^*\left( \phi (\rho (\xi )\psi )^*\right) + *\rho ^*\left( \psi (\rho (\xi )\phi )^*\right) ) \\&= -*\rho ^*\left( [\rho (\xi ),\phi \psi ^*] + \phi \psi ^*\rho (\xi ) - \rho (\xi )\phi \psi ^*\right) = 0. \end{aligned}$$

• For $\xi \in \Omega ^0(M,{\mathfrak g}_P)$, $a \in \Omega ^1(M,{\mathfrak g}_P)$, and $\phi \in \Gamma ({\mathfrak S})$ in degree 1, we have

  $$\begin{aligned} J(\xi ,a,\phi )&= \llbracket \xi ,\llbracket a,\phi \rrbracket \rrbracket + \llbracket a,\llbracket \phi ,\xi \rrbracket \rrbracket - \llbracket \phi ,\llbracket \xi ,a \rrbracket \rrbracket ] \\&= -\rho (\xi ){\bar{\gamma }}(a)\phi + {\bar{\gamma }}(a)\rho (\xi )\phi + {\bar{\gamma }}({[\xi ,a]})\phi = 0. \end{aligned}$$

• For $a \in \Omega ^1(M,{\mathfrak g}_P)$ and $\phi ,\psi \in \Gamma ({\mathfrak S})$ in degree 1, we have

  $$\begin{aligned} J(a,\phi ,\psi )&= - \llbracket a,\llbracket \phi ,\psi \rrbracket \rrbracket - \llbracket \phi ,\llbracket \psi ,a \rrbracket \rrbracket - \llbracket \psi ,\llbracket a,\phi \rrbracket \rrbracket \\&= 2{[a\wedge \mu (\phi ,\psi )]} + *\rho ^*\left( ({\bar{\gamma }}(a)\psi )\phi ^*\right) + *\rho ^*\left( ({\bar{\gamma }}(a)\phi )\psi ^*\right) = 0 \end{aligned}$$

  by Proposition B.1.

Step 2$(L^\bullet ,\delta _{\mathfrak c}^\bullet )$ is a DGA.

We need to show that $\delta _{\mathfrak c}\circ \delta _{\mathfrak c}= 0$. Using Proposition B.1, we compute that

and, using Proposition B.4 and Proposition B.1, we compute that

Step 3$(L^\bullet ,\llbracket \cdot ,\cdot \rrbracket ,\delta _{\mathfrak c}^\bullet )$ is a DGLA.

We need to verify that $\delta _{\mathfrak c}^\bullet$ satisfies the graded Leibniz rule with respect to $\llbracket \cdot ,\cdot \rrbracket$, that is for every two homogeneous elements $x,y \in L^\bullet$ we need to show that

$$\begin{aligned} D(x,y) = \delta \llbracket x,y \rrbracket - \llbracket \delta x,y \rrbracket - (-1)^{\deg x}\llbracket x,\delta y \rrbracket \end{aligned}$$

vanishes.

For degree reasons, $D(x,y) = 0$ unless $\deg x + \deg y \leqslant 2$; hence, only the following eight cases remain:

• For $\xi ,\eta \in \Omega ^0(M,{\mathfrak g}_P)$, we have

  $$\begin{aligned} D(\xi ,\eta ) = \begin{pmatrix} -\rho ([\xi ,\eta ])\Phi \\ \mathrm{d}_A[\xi ,\eta ] \end{pmatrix} - \llbracket \begin{pmatrix} -\rho (\xi )\Phi \\ \mathrm{d}_A\xi \end{pmatrix} , \eta \rrbracket - \llbracket \xi , \begin{pmatrix} -\rho (\eta )\Phi \\ \mathrm{d}_A\eta \end{pmatrix} \rrbracket = 0. \end{aligned}$$

• For $\xi \in \Omega ^0(M,{\mathfrak g}_P)$ and $\phi \in \Gamma ({\mathfrak S})$ in degree 1, we have

  

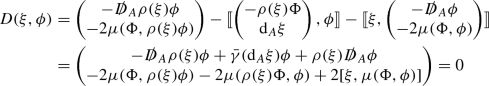
  by Proposition B.1.

• For $\xi \in \Omega ^0(M,{\mathfrak g}_P)$ and $a \in \Omega ^1(M,{\mathfrak g}_P)$, we have

  $$\begin{aligned} D(\xi ,a)&= \begin{pmatrix} -{\bar{\gamma }}([\xi ,a])\Phi \\ \mathrm{d}_A [\xi ,a] \end{pmatrix} - \llbracket \begin{pmatrix} -\rho (\xi )\Phi \\ \mathrm{d}_A\xi \end{pmatrix} , a \rrbracket - \llbracket \xi , \begin{pmatrix} -{\bar{\gamma }}(a)\Phi \\ \mathrm{d}_A a \end{pmatrix} \rrbracket \\&= \begin{pmatrix} -{\bar{\gamma }}([\xi ,a])\Phi - {\bar{\gamma }}(a)\rho (\xi )\Phi + \rho (\xi ){\bar{\gamma }}(a)\Phi \\ \mathrm{d}_A [\xi ,a] - [\mathrm{d}_A\xi \wedge a] - [\xi ,\mathrm{d}_A] \end{pmatrix} = 0. \end{aligned}$$

• For $\xi \in \Omega ^0(M,{\mathfrak g}_P)$ and $\phi \in \Gamma ({\mathfrak S})$ in degree 2, we have

  $$\begin{aligned} D(\xi ,\phi )&= *\rho ^*(\rho (\xi )\phi \Phi ^*) - \llbracket \rho (\xi )\Phi ,\phi \rrbracket - \llbracket \mathrm{d}_A\xi ,\phi \rrbracket - \llbracket \xi , *\rho ^*(\phi \Phi ^*) \rrbracket \\&= *\rho ^*(\rho (\xi )\phi \Phi ^*) - * \rho ^*( \phi \Phi ^* \rho (\xi )) - [\xi ,*\rho ^*(\phi \Phi ^*)] = 0. \end{aligned}$$

• For $\xi \in \Omega ^0(M,{\mathfrak g}_P)$ and $b \in \Omega ^2(M,{\mathfrak g}_P)$, we have

  $$\begin{aligned} D(\xi ,b) = \mathrm{d}_A [\xi ,b] - [\mathrm{d}_A\xi ,b] - [\xi ,\mathrm{d}_Ab] = 0. \end{aligned}$$

• For $\phi ,\psi \in \Gamma ({\mathfrak S})$ in degree 1, we have

  

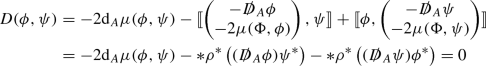
  by Proposition B.4.

• For $a \in \Omega ^1(M,{\mathfrak g}_P)$ and $\phi \in \Gamma ({\mathfrak S})$ in degree 1, we have

  

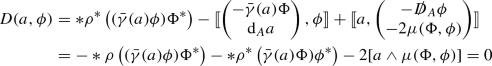
  by Proposition B.1.

• For $a,b \in \Omega ^1(M,{\mathfrak g}_P)$, we have

  $$\begin{aligned} D(a,b) = \begin{pmatrix} - {\bar{\gamma }}{ {[a\wedge b]}} \Phi \\ \mathrm{d}_A {[a\wedge b]} \end{pmatrix} - \llbracket \begin{pmatrix} {\bar{\gamma }}(a)\Phi \\ \mathrm{d}_A a \end{pmatrix} , b \rrbracket + \llbracket a , \begin{pmatrix} {\bar{\gamma }}(b)\Phi \\ \mathrm{d}_A b \end{pmatrix} \rrbracket = 0. \end{aligned}$$

Step 3 For every ${\hat{{\mathfrak c}}} :=(a,\phi ) \in L^1$, $(A+a,\Phi +\phi )$ solves (2.14) if and only if $\delta _{\mathfrak c}{\hat{{\mathfrak c}}} + \frac{1}{2}\llbracket {\hat{{\mathfrak c}}},{\hat{{\mathfrak c}}} \rrbracket = 0$.

For ${\hat{{\mathfrak c}}} :=(a,\phi ) \in L^1$, we have

which vanishes if and only if $(A+a,\Phi +a)$ solves (2.14). $\square$