1 Introduction and background

Turbulent flows in dilute polymer solutions (DPS) have been the subject of many studies since Toms (1948) discovered that a small amount of polymer added to a Newtonian solvent could drastically change the flow properties, leading among other consequences to a reduction of the drag in pipe flows (Virk 1975; Sreenivasan and White 2000). Many researchers have since then led investigations on how the elasticity of the so formed non-Newtonian fluids could influence the characteristics of turbulence (kinetic energy spectrum, length scales...) and its production, energy exchanges, and decay mechanisms (Lumley 1969; De Angelis et al. 2005; Crawford et al. 2008; Nguyen et al. 2016; Cocconi et al. 2017).

As a fundamental step, experiments have been made attempting to describe the influence of polymer elasticity on supposedly homogeneous and isotropic turbulence, using various set-ups such as washing machine (Liberzon et al. 2005, 2006; Crawford et al. 2008) , rotating grids (Cocconi et al. 2017) or oscillating grids (Liberzon et al. 2009), with very dilute solutions of long chained elastic polymers, e.g polyethylene oxide (PEO), as working fluids.

However in many applications, not only are the encountered fluids elastic, but also does their viscosity depend on the shear rate, making them shear-thinning, with a viscosity that decreases with increasing shear rate. This involves for example food processing (Katzbauer 1998), fermentation for vaccine production (Kawase et al. 1992; Pedersen et al. 1994) or blood fluid mechanics (Secomb 2016). Such real life fluids can also well be modelled by polymer solutions (which they sometimes are) either using higher concentrations of the above polymers (Pereira et al. 2013), or other polymers of more rigid conformation, such as Xanthan Gum (XG) (Garcia-Ochoa et al. 2000; Wyatt and Liberatore 2009). In that later case, shear-thinning is the first rheological feature to appear upon polymer addition, and the fluid can even be considered shear thinning and inelastic in a given range of polymer concentration (Cagney and Balabani 2019; Lacassagne et al. 2019b).

Contrary to turbulence in elastic non-Newtonian fluids, the topic of turbulence in such shear thinning inelastic DPS have been the subject of less experimental efforts, in particular regarding the case of polymer-turbulence interactions in shear thinning fluid (Rahgozar and Rival 2017). Recent works by the present authors Lacassagne et al. (2019a, b) present a description of shear-thinning polymer turbulence in an oscillatory grid set-up [as used once in elastic fluids by Liberzon et al. (2009)]. This is, to the authors knowledge, the only characterisation of oscillating grid turbulence (OGT) with shear thinning solutions, despite the device being commonly used to describe turbulence with complex suspensions of bubbles, cells, fibres or sediments in Newtonian fluids (Nagami and Saito 2013; San et al. 2017; Rastello et al. 2017; Mahamod et al. 2017; Colomer et al. 2019; Matinpour et al. 2019), or the interactions of homogeneous isotropic turbulence with solid boundaries (McCorquodale and Munro 2017, 2018a) or density stratifications (Thompson and Turner 1975; Hopfinger and Toly 1976; Xuequan and Hopfinger 1986; Verso et al. 2017).

In Lacassagne et al. (2019b), the flow displays several features specifically induced by the addition of polymer and the shear thinning property, such as an enhanced mean flow in the dilute regime, and variable decay rates and enhanced anisotropy of turbulence. Such features were similarly expected from studies on polymer solutions in other types of flows. While the properties of turbulence are checked to be homogeneous in the horizontal dimension of the PIV plane and can thus be assumed homogeneous also in the out of plane horizontal direction, one can not account for the three dimensional aspect of the mean flow structures (which would have required extensive additional measurements in parallel and orthogonal vertical planes). Moreover, the 2D2C (two dimensions, two velocity components) information does not allow to compute the true local shear rate, effective local viscosity, and shear stresses necessary to understand the mechanisms behind the flow changes observed.

In the present work, a 3D Particle tracking velocity (3D-PTV) method is applied to measure the flow velocity in oscillating grid flows of shear thinning, inelastic XG solutions.

The grid stirring conditions are similar to the ones used in the previous study (Lacassagne et al. 2019b), the same type of DPS are used (XG dissolved in distilled water), and focus is made on the dilute concentration regime. The objectives are threefold: first to compare this 3D-PTV approach to the available 2D PIV data, second, to use the three dimensional aspect to gain insight into the mean flow structure, and finally, to see how it can be used to extend the analysis of OGT in such fluids using the additional 3D3C information.

It is worth noting that the data collected by 3D-PTV is intrinsically Lagrangian. To achieve the first objective, the possibility of projecting Lagrangian velocity information on a Cartesian Eulerian grid so that it can be compared to PIV data has to be discussed here. However, the Lagrangian nature of the velocity measurement can be used as it is to extract relevant information on turbulence properties (Stelzenmuller et al. 2017; Polanco et al. 2018; Shnapp and Liberzon 2018) and on polymer turbulence interaction, as done in the elastic case for example by Liberzon et al. (2005), Crawford et al. (2008), Holzner et al. (2008). This Lagrangian analysis is beyond the scope of the present paper, but it still places the present data in a promising context for future investigations. A following objective would be to use the Lagrangian information to improve, for polymer solutions, Lagrangian stochastic modelling [as developed by Aguirre et al. (2006), Vinkovic (2005)].

In what follows, the experimental procedure is first presented: the oscillating grid set-up is described, working fluid’s properties are listed. The particle tracking device and innovative Shake the Box algorithm, allowing for particle tracking at high seeding concentration, are presented. Lagrangian results are then displayed, and their Eulerian projection is detailed and compared to PIV results by Lacassagne et al. (2019b). Finally, the perspective and limits of additional analysis offered by the 3D nature of measurements are discussed.

2 Experiments

Fig. 1
figure 1

Sketch of the experimental setup

Full size image

Experiments are similar to the ones performed by Lacassagne et al. (2019b) also detailed in Lacassagne (2018) for which liquid phase velocity has been measured using planar PIV. The flow generated by an oscillating grid in water or shear thinning polymer solutions of XG is studied, focusing on three concentrations in the dilute regime of XG entanglement. The experimental set-up is summarized in Fig. 1. The Volume Of Interest (VOI) is defined as the volume of fluid above the top grid position and below free surface, 175 mm wide in the x dimension and 80 mm deep in the y dimension. This volume is chosen large enough so that both mean flow structures and turbulence decay laws can be captured, in accordance with the particle tracking system capacity. Details on the working fluids, the oscillating grid apparatus, and the particle tracking system are provided in what follows.

2.1 Working fluids

The working fluid used in the tank can be either water or non-Newtonian, shear thinning solutions. Shear-thinning properties are conferred to the liquid by addition of XG, into distilled water. Here XG produced by Kelco under the commercial name Keltrol CG-T is used. Its average molar mass is \(M_\mathrm{w}=3.4\times 10^6\) g mol\(^{-1}\) and its polydispersity is equal to 1.12 (Rodd et al. 2000). XG is chosen for its high resistance to strong shear, extreme temperature and pH conditions (Garcia-Ochoa et al. 2000). Such features are useful when using it nearby a rigid oscillating grid where shear can be locally high and could destroy other long chained polymers (Vonlanthen and Monkewitz 2013). Three different mass concentrations \(C_\mathrm{XG}\) are studied, expressed in ppm (parts per million). The shear thinning behaviour is modelled by a Carreau–Yasuda (CY) equation :

$$\begin{aligned} \frac{\mu -\mu _{\infty }}{\mu _0-\mu _{\infty }}=\left( 1+\left( t_\mathrm{CY}\dot{\gamma }\right) ^a\right) ^{\frac{p-1}{a}} \end{aligned}$$
(1)

where the zero shear rate and infinite shear rate Newtonian viscosities (resp. \(\mu _0\) and \(\mu _{\infty }\)), characteristic time-scale \(t_\mathrm{CY}\), and exponents a and p depend on the polymer concentration \(C_\mathrm{XG}\). Their values are reported in Fig. 2 and Table 1.

Fig. 2
figure 2

Viscosity curves and Carreau–Yasuda fitting

Full size image
Table 1 Carreau–Yasuda fitting parameters for the shear thinning behaviour of XG solutions at various concentrations
Full size table

Concentrations are chosen inside the dilute regime of entanglement for XG in aqueous salt-free solutions defined by Cuvelier and Launay (1986) and Wyatt and Liberatore (2009). The 10 ppm and 25 ppm cases are hereinafter denoted XG10 and XG25.

2.2 Oscillating grid setup

Turbulence is generated in a transparent tank of a 277 mm by 277 mm inner cross section. The fluid height is set at \(H_\mathrm{f}=450\) mm and the distance between the surface and the average grid position is 250 mm. The vertical axis, oriented upwards, is noted z, and x and y are the axis defined by the grid bars. The origin of the reference frame is placed at the grid average position (\(z=0\)) at the crossing between the two central bars. In this study as in Lacassagne et al. (2019a, b), only polymer concentration is varied and all oscillations parameters are kept constant. The grid has square section bars of width equal to 7 mm, and the mesh parameter (distance between two grid bars) is \(M=35\) mm. This yields a solidity of 0.36, below the maximum value of 0.4 recommended by Thompson and Turner (1975). The frequency is fixed at \(f=1\) Hz and the stroke at \(S=45\) mm.

2.3 Particle tracking

2.3.1 Seeding and image acquisition

Seeding particles are DANTEC hollow glass spheres of 10 \(\mu \)m nominal diameter. The particle concentration used is approximately 0.03 g/L. The particle Stokes number is computed as \(\mathrm{{St}}=\frac{1}{18}\frac{\rho _p d_p^2 f}{\rho \nu }\) and it is found to be of order of magnitude always lower than \(\mathcal {O}(10^{-4})\) indicating that particles are good flow tracers. Particles are illuminated by a \(300 \times 100\) mm\(^2\) LED (FLASHLIGHT 300 array, LaVision). The recording system is a four-camera Minishaker L box (LaVision) of stereoscopic angle equal to \(11^\circ \), equipped with 12 mm focal length lenses placed at a 300 mm working distance from the central vertical plane of the volume of interest. The flashlight and set of cameras are triggered simultaneously using a LaVision Programmable Timing Unit (PTU) driven by DaVis 10 acquisition software. The whole system is operated at an acquisition frequency of \(f_\mathrm{a}=40\) fps (\(1/f_\mathrm{a}\) being an order of magnitude smaller than the fastest Kolmogorov time scale found in the water case). Multiple separate subsets of 2000 images corresponding to 50 s of measurement (50 grid oscillations) are acquired for each working fluid. This subset partition is needed to optimize the data recording and processing operations.

2.3.2 Image pre-treatment

Spatial calibration of the VOI is achieved by recording of a reference pattern placed in the working fluid prior to experiments. A LaVision stereo reference pattern is used, and placed in the \(y=0\) mm plane. This reference pattern is made of a crenellated dark plate with two series of evenly distributed white dots, inside and outside the gaps. Images of the two vertical planes of dots are acquired by each of the four cameras, and used by DaVis software for spatial reconstruction of the VOI.

Preliminary particle images are then acquired and used to perform a self calibration procedure (Wieneke 2018). This enables a refinement of the volumetric spatial calibration and of the optical transfer function used in the tracking algorithm (Schanz et al. 2016). Calibration is performed in water but valid also for DPS, as the optical index is not modified by XG addition in the dilute regime.

After their recording, particle images at each time t are pre-treated using the following operations

  1. 1.

    Background noise removal, by subtraction of the local sliding minimum value over a sample of 7 successive images (\(t-3\) to \(t+3\)).

  2. 2.

    Pixel intensity normalization by local average over surrounding square of 30 by 30 pixels.

  3. 3.

    Particle shape homogenisation by Gaussian smoothing using 3 by 3 pixels square windows.

  4. 4.

    Gray levels rescaling (subtraction of a fixed gray level count and multiplication by a fixed gain), allowing to artificially enhance the gray level dynamic range.

This pre-treatment process is used to improve the quality of particle images and ease their detection and tracking by the algorithm. It improves the sensitivity (number of detected particles) and selectivity (only particles detected) of the overall process. An example of a particle image before (a, b) and after (c, d) pre-treatment is presented in Fig. 3. The STB algorithm is then applied to pre-treated images using the DaVis software.

Fig. 3
figure 3

Example of particle image from camera 1, water run, before (a, b) and after pre-treatment (c, d). b, d Are zooms of respectively (a) and (c) on the same group of particles. Dashed circles stress the location of a dust particle crossing the VOI (blue, mixed) and of a shaded spot on the camera sensor (orange, dashed) efficiently removed by the pre-treatment

Full size image

2.3.3 Particle tracking velocimetry and Shake the Box algorithm

PTV methods are based on the identification and tracking of individual particle motions. They thus provide Lagrangian information on fluid particles. Assuming a particle can be tracked at several successive locations, and if it does follow even the fastest structures of the flow, the PTV method is then intrinsically time resolved since its velocity can be computed at any location and time along its continuous trajectory (Agüí and Jiménez 1987; Schanz et al. 2016). As for PIV, PTV can be either two dimensional if one uses one or two cameras (2D-PTV), or three dimensional with three or more (3D-PTV). Indeed identifying a particle from at least three angles of view allows its location in the 3D space at successive instants, and to measure the three components of its Lagrangian velocity (Kasagi and Nishino 1991). The major limit of PTV techniques resides in the unambiguous identification of particles and their tracking between successive images. Increasing the seeding particle concentration to enhance the spatial resolution of measurement results in a reduced efficiency of commonly used nearest neighbour search methods or particle screening (Cambonie and Aider 2014).

The Shake the Box algorithm is a Lagrangian tracking method developed by Schanz et al. (2016) and implemented in the latest version of LaVision DaVis 10 software, which offers an alternative to this nearest neighbour search, allowing to use typically higher seeding particle densities (Terra et al. 2019). Its principle is detailed in Schanz et al. (2016). Note that other hardware-based methods exist to achieve high seeding densities, such as scanning 3D-PTV (Hoyer et al. 2005).

The main idea is to use for each tracked particle, the information of its trajectory at previous times to predict its position at the subsequent time step. An image matching technique is then applied to improve the precision of the localisation: the particle image (or “box”) is “shook” around its predicted location until a maximum correlation is found (in a way similar to PIV cross correlation techniques), indicating that the new particle position has been identified. The first step makes the technique inherently time resolved, and this strong interaction with the temporal dimension makes it possible to extract information on local velocity and acceleration. Along with time resolution, the second specificity, namely the “shaking”, enables to track particles at high densities (above 0.1 particles per pixel, ppp) while almost completely suppressing ghost particles usually associated encountered with other iterative particle reconstruction methods (Schanz et al. 2016).

When pursuing 3D3C analysis of a flow, this method positions itself as a quicker and easier to implement than now commonly used Tomographic PIV approaches (Elsinga et al. 2006; Westerweel et al. 2013), in that the tracking algorithm does not involve full volumetric image cross correlation and is thus typically 10 times faster that Tomographic PIV correlation processes (Schanz et al. 2016; Aguirre-Pablo et al. 2019; Michaelis and Wieneke 2019).

2.3.4 Tracked particles

For each 2000 images subset, particles are triangulated and localized in space by the algorithm. They are associated to an active trajectory when at least 4 successive positions have been identified for the same particle. In the present experiments, about 15,000 particles are included in active trajectories at any instant. The volumetric particle density for active particles is thus 3.9 particles/cm\(^3\), corresponding to average inter-particle distance of respectively 6.35 mm.

3 Results

3.1 Trajectories and flow structures

Fig. 4
figure 4

Example of particle trajectories in a 0.275 s time sample for 25 ppm XG solution. The horizontal shaded rectangle denotes the location of the free surface. Black arrows and grey dots are a guide to the eye respectively illustrating the main flow direction and the center of side vortices

Full size image

An example of particle trajectories (thus for tracked particles only) for the XG25 run is displayed in Fig. 4. The trajectories visualisation is arbitrarily limited to 11 successive positions (corresponding to a time sampling of 0.275 s) for the sake of readability. Trajectories are coloured by the vertical velocity magnitude.

Such Lagrangian indicators allows to observe characteristic features of the (Eulerian) flow generated by an oscillating grid in dilute XG solution at 25 ppm (Lacassagne et al. 2019b): a central up-going motion associated with two side vortices. The intensity of the up-going motion, here expressed by the velocity magnitude in colorbar, quickly decreases with increasing distance to the grid in the central region. From this Lagrangian perspective, it is yet difficult to describe the mapping of turbulent velocity fluctuations generated by the grid motion. To do so, one can translate the data into an Eulerian description of the flow. This is discussed in Sect. 3.2, and a quantitative comparison with PIV data from Lacassagne et al. (2019b) is presented for both mean flow and turbulent velocities, for all three working fluids.

3.2 Eulerian reconstruction of flow statistics

Table 2 Eulerian projection parameters applied to all three working fluids
Full size table

To reconstruct Eulerian velocity fields from Lagrangian data, the VOI is first meshed by a Cartesian grid with cubic volumes of \(V \times V \times V\) px\(^3\). Note that the interest is here to compare Eulerian statistics: the following procedure is thus not a traditional interpolation routine of individual, instantaneous velocity fields (Agüí and Jiménez 1987; Stüer and Blaser 2000), but rather a statistical projection or binning (Godbersen and Schröder 2020). For each Eulerian volume, average and standard deviation of Lagrangian particle velocities passing through the volume of interest during a considered time interval are computed (Kasagi and Nishino 1991). This ultimately yields 3D 3C Eulerian average and standard deviation velocity fields with a spatial resolution of V. Any vertical or horizontal slice of this volume can then extracted to get a two dimensional, three component, Eulerian velocity field. A small V results in a higher spatial resolution of this spatial mean field, but also in a lower number of particles going through each volume of measurement in the given time, and hence in a possibly lower quality statistical convergence. The statistical convergence of Eulerian fields deduced from this reconstruction is discussed in Sect. 3.2.2. A lower threshold for particle count under which no velocity statistics are computed can be fixed. Thresholds listed in Table 2 correspond to a deletion of less than \(10\%\) of projected Eulerian vectors (excluding the 2 outer rows and columns of volume of control of the VOI that are prone to side effects, poor illumination, and in which the number of tracked particles is systematically lower).

Results of various Eulerian reconstructions are compared to each other, but also to inherently Eulerian 2D-PIV Data in similar flow conditions published in Lacassagne et al. (2019b). In the previous study, only one vertical plane has been investigated, parallel to one of the tank’s wall and aligned with the central bar (\(y=0\)). This central vertical plane is thus used as a probing plane to evaluate our measurement and our reconstruction. Note that it could also be used later to see in what extent Lagrangian statistics will depend on tested parameters, after comparison with the Eulerian results. In the 3D-PTV data, this PIV-equivalent plane corresponds to the central vertical slice (at \(y=0\)) of the 3D 3C projected velocity fields (average or standard deviation). In the following analysis and if not stated otherwise, reconstructed Eulerian velocity fields are considered in this slice only.

The mean flow is described by 2D norm of mean velocity fields, accessible trough both PIV and 3D-PTV, and computed as

$$\begin{aligned} U_\mathrm{2D}=\sqrt{\overline{U}_x^2+\overline{U}_z^2} \end{aligned}$$
(2)

For a quantitative comparison, profiles are extracted at \(z=2.5\) S from both PIV and projected 3D-PTV data fields. Still on this same central plane, turbulence properties are quantified by plotting width averaged (average along x) vertical profiles (plot along z) of horizontal velocity fluctuations root mean square. This quantity will here be called \(u^{\prime }_x\). It allows us to describe oscillating grid turbulence in the context the description made by Hopfinger and Toly (1976). From Lacassagne et al. (2019b), a power law decay with a slight variation of the exponent with polymer concentration is expected. Note that a similar analysis has been performed for either the second horizontal velocity component (\(u^{\prime }_y\)) or the vertical one (\(u^{\prime }_z\)), and the results agree with the conclusions presented hereinafter.

3.2.1 Effective particle count and spatial resolution

During Eulerian reconstruction, the total number of particles identified as belonging to each interrogation volume, and used in Eulerian statistics can be counted. The average amount of particles going through a given volume of interest on a 2000 snapshots sample is reported in Table 3. It can be noted that it is largely higher than the threshold indicated in Table 2. This is done for all working fluids, and compared for the three spatial resolution V considered for the XG25 case, all in the central plane of study. Excluding side effects for, particle counts are constant in most of the central plane, for \(2.5<Z<5.5M\) and \(-3.2M<X<3.2M\). Uncertainties are deduced as the standard deviation of particle count over the X dimension at a constant Z.

Table 3 Effective particle count
Full size table

The systematically lower count values for water is attributed to a lower particle mass added in the tank prior to the experiment. Using the previous results and knowing that particles are counted over 2000 snapshots, one can compute the average value of particles per volume of interest and per snapshot, also displayed in Table 3.

Fig. 5
figure 5

Influence of spatial resolution (32, 48 or 64 pixel side volumes) of the Eulerian projection on the horizontal turbulence profiles (\(u^{\prime }_x\)) scaled by the product fS, for the three working fluids. A zoom insert is associated for each case

Full size image

As evidenced by the XG25 case, higher spatial resolution yields lower particle counts in each volume and thus more scattered data on Fig. 5 (see also this figure for water and the XG10 case). However the shape of the curves are preserved both qualitatively and quantitatively, regardless of the spatial resolution chosen, within the tested range. This checked to be valid for all working fluids (Fig. 5), and the \(48 \times 48 \times 48\) px\(^3\) resolution is chosen for the rest of this study as a best compromise between particle count and data scattering.

3.2.2 Statistical convergence

Fig. 6
figure 6

Statistical convergence of \(u^{\prime }_x\) profiles for the example of the XG10 case. a Profiles of \(u^{\prime }_x/fS\) versus z/S for various \(N_s\). b Values of \(u^{\prime }_x\) extracted at \(z=3M \simeq 2.3S\) from these profiles and additional ones at other \(N_s\) values [not shown in (a)], as a function of \(N_S\)

Full size image

To check the statistical convergence of the chosen sampled profiles, statistical analysis is performed on several data sets of increasing number \(N_s\) of snapshots. The effective particle count previously allowed us to notice that for a given snapshots, some Eulerian volumes of the VOI may be free of particles. Using \(N_s\) snapshots thus does not necessarily mean that the average and rms Eulerian velocity will be computed using \(N_s\) particles, and it is of paramount importance to check statistical convergence.

Figure 6 displays an example (XG10) of the evolution of the vertical profile of horizontal turbulence with \(N_s\). On sub-figure (a), it appears than the profiles converge to a given curve with increasing \(N_s\). This convergence is evidenced by probing the value of \(u^{\prime }_x\) at a given altitude \(z=3M\simeq 2.3S\) a plotting it as a function of \(N_s\) [sub-figure (b), with additional points corresponding to profiles no shown in (a) for the sake of readability].

It is worth noting that since \(u^{\prime }_x\) is a second order statistical quantity, its convergence should be harder to achieve than that of the mean flow. Yet the convergence of \(u^{\prime }_x\) values is eased by the fact that the velocity information is already spatially averaged along x. Statistical convergence has thus also been tested for the mean flow (not shown here) and it is found that whenever \(N_s\) is sufficient to ensure convergence of \(u^{\prime }_x\), it is also sufficient for mean values.

3.2.3 Mean flow

Fig. 7
figure 7

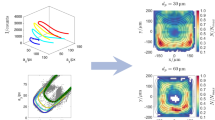
2D norm of mean flow velocity fields \(U_{2D}=\sqrt{\overline{U}_x^2+\overline{U}_z^2}\) measured by PIV in Lacassagne et al. (2019b) (central column) and accessed by Eulerian reconstruction of 3D-PTV data (left column). Quantitative comparison of horizontal profiles of \(U_{2D}\) at \(z=2.5S\) (horizontal white lines in the first two columns) is provided for each working fluid in the right column. Shaded areas correspond to \(\pm 20\%\) (light gray/pink) and \(\pm 10\%\) (darker gray/pink) uncertainties around each profile

Full size image

The mean flow (temporally averaged Eulerian velocities) are first compared through the observation of the 2D norm. This norm involves only the 2 components accessible by the reference PIV measurements, namely \(\overline{U}_x\) and \(\overline{U}_z\) (see Eq. 2). It is made non dimensional scaling by the (fS) product and its fields are represented in Fig. 7, left column for projected 3D-PTV results and central column for PIV results of Lacassagne et al. (2019b) (\(y=0\) slice of the 3D-PTV projected velocity field). A first qualitative comparison allows to see that

  • The mean flow enhancement effect described by Lacassagne et al. (2019b) is once again observed, with the apparition, upon polymer addition, of a central high velocity core corresponding to an up-going motion associated to side vortices.

  • Even if the mean flow enhancement trend is preserved, mean flow mappings for water and XG10 are qualitatively slightly different between the 3D-PTV and PIV cases, while quite similar for the XG25 case.

This last point is further evidenced by the horizontal profile plots in the right column of Fig. 7. The order of magnitudes and global increase with polymer concentrations are respected but the trend for XG10 and water are quite different, whereas the central peak is retrieved for XG25, with yet a lower amplitude.

The comparison between the two data sets is associated to several sources of imprecision. The first ones are the velocity measurement uncertainties relative to each method, that are accounted for by the shaded areas. The second one is inherent to the Eulerian projection method or 3D-PTV results: the width of the central vertical plane (slice) is set by the size of a voxel in the y direction, here 2.9 mm. This is more than 10 times larger than the laser sheet thickness of PIV measurements reported in Lacassagne et al. (2019b), meaning that 3D-PTV results are smoothed on a thicker slice compared to PIV measurements. The final explanation can be that of a poorly repeatable mean flow, not from a statistical point of view, but specific to OGT itself.

The lack of reproducibility of mean flows in oscillating grid stirred tanks filled with water is a well known issue of such devices. It is attributed to the high sensitivity the flow to initial conditions or default in grid/tank alignments (McKenna and McGillis 2004; Herlina 2005; McCorquodale and Munro 2018b). It is interesting to notice that here the more reproducible mean flow is the more structured and strong one. It appears that while structuring and enhancing the mean flow in the tank as described by Lacassagne et al. (2019b), the addition of polymer and the shear thinning property also tends to make it more reproducible. Due to higher initial viscosity some variations of initial conditions may be attenuated. This however would need to be confirmed by dedicated reproducibility experiments.

The 3D-PTV method employed here allows to gain additional information on the three-dimensional structure of the mean flow. Figure 8 shows the mean Eulerian velocity fields in three dimensions (vectors are colored by the velocity magnitude). The main features evidenced from the particle trajectories (Fig. 4) and 2D projections (Fig. 7) are confirmed: polymer addition enhances the central-up going motion and corresponding down-going velocities at the walls. From this figure however, it becomes clear that the mean flow in water and the most dilute polymer case are weaker but more complex, associated with horizontal swirling motion (see Fig. 8b), x/M=1; z/S=4).

Fig. 8
figure 8

Mean flow 3D Eulerian velocity fields \(\overline{U}\) coloured by the velocity magnitude \(\left| \overline{U}\right| =\sqrt{\overline{U}_x^2+\overline{U}_y^2+\overline{U}_z^2}\) for water (a), \(C_{XG}=10\) ppm (b) and \(C_{XG}=25\) ppm (c)

Full size image

3.2.4 Turbulence properties

The \(u^{\prime }_x\) profiles, which have already been displayed in Figs. 5 and 6, are finally compared to the PIV data of Lacassagne et al. (2019b) in Fig. 9.

Fig. 9
figure 9

a–c Width averaged vertical profiles of the RMS of horizontal velocity fluctuations along x (\(u^{\prime }_x\)) for the three working fluid considered. Profiles are compared to results obtained by Lacassagne et al. (2019b) using PIV. Shaded area correspond to a \(\pm 10\%\) uncertainty (and also \(\pm 20\%\) for water) around PIV profiles. d) Power law exponents (empty markers) derived from power law fitting of 3D-PTV profiles in (a–c). Error bar are 5\(\%\) confidence intervals on the the fitting parameter. Values and uncertainty reported in Lacassagne et al. (2019b) are added for comparison (full markers)

Full size image

The three set of curves are found to collapse surprisingly well, compared to mean flow profiles and in view of the usual variations around power law trends usually evidenced in the literature for water (Lacassagne et al. 2019b; Herlina 2005; Verso et al. 2017). Note that for this supposedly horizontally homogeneous turbulence, the differences in central plane thickness is of minor influence on the measured velocity fluctuations magnitude. The values of \(u^{\prime }_x\) obtained are very close to the PIV reference. For the polymer solutions, almost all 3D-PTV point fall within the \(\pm 10 \%\) uncertainty area drawn around PIV profiles, so one can say that the collapse is evidenced up to a \(\pm 10\%\) uncertainty. For water, a \(\pm 20\%\) uncertainty area is needed. In both the PIV and the 3D-PTV measurements, turbulence intensity decreases with increasing polymer concentration.

As evidenced in Lacassagne et al. (2019b) and from Figs. 7 and 9, turbulence intensity is always of at least the same order of magnitude than the mean flow. A basic feature of OGT is that the weaker mean flow is (almost) not involved in turbulence production mechanisms, turbulence being generated by the strong oscillatory flow in the grid swept zone (Lacassagne et al. 2019a). Poor reproducibility of the mean flow thus does not necessarily imply poor reproducibility of turbulence properties. Turbulence is here the topic of our study. The fact that the tolerances for matching turbulent profiles are lower than those required around mean flow profiles, and satisfactory, is an interesting result confirming the previous statement.

Based on the respective trends, the overall decay laws exponents \(-n\) are estimated by fitting power law functions to 3D-PTV profiles (Fig. 9d, empty markers). Values of \(-n\) reported in Lacassagne et al. (2019b) and their uncertainties are also displayed on the figure (full markers). It should be noted that estimating precisely power law exponents from the small z/S range available with 3D-PTV here can be difficult. However, the results are still in good agreement: the trend in concentration is retrieved, and the differences in exponent values stays within the range of uncertainty.

All of the above being mentioned, Fig. 9 consists in an important result of the present work. It shows that the properties of oscillating grid turbulence usually measured by PIV in grid stirred tanks can also be accessed by Eulerian reconstruction of 3D-PTV (Lagrangian) measurements. It thus legitimates the use of 3D-PTV in such flows, even if differences exist. Last but not least, it also opens new perspectives of investigation on the mechanisms of OGT in water and polymer solutions, thanks to the volumetric, time resolved data, either used after Eulerian reconstruction or in its initial Lagrangian state. This is the object of the following discussion and conclusions.

4 Discussion

4.1 Instantaneous Eulerian reconstruction

The Lagrangian information is instantaneous, time resolved, and volumetric even though not available on a Cartesian or regular mesh. The Eulerian projection presented here is statistical: the instantaneous information and time resolution asset is lost. However, it would be possible to project instantaneous Lagrangian velocities onto an Eulerian mesh: the only requirement would be to use only particles from one given instantaneous Lagrangian snapshot to compute the Eulerian velocity value in each sampling volume. This however requires a significant number of particle to be present in each volume of control at each time step. Here we saw in Sect. 3.2.1 that this number is at best of an order of magnitude of 10 for the coarsest spatial resolution. It thus should be kept in mind that the Eulerian velocity thus computed would be based on a rather small particle sample. Moreover, for the finest spatial resolution here studied, the particle count per snapshot per volume is typically below one. This indicates that for some snapshots and some volumes, no particle is present and thus no Eulerian velocity computation is possible. It would thus lead to “holes” in the projected Eulerian velocity fields that would then need to be filled or avoided using another interpolation post-processing (Agüí and Jiménez 1987; Stüer and Blaser 2000; Cambonie and Aider 2014; Schneiders and Scarano 2016; Steinmann et al. 2019).

In principle, interpolation of instantaneous Eulerian fields (and not statistical projection such as done here), would need to be done on Cartesian grids with mesh sizes at least twice the typical inter-particle distance (Agüí and Jiménez 1987), to satisfy the Nyquist criterion. Projecting reliable instantaneous Eulerian velocity fields would require in this case either to increase the seeding particle density or to further reduce the spatial resolution. The outputs of such an instantaneous projection would yet be very interesting, in that they would allow to access instantaneous and 3D fluctuating velocity fields after subtraction of the time averaged 3D velocity field. This could for example help to visualize 3D turbulent velocity structures rising from the grid to the interface, or compute instantaneous pressure, shear stress, or viscosity fluctuations.

Such instantaneous reconstructions have already been achieved (in Newtonian fluids), for example by Cambonie (2012, 2015) and co-workers for the study of pseudo periodic organization of jets in cross flows. Recently, major progress towards the possibility of Eulerian projections at high grid resolution have been made. They stem from the use of modern data assimilation utilizing physical laws (e.g Navier Stokes and vorticity transport equations) to interpolate the projection gaps (Schneiders and Scarano 2016). Such methods have been implemented in DaVis latest releases under the name VIC+ or VIC\(\#\) (Jeon et al. 2018b).

4.2 Three dimensional flow structures

Fig. 10
figure 10

Isosurface of vertical mean velocity \(\overline{U}_z\) scaled by fS at values \(-0.25\) (a), \(-0.075\) (b), 0.075 (c) and 0.25 (d) (XG25 case). Black arrows point the corresponding surface and indicate the vertical velocity direction (up for \(\overline{U}_z\)>0, down otherwise). The gray rectangle denotes the location of the free surface. Surface are colored by the local shear rate magnitude \(\left| \dot{\gamma }\right| \) made non dimensional dividing by f

Full size image

Despite the lost of the temporal information through Eulerian projection, three dimensional mean flow structures are still accessible through both Eulerian and Lagrangian description, which is a major advance compared to the existing PIV study. The up-going motion and side vortices is qualitatively retrieved and can be evidenced by looking at Fig. 4. After projection, a 3D Eulerian description of the mean flow for the XG25 case is available and presented in Fig. 10. Two iso-surfaces of vertical mean velocity \(\overline{U}_z\) scaled by fS are drawn at values \(-0.25\) (a), \(-0.075\) (b), 0.075 (c) and 0.25 (d). Surfaces are coloured by the local shear rate magnitude, computed as

$$\begin{aligned} \left| \dot{\gamma }\right| = \sqrt{0.5\left( \partial _i \overline{U}_j +\partial _j \overline{U}_i\right) ^2} \end{aligned}$$
(3)

(and made non dimensional dividing by f). i and j are equal to x, y or z and the Einstein summation convention is used. In the light of those results, it becomes possible to compute an effective local viscosity mapping induced by the mean flow established in the tanks with polymer solutions, and discuss the impact of shear variable viscosity on turbulence production and repartition in the tank. This mapping provides local yet time-averaged information on the viscosity. A possible extension would be to use accurately projected instantaneous Eulerian velocity fields [obtained for example by data assimilation methods (Schneiders and Scarano 2016; Jeon et al. 2018b)] to estimate instantaneous, local, effective viscosity mappings.

5 Conclusion and perspectives

As a conclusion, this work presents innovative 3D-PTV measurements of Lagrangian velocities in oscillating grid turbulence, in water and dilute polymer solutions. The shake the box algorithm implemented in DaVis 10 is used as a quick and efficient tracking way to track particles, establish their trajectory, and compute their Lagrangian velocities along it. Comparison with PIV data available from Lacassagne et al. (2019b) shows that 3D-PTV results can be used to estimate first (mean flow) and second order (rms of turbulent fluctuations) Eulerian statistics of OGT in water and dilute polymer solutions. The discrepancy in the mean flow results is attributed to the poor repeatability of mean flow structures inherent to oscillating grid flows in water. This however doesn’t pass on to turbulence decay laws, which are found to match the PIV profiles quite well. The relatively good comparison between mean flows obtained for the higher polymer concentration case suggests that the mean flow enhancement could be associated with an increase of its reproducibility.

Further three dimensional insight on the mean Eulerian velocity fields can be gained from 3D-PTV measurements. Projection of instantaneous Eulerian velocity fields would require further optimisation of both the seeding concentration and the resolution of Eulerian meshing. Yet statistical 3D3C Eulerian projected results already open the road to the computation and analysis of quantities that require velocity gradients in all three space dimensions (shear rate, viscosity, shear stress...), and would otherwise only be accessible by tomographic-PIV (Jeon et al. 2018a) or through scanning of the volume of measurement by several planar PIV measurement planes.

Finally, the nature of the available data opens many perspectives in terms of Lagrangian analysis of turbulence properties (Vinkovic 2005; Aguirre et al. 2006; Polanco et al. 2018; Stelzenmuller et al. 2017), which can bring an insight on mixing and de-mixing properties of turbulence via for example the analysis of forward and backward particles pair dispersion, (Polanco et al. 2018), or on the polymer-turbulence interactions via the analysis of structure functions (Ouellette et al. 2009) and stretching of material elements (Liberzon et al. 2005).