The ill-posedness of derivative interpolation and regularized derivative interpolation for band-limited functions by sampling

Abstract

In this paper, the ill-posedness of derivative interpolation is discussed, and a regularized derivative interpolation for band-limited signals is presented. The ill-posedness is analyzed by the Shannon sampling theorem. The convergence of the regularized derivative interpolation is studied by the combination of a regularized Fourier transform and the Shannon sampling theorem. The error estimation is given, and high-order derivatives are also considered. The algorithm of the regularized derivative interpolation is compared with derivative interpolation using some other algorithms.

1 Introduction

The computation of the derivative is widely applied in engineering, signal processing, and neural networks [1–3]. It is also widely applied in complex dynamical systems in networks [4].

In this section, we describe the problem of finding the derivative of band-limited signals by the Shannon sampling theorem [5]. Recall that a function is called Ω-band-limited if its Fourier transform has the property that $\hat f(\omega)=0$ for every ω∉[−Ω,Ω].

Shannon sampling theorem If f∈L²(R) and is Ω-band-limited, then it can be exactly reconstructed from its samples f(nh):

$$ f(t)={\lim}_{N\rightarrow \infty} \sum_{n=-N}^{N} \text{sinc} \Omega(t-nh) f(nh), $$

(1)

where $\text {sinc} \Omega (t-nh):= \frac {\sin \Omega (t-nh)} {\Omega (t-nh)}$ and h=π/Ω. Here, the convergence is in L² and uniform on R, which means the series approaches f(t) according to the L²-norm and L^∞-norm in R.

By the inversion formula, if f is band-limited

$$ \textbf{F}\ ^{-1} (\hat f)(t)= f(t)=\frac 1 {2\pi} \int_{-\Omega}^{\Omega}\hat f(\omega)e^{i\omega t}d\omega,~~\mbox{a.e.}~~ t\in \bf R. $$

(2)

By the Paley-Wiener theorem [6] p.67, f is real analytic.

It is an elementary property of the Fourier transform that F[f^(k)(t)]=(iω)^kF[f(t)], where f^(k)(t) is the kth derivative of f(t); consequently, if f is band-limited so is f^(k).

In [7], Marks presented an algorithm to find the derivative of band-limited signals by the sampling theorem:

$$ f^{(k)}(t)=\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} f(nh). $$

(3)

Here, again, the convergence is in L² and uniform on R.

In this paper, we study the problem of computing f^(k)(t) in the case the samples {f(nh)} are noisy:

$$ f(nh)\,=\,f_{E}\,+\,\eta_{n}=f_{E}(nh)+\eta(nh),~~~~~~~~||\{\eta_{n}\}||_{l^{\infty}}\leq \delta $$

(4)

where f_E(nh) is the exact signal and {η_n}={η(nh)} is the noise with the bound δ>0.

It was pointed out in [7] that the interpolation noise level increases significantly with k. In [8], Ignjatovic stated that numerical evaluation of higher-order derivatives of a signal from its samples is very noise sensitive and presented a motivation for the notions of chromatic derivatives. The Chromatic derivatives in [8] is too special since it is the operator polynomial ${\mathcal {K}}^{n}_{t}=(-i)^{n} P^{L}_{n}(i\frac d {dt})$, where $P^{L}_{n}$ are the normalized and scaled Legendre polynomials. A Fourier truncation method to compute high-order numerical derivatives was proposed in [9], and we will compare with the method in the simulation section. The advantage of [9] is that it does not require the function to be band-limited. The disadvantage is that the accuracy is not good for band-limited functions. In [10], the series to approximate a band-limited function and its derivative is given, but the ill-posedness and noise are not considered. In [11], an optimal algorithm for approximating band-limited functions from localized sampling is given. It is shown that a certain truncated series is the best estimate for using the local information operator; but the noisy case is not considered which means η_n=0 in (4). In [12], the noisy case is considered for approximating band-limited functions, but the computation of the derivatives is not considered in the noisy case.

In [13], pp. 235–249, cubic smoothing spline is discussed in noisy cases, but no proof of convergence is given. In [14–16], regularization methods are used to find the stable solutions in the computation of derivatives. In [14, 16], the approximation error is measured with respect to L²-norm. This means the regularized solution approximates the exact solution according to the L²-norm. Furthermore, the noise models are different: in [14], the disturbance is assumed to be bounded in the L²-norm, whereas in [16], it is bounded in the maximum norm. On a finite interval in R, the maximum norm is more strict. In [14], the error of the first derivative is given by $O(h) + O(\sqrt \delta)$. In [16], for the regularization parameter α=δ², the error of the jth derivative is given by

$$\begin{aligned} ||f^{(j)}_{\alpha}-f^{(j)}||_{L^{2}}&=\left[ \int_{0}^{1}|f^{(j)}_{\alpha}(t) -f^{(j)}(t)|^{2} dt \right]^{\frac 1 2}\\&\quad = O\left(h^{k-j}\right) + O\left(\delta^{\frac {k-j} k}\right) \end{aligned} $$

for 0≤j≤k−1 and f∈H^k(0,1)={g:g∈L²(0,1), g^(k)∈L²(0,1)} in the L²-norm which means the distance in H^k(0,1) is measured in the L²-norm. Here, $f^{(j)}_{\alpha }$ is the approximate jth derivative by regularization, δ is the error bound in (4), and h is the step size for the derivative interpolation. In the current paper, we measure the approximation error in the L^∞-norm on any finite interval in R and assume additive l^∞ noise. The notion of robustness naturally differs significantly for these different norms and spaces since the regularized solution approximates the exact solution according to the maximum norm on any finite interval in R implies the regularized solution approximates the exact solution according to the L²-norm on the same interval. In accordance to the estimated error in [14, 16], h must be close to zero to guarantee the accuracy. This is also needed in [15]. In this paper, since f is band-limited, there is no O(h) in the error estimate. So, the estimate of approximation error obtained in this paper is better since the condition h→0 is not required for the approximation.

In [17, 18], other kernels such as Gaussian functions and the power of sinc functions are studied. However, the noise and ill-posedness are not considered. In this paper, the kernel will be given by the regularized Fourier transform in [19]. The regularized transform is found by the Tikhonov regularization method in [20]. The estimate of approximation error is obtained in the noisy case. The ill-posedness is taken into account in the error estimation. In [21] and [22], the ill-posedness of the problem of computing f from the samples of f is analyzed and a regularized sampling algorithm is presented in [21].

In this paper, we will consider a more complex problem. In Section 2, we will analyze the ill-posedness of the problem of computing f^(k) from the samples of f and conclude that, in the presence of noise, formula (3) is not reliable even if k is relatively small. For the case k=1, we can see the ill-posedness by the bipolar δ noise in Section 2. In Section 3, a regularized derivative interpolation formula will be presented and its convergence property is proved. We will show the bipolar δ noise that causes ill-posedness can be controlled by the regularized solution. In Section 4, a regularized high -order derivative interpolation formula is presented and its convergence property is proved. In Section 5, applications will be shown by some examples. We will see that the error of the regularized solution is small for the bipolar δ noise. Finally, the conclusion is given in Section 6. In our algorithm, it is not necessary for the step size h of the samples to be close to 0.

2 The concepts of Paley-Wiener spaces and ill-posedness

In this section, we introduce the concepts of entire functions, Bernstein inequality, Plancherel-Pólya theorem, Paley-Wiener theorem ([6] pp. 48–68), and the ill-posedness.

Definition 1

A function $f(z):\mathbb {C}\rightarrow \mathbb {C}$ is said to be entire if is is holomorphic throughout the set of complex numbers $\mathbb {C}$.

By this definition, we can see that any band-limited function is an entire function.

Definition 2

An entire function f(z)is said to be exponential type if there exist positive constants A and B such that

$$|f(z)|\leq Ae^{B|z|},~~~~~~z\in \mathbb{C}. $$

Definition 3

An entire function f(z)is said to be exponential type at most τ if given ε>0 there exist a constant A_ε such that

$$|f(z)|\leq A_{\epsilon} e^{(\tau+\epsilon)|z|},~~~~~~z\in \mathbb{C}. $$

Definition 4

By E_σ we denote the class whose members are entire functions in the complex plane and are of exponential type at most σ.

According to this definition, if f(z)∈E_σ, then, given ε>0, there exist a constant A_ε such that

$$|f(z)|\leq A_{\epsilon} e^{(\sigma+\epsilon)|z|},~~~~~~z\in \mathbb{C}. $$

Definition 5

The Bernstein class $B^{p}_{\sigma }$ consists of those functions which belong to E_σ and whose restriction to R belongs to L^p(R).

This means $B^{p}_{\sigma }=\{f\in E_{\sigma }: f(z)|_{z=x+0i}\in L^{p}(\bf R)\}$.

Bernstein inequality For every $f\in B^{p}_{\sigma }$, positive r∈Z and p≥1, we have

$$||f^{(r)}||_{p}\leq \sigma^{r} ||f||_{p}. $$

Plancherel-Pólya inequality Let $f\in B^{p}_{\sigma }$, p>0, and let Λ=(λ_n), n∈Z be a real increasing sequence such that λ_n+1−λ_n≥2δ. Then,

$$\sum_{n=-\infty}^{\infty} |f(\lambda_{n})|^{p}\leq \frac {2e^{p\sigma\delta}} {\pi\delta} ||f||^{p}_{p}. $$

By this inequality, we can see that $f\in B^{p}_{\sigma }$ implies f∈L^∞(R).

Paley-Wiener theorem ([6], p. 67) The class functions {f(z)} whose members are entire, belong to L² when restricted to the real axis and are such that |f(z)|=o(e^σz) is identical to the class of functions whose members have a representation

$$f(z)=\int^{\sigma}_{-\sigma}\varphi (u)e^{iuz}du, $$

for some φ∈L²(−σ, σ).

By the Paley-Wiener theorem, the space of Ω-band-limited functions is equivalent to the classical Paley-Wiener space of entire functions. We denote

$${\rm{PW}}^{2}:=\left\{f\in L^{2}:~~f ~\text{is} ~\Omega-{\rm{band-limited}}\right\}. $$

Then, for each f∈PW², the Plancherel-Pólya inequality implies that also f∈L^∞; hence, the possibility of applying the Bernstein inequality on f and its derivatives f^(k) which yields that all f^(k)∈L^∞ have a bounded L^∞ norm for k≥1. We will consider a restricted function space which only includes derivatives of functions f∈PW² which are not only Ω-band-limited but also have a bounded Fourier transform. The condition $\hat f\in L^{\infty } (\bf R)$ is required to prove the approximation property of the derivative interpolation by regularization. This can be seen in the proof of Lemma 3 in Section 3. Let us denote the space by

$${\rm{PW}}^{\infty} :=\left\{f\in {\rm{PW}}^{2}:~~\hat f ~\rm is ~bounded\right\}. $$

The samples we considers are always bounded sequences in l^∞.

The concept of ill-posed problems was introduced in [20]. Here, we borrow the following definition from it:

Definition 6

Assume ${\mathcal {A}}:D\rightarrow U$ is an operator in which D and U are metric spaces with distances ρ_D(∗,∗) and ρ_U(∗,∗), respectively. The problem

$${\mathcal{A}}z=u $$

of determining a solution z in the space D from the “initial data” u in the space U is said to be well-posed on the pair of metric spaces (D,U) in the sense of Hadamard if the following three conditions are satisfied:

(i) For every element u∈U, there exists a solution z in the space D; in other words, the mapping $\mathcal {A}$ is subjective.

(ii) The solution is unique; in other words, the mapping $\mathcal {A}$ is one-to-one.

(iii) The problem is stable in the spaces (D,U): ∀ε>0,∃δ>0, such that

$$\rho_{U}(u_{1},u_{2})<\delta \Rightarrow \rho_{D}(z_{1},z_{2})<\epsilon. $$

In other words, the inverse mapping ${\mathcal {A}}^{-1}$ is uniformly continuous.

Problems that violate any of the three conditions are said to be ill-posed.

In this section, we discuss the ill-posedness of derivative interpolation by the sampling theorem in the pair of spaces (PW^∞, l^∞). For f^(k)∈PW^∞, its norm is defined by

$$||f^{(k)}(t)||_{{\rm{PW}}^{\infty}}:=\max_{t\in \textbf{R}}|f^{(k)}(t)|=||f^{(k)}(t)||_{L^{\infty}}, $$

and

$$l^{\infty} :=\left\{\{a(n):n\in \textbf{Z}\}:||\textbf{a}||_{l^{\infty}}<\infty\right\} $$

is the space of bounded sequences with the norm

$$||\textbf{a}||_{l^{\infty}}:=\sup_{n\in \textbf{Z}}|a(n)|. $$

We define the operator

$$\textbf{S}:~{\rm{PW}}^{\infty}\rightarrow l^{\infty},~~\text{by}~~ \textbf{S}f^{(k)}:=\{f(nh):n\in \textbf{Z}\}. $$

Here, f(nh) is the coefficient of [sincΩ(t−nh)]^(k) in (3).

Let us describe the case k=1 in (3). For the Ω-band-limited function f, the first derivative is

$$ {{\begin{aligned} f'(t)&=\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]' f(nh) \\&=\sum_{n=-\infty}^{\infty} \left[\frac {\cos \Omega(t-nh)} {t-nh}\,-\, \frac {\sin \Omega(t-nh)} {\Omega(t-nh)^{2}}\right] f(nh), \end{aligned}}} $$

(5)

where h=π/Ω. Here, the convergence is both in L² and uniformly on R. The proof of this fact is similar to the proof of the Shannon sampling theorem [23].

i) The existence condition is not satisfied.

The proof is given in (iii) that the stability condition is not satisfied. In the proof, we will find a kind of noise {η(nh):n∈Z} such that

$$\sum_{n=-\infty}^{\infty} \left [\text{sinc} \Omega(t-nh)\right ]' \eta_ (nh)=\infty $$

at some point t₀∈(−∞, ∞).

(ii) The uniqueness condition is satisfied.

Since S is a linear operator, it is one-to-one if and only if

$$\textbf{S}(f^{(k)})=\textbf{0}\in l^{\infty} \Rightarrow f^{(k)}\equiv 0. $$

Since f(nh)=0 for all n∈Z implies f(t)≡0 by the Shannon sampling theorem, then f^(k)(t)≡0. So S is one-to-one.

(iii) The stability condition is not satisfied, in other words, S⁻¹ is not continuous.

This can be seen from the following example.

Example 1

Consider any band-limited signal f along with f(nh)+η_b(nh) where η_b(nh) is a noise.

Assume the noise has the form η_b(nh)=δ·sgn{cosΩ(t₀−nh)/(t₀−nh)}, −N≤n≤N and η_b(nh)=0, for |n|>N, where t₀ is a given point in the time domain and δ is a small positive number. Then, the noise of the derivative in formula (5) is

$$\eta_{b}'(t)=\sum_{n=-N}^{N} \left [\text{sinc} \Omega(t-nh)\right ]' \eta_{b} (nh). $$

This is the noise of f^(k)(t) in which k=1.

At t=t₀ the noise of the derivative is

$${\begin{aligned} \eta_{b} '(t_{0})&=\delta\sum_{n=-N}^{N} \left|\frac {\cos \Omega(t_{0}-nh)} {t_{0}-nh}\right| \\&-\sum_{n=-N}^{N} \frac {\sin \Omega(t_{0}-nh)} {\Omega(t_{0}-nh)^{2}} \eta_{b}(nh) \rightarrow \infty, \end{aligned}} $$

as N→∞ if cosΩt₀≠0, since

$${\begin{aligned} &\sum_{n=-N}^{N} \left|\frac {\cos \Omega(t_{0}-nh)} {t_{0}-nh}\right| =\sum_{n=-N}^{N} \left|\frac {\cos \Omega t_{0}} {t_{0}-nh}\right| \\&\quad=|\cos \Omega t_{0}| \cdot \sum_{n=-N}^{N} \frac 1 {|t_{0}-nh|} \rightarrow \infty \end{aligned}} $$

by the divergence property of the Harmonic series and

$$\sum_{n=-N}^{N} \frac {\sin \Omega(t_{0}-nh)} {\Omega(t_{0}-nh)^{2}} \eta_{b}(nh) $$

converges by the convergence property of p-series in the case p=2.

If we do not set η_b(nh)=0, for |n|>N and define them in the same way as |n|≤N, then ηb′(t₀)=∞. This shows that the existence condition is not satisfied.

Also at any point, t=t₀+kπ/Ω, k∈Z

$${{}\begin{aligned} \eta_{b} '(t_{0}+ k\pi/\Omega) &= \sum_{n=-N}^{N} \frac {\cos \Omega(t_{0}+k\pi/\Omega -nh)} {t_{0}+ k\pi/\Omega-nh} \delta \\&\quad\cdot sgn \{\cos \Omega(t_{0}-nh)/(t_{0}-nh)\}\\ & - \sum_{n=-N}^{N} \frac {\sin \Omega(t_{0}+ k\pi/\Omega-nh)} {\Omega(t_{0}+ k\pi/\Omega-nh)^{2}} \eta_{b} (nh)\\ &=(-1)^{k}\delta\sum_{n=-N}^{N} \frac {t_{0} -nh} {t_{0}+ k\pi/\Omega-nh}\\&\quad \left|\frac {\cos \Omega(t_{0}-nh)} {t_{0}-nh}\right|\\ &-\sum_{n=-N}^{N} \frac {\sin \Omega(t_{0}+ k\pi/\Omega-nh)} {\Omega(t_{0}+ k\pi/\Omega-nh)^{2}} \eta_{b} (nh) \\&\quad\rightarrow \pm\infty, \end{aligned}} $$

as N→∞.

Thus, $||\{\eta _{b}(nh)\}||_{l^{\infty }}\leq \delta$, yet $||(f+\eta _{b})'-f'||_{\mbox{{PW}}^{\infty }}=||\eta _{b}'||_{L^{\infty }}$ can be made arbitrarily large. So (iii) in the definition of well-posedness fails.

Therefore, this is an ill-posed problem.

If we consider the problem on the pair of spaces (PW^∞, l²), the problem is well posed. But the condition $||\eta ||_{l^{2}}\leq \delta \rightarrow 0$ is too strict.

In Section 3, we will show that the regularized solution will converge to the exact signal as $||\eta ||_{l^{\infty }}\leq \delta \rightarrow 0$ according to the l^∞-norm for suitable regularization parameters.

3 The derivative interpolation by regularization

To solve the ill-posed problem in last section, we introduce the regularized Fourier transform [19]:

Definition 7

For α>0, we define

$$ \boldsymbol{F}_{\alpha}[f](\omega):=\textbf{F}[f_{W}](\omega)=\int_{-\infty}^{\infty} \frac {f(t)e^{-i\omega t}dt} {1+2\pi\alpha +2\pi\alpha t^{2}} $$

(6)

where

$$f_{W}(t):=\frac 1 {1+2\pi\alpha +2\pi\alpha t^{2}} f(t) $$

is the function f(t) multiplied with the weight function

$$K_{\alpha}(t):=(1+2\pi\alpha +2\pi\alpha t^{2})^{-1}. $$

The regularized Fourier transform was found by finding the minimum of a smoothing function and solving an Euler equation. The detail can be seen in [19].

In [19], we have proved that

$${\lim}_{\delta\rightarrow 0} \max_{\omega\in[-\Omega, \Omega]}|\textbf{F}_{\alpha}[f](\omega)-\hat f_{E}(\omega)|=0 $$

under the condition

$$||f_{\delta}(t)-f_{E}(t)||_{L^{2}}\leq\delta $$

if α(δ)→0 and δ²/α(δ) is bounded as δ→0. So the weight function K_α(t) has the function of stabilization. We have successfully used the regularization factor K_α(t) for band-limited extrapolations in [19]. In [24], we also successfully used the factor K_α(nh) in the computation of Fourier transform. The analysis of convergence property and the computation are in the frequency domain. In [21], the weight function K_α(nh) is applied to the Shannon sampling theorem. In this paper, we will compute the derivatives by the combination of (5) and (6). The analysis of convergence property and computation are in the time domain for the derivatives. The error estimations of the computation of the derivatives are also given. The proof is quite different.

Definition 8

Given {f(nh):n∈Z} in l^∞, define

$$f_{\alpha}(t):=\sum_{n=-\infty}^{\infty} \text{sinc} \Omega(t-nh) K_{\alpha}(nh) {f(nh)}. $$

The infinite series is uniformly convergent in R for any α>0 since both sincΩ(t−nh) and {f(nh):n∈Z} are bounded.

By the differentiation of f_α(t) in Definition 3.2, we obtain the regularized derivative interpolation:

$$ {\begin{aligned} f'_{\alpha}(t) &=\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]' K_{\alpha}(nh) {f(nh)}\\ &=\sum_{n=-\infty}^{\infty} \left[\frac {\cos \Omega(t-nh)} {t-nh}- \frac {\sin \Omega(t-nh)} {\Omega(t-nh)^{2}}\right] \quad K_{\alpha}(nh) {f(nh)}. \end{aligned}} $$

(7)

This derivative is well defined since the infinite series is also uniformly convergent on R.

Lemma 1

If f is band-limited, then $\textbf {F}_{\alpha }[f](\omega)=\frac 1 {4\pi a\alpha } \int _{-\Omega }^{\Omega } \hat f(u)e^{-a|u-\omega |} du$ where $a:=\left (\frac {1+2\pi \alpha } {2\pi \alpha }\right)^{\frac 1 2}$.

It can be seen from the convolution

$$\hat f_{W}=\frac 1 {2\pi} \hat f*\hat K_{\alpha} $$

where $\hat K_{\alpha }(\omega)=\frac 1 {2 a\alpha } e^{-\alpha |\omega |}$ is the Fourier transform of K_α(t). For the proof of the convergence of the regularized derivative interpolation, we will need the definition of periodic extension of the function e^iωt.

Definition 9

(e^iωt)_p[−Ω,Ω] denotes the periodic extension of the function e^iωt defined on the interval [−Ω,Ω] to the interval (−∞,∞) with period 2Ω.

Let E_t(ω):=(e^iωt)_p[−Ω,Ω]. Then, for ω∈[−Ω,Ω], E_t(ω)=e^iωt. For ω∈R∖[−Ω,Ω], E_t(ω) is the periodic extension of E_t(ω) for ω∈[−Ω,Ω].

The next Lemma is from [25].

Lemma 2

If $\hat f\in L^{1}(-\infty, \infty)$, then

$${{}\begin{aligned} \sum_{n=-\infty}^{\infty}\! \text{sinc} \Omega(t-nh)f(nh) \,=\,\frac 1 {2\pi} \int_{-\infty}^{\infty}\hat f(\omega)(e^{i\omega t})_{p[-\Omega, \Omega]}d\omega \end{aligned}} $$

for each t∈R.

In order to prove the convergence property of the regularized derivative interpolation, we need some more lemmas which are listed in the Appendix.

We are now in a position to state and prove our main theorem.

Theorem 1

Suppose

$$f(nh)=f_{E}(nh)+\eta_{n} $$

where $||\{\eta _{n}\}||_{l^{\infty }} \leq \delta$ and f_E∈PW^∞. Then, if we choose α=α(δ)=O(δ^μ), 0<μ<2 as δ→0, then $f^{\prime }_{\alpha }(t) \rightarrow f'_{E}(t)$ uniformly in any finite interval [-T, T] as δ→0. Furthermore,

$${\begin{aligned} ||f'_{\alpha}(t)-f'_{E}(t)||_{C[-T, T]} &=\max_{t\in [-T,T]}|f'_{\alpha}(t)-f'_{E}(t)| \\&\leq O(\alpha^{\frac 1 2})+O(\delta/\sqrt \alpha). \end{aligned}} $$

The proof is in the Appendix.

Theorem 2

Suppose

$$f(nh)=f_{E}(nh)+\eta_{w}(nh) $$

where {η_w(nh)} is white noise, Eη_w=0 and Var(η_w)=σ² and f_E∈PW^∞. Then, if we choose α=α(σ)=O(σ^μ), 0<μ<2 as σ→0, then $Ef^{\prime }_{\alpha }(t) \rightarrow f'_{E}(t)$ uniformly in any finite interval [-T, T] as σ→0. Furthermore,

$$|Ef'_{\alpha}(t) - f'_{E}(t)|=O(\alpha^{\frac 1 2}) $$

and

$$Var[f'_{\alpha}(t)-f'_{E}(t)]= O\left(\sigma^{2}\right)+O\left(\sigma^{2}/\sqrt \alpha\right). $$

The proof is in the Appendix.

4 Derivative interpolation of higher order

In this section, we prove the convergence property of the derivative interpolation formula of high order:

$$ f^{(k)}_{\alpha}(t)=\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} K_{\alpha}(nh) {f(nh)}. $$

(8)

Some lemmas are in the Appendix.

We can now state and prove a version of Theorem 1 for higher-order derivatives.

Theorem 3

If we choose α=α(δ)=O(δ^μ), 0<μ<2 as δ→0, then $f^{(k)}_{\alpha }(t) \rightarrow f^{(k)}_{E}(t)$ uniformly in any finite interval [-T, T] as δ→0. Furthermore, we have the estimate

$${\begin{aligned} ||f^{(k)}_{\alpha}(t)-f^{(k)}_{E}(t)||_{C[-T, T]}&=\max_{t\in [-T,T]} |f^{(k)}_{\alpha}(t)-f^{(k)}_{E}(t)|\\&\leq O(\alpha^{\frac 1 2})+O(\delta/\sqrt \alpha). \end{aligned}} $$

The proof is in the Appendix.

Remarks 1

This theorem shows that evaluation of higher order derivatives from Nyquist rate samples with any accuracy is possible. Here, the Nyquist rate samples mean the samples with the step size $h=\frac \pi \Omega$.

Theorem 4

Suppose

$$f(nh)=f_{E}(nh)+\eta_{w}(nh) $$

where {η_w(nh)} is white noise, Eη_w=0 and Var(η_w)=σ² and f_E∈PW^∞. Then, if we choose α=α(σ)=O(σ^μ), 0<μ<2 as σ→0, then $Ef^{(k)}_{\alpha }(t) \rightarrow f^{(k)}_{E}(t)$ uniformly in any finite interval [-T, T] as σ→0. Furthermore,

$$|Ef^{(k)}_{\alpha}(t) - f^{(k)}_{E}(t)|=O(\alpha^{\frac 1 2}) $$

and

$$Var[f^{(k)}_{\alpha}(t)-f^{(k)}_{E}(t)]= O(\sigma^{2})+O(\sigma^{2}/\sqrt \alpha). $$

The proof is similar to the proof of Theorem 2. We omit it here.

5 Methods, experimental results, and discussion

In this section, we give some examples to show that the regularized sampling algorithm is more effective in controlling the noise than some other algorithms. We will compare it with the Fourier truncation method ([9]) and Tikhonov regularization method ([16]). The procedure of how the Tikhonov regularization method was performed is described in detail in [16].

In practice, only finite terms can be used in (8), so we choose a large integer N and use next formula in computation:

$$ f^{(k)}_{\alpha N}(t)=\sum_{n=-N}^{N} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} K_{\alpha}(nh) {f(nh)} $$

(9)

where f(nh) is the noisy sampling data given in (4) in Section 1. Due to the weight function, the series above converges much faster than the series (3) of using Shannon’s sampling theorem. We give the estimate of the truncation error next.

Since t∈[−T, T], for |n|>N

$${\begin{aligned} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} &=\sum_{l=0}^{k} (^{k}_{l}) \left[\frac 1 {\Omega(t-nh)}\right]^{(l)} \\&[\sin \Omega(t-nh)]^{(k-l)}=O\left(\frac 1 N\right). \end{aligned}} $$

Then, the truncation error

$$\text{TR}=O\left(\frac 1 N \int_{N}^{\infty} K_{\alpha}(x) {dx} \right) $$

where

$${\begin{aligned} &\int_{N}^{\infty} K_{\alpha}(x) {dx} =\frac 1 {2\pi\alpha} \int_{N}^{\infty} \frac {dx} {a^{2} + x^{2}} \\&\quad=\frac 1 {2\pi\alpha a}\left(\frac \pi 2 - \arctan\frac N a\right)=O\left(\frac 1 {N\alpha}\right). \end{aligned}} $$

Therefore,

$$\text{TR}=O(\frac 1 {N^{2}\alpha}). $$

So, if N is large enough, the truncation error can be very small.

Theorem 5

If we choose α such that α(δ)=O(δ^μ), 0<μ<2 as δ→0, and α=O(N^γ), −2<γ<0 as N→∞, then we have the estimate

$${}||f^{(k)}_{\alpha N}(t)-f^{(k)}_{E}(t)||_{C[-T, T]}\,=\, O(\alpha^{\frac 1 2})+O(\delta/\sqrt \alpha)+O\left(\frac 1 {N^{2}\alpha}\right). $$

In this case, $\text {TR}=O(\frac 1 {N^{2+\gamma }}),$ which will vanish as N→∞.

In next three examples, we choose N=100 and α=0.01 in (9). We will consider three types of noise:

(i) Bipolar δ noise

$$\eta_{b}(nh)=\delta \cdot sgn \{\cos \Omega(t_{0}-nh)/ \Omega(t_{0}-nh)\} $$

where t₀=30, and δ=0.1, This is the noise given in Section 2 for which we have shown the stability condition is not satisfied.

(ii) White noise that is uniformly distributed in [−0.1,0.1].

(iii) White Gaussian noise whose variance is 0.01.

For the bipolar δ noise, we will give the square errors (SE). For the white noise, we use the three methods 100 times and will give the mean square errors (MSE).

Example 2

Suppose

$$f_{E}(t)=\frac {\sin (\Omega t)} {\pi t}. $$

Then,

$$\hat f_{E}(\omega)= \left\{ \begin{array}{l} 1,~~\omega \in [-\Omega,\Omega]\\ 0,~~\omega \notin [-\Omega,\Omega]. \end{array} \right. $$

where Ω=1.5.

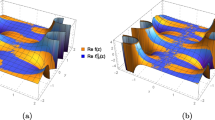
The simulation results for the bipolar δ noise are in Fig. 1. The solid curve is the exact derivative. The dot is the result by the Fourier truncation method. We choose α=0.01. The dot dashed is the result by the Tikhonov regularization method. The dashed is the result by the regularized sampling algorithm. We give the SE in the table:

Fig. 1

The simulation results for the bipolar δ noise in Example 2

The simulation results for the uniform noise are in Fig. 2. The MSE is in the table:

Fig. 2

The simulation results for the uniform noise in Example 2

The simulation results for the Gaussian noise are in Fig. 3. The MSE is in the table:

Fig. 3

The simulation results for the Gaussian noise in Example 2

Example 3

In this example, we choose a function that has a triangular spectrum. Let

$$f_{E}(t)=\frac {1-\cos (\Omega t)} {\pi t^{2}}. $$

Then,

$$\hat f_{E}(\omega)= \left\{ \begin{array}{l} \Omega -|\omega |,~~\omega \in [-\Omega,\Omega]\\ 0,~~\omega \notin [-\Omega,\Omega]. \end{array} \right. $$

where Ω=1.5.

We still choose α=0.01. The simulation results for the bipolar δ noise are in Fig. 4.

Fig. 4

The simulation results for the bipolar δ noise in Example 3

We give the SE in the table:

The simulation results for the uniform noise are in Fig. 5. The MSE is in the table:

Fig. 5

The simulation results for the uniform noise in Example 3

The simulation results for the Gaussian noise are in Fig. 6. The MSE is in the table:

Fig. 6

The simulation results for the Gaussian noise in Example 3

Example 4

In this example, we choose a function that is a raised-cosine filter. Let

$$f_{E}(t)=\frac 1 {1- (\frac {2\beta\omega_{c} t} \pi)^{2}} \frac {\sin\omega_{c} t} t \cos\beta t. $$

Then,

$${\begin{aligned} \hat f_{E}(\omega)= \left\{ \begin{array}{l} 1,~~|\omega| \leq \omega_{c}(1-\beta)\\ \frac 1 2 +\frac 1 2\cos\frac {\pi [|\omega|-\omega_{c}(1-\beta)]} {2\beta\omega_{c}},~\omega_{c}(1-\beta)<|\omega|<\omega_{c}(1+\beta).\\ 0,~~|\omega| \geq \omega_{c}(1+\beta). \end{array} \right. \end{aligned}} $$

where ω_c=1 and β=0.5. Here, Ω=ω_c(1+β)=1.5.

We still choose α=0.01. The simulation results for the bipolar δ noise are in Fig. 7. We give the SE in the table:

Fig. 7

The simulation results for the bipolar δ noise in Example 4

The simulation results for the uniform noise are in Fig. 8. The MSE is in the table:

Fig. 8

The simulation results for the uniform noise in Example 4

The simulation results for the Gaussian noise are in Fig. 9. The MSE is in the table:

Fig. 9

The simulation results for the Gaussian noise in Example 4

Next, we compare the three algorithms in dependence of the variance of the Gaussian noise. The MSE for variance = 1, 0.25, 0.04, 0.01, 0.0025 for the three algorithms are in the next three tables.

Fourier truncation method:

Tikhonov regularization method:

Regularized sampling algorithm:

Remarks 2

The results of the Fourier truncation method in [9] are not good since the condition $\phantom {\dot {i}\!}||\eta ||_{L^{2}}\leq \delta$ is not satisfied here. In this paper, the condition on the samples |η(nh)|≤δ is much weaker. The condition to apply the regularization method in [16] is the same, so the result is better than the Fourier truncation method, but it is not as good as the regularized sampling algorithm in this paper. This is just for band-limited signals. The Tikhonov regularization method is a general method for ill-posed problems. It may be better for other signals such as non-band-limited signals. For the Tikhonov regularization method in [16], one must solve a system of linear equations. The amount of computation is of the order O(N³) to compute the derivative of N points. For each t, the amount of computation of (9) is of the order O(N). Then, for N points, the amount of computation of (9) is of the order O(N²).

Example 5

In this example, we show how the square error depends on the regularization parameter α and give the optimal α. We choose the function in example 1 and the bipolar δ noise. The results are in the Fig. 10. For the first derivative, the optimal α=0.0590. For the second derivative, the optimal α=0.0650.

Fig. 10

The results the Square error as a function of α in Example 5

Remarks 3

By the proof of Theorem 1 and 3, the error bound depends on the exact signal f_E which is not known. So it is not easy to find an optimized α. However, there are some methods in which α can be determined such as discrepancy principle ([26]), the GCV and L-curve ([27], [28]). And by Example 4, we can see that the regularization parameter α should be a little larger in the computation of the second derivative than in the first derivative. This means higher derivatives are more sensitive to noise. So a larger regularization parameter α is required.

6 Conclusion

The interpolation formula obtained by differentiating the formula of the Shannon sampling theorem is not stable. The presence of noise can give rise to the unreliable results. For certain kind of noise, the error can even approach infinity. So, this is a highly ill-posed problem. The regularization method is an effective method for ill-posed problems. The derivative interpolation by regularized sampling algorithm is presented and the method is extended to high order derivative interpolation. The convergence property is proved and tested by some examples. The numerical results show that the derivative interpolation by regularized sampling algorithm is more effective in reducing noise for band-limited signals.

7 Appendix

Lemma 3

If f is band-limited and $\hat f\in L^{\infty } (\textbf {R})$, then

$${\begin{aligned} d(t)&:=\left|\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]' K_{\alpha}(nh) {f(nh)} \right. \\&\quad \left.- \left[K_{\alpha}(t) {f(t)}\right]'{\vphantom{\sum_{n=-\infty}^{\infty}}}\right|=O(\alpha^{\frac 1 2}), \end{aligned}} $$

where $O(\alpha ^{\frac 1 2})$ means $O(\alpha ^{\frac 1 2})\leq C\cdot \alpha ^{\frac 1 2}$, C=const.>0.

Proof

$${{}\begin{aligned} d(t) &=\left |\left[ \sum_{n=-\infty}^{\infty} \text{sinc} \Omega(t-nh) K_{\alpha}(nh) {f(nh)} - K_{\alpha}(t) {f(t)} \right]'\right |\\ &=\left |\left [ \frac 1 {2\pi} \int_{-\infty}^{\infty}(e^{i\omega t})_{p[-\Omega, \Omega]} \hat f_{W}(\omega)d\omega -K_{\alpha}(t) {f(t)} \right ] '\right |\\ &=\left |\left [\frac 1 {2\pi} \int_{-\infty}^{\infty}(e^{i\omega t})_{p[-\Omega, \Omega]} \hat f_{W}(\omega)d\omega \right. \right. \\&\quad \left. \left. - \frac 1 {2\pi} \int_{-\infty}^{\infty}e^{i\omega t} \hat f_{W}(\omega)d\omega \right ]'\right |\\ &=\left |\frac 1 {2\pi} \int_{-\infty}^{\infty}[(e^{i\omega t})_{p[-\Omega, \Omega]} - e^{i\omega t}]' \hat f_{W}(\omega)d\omega\right |. \end{aligned}} $$

We will see that this improper integral is uniformly convergent, so we can interchange the order of the differentiation and integration.

$${{}\begin{aligned} d(t) &=\left |\frac 1 {2\pi} \int_{|\omega|\geq\Omega}[(i\omega e^{i\omega t})_{p[-\Omega, \Omega]} - i\omega e^{i\omega t}] \hat f_{W}(\omega)d\omega\right |\\ &\leq \frac 1 {\pi} \int_{|\omega|\geq\Omega}|\omega \hat f_{W}(\omega)|d\omega =\frac 1 {\pi} \int_{\omega\geq\Omega}|\omega \hat f_{W}(\omega)|d\omega \\&\quad+\frac 1 {\pi} \int_{\omega\leq-\Omega}|\omega \hat f_{W}(\omega)|d\omega \end{aligned}} $$

where

$$\hat f_{W}(\omega) =\frac 1 {4\pi a\alpha} \int_{-\Omega}^{\Omega} \hat f(u)e^{-a|u-\omega|} du. $$

Assume $|\hat f(\omega)|\leq M$ where M is a positive constant. □

In the case ω≥Ω,

$${{}\begin{aligned} |\hat f_{W}(\omega)| & =\left |\frac 1 {4\pi a\alpha} \int_{-\Omega}^{\Omega} \hat f(u)e^{a(u-\omega)} du\right |\leq \frac M {4\pi a\alpha} e^{-a\omega} \int_{-\Omega}^{\Omega} e^{au} du\\ &=\frac M {4\pi a^{2}\alpha} e^{-a\omega} (e^{a\Omega}- e^{-a\Omega}) \leq \frac M {4\pi a^{2}\alpha} e^{-a\omega} e^{a\Omega}. \end{aligned}} $$

In the case ω≤−Ω, $|\hat f_{W}(\omega)| =\left |\frac 1 {4\pi a\alpha } \int _{-\Omega }^{\Omega } \hat f(u)e^{a(\omega -u)} du\right |$, we have the similar inequality.

So

$$\begin{aligned} d(t) &\leq \frac 2 {\pi} \int_{\omega\geq\Omega}\omega \frac M {4\pi a^{2}\alpha} e^{-a\omega} e^{a\Omega} d\omega\\&\quad= \frac {e^{a\Omega}} {2\pi^{2} a^{2}\alpha} \int_{\omega\geq\Omega}\omega e^{-a\omega} d\omega\\ &= \frac 1 {2\pi^{2} a^{3}\alpha} (\Omega + \frac 1 a) =\frac \Omega {2\pi^{2} \alpha}\left (\frac {2\pi\alpha} {1+2\pi\alpha}\right)^{\frac 3 2} \\&\quad+ \frac 1 {2\pi^{2} \alpha}\left (\frac {2\pi\alpha} {1+2\pi\alpha}\right)^{2}=O(\alpha^{1/2}) \end{aligned} $$

where the last equality uses the definition of a in lemma 3.1.

7.1 Proof of Theorem 1

Suppose t∈[−T,T], using formula (7), we obtain

$${{}\begin{aligned} |f'_{\alpha}(t)-f'_{E}(t)|&=\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh) \right ]' K_{\alpha}(nh) [f_{E}(nh)\right. \\&\quad \left. +\eta(nh)] -f'_{E}(t)\right |\\ &\leq \left |\sum_{n=-\infty}^{\infty} \left [\text{sinc} \Omega(t-nh)\right ]' K_{\alpha}(nh) {f_{E}(nh)} - f'_{E}(t)\right |\\ & +\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right ]' K_{\alpha}(nh) {\eta(nh)}\right |\\ & \leq\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right ]' K_{\alpha}(nh) {f_{E}(nh)}\right. \\&\quad \left. - \left[ K_{\alpha}(t) {f_{E}(t)} \right]'\right |\\ & +\left |\left[K_{\alpha}(t) {f_{E}(t)}\right]'- f'_{E}(t)\right | +\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]' K_{\alpha}(nh) {\eta(nh)}\right | \end{aligned}} $$

By Lemma 3,

$${\begin{aligned} &\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right ]' K_{\alpha}(nh) {f_{E}(nh)}\right. \\ &\quad \left. - {\vphantom{\sum_{n=-\infty}^{\infty}}}\left[ K_{\alpha}(t) {f_{E}(t)} \right]'\right |= O(\alpha^{\frac 1 2}). \end{aligned}} $$

Since −T≤t≤T,

$${{}\begin{aligned} &\left |\left[K_{\alpha}(t) {f_{E}(t)}\right]'- f'_{E}(t)\right |\\&= \left |\frac {(2\pi\alpha +2\pi\alpha t^{2})(1+2\pi\alpha +2\pi\alpha t^{2})f'_{E}(t)+4\pi\alpha f_{E}(t)} {(1+2\pi\alpha +2\pi\alpha t^{2})^{2}}\right |=O(\alpha). \end{aligned}} $$

We can calculate $\int _{0}^{\infty } K_{\alpha }(t) {dt}=\frac 1 {2a\alpha }$.

Since [sincΩ(t−nh)]^′ is bounded and

$$\left | K_{\alpha}(nh) {\eta(nh)} \right | \leq \frac \delta h \int_{(n-1)h}^{nh} K_{\alpha}(t) {dt} ~~~(n>0), $$

we have

$$\begin{aligned} &\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]' K_{\alpha}(nh) {\eta(nh)} \right|\\ &\leq \left |\left[ {\text{sinc} \Omega t} \right]' \frac {\eta(0)} {1+2\pi\alpha}\right |\\&\quad +\left |\sum_{n\not= 0} \left[\text{sinc} \Omega(t-nh)\right]' K_{\alpha}(nh) {\eta(nh)} \right |\\ &\quad=O(\delta)+O\left(\delta \int_{0}^{\infty} K_{\alpha}(t) {dt} \right) =O(\delta)+O(\delta /\sqrt \alpha), \end{aligned} $$

By the estimates above, we have

$$||f'_{\alpha}(t)-f'_{E}(t)||_{C[-T, T]}\leq O(\alpha^{\frac 1 2})+O(\delta/\sqrt \alpha). $$

7.2 Proof of Theorem 2

By the proof of Theorem 1, we can see that

$${{}\begin{aligned} |Ef'_{\alpha}(t)-f'_{E}(t)|&=\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh) \right ]' K_{\alpha}(nh) f_{E}(nh) \right.\\& \left. -f'_{E}(t) {\vphantom{\sum_{n=-\infty}^{\infty}}}\right|=O(\alpha^{\frac 1 2}) \rightarrow 0 \end{aligned}} $$

as σ→0.

$${{}\begin{aligned} &Var[f'_{\alpha}(t)-f'_{E}(t)]=\sum_{n=-\infty}^{\infty} \{\left[\text{sinc} \Omega(t-nh)\right]' K_{\alpha}(nh)\}^{2} {Var[\eta(nh)]} \\ &\leq \left[ (\text{sinc} \Omega t)' \right]^{2} \frac {\sigma^{2}} {(1+2\pi\alpha)^{2}} +\sum_{n\not= 0} \{\left[\text{sinc} \Omega(t-nh)\right]' K_{\alpha}(nh)\}^{2} \sigma^{2} \\ &=O(\sigma^{2})+O\left(\sigma^{2} \int_{0}^{\infty} [K_{\alpha}(t)]^{2} {dt} \right). \end{aligned}} $$

Since [K_α(t)]²≤|K_α(t)|,

$${\begin{aligned} Var[f'_{\alpha}(t)-f'_{E}(t)]&=O\left(\sigma^{2}\right)+O\left(\sigma^{2} \int_{0}^{\infty} K_{\alpha}(t) {dt} \right) \\&=O\left(\sigma^{2}\right)+O\left(\sigma^{2} /\sqrt \alpha\right). \end{aligned}} $$

Lemma 4

$$I_{k}:=\int_{\omega\geq\Omega}\omega^{k} e^{-a\omega} d\omega=\sum_{l=0}^{k}\frac {A_{k}^{l}} {a^{l+1}} \Omega^{k-l}e^{-a\Omega} $$

where $A_{k}^{l}=\prod _{j=1}^{l} (k-j+1)$ and $A_{k}^{0}=1$.

Proof

We can prove it by integration by parts:

$${\begin{aligned} I_{k}&=\frac 1 a\Omega^{k} e^{-a\Omega} + \frac k v6{k-1}=\frac {A_{k}^{0}} a\Omega^{k} e^{-a\Omega} + \frac k aI_{k-1} \\&\quad=\frac {A_{k}^{0}} a\Omega^{k} e^{-a\Omega} + \frac k a \left(\frac 1 a\Omega^{k-1} e^{-a\Omega} + \frac {k-1} aI_{k-2}\right) \end{aligned}} $$

$${\begin{aligned} &=\frac {A_{k}^{0}} a\Omega^{k} e^{-a\Omega} + \frac {A_{k}^{1}} {a^{2}}\Omega^{k-1} e^{-a\Omega} +\frac {k(k-1)} {a^{2}}I_{k-2} \\&\quad=......=\sum_{l=0}^{k}\frac {A_{k}^{l}} {a^{l+1}} \Omega^{k-l}e^{-a\Omega}. \end{aligned}} $$

□

Lemma 5

If f is band-limited, then

$${\begin{aligned} d(t)&:=\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} K_{\alpha}(nh) {f(nh)} \right. \\&\quad \left. - \left[K_{\alpha}(t) {f(t)} \right]^{(k)} {\vphantom{\sum_{n=-\infty}^{\infty}}}\right|=O\left(\alpha^{\frac 1 2}\right). \end{aligned}} $$

Proof

Since $(\text {sinc} \Omega t)^{(k)}\,=\, \frac 1 {2\Omega } \int _{-\Omega }^{\Omega }(i\omega)^{(k)}e^{i\omega t}d\omega$ is bounded on (−∞, ∞),

$$\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} K_{\alpha}(nh) {f(nh)} $$

is uniformly convergent.

$${{}\begin{aligned} d(t)&=\left |\left[\sum_{n=-\infty}^{\infty} \text{sinc} \Omega(t-nh) K_{\alpha}(nh) {f(nh)} - K_{\alpha}(t) {f(t)} \right]^{(k)}\right |\\ &=\left | \left[\frac 1 {2\pi} \int_{-\infty}^{\infty}\left(e^{i\omega t}\right)_{p[-\Omega, \Omega]} \hat f_{W}(\omega)d\omega - K_{\alpha}(t) {f(t)} \right]^{(k)}\right |\\ &=\left | \left[\frac 1 {2\pi} \int_{-\infty}^{\infty}\left(e^{i\omega t}\right)_{p[-\Omega, \Omega]} \hat f_{W}(\omega)d\omega - \frac 1 {2\pi} \int_{-\infty}^{\infty}e^{i\omega t} \hat f_{W}(\omega)d\omega \right]^{(k)}\right |\\ &=\left | \frac 1 {2\pi} \int_{-\infty}^{\infty}[(e^{i\omega t})_{p[-\Omega, \Omega]} - e^{i\omega t}]^{(k)} \hat f_{W}(\omega)d\omega\right |\\ &=\left | \frac 1 {2\pi} \int_{|\omega|\geq\Omega}[(i\omega)^{k} e^{i\omega t})_{p[-\Omega, \Omega]} - (i\omega)^{k} e^{i\omega t}] \hat f_{W}(\omega)d\omega\right |\\ &\leq \frac 2 {2\pi} \int_{|\omega|\geq\Omega}|\omega^{k} \hat f_{W}(\omega)|d\omega \leq \frac 2 {\pi} \int_{\omega\geq\Omega}\omega^{k} \frac M {4\pi a^{2}\alpha} e^{-a\omega} e^{a\Omega} d\omega \\&= \frac {e^{a\Omega}} {2\pi^{2} a^{2}\alpha} \int_{\omega\geq\Omega}\omega^{k} e^{-a\omega} d\omega\\ &\,=\,\frac {e^{a\Omega}} {2\pi^{2} a^{2}\alpha} \sum_{l=0}^{k}\frac {A_{k}^{l}} {a^{l+1}} \Omega^{k-l}e^{-a\Omega} \,=\,\frac 1 {2\pi^{2} a^{2}\alpha} \sum_{l=0}^{k}\frac {A_{k}^{l}} {a^{l+1}} \Omega^{k-l} \,=\,O\left(\alpha^{1/2}\right). \end{aligned}} $$

where $A_{k}^{l}=\prod _{j=1}^{l} (k-j+1)$ and $A_{k}^{0}=1$ by lemma 4 □

Lemma 6

For t∈[−T,T], if k is even

$$\left[K_{\alpha}(t) \right]^{(k)} =\frac 1 {2\pi\alpha} \left[\frac 1 {a^{2} + t^{2}}\right]^{(k)} =O\left(\alpha^{k/2}\right), $$

and if k is odd

$$\left[K_{\alpha}(t) \right]^{(k)} =\frac 1 {2\pi\alpha} \left[\frac 1 {a^{2} + t^{2}}\right]^{(k)} =O\left(\alpha^{(k+1)/2}\right), $$

as α→0.

Proof

$$\frac 1 {2\pi\alpha} \left[\frac 1 {a^{2} + t^{2}}\right]^{(k)} =\frac 1 {2\pi\alpha} \frac 1 {2ai} \left[\frac 1 {t-ai}-\frac 1 {t+ai}\right]^{(k)} $$

$${\begin{aligned} &=\frac 1 {2\pi\alpha} \frac {(-1)^{k}} {2ai} \left[\frac {k!} {(t-ai)^{k+1}}-\frac {k!} {(t+ai)^{k+1}}\right] \\&\quad=\frac {(-1)^{k}k![(t+ai)^{k+1}-(t-ai)^{k+1}]} {4\pi\alpha ai~(t^{2}+a^{2})^{k+1}} \end{aligned}} $$

$${\begin{aligned} =\frac {(\!-1)^{k}k!\{[(ai)^{k+1}\!+ k(ai)^{k} t\!+...]\!- [(-ai)^{k+1}\!+ k(-ai)^{k} t+...)]\}} {4\pi\alpha ai~(t^{2}+a^{2})^{k+1}}. \end{aligned}} $$

If k is even, this is of the order $O\left (\frac {a^{k+1}} {\alpha a a^{2k+2}}\right)=O\left (\alpha ^{k/2}\right)$.

If k is odd, this is of the order $O\left (\frac {a^{k}} {\alpha a a^{2k+2}}\right)=O\left (\alpha ^{(k+1)/2}\right)$. □

Lemma 7

For t∈[−T,T],

$$\left[K_{\alpha}(t) {f_{E}(t)} \right]^{(k)}- f^{(k)}_{E}(t)=O(\alpha). $$

Proof

$$\begin{aligned} &\left[{K_{\alpha}(t) f_{E}(t)} \right]^{(k)}- f^{(k)}_{E}(t) = K_{\alpha}(t) f^{(k)}_{E}(t) \\&\quad+\sum_{l=1}^{k} (^{k}_{l}) \left[K_{\alpha}(t) \right]^{(l)}f^{(k-l)}_{E}(t) - f^{(k)}_{E}(t)\\ & =-\left[\frac {2\pi\alpha +2\pi\alpha t^{2}} {1+2\pi\alpha +2\pi\alpha t^{2}}\right]f^{(k)}_{E}(t) \\&\quad+\sum_{l=1}^{k} (^{k}_{l}) \left[K_{\alpha}(t) \right]^{(l)}f^{(k-l)}_{E}(t) =O(\alpha) \end{aligned} $$

by Lemma 6. □

8 Proof of Theorem 3

$${{}\begin{aligned} |f^{(k)}_{\alpha}(t)\,-\,f^{(k)}_{E}(t)|& \,=\,\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t\,-\,nh)\right]^{(k)} K_{\alpha}(nh) [f_{E}(nh)\,+\,\eta(nh)] -f^{(k)}_{E}(t)\right |\\ &\!\leq\! \left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t\,-\,nh)\right]^{(k)} K_{\alpha}(nh) {f_{E}(nh)} \,-\, f^{(k)}_{E}(t)\right |\\ &\,+\,\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t\,-\,nh)\right]^{(k)} K_{\alpha}(nh) {\eta(nh)}\right |\\ & \!\leq\! \left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t\,-\,nh)\right]^{(k)} K_{\alpha}(nh) {f_{E}(nh)} \,-\, \left[K_{\alpha}(t) {f_{E}(t)} \right]^{(k)}\right |\\ &\,+\,\left |\left[K_{\alpha}(t) {f_{E}(t)} \right]^{(k)}- f^{(k)}_{E}(t)\right | \\&\quad\,+\,\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} K_{\alpha}(nh) {\eta(nh)}\right | \end{aligned}} $$

where

$$\begin{aligned} &\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} K_{\alpha}(nh) {f_{E}(nh)} \right. \\& \left.- \left[K_{\alpha}(t) {f_{E}(t)} \right]^{(k)}{\vphantom{\sum_{n=-\infty}^{\infty}}}\right|=O(\alpha^{\frac 1 2}) \end{aligned} $$

by lemma 5,

$$\left |\left[K_{\alpha}(t) {f_{E}(t)} \right]^{(k)}- f^{(k)}_{E}(t)\right |=O(\alpha) $$

by lemma 7, and

$$\left |\sum_{n=-\infty}^{\infty} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} K_{\alpha}(nh) {\eta(nh)} \right| $$

$$\begin{aligned} & \leq \left |\left[ {\text{sinc} \Omega t} \right]^{(k)} \frac {\eta(0)} {1+2\pi\alpha}\right | \\&\quad+\left |\sum_{n\not= 0} \left[\text{sinc} \Omega(t-nh)\right]^{(k)} K_{\alpha}(nh) {\eta(nh)} \right |\\ &=O(\delta)+O\left(\delta \int_{0}^{\infty} K_{\alpha}(t) {dt} \right) =O(\delta)+O(\delta /\sqrt \alpha). \end{aligned} $$

This implies

$$||f^{(k)}_{\alpha}(t)-f^{(k)}_{E}(t)||_{C[-T, T]}\leq O(\alpha^{\frac 1 2})+O(\delta/\sqrt \alpha). $$