Finding Needles in a Haystack

Abstract

Convex polygons are distinguishable among the piecewise $C^\infty$ convex domains by comparing their visual angle functions on any surrounding circle. This is a consequence of our main result, that every segment in a $C^\infty$ multicurve can be reconstructed from the masking function of the multicurve given on any surrounding circle.

1 Introduction

Given a compact convex domain ${\mathcal {K}}$ inside a circle, we say it is distinguishable if no other convex disc exists in the circle that subtends the same angle at each point of the circle as ${\mathcal {K}}$ does. Green proved in [3] that a compact convex domain inside a circle which subtends a constant(!) angle $\nu$ at each point of the circle is not distinguishable if and only if $\nu /\pi$ is a rational number with even denominator in its smallest terms.

However it is proved in [6, 8], that two polygons are always distinguishable from each other, so the question

$$\begin{aligned} {\textit{Are convex polygons distinguishable among convex domains?}} \end{aligned}$$

(1)

emerged naturally in [4, Quest. 3.2], where it is proved that all triangles [4, Cor. 2.4], and the regular octagon surrounded by the regular star octagon inscribed in the circle [4, Exam. 2.5] are distinguishable. Further, the midpoint square of the inscribed square are distinguishable too by [5].

In this article we prove in Theorem 4.1, that every segment in a $C^\infty$ multicurve can be determined by knowing the masking function of the multicurve on any surrounding circle. This implies an affirmative answer for (1) formulated in Corollary 4.2, i.e., that every convex polygon is distinguishable among the convex domains of piecewise $C^\infty$ boundary.

2 Notations and Preliminaries

We work in the plane ${\mathbb {R}}^2$; the open unit ball centered at (0, 0) is ${\mathcal {B}}^2$ and its boundary, the unit circle, is ${\mathcal {S}}^1=\partial {\mathcal {B}}^2$. Unit vectors are shorthanded as ${\textit{\textbf{u}}}_{\beta }=(\cos \beta ,\sin \beta )$. The linear map $\cdot ^{\perp }$ on ${\mathcal {S}}^1$ is defined by ${\textit{\textbf{u}}}_{\beta }^{\perp }={\textit{\textbf{u}}}_{\beta +\pi /2}=(-\sin \beta ,\cos \beta )$. The Euclidean multiplication is denoted by $\langle \cdot ,\cdot \rangle$.

Let ${\textit{\textbf{r}}}:[a,b]\rightarrow {\mathbb {R}}^2$ be a differentiable curve parameterised by arc-length parameter s. The trace ${\mathrm{Tr}}\,{\textit{\textbf{r}}}$ of ${\textit{\textbf{r}}}$ is the set of points in ${\mathbb {R}}^2$ that are in the range of the function ${\textit{\textbf{r}}}$. A non-degenerate segment of the form ${\textit{\textbf{r}}}([s_0,s_1])$, $s_0<s_1$, in ${\mathrm{Tr}}\,{\textit{\textbf{r}}}$ is said to be traced. We call also a straight line traced if there is a traced segment on it.

A multicurve $\textit{\textbf{r}}_{_{\!\!\mathcal J}}$ is a finite set of differentiable curves ${\textit{\textbf{r}}}_j:[a_j,b_j]\rightarrow {\mathbb {R}}^2$, $j\in {\mathcal {J}}\subset {\mathbb {N}}$, the members of the multicurve, such that the members are of finite length and do not intersect each other in open arc. The trace ${\mathrm{Tr}}\,\textit{\textbf{r}}_{_{\!\!\mathcal J}}$ of a multicurve $\textit{\textbf{r}}_{_{\!\!\mathcal J}}$ is the union $\bigcup _{j\in {\mathcal {J}}} {\mathrm{Tr}}\,{\textit{\textbf{r}}}_j$. A multicurve is said to have a property if each of its members satisfies that property. Let ${\mathfrak {C}}$ be the set of curves that

• are twice differentiable,

• are not self-intersecting,

• are parameterised by arc-length on a finite closed interval,

• are intersecting every straight line in only finitely many closed (maybe degenerate) segments,

• have only finitely many tangents through any point of its exterior,

• have only finitely many points of vanishing curvature beside a finite set of traced straight lines, and

• have only finitely many multiple tangent lines.

A multicurve is called regular if all of its members are in ${\mathfrak {C}}$. A multicurve is a multisegment if all of its members are segments. A multisegment is obviously regular. To avoid long analytic technicalities, we confine ourselves to considering only regular multicurves.

Following [9], the masking number¹$M_{{\mathcal {T}}}(P)$ of the trace $M_{\mathcal T}={\mathrm{Tr}}\,\textit{\textbf{r}}_{_{\!\!\mathcal J}}$ of a regular multicurve $\textit{\textbf{r}}_{_{\!\!\mathcal J}}$ is $M_{{\mathcal {T}}}(P)=(1/2)\int _{{\mathcal {S}}^1}{\#}({\mathcal {T}}\cap \ell (P,{\textit{\textbf{w}}}))\,d{{\textit{\textbf{w}}}}$, where $\ell (P,{\textit{\textbf{w}}})$ is the straight line through the point $P\in {\mathbb {R}}^2$ with direction ${\textit{\textbf{w}}}\in {\mathcal {S}}^1$ and $\#$ is the counting measure. If ${\mathcal {T}}$ is a closed convex curve, then the masking number $M_{{\mathcal {T}}}(P)$ is twice of the point projection (see [2]) and the shadow picture (see [6]).

We define the masking function $M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ of a regular multicurve $\textit{\textbf{r}}_{_{\!\!\mathcal J}}$ by

$$\begin{aligned} M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}(X)=\int _{0}^{\pi }\#({\mathrm{Tr}}\,{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}\cap \ell (X,{\textit{\textbf{u}}}_{\alpha }))\,d\alpha . \end{aligned}$$

We clearly have $M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}(X)=\sum _{j\in {\mathcal {J}}}M_{{\textit{\textbf{r}}}_j}(X)$ and also $M_{{\mathrm{Tr}}{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}}=M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}$.

Proposition 2.1

[9, Prop. 3.2]  If ${\textit{\textbf{r}}}:[0,h]\ni s\mapsto {\textit{\textbf{r}}}(0)+s{\textit{\textbf{v}}}$, ${\textit{\textbf{v}}}\in {\mathcal {S}}^1$, then

$$\begin{aligned} \partial _{{\textit{\textbf{w}}}}M_{{\textit{\textbf{r}}}}(X)={\left\{ \begin{array}{ll} -|\langle {\textit{\textbf{v}}},{\textit{\textbf{w}}}^{\perp }\rangle |\displaystyle \biggl (\frac{1}{x}+\frac{1}{h-x}\biggr )&{} \ \text {if } X={\textit{\textbf{r}}}(0)+x{\textit{\textbf{v}}}\text { and }x\in {\mathbb {R}}\setminus \{0,h\},\\ -\partial _{-{\textit{\textbf{w}}}}M_{{\textit{\textbf{r}}}}(X)&{}\hbox { if}\ X\notin \ell ({\textit{\textbf{r}}}(0),{\textit{\textbf{v}}}), \end{array}\right. } \end{aligned}$$

where ${\textit{\textbf{w}}}\in {\mathcal {S}}^1$ and $\partial _{{\textit{\textbf{w}}}}$ denotes the one sided directional derivation.

Lemma 2.2

[9, Lem. 4.1]  Let $\textit{\textbf{r}}_{_{\!\!\mathcal J}}$ be a regular multicurve, and let ${\textit{\textbf{w}}}\in {\mathcal {S}}^1$ be not parallel² to any traced segment.

• (1) If no traced line goes through X, then $\partial _{{\textit{\textbf{w}}}}M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}(X)+\partial _{-{\textit{\textbf{w}}}}M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}(X)=0$.

• (2) If $X\notin {\mathrm{Tr}}\,\textit{\textbf{r}}_{_{\!\!\mathcal J}}$, then $\partial _{{\textit{\textbf{w}}}}M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}(X)+\partial _{-{\textit{\textbf{w}}}}M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}(X)\ge 0$, and it is positive if and only if X is on a traced straight line.

• (3) Except for finitely many points X of a traced segment of $\textit{\textbf{r}}_{_{\!\!\mathcal J}}$ we have $\partial _{{\textit{\textbf{w}}}}M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}(X)+\partial _{-{\textit{\textbf{w}}}}M_{\textit{\textbf{r}}_{_{\!\!\mathcal J}}}(X)\ne 0$.

For multicurves of class $C^k$, $k\in {\mathbb {N}}$, item (1) can be obviously replaced with:

(1$'$):

If no traced line goes through X, then $\partial _{{\textit{\textbf{w}}}}^kM_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}(X)=(-1)^k\partial _{-{\textit{\textbf{w}}}}^k M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}(X)$.

Finally, the following known result on harmonic functions is displayed here for the sake of completeness, and because it is crucial in what follows.

Theorem 2.3

[1, I.4. Thm. (c)]   If the function f is harmonic on the open subset ${\mathcal {D}}$ of ${\mathbb {R}}^n$, and f has a continuous extension to ${\mathcal {D}}\cup \partial {\mathcal {D}}$, then the supremum and infimum of the extension are attained on $\partial {\mathcal {D}}$.

Here the space ${\mathbb {R}}^n$ is with the Euclidean topology and is compactified by the ideal point at infinity, which is not included in ${\mathbb {R}}^n$, but is included in the boundary of every unbounded subset of ${\mathbb {R}}^n$.

3 Utilities

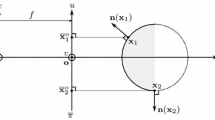
Let $\phi _j({\textit{\textbf{p}}})\in (-\pi ,\pi )$ be the oriented visual angle of the jth member segment ${\textit{\textbf{r}}}_j:[0,h]\ni s\mapsto {\textit{\textbf{r}}}(0)+s{\textit{\textbf{v}}}$, ${\textit{\textbf{v}}}\in {\mathcal {S}}^1$, of the multisegment ${\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$ at ${\textit{\textbf{p}}}\in {\mathbb {R}}^2\setminus {\mathrm{Tr}}\,{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$, i.e.,

$$\begin{aligned} \begin{aligned}&(\cos \phi _j({\textit{\textbf{p}}}),\sin \phi _j({\textit{\textbf{p}}}))\\&\qquad =\biggl (\frac{\langle {\textit{\textbf{r}}}_j(0)-{\textit{\textbf{p}}},\,{\textit{\textbf{r}}}_j(h)-{\textit{\textbf{p}}}\rangle }{|{\textit{\textbf{r}}}_j(0)-{\textit{\textbf{p}}}|\cdot |{\textit{\textbf{r}}}_j(h)-{\textit{\textbf{p}}}|},\frac{\langle ({\textit{\textbf{r}}}_j(0)-{\textit{\textbf{p}}})\times ({\textit{\textbf{r}}}_j(h)-{\textit{\textbf{p}}}),\,\textit{\textbf{m}}\rangle }{|{\textit{\textbf{r}}}_j(0)-{\textit{\textbf{p}}}|\cdot |{\textit{\textbf{r}}}_j(h)-{\textit{\textbf{p}}}|}\biggr ), \end{aligned} \end{aligned}$$

(2)

where $\textit{\textbf{m}}$ is a fixed unit normal vector of the plane. Observe that $\phi _j$ changes sign if the parameterisation of ${\textit{\textbf{r}}}_j$ is reversed, so the definition

$$\begin{aligned} \Phi _{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}^{}}^{}:{\mathbb {R}}^2\ni {\textit{\textbf{p}}}\mapsto \sum \nolimits _{j\in {\mathcal {J}}}^{}\phi _j({\textit{\textbf{p}}}) \end{aligned}$$

is valid only if a choice of the parameterisation was fixed for every segment.

We need the following slight generalisation of the observation given in the proof of [6, Lem. 2.2].

Lemma 3.1

Let ${\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}^{}$ be a multisegment.

• (1) If no traced line of ${\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$ goes through ${\textit{\textbf{p}}}$, then $M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ is real analytic around ${\textit{\textbf{p}}}$.

• (2) The function $\Phi _{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ is real analytic on ${\mathbb {R}}^2\setminus {\mathrm{Tr}}\,{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$.

Proof

As $M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ and $\Phi _{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ are locally the sum of the functions $\pm \phi _j$, we can assume without loss of generality that ${\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$ is the segment ${\textit{\textbf{r}}}:[0,h]\ni s\mapsto {\textit{\textbf{r}}}(0)+s{\textit{\textbf{v}}}$, ${\textit{\textbf{v}}}\in {\mathcal {S}}^1$. Since both $\arccos$ and $\arcsin$ are analytic on $(-1,1)$, the equality of the first coordinates in (2) proves both statements if the traced line avoids ${\textit{\textbf{p}}}$, and the equality of the second coordinates in (2) proves the second statement if the traced line goes through $\textit{\textbf{p}}$. $\square$

The following lemma is an obvious extension of [9, Thm. 6.1(1)].

Lemma 3.2

For every multisegment ${\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$ the functions $M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ and $\Phi _{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ are locally harmonic, where they are differentiable.

For a more direct proof one observes that $M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ and $\Phi _{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ are locally the sum of the functions $\pm \phi _j$, hence one can assume without loss of generality that ${\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$ is a segment for which [7, Lem. A.1(2)] implies the harmonicity directly.

4 Finding the Needles in a Haystack

Theorem 4.1

The traced segments of a regular multicurve of class $C^\infty$ can be reconstructed if the masking function is given on any rounding circle.

Proof

Let ${\mathrm{Tr}}\,{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$ be in ${\mathcal {B}}^2$ and suppose that $M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}$ is given on ${\mathcal {S}}^1$. By (1) and (2) of Lemma 2.2 the set of the intersections of ${\mathcal {S}}^1$ with the traced lines is

$$\begin{aligned} {\mathcal {P}}:=\bigl \{{\textit{\textbf{u}}}_\xi :\partial _{{\textit{\textbf{u}}}_\xi ^\perp }M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}({\textit{\textbf{u}}}_\xi )+\partial _{-{\textit{\textbf{u}}}_\xi ^\perp } M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}({\textit{\textbf{u}}}_\xi )>0\bigr \}. \end{aligned}$$

This is a finite set, so we can enumerate its elements in anticlockwise order: ${\textit{\textbf{u}}}_{\xi _0},\ldots ,{\textit{\textbf{u}}}_{\xi _i},\dots ,{\textit{\textbf{u}}}_{\xi _n}$.

Fig. 1

Traced segments, traced lines and the “first” arc they determine

Let ${\textit{\textbf{p}}}_{{\mathcal {I}}}$ be the multisegment of all the traced segments in ${\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}$. Let ${\textit{\textbf{p}}}_{{\mathcal {I}}_i}$ be the multisegment of the segments in ${\textit{\textbf{p}}}_{{\mathcal {I}}}$ that are collinear with ${\textit{\textbf{u}}}_{\xi _{i}}$, $i=0,\dots ,n$. Let ${\textit{\textbf{u}}}_{\xi _i^0}={\textit{\textbf{u}}}_{\xi _i}$, and let ${\textit{\textbf{u}}}_{\xi _i^{1}},\dots ,{\textit{\textbf{u}}}_{\xi _i^m},\dots ,{\textit{\textbf{u}}}_{\xi _i^{p_i}}$ be the remaining intersections of ${\mathcal {S}}^1$ with the traced lines of ${\textit{\textbf{p}}}_{{\mathcal {I}}_i}$ enumerated in anticlockwise order. Let ${\textit{\textbf{p}}}_{{\mathcal {I}}_i^m}$ be the multisegment of the segments in ${\textit{\textbf{p}}}_{{\mathcal {I}}_i}$ lying on the straight line ${\textit{\textbf{u}}}_{\xi _{i}}{\textit{\textbf{u}}}_{\xi _i^{m}}$, and let ${\mathcal {A}}_i^{m}$ be the counterclockwise arc $\widehat{{\textit{\textbf{u}}}_{\xi _i^m}{\textit{\textbf{u}}}_{\xi _i^{m+1}}}$ of ${\mathcal {S}}^1$ for every $m=1,\dots ,p_i$, where $p_i+1$ is understood as 0. (See Fig. 1.) With these notations in hand (1$'$) of Lemma 2.2 gives for every $k\in {\mathbb {N}}$ that

$$\begin{aligned} \begin{aligned} \partial _{{\textit{\textbf{u}}}_{\xi }^\perp }^k M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}({\textit{\textbf{u}}}_{\xi })&+(-1)^{k+1}\partial _{-{\textit{\textbf{u}}}_{\xi }^\perp }^k M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}({\textit{\textbf{u}}}_{\xi })\\&={\left\{ \begin{array}{ll} 2\partial _{{\textit{\textbf{u}}}_{\xi _i}^\perp }^k M_{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}({\textit{\textbf{u}}}_{\xi _i})&{} \text {if }\xi =\xi _i\text { for an }i\in \{0,\dots ,n\}, \\ 0&{}\text {if }\xi \ne \xi _i\text { for every }i\in \{0,\dots ,n\}. \end{array}\right. } \end{aligned} \end{aligned}$$

(3)

According to (1) of Lemma 3.1 function $M_{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ is analytic on the arc ${\mathcal {A}}_i^0$, so the values in (3) determine the function $M_{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ on the arc ${\mathcal {A}}_i^0$.

Take the parameterisation ${\textit{\textbf{r}}}_e$ on every segment in ${\textit{\textbf{p}}}_{{\mathcal {I}}_i}$ so that $\phi _e>0$ on ${\mathcal {A}}_i^0$. Then $\Phi _{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}\equiv M_{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ on ${\mathcal {A}}_i^0$ so (2) of Lemma 3.1 gives $\Phi _{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ all over ${\mathcal {S}}^1$. From this, Theorem 2.3 implies that $\Phi _{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ is determined all over the exterior of ${\mathcal {B}}^2$, because $\Phi _{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ vanishes at infinity and is harmonic in the exterior of ${\mathcal {B}}^2$ by Lemma 3.2.

On the other hand, $\Phi _{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ is real analytic on ${\mathbb {R}}^2\setminus {\mathrm{Tr}}{\textit{\textbf{p}}}_{{\mathcal {I}}_i}$ by (2) of Lemma 3.1, so it is determined on ${\mathbb {R}}^2\setminus {\mathrm{Tr}}{\textit{\textbf{p}}}_{{\mathcal {I}}_i}$ by the unique analytic extension from the outside of ${\mathcal {B}}^2$. However, $\Phi _{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ cannot extend continuously to ${\mathrm{Tr}}{\textit{\textbf{p}}}_{{\mathcal {I}}_i}$ because it has different limits from different sides of the traced line of every segment in the multisegment ${\textit{\textbf{p}}}_{{\mathcal {I}}_i}$. Thus ${\textit{\textbf{p}}}_{{\mathcal {I}}_i}$ is determined as the set of points where $\Phi _{{\textit{\textbf{p}}}_{\mathcal {I}_i}}$ cannot extend to.

Considering the difference $M_{{\textit{\textbf{r}}}_{_{\mathcal {\!\!J}}}}-M_{{\textit{\textbf{p}}}_{{\mathcal {I}}_i}}$ puts us into the same situation as at the start of the proof, but with less traced straight lines, so repeating our procedure over and over again will lead to the determination of all traced segments. $\square$

As a special case we obtain from Theorem 4.1 the following nice result.

Corollary 4.2

Every segment of the piecewise $C^\infty$ boundary of a convex domain ${\mathcal {D}}$ is determined by the visual angle function of ${\mathcal {D}}$ given on a surrounding circle.

Since a point of a surrounding circle can be collinear with at most two traced segments of the boundary of a convex domain, the following comes up.

Conjecture 4.3

In the interior of ${\mathcal {B}}^2$ any closed convex polygon and any closed convex disc with piecewise $C^5$ boundary can be distinguished from each other by their visual angle functions restricted to ${\mathcal {S}}^1$.