1 Introduction

The last two decades have seen several large-scale epidemics outbreaks such as Ebola, SARS, Zika virus, and swine flu, which leads to low socioeconomic status and inadequate access to health care. People get information about these outbreaks quite quickly due to significant advances in social media, which can have an insightful effect on the actual epidemic dynamics [17, 31]. Therefore, at the beginning of an epidemic outbreak, the initial step is to make the individuals aware of the disease and its preventive methods. Awareness programs can alert the susceptible population toward the contagious disease [23]. If susceptible individuals have adequate knowledge and proper information about the infection, then they take precautionary measures such as regular hand sanitization, the use of face masks, wear hand gloves, vaccination, and even quarantine, which can reduce the impact of illness, for instance, ranging from the plague outbreak in the English village of Eyam in 1665–1666 [9], where the town completely sealed itself off to prevent further transmission of plague, to more recent outbreaks of swine influenza [17] and Ebola [31]. In the situation of rural health services, the challenge of government health-care scheme is that there are numerous gaps in primary health services, and the health-care facilities are mainly urban centric. The rural residents may have low health knowledge awareness, and their receiving way of health knowledge can be traditional and straightforward. Knowledge level increases with higher education levels; therefore, one of the main factors is their education level. Therefore, a lot of people are not fully but partially aware of the spread and control of infectious diseases. Due to partial awareness, some individuals often medicate themselves adopting antibiotics, even when advised against doing so which weakens their immune system makes them at a high risk of catching the infection [18]. Therefore, complete awareness about the cycle of disease, along with the utilization of appropriate precautions and adequate decontamination procedures, is vital. Full awareness of the disease in humans develops a habit of taking precautionary measures against it, and they follow the instructions given by health workers and government and lower their risk of becoming infected.

In the study of the transmission of infectious diseases, the incidence rate has a vital role as it determines the number of infectives per unit of time. In 1927, Kermack Mckendrick considered the bilinear incidence rate, which follows the law of mass action [1]. In the bilinear incidence rate, the number of infectives linearly increases, which might be real for a small population of infected individuals, but it is impractical for a large number of infectives. Therefore, several studies are devoted to consider nonlinear incidence rate for disease transmission dynamics (e.g., [2, 3, 15, 16, 26, 34,35,36,37,38,39,40]. In the present study, we have incorporated the nonlinear saturated incidence rate, where the interaction term is of the form Sg(I), \(g(I)=\beta I/(1+\varepsilon I)\). Here, \(\beta I\) measures the force of infection, and \(1/(1 + \varepsilon I)\) measures the inhibition effect of the behavioral change of the susceptibles when their number increases and crowding effect of the infective individuals [2, 22]. In this incidence rate, the number of infectives depends on the nonlinear bounded map g(I), which tends to saturation level \(\beta /\varepsilon \) when I gets large. It prevents the unboundedness of the contact rate as it includes the psychological effects and, thus, more realistic than the bilinear incidence rate.

Treatment is vital to cure the infection and prevent the development of resistant bacteria. Therefore, consideration of the treatment rate in the epidemic model is of great importance. In 2004, Wang and Ruan [10] studied the SIR epidemic model with the constant treatment rate and showed various bifurcations. The consideration of constant treatment rate might be real when there are small infected populations because there are limited medical resources available in society. Therefore, in 2012, Zhou and Fan [24] improved the treatment rate by considering Holling type II functional response as given below:

$$\begin{aligned} h (I)&= \frac{\beta I}{1+\alpha I}, \quad I \ge 0, \quad \beta \ge 0, \quad \alpha \ge 0. \end{aligned}$$

and explore the SIR epidemic model to understand the effect of the limited medical resources and their supply efficiency on the transmission of infectious diseases. Motivated by the work mentioned above, we deliberate the Holling type II treatment rate (also called saturated treatment rate) and study the effect of treatment rate with limited medical resources in the current epidemic model.

The inclusion of time delay in the study of epidemiology is an important aspect. Persons with asymptomatic infections play an essential role in the spread of infectious disease, especially as they are unaware of their infection and therefore take no special hygiene precautions. Thus, the study of epidemiology involves time delay, which needs to be considered for practical purposes. The inclusion of time delay may arise due to delays caused by the latency in a vector and delay caused by a latent period in the host [4]. Recently, many mathematical models studied the impact of time delay in their epidemic model [7, 13, 35,36,37, 40].

The impact of information and awareness on the spread of epidemics has been studied by many authors [14, 19,20,21, 27,28,29, 33, 34]. Funk et al. [19] considered the aware susceptible and aware infected populations in their epidemic model, on the assumption that the aware susceptibles will be at a lower rate of catching the infection than the unaware susceptibles, and studied that disease dynamics in a well-mixed population. Kiss et al. [20] studied the effect of information transmission on the dynamics of sexually transmitted diseases. They assumed that the entire population is aware of the risk of infection; however, only a specific portion decides to react by constraining their contact with contaminated people. Misra et al. and Dubey et al. [21, 34] investigated the impact of awareness programs on the transmission dynamics of infectious diseases in their nonlinear epidemic models. Some researchers studied the impact of awareness on the disease transmission dynamics along with the influence of time delay. Zuo et al. [29] introduced a time delay in the media variable to emphasize the delay in reporting cases of infections. Zhao et al. [27] studied the SIRS epidemic model by incorporating time delay in media coverage. Zuo and Liu [28] studied the effect of awareness programs driven by media and the delay on the prevalence of the infectious disease. In all these models, the study reveals that the disease-free equilibrium (DFE) is stable when a basic reproduction number \(R_0\) is less than one, unstable when \(R_0 > 1\), irrespective of the value of the time delay, and has a stable endemic equilibrium for time delay equals to zero. In the study of Zuo et al. [29], Zhao et al. [27], and Misra et al. [21], the occurrence of Hopf bifurcation is shown for the particular value of the time delay. Greenhalgh et al. [33] included two delays, one in reporting of infected cases and another delay representing the loss of disease awareness after a fixed period. Their study reveals the reduction in infected individuals with an increment in the duration of awareness. It is also shown that both the time delays can produce oscillations and destabilize the endemic equilibrium.

The public is a coalition of many subgroups of individuals with vastly different social, educational, and economic backgrounds. During an outbreak, people adopt full or partial awareness, depending on the understanding of how they perceive risks, and communicate about the effectiveness of protective measures. Therefore, instead of going directly from susceptible to infected class, we introduce fully aware and partial aware susceptible compartments into the SIR epidemic model due to heterogeneous protection level and extend the epidemic model to include the behavioral change of susceptibles, which can change the transmission patterns and reduce the prevalence of disease to the more extent. The precaution level of susceptible individuals is heterogeneous as they may take different levels of precautions to protect themselves from being infected based on the severity of epidemics or their characteristics. We consider three specific nonlinear incidence rates of unaware susceptibles, fully aware susceptibles, and partially aware susceptible, respectively, with the inclusion of time delay as a latent phase having a fixed duration. Also, with awareness, treatment to infectives is essential to mitigate the infection. Therefore, we consider the nonlinear saturated treatment rate, which includes the fact of limitation in the availability of resources. We formulate the nonlinear time-delayed mathematical epidemic model and perform the stability analysis to demonstrate the eradication or persistence of the disease with the help of the basic reproduction number \(R_0\) for the time delay \(\varrho \ge 0\). The bifurcation theory approach using the center manifold theory is performed, revealing the existence of backward and forward bifurcations, which shows that reducing \(R_0\) below unity is not sufficient to eradicate the disease due to the presence of backward bifurcation, which has an important implication in the study of disease dynamics. Further, choosing time delay as a bifurcation parameter, the periodic and oscillatory solutions appear via Hopf bifurcation. Moreover, the numerical experiments show the importance of considering full and aware susceptible individuals and nonlinear terms such as time delay, incidences, and treatment.

The rest of the manuscript is organized as follows: The model and its basic properties are presented in Sect. 2. In Sect. 3, the existence of disease-free and endemic equilibria is presented, and stability analysis is performed using the basic reproduction number. The conditions for the backward and forward bifurcations are derived. Also, the existence of stability switches is shown via the presence of Hopf bifurcation by choosing the time delay as a bifurcation parameter. In Sect. 4, numerical simulations are presented to signify the theoretical results. Lastly, Sect. 5 is devoted to a brief discussion.

2 Mathematical model and basic properties

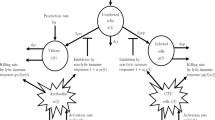
We assume that N denotes the total constant population, and it is divided into five compartments according to the disease status: unaware susceptible class S(t), fully aware class \(A_F(t)\), partially aware class \(A_P(t)\), infected individuals class I(t), and removed individuals class R(t). The unaware susceptible class consists of those individuals who are vulnerable to the disease and taking no precautions against it. A fully aware susceptible class involves those individuals who have adequate knowledge and proper information about the spread of the disease and taking precautionary measures against it. Partially aware susceptibles consist of those individuals who have an incomplete understanding of the spread and prevention of the disease and have low resources available to escape from the infection. Including a behavioral response among unaware susceptibles would unavoidably call for response among fully aware susceptibles and partially aware susceptibles. Therefore, we have considered three explicit same functional types of saturated incidence rates described below:

  1. (i)

    \(F_1(S(t-\varrho ),I(t-\varrho ))=(\beta _1 S(t-\varrho )I(t-\varrho ))/(1+\varepsilon I(t-\varrho ))\), representing the saturated incidence rate among unaware susceptibles,

  2. (ii)

    \(F_2( A_F(t-\varrho ),I(t-\varrho ))=(\beta _2 A_F(t-\varrho )I(t-\varrho ))/(1+\varepsilon I(t-\varrho ))\), representing the saturated incidence rate among fully aware susceptibles,

  3. (iii)

    \(F_3( A_P(t-\varrho ),I(t-\varrho ))=(\beta _2 A_F(t-\varrho )I(t-\varrho ))/(1+\varepsilon I(t-\varrho ))\), representing the saturated incidence rate among partially aware susceptibles,

where \(\varrho \) denotes the time delay, representing the latent period. The latent period is defined as the period between exposure and infection, since the pathogen is present in a latent stage, without clinical symptoms or signs of infection in the host. The delay term in S(t), \(A_F(t)\), and \(A_P(t)\) is introduced because people, who are unaware, fully aware, or partially aware of the disease may consider themselves in their respective classes after becoming infected. We assume that such individuals are in the latent period.

Let \(\kappa \) denote the constant rate of inflow of new unaware susceptibles due to the recruitment of new members by the current members or immigration. Let \(\delta _1\) denote the rate at which unaware susceptibles S(t) become fully aware. \(\delta _2\) denotes the rate at which S(t) becomes partially aware of the disease. The parameters \(\beta _1\), \(\beta _2\), and \(\beta _3\) are the transmission rates of infection of unaware, fully aware, and partially aware susceptible populations, respectively. We suppose that all the susceptible classes can become infected by contact with infected individuals, but the fully aware class has less chance to be infected as compared to the unaware susceptible and partially aware susceptible individuals [33]. Therefore, it is assumed that \(\beta _1 ~\text {and}~ \beta _3~ \text {are greater }~ \beta _2\). The parameter \(\varepsilon \) represents the behavioral changes or measures of inhibition adopted by infectives. \(\vartheta \) denotes the natural mortality rate of all individuals, whereas d and \(\theta \) denote the disease-induced mortality rate and recovery rate of the infectives, respectively. The function \(h(I(t))=aI/(1+bI)\) represents the treatment rate of infectives, where a and b denote the cure rate and limitation rate in the availability of resources, respectively. The symbols and description of the parameters and state variables are given in Table 1 briefly.

Table 1 Notations of model variables and parameters
Full size table

The flow diagram of the proposed epidemic model is given in Fig. 1, and model is represented mathematically under the following system of delay differential equations:

$$\begin{aligned} \begin{aligned} \frac{{\mathrm {d}}S}{{\mathrm {d}}t}&=\kappa -\delta _1 S-\delta _2 S-\frac{\beta _1 S(t-\varrho ) I(t-\varrho )}{1+\varepsilon I(t-\varrho )}- \vartheta S, \\ \frac{{\mathrm {d}}A_F}{{\mathrm {d}}t}&=\delta _1 S-\frac{\beta _2 I(t-\varrho ) A_F(t-\varrho )}{1+\varepsilon I(t-\varrho )}-\vartheta A_F,\\ \frac{{\mathrm {d}}A_P}{{\mathrm {d}}t}&= \delta _2 S -\frac{\beta _3 I(t-\varrho ) A_P(t-\varrho )}{1+\varepsilon I(t-\varrho )}-\vartheta A_P, \\ \frac{{\mathrm {d}}I}{{\mathrm {d}}t}&= \frac{\beta _1 S(t-\varrho ) I(t-\varrho )}{1+\varepsilon I(t-\varrho )}+\frac{\beta _2 I(t-\varrho ) A_F(t-\varrho )}{1+\varepsilon I(t-\varrho )}\\&\quad +\frac{\beta _3 I A_P(t-\varrho )}{1+\varepsilon I(t-\varrho )}-(d+\theta +\vartheta ) I-\frac{aI}{1+b I},\\ \frac{{\mathrm {d}}R}{{\mathrm {d}}t}&= \theta I+ \frac{aI}{1+b I}-\vartheta R. \end{aligned} \end{aligned}$$
(1)

Suppose that the initial conditions of the model (1) take the form

$$\begin{aligned} \begin{aligned}&S(\nu )=\chi _1(\nu ),~ A_F(\nu )=\chi _2(\nu ),~A_P(\nu )=\chi _3(\nu ),\\&I(\nu )=\chi _4(\nu ),~R(\nu )=\chi _5(\nu ),\\&\quad \chi _i(\nu ).~\nu \in [-\varrho ,~0], ~\chi _i(0)>0~(i=1,2,3,4,5), \end{aligned} \end{aligned}$$
(2)

where \(\left( \chi _1(\nu ),\chi _2(\nu ),\chi _3(\nu ),\chi _4(\nu ),\chi _5(\nu )\right) \in C\left( [-\varrho ,~0],~ \mathbb {R}^5_+\right) \), which is the Banach space of continuous functions mapping the interval \([-\varrho ,~0]\) into \(\mathbb {R}^5_+\), where

$$\begin{aligned}&\mathbb {R}^5_+=\left\{ \left( S,A_F,A_P,I,R\right) / S \ge 0,A_F \ge 0,\right. \\&\quad \left. A_P \ge 0,I \ge 0,R \ge 0\right\} . \end{aligned}$$
Fig. 1
figure 1

Flow diagram of the model (1)

Full size image

Using Proposition 2.3 in [32] and Proposition 2.1 in [25], it follows that all state variables of the model (1) are nonnegative, i.e., \((S,A_F,A_P,I,R) \in {{\mathbb {R}}^5_+}\). For biological reasons, we assume that the model parameters \(\kappa \), \(\delta _1\), \(\delta _2\) \(\beta _1\), \(\beta _2\), \(\beta _3\), \(\varepsilon \), \(\vartheta \), \(\theta \), d, a, b are positive. By the fundamental theory of functional differential equations [6], the model (1) has a unique solution \(\left( S(t)\,A_F(t),A_P(t),I(t),R(t)\right) \) satisfying the initial conditions (2).

Lemma 1

The compact set

$$\begin{aligned} \Omega= & {} \left\{ (S(t),A_F(t),A_P(t),I(t),R(t)) \in \mathbb {R}_+^5 : S(t)\right. \\&\left. +A_F(t)+A_P(t)+I(t)+R(t) \le \frac{\kappa }{\vartheta } \right\} \end{aligned}$$

is invariant for the solutions of the model (1).

Proof

Since the right-hand side of the model (1) and its derivatives are continuous, it assures the well-posedness of the model (1).

On adding the equations of the model (1), we get

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm {d}}}{{\mathrm {d}}t }\left( S(t)+A_F(t)+A_P(t)+I(t)+R(t)\right) \\&\quad =\kappa -\vartheta (S(t)+A_F(t)+A_P(t)\\&\qquad +I(t)+R(t))-dI \\&\quad \le \kappa -\vartheta (S(t)+A_F(t)+A_P(t)+I(t)+R(t)). \end{aligned} \end{aligned}$$
(3)

Thus, the invariant region for the existence of the solutions is given as

$$\begin{aligned} 0< \lim _{t\rightarrow \infty } (S(t){+}A_F(t){+}A_P(t)+I(t)+R(t)) \le \frac{\kappa }{\vartheta }.\nonumber \\ \end{aligned}$$
(4)

Hence, the solution of the model (1) is compact. \(\square \)

In the next section, we obtain the model’s equilibria and perform stability analysis to investigate the behavior of the equilibrium points.

3 Mathematical Analysis

Since R(t) does not appear in the first four equations of the model (1), without loss of generality, it is sufficient to consider first four equations of the model for the analysis purpose:

$$\begin{aligned} \begin{aligned} \frac{{\mathrm {d}}S}{{\mathrm {d}}t}&=\kappa -\delta _1 S-\delta _2 S-\frac{\beta _1 S(t-\varrho ) I(t-\varrho )}{1+\varepsilon I(t-\varrho )}- \vartheta S, \\ \frac{{\mathrm {d}}A_F}{{\mathrm {d}}t}&=\delta _1 S-\frac{\beta _2 I(t-\varrho ) A_F(t-\varrho )}{1+\varepsilon I(t-\varrho )}-\vartheta A_F,\\ \frac{{\mathrm {d}}A_P}{{\mathrm {d}}t}&= \delta _2 S -\frac{\beta _3 I(t-\varrho ) A_P(t-\varrho )}{1+\varepsilon I(t-\varrho )}-\vartheta A_P, \\ \frac{{\mathrm {d}}I}{{\mathrm {d}}t}&= \frac{\beta _1 S(t-\varrho ) I(t-\varrho )}{1+\varepsilon I(t-\varrho )}+\frac{\beta _2 I(t-\varrho ) A_F(t-\varrho )}{1+\varepsilon I(t-\varrho )}\\&\quad +\frac{\beta _3 I A_P(t-\varrho )}{1+\varepsilon I(t-\varrho )}-(d+\theta +\vartheta ) I-\frac{aI}{1+b I}. \end{aligned} \end{aligned}$$
(5)

For the existence of model equilibrium, we set the right-hand side terms of the (5) to zero and obtain that the model (5) has two equilibria given below:

  1. 1.

    Disease-free equilibrium \(E_0(S_0,A_{F_0},A_{P_0},0)\) (represents the eradication of infected individuals, i.e., \( I\equiv 0 ~\text {for all}~ t > 0\)), discussed in Sect. 3.1.

  2. 2.

    Endemic equilibrium \(E_e(S^*,A_F^*,A_P^*,I^*)\) (represents the persistence of infected individuals above a certain positive level, i.e., \(I>0\) for all \(t > 0\)), discussed in Sect. 3.2.

3.1 Disease-free equilibrium

The system (5) has a disease-free equilibrium of the form \(E_0(S_0,A_{F_0},A_{P_0},0)\), where

$$\begin{aligned} S_0= & {} \frac{\kappa }{\delta _1+\delta _2+\vartheta },~ A_{F_0}=\frac{\delta _1\kappa }{\vartheta (\delta _1+\delta _2+\vartheta )},\\ A_{P_0}= & {} \frac{\delta _2\kappa }{\vartheta (\delta _1+\delta _2+\vartheta )}. \end{aligned}$$

The characteristic equation of the system (5) at disease-free equilibrium is obtained as

$$\begin{aligned}&\left( -\vartheta -\lambda \right) ^2 \left( -\delta _1{-}\delta _2{-}\vartheta {-}\lambda \right) \left( \lambda +\left( \vartheta +d+\theta +a\right) \right. \nonumber \\&\quad \left. -\left( \beta _1 S_0+\beta _2 A_{F_0}+\beta _3 A_{P_0}\right) \mathrm {e^{-\lambda \varrho }}\right) =0. \end{aligned}$$
(6)

Equation (6) is fourth-degree transcendental equation in \(\lambda \) with roots \(\lambda _1=-\vartheta ,~\lambda _2=-\vartheta ,~\lambda _3= -(\delta _1+\delta _2+\vartheta )\), and the other roots are the solution of

$$\begin{aligned}&\lambda +\left( \vartheta +d+\theta +a\right) \nonumber \\&\quad -\left( \beta _1 S_0+\beta _2 A_{F_0}+\beta _3 A_{P_0}\right) \mathrm {e^{-\lambda \varrho }}=0. \end{aligned}$$
(7)

On simplification, Eq. (7) can be written as

$$\begin{aligned} X(\lambda ):= & {} \lambda +\left( \vartheta +d+\theta +a\right) \nonumber \\&-\frac{\kappa \left( \beta _1 \vartheta +\beta _2 \delta _1+\beta _3 \delta _2\right) }{\vartheta \left( \delta _1+\delta _2+\vartheta \right) }\mathrm {e^{-\lambda \varrho }}=0. \end{aligned}$$
(8)

The term \(\frac{\kappa \left( \beta _1 \vartheta +\beta _2 \delta _1+\beta _3 \delta _2\right) }{\vartheta \left( \vartheta +d+\theta +a\right) \left( \delta _1+\delta _2+\vartheta \right) }\mathrm {e^{-\lambda \varrho }}\) at \(\varrho =0\) is defined as the basic reproduction number of the system (5). Thus, the basic reproduction number of the system (5) is

$$\begin{aligned} R_0=\frac{\kappa \left( \beta _1 \vartheta +\beta _2 \delta _1+\beta _3 \delta _2\right) }{\vartheta \left( \vartheta +d+\theta +a\right) \left( \delta _1+\delta _2+\vartheta \right) }. \end{aligned}$$

The basic reproduction number \(R_0\) is the average number of secondary infections caused by a single infected agent, during his/her entire infectious period, in an entirely susceptible population [8].

3.1.1 Analysis for \(\mathbf {{R_0} \ne 1}\)

As mentioned above, Eq. (6) has three negative real roots \(\lambda _1=-\vartheta ,~\lambda _2=-\vartheta ,~\lambda _3= -(\delta _1+\delta _2+\vartheta )\), and other roots are the solutions of Eq. (8).

Note that

$$\begin{aligned} X(0)=\left( \vartheta +d+\theta +a\right) (1-R_0). \end{aligned}$$
(9)

If \(R_0>1\), then \(X(0)<0\). Also,

$$\begin{aligned} X'(\lambda )=1+\frac{\kappa \left( \beta _1 \vartheta +\beta _2 \delta _1+\beta _3 \delta _2\right) }{\vartheta \left( \delta _1+\delta _2+\vartheta \right) }\mathrm {e^{-\lambda \varrho }}\varrho >0. \end{aligned}$$
(10)

Thus, \(\mathop {\lim }\limits _{\lambda \rightarrow \infty } X(\lambda ) = + \infty \).

Hence, \(X(\lambda )=0\), \(X(0)<0\), \(X'(\lambda )>0\), and \(\mathop {\lim }\limits _{\lambda \rightarrow \infty } X(\lambda ) = + \infty \) indicate that there always exists a unique and positive real root of \(X(\lambda )=0\) if \(R_0>1\).

Now, if \(R_0<1\), then

$$\begin{aligned} {\text {Re}}\,\lambda&= \frac{\kappa \left( \beta _1 \vartheta +\beta _2 \delta _1+\beta _3 \delta _2\right) {\mathrm {e}^{ - ({\text {Re}}\,\lambda )\varrho }}\cos (Im\lambda )\varrho }{\vartheta \left( \delta _1+\delta _2+\vartheta \right) }\nonumber \\&\quad -\left( \vartheta +d+\theta +a\right) \nonumber \\&<\frac{\kappa \left( \beta _1 \vartheta +\beta _2 \delta _1+\beta _3 \delta _2\right) }{\vartheta \left( \delta _1+\delta _2+\vartheta \right) }-\left( \vartheta +d+\theta +a\right) \nonumber \\&=\left( \vartheta +d+\theta +a\right) \left( R_0-1\right) \nonumber \\&<0. \end{aligned}$$
(11)

Therefore, \(R{}_0 < 1\) implies that \(\lambda \) is a root of Eq. (6) with negative real part.

3.1.2 Analysis at \(\mathbf {R_0 = 1}\)

In this subsection, the system (5) is analyzed at \(E_0(S_0,A_{F_0},A_{P_0},0)\) and \(R_0=1\) for the time delay \(\varrho \ge 0\).

Case (i) \(\varvec{\varrho }>\textit{\textbf{0}}\)

If \(R_0 = 1\), then \(\lambda = 0\) is a simple characteristic root of Eq. (8). Note that \(R_0=1\) implies that \({\kappa \left( \beta _1 \vartheta +\beta _2 \delta _1+\beta _3 \delta _2\right) }{=}{\vartheta \left( \vartheta {+}d{+}\theta {+}a\right) \left( \delta _1{+}\delta _2{+}\vartheta \right) }.\)

Let \(\lambda =r+\mathrm {i} s\) be any of the other solutions, then (8) becomes:

$$\begin{aligned}&r+\mathrm {i} s+ \left( \vartheta +d+\theta +a\right) \nonumber \\&\quad -\left( \vartheta +d+\theta +a\right) \mathrm {e}^{-r \varrho } \left( \cos {s \varrho }-\mathrm {i}\sin {s \varrho }\right) =0.\nonumber \\ \end{aligned}$$
(12)

By applying Euler’s formula and splitting real and imaginary parts, Eq. (12) can be written as

$$\begin{aligned} \begin{aligned} r+\vartheta +d+\theta +a&=(\vartheta +d+\theta +a)\cos {s \varrho } \ \mathrm {e}^{-r \varrho },\\ s&=-(\vartheta +d+\theta +a) \sin {s \varrho } \ \mathrm {e}^{-r \varrho }. \end{aligned} \end{aligned}$$
(13)

On squaring and adding both the equations of Eq. (13), we obtain

$$\begin{aligned}&\left( r+\vartheta +d+\theta +a\right) ^2+s^2\nonumber \\&\quad =\left( r+\vartheta +d+\theta +a\right) ^2 \mathrm {e}^{-2 r \varrho }. \end{aligned}$$
(14)

If there exists a root satisfying both the equations of (13), then this root also satisfies Eq. (14) obtained by squaring and adding these equations. For Eq. (14) to be verified, we must have \(r \le 0\). Therefore, \(E_0\) is linearly neutrally stable.

Case (ii) \(\varvec{\varrho =0}\)

We now analyze the qualitative behavior of the system (5) without time delay, i.e., we take \(\varrho =0\). This analysis has an interest in itself and will also allow getting some information on the stability of the coexistence equilibrium in the case with delay [30]. The bifurcation theory approach obtained in [11], which is based on the center manifold theory [5], has been used to decide the local stability of a nonhyperbolic equilibrium (i.e., linearization matrix has at least one eigenvalue with zero real part) near the criticality \(E_0\) and \(R_0=1\). It allows us to clarify the direction of the bifurcation and describes the local behavior of disease-free equilibrium near \(R_0=1\). For simplicity, we redefine the state variables as \(S=x_1,~ A_F=x_2,~A_P=x_3\), and \(I=x_4\). So, the system (5) takes the form:

$$\begin{aligned} \begin{aligned} \frac{{\mathrm {d}}x_1}{{\mathrm {d}}t}&=\kappa -\delta _1 x_1-\delta _2 x_1-\frac{\beta _1 x_1 x_4}{\varepsilon x_4+1}-x_1 \vartheta \equiv g_1, \\ \frac{{\mathrm {d}}x_2}{{\mathrm {d}}t}&=-\frac{\beta _2 x_2 x_4}{\varepsilon x_4+1}-\vartheta x_2+\delta _1 x_1 \equiv g_2,\\ \frac{{\mathrm {d}}x_3}{{\mathrm {d}}t}&= -\frac{\beta _3 x_3 x_4}{\varepsilon x_4+1}-\vartheta x_3+\delta _2 x_1 \equiv g_3, \\ \frac{{\mathrm {d}}x_4}{{\mathrm {d}}t}&= \frac{\beta _1 x_1 x_4}{\varepsilon x_4+1}+\frac{\beta _2 x_2 x_4}{\varepsilon x_4+1}+\frac{\beta _3 x_3 x_4 }{\varepsilon x_4+1}\\&\quad -(d+\theta +\vartheta ) x_4-\frac{ax_4}{b x_4+1}\equiv g_4. \end{aligned} \end{aligned}$$
(15)

We observe that when \(R_0=1\), the chosen bifurcation parameter \(\beta _2\) takes the form

$$\begin{aligned}&\beta _2=\beta _2^*\\&\quad =\frac{\delta _2 \left( \vartheta (a+d+\theta +\vartheta )-\beta _3 \kappa \right) +\vartheta \left( \delta _1+\vartheta \right) (a+d+\theta +\vartheta )+\beta _1 \kappa (-\vartheta )}{\delta _1 \kappa }. \end{aligned}$$

The Jacobian matrix \(J(E_0, \ \beta _2^*)\) of the system (15) obtained at criticality (that is, at \(E_0\) and \(\beta _2^*\)) is

$$\begin{aligned} J(E_0, \beta _2^*) = \left( \begin{array}{cccc} -\vartheta -\delta _1-\delta _2 &{} 0 &{} 0 &{} -\frac{\kappa \beta _1}{\vartheta +\delta _1+\delta _2} \\ \delta _1 &{} -\vartheta &{} 0 &{} -\frac{\kappa \beta _2^* \delta _1}{\vartheta \left( \vartheta +\delta _1+\delta _2\right) } \\ \delta _2 &{} 0 &{} -\vartheta &{} -\frac{\kappa \beta _3 \delta _2}{\vartheta \left( \vartheta +\delta _1+\delta _2\right) } \\ 0 &{} 0 &{} 0 &{} 0\\ \end{array} \right) . \end{aligned}$$

The eigenvalues of the Jacobian matrix \(J(E_0, \beta _2^*)\) are \(\lambda _1= -\vartheta ,~\lambda _2= -\vartheta ,~\lambda _3= -\vartheta - \delta _1 -\delta _2,~\lambda _4=0\). We see that \(\lambda _1, \lambda _2,\) and \(\lambda _3\) are real and negative eigenvalues and \(\lambda _4=0\) is a simple zero eigenvalue (since the algebraic multiplicity of \(\lambda _4=0\) is 1) of \(J(E_0, \beta _2^*)\). Thus, when \(R_0 = 1\), the DFE \(E_0\) is a non-hyperbolic equilibrium.

The right eigenvector \(v=(v_1,v_2,v_3,v_4)\) of \(J(E_0, \beta _2^*)\) corresponding to \(\lambda _4=0\) is obtained as

$$\begin{aligned} v_1&=-\frac{\beta _1 \kappa }{\left( \delta _1+\delta _2+\vartheta \right) {}^2},\\ v_2&=-\frac{\delta _1 \kappa \left( \beta _2 \left( \delta _1+\delta _2+\vartheta \right) +\beta _1 \vartheta \right) }{\vartheta ^2 \left( \delta _1+\delta _2+\vartheta \right) {}^2},\\ v_3&=-\frac{\delta _2 \kappa \left( \beta _3 \left( \delta _1+\delta _2+\vartheta \right) +\beta _1 \vartheta \right) }{\vartheta ^2 \left( \delta _1+\delta _2+\vartheta \right) {}^2},\\ v_4&=1. \end{aligned}$$

The left eigenvector \(w=(w_1, w_2, w_3,w_4)\) of \(J(E_0,\ \beta _2^*)\) corresponding to \(\lambda _4=0\) is obtained as

$$\begin{aligned} w_1&=0,\\ w_2&=0,\\ w_3&=0,\\ w_4&=1. \end{aligned}$$

Let \(g_k\)’s, \(k=1,2,3,4\), denote the right-hand side of the system (15). The bifurcation coefficients \(a_1\) and \(b_1\) defined in Theorem 4.1 of [33] are given by:

$$\begin{aligned} \begin{aligned} {a_1}&= {\sum \limits _{k,i,j = 1}^4 {{w_k}{v_i}{v_j}\left( {\frac{{{\partial ^2}{g_k}}}{{\partial {x_i}\partial {x_j}}}} \right) } _{{E_0}}},\\ b_1&={\sum \limits _{k,i = 1}^4 {{w_k}{v_i}\left( {\frac{{{\partial ^2}{g_k}}}{{\partial {x_i}\partial {\beta _2 ^*}}}} \right) } _{{E_0}}}. \end{aligned} \end{aligned}$$

The nonzero partial derivatives of the functions \(g_k\)’s at \(E_0\) are evaluated as

$$\begin{aligned} {\left( {\frac{{{\partial ^2}{g_4}}}{{\partial x_4 \partial x_1}}} \right) _{{E_0}}}= & {} \beta _1, {\left( {\frac{{{\partial ^2}{g_4}}}{{\partial x_4 \partial x_2}}} \right) _{{E_0}}}=\beta _2^*, \\ {\left( {\frac{{{\partial ^2}{g_4}}}{{\partial x_4 \partial x_3}}} \right) _{{E_0}}}= & {} \beta _3, {\left( {\frac{{{\partial ^2}{g_4}}}{{\partial x_1 \partial x_4}}} \right) _{{E_0}}}=\beta _1, \\ {\left( {\frac{{{\partial ^2}{g_4}}}{{\partial x_2 \partial x_4}}} \right) _{{E_0}}}= & {} \beta _2^*, \\ {\left( {\frac{{{\partial ^2}{g_4}}}{{\partial x_3 \partial x_4}}} \right) _{{E_0}}}= & {} \beta _3, {\left( {\frac{{{\partial ^2}{g_4}}}{{ \partial x_4^2}}} \right) _{{E_0}}}\\= & {} -\frac{2 \varepsilon \beta _1 \kappa }{\delta _1+\delta _2+\vartheta }-\frac{2 \varepsilon \beta _2^* \delta _1 \kappa }{\vartheta \left( \delta _1+\delta _2+\vartheta \right) }\\&-\frac{2 \varepsilon \beta _3 \delta _2 \kappa }{\vartheta \left( \delta _1+\delta _2+\vartheta \right) }+2 a b, and \\ {\left( {\frac{{{\partial ^2}{g_4}}}{{\partial x_4 \partial \beta _2^*}}} \right) _{{E_0}}}= & {} \frac{\delta _1 \kappa }{\vartheta \left( \delta _1+\delta _2+\vartheta \right) }. \end{aligned}$$

The bifurcation coefficients \(a_1\) and \(b_1\) are calculated at the bifurcation parameter \(\beta _2^*\) as follows:

$$\begin{aligned} \begin{aligned} a_1&=-\frac{2}{\delta _1 \kappa \vartheta ^2 \left( \delta _1+\delta _2+\vartheta \right) } \big ( \delta _1 (\delta _2 (\vartheta ^2 \left( \kappa (a (\varepsilon -b)\right. \\&\quad \left. +\varepsilon (d+\theta +\vartheta ))+2 (a+d+\theta +\vartheta )^2\right) \\&\quad +\beta _3 \kappa \left( \beta _3 \kappa -2 \vartheta (a+d+\theta +\vartheta )\right) )\\&\quad +\vartheta ^3 \left( \kappa (a (\varepsilon -b)+\varepsilon (d+\theta +\vartheta ))\right. \\&\quad \left. +2 (a+d+\theta +\vartheta )^2\right) )\\&\quad +\delta _1^2 \vartheta ^2 \left( \kappa (a (\varepsilon -b)+\varepsilon (d+\theta +\vartheta ))\right. \\&\quad \left. +(a+d+\theta +\vartheta )^2\right) \\&\quad +(\delta _2 \left( \vartheta (a+d+\theta +\vartheta )-\beta _3 \kappa \right) \\&\quad +\vartheta ^2 (a+d+\theta +\vartheta )){}^2\\&\quad -\beta _1 \kappa \vartheta \left( 2 \delta _2 \left( \vartheta (a+d+\theta +\vartheta )-\beta _3 \kappa \right) \right. \\&\quad \left. +\vartheta \left( \delta _1+2 \vartheta \right) (a+d+\theta +\vartheta )\right) \\&\quad +\beta _1^2 \kappa ^2 \vartheta ^2 \big )\\&=-\frac{2}{\delta _1 \kappa \vartheta ^2 \left( \delta _1+\delta _2+\vartheta \right) } \times G(\beta _3),\\ b_1&=\frac{\kappa }{\delta _1+\delta _2+\vartheta }. \end{aligned} \end{aligned}$$

where

$$\begin{aligned} G(\beta _3)&=\left( \zeta _2 \ \beta _3^2+\zeta _1 \ \beta _3+\zeta _0\right) , \end{aligned}$$
(16)

where the coefficients \(\zeta _0, ~ \zeta _1\) and \(\zeta _2\) are

$$\begin{aligned} \zeta _2&=\delta _2 \left( \delta _1+\delta _2\right) \kappa ^2,\nonumber \\ \zeta _1&=2 \delta _2 \kappa \vartheta \left( \beta _1 \kappa -\left( \delta _1+\delta _2+\vartheta \right) (a+d+\theta +\vartheta )\right) ,\nonumber \\ \zeta _0&=\vartheta ^2 \big (\big (\delta _1+\delta _2+\vartheta \big ) \big (\delta _1 \big (\kappa (a (\varepsilon -b)\nonumber \\&\quad +\varepsilon (d+\theta +\vartheta ))\nonumber \\&\quad +(a+d+\theta +\vartheta )^2\big )\nonumber \\&\quad +\big (\delta _2+\vartheta \big ) (a+d+\theta +\vartheta )^2\big )\nonumber \\&\quad +\beta _1 \delta _1 \kappa (a+d+\theta +\vartheta )\nonumber \\&\quad +\beta _1 \kappa \big (\beta _1 \kappa -2 \big (\delta _1+\delta _2+\vartheta \big ) (a+d+\theta +\vartheta )\big )\big ). \end{aligned}$$
(17)

It can be seen that the bifurcation coefficient \(b_1\) is always positive and the sign of \(a_1\) depends the sign of \(G(\beta _3)\), given in Eq. (16). If \(G(\beta _3)<0\), then \(a_1>0\), whereas if \(G(\beta _3)>0\), then \(a_1<0\).

The discriminant of quadratic polynomial \(G(\beta _3)\) is obtained as

$$\begin{aligned} \begin{aligned}&D=a \big (\delta _1+\delta _2\big ) \kappa (b-\varepsilon ) \big (\delta _1+\delta _2+\vartheta \big )\\&\quad +\big (-\delta _1{-}\delta _2{-}\vartheta \big ) \big (\big (\delta _1+\delta _2+\vartheta \big ) (a+d+\theta +\vartheta )^2\\&\quad +\varepsilon \big (\delta _1+\delta _2\big ) \kappa (d+\theta +\vartheta )\big )\\&\quad +\beta _1 \kappa \big (\delta _1+\delta _2+2 \vartheta \big ) (a+d+\theta +\vartheta )\\&\quad +\beta _1^2 \big (-\kappa ^2\big ). \end{aligned} \end{aligned}$$
(18)

Let \(\beta _3^*\) and \(\beta _3^{**}\) be two roots of Eq. (16), then we get

$$\begin{aligned} \beta _3^*= \frac{-\zeta _1+D}{2 \zeta _2},~\text {and}~ \beta _3^{**}=\frac{-\zeta _1-D}{2 \zeta _2}. \end{aligned}$$
(19)

Using Theorem 4.1(iv) in [11], the type of bifurcation is governed by the sign of \(a_1\) and hence by the sign of \(G(\beta _3)\). If \(G(\beta _3)\) is of positive sign, then forward bifurcation occurs, whereas if the sign of \(G(\beta _3)\) is negative, then the system (15) reveals a backward bifurcation. The study of forward and backward bifurcation is important in the study of epidemiology as they play a relevant role in disease control and eradication. In the case of forward bifurcation, the condition \(R_0 < 1\) is a necessary and sufficient condition for disease eradication, whereas reducing \(R_0\) below unity is no longer sufficient for disease eradication when a backward bifurcation occurs. These behavior differences are essential in planning how to control a disease; a backward bifurcation at \(R_0 = 1\) makes control more difficult. These two cases are discussed below separately.

(I) Forward bifurcation: When there is a forward bifurcation at \(R_0 = 1\), it is not possible for a disease to invade a population if \(R_0 < 1\) because the system will return to the disease-free equilibrium \(I = 0\) if some infectives are introduced into the population. For values of \(R_0\) slightly greater than 1, \(E_0\) changes its stability from stable to unstable and the model admits a unique endemic equilibrium, which is locally asymptotically stable [11]. Therefore, it is imperative to find the range for which forward bifurcation occurs. The range of forward bifurcation is governed by the positivity of \(G(\beta _3)\). Thus, there are two cases in which \(G(\beta _3)\) is found to be positive. These are given as follows:

$$\begin{aligned} \left\{ \begin{array}{r} \zeta _1>0,\\ \zeta _0>0. \end{array}\right. \end{aligned}$$
(20)
$$\begin{aligned} \hbox {or} \end{aligned}$$
$$\begin{aligned} \left\{ \begin{array}{r} D>0,\\ \text {either of} ~ \left( \zeta _1>0,~\zeta _0 {<}0\right) ,~ \left( \zeta _1{<}0.~\zeta _0 {>}0\right) ,~ \text {or}~ \left( \zeta _1 {<}0,~ \zeta _0 {<}0\right) ~\text {holds},\\ \beta _3<\beta _3^{*}~ \text {or}~\beta _3>\beta _3^{**}. \end{array}\right. \nonumber \\ \end{aligned}$$
(21)

(II) Backward bifurcation: The backward bifurcation is characterized as when \(R_0<1\); a small unstable endemic equilibrium appears while the disease-free equilibrium and a larger endemic equilibrium are locally asymptotically stable. When \(R_0>1\), then an unstable disease-free equilibrium and a stable endemic equilibrium exist [11]. It is illustrated in Fig. (4). The range of existence of backward bifurcation (i.e., when \(G(\beta _3)<0\)) as follows:

$$\begin{aligned} \left\{ \begin{array}{r} D>0,\\ \text {either of} ~ \left( \zeta _1 {>}0,~\zeta _0 {<}0\right) ,~ \left( \zeta _1{<}0.~\zeta _0 {>}0\right) ,~ \text {or}~ \left( \zeta _1 {<}0,~ \zeta _0 {<}0\right) ~\text {holds},\\ \beta _3^{**}{<}\beta _3 {<}\beta _3^*. \end{array}\right. \nonumber \\ \end{aligned}$$
(22)

Based on the analysis above, we state the following theorems:

Theorem 1

The disease-free equilibrium \(E_0(S_0,A_{F_0},A_{P_0},0)\) of the delayed system (5) is asymptotically stable if \(R_0 < 1\) and unstable if \(R_0 > 1\) for \(\varrho >0\).

Theorem 2

The disease-free equilibrium \(E_0(S_0,A_{F_0}, A_{P_0},0)\) of the delayed system (5) at \(R_0=1\) is linearly neutrally stable for \(\varrho >0\).

Theorem 3

When \(R_0=1\), then the undelayed system (15) reveals a backward (forward) bifurcation at disease-free equilibrium \(E_0(S_0,A_{F_0},A_{P_0},0)\) if and only if \(G(\beta _3)<0~ (>0)\).

The graphical presentations of the forward and backward bifurcations are shown in Figs. 2, 3, and 4 for the experimental data mentioned below:

\(\kappa =2,~ \varepsilon =0.1,~ \vartheta =0.01,~ d=0.001,~b=0.8,~\theta =0.01,~a=0.9,~ \beta _1=0.004,~ \delta _1=0.01,~\delta _2=0.009\). At these values of parameters, we evaluate that the range of \(\beta _3\) is \(\beta _3^{**}=0.00098164 \le \beta _3 \le 0.0088652 =\beta _3^*\). The cases of occurrence of forward and backward bifurcations, given in the inequalities (20), (21), and (22), are illustrated from (1)–(3) as below:

  1. (1)

    If we take \(\beta _3=0.00008\), then we obtain that \(\zeta _2=0.000522\), \(\zeta _1=1.242\times 10^{-6}>0\), and \(\zeta _0=7.75344 \times 10^{-9}>0\). This case illustrates the inequality (20), and the graph is shown in Fig. 2.

  2. (2)

    On considering \(\beta _3=0.01\), we obtain that \(\zeta _2=0.000522\), \(\zeta _1=1.242\times 10^-6>0\), \(\zeta _0=-5.44699\times 10^{-8}<0\), and the discriminant \(D=1.15276\times 10^{-10}>0\). It illustrates the inequality (21), and the graph is shown in Fig. 3.

  3. (3)

    If we take \(\beta _3=0.006\), which lies between \(\beta ^{**}_3\) and \(\beta _3^*\), then we obtain that the coefficients \(\zeta _2=0.000522\), \(\zeta _1=1.242 \times 10^{-6}>0\) and \(\zeta _0= -4.05047 \times 10^{-8}<0\), and the discriminant \(D=8.61164 \times 10^{-11}>0.\) This case illustrates the inequality (22), and the graph is shown in Fig. 4.

In Figs. 2, 3, and 4, the solid lines show stability and the dashed lines show instability.

3.2 Endemic equilibrium and stability

Assuming that \(S,~A_F,~A_P,~I \ne 0\). To determine the conditions for the existence of endemic (positive) equilibrium \(E_e(S^*,A_F^*,A_P^*,I^*)\), we put the right-hand side of the system (5) to zero. We get:

$$\begin{aligned}&\kappa -\delta _1 S-\delta _2 S-\frac{\beta _1 S I}{1+\varepsilon I}-S \vartheta =0, \end{aligned}$$
(23)
$$\begin{aligned}&-\frac{\beta _2 A_F I}{1+\varepsilon I}-\vartheta A_F+\delta _1 S=0,\end{aligned}$$
(24)
$$\begin{aligned}&-\frac{\beta _3 A_P I }{1+\varepsilon I}-\vartheta A_P+\delta _2 S=0, \end{aligned}$$
(25)
$$\begin{aligned}&\frac{\beta _1 S I}{1+\varepsilon I}+\frac{\beta _2 A_F I}{1+\varepsilon I}+\frac{\beta _3 A_P I}{1+\varepsilon I}\nonumber \\&\quad -(d+\theta +\vartheta ) I-\frac{aI}{1+b I}=0 . \end{aligned}$$
(26)

Solving for S, \(A_F\) and \(A_P\) in terms of I, from Eqs. (23), (24), and (25), respectively, and substituting the resulting expression in Eq. (26), after simplification, we obtain the following equation in I:

$$\begin{aligned} P(I):=A_0+A_1 I+ A_2 I^2+A_3 I^3+A_4 I^4=0,\nonumber \\ \end{aligned}$$
(27)
Fig. 2
figure 2

Plot of \(R_0\) versus I(t), showing the occurrence of forward bifurcation

Full size image
Fig. 3
figure 3

Plot of \(R_0\) versus I(t), showing the occurrence of forward bifurcation

Full size image
Fig. 4
figure 4

Plot of \(R_0\) versus I(t), showing the presence of backward bifurcation

Full size image

where

$$\begin{aligned} A_0= & {} \vartheta \left( \delta _1+\delta _2+\vartheta \right) (a+d+\theta +\vartheta ) (1-R_0), \nonumber \\ A_1= & {} \vartheta \left( \left( \delta _1+\delta _2+\vartheta \right) \left( 3 \varepsilon \vartheta +\beta _2+\beta _3\right) +\beta _1 \vartheta \right) \nonumber \\&\quad (a+d+\theta +\vartheta )-\beta _2 \delta _1 \kappa \vartheta (2 \varepsilon +b) \nonumber \\&\qquad -\beta _3 \delta _2 \kappa \vartheta (2 \varepsilon +b) \nonumber \\&\qquad -\beta _1 \kappa \vartheta ^2 (2 \varepsilon +b)+b \vartheta ^2 \left( \delta _1+\delta _2+\vartheta \right) \nonumber \\&\qquad (d+\theta +\vartheta )-\beta _2 \beta _3 \delta _1 \kappa -\beta _2 \beta _3 \delta _2 \kappa \nonumber \\&\qquad -\beta _1 \left( \beta _2+\beta _3\right) \kappa \vartheta ,\nonumber \\ A_2= & {} \vartheta \Big (\beta _3 \left( \delta _2 (2 a \varepsilon -\varepsilon \kappa (\varepsilon +2 b)+(2 \varepsilon +b) (d+\theta +\vartheta ))\right. \nonumber \\&\qquad \left. +\left( \delta _1+\vartheta \right) (2 a \varepsilon +(2 \varepsilon +b) (d+\theta +\vartheta ))\right) \nonumber \\&\qquad +3 \varepsilon \vartheta \left( \delta _1+\delta _2+\vartheta \right) (a \varepsilon +(\varepsilon +b) (d+\theta +\vartheta ))\Big ) \nonumber \\&\qquad +\beta _2 \Big (\beta _3 \Big (\left( \delta _1+\delta _2\right) (a-\kappa (\varepsilon +b)+d+\theta +\vartheta )\nonumber \\&\qquad +\vartheta (a+d+\theta +\vartheta )\Big )+\vartheta \big (\delta _1 (2 a \varepsilon -\varepsilon \kappa (\varepsilon +2 b)\nonumber \\&\qquad +(2 \varepsilon +b) (d+\theta +\vartheta ))\nonumber \\&\qquad +\left( \delta _2+\vartheta \right) (2 a \varepsilon +(2 \varepsilon +b) (d+\theta +\vartheta ))\big )\Big )\nonumber \\&\qquad -\beta _1 \Big (\beta _2 \left( -\vartheta (a+d+\theta +\vartheta )+\kappa \vartheta (\varepsilon +b)+\beta _3 \kappa \right) \nonumber \\&\qquad +\vartheta \left( \vartheta (-2 a \varepsilon +\varepsilon \kappa (\varepsilon +2 b)\right. \nonumber \\&\qquad -(2 \varepsilon +b) (d+\theta +\vartheta )) \nonumber \\&\qquad \left. -\beta _3 (a-\kappa (\varepsilon +b)+d+\theta +\vartheta )\right) \Big ), \nonumber \\ A_3= & {} -\left( \varepsilon \vartheta +\beta _3\right) \left( \left( \varepsilon \vartheta +\beta _2\right) \left( -a \varepsilon \vartheta -\beta _1 (a-b \kappa )\right) \right. \nonumber \\&\qquad \left. -\varepsilon \delta _1 \left( a \varepsilon \vartheta +\beta _2 (a-b \kappa )\right) \right) +\varepsilon \delta _2 \left( \varepsilon \vartheta +\beta _2\right) \big (a \varepsilon \vartheta \nonumber \\&\qquad +\beta _3 (a-b \kappa )\big )-(d+\theta +\vartheta ) \big (\beta _1 \left( \vartheta \left( -\beta _3 (\varepsilon +b)\right. \right. \nonumber \\&\qquad \left. \left. -\varepsilon \vartheta (\varepsilon +2 b)\right) -\beta _2 \left( \vartheta (\varepsilon +b)+\beta _3\right) \right) \nonumber \\&\qquad -\left( \delta _1+\delta _2+\vartheta \right) \left( \beta _2 \left( \beta _3 (\varepsilon +b)+\varepsilon \vartheta (\varepsilon +2 b)\right) \right. \nonumber \\&\qquad \left. +\varepsilon \vartheta \left( \beta _3 (\varepsilon +2 b)+\varepsilon \vartheta (\varepsilon +3 b)\right) \right) \big ), \nonumber \\ A_4= & {} b \left( \varepsilon \vartheta +\beta _2\right) \left( \varepsilon \vartheta +\beta _3\right) (d+\theta +\vartheta )\nonumber \\&\qquad \left( \varepsilon \left( \delta _1+\delta _2+\vartheta \right) +\beta _1\right) . \end{aligned}$$
(28)

For a positive root of \(I^*\) of the polynomial P(I), we have

$$\begin{aligned} S^*&=\frac{\kappa +\varepsilon \kappa I^*}{\left( \delta _1+\delta _2+\vartheta \right) (\varepsilon I^*+1)+\beta _1 I^*},\end{aligned}$$
(29)
$$\begin{aligned} A_F^*&=\frac{\delta _1 S^* (\varepsilon I^*+1)}{\varepsilon I^* \vartheta +\beta _2 I^*+\vartheta },\end{aligned}$$
(30)
$$\begin{aligned} A_P^*&=\frac{\delta _2 S^* (\varepsilon I^*+1)}{\varepsilon I^* \vartheta +\beta _3 I^*+\vartheta }. \end{aligned}$$
(31)

So, \(E_e(S^*,A_F^*,A_P^*,I^*)\) is a positive equilibrium of the system (5).

Theorem 4

When \(R_0>1\), then there is either a unique or three positive endemic equilibria if all equilibria are simple roots.

Proof

Let \(R_0>1\). We see that the coefficient \(A_4\) is always positive. On the other hand, \(A_0<0\) when \(R_0>1\). From Eq. (27), we have a fourth-degree polynomial in I, given below:

$$\begin{aligned} P(I):=A_0+A_1 I+ A_2 I^2+A_3 I^3+A_4 I^4=0. \end{aligned}$$

The following possibilities for the signs of \(A_1,~A_2\), and \(A_3\) exist:

$$\begin{aligned} \begin{aligned} {\mathbf{V }_1:}~&A_1>0,~ A_2>0,~\text {and}~ A_3>0,\\ {\mathbf{V }_2:}~&A_1<0,~ A_2<0,~\text {and}~ A_3>0,\\ {\mathbf{V }_3:}~&A_1<0,~ A_2>0,~\text {and}~ A_3>0,\\ {\mathbf{V }_4:}~&A_1<0,~ A_2<0,~\text {and}~ A_3<0,\\ {\mathbf{V }_5:}~&A_1>0,~ A_2>0,~\text {and}~ A_3<0,\\ {\mathbf{V }_6:}~&A_1>0,~ A_2<0,~\text {and}~ A_3>0,\\ {\mathbf{V }_7:}~&A_1>0,~ A_2<0,~\text {and}~ A_3<0,\\ {\mathbf{V }_8:}~&A_1<0,~ A_2>0,~\text {and}~ A_3<0. \end{aligned} \end{aligned}$$

Using Descartes’ rule of signs [12], P(I) can have either a unique or three positive roots. If any of the conditions V \(_1\)–V \(_4\) holds, then there is unique endemic equilibrium, whereas for the existence of three endemic equilibria, any one of the conditions V \(_5\)–V \(_8\) must satisfy. \(\square \)

For the present study, we consider the case of unique endemic equilibrium only. H1: Suppose that any of the conditions (V \(_1\)–V \(_4\), and \(R_0>1\)) holds, then the system (5) admits a unique endemic equilibrium.

Now, we study the local stability behavior of endemic equilibrium \(E_e(S^*,A_F^*,A_P^*,I^*)\). For this, we obtain the characteristic equation of the system (5) at \(E_e(S^*,A_F^*,A_P^*,I^*)\) as given below:

$$\begin{aligned} P_0(\lambda )+\mathrm {e}^{-\lambda \varrho } P_1(\lambda )+\mathrm {e}^{-2\lambda \varrho }P_2(\lambda )+\mathrm {e}^{-3\lambda \varrho } P_3(\lambda )=0,\nonumber \\ \end{aligned}$$
(32)

where,

$$\begin{aligned} \begin{aligned} P_0(\lambda )&=\lambda ^4 +K_1 \lambda ^3+K_2 \lambda ^2+K_3\lambda +K_4,\\ P_1(\lambda )&=K_5 \lambda ^3+K_6 \lambda ^2+K_7\lambda +K_8,\\ P_2(\lambda )&= K_9 \lambda ^2+K_{10} \lambda +K_{11},\\ P_3(\lambda )&= K_{12} \lambda +K_{13}. \end{aligned} \end{aligned}$$
(33)

where the coefficients \(K_i\), \(i=1\) to 13 are given in Appendix. For \(\varrho =0\), the characteristic equation becomes:

$$\begin{aligned} \lambda ^4+Q_3 \lambda ^3+Q_2 \lambda ^2+Q_1 \lambda +Q_0=0, \end{aligned}$$
(34)

where \(Q_i's\), \(i=0,1,2,3\), are given in Appendix.

Based on Routh–Hurwitz criterion, it can be concluded that all the roots of Eq. (34) have negative real parts if the following inequalities hold:

$$\begin{aligned}&\mathbf{H2}: ~{Q_i>0~(i=0,1,2,3)},~Q_3Q_2-Q_1>0,~\text {and}~\nonumber \\&\quad Q_3Q_2Q_1-Q_1^2-Q_3^2Q_0>0. \end{aligned}$$
(35)

Thus, we state the following theorem:

Theorem 5

At \(\varrho =0\), the endemic equilibrium \(E_2(S^*,A_F^*,A_P^*,I^*)\) is locally asymptotically stable if H2 holds.

Now multiplying by \(e^{-\lambda \varrho }\) on both sides of the characteristic equation (32), we get:

$$\begin{aligned} P_0(\lambda )\mathrm {e}^{\lambda \varrho }+ P_1(\lambda )+\mathrm {e}^{-\lambda \varrho }P_2(\lambda )+\mathrm {e}^{-2\lambda \varrho } P_3(\lambda )=0.\nonumber \\ \end{aligned}$$
(36)

Change of stability and hence the existence of oscillatory solution may appear if the roots of the characteristic equation are purely imaginary. Therefore, to study the stability of \(E_e\), assuming that \(\lambda =\mathrm {i}\omega ,~ (\omega >0)\) is a root of Eq. (36). Then, Eq. (36) becomes:

$$\begin{aligned}&P_0(\mathrm {i}\omega )\mathrm {e}^{\mathrm {i}\omega \varrho }+ P_1(\mathrm {i}\omega )+\mathrm {e}^{-\mathrm {i}\omega \varrho }P_2(\mathrm {i}\omega )\nonumber \\&\quad +\mathrm {e}^{-2\mathrm {i}\omega \varrho } P_3(\mathrm {i}\omega )=0. \end{aligned}$$
(37)

Equation (37) can be rewritten as

$$\begin{aligned} \begin{aligned}&\left( M_0+\mathrm {i}N_0\right) \left( \cos {\omega \varrho }+\mathrm {i}\sin {\omega \varrho }\right) + \left( M_1+\mathrm {i}N_1\right) \\&\quad +\left( M_2+\mathrm {i}N_2 \right) \left( \cos {\omega \varrho }-\mathrm {i}\sin {\omega \varrho }\right) \\&\quad +\left( M_3+\mathrm {i}N_3 \right) \left( \cos {2\omega \varrho }-\mathrm {i}\sin {2\omega \varrho }\right) =0, \end{aligned} \end{aligned}$$
(38)

where \(M_0,~M_1,~M_2,~M_3,~N_0,~N_1,~N_2\) and \(N_3\) denote the real and imaginary parts of \(P_0(\mathrm {i}\omega ),~P_1(\mathrm {i}\omega )\), \(P_2(\mathrm {i}\omega )\) and \(P_3(\mathrm {i}\omega )\), respectively, given as:

$$\begin{aligned} \begin{aligned} M_0&=\omega ^4-K_2 \omega ^2+K_4,~ N_0=-K_1 \omega ^3+K_3 \omega ,\\ M_1&=-K_6 \omega ^2+K_8,~ N_1=-K_5 \omega ^3+K_7 \omega ,\\ M_2&=-K_9 \omega ^2+K_{11},~ N_2=K_10 \omega ,\\ M_3&=K_{13},~ N_3=K_{12} \omega . \end{aligned} \end{aligned}$$

When Eq. (38) splits into its real and imaginary parts, we get

$$\begin{aligned}&M_1+M_4 \cos {\omega \varrho }+V_4 \sin {\omega \varrho }\nonumber \\&\quad =-N_3 \sin {2 \omega \varrho }-M_3 \cos {2\omega \varrho }, \end{aligned}$$
(39)
$$\begin{aligned}&N_1+N_5 \cos {\omega \varrho }+M_5\sin {\omega \varrho }\nonumber \\&\quad =-N_3 \cos {2\omega \varrho }+M_3 \sin {2\omega \varrho }, \end{aligned}$$
(40)

where \(M_4=M_0+M_2, ~N_4=N_2-N_0,~ M_5=M_0-M_2\) and \(N_5=N_2+N_0\).

On squaring Eqs. (39) and (40) and then adding, we obtain

$$\begin{aligned}&\left( M_1+M_4 \cos {\omega \varrho }+N_4 \sin {\omega \varrho }\right) ^2+\left( N_1+N_5\cos {\omega \varrho }\right) \nonumber \\&\quad +M_5 (\sin {\omega \varrho })^2-N_3^2-M_3^2=0. \end{aligned}$$
(41)

On substituting \(\sin {\omega \varrho }=\sqrt{1-\cos ^2{\omega \varrho }}\) in Eq. (41), we obtain

$$\begin{aligned}&L_1 \cos ^4{\omega \varrho }+L_2 \cos ^3{\omega \varrho }+L_3\cos ^2 {\omega \varrho }\nonumber \\&\quad +L_4 \cos {\omega \varrho }+L_5=0, \end{aligned}$$
(42)

where

$$\begin{aligned}&L_1=p_1^2+4p_5^2,~ L_2=4p_1 p_2+8p_4p_5,\\&L_3=4p_2^2+2p_1p_3+4p_4^2-4p_5^2,\\&L_4=4p_2p_3-8p_4p_5,\\&L_5=p_3^2-4p_4^2,\\&p_1=M_4^2+N_5^2-N_4^2-M_5^2,~ p_2=M_1M_4+N_1N_4,\\&p_3=M_1^2+N_4^2+N_1^2+M_5^2-N_3^2-M_3^2,~ \\&p_4=M_1N_4+N_1M_5,\\&p_5=M_4N_4+M_5N_5. \end{aligned}$$

Let \(\cos {\omega \varrho }=x\), then Eq. (42) can be written as

$$\begin{aligned} f(x):= L_1 x^4+L_2 x^3+L_3 x^2+L_4 x+L_5=0. \end{aligned}$$
(43)

From Eq. (43), we obtain

$$\begin{aligned} f'(x)=4L_1 x^3+3L_2 x^2 +2 L_3 x+L_4=0. \end{aligned}$$
(44)

For convenience, we assume that \(x=y-L_2/4L_1\). Then, Eq. (44) becomes:

$$\begin{aligned} y^3+Ay+B=0, \end{aligned}$$
(45)

where

$$\begin{aligned} A&=\frac{L_3}{2L_1}-\frac{3}{16} \left( \frac{T_2}{T_1}\right) ^2,\\ B&=\frac{1}{32}\left( \frac{L_2}{L_1}\right) ^3-\frac{L_2 L_3}{8 L_1^2}+\frac{L_4}{4 L_1}. \end{aligned}$$

Now, roots of Eq. (45) are given as

$$\begin{aligned} y_1&=\root 3 \of {-\frac{B}{2}+\sqrt{O}}+\root 3 \of {-\frac{B}{2}-\sqrt{O}},\\ y_2&=\eta _1 \root 3 \of {-\frac{B}{2}+\sqrt{O}}+\eta _2 \root 3 \of {-\frac{B}{2}-\sqrt{O}},\\ y_3&=\eta _2 \root 3 \of {-\frac{B}{2}+\sqrt{O}}+\eta _1 \root 3 \of {-\frac{B}{2}-\sqrt{O}},\\ \end{aligned}$$

where \(\eta _1=\frac{-1+\sqrt{3}\mathrm {i}}{2},~\eta _2=\frac{-1-\sqrt{3}\mathrm {i}}{2}\) and \(O=\frac{B^2}{4}+\frac{A_3}{27}\).

It follows from \(\cos {\omega \varrho }=x\) and \(x=y-L_2/4L_1=F_1(\omega )\) that

$$\begin{aligned} \cos {\omega \varrho }=F_1(\omega ). \end{aligned}$$
(46)

On substituting Eq. (46) in Eq. (41) and solving for \(\sin {\omega \varrho }\), we obtain

$$\begin{aligned} \sin {\omega \varrho }=F_2(\omega ). \end{aligned}$$
(47)

From Eqs. (46) and (47), we get

$$\begin{aligned} F_1^2(\omega )+F_2^2(\omega )=1. \end{aligned}$$
(48)

Assume that H3:, Eq. (48) has at least one positive root \(\omega _0\), such that the characteristic equation (32) has a pair of purely imaginary roots \(\mathrm {i} \omega _0\).

For \(\omega _0\), the corresponding critical value of time delay \(\varrho _k\) can be obtained as:

$$\begin{aligned} \varrho _k=\frac{1}{\omega _0} \left( \arccos {F_1(\omega _0)}+2k \pi \right) ,~k=0,1,2,\ldots .\nonumber \\ \end{aligned}$$
(49)

Assume that \(\varrho \) is a bifurcation parameter and \(\varrho _0\)=\(\min {\varrho _k},~k=0,1,2,\ldots \) is the critical value.

To establish the Hopf bifurcation, we show that \(Re\,\left[ \frac{{\mathrm {d}}\lambda }{{\mathrm {d}}\varrho }\right] ^{-1}\Big |_{\lambda =\mathrm {i} \omega _0} \ne 0\).

Differentiating Eq. (32) with respect to \(\varrho \), we obtain:

$$\begin{aligned}&\frac{{\mathrm {d}}\lambda }{{\mathrm {d}}\varrho } \left( P_0'(\lambda )+\mathrm {e}^{-\lambda \varrho } P_1'(\lambda )-\varrho \mathrm {e}^{-\lambda \varrho } P_1(\lambda ) +\mathrm {e}^{-2\lambda \varrho } P_2'(\lambda )-2 \varrho P_2(\lambda )\mathrm {e}^{-2\lambda \varrho } +\mathrm {e}^{-3\lambda \varrho } P_3'(\lambda ) -3\varrho P_3(\lambda ) \mathrm {e}^{-3\lambda \varrho }\right) \\&\quad -\lambda \mathrm {e}^{-\lambda \varrho } P1(\lambda )-2\lambda P_2(\lambda ) \mathrm {e}^{-2\lambda \varrho }-3\lambda P_3(\lambda ) \mathrm {e}^{-3\lambda \varrho }=0.\\&\implies \frac{{\mathrm {d}}\lambda }{{\mathrm {d}}\varrho } \left( P_0'(\lambda )+\mathrm {e}^{-\lambda \varrho } P_1'(\lambda )-\varrho \mathrm {e}^{-\lambda \varrho } P_1(\lambda ) +\mathrm {e}^{-2\lambda \varrho } P_2'(\lambda )-2 \varrho P_2(\lambda )\mathrm {e}^{-2\lambda \varrho } +\mathrm {e}^{-3\lambda \varrho } P_3'(\lambda )-3\varrho P_3(\lambda ) \mathrm {e}^{-3\lambda \varrho }\right) \\&\quad =\lambda \mathrm {e}^{-\lambda \varrho } P1(\lambda )+2\lambda P_2(\lambda ) \mathrm {e}^{-2\lambda \varrho }+3\lambda P_3(\lambda ) \mathrm {e}^{-3\lambda \varrho }.\\&\implies \frac{{\mathrm {d}}\lambda }{{\mathrm {d}}\varrho }=\frac{\lambda \left( P_1(\lambda )+2 P_2(\lambda )\mathrm {e}^{-\lambda \varrho }+3 P_3(\lambda ) \mathrm {e}^{-2\lambda \varrho }\right) }{\left( P_0'(\lambda )\mathrm {e}^{\lambda \varrho }{+}P_1'(\lambda ){-}\varrho P_1(\lambda ){+}\mathrm {e}^{-\lambda \varrho }\left( P_2'(\lambda ){-}2\varrho P_2(\lambda )\right) {+}\mathrm {e}^{-2\lambda \varrho }\left( P_3'(\lambda ){-}3\varrho P_3(\lambda )\right) \right) }. \end{aligned}$$

Thus, we get

$$\begin{aligned}&\left[ \frac{{\mathrm {d}}\lambda }{{\mathrm {d}}\varrho }\right] ^{-1} =\frac{\left( P_0'(\lambda )\mathrm {e}^{\lambda \varrho }{+}P_1'(\lambda ){+}\mathrm {e}^{-\lambda \varrho }P_2'(\lambda ){+}\mathrm {e}^{-2\lambda \varrho }P_3'(\lambda )\right) {-}\left( \varrho P_1(\lambda ){+}2 \varrho P_2(\lambda )\mathrm {e}^{-\lambda \varrho }{+}3\varrho P_3(\lambda )\mathrm {e}^{-2\lambda \varrho }\right) }{\lambda \left( P_1(\lambda )+2 P_2(\lambda )\mathrm {e}^{-\lambda \varrho }{+}3P_3(\lambda )\mathrm {e}^{-2\lambda \varrho }\right) }.\\&\text {i.e.,} \left[ \frac{{\mathrm {d}}\lambda }{{\mathrm {d}}\varrho }\right] ^{-1} =\frac{\left( P_0'(\lambda )\mathrm {e}^{\lambda \varrho }+P_1'(\lambda )+\mathrm {e}^{-\lambda \varrho }P_2'(\lambda )+\mathrm {e}^{-2\lambda \varrho }P_3'(\lambda )\right) }{\lambda \left( P_1(\lambda )+2 P_2(\lambda )\mathrm {e}^{-\lambda \varrho }+3P_3(\lambda )\mathrm {e}^{-2\lambda \varrho }\right) } -\frac{\varrho }{\lambda }.\\&Re\left[ \frac{d \lambda }{d\varrho }\right] ^{-1}\Big |_{\lambda =\mathrm {i} \omega _{0}}=\frac{X_1X_2+Y_1Y_2}{X_2^2+Y_2^2}, \end{aligned}$$

where

$$\begin{aligned} X_1&=-\sin {\omega _0 \varrho _0} \left( -4 \omega _0^3+2K_2 \omega _0\right) \\&\quad +\cos {\omega _0 \varrho _0} \left( -3K_1 \omega _0^2+K_3\right) +\left( -3K_5 \omega _0^2+K_7\right) \\&\quad +\left( K_{10}\cos {\omega _0 \varrho _0}+2 \omega _0 K_9 \sin {\omega _0 \varrho _0}\right) \\&\quad +K_{16}\cos {2 \omega _0 \varrho _0},\\ X_2&=K_5 \omega _0^4-K_7 \omega _0^2-2K_{10} \omega _0^2 \cos {\omega _0 \varrho _0}\\&\quad +2\left( -K_9 \omega _0^2+\omega _0 K_{11}\right) \sin {\omega _0 \varrho _0}\\&\quad -3\omega _0^2K_{12} \cos {2 \omega _0 \varrho _0}\\&\quad +3\omega _0K_{13}\sin {2\omega _0 \varrho _0},\\ Y_1&=\cos {\omega _0 \varrho _0}\left( -4 \omega _0^3+2K_2 \omega _0\right) \\&\quad +\sin {\omega _0 \varrho _0}\left( -3K_1 \omega _0^2+K_3\right) +2\omega _0K_6 \\&\quad +2 \omega _0 K_9 \cos {\omega _0\varrho _0}-K_{10}\sin {\omega _0 \varrho _0}\\&\quad -K_{16}\sin {2 \omega _0 \varrho _0},\\ Y_2&=-K_6 \omega _0^3+\omega _0 K_8+2\left( -K_9 \omega _0^3+\omega _0 K_{11}\right) \cos {\omega _0 \varrho _0}\\&\quad +3\left( \omega _0^2 K_{12}\sin {2\omega _0 \varrho _0}+\omega _0 K_{13}\cos {2\omega _0 \varrho _0}\right) \\&~~~~+2 \omega _0^2 K_{10} \sin {\omega _0 \varrho _0}. \end{aligned}$$

Obviously, if H4: \(X_1X_2+Y_1Y_2 \ne 0\), then \(Re\left[ \frac{d \lambda }{d\varrho }\right] ^{-1}\Big |_{\lambda =\mathrm {i} \omega _0} \ne 0.\)

Thus, we state the following theorem:

Theorem 6

For the system (5), if the conditions (H1–H4) hold, then the endemic equilibrium \(E_e=(S^*, A_F^*,A_P^*, I^*)\) is locally asymptotically stable when \(\varrho \in [0, \varrho _0)\); the system (5) undergoes a Hopf bifurcation at \(E_e=(S^*, A_F^*,A_P^*, I^*)\) when \(\varrho =\varrho _0\), and a family of periodic solutions bifurcate from \(E_e=(S^*, A_F^*,A_P^*, I^*)\).

4 Numerical simulation

In this section, numerical experiments are presented to show the analytical results using Mathematica 11.

We have considered the following set of experimental data: \(\kappa =2,~\vartheta =0.01,~ \beta _1= 0.02,~\beta _2= 0.006,~\beta _3 = 0.008,~\delta _1 = 0.1,~\delta _2= 0.02,~a = 0.04,~d= 0.009,~\theta = 0.004,~\varepsilon = 0.5,~ b = 0.09.\)

At these parameters values, the endemic equilibrium is \(E_e(S^*,A_F^*,A_P^*,I^*)=(11.903, 55.602, 9.443, 38.504)\) with \(R_0>1\).

Fig. 5
figure 5

Subpopulations \(S-A_P-A_F-I-R\) at \(\varrho =1\)

Full size image

Figure 5 shows the behavior of different subpopulations for the time delay \(\varrho =1\). Evidently, as time increases, unaware susceptibles decrease, and the fully aware and partially aware, infected, and removed individuals population increase and then start decaying and settle down to steady state \(E_e(11.903, 55.602, 9.443, 38.504)\).

Fig. 6
figure 6

Infected population I(t) at different values of time delay \(\varrho \)

Full size image

Figure 6 depicts the effect of time delay on the infected population. We plot the infected population for different values of time delay \(\varrho =1, 7\), and 14, respectively. It reveals that the large value of time delay causes an increment in the infected population.

Fig. 7
figure 7

Infected population for the transmission rates of unaware, fully aware, and partially aware susceptibles for the time delay \(\varrho =1\)

Full size image

Figure 7a–c shows the influence of different transmission rates on infected population I(t). It validates the increment in the number of infected population as the transmission rates increase, which is biologically true.

Fig. 8
figure 8

Impact of full and partial awareness rates on Infected population for the time delay \(\varrho =1\)

Full size image
Fig. 9
figure 9

Dynamics of infectious diseases showing the impact of aware classes on infected individuals I(t) for the time delay \(\varrho =1\)

Full size image
Fig. 10
figure 10

Impact of cure rate, awareness, and saturated treatment on the infected population for \(\varrho =1\)

Full size image

Figure 8a, b shows the impact of full and partial awareness rates (\(\delta _1\) and \(\delta _2\)) on the infected population for the time delay \(\varrho =1\). It is evident that if the full awareness rate is high, then infection diminishes at a high level. Partially awareness in humans also helps them to escape from the infection, as depicted in Fig. 8b. Thus, more efforts should be put to spread full awareness among people.

Figure 9 examines the potential of fully and partially aware classes in minimizing the impact of an epidemic. From the graph, it is evident that when people are not aware of the spread of disease at all (shown by a solid red line), then the infection occurs at a higher rate. Awareness in humans motivates them to escape from the infection. By the full and right information about a disease, individuals change their attitudes and actions to reduce their chances of becoming infected, spreading the disease further, or experiencing prolonged periods of medical treatment. Attempts to raise awareness of an infectious disease may also build a sense of threat in individuals who are inadequately informed. When there is only partial information available, then infection reduces, but a low level (as shown by the dashed green line). Because of weak, inaccessible, and absence of education, uneducated individuals are rarely formally trained in the process of handling diseases, its prognosis, and diagnosis, preventions, and cures. They take preventive measures by word of mouth or by social media, which leads to a reduction in the infection at a low level. Also, if people are partially mindful, then there are chances that they can take unnecessary medications due to fear of catching the infection, which can weaken their immune system. So those people are at more risk of getting infected (shown by the dot-dashed blue line). Therefore, the absence of partial awareness and presence of full awareness about the spread and prevention of disease are leading to a reduction in the range of illness at the high rate (shown by the dotted black line).

Figure 10a shows that the increase in the cure rate can increase the reduction in infected individuals. Figure 10b shows the influence of saturated treatment rate on infected population I(t). We have plotted the infected population when there is neither treatment nor awareness available. Clearly, in this case, infection is spreading at a very high rate. Purple dashed line shows the infected population when people are aware, but treatment is not available, and the solid red line shows the infected population in the absence of awareness and treatment. The major difference can be seen between these two lines. Blue dashed line shows the infected population when both awareness and treatment are present, which is stabilizing at the lowest level among three lines. Thus, the treatment rate with awareness helps in reducing infection at a faster rate.

To show the presence of Hopf bifurcation, we take the following experimental data: \(\kappa =10,~ \varepsilon =0.92,~ \beta _1=0.2,~\beta _2=0.02,~\beta _3=0.04,~\delta _1=0.05,~\delta _2=0.03,~\vartheta =0.1,~ a=0.2,~b=0.5,~ \theta =0.01,~d=0.01.\)

We obtain that \(E_e(S^*,A_F^*,A_P^*,I^*)=(25.5152,10.5267,5.37598,42.1257)\), at these values of parameters.

Fig. 11
figure 11figure 11

Graphs depicting the presence of Hopf bifurcation for different values of time delay \(\varrho \)

Full size image

Figure 11 depicts the time series solutions of the model (1) with their respective SIR phase plot for distinct values of time delay \(\varrho \). It is observed that the spread of infectious disease can be controlled for \(\varrho =14\), and \(\varrho =21\). That is, Fig. 11a–d shows that initially periodic solutions appear but after a time; the endemic equilibrium \(E_e\) reached to its steady state. Figure 11e–h shows the unstable limit cycle around the endemic equilibrium when time delay \(\varrho >\varrho _0=24\).

5 Discussion

In the present article, we divide the total population into five compartments: unaware susceptibles, fully aware susceptibles, partially aware susceptibles, infected, and removed individuals and study a time-delayed epidemic model with the inclusion of saturated incidences and treatment rates. We analyze the model mathematically and study the dynamic behaviors of the epidemic model with and without time delay \(\varrho \). The mathematical analysis of the model shows that it exhibits two equilibria: disease-free and endemic. By deriving the basic reproduction number \(R_0\), we prove that the disease-free equilibrium is locally asymptotically stable when \(R_0<1\), unstable when \(R_0>1\), and linearly neutrally stable when \(R_0=1\) for the time delay \(\varrho > 0\). When we don’t consider the time delay, then using the center manifold theory, it is obtained that the forward or backward bifurcation occurs when \(R_0 = 1\). We obtain the bifurcation range of forward and backward bifurcations, given in the inequalities (20), (21), and (22), respectively. In the presence of forward bifurcation, as \(R_0\) increases through unity, the disease-free equilibrium loses its stability, and a stable endemic equilibrium appears. In contrast, the presence of backward bifurcation shows that a stable endemic equilibrium coexists with a stable DFE when \(R_0 < 1\). It has an important implication as it fails the ideal condition of reducing \(R_0\) below unity to eradicate the diseases from society. Thus, the control programs must reduce \(R_0\) further than below unity to eliminate the disease. Schematic diagrams of forward and backward bifurcation are depicted in Figs. (2), (3), and (4). Further, the local stability of the endemic equilibrium has been studied, which demonstrates that by choosing time delay as a bifurcation parameter, the Hopf bifurcation occurs near the endemic equilibrium, revealing the presence of oscillatory and periodic solutions.

The numerical simulations show the graphical representation of the effectiveness of theoretical results. We see that the consideration of time delay has a significant role as it has an impact on the number of infectives. It is seen that when the time delay is high, then infection spreads at a higher rate. The periodic and oscillatory solutions have been plotted near endemic equilibrium, which shows the presence of Hopf bifurcation at different values of time delay \(\varrho \). As the delay \(\varrho \) passes through the critical value \(\varrho _0\), the endemic equilibrium loses its stability, and an unstable limit cycle appears. When there is no treatment available, then knowledge about the spread of disease is the main focus. The role of full and partial awareness in susceptibles, with and without saturated treatment, has been shown numerically. When treatment is not given to infected individuals, then only susceptibles’ full or partial awareness shows the significant difference in the number of infectives (Figs. 9, 10b), whereas if we consider saturated treatment rate along with awareness in the susceptibles, then the transmission pattern of infectious diseases changes more effectively, and the reduction in the prevalence of the disease can be seen to the more extent.

The findings of the model, consisting of explicit saturated incidences with latent period and saturated treatment rate, are capable of demonstrating the significant role of the latent period, the behavior of susceptibles through different subclasses, and limitation in available facilities of treatment. The results are capable of understanding the role of varying protection levels of susceptibles in the transmission pattern of the infectious diseases and hence further suggesting the control strategies to prevent the spread of infections at a massive scale. The full awareness about the spread of infectious disease increases public perception to avert infection and willingness to adopt prevention methods, which mitigates the transmission of disease. Due to the different social, educational, and limited information resources, some people may have incomplete information. Therefore, these partially aware individuals adopt insufficient preventive methods, through which infection reduces but at a low level. Public health initiatives can put extra effort into making individuals fully aware by enhancing health literacy and providing sufficient information resources. It can contribute to early case detection and help in reducing the transmission of infection. Thus, for the eradication of the disease, programs related to regular knowledge, full information, education, and communication, concerning the spread of infectious diseases and its importance to the public and health-care workers, will help them in improving their general attitude toward it. Timely disease pieces of information updates are highly needed. Together with awareness, appropriate treatment to infectives and the availability of health resources will help in diminishing the infection from society, effectively.