1 Introduction

Planners and decision makers in power utility companies like Eskom, South Africa’s power utility company, face uncertainties in the demand for electricity [1]. This is due to several factors that include weather conditions like temperature which is a global major driver of electricity demand [1, 2]. Modelling of electricity demand using climate variables such as temperature as one of the covariates is discussed in literature. However, various statistical techniques are used in the energy sector, depending on the nature of the problem at hand.

In the current paper, we demonstrate the use of the point process (PP) approach of extreme value theory (EVT) in modelling temperature extremes in South Africa. The PP modelling approach is considered as a more elegant alternative of extreme value analysis because of its capability in modelling and quantifying both the frequency and intensity rates of the occurrence of extremes [3]. This is the principal advantage of using the PP approach over the block-maxima (BM) approach and the peaks-over-threshold (POT) approach which are unified by the PP approach as emphasised in Coles [3]. The stationary and non-stationary PP models are fitted in modelling the average maximum daily temperature (AMDT) in South Africa. We discuss the details of the case study in Section 3.

The principal motivation for this paper is based on the fact that the occurrence of extremely low or extremely high temperatures influences electricity demand in both the domestic and industrial electricity users. During non-winter season, the electricity users switch on cooling systems until a point at which all the cooling systems are on, implying an extreme increase in electricity demand [1]. The purpose of this paper is to demonstrate and compare the extent to which the PP and the generalised Pareto distribution (GPD) modelling approaches can be used in modelling AMDT in South Africa. The temperatures are modelled for the purpose of studying the impact of extreme AMDT on electricity demand in South Africa.

1.1 Literature Review on Related Problems

Abatan et al. [4] analyse trends in extreme temperature over Nigeria from percentile-based threshold indices. The study focuses on spatial and temporal trends in extreme temperature for 21 stations in Nigeria over the years 1971–2012. It was concluded in Abatan et al. [4] that although a majority of the stations have significant trends on warm days and warm nights, the annual trend is greatest on warm nights. Thornton et al. [5] discuss the role of temperature in the variability and extremes of electricity and gas demand. The paper investigates the daily relationship of electricity and gas demand with temperature in Great Britain from 1975 to 2013 and 1996 to 2013, respectively. Extreme demand periods are assessed using detrended daily temperature observations from 1772. The results establish that 1 in 20 year peak day electricity and gas demand estimates are above their average winter day demand [5].

Chikobvu and Sigauke [6] discuss the modelling of the influence of temperature on average daily electricity demand in South Africa using a piecewise linear regression model and the generalised extreme value theory approach over the years 2000–2010. The empirical results show that electricity demand in South Africa is highly sensitive to cold temperatures. It was further concluded that extreme low average daily temperatures of the order of 8.2 ∘C are very rare in South Africa and that they only occur about 8 times in a year, resulting in huge increases in electricity demand [6].

Lebotsa et al. [7] discuss an application of partially linear additive quantile regression models for predicting short-term electricity demand during the peak demand hours from 18:00 to 20:00 using South African data for January 2009 to June 2012. Results from the unit commitment problem show that it is very costly to use gas-fired generating units and that for any increase in demand above the median quantile forecasts, it will be economical to increase the generation of electricity from generating unit [7]. Although temperature is an important weather variable in the energy sector, it is important to study the impact of other climate variables such as water supply, wind speed, and humidity on electricity demand.

Sridharan et al. [8] develop a framework consisting of long-term models for electricity supply and water systems management to assess the vulnerability of potential expansion plans to the effects of climate change. This study demonstrates that failing to climate-proof infrastructure investments can result in significant electricity price fluctuations in selected countries such as Uganda and Tanzania, while others such as Egypt are less vulnerable [8].

Wangsa and Wee [9] propose an integrated distribution system model for electricity supply chain consisting of a power plant, a transmission substation, a distribution substation, and multi-customers. A procedure to derive the optimal solution and the decision variables is developed using differential calculus. The results of the study revealed that the cost decreases as the blackout ratio and distribution substation capacity increase and that the cost is insensitive to the changing electricity consumption time [9].

Like any other country, South Africa faces problems when it comes to the sufficient supply of electricity. Depending on the availability of necessary resources, the use of renewable energy can be more beneficial to both the energy sector and electricity consumers. Aliyu et al. [10] review the prospects of four major renewable energy sources which are hydro, solar, wind, and biomass for each of the three leading countries in Africa, namely South Africa, Egypt, and Nigeria. Of these three countries, it is emphasised that South Africa has the best model for tackling its energy challenge through the use of wind and solar energy. In the three countries and indeed across the African continent, access to renewable energy for off-grid, small-scale application is key to successful resolution to energy crisis, sustainable development, and fighting climate change [10].

Flowers et al. [11] assess climate impacts on the cost of solar energy in the United States of America. The assessment is based on the formulation of an extended levelised cost of energy calculation which considers photovoltaic module performance and lifespan as a function of local climate. This assessment is considered to be the first to quantify trade-offs between technologies, geographies, and policies in a unified manner [11].

The occurrences of extreme observations lead to the use of EVT which comprises a rich family of techniques that are suitable for modelling tail behaviour of thin or heavy-tailed distributions [12]. The use of symmetrical techniques in such cases leads to limitations such as unreliable estimates since most of the sample values fall outside the tail of the distribution, as well as the difficulty in estimating the model parameters that would lead to a good fit in the tails [3, 12]. The use of EVT in modelling electricity demand is usually preferred in the energy sector because of the capability of EVT in modelling tail behaviour of thin or heavy-tailed distributions.

The use of generalised additive models in predicting medium-term hourly electricity demand using South African data for the years 2009 to 2013 is discussed in Sigauke [13]. The selection of variables is done using least absolute shrinkage and selection operator via hierarchical interactions. The study shows significantly improved accuracy of forecasts that may serve as a useful tool for decision makers and system operators in power utility companies, particularly in maintenance planning including medium-term risk assessment [13].

One of the vital tasks in statistical modelling is the assessment of the extent to which the models fit the data. Davison and Smith [14] fit the GPD over several thresholds with applications in hydrology, followed by calculating the Anderson-Darling and the Kolmogorov-Smirnov statistics to test fit. The limitation that was encountered is the lack of the formal tests that are suitable to diagnose fit of the GPD. Because of this limitation, the authors opted for the use of tables in testing for exponential property, which was unsuccessful since there were too high test statistics [14]. Choulakian and Stephens [15] discuss the formal goodness-of-fit tests of the GPD models together with applications. These tests are based on the Cramér-von Mises and the Anderson-Darling statistics.

2 Modelling Non-stationary Extremes Using the Point Process Approach

The key benefit of using the PP tail model over the GPD is that the former can more easily be extended to the non-stationary case by allowing a change in the intensity or number of threshold exceedances over time or space, which has a natural physical interpretation [16]. Furthermore, since the PP model describes the threshold exceedance process over time or space, it is more straightforward to consider representation of dependence in the extremes. This includes for example, clustering of exceedances, which are frequently observed in various applications such as finance and hydrology [16].

Let \(\mathbf {Y} = \left \{Y_{1},\dots ,Y_{n} \right \}\) denote a sequence of AMDT with one observed covariate x such that \(\mathbf {X}=\left \{X_{1},\dots ,X_{n}\right \}\). Of these n observations, let nτ denote the number of exceedances above a sufficiently high predetermined threshold, τ. In this paper, a time-varying covariate is used. Pickands [16] showed that the point process defined by:

$$ P_{n}=\left\{\left( \frac{i}{n+1},x_{i}\right); i=1,\dots,n\right\} $$

is well approximated in the limits as \(n\to \infty \), by an inhomogeneous Poisson process on the region \(A=[0,1]\times (\tau ,\infty )\), for a sufficiently high threshold τ, with the intensity function on the subregion \(B=(t_{1},t_{2})\times (x,\infty )\) given by:

$$ {\Lambda}(B)= \left\{\begin{array}{ll} (t_{2}-t_{1})n_{\tau}\left[1+\xi\left( \frac{x-\mu}{\sigma}\right)\right]_{+}^{-\frac{1}{\xi}} & \text{for} ~ \xi\neq0,\\ (t_{2}-t_{1})n_{\tau}\exp\left\{-\left( \frac{x-\mu}{\sigma}\right)\right\} & \text{for} ~ \xi=0, \end{array}\right. $$
(1)

where x > τ and the scaling constant nτ is the number of blocks of observations [16]. In this paper, nτ is considered as the number of exceedances with probability shown in the first component of Eq. 2.

Modelling threshold exceedances using the PP framework follows a process similar to that of threshold modelling via the GPD, with the PP conditional probability model parameterised by (μ,σ,ξ) [16]. The application of the PP modelling framework relies on the choice of a suitably high threshold τ, above which the asymptotically motivated models provide a reliable approximation. The likelihood for the extreme value mixture (EVM) model is separable out into the contribution from the observations below the threshold (the kernel density component) and those above the threshold (the GPD or PP tail model). The PP likelihood used in this paper is obtained by straightforward application of the Poisson likelihood with inhomogeneous intensity function given in Eq. 1.

The non-stationary likelihood function of the PP model over the region \([0,1]\times (\tau ,\infty )\) is given by Macdonald et al. [17]:

$$ \begin{array}{@{}rcl@{}} L(\tau,\boldsymbol{\theta};\mathbf{Y,X}) &=&\exp\left\{-\frac{1}{n}\sum\limits_{i=1}^{n}\left[1+\xi(x_{i})\left( \frac{\tau-\mu(x_{i})}{\sigma(x_{i})}\right)\right]^{-\frac{1}{\xi(x_{i})}}\right\} \\ &&\times \prod\limits_{i:Y_{i}>\tau}\frac{1}{\sigma(x_{i})}\left[1+\xi(x_{i})\!\left( \frac{y_{i}-\mu(x_{i})}{\sigma(x_{i})}\!\right)\right]^{-\frac{1}{\xi(x_{i})}-1},\\ \end{array} $$
(2)

for ξ(xi)≠ 0,𝜃 = (μ(x),σ(x),ξ(x)) the parameters modelled as functions of the covariate x, where B = {i : xi > τ}.

In Eq. 2, 𝜃 denote a vector of parameters, μ is the location parameter, σ is the scale parameter, and ξ is the shape parameter. If the covariate x is the time-varying effect denoted by t, the model is then written in a non-stationary context as follows:

$$ \begin{array}{@{}rcl@{}} \mu(t)&=&\mu_{0}+\mu_{1}t, \log\sigma(t) =\sigma_{0}+\sigma_{1}t, \xi(t)=\xi_{0}+\xi_{1}t. \end{array} $$

The first component of the likelihood function in Eq. 2 represents the probability of getting nτ exceedances, where nτ is Poisson distributed and discussed under Eq. 1. We now define a stationary model and various non-stationary models for modelling the variation on the location and scale parameters using linear, exponential, and quadratic transformations.

According to Coles [3], it is usually challenging to model the variation in the shape parameter. In this paper, we also limit the non-stationary modelling to the location and the scale parameters only. The models \((M_{0},\dots ,M_{3})\) are considered in this paper:

$$ \begin{array}{@{}rcl@{}} M_{0}:\mu(t)&=&\mu_{0},\qquad \quad \sigma(t) =\sigma_{0}, \qquad \xi(t)=\xi_{0} \end{array} $$
(3)
$$ \begin{array}{@{}rcl@{}} M_{1}:\mu(t)&=&\mu_{0}+\mu_{1}t, \quad \sigma(t) =\sigma_{0},\qquad\xi(t)=\xi_{0} \end{array} $$
(4)
$$ \begin{array}{@{}rcl@{}} M_{2}:\mu(t)&=&\mu_{0}, \qquad\quad~ \sigma(t)=\exp(\sigma_{0}+\sigma_{1}t), \\ & & \qquad\qquad\qquad\qquad\qquad\quad \xi(t)=\xi_{0} \end{array} $$
(5)
$$ \begin{array}{@{}rcl@{}} M_{3}:\mu(t)&=&\mu_{0}, \qquad\quad \sigma(t)=\sigma_{0}+\sigma_{1}t+\sigma_{2}t^{2}, \\ & &\qquad\qquad\qquad\qquad\qquad\quad\xi(t)=\xi_{0}. \end{array} $$
(6)

Model M0 is stationary and the rest of the models involve linear, exponential, and quadratic transformations to cater for non-stationarity of the location and scale parameters. Model M1 uses a linear transformation of the location parameter, whereas model M2 uses an exponential transformation of scale parameter. A quadratic transformation of the scale parameter is used in model M3.

The models are nested and we carry out likelihood ratio tests based on the deviance statistic. This is useful for examining the fit of the models and choosing the best out of several candidate models. The deviance statistic is given as:

$$ D=2\left\{\ln\lambda(M_{j})-\ln\lambda(M_{0})\right\}{\thicksim\chi^{2}_{k}}, \quad \text{for}\quad j=1,\dots,3, $$
(7)

where Mj is the model tested against model M0 and if \(D>{\chi ^{2}_{k}}\) we reject the null hypothesis and conclude that model Mj provides a significant improvement over model M0.

2.1 Frequency Analysis Using the Poisson-Generalised Pareto Distribution

The frequency and intensity of occurrence of extremely high temperatures constitute the core of the analyses in this paper. This forms part of the results that could be useful to the planners and decision makers in the energy sector. This section discusses the use of the orthogonal and the reparameterisation approaches for estimating the frequency and intensity of the annual occurrence of extremely high temperatures.

The orthogonal approach is described in Smith [18] as the one that separately estimates the frequency and the intensity rates of the occurrence of extremes and hence difficult to interpret under non-stationary context. Due to this limitation, this paper considers time-homogeneous point process models for calculating intensity rates and frequency using the reparameterisation approach.

The Poisson-GPD is briefly discussed in this section. We show how the Poisson-GPD can be used to estimate the frequency of occurrences of extreme AMDT per year. Let \(Y_{j}, j=1,\dots ,n\) be AMDT. The interest is in observing Yj > τ, where τ is a sufficiently high threshold. Let \(X_{1},\dots ,X_{n}\) be independent and identically distributed (i.i.d) random variables with the observed indices i for which Xi > τ. In case these indices are rescaled to points \(\frac {j}{n}\), they are considerable as a point process of rescaled exceedance times on [0,1]. If \(n\rightarrow \infty \) and \((1-F(\tau ))\rightarrow 0\) such that \(n(1-F(\tau ))\rightarrow \lambda (0<\lambda <\infty )\), the process converges weakly to a homogeneous Poisson process on [0,1], of intensity λ, i.e. \(n(1-F(\tau ))\rightarrow \theta \) [18].

The number of exceedances, denoted by nτ in some specified unit time, say a year, follows a Poisson distribution with mean 𝜃. The observations \(Y_{1},\dots ,Y_{n_{\tau }}\) are then assumed to follow the GPD [18]. The stationary PP model M0 is used for calculating the frequency of occurrence of extremely hot days. This is done using the reparameterisation approach that is discussed in Smith [18] and given in Eq. 9.

We show the relationship between the Poisson-GPD process with the survival function of the generalised extreme value distribution (GEVD) for annual maxima. If we let x > τ, then the probability that the annual maximum of the Poisson-GPD process is greater than x is given as:

$$ \begin{array}{@{}rcl@{}} P\left( \max_{1\leq j\leq n_{\tau}}Y_{j}>x\right)&=&1-P(N_{\tau}=0)- \sum\limits_{n=1}^{\infty} P\\ &&\times\left( N_{\tau}=n,Y_{1}\leq x,\dots,Y_{n}\leq x\right)\\ &=&1-e^{-\theta}- \sum\limits_{n=1}^{\infty} \frac{\theta^{n} e^{-\theta}}{n!}\left[1-\left( 1+\xi\frac{x-\mu}{\sigma}\right)^{-\frac{1}{\xi}}\right]^{n}\\ &=&1-\exp\left[-\theta\left( 1+\xi\frac{x-\mu}{\sigma}\right)^{-\frac{1}{\xi}}\right]. \end{array} $$
(8)

Now if

$$ \sigma=\psi+\xi(\tau-\mu) \quad \text{and} \quad \theta=\left( 1+\xi\frac{x-\mu}{\psi}\right)^{-\frac{1}{\xi}} $$

are substituted in Eq. 8, we get the survival function of the GEVD, which is:

$$ 1-\exp\left\{-\left[1+\xi\left( \frac{x-\mu}{\psi}\right)\right]^{-\frac{1}{\xi}}\right\}. $$

The derivation in Eq. 8 results in the reparameterisation approach that is discussed in Smith [17] and given in Eq. 9 as follows:

$$ \hat\sigma^{*}=\sigma+\xi(\tau-\mu)\quad\text{and}\quad\hat\lambda=\left[1+\xi\left( \frac{\tau-\mu}{\hat\sigma^{*}}\right)\right]^{-\frac{1}{\xi}}. $$
(9)

According to Smith [18], the GEV and GPD models are entirely consistent with one another above the threshold τ, and Eq. 9 gives an explicit relationship between the two sets of parameters σ∗ and λ. These parameters are then estimated in this paper as \(\hat \sigma ^{*}\) and \(\hat \lambda \) in the process of calculating the frequency and intensity of the annual occurrence of extremely hot days in South Africa. This is carried out using the stationary PP model that is fitted in Section 4.

3 Description of the Case Study

The modelling framework discussed in Section 2 is then applied to a real-life data set. The data that is used in this paper is a time series of AMDT that were collected by the South African Weather Service (SAWS) from the 28 weather stations in South Africa. The data was collected over the period 1 January 2000 to 30 August 2010 and was then divided into winter and non-winter seasonal versions, where non-winter is defined as the period from 1 September to 30 April of each year and the rest of the data is for the winter season [1, 2].

Only the data for non-winter season is used in this paper for the purpose of modelling the frequency of occurrence of extremely high temperatures. There are several packages that are discussed in literature as relevant for addressing issue of missing observations in the data set. We impute the missing data using the R package “Mice” [19]. The use of this package is preferred because it performs multiple imputations based on fully conditional specifications that are implemented by the Mice algorithm described in Van Buuren et al. [19].

Suppose that \(x_{1},\dots ,x_{n}\) denote a series of AMDT that are i.i.d and let τ be a sufficiently high threshold. The values \(x_{(1)}\le \dots \le x_{(k)}\) are k positive residuals above τ if {xi : xi > τ} and the observations yj = x(j) − τ, for \(j=1,\dots ,k\) are threshold excesses [12, 20]. When the threshold is too high, there are few positive excesses above the threshold and hence a large variance [3, 12, 20]. A low value of the threshold leads to the violation of the asymptotic feature of the GPD, implying bias [3, 12, 20]. There are various threshold selection tools that are discussed in literature, including Pareto quantile plot, mean excess plot, threshold stability plot, and the mean residual life plot [3, 12].

In this paper, we prefer the use of a non-parametric EVM model for the purpose of avoiding consequences of fixed threshold approach such as ignorance of uncertainties and inability to compare GPD or PP parameters of an entire model at different thresholds as discussed in Hu and Scarrott [21]. In addition to the use of non-parametric EVM models, we use threshold stability plots. Amongst various smoothing techniques, the penalised cubic smoothing spline (PCSS) function is used for non-linear detrending the data and for determining the sufficiently high time varying threshold.

The PCSS has become a very powerful and applicable smoothing technique over the last decade as emphasised in Krivobokova [22]. This non-parametric method can be viewed as a generalisation of smoothing splines with a more flexible choice of bases and penalties. The main benefit of using PCSS as emphasised in Krivobokova [22] is that it ties with various modelling frameworks including EVT, ridge regression, mixed models, and Bayesian statistics.

Initially, we fit a PCSS as a time-varying threshold which is given as:

$$ \begin{array}{@{}rcl@{}} \sum\limits_{t=1}^{n}\left( x_{t}-f(t)\right)^{2}+\lambda\int\left( f^{\prime\prime}(t)\right)^{2}\text{d}t, \end{array} $$
(10)

where xt is the temperature, f(t) is a PCSS function, and λ is a smoothing parameter that is chosen based on the generalised cross-validation (GCV) approach [23].

We then extract the residuals (excesses) above this threshold and fit a fixed threshold above the positive residuals (excesses above the time varying threshold) using the non-parametric EVM model proposed in Hu and Scarrott [21] (Fig. 1). The procedure for the application of non-parametric EVM model is to fit a kernel density to a bulk model that is given in Eq. 11, followed by fitting GPD to the tail of the distribution. The sufficiently high threshold is then determined by estimating τ as shown in Fig. 2. See MacDonald et al. [17] for details.

Fig. 1
figure 1

Time series plot of the average maximum daily temperature. The blue dots indicate the observations and the red solid line indicates the smoothing parameter

Full size image
Fig. 2
figure 2

Threshold estimation using a non-parametric extremal mixture model where a boundary corrected kernel density is fitted to the bulk model and a GPD fitted to the tail of the distribution (\(\hat {\tau }= 2.91\))

Full size image

The distribution function of the boundary corrected EVM model is given in Eq. 11.

$$ F(x\vert\tau,\boldsymbol{\beta},\sigma_{\tau},\xi,\phi_{\tau})= \begin{cases} (1-\phi_{\tau})\times\frac{H(x\vert\boldsymbol{\beta})}{H(\tau\vert\boldsymbol{\beta})}, & x\le\tau,\\ (1-\phi_{\tau})+\phi_{\tau}\times G(x\vert\tau,\sigma_{\tau},\xi), & x>\tau, \end{cases} $$
(11)

where ϕτ is the proportion of observations that exceed the threshold such that 0 < ϕτ < 1, H(.|β) is a boundary corrected kernel density and G(.|τ,στ,ξ) is the GPD [17].

In stationary sequences, extreme values can occur in clusters, for which asymptotic characterisations and methods of inference are detailed in Ferro and Segers [24]. The first step in making inferences is to identify clusters in the data, followed by declustering. However, prior to the process of declustering, the extremal index (reciprocal of the mean cluster size) which is an important parameter (0 ≤ 𝜃n(τ) ≤ 1) for measuring the degree of clustering of extremes in a stationary process needs to be calculated.

Apart from the extremal index being of interest in its own right, it is a crucial parameter for determining the limiting distribution of extreme values from the process as emphasised in Smith and Weissman [25]. Considering the point process of exceedance times over a sufficiently high threshold, the extremal index can be shown to converge asymptotically to a clustered Poisson process [25].

Smith [26] argues that the seasonality component is associated with short-range dependence since a hot day is likely to be followed by hot days and that the same applies to other seasons. The dependence feature leads to a weakness whereby the observations are clustered or grouped together, violating the i.i.d condition [26]. We decluster the exceedances above the threshold to get rid of short-range dependence. See the ‘texmex’ R package of Southworth and Heffernan [27] for theoretical and software details of the declustering algorithm. We apply the interval estimator method of Ferro and Segers [24] to decluster positive residuals above the threshold.

Let T denote a random variable on the positive integers whose distribution is given by:

$$ P(T>n)=\theta p^{n\theta}, \quad\text{for}\quad n\ge1, $$
(12)

where 𝜃 ∈ (0,1] and p ∈ (0,1) may be viewed as F(τn). From the mathematical details of the declustering algorithm discussed in Ferro and Segers [24], it then follows that:

$$ E\left\{\frac{T(T-1)}{2}\right\}=\sum\limits_{n=1}^{\infty} n P(T>n)=\theta p^{\theta}(1-p^{\theta})^{-2}. $$

The first-order bias of 𝜃 at a threshold τ is \(\theta (2-3\theta /2)\bar F(\tau )\). The relationship:

$$ \theta=\frac{2\{E(T-1)\}^{2}}{E\{(T-1)(T-2)\}} $$
(13)

which motivates the interval estimator given in Eq. 14.

$$ \hat\theta_{n}(\tau)=\frac{2\left[{\sum}_{i=1}^{N-1}(T_{i}-1)\right]^{2}}{(N-1){\sum}_{i=1}^{N-1}(T_{i}-1)(T_{i}-2)}, $$
(14)

whose first-order bias is 0, where τ is a sufficiently high threshold and Ti denotes interexceedance times [24]. The extremal index, 𝜃n(τ) is calculated prior to the declustering and used for measuring the amount of clustering and 0 ≤ 𝜃n(τ) ≤ 1, where \(\frac {1}{\theta _{n}(\tau )}\) is the limiting mean cluster size [24].

After determining the sufficiently high threshold and declustering, the stationary and non-stationary point process models that are discussed in Section 2 were then fitted to cluster maxima using the MLE method. The parameters were estimated in this paper using the method of maximum likelihood estimation (MLE) with the likelihood function that is given in Eq. 2. These procedures were carried out using R, a programming language for statistical computing [28].

The R packages used in this paper include, but not limited to, ‘texmex’ by Southworth and Heffernan [27], ‘Evmix’ by Hu and Scarrott [21], and ‘evd’ by Stephenson [29]. The stationary (time-homogeneous) model that is fitted and used as a base model in comparison with various non-stationary models is given in Eq. 3. The non-homogenous model with linear transformation of the location parameter is M1 in Eq. 4. In Eqs. 5 and 6 we fit the non-homogeneous point process models with exponential and quadratic transformations of the scale.

The models that are used in this paper are nested and to that effect, the likelihood ratio tests are carried out based on the deviance statistic. The tests support fit of the stationary point process model. We further fitted the stationary GPD in comparison with the stationary PP model. The formal tests which are the Anderson-Darling test and the Cramér-von Mises test are conducted to assess goodness of fit of the GPD. These tests are conducted using the ‘evd’ package [29]. The Cramér-von Mises statistic W2 and the Anderson-Darling statistic A2 are calculated using Eqs. 15 and 16 that are respectively discussed in Hosking [30].

$$ W^{2}=\sum\limits_{i=1}^{n}\left\{F(x_{(i)})-(2i-1)/(2n)\right\}^{2}+1/(12n) $$
(15)

and

$$ \begin{array}{@{}rcl@{}} A^{2}&=&-n-(1/n)\sum\limits_{i=1}^{n}\left( 2i-1\right)\left[\log\left\{F(x_{(i)})\right\}\right.\\ &&\left.+\log\left\{1-F(x_{(n+1-i)})\right\}\right], \end{array} $$
(16)

where F(x(i)) is the empirical distribution function at the i th point [30]. The frequency of occurrence of extremely hot days is the main focus of analysis in this paper as this information is useful to the planners and decision makers in the energy sector. We calculate and interpret the intensity of occurrence of extremely hot days based on the stationary point process model and the reparameterisation approach [18].

4 Results

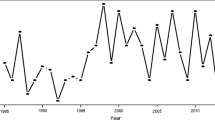
Figure 1 is a time series plot of AMDT with a time-varying threshold which is a PCSS. The smoothing parameter is chosen based on the GCV criterion and found to be \(\hat \lambda =1.028421\textit {e}^{-08}\). The detrended version of the data (residuals above the threshold) is given in Fig. 3 at the top left panel. It is noticeable in the panels of threshold stability plots in Fig. 3 that when threshold exceeds \(\hat \tau =2.9134\), the parameters begin diverging from their mean. Figure 2 shows the results of fitting the non-parametric EVM model and the threshold is found to be \(\hat \tau =2.9134\).

Fig. 3
figure 3

From left to right: Positive residuals (excesses) above the threshold (top left panel), threshold stability plot for the extremal index (top right panel), threshold stability plot for the scale parameter (bottom left panel), and threshold stability plot for the shape parameter (bottom right panel)

Full size image

The extremal index is estimated prior to the declustering process and found to be 𝜃 = 0.5908, which is large enough to give a low rate of exceedance. The rate of exceedance is 1/0.5908 = 1.69 ≈ 2, meaning that the cluster maxima occur in groups of approximately 2. From these findings, we establish that temperature tends to be very high on consecutive days but very hot spells tend not to last longer than 1 or 2 days. The original series contains 1407 observations and there are 81 identified cluster maxima (Figs. 4 and 5). Excesses above the threshold are found to be 144. The GPD is fitted to cluster maxima and the exceedances above the threshold are indicated in Fig. 6.

Fig. 4
figure 4

Threshold diagnostic plots for the point process models fitted to average maximum daily temperature. From left to right: Scale parameter threshold stability plot (top left panel), shape parameter threshold stability plot (top right panel), and mean residual life plot (bottom panel)

Full size image
Fig. 5
figure 5

Q-Q plots of normalised interexceedance times against standard exponential quantiles. Vertical line shows the \((1-\boldsymbol {\hat \theta })\) quantile; sloping line has gradient \(1/\boldsymbol {\hat \theta }\). Data is the AMDT in degrees Celsius that are simulated from a max-autoregressive process with extremal index \(\boldsymbol {\hat \theta }=0.5908\)

Full size image
Fig. 6
figure 6

GPD fitted to cluster maxima (excesses) of the average maximum daily temperature. The extreme observations above the threshold are indicated by the purple dots

Full size image

Threshold diagnostic plots are given in Fig. 3 which shows on the top right panel, the threshold stability plot for extremal index. The bottom panel shows threshold stability plot for scale parameter on the left and threshold stability plot for shape parameter on the right. Further assessment of parameter estimates at several thresholds is given in Fig. 4 which shows at the top left panel, the threshold stability plot of logarithmic scale; threshold stability plot of shape parameter at the top right panel; and mean residual life plot at the bottom panel.

4.1 Results from the Stationary GPD and the Point Process Approach

4.1.1 Results from Fitting the GPD

Figure 5 shows quantile-quantile (Q-Q) plots for normalised interexceedance times against standard exponential quantiles. The Q-Q plots are mainly useful for the purpose of assessing several thresholds for estimated value of extremal index. The chosen threshold (\(\hat \tau =2.9134\)) is compared with various candidate thresholds (\(\hat \tau =2.5\), \(\hat \tau =2.4\), and \(\hat \tau =2.35\)) in Fig. 5. Although the Q-Q plots for \(\hat \tau =2.9134\) and \(\hat \tau =2.5\) look quite similar, the one for \(\hat \tau =2.9134\) appears to be more approximately linear. The Q-Q plots shown in Fig. 5 show that a threshold of \(\hat {\tau }=2.91\) gives a good fit of the model to the AMDT data.

The GPD is fitted to cluster maxima of AMDT using the MLE method and the results are summarised in Table 1. The parameter estimates are found to be \(\hat \theta =0.9168(0.1285)\) and \(\hat \xi =-0.1855(0.0956)\) with standard errors in parentheses, respectively. The negative value of the shape parameter reveals evidence that Wξ belongs to the Weibull class of the GPD and hence the appropriateness of the Weibull class of distributions in modelling maximum daily temperature in South Africa.

A 95% confidence interval for the shape parameter ξ is calculated to justify that the shape parameter is indeed estimated by a negative value. This is accomplished as follows:

$$ \begin{array}{@{}rcl@{}} \hat\xi\pm z_{\alpha/2}\times(\text{standard error})&\Rightarrow&-0.1855\pm 1.96\times0.0956\\ &=&(-0.3729;0.001876). \end{array} $$

The shape parameter is enclosed within the interval (− 0.3729;0.001876) at a 95% level of confidence. Since this confidence interval contains zero, we carry out a formal test of hypothesis at 5% level of significance to test whether the shape parameter is zero or not.

Table 1 Parameter estimates of GPD fitted to cluster maxima of the average maximum daily temperature above 22 ∘C
Full size table

We use the likelihood ratio (LR) test under the null hypothesis that the value of the shape parameter is 0. The null and alternate hypotheses of the test are given as follows:

$$ H_{0}:\xi=0 \quad \text{versus}\quad H_{1}:\xi\neq0. $$

The deviance statistic of the LR test is given in Eq. 7. We prefer the use of the modified LR test that is suggested by Hosking [30] with the modified test statistic that is denoted by LR∗. It is argued that LR∗ gives a more precise approximation to the asymptotic distribution of LR [30].

$$ \text{LR}^{*}=\left( 1-\frac{2.8}{n}\right)\text{LR}, $$
(17)

where LR follows \(\chi _{1,(\alpha )}^{2}\) under H0, implying that LR = 3.841. Since there are 2 543 observations in the data set, substituting n = 2543 in Eq. 17, it follows that LR∗ = 3.8368. The rule is to reject H0 if \(\text {LR}^{*}>\chi _{1,(1-\alpha )}^{2}\). Since 3.8368 > 0.004, the null hypothesis is rejected and we concluded that indeed the Weibull class of distributions is a good fit to the cluster maxima. The diagnostic plots that are given in Fig. 7 show a good fit of the GPD to cluster maxima.

Fig. 7
figure 7

Diagnostic plots of the stationary generalised Pareto distribution fitted to cluster maxima of average maximum daily temperature

Full size image

The shaded area on the probability and the quantile plots show the linearity of the dots to guide in suggesting good fit of the GPD to the AMDT data. The same applies to the return level plot. The estimated rate of excess is calculated as the ratio of the number of cluster maxima and the number of the observations above the time-varying threshold, which is \(\frac {81}{144}\approx 0.5625\). Since \(\theta =\log (\sigma _{\tau })\), this implies that the scale parameter is estimated as \(\hat \sigma _{\tau }=e^{\hat \theta }=e^{0.9168}\approx 2.5013\).

The estimation of target parameters in statistical modelling is usually associated to some level of uncertainty which needs to be quantified. One of the techniques that are useful for assessing uncertainty in parametric and non-parametric estimation is the bootstrap resampling approach [31]. We apply the bootstrap resampling approach in this paper for assessing uncertainty on the estimates of GPD parameters (Table 2). The bootstrap statistics for GPD estimates are calculated and summarised in Table 3. The biases for the scale and shape estimates are given by 0.0320 and − 0.0461, whereas the standard deviations are estimated as 0.1552 for scale estimate and 0.1124 for estimate of the shape. These statistics are small in comparison with the theoretical values, implying a less level of uncertainty. The bootstrap densities for the estimates of the scale and shape respectively are given in Fig. 8, which shows good fit of the density functions to the estimated values.

Table 2 Cramér-von Mises and Anderson-Darling goodness-of-fit tests of the GPD
Full size table
Table 3 GPD parameter uncertainty using parametric bootstrap resampling approach
Full size table
Fig. 8
figure 8

Parametric bootstrap densities of the GPD parameters

Full size image

In this paper, we conduct both the Cramér-von Mises and the Anderson-Darling tests to assess fit of the GPD toward modelling AMDT in South Africa. The results of the tests are given in Table 2, where column 2 shows the test statistics and the p values of the test are given in column 3. We wish to test the hypothesis H0: The random sample \(x_{1},x_{2},\dots ,x_{n}\) comes from the GPD, against H1: H0 is false. Looking at the Cramér-von Mises test, the p value 0.6187 is large in comparison with 5% level of significance.

We fail to reject H0 at 5% level of significance and conclude that the random sample \(x_{1},x_{2},\dots ,x_{n}\) comes from the GPD. This decision is supported by the test statistic 0.0506 in comparison with the critical region zα/2 = 1.645. The Anderson-Darling test has the p value 0.5919 and the test statistic 0.3809. In this test, we fail to reject the null hypothesis. The conclusion based on these formal tests is that the fit of the GPD is appropriate for modelling AMDT in South Africa.

4.1.2 Results from Point Process Modelling Approach

Table 4 presents the estimation of the target parameters of the point process model with standard errors given in parentheses. The parameter estimates of the stationary model together with their standard errors in parentheses are \(\hat {\mu }=6.098(0.3434)\), \(\hat {\sigma }=0.340 (0.0998)\), and \(\hat {\xi }=-0.193(0.0612)\). In models M0 and M1, parameter estimates reveal the existence of a zero trend component. The null hypothesis is not rejected and the conclusion is an insignificance of a trend component. The estimates of the shape parameter reveal appropriateness of Weibull class of distributions in modelling AMDT. The LR tests were carried out based on the deviance statistic that is given in Eq. 7 (Fig. 9).

Table 4 Parameter estimates for time-homogeneous and non-homogeneous point process models fitted to average maximum daily temperature with standard errors in parentheses
Full size table
Fig. 9
figure 9

Diagnostic plots of the stationary point process model fitted to cluster maxima of average maximum daily temperature

Full size image

Model M0 is used as a base model and the rest of the models are compared to M0 to assess significant improvements. It follows that D(1,0) = 0.0016, D(2,0) = 0.0004, and D(3,0) = 0.0094. These deviance statistics are small in comparison with \(\chi ^{2}_{1,(0.05)}=3.841\). We fail to reject the null hypothesis at 5% level of significance and conclude that model Mj, j = 1,2,3 does not provide any significant improvement. From Eq. 9, it follows that \(\hat \sigma ^{*}= 1.0633\) and \(\hat \lambda =15.1471\approx 15\), which implies that the frequency of the occurrence of extremely hot days is approximately 15 times per annum. This is the annual number of days in which Eskom experiences an extremely high demand of electricity.

The frequency analysis of the occurrence of cluster maxima above the sufficiently high threshold \(\hat {\tau }= 2.91\) is discussed. Figure 10 is a bar graph that shows monthly frequency of occurrence of cluster maxima above \(\hat {\tau }= 2.91\) over the period 2000 to 2010. This graph reveals that the least cluster maxima is 4 and it occurred during October, followed by 6 which occurs in June. The modal occurrence of the cluster maxima is 7 which occurred in August, September, and November. January, February, and May had the occurrence of 8 cluster maxima whereas the highest count of 11 was encountered in July.

Fig. 10
figure 10

Bar chart of monthly frequency of occurrence of cluster maxima above \(\hat {\tau }= 2.9134\) for the period 2000 to 2010

Full size image

5 Discussion

Stationary and non-stationary point process models were fitted so as to model AMDT in South Africa. The PCSS function was used for non-linear detrending the data, after which residuals above the threshold were extracted. The boundary-corrected EVM model was fitted to determine the fixed threshold. The data had revealed short-range dependence and heavy seasonality which led to declustering of exceedances. The interval estimator method was used for declustering the data. Stationary and non-stationary candidate models were fitted using the MLE method.

Model adequacy was checked using graphical diagnostic tools which showed support of the stationary model. Inclusion of covariate did not result in any improvement in the models. We further fitted the stationary GPD model to compare its fit with that of the stationary point process model. The goodness-of-fit of the GPD was checked using the formal tests which are the Cramér-von Mises test and the Anderson-Darling test. It is established based on these tests that the GPD is an appropriate model for modelling AMDT in South Africa.

The fit was also supported by the diagnostic plots. We then used the stationary point process model for calculating the frequency of the occurrence of extremely hot days based on the reparameterisation approach. It has been found in this study that the number of extremely hot days occur at the rate of 15 times per annum. These are the days in which Eskom experiences an extremely high demand for electricity. We further discussed the frequency analysis of monthly occurrence of cluster maxima above the threshold over the period of the study (2000–2010). It is established that the least occurrence of cluster maxima was during October and that the modal occurrence of 7 was encountered during the months August, September, and November. There was the highest occurrence of cluster maxima in July.

6 Conclusions

This paper has discussed the modelling of temperature extremes using the point process approach. The modelling framework uses penalised cubic smoothing spline as a time-varying threshold, followed by fitting the extreme value mixture model to determine a fixed threshold. The exceedances above the fixed threshold are then declustered. The stationary and non-stationary point process models, and the stationary GPD are then fitted to cluster maxima. Inclusion of trend or covariate in the point process models that are used for modelling temperature extremes in South Africa during the non-winter season (1 September 2000 to 30 April 2010) does not result in any significant improvement of the models.

Use of the formal tests (Anderson-Darling test and Cramér-von Mises test) for testing goodness of fit for the models supports the fit of stationary GPD in modelling temperature extremes in South Africa during the non-winter season (1 September 2000 to 30 April 2010). The use of the reparameterisation approach of the Poisson-GPD has established that the frequency of the occurrence of extremely hot days over the non-winter season (1 September 2000 to 30 April 2010) is approximately 15 times per annum. The results of the study based on the data for the years 2000–2010 establish that temperature tends to be very high on consecutive days but very hot spells tend not to last longer than 1 or 2 days.

Major findings and contributions of this study are as follows:

  • A major contribution for this paper is on the use of the PCSS function for non-linear detrending temperature observations together with the use of the non-parametric EVM model in determining the fixed threshold.

  • The methodology and results may be useful to power utility companies based on the fact that the frequency analysis of the occurrence of extremely high temperatures is directly relevant to the modelling of electricity demand based on the fact that the frequency and the duration of a hot spell are the important issues from the viewpoint of both the energy statisticians and the disaster risk analysts.

  • The major results of this paper establish that temperature tends to be very high on consecutive days but very hot spells tend not to last longer than 1 or 2 days, a remark that may be relevant to the meteorologists and disaster risk managers.

  • The reparameterisation approach of the Poisson-generalised Pareto distribution (Poisson-GPD) has been used to determine the number of extremely hot days, which is 15 per annum. This remark is as well important to the meteorologist for the purpose of predicting the future occurrence of hot spells. This is the number of days on which Eskom experiences extremely high demand for electricity (Fig. 11).