Coupling XFEM and Peridynamics for brittle fracture simulation: part II—adaptive relocation strategy

Abstract

An adaptive relocation strategy for a coupled XFEM–Peridynamic (PD) model is introduced. The motivation is to enhance the efficiency of the coupled model and demonstrate its applicability to complex brittle fracture problems. The XFEM and PD approximation domains can be redefined during the simulation, to ensure that the computationally expensive PD model is applied only where needed. To this end a two-step expansion/contraction process, allowing the PD patch to adaptively change its shape, size and location, following the propagation of the crack, is employed. No a priori knowledge of the crack path or re-meshing is required, and the methodology can automatically switch between PD and XFEM. Three 2D fracture examples are presented to highlight the performance of the methodology and the ability to follow multiple crack tips. Results indicate significant computational savings. Furthermore, the characteristic length scale of PD theory bestows a nonlocal and multiscale component to the methodology.

1 Introduction

Many studies have been devoted to the coupling of FE meshes and PD grids, for the mitigation of the computational restrictions associated with the numerical implementation of the PD theory. Here, we focus our attention to the contributions presented by Zaccariotto et al. [1] and Han et al. [2].

In [1], Zaccariotto et al. employ the coupling methodology developed in [3] to study dynamic fracture problems. Coupling is enforced through the introduction of ghost nodes and particles and it is similar to the coupling approach employed here. To improve the computational efficiency of the coupled model during fracture, a trigger is introduced that is based on the relative displacement between two FE nodes. The trigger signifies the switch from FE nodes to PD particles near the areas where large strains develop. Although in [1] the coupling procedure used has the requirement of coincident FE nodes and PD particles, this restriction is lifted in a subsequent publication [4]. Effectively, during the initial stages of the simulation $\varOmega^{PD}$ is small and restricted only near the crack tip and expands as the crack propagates, to follow the updated location of the crack.

A similar procedure was also used by Han et al. [2] where the ‘morphing’ strategy was used to couple classical elasticity with the PD theory [2], [5]. According to the morphing strategy both local and non-local interactions appear in the formulation of the model and their contributions are controlled by introducing a special weighting function that ensures energy equilibrium. Thus, there are areas of the material that are described through interactions that are purely local, non-local, or a combination of the two. The effect of the weighting function choice and the length of the transitioning area is investigated in [5]. A critical damage index based on the loss of material stability is introduced that triggers the switch from local to non-local interactions. Similar to [1], $\varOmega^{PD}$ expands and follows the propagation of the crack.

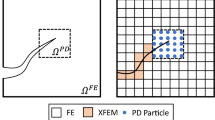
Since a crack can propagate only inside $\varOmega^{PD}$, a priori knowledge of the final crack path is required to define $\varOmega^{PD}$ and $\varOmega^{FE}$ at the beginning of the simulation. This requirement is removed with the expansion process used [1] and [2] that adaptively expands $\varOmega^{PD}$. This has been proven to be an efficient procedure to simulate complex problems such as dynamic crack branching. Yet, the size of $\varOmega^{PD}$ increases monotonically with each subsequent expansion that can lead to computational restrictions. Use of PD to capture the displacement jump near the crack body, however; adds unnecessary computational burden. The relocation methodology presented here allows to switch from FEs to PD particles in order to capture the propagation of the crack but also switch from PD particles back to FEs in areas where the PD model is no longer needed. Relocation of $\varOmega^{PD}$ takes place through a two-step expansion/contraction process, illustrated schematically in Fig. 1. Similar to [1] and [2], the expansion step is used to transfer part of $\varOmega^{FE}$ to $\varOmega^{PD}$ to capture the updated location of the crack. Subsequently, the contraction step is used to limit $\varOmega^{PD}$ only near the vicinity of the crack tip and reduce the total number of particles by transferring part of $\varOmega^{PD}$ to $\varOmega^{FE}$.

Fig. 1

Schematic illustration of the two-step process for the adaptive relocation of $\varOmega^{PD}$

With the proposed relocation strategy, the size of $\varOmega^{PD}$ remains small during the simulation while its location is adaptively redefined. Key ingredients for its successful implementation are:

• (A) An effective technique to couple the PD theory with classical elasticity, that allows the independent discretization of $\varOmega^{PD}$ and $\varOmega^{FE}$, and generates small wave reflections during dynamic problems.

• (B) The ability to localize the implementation of the computationally expensive PD theory to the vicinity of the crack tip (see Fig. 1). Since the method is intended for crack propagation problems, it is desirable to avoid remeshing during the analysis.

• (C) An algorithm to adaptively relocate the PD patch so that it automatically follows the crack tip(s) and cover its (their) vicinity efficiently.

The actual implementation of the strategy proposed, and its success, relies on achieving the three objectives (A), (B) and (C). A possible coupling between XFEM and PD, that addresses objectives (A) and (B) is discussed in “Coupling XFEM and Peridynamics for Brittle Fracture Simulation—Part I: Feasibility and Effectiveness” [6]. For consistency, the same notation and definitions are adopted here. In this part, the development for a possible relocation strategy to fulfil objective (C), is presented. The performance of the coupled XFEM–PD model, with the ability to relocate $\varOmega^{PD}$ is demonstrated through a series of fracture examples.

Obviously, different coupling approaches, model combinations and relocation strategies are possible. In [7], Talebi et al. present an open source software called PERMIX that allows the creation of multiscale models using the Arlequin framework [8] with the capability of coupling continuum models with molecular dynamics, Peridynamics and smooth particle hydrodynamics. Examples of coupling PD with FE using the Arlequin method can also be found in [9] and [10]. PERMIX was also used in [11] to couple XFEM with atomistic models to study crack propagation in 3D examples. The present contribution is an attempt towards the efficient combination of local and non-local models, with dynamic relocation capabilities, aiming at true multiscale simulations. Multiscale methodologies for fracture problems with adaptive capabilities are also proposed in [12] and [13]. In [13] specifically, a strategy similar to the one presented here is proposed. As the crack propagates, an adaptive refinement process redefines the location where the coarse (FE) and fine scale (atomistic) models are used while the phantom node method is implemented to model the discontinuity within the continuum domain.

A different approach to minimize the computational cost of full PD models it to adopt refinement strategies. Coarse discretization can be used away from the crack tips while in the vicinity of the crack, the particle grid can be refined. The dual-horizon methodology presented in [14] is such an approach that also avoids the appearance of spurious reflections. Furthermore, the nonlocal operator method, that can be considered a generalization of the dual-horizon PD model, has been proposed in [15, 16]. Our study is limited to methodologies that combine the FE method with PD as it is envisaged to take advantage already established FE solvers and potentially port PD models to commercially available FE packages. Nevertheless, refinement strategies can still be used in $\varOmega^{PD}$ to further boost the efficiency of the solution.

This paper is organized as follows: in Sect. 2 the implementation of the XFEM–PD model for dynamic fracture problems with multiple or intersecting cracks is presented. Then, the expansion and contraction steps of the adaptive relocation strategy are presented in Sect. 3. A simple algorithm to monitor the crack tip location is also included in this section. In Sect. 4 three fracture examples are used to demonstrate the performance of the methodology. The complex case of dynamic crack branching is also considered. Finally, concluding remarks and recommendations for future work are included in Sect. 5.

2 Implementation of the XFEM: PD model for dynamic crack propagation and crack branching

In certain problems (e.g. crack branching) multiple cracks, or their intersection, might appear in a single element. Consider the case of a crack with two branches, as illustrated in Fig. 2. The initial crack and one of the branches are termed main crack (solid green line) and the other branch is termed secondary crack (dashed red line). White and yellow squares are used to indicate the standard and the enriched elements, respectively. Daux et al. [17, 18] were the first to implement the junction enrichment function to capture the discontinuous displacement field in an element where a junction appears. Later Zi et al. [19] proposed the enrichment of multiple cracks by overlaying Heaviside step functions. A signed distance function, $\phi^{m} \left( {\varvec{x}^{FE} } \right)$ and $\phi^{s} \left( {\varvec{x}^{FE} } \right)$, is assigned to the main and the secondary crack, respectively. The nodes whose support is intersected by the main crack, indicated with green dots, are enriched in the absence of the secondary crack. Subsequently, the nodes whose support is intersected by the secondary crack, indicated by larger red dots, are enriched in the absence of the main crack. Consequently, the elements that are cut by multiple cracks or contain a junction will be enriched multiple times. This is required because a single step function is not adequate to capture the complex discontinuous displacement field in these elements [20].

Fig. 2

Enrichment strategy for multiple cracks and junctions. Green dots indicate the nodes enriched due the main crack (green solid line), while red dots the nodes enriched due to the secondary crack (red dashed line). (Color figure online)

Following [20], the displacement field in an element with multiple cracks is approximated as:

$$ \varvec{u}\left( {\varvec{x}^{FE} } \right) \approx \mathop \sum \limits_{i = 1}^{K} N_{i} \left( {\varvec{x}^{FE} } \right)\varvec{u}_{i} + \mathop \sum \limits_{j = 1}^{M} N_{j}^{m} \left( {\varvec{x}^{FE} } \right)\left( {H\left( {\varvec{x}^{FE} } \right) - H\left( {\varvec{x}_{j}^{FE} } \right)} \right)\varvec{a}_{j}^{m} + \mathop \sum \limits_{k = 1}^{G} N_{j}^{s} \left( {\varvec{x}^{FE} } \right)\left( {H\left( {\varvec{x}^{FE} } \right) - H\left( {\varvec{x}_{k}^{FE} } \right)} \right)\varvec{a}_{k}^{s} $$

(1)

where $K$ is the total number of FE nodes, $M$ and $G$ are the total number of nodes enriched due to the main and the secondary crack, respectively, $\varvec{u}_{i}$ are the nodal displacements, $\varvec{ a}_{j}^{m}$ are the enriched dofs associated with the main crack and $\varvec{a}_{k}^{s}$ are the dofs associated with the secondary crack. In the element where the crack junction takes place, the approximation is modified to:

$$ \varvec{u}\left( {\varvec{x}^{FE} } \right) \approx \mathop \sum \limits_{i = 1}^{K} N_{i} \left( {\varvec{x}^{FE} } \right)\varvec{u}_{i} + \mathop \sum \limits_{j = 1}^{M} N_{j}^{m} \left( {\varvec{x}^{FE} } \right)\left( {H\left( {\varvec{x}^{FE} } \right) - H\left( {\varvec{x}_{j}^{FE} } \right)} \right)\varvec{a}_{j}^{m} + \mathop \sum \limits_{k = 1}^{G} N_{j}^{s} \left( {\varvec{x}^{FE} } \right)\left( {J\left( {\varvec{x}^{FE} } \right) - J\left( {\varvec{x}_{k}^{FE} } \right)} \right)\varvec{a}_{k}^{s} $$

(2)

where $J\left( {\varvec{x}^{FE} } \right)$ is the junction function defined as:

$$ J\left( {\varvec{x}^{FE} } \right) = \left\{ {\begin{array}{*{20}c} { H\left( {\varphi^{m} \left( {\varvec{x}^{FE} } \right)} \right),} & {\varphi^{m} \left( {\varvec{x}^{FE} } \right) < 0} \\ {H\left( {\varphi^{s} \left( {\varvec{x}^{FE} } \right)} \right),} & {\varphi^{m} \left( {\varvec{x}^{FE} } \right) > 0} \\ \end{array} \varvec{ }} \right. $$

(3)

It is noted that for an element that contains two cracks or the junction of two cracks, the dimensions of the local stiffness matrix will be $24 \times 24$, referring to 8 standard and 16 enriched dofs.

Static and dynamic problems involving crack propagation are considered. The formulation of the system of equations for the coupled XFEM–PD model is presented in [6]. In static problems, the solution is approximated using the implicit Newton–Raphson iterative method. In order to capture the rapid nature of the fracture phenomenon in dynamic problems, sufficiently small time steps need to be employed [17]. When a large number of time steps is required, explicit time integration schemes can be computationally more efficient compared to the implicit ones [21]. However, explicit methodologies are only conditionally stable.

Belytschko et al. [22] pointed out that if conventional mass lumping techniques are implemented in XFEM, the critical time step tends to zero as the discontinuity approaches the element nodes [23]. To circumvent this restriction, Menouillard et al. [24], proposed an approximation of the lumped mass matrix by considering kinetic energy conservation for some special motions of the body. The methodology provides a lower bound on the critical time step, even in cases where the discontinuity coincides with a nodal position. Xu et al. [20], followed the formulation of Menouillard et al. [24], to propose a mass lumping when the shifted Heaviside enrichment is used and extended the applicability of the approximation to cases with multiple discontinuities.

Considering a 2D bilinear element, and following [20] and [24], the mass associated with the enriched nodes of the element is computed as:

$$ m = \rho \int \psi^{m} \left( {\varvec{x}^{FE} } \right)^{2} d\varOmega , $$

(4)

where $\psi^{m} \left( {\varvec{x}^{FE} } \right) = \mathop \sum \limits_{j = 1}^{4} N_{j}^{m} \left( {\varvec{x}^{FE} } \right)\left( {H\left( {\varvec{x}^{FE} } \right) - H\left( {\varvec{x}_{j}^{FE} } \right)} \right)$ is the enrichment function (in this case the shifted Heaviside enrichment). Then, the element mass is distributed to the nodes of the elements and subsequently, to the respective dofs. Xu et al. [20] present a weighting procedure for the distribution of the mass considering the area of each subarea in the element that is defined by the crack. The integral in Eq. 4 can be approximated numerically using the same Gauss integration procedure described in [6]. Then, the weighted mass for each node can be approximated by creating a uniform grid within the element and using the expression:

$$ m_{J} = \frac{{n_{subJ}^{intI} }}{{n_{ele}^{int} \cdot n_{subJ}^{nodeI} }} \cdot m, $$

(5)

where $J = 1, 2, 3, 4$ is the element node number, $n_{subJ}^{intI}$ is the number of grid points in the subarea that contains node $J$, $n_{ele}^{int}$ is the total number of grid points and $n_{subJ}^{nodeI}$ is the number of nodes in the subarea that contains node number $J$. The process is repeated if multiple cracks or a junction exists in the element. For example, considering the secondary crack from Fig. 2, evaluation of Eq. 4 is repeated in the absence of the main crack and the superscript $( \cdot )^{m}$ is replaced with $( \cdot )^{s}$. The weighted mass is computed again using Eq. 5 but this time the mass is associated with the dofs of the secondary crack.

By repeating Eq. 5 for all the elements that have been enriched and for each crack, the diagonal lumped mass matrix $\varvec{M}^{enr,enr}$ is computed. The superscript $\left( \cdot \right)^{enr,enr}$ is used to denote that this matrix refers only to the enriched dofs. For the standard dofs, the mass is computed using the conventional row summation technique on the consistent mass matrix as:

$$ \varvec{M}_{i,i}^{std,std} = \mathop \sum \limits_{j} \varvec{M}_{i,j}^{consistent} . $$

(6)

Then the final mass matrix is then defined as:

$$ \varvec{M}^{FE} = \left[ {\begin{array}{*{20}c} {\varvec{M}^{std,std} } & 0 \\ 0 & {\varvec{M}^{enr,enr} } \\ \end{array} } \right], $$

(7)

Finally, the discretized system of equations is written in matrix notation as:

$$ \varvec{M}^{FE} \varvec{\ddot{\bar{u}}} + \varvec{K}^{FE} \bar{\varvec{u}} = \varvec{F}^{FE} , $$

(8)

where $\bar{\varvec{u}} = \left\{ {\varvec{u}^{T} ,\varvec{a}^{T} } \right\}\varvec{ }^{T}$ is the vector that contains the standard and enriched dofs values and $\varvec{F}^{FE}$ is the external force vector. In the absence of cracks, $\varvec{M}^{FE} = \varvec{M}^{std,std}$.

Using the coupled XFEM–PD model we need to consider two time steps, the first is associated with the discretization of the PD particle grid while the second, with the discretization of the FE mesh and the position of the crack relative to the FE nodes. Although the mass lamping technique implemented provides a lower bound on the critical time step, computation of the exact value is not straightforward. Besides, since the discretization in $\varOmega^{PD}$ is typically finer compared to that in $\varOmega^{FE}$, it is expected that the PD critical time step will be the smaller of the two.

3 Adaptive relocation strategy

In this section, the relocation strategy for $\varOmega^{PD}$ is presented. As mentioned in the introduction, the aim is to re-define $\varOmega^{PD}$ in an adaptive way that follows the propagation of the crack. A possible way to perform this could be to directly relocate the whole PD domain to the updated location of the crack tip. This approach however can be cumbersome in static problems and when complex crack patterns are considered. Instead, the strategy followed for the adaptive relocation of $\varOmega^{PD}$ is performed through a two-step process:

Step 1—Expansion Step As the crack propagates within $\varOmega^{PD}$, it will eventually reach the XFEM-PD coupling interface, $\partial \varOmega_{1}$. The area where the PD theory is applied needs to be expanded to ensure that the crack tip is always sufficiently covered within $\varOmega^{PD}$. Consequently, the coupling interface is shifted, and additional PD particles are introduced to cover the updated location of $\varOmega^{PD} .$ The FEs that are now located within the new boundary are deactivated and their contribution is removed from $\varvec{K}^{FE}$ and $\varvec{M}^{FE}$.

Step 2—Contraction Step After $\varOmega^{PD}$ has been expanded, the PD particles that are away from the crack tip are no longer required as the displacement jump due to the crack body can be captured accurately with the XFEM enrichment. During this step, $\partial \varOmega_{1}$ is shifted again, focusing around the crack tip(s) and $\varOmega^{PD}$ is restricted to a smaller area. The approximation of the solution switches back to the FE method in the area that is no longer inside $\varOmega^{PD}$. Additional enriched dofs are introduced to capture the new crack segment that is now revealed in $\varOmega^{FE}$.

The location of $\varOmega^{PD}$ is updated and follows the propagation of the crack through this two-step process, as illustrated schematically in Fig. 1. Because $\varOmega^{PD}$ virtually propagates with this expansion/contraction type of movement, leaving behind a trail of Heaviside functions, the algorithm is termed the “Peridynamic snail”. The advantage of this two-step process is that each time only a small portion of $\varOmega^{PD}$ and $\varOmega^{FE}$ is modified, minimizing the requirement for interpolations and allowing for the crack pattern to first emerge naturally within $\varOmega^{PD}$ prior to the relocation. A requirement that arises during the contraction step is the need for information regarding the vicinity of the crack tip and the path it has followed. This is necessary to identify which particles are no longer needed and update the location of $\partial \varOmega_{1}$ as well as for the definition of the enrichment functions. A tracking methodology is thus required to monitor the evolution of the crack.

4 Crack tracking algorithm

The requirement to monitor the location of the crack during the simulation is counter-intuitive for the PD theory. In fact, one of the attractive properties of PD is the ability to incorporate damage and simulate its evolution without the need for special algorithms that monitor its location or the path it has travelled [9]. A simple approach is implemented here to identify the location of the crack tip, leading to a piecewise linear estimation of the final crack path.

The current location of the crack tip is estimated numerically using the local damage index $\phi \left( {\varvec{x}^{PD} ,t} \right)$. Consider a square plate with an edge breaking crack, as illustrated in Fig. 3a. In Fig. 3b a schematic representation of a PD grid and the particle bonds is illustrated, where the bonds that are intersected by the crack have been removed. It is not easy to pinpoint exactly the location of the crack tip as the bonds cannot be directly related to geometrical information. The process is based on the observation that when taking the gradient of the local damage index, the vector field near the crack will point towards the location of the crack body and converge near the location of the tip. It is thus expected that a discrete version of the Laplacian $\nabla \cdot \nabla \phi \left( {\varvec{x}^{PD} ,t} \right)$ will exhibit a local minimum at this location. Since $\phi \left( {\varvec{x}^{PD} ,t} \right)$ is a discrete field, the discrete Laplacian is calculated as:

$$ \nabla \cdot \nabla \phi \left( {\varvec{x}^{PD} ,t} \right) = \left( {D_{xx}^{2} \phi } \right) + \left( {D_{yy}^{2} \phi } \right), $$

(9)

where $D_{xx}^{2} \phi = \left( {\phi \left( {x + \Delta x,y,t} \right) - 2\phi \left( {x,y,t} \right) + \phi \left( {x + \Delta x,y,t} \right)} \right)/\Delta x^{2}$ denotes the second central difference operator. Working similarly for $y$ direction, a discrete version of $\nabla \cdot \nabla \phi \left( {\varvec{x}^{PD} ,t} \right)$ is produced numerically.

Fig. 3

a Illustration of a plate with an edge crack using the local damage index $\phi \left( {\varvec{x}^{PD} ,t} \right)$, b representation of a PD grid and the bond network. A red triangle indicates the location of the tip as identified from the tracking algorithm and c plot of $\nabla \cdot \nabla \phi \left( {\varvec{x}^{PD} ,t} \right)$ and $\nabla \phi \left( {\varvec{x}^{PD} ,t} \right)$ near the location of the crack tip

The gradient and the Laplacian of $\phi \left( {\varvec{x}^{PD} ,t} \right)$ are plotted in Fig. 3c. In the examples presented here, $\nabla \cdot \nabla \phi \left( {\varvec{x}^{PD} ,t} \right)$ has been normalized with respect to its minimum value. The predicted location of the local minimum is indicated in Fig. 3b with a red triangle. A very good estimation of the crack tip location can be obtained through this simplistic approach.

The Laplacian $\nabla \cdot \nabla \phi \left( {\varvec{x}^{PD} ,t} \right),$ is computed numerically during the simulation and the current location of the crack tip is stored in an array to be used during the contraction step of the relocation process. This tracking method can also be used to monitor the damage evolution when multiple cracks are present. The performance of the tracking methodology is evaluated by taking an example from an earlier investigation made by the authors. In [25], the thermal cracking of alumina specimens under cold shock was studied. This example is borrowed as multiple cracks nucleate at the boundary of the domain and propagate towards its interior. The final length of each crack varies which result in a hierarchical crack pattern. Although this simulation was performed using a PD only model, it is a good example to evaluate the method’s performance.

The tracking process for the cold shocked alumina at different time steps, is illustrated in Fig. 4. Using this approach, it was possible to capture automatically the propagation and the arrest of each individual crack. The current location of the crack tip is indicated with a black circle and the path it followed with a black line. At each time step the tracking process is applied, possible tip locations are identified. To sort which tip location corresponds to which crack, a straight line is used to connect each crack with each possible tip location. The local damage index is then computed along each of the lines and the tip corresponds to the crack that produces the highest value. The method is applied by simply comparing a current with a previous step and no prior knowledge regarding the direction of propagation is required. In the examples presented here for instance, some of the cracks propagate in the vertical while others in the horizontal direction.

Fig. 4

Application of the tracking algorithm on the damage evolution of an alumina specimen under cold shock [25]

4.1 Expansion step

The expansion and the contraction steps are performed sequentially to achieve the adaptive relocation of $\varOmega^{PD}$. It is desirable, during the relocation process, to limit as much as possible the remeshing requirements for $\varOmega^{FE}$. With regards to the body of the crack that appears within $\varOmega^{FE}$, this requirement is lifted with the introduction of the XFEM enrichment. However, in order to achieve relocation, $\varOmega^{FE}$, $\varOmega^{PD}$ and $\partial \varOmega_{1}$ must be redefined. Since the shape and the size of $\varOmega^{PD}$ will vary during the simulation, at least partial redefinition of the PD grid is unavoidable. Remeshing of $\varOmega^{FE}$ can be avoided, however; by initially discretizing with FEs the whole problem domain $\varOmega$. Then, the PD patch is overlaid on the FE mesh and $\partial \varOmega_{1}$ is defined along element edges. Then, the FE nodes with $\varvec{x}^{FE} \in \varOmega^{PD}$ as well as the stiffness and mass contributions of the elements within $\varOmega^{PD}$ are removed. Thus, during relocation, the FE mesh remains unchanged by activating and deactivating the appropriate elements and no restrictions are applied with regards to its initial definition.

An example of the expansion/contraction process is illustrated in Fig. 5. For simplicity, uniform discretization is used for both $\varOmega^{PD}$ and $\varOmega^{FE}$. Initially, $\varOmega^{PD}$ is constructed as a square, centred at the crack tip. Blue and grey dots in this figure indicate normal and ghost particles, respectively. White squares have been used to indicate the FE mesh, while yellow squares indicate the elements that are cut by the crack and have been enriched. As the crack propagates, it will eventually reach the coupling interface $\partial \varOmega_{1}$ (see Fig. 5b).

Fig. 5

Illustration of the relocation process through the subsequent application of the expansion and contraction steps

During the expansion step, the knowledge of the location of the crack or its tip is not required. The expansion step is activated when:

$$\| \varvec{x}^{PD,b} - \varvec{x}^{PD,*}\| < l^{crit} , $$

(10)

where $\varvec{x}^{PD,b}$ are the PD particles that lost at least one bond in the current step increment $t$, $\varvec{x}^{PD,*}$ is the closest point to $\varvec{x}^{PD,b}$ on $\partial \varOmega_{1}$ and $l^{crit}$ is a threshold distance. The term step increment refers to time and load increments for dynamic and static problems, respectively.

Equation 10 is the expansion trigger and identifies if and where expansion is required. Let $\varvec{x}^{PD,Exp}$ be the set of $\varvec{x}^{PD}$ that violates Eq. 10 i.e.:

$$ \varvec{x}^{PD,Exp} = \left\{ {\varvec{x}^{PD} \in \varvec{x}^{PD,b} :\| \varvec{x}^{PD} - \varvec{x}^{PD,*}\| > l^{crit} } \right\} $$

(11)

Then $\varOmega^{PD}$ must be expended for each entry in $\varvec{x}^{PD,Exp}$ till the expansion trigger is no longer violated at any location. Multiple expansions might be required within a single expansion step depending on the number and the locations defined by $\varvec{x}^{PD,Exp}$. The threshold value ensures that a minimum distance of $l^{crit}$ covers at any given time step a damaged particle. As such it is the location of the damaged particles that drive the activation of the expansion step regardless of the exact position of the crack. This property allows to easily reshape $\varOmega^{PD}$ even when complex crack patterns or multiple cracks are considered (see branching example in the following paragraphs). A red dot is used in Fig. 5b to indicate a particle that has tripped the expansion trigger and the distance $l^{crit}$ around the particle is plotted with a solid red line.

The extent to which the area of $\varOmega^{PD}$ expands during the expansion step is defined through the expansion length $l^{Exp}$. Since the final crack path is not known, the expansion is performed in a radial sense, centred at the location of the expansion trigger, to allow for all possible directions of crack propagation. A circle with radius $l^{Exp}$, is plotted in Fig. 5b with a dashed red line to define the part of $\varOmega^{FE}$ that will switch to $\varOmega^{PD}$ in the subsequent steps. The expansion domain is defined as:

$$ \varOmega^{Exp} = \left\{ {\varvec{x}^{FE} \in \varOmega^{FE} :\|\varvec{x}^{FE} - \varvec{x}^{PD,Exp}\| < l^{Exp} } \right\} $$

(12)

Obviously, $\varOmega^{Exp} \subseteq \varOmega^{FE}$ and $\partial \varOmega^{Exp}$ is its boundary. Thus, for the next step:

$$ \varOmega^{PD,t + \Delta t} = \varOmega^{PD,t} \cup \varOmega^{Exp} , $$

(13a)

$$ \varOmega^{FE,t + \Delta t} = \varOmega^{FE,t} \backslash \varOmega^{Exp} , $$

(13b)

The superscripts $t$ and $t + \Delta t$ are used to denote the current and next steps, respectively. The new coupling interface $\partial \varOmega_{1}^{t + \Delta t}$ is now updated and it is the boundary of $\varOmega^{PD,t + \Delta t}$, illustrated with a black dotted line in Fig. 5b. The FEs that lie within $\varOmega^{Exp}$ are deactivated by removing their contribution from $\varvec{K}^{FE}$ and $\varvec{M}^{FE}$ and additional normal and ghost PD particles are introduced to discretize $\varOmega^{Exp}$, indicated by yellow and orange dots, respectively, in Fig. 5b.

The displacement, velocity and acceleration of the PD particles that were added in $\varOmega^{Exp}$ must be initialized. Let $n^{a}$ be the total number of the added particles. Since these particles are added ahead of the crack tip, these elements are not enriched, and the interpolation can be written as:

$$ \varvec{Y}_{k}^{a} = \mathop \sum \limits_{{{\text{i}} = 1}}^{K} N_{i} \left( {\varvec{x}_{k}^{PD} } \right)\varvec{X}_{i} ,\varvec{ }k = 1,2, \ldots n^{a} $$

(14)

where $\varvec{Y}_{k}^{a}$ and $\varvec{X}_{i}$ can be replaced by $\varvec{d}_{k}^{a} ,\dot{\varvec{d}}_{k}^{a} \varvec{ }{\text{or}} \varvec{\ddot{d}}_{k}^{a}$ and $\varvec{u}_{i} ,\dot{\varvec{u}}_{i} \varvec{ }{\text{or}}\varvec{ \ddot{u}}_{i}$ respectively.

4.2 Contraction step

The expansion and the contraction steps are independent. A trigger can also be used to activate the contraction step such as:

$$ k < k^{crit} $$

(15)

Here we define $k$ as the number of times the expansion step has been executed. By setting $k^{crit} = 1$, the contraction step is activated after each expansion step. Other definitions of the trigger for the contraction step are possible. For example, a limit can be set based on the total number of dofs in the system to keep in control the memory requirements of the solution.

During the contraction step, the area of $\varOmega^{PD}$ is limited to a certain distance from the location of the crack tip, $\varvec{x}^{tip}$. This limits the use of the PD theory and improves the computational efficiency. Similar to the expansion step, a threshold value, $l^{Con}$, is used to define the part of $\varOmega^{PD}$ that will remain unchanged (green dotted line in Fig. 5c). Just like the expansion step converts part of $\varOmega^{FE}$ into $\varOmega^{PD}$, the contraction step converts part of $\varOmega^{PD}$ into $\varOmega^{FE}$. The part of the domain that needs to be converted is defined as:

$$ \varOmega^{Con} = \left\{ {\varvec{x}^{FE} \in \varOmega^{PD} :\|\varvec{x}^{FE} - \varvec{x}^{tip}\| > l^{Con} } \right\}. $$

(16)

The particles that are inside the contracted PD domain are defined as $\varvec{x}^{PD,n} = \left\{ {\varvec{x}^{PD} \in \varOmega^{PD} \backslash \varOmega^{Con} } \right\}$. The particles that will finally remain in the subsequent steps are defined as:

$$ \varvec{x}^{PD,f} = \left\{ {\varvec{x}^{PD} :\|\varvec{x}^{PD,n} - \varvec{x}^{PD} \|< \delta } \right\} $$

(17)

i.e. $\varvec{x}^{PD,f}$ contains the particles in $\varvec{x}^{PD,n}$ and all the particles in $\varvec{x}^{PD}$ that are located within one horizon $\delta$ of the particles in $\varvec{x}^{PD,n}$. The particles in $\varvec{x}^{PD,n}$ are the new normal particles while the additional particles in $\varvec{x}^{PD,f}$ are needed to be used as ghost particles and enforce the coupling. The normal and the ghost particles are indicated with blue and grey dots in Fig. 5c. In the same figure, red circles indicate the particles that are not contained in $\varvec{x}^{PD,f}$ and that are removed from subsequent computations. The elements in $\varOmega^{Con}$ are activated again and their stiffness and mass contributions are added back to $\varvec{K}^{FE}$ and $\varvec{M}^{FE}$, respectively. Furthermore, the elements in $\varOmega^{Con}$, that are cut by the crack body, are enriched and the signed distance function $\varphi \left( {\varvec{x}^{FE} } \right)$ is updated. The enrichment is necessary since after moving the coupling interface, an additional segment of the crack body now exists in $\varOmega^{FE}$.

Since the FE nodes in $\varOmega^{Con}$ are activated, their values need to be initialized. The initialization of the values depends on whether the support of the node is cut by the crack body or not. If it is not cut, linear interpolation is implemented using the PD values that enclose the FE node. This interpolation procedure is also used in [4]. If, however, the crack intersects the nodal support, the enriched dofs must also be considered. Since the values of the enriched dofs do not have a physical meaning, their values cannot be easily related to information from the PD model. In this case, the initialization is performed in an approximate manner through least squares fitting.

Consider the isolated element in Fig. 6. Let $n_{1} = 4$ be the total FE nodal numbers and $n_{2} = 16$ the number of PD particle numbers inside the element. The FE nodes have been enriched with shifted Heaviside functions to capture the discontinuous displacement field due to the crack (red dash line). Considering the displacement field first, we write:

$$ \varvec{d}_{k} = \mathop \sum \limits_{{{\text{i}} = 1}}^{{ n_{1} }} N_{i} \left( {\varvec{x}_{k}^{PD} } \right)\varvec{u}_{i} + \mathop \sum \limits_{j = 1}^{{ n_{1} }} N_{j} \left( {\varvec{x}_{k}^{PD} } \right)\left( {H\left( {\varvec{x}_{k}^{PD} } \right) - H\left( {\varvec{x}_{j}^{FE} } \right)} \right)\varvec{a}_{j} ,\quad k = 1, \ldots ,n_{2} . $$

(18)

Fig. 6

Illustration of a FE cut by a crack and the PD particles it contains

The above expression describes an overdetermined system of Eqs. (32 equation for 16 unknowns in this example). Denoting with:

$$ \begin{aligned} & \varvec{y} = \left[ {\left( {\varvec{d}_{1} } \right)^{T} , \ldots ,\left( {\varvec{d}_{{n_{2} }} } \right)^{T} } \right]^{T} ,\quad \varvec{A} = \left[ {\begin{array}{*{20}c} {\left[ {\varvec{N}\left( {\varvec{x}_{1}^{PD} } \right)} \right]\varvec{ }\left[ {\varvec{\varPsi}^{enr} \left( {\varvec{x}_{1}^{PD} } \right)} \right]} \\ \vdots \\ {\left[ {\varvec{N}\left( {\varvec{x}_{k}^{PD} } \right)} \right]\varvec{ }\left[ {\varvec{\varPsi}^{enr} \left( {\varvec{x}_{k}^{PD} } \right)} \right]} \\ \end{array} } \right]\;{\text{and}} \\ & \quad \quad \quad \varvec{b} = \left[ {\left( {\varvec{u}_{1} } \right)^{T} , \ldots ,\left( {\varvec{u}_{{n_{1} }} } \right)^{T} ,\left( {\varvec{a}_{1} } \right)^{T} , \ldots ,\left( {\varvec{a}_{{n_{1} }} } \right)^{T} } \right]^{T} \\ \end{aligned} $$

(19)

the vector of inputs, the matrix of coefficients and the unknown vector, respectively, then:

$$ \varvec{b} = \left( {\varvec{A}^{T} \varvec{A}} \right)^{ - 1} \varvec{A}^{T} \varvec{y}. $$

(20)

Equation 20 describes the least square estimation of $\varvec{ b}$ and allows for the approximation of the enriched dofs values. For short, $\varvec{\varPsi}^{enr} \left( {\varvec{x}_{1}^{PD} } \right)$ is used to denote the second term of Eq. 18. The velocity and acceleration fields are estimated in a similar manner.

After the initialization of the FE values is completed, the PD particles that are not contained in $\varvec{x}^{PD,f}$ can be removed and the domains are updated as:

$$ \varOmega^{PD,t + \Delta t} = \varOmega^{PD,t} \backslash \varOmega^{Con} , $$

(21a)

$$ \varOmega^{FE,t + \Delta t} = \varOmega^{FE,t} \cup \varOmega^{Con} , $$

(21b)

The updated $\partial \varOmega_{1}^{t + \Delta t}$ is the boundary of $\varOmega^{PD,t + \Delta t}$ and it is indicated with a black dotted line in Fig. 5c, d. The additional FE that have been enriched due to the contraction of $\varOmega^{PD}$ are indicated in Fig. 5d with green colour. It is also possible to see in Fig. 5 that after the execution of the expansion/contraction steps, the PD domain has been displaced, following the propagation of the crack. The incorporation of the XFEM enrichment for the description of the discontinuous displacement field near the crack body alleviates the need for remeshing each time the contraction step is executed, and an additional part of the crack appears in $\varOmega^{FE}$. Still, local modification of $\varvec{K}^{FE}$ and $\varvec{M}^{FE}$ is required to account for the relocation of the two domains.

4.3 Parameter selection

The behaviour of the expansion/contraction steps depends on the definition of the parameters $l^{crit}$, $l^{Exp}$, and $l^{Con}$. These values are auxiliary and do not arise from the formulation of the problem. Nevertheless, the following observations can be made that corelate the values of these parameters. Consider the simplified illustration in Fig. 7; after the application of the contraction step, $\varOmega^{PD}$ is limited within a circle of radius $l^{Con}$, centred at the crack tip (orange circle). The crack can propagate within a distance of $l^{crit}$ of the orange circle without triggering the expansion step (green circle).

Fig. 7

Schematic illustration of the relationship between $l^{crit}$, $l^{Exp}$ and $l^{Con}$

Let the crack propagate in a straight line and trigger the expansion step. If $l^{Exp} < l^{crit}$ then then $\varOmega^{Exp}$ would be empty and no expansion occurs through Eqs. 13. Furthermore, there is a maximum value $l_{max}^{Exp} = 2l^{Con} - l^{crit}$ above which the expanded domain will cover a larger portion of the crack, compared to the initial domain. This is counterproductive for the purposes of this algorithm. Thus $l^{Exp}$ is bounded as:

$$ l^{crit} < l^{Exp} \le 2l^{Con} - l^{crit} $$

(22)

Additionally, if $l^{Exp} > l^{Con}$ then the contraction step might cancel out big portion of the expansion, if they are used in turn. Therefore, in the following paragraphs, it is selected $l^{Exp} \approx l^{Con}$ and Eq. 22 is satisfied for $l^{Con} > l^{crit}$.

A difference in the execution of the expansion and contraction steps arise based on whether a static or a dynamic problem is considered. It is noted that time integration is performed using a central difference scheme for dynamic problems while a full Newton–Raphson iterative solver is implemented for static. The implementation of both approaches is described in Part I of the current study. During a dynamic simulation, the expansion trigger is checked after each time increment to evaluate if every damaged particle is sufficiently covered. Subsequently the contraction step is used. Static simulations, however; require a different approach. When the Newton–Raphson approximation has converged for a given load increment, the expansion trigger is evaluated. If it is not satisfied, $\varOmega^{PD}$ is expanded and the same load increment is re-evaluated. This process is repeated till the expansion trigger is not tripped and the solution is accepted for this load increment. After this the contraction step can be executed. Thus, multiple expansion steps might be required for a single load increment till $\varOmega^{PD}$ is sufficiently large to facilitate the initial and the propagated crack location. This is required because the direction and the propagation length are not known and in static problems even small increases in the load step can lead to large crack extension. This feature is particularly important for unstable crack propagation. Two flowcharts that illustrate the algorithmic implementation of the adaptive relocation strategy are included in “Appendix”.

5 Brittle fracture simulation using the XFEM: PD with the adaptive relocation strategy

5.1 Static mode I propagation in a double cantilever beam

As a first example we use the problem of a mode I crack propagation in a double cantilever beam under plane stress assumptions. This example was also used in the first part of this study [6] to evaluate the size influence of $\varOmega^{PD}$ on the accuracy of the XFEM–PD model. For completeness the problem set-up is also included here. The plate is assumed linear, isotropic with Young’s modulus $E = 75 {\text{GPa}}$, Poisson’s ratio $v = 1/3$ and the critical energy release rate $G_{c} = 5 {\text{N}}/{\text{m}}$. External loads are assumed to be applied slowly so that the inertia terms can be neglected. To ensure stable crack propagation, a prescribed displacement, $\delta_{y} = 1.5 \cdot 10^{ - 3} \,{\text{mm}}$, is applied that the two clamps, illustrated in Fig. 8. The initial crack length is taken as $a = 0.3 {\text{mm}}$. Only uniform grids are considered for the discretization of $\varOmega^{PD}$ and $\varOmega^{FE}$ with $\Delta x^{PD} = \Delta y^{PD}$ and $\Delta x^{FE} = \Delta y^{FE}$, respectively.

Fig. 8

Geometry and boundary conditions of the double cantilever beam with a pre-existing crack

Since the XFEM–PD model is combined with the adaptive relocation algorithm, $\varOmega^{PD}$ can be constructed as a square with $L^{PD} = H^{PD}$. The problem geometry is illustrated schematically in Fig. 8. We employ the same parameters as in Part I with $L^{PD} = 0.15 {\text{mm}}$, $\Delta x^{PD} = 2.5 \cdot 10^{ - 3} \,{\text{mm}}$ and $\Delta x^{FE} = 10 \cdot 10^{ - 3} \,{\text{mm}}$. The micromodulus function $c\left(\varvec{\xi}\right)$ is assumed conical and the PD horizon is set to $\delta = 4\Delta x^{PD}$. Additionally, it was demonstrated in Part I [6], that the XFEM–PD model remains accurate when the crack tip is covered with PD particles by a layer of thickness $2.5\delta$. To ensure during crack propagation that this is satisfied, the parameters used for the expansion/contraction steps are $l^{crit} = 3\delta$, $l^{Exp} = 7\delta$ and $l^{Con} = 8\delta$.

In total 17,716 dofs are used after the discretization of the problem domain (9248 PD dofs and 8468 FE dofs). Although this example is simple in the sense that the crack is expected to propagate in a straight line, it is used to illustrate certain aspects of the methodology. The prescribed displacement is applied over 200 increments and the solution of the system of equations is approximated using the Newton–Raphson iterative solver. After each load increment, the expansion trigger from Eq. 10 is evaluated to determine if the crack is sufficiently covered by the PD domain. The contraction step is executed after each expansion to minimize the total number of dofs in the system.

In Fig. 9 the crack propagation using the proposed relocation strategy is presented for three different load increments. In the left column the white squares indicate the standard FEs, the yellow ones the enriched FEs and a grey line is used to indicate the location of $\partial \varOmega_{1}$. The local damage index $\phi \left( {\varvec{x}^{PD} ,t} \right),$ is plotted in the region of the PD domain to indicate the crack location. In the right column of Fig. 9, the deformed configuration is plotted near $\varOmega^{PD}$. No remeshing is required for the FE mesh and the discretization of $\varOmega^{FE}$ remains unchanged from the beginning till the end of the simulation. Meanwhile, $\varOmega^{PD}$ follows the crack propagation and relocates each time Eq. 10 is violated (see Fig. 9a, g). The crack path can be traced from the trail of enrichment functions, which gives the name Peridynamic snail to the algorithm.

Fig. 9

Left column: adaptive relocation of $\varOmega^{PD}$ and tip tracking during crack propagation at different load increments. For clarity, the local damage index is plotted in $\varOmega^{PD}$ to indicate the crack location. Right column: close up at the coupling interface indicating the PD particles and the FEs. Displacements have been magnified by a factor of 50

A load increment is also isolated before and after the application of the relocation method in Fig. 9c, f. The load increment 0.58 is initially solved with the current XFEM-PD configuration and the crack propagation is approximated. In Fig. 9c, d the current XFEM-PD configuration and a close-up near the PD domain are plotted, respectively. At the end of this solution step, some of the damaged particles due to the crack propagation violate the expansion trigger. $\varOmega^{PD}$ is expanded and load increment 0.58 is solved again. With the expanded PD domain, the expansion trigger is not activated after the crack propagation and the solution is accepted. The contraction step is subsequently used and the new XFEM-PD configuration and a close-up near the PD domain are plotted in Fig. 9e, f respectively.

The peak reaction force is $P = 20.90 \cdot 10^{ - 3} \,{\text{N}}$ and the final crack length is $a_{f} = 0.6513 {\text{mm}}$. These values are in close agreement with the results reported in Part I of this study [6]. For comparison purposes we consider 4 possible cases: in Case 1 the problem is solved using a pure PD model. In Case 2 the XFEM–PD model is used and $\varOmega^{PD}$ is constructed as such that contains both the initial and the final location of the crack tip. Cases 1 and 2 refer to the numerical models used in [6]. In Cases 3 and 4 the XFEM–PD model with the adaptive relocation strategy is used. The difference is that in Case 3, $\varOmega^{PD}$ can expand only. This can be achieved in the proposed algorithm by assigning a high value for $k^{crit}$ in Eq. 15, to recreate a similar expansion only methodology to the one used in [1] and [2]. In both Cases 3 and 4 $\varOmega^{PD}$ is initially constructed as a square with $L^{PD} = H^{PD} = 0.15 {\text{mm}}$. In all cases $\Delta x^{PD} = 2.5 \cdot 10^{ - 3} \,{\text{mm}}$ while in Cases 2, 3 and 4, $\Delta x^{FE} = 10 \cdot 10^{ - 3} \,{\text{mm}}$.

A comparison of the reaction force versus the applied displacement is plotted for each case in Fig. 10a. All cases considered produce results that are in close agreement. The introduction of a relocation strategy allows to minimize the use of the computationally expensive PD model in both Cases 3 and 4. This is possible because there is no need to pre-construct $\varOmega^{PD}$ to match the expected propagation path. The definition of $l^{crit} = 3\delta$ in the relocation process is adequate to ensure that at all time instants the crack tip is sufficiently covered within $\varOmega^{PD}$.

Fig. 10

a Comparison of the predicted reaction force for each case. b Total number of dofs. Vertical axis is plotted in logarithmic scale

In Fig. 10b, the total number of dofs used for the discretization of each case is plotted versus the applied displacement. For Cases 1 (the PD only model) and 2 (XFEM–PD with no relocation capabilities), the total number of dofs are 131,040 and 42,196, respectively, and remain constant throughout the simulation. Cases 3 and 4 have initially the same number of dofs (17,716) however, at the end of the simulation the dofs of Case 3 have increased to 35,000 while for Case 4 they are approximately the same (15,148). The variation in Case 4 is caused by the shape variation of $\varOmega^{PD}$ from the initial to the final configuration (see Fig. 9b, h).

The ability to focus the use of PD to specific locations during the evolution of the crack leads to significant computational savings. The CPU time required for each case is plotted in Fig. 11. Different values of $\Delta x^{PD}$ are considered while all other parameters are kept constant. Compared to a pure PD model, the total CPU time is reduced for all cases. When $\Delta x^{PD} = 2.5 \cdot 10^{ - 3} \,{\text{mm}}$ specifically, Cases 2, 3 and 4 accelerated the simulation by factors of $5.79,$$11.07$ and $17.4$, respectively. Despite having to manage the relocation of $\varOmega^{PD}$, both Cases 3 and 4 improve significantly the efficiency of the XFEM–PD model.

Fig. 11

Comparison of the CPU time required to solve the resulting system of equations when the PD only and the proposed approaches are used, for different $\Delta x^{PD}$

5.2 Dynamic example of a plate with a central crack

Often, it is required to address problems that contain multiple crack tips, either due to the existence of multiple edge breaking cracks (see e.g. Fig. 4) or because the crack is embedded into the body. To this end, a plate containing a central crack is considered here, to illustrate the ability of the proposed methodology to monitor and follow the evolution of multiple tips. The same example has been presented in [26] where a PD only model was implemented for the simulation of crack propagation. For comparison, the example is recreated here using the XFEM-PD model with the adaptive relocation algorithm.

The inertia forces are not neglected in this example and the plate behaves elastically with Young’s modulus $E = 192 {\text{GPa}}$, Poisson’s ratio $v = 1/3$ and density $\rho = 7850 {\text{kg}}/{\text{m}}^{3}$. Following [26], the critical bond elongation is set to $s_{0} = 0.04472$ and the plate thickness to $h = 1 \cdot 10^{ - 4} \,{\text{m}}$. The total duration of the analysis is $t_{tot} = 16.6 \cdot 10^{ - 6} {\text{s}}$ with $\Delta t = 1 \cdot 10^{ - 8} {\text{s}}$ and a prescribed velocity $v_{0} = 20\,{\text{m/s}}$ is applied at the top and bottom faces of the plate. The discretization length is set to $\Delta x^{PD} = \Delta y^{PD} = 1.02 \cdot 10^{ - 4} \,{\text{m}}$ and $\Delta x^{FE} = \Delta y^{FE} = 1 \cdot 10^{ - 3} \,{\text{m}}$ for $\varOmega^{PD}$ and $\varOmega^{FE}$, respectively. For consistency and to ensure comparability of the results obtained using the proposed approach with those reported in [26], $c\left(\varvec{\xi}\right)$ is assumed uniform and the PD horizon is set to $\delta = 3\Delta x^{PD}$. A sampling rate of 1/20 steps is used to monitor the crack location and check if expansion is required.

The tips at both ends of the crack are monitored and the PD domain relocates according to their propagation. It is of interest to ensure that only the tips are covered within $\varOmega^{PD}$ and not the whole crack. Multiple PD patches, or subdomains $\varOmega_{i}^{PD}$, can be defined depending on the number of tips. Each subdomain $\varOmega_{i}^{PD}$ can expand and contract independently. Here, the patches are square with side $0.005 {\text{m}}$, centered at the location of each crack tip and $\varOmega^{PD}$ is defined as $\varOmega^{PD} = \varOmega_{1}^{PD} \cup \varOmega_{2}^{PD}$. The geometry and loading conditions are illustrated schematically in Fig. 12. Although in this example the patch number and location were pre-defined, these patches can emanate naturally through the expansion/contraction process in more complex problems. This property is presented in the following section where the dynamic crack branching problem is considered.

Fig. 12

Schematic illustration of the plate with a central crack

The velocity fields applied on the top and bottom faces of the plate stretch the plate in the vertical direction. The cark evolution is presented in Fig. 13 at three different time instants. Each of the PD subdomains $\varOmega_{1}^{PD} {\text{and}} \varOmega_{2}^{PD}$ follow the propagation of the tip they contain and adaptively relocate when it reaches close to the coupling interface (indicated with a grey line in the same figure). The location of each tip is monitored using the tracking algorithm discussed earlier and the crack length versus time is plotted in Fig. 14 for both tips. For the material and loading parameters selected in this problem crack propagation is expected in the horizontal direction in a self-similar manner. The proposed methodology can capture the self-similar growth of the crack while relocating $\varOmega^{PD}$ during the analysis. The results are also in very good agreement with those reported by Madenci and Oterkus [26]. A difference between the results is observed at $t = 0.77 \cdot 10^{ - 5} \,{\text{s}}$. In the results reported in [26] the crack length suddenly increases while in the present study this effect was not captured. This difference could be attributed to the different way of monitoring the tip location and the sampling rate of the measurements taken. The proposed method is thus capable of monitoring multiple tips and adaptively relocate each individual subdomain contained in $\varOmega^{PD}$.

Fig. 13

Crack location at time instants $t = 0, t = 0.1041 \cdot 10^{ - 4}$ and $t = 0.1660 \cdot 10^{ - 4} {\text{s}}$. The local damage index $\phi \left( {\varvec{x},t} \right)$ is plotted to indicate the location of $\varOmega^{PD}$ and the crack

Fig. 14

Comparison of the crack propagation with the results presented by Madenci and Oterkus [26]

In the example addressed here, apart from the external loading, pulses are generated at each tip during crack growth. An interesting case arises when the $\varOmega^{PD}$ is completely embedded in $\varOmega^{FE}$ and the source lies within $\varOmega^{PD}$. In this case, the spurious reflections will be confined and will not be able to be transmitted in $\varOmega^{FE}$, leading to energy entrapment. Such an example was presented and discussed in [10]. Stress pulses originate in $\varOmega^{PD}$ due to crack extension. If the coupling between the two domains is not accurate the entrapment of the spurious reflections is pronounced and can lead to a fictitious energy build-up.

Although it is not easy to isolate these reflections, the vertical component of the velocity $v_{y}$ near the tip at the right side of the plate is plotted in Fig. 15. As the crack starts to grow pulses are generated and propagate towards the coupling interface (see Fig. 15a). At a later time instant, these pulses cross the interface and spurious reflections appear inside $\varOmega^{PD}$. These reflections can be seen near the top and bottom faces in Fig. 15b. The sudden and rapid nature of fracture excites a broad spectrum of frequencies. In $\varOmega^{PD}$ the discretization is one order of magnitude smaller than $\varOmega^{FE}$. A possible explanation for these reflections is that part of the frequency spectrum of the pulse is above the cut-off frequency of the discretized model in $\varOmega^{FE}$. As waves if these frequencies cannot enter $\varOmega^{FE}$ they become trapped in $\varOmega^{PD}$.

Fig. 15

Plots of $v_{y}$ near the right crack tip during the initial stages of the crack growth. The coupling interface is indicated with a black dashed line

The results illustrated in Fig. 14, indicate that these reflections did not affect significantly the propagation of each crack tip. Inevitably during the contraction step a region of $\varOmega^{PD}$ that contains reflections is switched to $\varOmega^{FE}$. Because of the interpolation and the least squares fitting that take place, these reflections are smoothed during the transition. It is of interest to evaluate whether significant energy is lost during the simulation because of this approximation. During crack growth, there is energy loss due to the removal of the broken bonds from the simulation. Additionally, using the current problem set-up, energy is constantly provided into the system. This complicates the evaluation of the energy loss due to the switch from PD to FEs. Thus, we modify the problem and instead of a constant velocity, a distributed load $f_{y}$ is applied at the top and bottom faces of the plate with:

$$ f_{y} = \left\{ {\begin{array}{*{20}l} {f_{max} } \hfill &\quad {t \le 6 \cdot 10^{ - 4} \,{\text{s}}} \hfill \\ 0 \hfill & \quad {\text{otherwise}} \hfill \\ \end{array} } \right., $$

(23)

where $f_{max} = 8\,{\text{kN/m}}$. All other parameters in the analysis remain the same as before apart from the total duration of the simulation that is increased to $t_{tot} = 20 \cdot 10^{ - 6} {\text{s}}$.

Using the modified loading from Eq. 23, crack propagation is again self-similar, but growth is arrested after each side of the crack has extended by $6.93 \cdot 10^{ - 3} \,{\text{m}}$. To evaluate the influence of the expansion/contraction process the analysis is conducted twice: (i) the first time the proposed methodology is implemented again with the new loading. The dimensions and the location of $\varOmega^{PD}$ is the same as illustrated in Fig. 4. (ii) The second time, the dimensions of $\varOmega^{PD}$ are selected as such that it contains both the initial and the final crack location. The initial and final configurations for each case are illustrated in Fig. 16. By comparing the total energy in each case, it is attempted to obtain an indication of the induced error because of the smoothing of the reflections during the contraction step.

Fig. 16

Initial and final configuration when a$\varOmega^{PD}$ is initially small and the expansion/contractions steps are executed for the relocations and b$\varOmega^{PD}$ is constructed as such that contain both the initial and the final location of the crack

The total energy in each case is plotted in Fig. 17. Based on the total energy in the system three distinct areas can be observed. The first is the initial stage where energy is provided into the system. At approximately $t = 0.6 \cdot 10^{ - 5} \,{\text{s}}$ crack propagation is observed, and the total energy of the system is reduced. The crack extends till $t = 1.34 \cdot 10^{ - 5} \,{\text{s}}$ when crack is arrested, and the total energy remains constant. The two cases capture the same behaviour and the computed total energy is in close agreement. Comparing the two curves the maximum value of the absolute relative error is $4.1 \cdot 10^{ - 3}$. As such, the expansion/contraction process does not lead to significant variations in the energy of the system.

Fig. 17

Comparison of the total energy computed when (1) the proposed method with the expansion/contraction steps is used and (2) when $\varOmega^{PD}$ is specifically constructed to include both the initial and the final location of the crack

5.3 Dynamic crack branching

Although the previous two examples where useful to highlight key advantages of the proposed methodology, they referred to simple mode I cases where the crack propagates in a straight line. As a final example, the case of dynamic crack branching is included. Dynamic crack branching is an open subject in fracture mechanics as no unified theory has been able to explain the phenomenon. Many researchers have simulated numerically this problem using a variety of tools to gain understanding on the fundamental mechanisms behind the branching phenomenon (see e.g. [14, 22, 27,28,29]). In the contributions by Ha and Bobaru [30] and Bobaru and Zhang [31] specifically, the application of the PD theory for the dynamic crack branching problem is discussed in detail. This problem is used here to illustrate the ability of the XFEM-PD model to adaptively relocate and follow the damage evolution when complex crack patterns emerge. It is also used to illustrate the ability of $\varOmega^{PD}$ to split into different subdomains, each following the propagation of a different crack tip, through the implementation of the expansion/contraction step.

Consider a rectangular plate with an edge-breaking pre-existing crack. The plate is made of soda-lime glass and it is assumed to behave elastically with Young’s modulus $E = 72 {\text{GPa}}$, Poisson’s ratio $v = 1/3$, density $\rho = 2440 {\text{kg}}/{\text{m}}^{3}$ and energy release rate $G_{C} = 135 {\text{N}}/{\text{mm}}$. It is also assumed that plane stress conditions apply. The initial length of the crack is $a = 0.05 {\text{m}}$ while the length and the height of the plate are $L = 0.1 {\text{m}}$ and $H = 0.04 {\text{m}}$, respectively. The geometry and loading conditions of the current set-up are illustrated schematically in Fig. 18.

Fig. 18

Schematic illustration of the problem set-up for the dynamic branching example

The example presented here is taken from [30] where $m$ and $\delta$ convergence studies were performed. Based on the numerical results in [30], it was observed that if a pressure $p = 14\,{\text{MPa}}$ is applied at the top and bottom faces of the plate, the crack will propagate initially on a horizontal line and then branch into two cracks. The final crack pattern will change depending on the value of the load applied.

The discretization length of $\varOmega^{FE}$ and $\varOmega^{PD}$ is set to $\Delta x^{FE} = \Delta y^{FE} = 7.5 \cdot 10^{ - 4} \,{\text{m}}$ and $\Delta x^{PD} = \Delta y^{PD} = 1.25 \cdot 10^{ - 4} \,{\text{m}}$ and the PD horizon selected is $\delta = 4 \Delta x^{PD}$. The discretization in $\varOmega^{PD}$ was selected is the finer case that was presented during the converge study in [30]. The total duration of the simulation is $t_{total} = 4 \cdot 10^{ - 5} \,{\text{s}}$ with time step equal to $\Delta t = 2.5 \cdot 10^{ - 8} \,{\text{s}}$. The bond constant is assumed uniform. Similar to the previous examples, $\varOmega^{PD}$ is constructed initially as a square with $L^{PD} = H^{PD} = 0.01 {\text{m}}$, centered at the location of the tip. In total $30,204$ dofs are used for the discretization of the problem, $15,488$ for $\varOmega^{PD}$ and $14,716$ for $\varOmega^{FE}$ ($14,472$ standard and 244 enriched dofs). Because the crack pattern is more complex in this example, the contraction step is executed when three expansion steps have been completed. This allows $\varOmega^{PD}$ to first follow the propagation of the crack and adapt to the complex geometry during branching and then it is contracted to reduce the total number of dofs.

The local damage index $\phi \left( {\varvec{x},t} \right)$ is plotted in Fig. 19 at $t = 0.1950 \cdot 10^{ - 4} {\text{s}}$. Although $\phi \left( {\varvec{x},t} \right)$ is not defined in classical elasticity, a zero value is used in $\varOmega^{FE}$ as it is in its pristine condition. A white and a grey solid line is used to indicate the current and the initial location of $\partial \varOmega_{1}$. The crack propagation is initially straight. However, prior to the branching the damage area becomes wider, as illustrated in Fig. 19.

Fig. 19

Surface plot of the local damage index illustrating the initial propagation of the crack

The onset of branching and the adaptive relocation of $\varOmega^{PD}$ that follows the complex pattern and eventually splits into two subdomains is illustrated in Fig. 20. It is difficult to define the exact time and location that crack branching takes place. Based on the damage plots in Fig. 20a, b an estimation between $t = 20.00 \sim 20.50\,\upmu{\text{s}}$ and $x = 6.7 \sim 6.73\,\upmu{\text{m}}$ can be made. These values are in close agreement with the results reported in [30]. Based on their results, crack branching takes place between $t = 20.50 \sim 21.50\,\upmu{\text{s}}$ and is located approximately at $x = 6.80\,\upmu{\text{m}}$. As discussed in [30], dynamic crack branching is affected by the reflections of the stress waves from the geometrical boundaries.

Fig. 20

Adaptive relocation and splitting of $\varOmega^{PD}$ during branching

Creating automatically specific patches that conform to the geometry of the branching crack can be challenging. By applying the expansion step, $\varOmega^{PD}$ can change in size and shape to follow the evolution of the damage. This can be seen in Fig. 20a, e. Since no information regarding the number and location of the crack(s) is required, this approach can accommodate such complex geometries. A restriction was applied on the contraction step to allow for a smooth transition from PD to FE near the branching site. When branching is identified, the contraction step can be executed only when the new interface will be away from that location (see Fig. 20f) as creating the coupling near the branching location can be challenging. From Fig. 20a, f it can also be seen how the initial $\varOmega^{PD}$ is split into two subdomains, each one following a crack tip. The splitting of $\varOmega^{PD}$ is better illustrated in Fig. 21 where the final configuration is plotted. Additionally, the deformed plate is plotted in Fig. 22, where the displacements have been magnified by a factor of 20. Solid green and red lines are used to indicate the main and the secondary branch of the crack, respectively.

Fig. 21

Final crack path and location of $\varOmega^{PD}$

Fig. 22

Illustration of the deformed plate at different time instants. Displacements have been magnified by a factor of 20

The final crack path that was obtained using the proposed methodology is compared with the path reported by Ha and Bobaru [30] in Fig. 23. Because the path from [30] is inferred from a figure, to improve the fidelity of the comparison the path predicted using a PD only model is also included. The parameters for the PD only model are the same as those used for $\varOmega^{PD}$ in the XFEM-PD model. In total, the PD only model requires $515,200$ dofs for the discretization of the domain. The predicted crack paths are in close agreement for all cases considered. It is possible to capture the location where the branching occurs as well as the same change of propagation angle following the branching event.

Fig. 23

Comparison of the final crack path as predicted using the proposed method, a PD only model and the results presented in [30]

The maximum theoretically attainable crack propagation speed is the Rayleigh wave speed $c_{R}$. Numerous experimental observations suggest that the propagation speed is limited in the region of $0.4 \sim 0.7c_{R}$ [32, 33]. When the propagation speed reaches this value, branching typically occurs. The crack propagation speed computed using the proposed method is plotted in Fig. 24. In the same figure the propagation speed for the same discretization parameters from [30] is included. In soda lime glass, terminal velocities between $1460\sim 1600 {\text{m}}/{\text{s}}$ have been reported by various experimental investigations [34]. For consistency, the max propagation speed of $v_{c} = 1580 {\text{m}}/{\text{s}}$ is indicated in Fig. 24, as this value was used in [30] for the purposes of the comparison. The results from the proposed method follow the same trend as those reported in the literature. The propagation speed approaches $v_{c}$ prior to crack branching at approximately $t = 1.92 \cdot 10^{ - 5} {\text{s}}$, followed by a reduction in the propagation speed. Additionally, the same fluctuations in speed are observed that are similar to the observations presented in [30]. As discussed in [30] and [31], these fluctuations can be correlated to the concertation or dispersion of the stress waves that reflect from the boundaries. It is evident that although the trend is followed between the two curves, the curve of the present model is shifted slightly to the left. This is also collaborated by the fact that in our simulations the branching event took place earlier. Small differences in the results were expected because when the proposed method is used, the loading and the geometrical boundaries are defined on $\varOmega^{FE}$. Furthermore, use of classical elasticity to model the bulk of the material induces differences in the wave propagation characteristics. Nevertheless, the when the XFEM-PD model is used with the adaptive relocation algorithm to recreate the problem, the results are comparable with those obtained using a PD only solution.

Fig. 24

Comparison of the crack propagation speed observed when the proposed method is implemented compared to Ha and Bobaru [30]. The maximum crack speed that was observed during experimental studies is indicated with a grey line

6 Conclusions and future work

In this study, an adaptive relocation strategy for the XFEM–PD model is developed proposed that allows to automatically redefine the areas where each model is used during the evolution of damage. The relocation of $\varOmega^{PD}$ is realized through the sequential execution of expansion and contraction steps that signify the switch from FE nodes to PD particles and from PD particles to FE nodes. A series of static and dynamic examples were presented to illustrate the performance of the methodology.

The key advantages and observations behind the proposed approach are:

• I. A PD patch is employed around the crack tip. The PD patch covers sufficiently the vicinity of the crack tip but remains always as small as possible to avoid excessive computational cost.

• II. Since the crack body away from the tip remains in the domain where classical continuum elasticity is used, treatment of the discontinuous displacement field is required. Heaviside functions are used to enrich the basis functions of the finite elements that are cut by the crack. Crack tip enrichment based on solutions from linear elastic fracture mechanics to capture the stress state near the tip is not required since this part is handled by the PD theory. Incorporation of XFEM enrichment in $\varOmega^{FE}$ allows to avoid remeshing during the relocation.

• III. The existence of single and multiple crack tip(s) is allowed only in $\varOmega^{PD}$. If a crack propagates the PD patch will also follow the propagation and the crack is free to propagate anywhere in the problem domain regardless of the initial position of $\varOmega^{PD}$. The crack propagation length and direction are captured by the PD model and knowledge of the final crack path is not required.

• IV. Limiting the area where the PD theory is applied can lead to improvement of the overall computational cost of the solution. The numerical results presented here indicate significant savings in terms of memory requirements and CPU time.

• V. The expansion/contraction procedure allows to first capture the crack pattern and then relocate as necessary, with the ability of splitting in case the initial crack branches. Furthermore, in static problems that the final crack length is not known, the expansion step can be repeated as many times as necessary till convergence is achieved.

• VI. Switching to a nonlocal model near the crack tip introduces an internal length scale to the simulation. The microstructure of the material incorporated in the model, aiming at true multiscale simulations.

The use of the Bond-Based Peridynamic theory implies the restriction on the Poisson’s ratio and limits the applicability of the current methodology. In the future, coupling of the State-Based Peridynamic theory with classical elasticity could be explored to circumvent this limitation. Such coupling approaches have been proposed recently in the literature. Without being exhaustive, the interested reader is referred to [35,36,37] and the references therein. Additionally, the crack tracking algorithm presented here is simplistic, and although accurate for the applications considered here, false front identification, due to inaccuracies of the herein proposed algorithm, could lead to improper relocation of $\varOmega^{PD}$ and induce errors in the definition of the Heaviside functions, impairing significantly the accuracy of the results. The considerable reduction of dofs is significant for extensions to 3D applications where the computational cost of full PD models can be restrictive. For such extensions however a robust crack font tracking method is necessary to allow the implementation of the coupled XFEM-PD model. This will allow the extension of the methodology presented here to 3D problems. It is also expected that the selection of appropriate indicators and norms and the use of e.g. a posteriori error estimates will enhance the performance of the relocation strategy. The aforementioned points can be the subject of a future study.

The algorithmic realization of the expansion and contraction steps requires the execution of multiple conditional and looping statements. The extension, scalability and efficiency of such algorithm to a highly parallelized platform is not straightforward. For example, Mossaiby et al. [38] demonstrate significant computational gains through the execution of PD algorithms using graphics processing units (GPUs). The performance of the methodology on such platforms needs to be studied. On the other hand, GPUs are usually limited in terms of available memory. Thus, methodologies like the one presented here, capable of reducing significantly the total number of dofs, can be very appealing.

Appendix: Flowcharts for the algorithmic implementation of the adaptive relocation strategy

In this Appendix two flowcharts are presented to illustrate the algorithmic implementation of the adaptive relocation strategy. The steps for the execution of the expansion and the contraction steps are illustrated first in Fig. 25. The difference in the implementation of the relocation strategy in static and dynamic problems is then depicted in Fig. 26.

Fig. 25

Flowcharts for the expansion and contraction steps

Fig. 26

Overview of the algorithmic implementation of the expansion/contraction steps in static and dynamic problems