Introduction

Silicon and oxygen are considered major impurities present in Earth’s iron-nickel core as a consequence of metal-silicate partitioning during core formation (Wade and Wood 2005; Rubie et al. 2011; Siebert et al. 2013). However, suggested concentrations of Si and O from element partitioning in the magma ocean vary among studies: 5-7 wt% Si + 0 wt% O (Wade and Wood 2005), 8 wt% Si + 0.5 wt% O (Rubie et al. 2011), and 1.5–2.2 wt% Si + 4.5–5.5 wt% O (Siebert et al. 2013). The validity of a hypothetical Si- and O-bearing iron core can be tested by comparing its predicted physical properties with seismologically constrained parameters which include the seismic P-wave velocity (Vp) and density. For a liquid core, the Vp and density can be calculated from a thermodynamic potential such as the Gibbs free energy as a function of pressure (P), temperature (T), and composition (e.g., Komabayashi 2014).

While thermodynamic models including mixing property of liquids were established for the system Fe–FeO under core P–T conditions (Frost et al. 2010; Komabayashi 2014), a self-consistent thermodynamic model for the system Fe–(Fe)Si which can be applicable to Earth’s core has yet to be constructed although the system has extensively been studied by both experiment and first-principles calculation (Alfe et al. 2002; Dobson et al. 2002; Lin et al. 2002; Kuwayama and Hirose 2004; Tateno et al. 2015; Ozawa et al. 2016; Komabayashi et al. 2019). A thermodynamic model for the system Fe–Si needs to address mixing property of Fe and Si in iron phases, since these phases form solutions and their nonideality affects the P–T locations of chemical reactions involving them. The thermodynamic model established at 1 bar in metallurgy indicates that the body-centred cubic (bcc), face-centred cubic (fcc), and liquid phases show strong negative nonideality which stabilizes them more than what expected from ideal mixing (e.g., Kanibolotsky et al. 2003; Ohnuma et al. 2012). Although Huang et al. (2019) reported that the mixing of Fe, Si, and O in liquids under core pressures would be ideal from the first-principles calculations, the evolution of the mixing properties with increasing pressure and temperature needs to be evaluated from experimental data.

Another important part of thermodynamic modelling of the system Fe–Si is inclusion of melting relations. The width of the melting loops of iron phases was studied by both experiment and theory because it is the key to understanding the Si partitioning between the solid inner core and liquid outer core when the inner core crystallises (Kuwayama and Hirose 2004; Ozawa et al. 2016; Alfe et al. 2002). At 1 bar the width of the melting phase loop for the bcc phase is as narrow as 2 wt%Si for Fe-5 wt%Si (Kubaschewski 1993). Kuwayama and Hirose (2004) from high-pressure experiments in a multianvil apparatus suggested that the width of the melting loop for the fcc phase would be less than 2 wt%Si at 21 GPa. Recently Ozawa et al. (2016) demonstrated from a DAC experiment that the fcc melting loop was as narrow as less than 1 wt%Si at 58 GPa. Alfe et al. (2002) reported by first-principles calculation that silicon is almost equally partitioned between hexagonal close-packed (hcp) iron and liquid at 370 GPa. As such the width of melting loop of the iron phases seems to become narrower with increasing pressure from 1 bar to over 3 Mbar. However, those studies at pressures greater than 21 GPa only determined the solid–liquid partitioning of silicon and the melting/crystallising point for Fe–Si alloy was not determined (Ozawa et al. 2016; Alfe et al. 2002). The crystallising (i.e., liquidus) temperature of a Si-bearing iron system is important for constraining the temperature at the inner core-outer core boundary (ICB, at 330 GPa).

In this study, the mixing properties of Si-bearing iron phases are first examined by thermodynamic calculation of a phase transition loop. Komabayashi et al. (2019) constrained the width of the transition between fcc and hcp structures in Fe-4wt%Si to 71 GPa and 2000 K in an internally resistive-heated diamond anvil cell (DAC) which enabled very precise measurements (Fig. 1). Then I extend the thermodynamic modelling to higher temperature to calculate the melting point under high pressure. By reproducing the reported Si partitioning data, I place constraints on the crystallising points of Si-bearing iron liquids to the inner core pressures. From the constrained melting temperatures over a wide pressure range, I evaluate a thermal equation of state (EoS) of an Fe–Si liquid. Then, combining Komabayashi (2014)’s model for the system Fe–FeO with the results of this study, I address the nature of Fe-rich liquids in the system Fe–Si–O; I calculate the density and Vp of liquids in the ternary system over the outer core pressure range and discuss the likely amounts of Si and O in Earth’s outer core. I then calculate the density of the solid iron phase precipitating from the determined outer core composition. From these calculations, I finally discuss whether or not the system Fe–Si–O can represent Earth’s core.

Fig. 1
figure 1

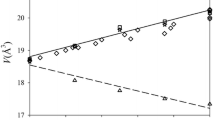
Calculated fcc–hcp transition boundaries for Fe-4 wt%Si with the ideal mixing model (red line) and nonideal mixing model (blue dashed line). Experimental results with in situ X-ray diffraction in an internally resistive-heated DAC are also plotted: inversed triangle, hcp + bcc; square, hcp; normal triangle, fcc + hcp; circle, fcc (Komabayashi et al. 2019). The black line is an experimentally constrained fcc–hcp transition boundary in pure iron (Komabayashi et al. 2009). The typical experimental uncertainty in temperature is 50 K while the data with asterisk have larger uncertainty of about 100 K

Full size image

Method

To develop thermodynamic models for the fcc–hcp transitions and melting curve in the system Fe–Si, I followed the approach in metallurgy to modelling the Gibbs free energy (chemical potential) curves of Fe phases (e.g., hcp) as a function of the Si content; they were modelled between pure Fe and pure Si with the same structures. The thermodynamic properties of hypothetical fcc and hcp Si at 1 bar were reported by the metallurgy literature (e.g., Dinsdale 1991) and their mixing properties were also available (e.g., Ohnuma et al. 2012). In the system Fe–Si, intermediate phases such as FeSi are stable depending on the P–T condition, but those phases do not form a solid solution with the Fe phase as they have different structures. Instead, one can model the chemical potential curve of the Fe solid solution between Fe and hypothetical Si with the hcp structure; this does not violate the laws of thermodynamics as the chemical potentials of the (sub)system Fe–FeSi are properly buffered by Fe and FeSi phases when they have a common tangent in the potential-composition diagram. This is the most reasonable and practical approach as this provides the largest applicable range to the solid solution. For instance, when different intermediate phases become stable at different P–T conditions, one would have to keep redefining their new end-members if one has to model the system with those intermediate phases, which is not sensible at all as this will likely introduce inconsistent behaviour of the system on a phase change. Indeed, the approach taken in this study was also adopted in Mineral Physics as well (Fei and Brosh 2014; Saxena and Eriksson 2015).

A phase transition in a binary system at constant pressure can be modelled with simultaneous equations (e.g., Cemič 2005):

$$\ln \left( {\frac{{a_{\text{Fe}}^{\text{fcc}} }}{{a_{\text{Fe}}^{\text{hcp}} }}} \right) = \frac{{\Delta S_{\text{Fe}}^{{{\text{fcc}} - {\text{hcp}}}} }}{R}\left( {1 - \frac{{T_{\text{Fe}}^{{{\text{fcc}} - {\text{hcp}}}} }}{T}} \right)$$
(1)
$$\ln \left( {\frac{{a_{\text{Si}}^{\text{fcc}} }}{{a_{\text{Si}}^{\text{hcp}} }}} \right) = \frac{{\Delta S_{\text{Si}}^{{{\text{fcc}} - {\text{hcp}}}} }}{R}\left( {1 - \frac{{T_{\text{Si}}^{{{\text{fcc}} - {\text{hcp}}}} }}{T}} \right)$$
(2)

where R is the gas constant, and for instance, \(a_{\text{Fe}}^{\text{fcc}}\) is the activity of Fe in the fcc phase, \(\Delta S_{\text{Fe}}^{{{\text{fcc}} - {\text{hcp}}}}\) is the entropy change upon the fcc–hcp transition for the Fe end-member, \(T_{\text{Fe}}^{{{\text{fcc}} - {\text{hcp}}}}\) is the transition temperature for the Fe end-member. The parameters for the Fe end-member were from an experimental determination of the fcc–hcp transition (Komabayashi et al. 2009) and a thermodynamic model (Komabayashi 2014). For the hypothetical Si end-member phases with the fcc and hcp structures, the database for 1 bar by Dinsdale (1991) was adopted. The value for \(\Delta S_{\text{Si}}^{{{\text{fcc}} - {\text{hc}}p}}\) was assumed to be constant over the P–T range studied here, which is a reasonable assumption for a solid–solid phase transition when the detailed thermodynamic data is not available.

The activity is described as:

$$a = \, \gamma X$$
(3)

where γ is the activity coefficient and X is the mole fraction of a component. I employed ideal mixing (γ = 1) and nonideal mixing for the fcc–hcp transitions. The Gibbs free energy of a nonideal solution (Gm) is expressed as (Guggenheim 1937; Redlich and Kister 1948; Ohnuma et al. 2012):

$$G_{\text{m}} = {}^{ \circ }G_{\text{Fe}} *X_{\text{Fe}} + {}^{ \circ }G_{\text{Si}} *X_{\text{Si}} + {\text{RT}}\left( {X_{\text{Fe}} \ln X_{\text{Fe}} + X_{\text{Si}} \ln X_{\text{Si}} } \right) + X_{\text{Fe}} X_{\text{Si}} *L_{\text{Fe,Si}}$$
(4)

where \({}^{ \circ }G_{\text{Fe}}\) and \({}^{ \circ }G_{\text{Si}}\) are the Gibbs energies of the end-member pure phases, \(L_{\text{Fe,Si}}\) represents the interaction parameters which is based on a power series representation:

$$L_{\text{Fe,Si}} = \sum\limits_{n} {\left( {X_{\text{Fe}} - X_{\text{Si}} } \right)}^{n} *{}^{{^{n} }}L_{\text{Fe,Si}}$$
(5)

Equations (4) and (5) yield,

$${\text{RT}}\ln \gamma_{\text{Fe}} = X_{\text{Si}}^{2} \left\lfloor {{}^{0}L_{\text{Fe,Si}} + {}^{1}L_{\text{Fe,Si}} \left( {3 - 4X_{\text{Si}} } \right) + {}^{2}L_{\text{Fe,Si}} \left( {1 - 2X_{\text{Si}} } \right)\left( {5 - 6X_{\text{Si}} } \right)} \right\rfloor$$
(6)
$${\text{RT}}\ln \gamma_{\text{Si}} = \left( {1 - X_{\text{Si}} } \right)^{2} \left\lfloor {{}^{0}L_{\text{Fe,Si}} + {}^{1}L_{\text{Fe,Si}} \left( {1 - 4X_{\text{Si}} } \right) + {}^{2}L_{\text{Fe,Si}}\left( {2X_{\text{Si}} - 1} \right)\left( {6X_{\text{Si}} - 1} \right)} \right\rfloor$$
(7)

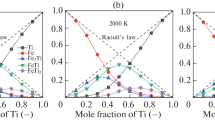
See Cemič (2005, pp. 194–195) for the details of the derivation of the above equations. In the present calculations, Eqs. (6) and (7) were used to obtain γ and (4) and (5) were not directly used. We adopted an activity model for the fcc phase at 1 bar in the system Fe–Si (Ohnuma et al. 2012). As there is no mixing model for the hcp phase available, I assumed the same activity model for the fcc and hcp phases as they have similar stacking structures.

Results

Fcc–hcp transition in Fe-4wt%Si

Figure 1 shows calculated phase boundaries for the fcc–hcp transitions in Fe-4wt%Si. With all the parameters for Fe well-constrained (Komabayashi 2014), the calculated dP/dT slope of the fcc–hcp transition depends on (i) \(T_{\text{Si}}^{{{\text{fcc}} - {\text{hcp}}}}\) and its pressure dependence and (ii) mixing properties of the phases. For (i), the value at 1 bar (Dinsdale 1991) was adopted and its pressure dependence was assessed in this study so that the calculation reproduces the experimental data (Komabayashi et al. 2019) (Fig. 1). For (ii), I tested two mixing models for the phases: (a) nonideal mixing and (b) ideal mixing. For (a), Ohnuma et al. (2012) proposed a sub-regular solution model for the fcc phase at 1 bar. Their mixing model was used to calculate the fcc–hcp transition boundaries assuming no pressure and temperature dependence on the interaction parameters. As mentioned above, the same interaction parameters were employed for the fcc and hcp phases. The used parameters are listed in Table 1. Note that Asanuma et al. (2008) earlier reported fcc–hcp transition boundaries in Fe-3.4 wt%Si using a laser-heated DAC, and found a much wider fcc + hcp coexistence region than in Komabayashi et al. (2019) under the same P–T conditions. In addition, the fcc-in boundary in Asanuma et al. (2008) was located at temperatures lower than the pure Fe boundary. As was extensively discussed in Komabayashi et al. (2019), the appearance of fcc peaks in X-ray diffraction patterns was not clearly recognized in Asanuma et al. (2008). The results of Komabayashi et al. (2019) on the P–T location of the fcc–hcp boundaries are consistent with more recent works by Fischer et al. (2013) and Tateno et al. (2015).

Table 1 Thermodynamic parameters used in the calculations
Full size table

The calculated transition boundaries with the nonideal mixing model yielded a slightly narrower phase loop than with the ideal mixing model under high pressures (Fig. 1). Figure 2 shows misfits of calculated transition temperatures to experimental data. The experimental data points in the 1st run are at much (a few 10 K) higher temperatures than the equilibrium reactions lines, namely they lie well within the fcc stability field. In the experiment by Komabayashi et al. (2019), the sample was directly heated from 300 K to the fcc stability field at 1050–1060 K, and therefore the equilibrium point was not bracketed. On the 3rd run, the misfits of the fcc-in data point are as large as 160–180 K because of larger experimental uncertainties in temperature (Komabayashi et al. 2019) (Fig. 2). Those data points were not considered when I fitted the thermodynamic parameters simply due to the larger experimental uncertainty. Except for those data points in the 1st and 3rd runs, the transition temperatures were reasonably reproduced by both ideal and nonideal mixing models (Fig. 2). Note that the experimental data in Figs. 1 and 2 are of the greatest precision in temperature (50 K) for a diamond anvil cell experiment at temperatures greater than 1400 K (i.e., temperatures are measured with the spectroscopic method) as it was conducted in the internally-resistive heating system.

Fig. 2
figure 2

Misfits of calculated transition temperatures to experimental data on the fcc–hcp transition boundaries (Komabayashi et al. 2019). Typical temperature uncertainties (50 K) are shown as the green band. The error bar attached to each data point denotes the range of bracketing equilibrium point. In the 1st run, the fcc-in reaction was not constrained and the hcp-out reaction might have been overshot in the experiment (Komabayashi et al. 2019). For the fcc-in data in the 3rd run (asterisk) were with a larger temperature uncertainty and not considered when evaluating the thermodynamics of the boundaries in this study

Full size image

The above analysis demonstrates that the ideal mixing model can be applied to the hcp and fcc phases under high pressures as well as the nonideal model. As the nonideal mixing model was established at 1 bar and can be used up to 3500 K (Ohnuma et al. 2012), I will use the ideal mixing model for the phases in the following calculations under core P–T conditions.

Melting of Si-bearing fcc and hcp Fe phases under high pressure

The melting temperature of a Si-bearing iron phase (fcc or hcp) was not measured at pressures greater than 21 GPa (Kuwayama and Hirose 2004), although high-pressure experiments observed melting of the B2 phase or eutectic of Fe + B2 in the system Fe–(Ni)–Si at the Si-rich side (Si > 10 wt%) (Asanuma et al. 2010; Morard et al. 2011; Fischer et al. 2013; Lord et al. 2014). Here I estimated the melting temperatures of Si-bearing fcc and hcp phases through calculations of the melting phase loops. An experimental study reported narrow melting loops, < 1 wt%Si, at about 60 GPa (Ozawa et al. 2016) and a theoretical study (Alfe et al. 2002) predicted a much narrower loop in that Si is almost equally partitioned between solid and liquid at 370 GPa. I calculated the melting loops using Eqs. (1) and (2) adopting ideal mixing as discussed above so that the loops reproduce those Si partitioning data. Indeed, Alfe et al. (2002) discussed that the deviation from ideal mixing is weak at low Si content.

The parameters for pure Fe melting were from Komabayashi (2014). The entropy changes upon melting for the end-member Si (\(\Delta S_{\text{Si}}^{\text{melting}}\)) with the fcc and hcp structures at 1 bar were obtained from Dinsdale (1991) and I applied them to high-pressure melting at 60 (fcc) and 330 (hcp) GPa. The constant \(\Delta S_{\text{Si}}^{\text{melting}}\) without a phase change is supported by Richard’s rule (a constant entropy change on melting for metals on the order of the gas constant) (e.g., Tiwari 1978). The end-member melting temperatures for Si (\(T_{\text{Si}}^{\text{melting}}\)) under high pressures were considered as follows. The ∆Smelting for both end-members are as large as 7–10 J/K/mol (cf. \(\Delta S_{\text{Fe}}^{{{\text{fcc}} - {\text{hcp}}}}\) = 3 J/K/mol at 60 GPa) (Table 1). Yamasaki and Banno (1972) analysed effects of ∆S for the end-members on the shape of a two-phase loop in a binary system (Fig. 3). Assuming both phases are ideal solutions, when ∆S is large for both end-members, a phase transition loop would be wide, depending on the difference in transition temperature between the end-members, i.e., \(\Delta T_{\text{Fe - Si}}^{\text{melting}}\) for the present discussion (Fig. 3). As such \(\Delta T_{\text{Fe - Si}}^{\text{melting}}\) needs to be small in order to account for the reported narrow melting loops. Since \(T_{\text{Fe}}^{\text{melting}}\) was rather well constrained by the thermodynamic database (Komabayashi 2014), the width of the calculated melting loop can be narrowed to fit the reported Si partitioning data only if \(T_{\text{Si}}^{\text{melting}}\) is close to \(T_{\text{Fe}}^{\text{melting}}\).

Fig. 3
figure 3

Variation in the shape of a two-phase loop in the binary system AB as a function of ∆SA and ∆SB (after Yamasaki and Banno 1972). Ideal mixing is assumed. When both ∆S are large, the loop is wide, unless ∆T is small

Full size image

When the melting phase loop was calculated to match the data by Ozawa et al. (2016) at 60 GPa, \(T_{\text{Si}}^{\text{melting}}\) needed to be 2600 K (Fig. 4a) which is only 300 K lower than \(T_{\text{Fe}}^{\text{melting}}\) = 2910 K. Alfe et al. (2002) concluded that Si is almost equally partitioned between solid and liquid to 20 mol%Si (11 wt%Si) at 7000 K and 370 GPa. Assuming an ideal solution for both liquid and solid, an equal partitioning of Si between solid and liquid implies composition-independent melting, which is expressed as a single horizontal line in Fig. 4b (green line). To investigate the sensitivity of the width of the phase loop to \(T_{\text{Si}}^{\text{melting}}\) and to provide a guide for future experiments, I calculated the melting loops at 330 GPa assuming a minimum fractionation detectable by experiment (ca. ± 0.3 wt%Si at Fe–6 wt%Si) (Fig. 4b, black line). The results showed that \(T_{\text{Si}}^{\text{melting}}\) was between 6100 and 6660 K when \(T_{\text{Fe}}^{\text{melting}}\) was 6380 K. As such, the small fractionation of Si would hardly change the liquidus temperature and the melting temperature in the Fe-rich region of the phase diagram may be essentially composition independent. Note that here I only discussed the melting temperatures of the Fe–Si hcp phases at 330 GPa and the eutectic relations shown in Fig. 4b needs to be examined by experiment and first-principles calculation because there are no reports of direct measurements. In particular, the eutectic compositions were assumed to be about Fe-6 wt%Si from the only experimental constraint of a subsolidus reaction between hcp and hcp + B2 occurring at 4750 K at 330 GPa for Fe-9 wt%Si (Tateno et al. 2015). The parameters used in the calculations are listed in Table 1.

Fig. 4
figure 4

Calculated melting loops of a the fcc and b hcp phases at 60 and 330 GPa respectively, with ideal mixing assumed between Fe and Si. The green lines were obtained so that the calculations reproduce the reported Si partitioning data (Ozawa et al. 2016; Alfe et al. 2002). At both pressure conditions, inferred eutectic relations were also drawn. The used parameters are listed in Table 1. In a, Si partitioning data between the liquid and B2 phases are also plotted (Ozawa et al. 2016). In b, the hcp melting line in green corresponds to the equal Si partitioning (Alfe et al. 2002). The black lines represent the present calculations assuming a small, i.e., experimentally detectable fractionation of Si (ca. ± 0.3 wt%Si at Fe-6 wt%Si), resulting in \(T_{\text{Si}}^{\text{melting}}\) = 6100 and 6660 K when \(T_{\text{Fe}}^{\text{melting}}\) was 6380 K. The melting temperatures of the Fe–Si hcp phases are only discussed in b and the eutectic compositions at about 6 wt %Si were tentatively assumed based on the subsolidus phase relations (Tateno et al. 2015)

Full size image

For 1–8 wt%Si-bearing iron systems, which span the proposed values for the Si content in Earth’s core (Wade and Wood 2005; Antonangeli et al. 2010; Rubie et al. 2011; Badro et al. 2015; Antonangeli et al. 2018), the expected change of liquidus temperature of Fe due to Si is about − 50 K at 60 GPa and about 0 K at 330 GPa (Fig. 4). This suggests that the addition of Si to Earth’s core would not significantly affect the temperature at the ICB where the inner core is believed to be crystallised from the outer core.

Discussions

Phase diagram and liquid EoS of Fe-4 wt%Si

Figure 5 shows a phase diagram of Fe-4 wt%Si to the ICB condition. As discussed above the width of the melting loop is very narrow above 60 GPa and I will not distinguish liquidus and solidus in the following discussions. The difference in melting point between the alloy and pure Fe is very small at 60 GPa and diminishes with increasing pressure, which places tight constraints on the P–T location of the melting curves of Fe-4 wt%Si from 60 to 360 GPa.

Fig. 5
figure 5

A phase diagram for Fe-4 wt%Si in comparison to that of pure iron (Komabayashi 2014). The fcc–hcp transition boundaries and melting curve of the hcp phase were calculated with ideal mixing of Fe and Si, while the other boundaries including the melting curve of the fcc phase were schematically drawn. The melting curves of the fcc and hcp phases are compared with of pure Fe (Komabayashi 2014), namely, 20 K lower than pure iron at 60 GPa and the same as for iron above 90 GPa. Pure iron melting data by experiment are plotted (Anzellini et al. 2013; Jackson et al. 2013; Sinmyo et al. 2019)

Full size image

A melting curve constrained over a wide P–T range can be used to deduce a thermal EoS for the liquid phase when the other thermodynamic parameters are available including the EoS of the subsolidus crystalline phase (Komabayashi 2014). A high-pressure phase equilibrium relation can be calculated based on the Gibbs free energy of phases as a function of P and T. The Gibbs free energy of a phase at a given P–T condition is expressed as:

$$G = G_{{ 1 {\text{bar, }}T}} + \int_{{1{\text{bar}}}}^{P} {V_{{^{T} }} {\text{d}}P}$$
(8)

where G1bar, T is the Gibbs free energy at 1 bar and T of interest and VT is the molar volume at T. The volumetric term in Eq. (8) is calculated from a P–V–T EoS of the phase. In this study, the room-temperature volume is expressed with the Vinet EoS as:

$$P_{298} = 3K_{0} x^{ - 2} (1 - x)\exp \left[ {\frac{3}{2}(K' - 1)*(1 - x)} \right]$$
(9)

where x ≡ (V/V0)1/3 and, P298, K0, K′, and V0 are the pressure at 298 K, the isothermal bulk modulus, its pressure derivative, and the molar volume at the reference P–T conditions of 1 bar and 298 K, respectively.

The thermal expansion of a phase under high pressure was formulated using the Anderson–Grüneisen parameter, δT (Anderson et al. 1992):

$$\frac{\partial \ln \alpha }{\partial \ln V} = \, \delta_{\text{T}} = \, \delta_{0} \eta^{\kappa }$$
(10)

where η ≡ V/V0, δ0 is the value of δT at 1 bar and κ is a dimensionless parameter. This equation yields:

$$\frac{\alpha }{{\alpha_{0} }} = \exp \left[ { - \frac{{\delta_{0} }}{\kappa }\left( {1 - \eta^{\kappa } } \right)} \right]$$
(11)

where α0 is the thermal expansivity at 1 bar.

G1bar, T was obtained from ideal mixing of the end-member phases (Komabayashi 2014; Dinsdale 1991) (Table 2). The EoS parameters for the Fe-4 wt%Si hcp phase were evaluated in Komabayashi et al. (2019) based on the parameters of the pure Fe (Dewaele et al. 2006) and of Fe-9 wt%Si (Tateno et al. 2015). I have evaluated the EoS parameters for the Fe-4 wt%Si liquid phase by calculating the melting curve which reproduces that of the pure Fe hcp phase at 100–350 GPa (Komabayashi 2014). The obtained parameters are listed in Table 3.

Table 2 Gibbs energies of pure phases (°G) at 1 bar, T (J·mol−1) = a + bT + cTlnT + dT2 + eT−1 + fT0.5 + gT−9
Full size table
Table 3 Thermophysical parameters in the Vinet–Anderson–Grüneisen equation
Full size table

The melting of the Fe-4 wt%Si hcp phase at the ICB is accompanied with a volume change of 1.6%, which is slightly smaller than the case of pure Fe of 2.0%. Selected thermodynamic properties for the hcp and liquid phases of Fe-4 wt%Si are presented in Table S1.

The derivation of the EoS of the Fe–Si liquid phase presented above depends on the choice of melting curves of iron. The high-pressure melting curve of iron used in this study was from Komabayashi (2014) which is consistent with experimental data of Anzellini et al. (2013) and Jackson et al. (2013). Very recently a new melting curve of iron was proposed by Sinmyo et al. (2019) on the basis of high-P–T experiment. Those high-pressure melting data by experiment are shown in Fig. 5 for comparison. Sinmyo et al. (2019)’s melting points are systematically lower than Anzellini et al. (2013)’s data. If one models an EoS for liquid iron using Sinmyo et al. (2019)’s melting curve, its resulting density will be greater than the case of Komabayashi (2014)’s melting curve. However incorporation of the new data into the thermodynamic model needs very careful treatment as the model by Komabayashi (2014) is consistent with many different types of measurements. For example, Komabayashi (2014)’s database, starting with the 1 bar metallurgy data, is consistent with phase relations in the system Fe–FeO determined in multianvil apparatus (e.g., Tsuno et al. 2007) and melting points of fcc iron (Jackson et al. 2013) and of hcp iron (Anzellini et al. 2013) determined in DACs. Also, the eutectic melting relationships of Fe–FeO at high pressures calculated by Komabayashi (2014) using Frost et al. (2010)’s mixing model were recently confirmed by a DAC experiment by Oka et al. (2019). In addition, the entropy change on melting of iron in Komabayashi (2014) follows Richard’s rule along the melting curve. As such the phase relations calculated by Komabayashi (2014) are consistent with many experimental data using the DAC and multianvil, and of 1 bar measurements. Furthermore, the validity of his EoS for liquid iron was confirmed by the first-principles calculation to 2 terapascals and 10,000 K (Wagle and Steinle-Neumann 2019 and reference therein). As such, the Fe database of Komabayashi (2014) has been tested and validated. The newly proposed melting curve of iron by Sinmyo et al. (2019) will have to be tested by comparing with those different types of measurements in the future.

Liquids in the system Fe–Si–O and silicon and oxygen in the core

Silicon and oxygen are considered to be major light elements in the core as a consequence of metal-silicate partitioning in the magma ocean during core formation. Although the seismic velocity and density of Si- and O-bearing Fe liquids were examined and possible ranges for their amounts in the core were proposed by first-principles calculation (Badro et al. 2014), there is no such a model reported from experimental data sources. Here I predict the nature of Si- and O-bearing outer cores from the thermodynamic models of Fe–FeO (Komabayashi 2014) and Fe–Si (this study) which are based on experimental data.

Komabayashi (2014) discussed that the liquids of the system Fe and FeO can be modelled with ideal mixing of the end-member liquids under core P–T conditions. This study has shown that mixing of Fe and Si liquids can be represented by ideal mixing as well. I therefore assume that mixing of Fe, FeO, and Si liquids would be ideal mixing under core P–T conditions. This enables us to compare the physical properties of iron liquids and resulting core composition with those by theory (Badro et al. 2014) which placed the same assumption on the ideality of mixing liquids in the system Fe–Si–O for Earth’s core. A more recent theoretical work reported that Fe-rich liquids in the same ternary system would indeed behave as ideal solutions under core conditions (Huang et al. 2019). As Komabayashi (2014) demonstrated, the ideality of liquids can be tested by comparing calculated phase relations with experimental data, such as eutectic temperature, which should be made in the near future. Below I discuss the isentrope, density, and Vp of hypothetical outer cores in the systems Fe–Si and Fe–Si–O.

Figure 6 shows isentropes of the outer cores with compositions of Fe (Komabayashi 2014), Fe-5.9 wt%O (Komabayashi 2014), Fe-4 wt%Si (this study), and Fe-5.8 wt%Si–0.8 wt%O (this study, see below). Each isentrope starts at the liquidus temperature of the respective composition at the ICB. I assume the liquidus temperature of the system Fe–Si–O is the same as of Fe–FeO since the addition of Si would not change the liquidus temperature under the core pressures. The temperatures at the core-mantle boundary (CMB) are 4750 K for Fe; 4070 K for Fe-5.9 wt%O; 4660 K for Fe-4 wt%Si; 4560 K for Fe-5.8 wt%Si–0.8 wt%O. The Fe-4 wt%Si-outer core shows a very similar isentrope to that of the pure Fe core due to similar Grüneisen parameters (Table S1) (Komabayashi 2014). As such the thermal structure of the core would not be greatly affected by the presence of silicon.

Fig. 6
figure 6

Isentropic temperature profiles of Fe-4 wt%Si and Fe-5.8 wt%Si–0.8 wt%O outer cores. Reported profiles of outer cores with pure Fe and Fe-5.9 wt%O (Komabayashi 2014) are also shown. The mantle profile is from Brown and Shankland (1981)

Full size image

Figure 7 shows calculated density and Vp for each outer core composition along its isentrope together with seismologically constrained values (PREM, Dziewonski and Anderson 1981). Pure iron shows greater density and slower velocity than the PREM (Anderson and Ahrens 1994; Komabayashi 2014). The addition of silicon increases the velocity, contrary to the case of oxygen. Figure 8 plots the Si and O contents which satisfy the Vp or density of the PREM. The intersection of the Vp- and density-satisfying lines yields the best-fit solution of Fe-5.8(0.6) wt%Si-0.8(0.6) wt%O, taking the errors for density (0.2% from EoS and 0.5% from observation) and velocity (0.2% from EoS and 0.2% from observation) into account. As discussed in Komabayashi (2014), oxygen may not be the primary light element in the core mostly due to its distinctive nature reducing the velocity of liquid iron alloy. Selected thermodynamic properties for the best-fit outer core at the CMB and ICB are presented in Table 4.

Fig. 7
figure 7

P-wave velocities (Vp) and densities of iron alloys: pure Fe (Komabayashi 2014), Fe-5.9 wt%O (Komabayashi 2014), Fe-4 wt%Si (this study), and Fe-5.8 wt%Si-0.8 wt%O (this study). Each profile was along its isentrope (Fig. 6). The star represents the density of the Fe-Si hcp phase which would precipitate from the Fe-5.8 wt%Si–0.8 wt%O outer core

Full size image
Fig. 8
figure 8

The amounts of silicon and oxygen which satisfy the velocity (Vp) or density (ρ) of the PREM for the outer core at 330 GPa. The temperature is at the liquidus temperature for each composition, projected onto the system Fe–FeO (Komabayashi 2014). The star indicates the best-fit outer core composition, Fe-5.8 wt%Si–0.8 wt %O

Full size image
Table 4 Calculated physical properties of Fe–Si–O liquids
Full size table

The best-fit composition of the outer core is close to the binary system Fe–Si and here I compare it with earlier estimates in the system Fe–Si. Fischer et al. (2014) and Tateno et al. (2015) estimated the Si content in the outer core based on compression experiments on Fe-9 wt%Si hcp phases, assuming silicon is the sole light element there. Figure 8 shows that the Si content in an Fe–Si liquid needed to reconcile the PREM density is 6.2 wt% in my model. This value should be consistent with the data in Tateno et al. (2015) as the EoS of the Fe–Si hcp phase in this study was evaluated based on their data (Komabayashi et al. 2019). On the other hand, Fischer et al. (2014)’s estimate of the Si content in the outer core was about 11 wt%. The outer core thermal profile in Fischer et al. (2014) assumed 4000 K at the CMB, indicating 600–700 K lower than in this study, corresponding to a density difference of about 1%. Furthermore, the density change upon melting of iron at the CMB pressure is 2.6% (Komabayashi 2014) while Fischer et al. (2014) assumed between 1 and 2%. Adding all these factors up will reduce the estimated Si content in the outer core with Fischer et al. (2014)’s model to about 9 wt%, which is 3% different from the case of this study. The remaining unresolved factor likely lies in the thermal pressure term in the EoS of the Fe–Si hcp phases as the experiments in Fischer et al. (2014) and Tateno et al. (2015) were based on different pressure scales. Note that all the data in Komabayashi (2014) and Komabayashi et al. (2019) were based on pressure scales consistent with Tateno et al. (2015).

Badro et al. (2014) also predicted the effects of several light elements on the density and velocity of iron liquid from the first-principles calculations and proposed a seismologically consistent compositional range for the outer core. Figure 9 compares the results of this study with the range of Si and O contents in Fe–Ni core melt by Badro et al. (2014). The outer core composition of this study is placed slightly outside their range which was up to 4.5 wt%Si at the minimum oxygen content of 1.2 wt%. The major source for the discrepancy lies in the effect of oxygen on the velocity of iron liquid. Figure 10 shows the effects of silicon and oxygen on the liquid iron properties: density, adiabatic bulk modulus, and Vp. Komabayashi (2014)’s model predicted a negative effect (i.e., decrease) on the velocity by the addition of oxygen while Badro et al. (2014)’s model predicted a positive effect. Another recent first-principle calculations by Ichikawa and Tsuchiya (2020) predicted similar trends to those in Badro et al. (2014) (Fig. 10). However, this does not necessarily indicate that the experiment-based and theory-based models are complete opposite. The result depends on the magnitude of reduction of the bulk modulus of iron liquid due to oxygen. All Badro et al. (2014), Komabayashi (2014), and Ichikawa and Tsuchiya (2020) show that the addition of oxygen reduces both the bulk modulus and density (Fig. 10b). The Vp is reduced in Komabayashi (2014) because the bulk modulus decreases more than density by mixing an oxygen component. This indicates that increase/decrease of Vp depends on the difference in the elastic parameter between the end-members [i.e., Fe and FeO in Komabayashi (2014)]. In his modelling of the EoS of liquid phases, Komabayashi (2014) demonstrated that the compressibility of a liquid should be close to that of the counterpart crystalline phase under core pressures, and the small bulk modulus of liquid FeO was a consequence of a small bulk modulus of solid B1 FeO. The EoS of solid B1 FeO was established based on experimental data to 207 GPa and 3800 K (Fischer et al. 2011; Ozawa et al. 2010) which are relevant to core conditions and therefore its elastic behaviour can be reliably applied.

Fig. 9
figure 9

The silicon and oxygen contents in the outer core which match the density and Vp of the PREM (Figs. 7 and 8). The reported range for the Si and O contents in an Fe–Ni outer core from the first-principles calculations is shown as the green area (Badro et al. 2014)

Full size image
Fig. 10
figure 10

Effects of a silicon and b oxygen on the P-wave velocity (Vp), adiabatic bulk modulus (Ks) and density (ρ) of liquid iron at 330 GPa. Data from the first principles studies are compared (Badro et al. 2014; Ichikawa and Tsuchiya 2020). Note that the parameters are normalized to those for pure iron. The effect of oxygen on Ks is more pronounced than on ρ, resulting in a reduction of Vp (this study; Komabayashi 2014)

Full size image

Similarly the effects of silicon on the bulk modulus are in contrast between the experiment-based (this study) and theory-based models (Badro et al. 2014; Ichikawa and Tsuchiya 2020) although all the papers show positive effects on the Vp (Fig. 10a). The EoS parameters for the Fe–Si hcp phase in this study was based on the compression experiments by Tateno et al. (2015) to 305 GPa who demonstrated that the addition of silicon surely increases the bulk modulus of hcp iron. Table 3 lists a set of EoS for solids and liquids in the system Fe–Si while the first-principles calculations did not provide such a self-consistent set of EoS for solids and liquids in the system Fe–Si or Fe–O. Further comparison is needed to resolve the difference between experiment and theory.

The best-fit outer core composition in this study is here compared with previously proposed core compositions based on metal-silicate partitioning experiments which placed constraints on core formation processes. Si-rich and O-poor models were proposed by Wade and Wood (2005) (5–7 wt%Si + 0 wt%O) and Rubie et al. (2011) (8 wt%Si + 0.5 wt%O), which are close to my best-fit outer core composition. In contrast, Siebert et al. (2013) proposed an O-rich core with a compositional range of 1.5–2.2 wt%Si + 4.5–5.5 wt%O. This oxygen-rich composition falls within the range of Si and O contents by Badro et al. (2014) in Fig. 9. Therefore, resolving the above-discussed discrepancy in the effects of Si and O on liquid iron properties will help to narrow down the possible core formation scenarios.

I also calculated the density of the hcp phase at 330 GPa which would crystallise from the Fe-5.8 wt%Si–0.8 wt%O outer core melt, i.e., to form the inner core. As oxygen is not partitioned into hcp iron upon crystallization (Ozawa et al. 2010), the composition of the precipitating phase is going to be Fe-5.85 wt%Si. From the EoS of hcp iron phases in the system Fe–Si (Dewaele et al. 2006; Tateno et al. 2015), the density of the crystallising phase at 330 GPa and 6180 K is calculated to be 12.42 g/cm3, which is much less dense than the inner core (12.77 g/cm3) (Fig. 7). Therefore, while Fe-5.8 wt%Si–0.8 wt%O can account for the seismic properties of the outer core, it does not produce a consistent inner core phase. This is mainly because the melting loop is very narrow and a significant amount of silicon is partitioned into the inner core upon crystallisation. On the other hand, Ozawa et al. (2016) proposed that the Si-rich B2 phase would crystallise in an Fe–Si outer core as they reported a Si-poor eutectic composition (< 1.5 wt%Si) at 127 GPa. As mentioned above, there have been no direct measurements on the eutectic composition in the system Fe–Si at 330 GPa, and the crystallising phase needs to be examined in the future studies. Nevertheless, since the B2 phase contains much more silicon than the hcp phase, it should be much less dense and cannot account for the inner core density either (Ozawa et al. 2016). Therefore, in either case, Earth’s core cannot be fully represented by the system Fe–Si–O and it must include another light element although silicon and oxygen are likely major impurities (Wade and Wood 2005; Rubie et al. 2011; Siebert et al. 2013).

Summary and conclusions

In summary: (1) I have constructed a thermodynamic model for the fcc–hcp phase transition in the Si-bearing iron system based on experimental data; (2) the model suggests that mixing of Si and Fe can be represented by ideal mixing under high P and T; (3) the melting temperature for the Si-bearing iron phases should be insensitive to the Si content, otherwise the melting phase loop would be too wide because of the large ∆S of melting for both end-members; (4) I have evaluated a thermal EoS for the Si-bearing iron liquid from the determined melting temperatures; (5) Assuming ideal mixing between Fe, FeO, and Si, the best-fit composition to the PREM density and velocity of the outer core is Fe-5.8 wt%Si–0.8 wt%O; (6) the determined outer core composition however does not produce a consistent inner core phase; (7) Earth’s core must contain another light element in addition to silicon and oxygen.