Rate-dependent viscoelasticity of an impact-hardening polymer under oscillatory shear

The IHP used in this study, called ESA (figure 1(c)), was provided by Shenzhen Innovation Advanced Materials Co. Ltd, Shenzhen, China. The components of ESA are similar to those of Silly Putty produced by Dow Corning Corporation, which is a type of boric acid-modified polydimethylsiloxane (PDMS). The strain rate effect of ESA is closely related to the pre-existing B–O bonds in ESA. In this study, we primarily focus on a quantitative description of the real rate-dependent viscoelasticity of ESA, the microscopic mechanism is not discussed in detail.

Zoom In Zoom Out Reset image size

We used a parallel-plate rheometer (TA instrument, discovery HR-2) to carry out DMA (figure 1(a)). As shown in figure 1(b), oscillatory shear can be carried out directly using a discovery HR-2 rheometer on a sample of ESA with a geometry of Φ25 mm × 1 mm. The range of oscillatory angular frequency was 10⁻¹ rad s∼10² rad/s, and the temperature was controlled between 20 °C and 200 °C. By implementing a large amplitude oscillatory shear (LAOS), we could determine the linear viscoelastic (LVE) range [28]. We then chose a suitable loading condition to ensure the measurements outlined below were implemented within the LVE range. The shape of the Lissajous curves within each cyclical loading period was monitored in situ using a discovery HR-2 rheometer to evaluate the linear viscoelasticity, thus providing an assistant method. The different loading conditions are shown in the captions of the related figures.

Differential scanning calorimetry was performed using a DSC 8500 (PerkinElmer Inc., USA) with a heating rate of 15 °C min⁻¹ in a nitrogen environment. The temperature range for DSC was set to −50 °C∼200 °C. A TGA 8000 (PerkinElmer Inc., USA) was used to perform thermogravimetric analysis. The heating rate was 15 °C min⁻¹ from 30 °C to 200 °C, and the nitrogen flow was set at 20 ml min⁻¹.

Within the LVE range, the dynamic viscoelastic moduli, i.e., the storage modulus and the loss modulus, fully describe the viscoelastic response of soft material or complex fluids and are endowed with specific physical meanings [28]. When a sinusoidal strain is applied, the response stress of a linear viscoelastic material is also sinusoidal, with the same oscillatory frequency and a phase shift. In other words, the dynamic viscoelastic moduli are independent of oscillatory strain amplitude within the LVE range [29], which is a valuable criterion to determine the LVE range of viscoelastic materials [30–32]. In this work, we discuss the linear viscoelasticity of ESA and its frequency and temperature dependence. To begin, we determined the LVE range of ESA using large amplitude oscillatory shear (LAOS) method.

As shown in figure 2, if we use the range of strain amplitude to describe the LVE range, we find that ESA is always linear viscoelastic within the selected strain amplitude range (0.08%∼10%), and no Payne effect is observed. However, note that the deformation is related to the position of the sample for the mode of oscillatory shear. When the strain at the edge of the sample reaches the critical value of linear viscoelasticity, the other part of the sample is still within the LVE range, although the dynamic viscoelastic moduli of ESA are mainly independent of the strain amplitude [33]. Therefore, we apply a small strain amplitude of 0.2% under oscillatory shear and monitor the shape of Lissajous curves to ensure ESA falls within the LVE range.

Zoom In Zoom Out Reset image size

When the loading frequency increases to a critical value, the Lissajous curve distorts because of the inertial effect, depending on the strain amplitude as well [29]. We do not observe a the distortion of the Lissajous curves under the loading conditions shown in figure 3, indicating that the loading frequency does not induce nonlinear behavior here. Figure 3 indicates that the dynamic viscoelastic properties (i.e., storage modulus, loss modulus, and loss factor) of ESA are very sensitive to oscillatory frequency under oscillatory shear at different temperatures. As previously mentioned, the oscillatory frequency can be equivalently expressed as the strain rate. 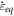Yi et al described an equivalent relationship as ${\dot{\varepsilon }}_{eq}=2\gamma \omega ,$ where ${\dot{\varepsilon }}_{eq}$ is the equivalent strain rate, γ is the shear strain, and ω is the angular frequency [21]. Thus, we can conclude that the viscoelasticity of ESA is strain rate-dependent according to the results shown in figure 3. Below, we describe how to characterize the rate-dependence of ESA quantitatively.

Zoom In Zoom Out Reset image size

Calculating the relative increment of storage modulus within the experimental range is the most widely used quantitative method to characterize the frequency-dependent effect, which can be achieved experimentally (usually 0.1 Hz∼100 Hz under oscillatory shear) [13, 22]. We extract the storage modulus at 0.1 rad/s and 100 rad/s from figure 3(a). As shown in figure 4(a), G'₁₀₀ is larger than G'_0.1 at different temperatures because the storage modulus monotonically increases with frequency. Therefore, the relative increment of storage modulus, i.e., G'₁₀₀/G'_0.1, can be defined to describe the frequency-dependent effect (or rate-dependent effect) of ESA within the experimental range. Figure 4(b) shows that G'₁₀₀/G'_0.1 varies between 1.31 × 10³ and 1.77 × 10⁴ within the temperature range of 20 °C∼160 °C. However, limited by the experimental technique, the frequency range is still too narrow to fully describe the rate-dependent effect of the IHPs. This is especially true when the frequency-sensitive storage modulus does not fall within the measurable frequency range of commercial devices (most frequency-dependent storage moduli of viscoelastic polymers present an 'S' shape, i.e., the frequency-sensitive storage modulus falls within a narrow frequency range). Furthermore, the relative increment of storage modulus cannot reflect the real rate-dependent effect.

Zoom In Zoom Out Reset image size

To solve this problem, we introduce the Havriliak-Negami (H–N) model to describe the frequency-dependent dynamic viscoelastic behaviors of ESA for a wider frequency range than our experimental frequency range. The H–N model is a powerful theoretical tool to analyze viscoelastic damping materials [34–37]. This model connects the modulus between the low-and high-frequency range (theoretically from zero to infinity) and greatly extends the achievable experimental frequency range, thus allowing to capture the rate-dependent effect fully. Furthermore, the dynamic mechanical properties of viscoelastic materials can be accurately described within wide ranges of temperature and frequency by introducing four temperature-independent parameters and one temperature-dependent parameter. The parameters in the H–N model are relatively straightforward compared to other phenomenological models such as the generalized Maxwell model and the fractional derivative model. The H–N model can be expressed as follows:

$$\begin{eqnarray}&&{G}^{* }(\omega ,\tau )=G^{\prime} (\omega ,\tau )+iG^{\prime\prime} (\omega ,\tau )={G}_{+\infty }+\displaystyle \frac{{G}_{0}-{G}_{+\infty }}{{[1+{(i\omega \tau )}^{\alpha }]}^{\beta }},\end{eqnarray} \tag{ 1 }$$

$$\begin{eqnarray}&&G^{\prime} (\omega ,\tau )={G}_{+\infty }+\displaystyle \frac{({G}_{0}-{G}_{+\infty })\cos (\beta \theta )}{{[1+2{(\omega \tau )}^{\alpha }\cos (\alpha \pi /2)+{(\omega \tau )}^{2\alpha }]}^{2\beta }},\end{eqnarray} \tag{ 2 }$$

$$\begin{eqnarray}&&G^{\prime\prime} (\omega ,\tau )=\displaystyle \frac{({G}_{0}-{G}_{+\infty })\sin (\beta \theta )}{{[1+2{(\omega \tau )}^{\alpha }\cos (\alpha \pi /2)+{(\omega \tau )}^{2\alpha }]}^{2\beta }},\end{eqnarray} \tag{ 3 }$$

$$\begin{eqnarray}&&\tan \,\delta =\displaystyle \frac{G^{\prime\prime} }{G^{\prime} }=\displaystyle \frac{({G}_{+\infty }-{G}_{0})\sin (\beta \theta )}{{G}_{+\infty }{\left[1+2{(\omega \tau )}^{\alpha }\cos (\alpha \pi /2)+{(\omega \tau )}^{2\alpha }\right]}^{\beta /2}+({G}_{+\infty }-{G}_{0})\cos (\beta \theta )},\end{eqnarray} \tag{ 4 }$$

$$\begin{eqnarray}&&\theta =\arctan \left[\displaystyle \frac{{(\omega \tau )}^{\alpha }\,\sin (\alpha \pi /2)}{1+{(\omega \tau )}^{\alpha }\,\cos (\alpha \pi /2)}\right].\end{eqnarray} \tag{ 5 }$$

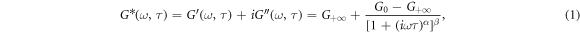
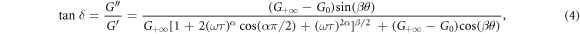
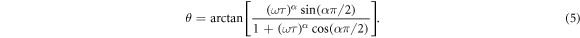
There are five parameters (G₀, G_+∞, α, β and τ) in the H–N model. G₀ and G_+∞ represent the moduli limits at the frequency trending to zero and infinity, respectively. Therefore, G_+∞/G₀ can be used to evaluate the rate-dependent effect of the IHPs quantitatively. G_+∞/G₀ can be considered as the theoretical limit of rate-dependent viscoelasticity, which reflects the intrinsic material properties. To begin, we choose a set of trial values of τ, α, β, G₀ and G_+∞, and set τ as 1. Because 0 < α, β ≤ 1, we set α = β = 0.5. According to the physical meaning, we set the initial values of G₀ and G_+∞ as the storage moduli at the frequency of 0.1 rad/s and 100 rad/s, respectively. Then, we use the multi-parameter optimization function (we choose the constrained nonlinear minimization solver) in the optimization toolbox of Matlab^® software to fit the parameters based on the experimental data shown in figure 3 [38]. The error function we use here is defined as:

$$\begin{eqnarray}&&{F}_{error}=\sqrt{\displaystyle {\sum }_{G^{\prime} }{\left(1-\displaystyle \frac{\tan {\delta }_{cal}}{\tan {\delta }_{\exp }}\right)}^{2}},\end{eqnarray} \tag{ 6 }$$

where tanδ_cal and tanδ_exp are the loss factor calculated from equation (4) and the corresponding experimental data, respectively. The parameters (G₀, G_+∞, α, β and τ) in the H–N model can be quickly converged to achieve the optimal values for the condition mentioned above.

The relationship between the loss factor and storage modulus on a logarithmic scale is referred to as a Wicket plot, which is a useful tool to analyze dynamic viscoelastic data [35]. Figure 3(d) shows that the H–N model fits the related experimental results well. We also compare the experimental and calculated results of the storage modulus at angular frequencies of 0.1 rad/s and 100 rad/s, as shown in figure 5. The calculated results are also consistent with the experimental results, which implies that the results calculated by the H–N model are credible for the given experimental conditions. However, predictive ability of the H–N model beyond the experimental range still needs to be verified. As figure 3(d) shows, the Wicket plots, which is similar with Van Gurp-Palmen and Cole-Cole plots, can prove that ESA is a simple heat flow material and indicate that the time-temperature superposition principle (TTSP) can be used to extend the experimental data to a wider frequency range (Wicket plots are almost superimposed at different temperatures). If the H–N model can predict the experimental data within the extended frequency range, we can further evaluate the reliability of G_∞/G₀.

Zoom In Zoom Out Reset image size

We choose 20 °C as the reference temperature and assume that the density of ESA does not change at different temperatures. Then, the relationship of time-temperature transition [39]

$$\begin{eqnarray}&&G^{\prime} {(\omega )}_{{T}_{0}}=\displaystyle \frac{{\rho }_{0}{T}_{0}}{{\rho }_{T}T}G^{\prime} {\left(\displaystyle \frac{\omega }{{a}_{T}}\right)}_{T}\end{eqnarray} \tag{ 7 }$$

can be simplified to:

$$\begin{eqnarray}&&G^{\prime} {(\omega )}_{{T}_{0}}=\displaystyle \frac{{T}_{0}}{T}G^{\prime} {\left(\displaystyle \frac{\omega }{{a}_{T}}\right)}_{T},\end{eqnarray} \tag{ 8 }$$

where a_T is a shift factor (the ratio of the relaxation time at T and T₀), and ρ₀ and ρ_T represent the density of ESA at temperature T₀ and T, respectively.

We choose the experimental data from figure 3(a) that ranges from 20 °C to 120 °C to perform the time-temperature superposition, as shown in figure 6. Figure 5 shows that G' at 140 °C and 160 °C does not decrease monotonously with temperature, and does do not contribute to the extension of the frequency range by TTSP. The temperature-dependent shift factor (a_T, the inset of figure 6) follows the Arrhenius equation well [37]. We calculate the activation energy of ESA to be 27.4299 kJ mol⁻¹. Figure 6 shows that the master curve (G'-frequency curve) by TTSP extends the lower angular frequency of the experimental data at 20 °C from 0.1 rad/s to 0.005 rad/s. The H–N model calculated based on the experimental data at 20 °C is acceptable to predict the data within the extended experimental range (0.005 rad/s∼0.1 rad/s) considering the errors from experiment and TTSP. Based on the data shown in figure 6, we calculate three different relative increments of storage moduli at 20 °C: G'₁₀₀/G'_0.1 = 1.31 × 10³; G'₁₀₀/G'_0.005 = 3.19 × 10⁴; G_+∞/G₀ = 2.32 × 10⁵. This illustrates that the relative increment of storage modulus is relevant within the frequency range (i.e., not an intrinsic material property). Furthermore, we calculate G_+∞/G₀ at different temperatures using the H–N model (figure 4). The range of modulus (i.e., G₀ ∼ G_+∞) calculated by the H–N model is much wider than that obtained from the experiment (figure 4(a)). We find that each theoretical limit of the rate-dependent viscoelasticity (G_+∞/G₀) is larger than the experimental rate-dependent viscoelasticity (G'₁₀₀/G'_0.1): at least 27 times larger (at 80 °C). Therefore, G_+∞/G₀ is more reasonable to characterize the rate-dependent viscoelasticity of ESA. For example, the modulus of ESA can theoretically change from 1.03 Pa (G₀) to 3.94 × 10⁷ Pa (G_+∞) at 160 °C, indicating that ESA can switch between extremely soft and extremely hard under different loading rates. This characteristic reveals why ESA can be considered an impact-hardening polymer, which is quite beneficial for some applications such as impact protection [9] and highly sensitive electromechanical sensors [8], etc.

Zoom In Zoom Out Reset image size

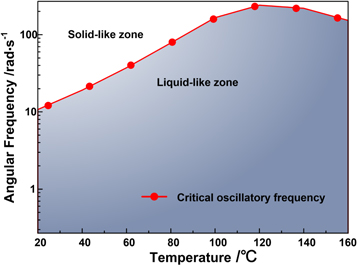
Temperature greatly influences polymer properties, including IHPs [4]. In section 3.2, we concentrated on the frequency-dependent dynamic viscoelastic behaviors of ESA at different temperatures. Here we analyze the influence of temperature on the dynamic viscoelastic behaviors of ESA. Within the linear viscoelastic range, the storage modulus of IHPs represents the ability to store energy, and the loss modulus represents the ability to dissipate energy [29]. The intersection of the frequency-dependent curves of the storage modulus and loss modulus is defined as the point of the phase transition between a solid-like and liquid-like state [33]. Thus, the material is solid-like when the storage modulus is larger than the loss modulus (i.e., tanδ < 1), and the material is liquid-like when the loss modulus is larger than the storage modulus. The phase transition points (the critical angular frequency at the intersection of the storage modulus and loss modulus, or when tanδ = 1) of ESA can be found under oscillatory shear at different temperatures and plotted as a temperature-dependent phase diagram, as shown in figure 7.

Zoom In Zoom Out Reset image size

As shown in figure 7, as the temperature increases, the critical frequency (the solid red dots in figure 7) of the phase transition increases gradually up to 120 °C and then decreases slightly. At higher temperatures, the polymer chains are more active and more energy is dissipated at the same frequency. On the other hand, ESA is frequency-sensitive (figure 3), the polymer chains are restricted at a higher frequency, and more energy is stored at the same temperature. In other words, temperature and frequency play opposite roles in the dynamic viscoelastic properties of ESA, which is consistent with the experimental data (figure 7). This phase diagram is valuable for engineering applications for choosing suitable or desired loading conditions. For example, if the loading conditions (in this case, we mean the oscillatory frequency and temperature) fall into the liquid-like zone (blue zone) of figure 7, the ESA dissipates more input energy. If more input energy is need to be stored, the loading conditions should be maintained within the solid-like zone (white zone).

We measured the temperature-dependent dynamic viscoelastic properties of ESA at a fixed oscillatory frequency. As shown in figure 8, G' decreases initially with increasing temperature but then clearly increases when the temperature exceeds 140 °C. The largest reduction of G' induced by temperature (in the range of 20 °C∼140 °C) is 104.58, indicating that adjusting the temperature is another method to change the modulus of ESA. The change of modulus induced by temperature is equivalent to the rate-dependent viscoelasticity according to the time-temperature superposition principle (TTSP).

Zoom In Zoom Out Reset image size

The temperature-dependent tanδ is calculated based on the relationship of tanδ = G''/G [29]. When the temperature is higher than 24 °C, ESA behaves in a liquid-like state (tanδ > 1), as shown in figure 8. Furthermore, we observe an distinct peak in the tanδ-temperature curve of ESA under oscillatory shear at around 130 °C. Correspondingly, G' and G'' increase when the temperature exceeds to 130 °C and decrease when the temperature is less than 130 °C. No endothermic or exothermic peak is observed in the DSC measurements (figure 9(a)) within the temperature range of −50∼200 °C, indicating that ESA is non-crystalline; thus, TTSP can feasibly be performed. The TG measurements (figure 9(b)) indicate that no degradation takes place in the tested region. Moreover, the results shown in figure 8 are reproducible for the same sample, indicating that the peak is not caused by an irreversible chemical reaction and that the reversible strain rate-hardening behavior is primarily due to reversible breaking and recombining of B-O dative bonds [23]. The storage modulus decreases with increasing temperature because the molecules of the polymer move more easily under high temperatures. When the temperature exceeds a critical value (130 °C in this instance), the configuration of the molecular chains changes and the configuration entropy also increases. A higher configuration entropy induces polymers with a higher elastic modulus [40]. When the temperature exceeds 130 °C, the increment in elastic modulus induced by the configuration entropy exceeds the reduction in elastic modulus induced by temperature; thus we observe an increase of storage modulus and a corresponding decrease of tanδ.

Zoom In Zoom Out Reset image size