Piezoelectric vibration controller in a parametrically-excited system with modal localisation

Abstract

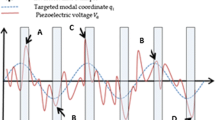
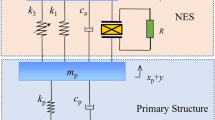
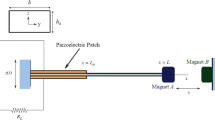
In a previous work, the authors investigated, with promising results, the use of a piezoelectric element for the sake of energy harvesting from a rod assemblage subjected to varying normal force. However, in that occasion it was also observed that, depending on the initial voltage applied to the piezoelectric element, the system’s vibrations could actually be controlled, due to structural stiffening associated to the so-called inverse effect, inherent to piezoelectric coupling. In this work, this duality (energy harvesting and vibration control) is further exploited. It is shown that one or the other feature may arise in a parametric-instability scenario. The same trend was also captured with the aid of a reduced-order model.

Appendices

Appendix A

The unveiled terms of the stiffness matrix ${\mathbf{K}}\left( {\varvec{q},\dot{\varvec{q}},\tau } \right)$, not detailed in (31) for brevity, read

$$ \begin{aligned} k_{12} & = k_{21} = - 4\alpha - \uptheta + 2\sigma - \Delta \uptheta \sin \left( {n\sqrt \lambda \tau } \right) \\ & \quad + \left( { - \frac{3}{2}\alpha - \frac{1}{3}\uptheta + \frac{2}{3}\sigma - \frac{1}{3}\Delta \uptheta \sin \left( {n\sqrt \lambda \tau } \right)} \right)\left( {q_{1}^{2} + q_{2}^{2} } \right) \\ & \quad + \alpha q_{1} q_{3} + \alpha q_{2} q_{3} - \frac{1}{2}\alpha q_{3}^{2} \\ \end{aligned} $$

(63)

$$ \begin{aligned} k_{22} & = 1 + 6\alpha + 2\theta - 3\sigma + 2\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right) \\ & \quad + \left( {6\alpha + \frac{3}{2}\theta - 3\sigma + \frac{3}{2}\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right)} \right)q_{1}^{2} \\ & \quad + \left( { - 3\alpha - \frac{2}{3}\theta + \frac{4}{3}\sigma - \frac{2}{3}\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right)} \right)q_{1} q_{2} \\ & \quad + \left( { - 3\alpha - \frac{2}{3}\theta + \frac{2}{3}\sigma - \frac{2}{3}\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right)} \right)q_{2} q_{3} \\ & \quad + \left( { - \frac{2}{3} - \frac{1}{3}\theta + \frac{1}{2}\sigma - \frac{1}{3}\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right)} \right)q_{2}^{2} \\ & \quad + \left( {6\alpha + \frac{3}{2}\theta - \frac{3}{2}\sigma + \frac{3}{2}\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right)} \right)q_{3}^{2} - \dot{q}_{2}^{2} \\ \end{aligned} $$

(64)

$$ \begin{aligned} k_{23} & = k_{32} = - 4\alpha - \uptheta + \sigma - \Delta \uptheta \sin \left( {n\sqrt \lambda \tau } \right) \\ & \quad + \left( { - \frac{3}{2}\alpha - \frac{1}{3}\uptheta + \frac{1}{3}\sigma - \frac{1}{3}\Delta \uptheta \sin \left( {n\sqrt \lambda \tau } \right)} \right)\left( {q_{2}^{2} + q_{3}^{2} } \right) + \alpha q_{1} q_{2} - \frac{1}{2}\alpha q_{1}^{2} \\ \end{aligned} $$

(65)

$$ \begin{aligned} k_{33} & = 1 + 5\alpha + 2\theta - \sigma + 2\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right) \\ & \quad - \alpha q_{1} q_{2} + \left( {6\alpha + \frac{3}{2}\theta - \frac{3}{2}\sigma + \frac{3}{2}\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right)} \right)q_{2}^{2} \\ & \quad + \left( { - 3\alpha - \frac{2}{3}\theta + \frac{2}{3}\sigma - \frac{2}{3}\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right)} \right)q_{2} q_{3} \\ & \quad + \left( { - \frac{2}{3} - \frac{1}{3}\theta + \frac{1}{6}\sigma - \frac{1}{3}\Delta \theta \sin \left( {n\sqrt \lambda \tau } \right)} \right)q_{3}^{2} - \dot{q}_{3}^{2} \\ \end{aligned}. $$

(66)

Appendix B

The unveiled terms of (59) read

$$ A = - 0.7175q^{2} + 5.5693v_{0} q - 10.8010v_{0}^{2} + 1 $$

(67)

$$ B_{1} = - 0.7175q + 2.7846v_{0} $$

(68)

$$ B_{2} = 0.0014 $$

(69)

$$ B_{3} = - 0.0223v_{0} $$

(70)

$$ B_{4} = 0.1296v_{0}^{2} - 0.0072 $$

(71)

$$ B_{5} = 0.0557v_{0} - 0.3347v_{0}^{3} $$

(72)

$$ B_{6} = 0.3241v_{0}^{4} - 0.1081v_{0}^{2} + 0.0099 $$

(73)

$$ C_{1} = 0.0261\Delta \theta \sin \left( {\frac{\sqrt \Lambda \tau }{\sqrt \delta }} \right) - 0.5386 $$

(74)

$$ C_{2} = - 0.3150v_{0} \Delta \theta \sin \left( {\frac{\sqrt \Lambda \tau }{\sqrt \delta }} \right) + 6.3059v_{0} $$

(75)

$$ C_{3} = \left( {1.2653v_{0}^{2} + 0.1050} \right)\Delta \theta \sin \left( {\frac{\sqrt \Lambda \tau }{\sqrt \delta }} \right) - 24.6160v_{0}^{2} + 0.6103 $$

(76)

$$ D = \left( { - 1.6932v_{0}^{3} - 0.4139v_{0} } \right)\Delta \theta \sin \left( {\frac{\sqrt \Lambda \tau }{\sqrt \delta }} \right) + 32.0382v_{0}^{3}. $$

(77)