Convergence rates for an inertial algorithm of gradient type associated to a smooth non-convex minimization

Abstract

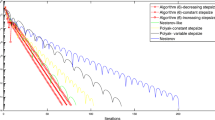
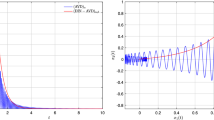
We investigate an inertial algorithm of gradient type in connection with the minimization of a non-convex differentiable function. The algorithm is formulated in the spirit of Nesterov’s accelerated convex gradient method. We prove some abstract convergence results which applied to our numerical scheme allow us to show that the generated sequences converge to a critical point of the objective function, provided a regularization of the objective function satisfies the Kurdyka–Łojasiewicz property. Further, we obtain convergence rates for the generated sequences and the objective function values formulated in terms of the Łojasiewicz exponent of a regularization of the objective function. Finally, some numerical experiments are presented in order to compare our numerical scheme and some algorithms well known in the literature.

Appendix

1.1 Second order continuous dynamical systems that are modelling Algorithm (2)

In what follows we emphasize the connections between Algorithm (2) and the continuous dynamical systems (3) and (4).

Consider (4) with the initial conditions $x(t_0)=u_0,\,{\dot{x}}(t_0)=v_0,\,u_0,v_0\in {\mathbb {R}}^m$ and the governing second order differential equation

$$\begin{aligned} \ddot{x}(t)+\left( \gamma +\frac{\alpha }{t}\right) {\dot{x}}(t)+{\nabla }g(x(t))=0,\,\gamma >0,\,\alpha \in {\mathbb {R}}. \end{aligned}$$

We will use the time discretization presented in [6], that is, we take the fixed stepsize $h> 0,$ and consider $\beta =1-\gamma h>0$, $t_n = \frac{1}{\beta } nh$ and $x_n = x(t_n).$ Then the implicit/explicit discretization of (3) leads to

$$\begin{aligned} \frac{1}{h^2}(x_{n+1}-2x_n+x_{n-1})+\left( \frac{\gamma }{h}+\frac{\alpha \beta }{nh^2}\right) (x_n-x_{n-1})+{\nabla }g(y_n)=0, \end{aligned}$$

(55)

where $y_n$ is a linear combination of $x_n$ and $x_{n-1}$ and will be defined below.

Now, (55) can be rewritten as

$$\begin{aligned} x_{n+1}= x_n+\left( \beta -\frac{\alpha \beta }{ n}\right) (x_n-x_{n-1})-h^2{\nabla }g(y_n), \end{aligned}$$

which suggest to choose $y_n$ in the form

$$\begin{aligned} y_n=x_n+\left( \beta -\frac{\alpha \beta }{ n}\right) (x_n-x_{n-1}). \end{aligned}$$

However, for practical purposes, it is convenient to work with the re-indexation $n\rightarrowtail n+\alpha$ and we obtain the following equivalent formulation

$$\begin{aligned} y_n=x_n+\frac{\beta n}{ n+\alpha }(x_n-x_{n-1}). \end{aligned}$$

Hence, by taking $h^2=s$ we get

$$\begin{aligned} x_{n+1}= x_n+\frac{\beta n}{ n+\alpha }(x_n-x_{n-1})-s{\nabla }g(y_n), \end{aligned}$$

which is exactly Algorithm (2).

Remark 25

Obviously, already the form $\beta =1-\gamma h>0$ shows that $\beta \in (0,1).$ We could not obtain Algorithm (2) via some similar discretization of the continuous dynamical system (3) as the discretization method presented above. Nevertheless, we can show that (3) is the exact limit of Algorithm (2) in the sense of Su, Boyd and Candès [50].

In what follows we show that by choosing appropriate values of $\beta$, both the continuous second order dynamical systems (3) and the continuous dynamical system (4) are the exact limit of the numerical scheme (2).

To this end we take in (2) small step sizes and follow the same approach as Su, Boyd and Candès in [50], (see also [27] for similar approaches). For this purpose we rewrite (2) in the form

$$\begin{aligned} \frac{x_{n+1}-x_n}{\sqrt{s}}=\frac{\beta n}{n+\alpha }\cdot \frac{x_n-x_{n-1}}{\sqrt{s}}-\sqrt{s}{\nabla }g(y_n) \ \forall n \ge 1 \end{aligned}$$

(56)

and introduce the Ansatz $x_n\approx x(n\sqrt{s})$ for some twice continuously differentiable function $x : [0,+\infty ) \rightarrow {\mathbb {R}}^m$. We let $n=\frac{t}{\sqrt{s}}$ and get $x(t)\approx x_n,\,x(t+\sqrt{s})\approx x_{n+1},\,x(t-\sqrt{s})\approx x_{n-1}.$ Then, as the step size s goes to zero, from the Taylor expansion of x we obtain

$$\begin{aligned} \frac{x_{n+1}-x_n}{\sqrt{s}}={\dot{x}}(t)+\frac{1}{2}\ddot{x}(t)\sqrt{s}+o(\sqrt{s}) \end{aligned}$$

and

$$\begin{aligned} \frac{x_n-x_{n-1}}{\sqrt{s}}={\dot{x}}(t)-\frac{1}{2}\ddot{x}(t)\sqrt{s}+o(\sqrt{s}). \end{aligned}$$

Further, since

$$\begin{aligned} \sqrt{s}\Vert {\nabla }g(y_n)-{\nabla }g(x_n)\Vert \le \sqrt{s} L_g\Vert y_n-x_n\Vert =\sqrt{s} L_g\left| \frac{\beta n}{n+\alpha }\right| \Vert x_n-x_{n-1}\Vert =o(\sqrt{s}), \end{aligned}$$

it follows $\sqrt{s} {\nabla }g(y_n)=\sqrt{s}{\nabla }g(x_n)+ o(\sqrt{s})$. Consequently, (56) can be written as

$$\begin{aligned}&{\dot{x}}(t)+\frac{1}{2}\ddot{x}(t)\sqrt{s}+ o(\sqrt{s})\\&\quad = \frac{\beta t}{t+\alpha \sqrt{s}}\left( {\dot{x}}(t)-\frac{1}{2}\ddot{x}(t)\sqrt{s}+ o(\sqrt{s})\right) -\sqrt{s}{\nabla }g(x(t))+ o(\sqrt{s}) \end{aligned}$$

or, equivalently

$$\begin{aligned}&(t+\alpha \sqrt{s})\left( {\dot{x}}(t)+\frac{1}{2}\ddot{x}(t)\sqrt{s}+o(\sqrt{s})\right) \\&\quad = \beta t\left( {\dot{x}}(t)-\frac{1}{2}\ddot{x}(t)\sqrt{s}+o(\sqrt{s})\right) -\sqrt{s}(t+\alpha \sqrt{s}){\nabla }g(x(t))+o(\sqrt{s}). \end{aligned}$$

Hence,

$$\begin{aligned} \frac{1}{2}\left( \alpha \sqrt{s}+(1+\beta )t\right) \ddot{x}(t)\sqrt{s}+\left( (1-\beta )t+\alpha \sqrt{s}\right) {\dot{x}}(t)+\sqrt{s}(t+\alpha \sqrt{s}){\nabla }g(x(t))=o(\sqrt{s}).\nonumber \\ \end{aligned}$$

(57)

Now, if we take $\beta =1-\gamma {s}<1$ in (57) for some $\frac{1}{{s}}>\gamma >0$, we obtain

$$\begin{aligned} \frac{1}{2}\left( \alpha \sqrt{s}+(2-\gamma {s})t\right) \ddot{x}(t)\sqrt{s}+\left( \gamma {s}t+\alpha \sqrt{s}\right) {\dot{x}}(t)+\sqrt{s}(t+\alpha \sqrt{s}){\nabla }g(x(t))=o(\sqrt{s}). \end{aligned}$$

After dividing by $\sqrt{s}$ and letting $s\rightarrow 0$, we obtain

$$\begin{aligned} t\ddot{x}(t)+\alpha {\dot{x}}(t)+t{\nabla }g(x(t))=0, \end{aligned}$$

which after division by t gives (3), that is,

$$\begin{aligned} \ddot{x}(t)+\frac{\alpha }{t}{\dot{x}}(t)+{\nabla }g(x(t))=0. \end{aligned}$$

Similarly, by taking $\beta =1-\gamma \sqrt{s}<1$ in (57), for some $\frac{1}{\sqrt{s}}>\gamma >0$, we obtain

$$\begin{aligned} \frac{1}{2}\left( \alpha \sqrt{s}+(2-\gamma \sqrt{s})t\right) \ddot{x}(t)\sqrt{s}+\left( \gamma \sqrt{s}t+\alpha \sqrt{s}\right) {\dot{x}}(t)+\sqrt{s}(t+\alpha \sqrt{s}){\nabla }g(x(t))=o(\sqrt{s}). \end{aligned}$$

After dividing by $\sqrt{s}$ and letting $s\rightarrow 0$, we get

$$\begin{aligned} t\ddot{x}(t)+(\gamma t+\alpha ){\dot{x}}(t)+t{\nabla }g(x(t))=0, \end{aligned}$$

which after division by t gives (4), that is,

$$\begin{aligned} \ddot{x}(t)+\left( \gamma +\frac{\alpha }{t}\right) {\dot{x}}(t)+{\nabla }g(x(t))=0. \end{aligned}$$