1 Introduction

In recent years, with the growth of the increasing requirements for travel safety, environmental protection and efficiency, as well as advanced technology, intelligent transportation tools have developed rapidly, especially electric vehicles. As one of the effective ways to alleviate the energy and environment issue, the electric vehicles have received considerable attention [1,2,3,4,5]. Each wheel is independently driven by an in-wheel motor in the electric vehicle systems, which shows superior actuation flexibility and maneuverability [6]. Many fruitful results of vehicle control strategies have been provided, such as fuzzy logic control [7], coordinated control [8], optimal control [9], and fault-tolerant control [10]. Based on the differential steering, the yaw control problem for electric vehicles was discussed in [11]. Considering the parameter uncertainties, Kazemi et al. [12] designed an adaptive sliding mode controller for Steer-by-Wire (SbW) systems. Using the delta operator approach, a fault-tolerant controller for SbW systems was designed in [13]. As an effective strategy of chassis control, the yaw-moment control technique for vehicle dynamic systems was proposed in [14].

It should be noted that all the aforementioned control results of electric vehicle systems are assumed to be under the ideal working conditions. However, owing to the wear or overtime operation of machinery, the electric vehicle systems may suffer from sensor failures. The sensor failures may affect the system performance and cause instability of the system. To handle such a problem, many results have been published [15,16,17,18,19,20]. For instance, in the presence of random state delay and sensor failures, Takagi–Sugeno (T-S) fuzzy model for vehicle suspension systems was developed to tackle the uncertainties in [18]. Su et al. [19] provided a reliable filter design strategy for fuzzy systems when the sensor failures and time-delay existed. By means of the T-S fuzzy approach, a reliable fuzzy controller for networked control systems subject to sensor failures was constructed in [20]. In addition, the actuator saturation issue should be considered in the controller design procedure. Up to now, many theoretical achievements subject to actuator saturation have been presented in [21,22,23,24]. For ground-vehicle lateral dynamic systems, a robust yaw-moment controller with the actuator saturation was designed in [25]. Considering the actuator saturation, Li et al. [26] discussed the adaptive sliding mode control problem for fuzzy systems. In [27], a saturated adaptive control scheme for active suspension systems was presented to tackle the actuator saturation issue.

On the other hand, the uncertainties caused by the payload or number of passengers should be considered in the electric vehicle systems. Unlike the type-1 fuzzy sets [28,29,30,31], the interval type-2 (IT2) fuzzy sets [32,33,34,35,36] are presented to describe the uncertainties, especially when the membership functions (MFs) have the uncertainties. To handle the uncertainties, an IT2 fuzzy model for nonlinear systems was constructed in [37]. In [38], the nonlinear systems were modeled as IT2 fuzzy systems and the problem of fault detection filter design was discussed. Based on the mismatched MFs, an IT2 fuzzy controller was designed to stabilize the control systems in [39, 40]. According to the IT2 fuzzy logic strategy, a novel reactive control scheme for autonomous mobile robots was provided in [41]. Under the effect of cyberattacks, Zhang et al. [42] discussed the sliding mode control problem for IT2 fuzzy systems. Based on the IT2 fuzzy model, the sliding mode fault-tolerant control issue was addressed in [43]. However, the IT2 fuzzy control problem for uncertain electric vehicle systems with sensor failures and actuator saturation has not been fully studied, which motivates our work.

This paper considers the IT2 fuzzy control problem for uncertain electric vehicle systems, in which the sensor failures and actuator saturation are taken into account. The main contributions are summarized as follows. (1) According to the IT2 fuzzy sets, an IT2 fuzzy system for electric vehicle system with uncertainties is established. Different from [44], the uncertainties in the IT2 fuzzy system are effectively described by the lower and upper membership functions (LUMFs). (2) To make the implementation of controller more practical, the saturation nonlinearity and sensor failures are taken into account in the design process of IT2 fuzzy controller.

The remaining of this paper is structured below. The problem statement is given in Sect. 2. In Sect. 3, the main results are proposed. Section 4 provides some simulation results. Section 5 gives the conclusion.

Notations The matrix transposition and matrix inverse are represented by superscript “T” and “\(-1\)”, respectively. The symbol “\(\text {diag}\{\cdots \}\)”is the block diagonal matrix and the notation “\(*\)” stands for a symmetric term in a symmetric block matrix. Meanwhile, the zero matrix and identity matrix are denoted by “0” and “I”, respectively. \([A]_{s}\) is defined as \(A+A^{T}\). If a matrix is not specified in dimension, we can suppose that it has a suitable dimension.

2 Problem Statement

2.1 Description of Electric Vehicle Systems

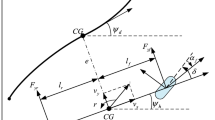
Figure 1 depicts the electric vehicle model. The sideslip angle and yaw rate can be represented by \(\beta\) and \(\varOmega _{z}\), respectively. The vehicle mass is denoted by m. \(l_{f}\) and \(l_{r}\) are the distances from front and rear (FR) wheel axles to the center of gravity (CG), respectively. \(I_{z}\) stands for moment of inertia. \(v_{x}\) and \(v_{y}\) represent the vehicle longitudinal velocity and lateral velocity, respectively, where \(v_{x}\) is a constant. The yaw moment \(M_{z}\) is written as [45]

$$\begin{aligned} M_{z}=({F}_{xfl}cos\delta _{f}+{F}_{xrl})l_{s}-({F}_{xfr}cos\delta _{f}+{F}_{xrr})l_{s} \end{aligned}$$

where \(\delta _{f}\) and \({F}_{xi}\) denote the steering input angle and the longitudinal force, respectively.

Fig. 1
figure 1

Schematic diagram of the electric vehicle model

Full size image

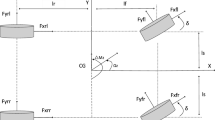
Since the four wheels of electric vehicle model are symmetrical on both sides, it is reasonable to give the bicycle model depicted in Fig. 2 for the simplification of controller design. Then, we construct the following vehicle handling dynamic model [25]:

Fig. 2
figure 2

Schematic diagram of the bicycle model

Full size image
$$\begin{aligned} \left\{ \begin{array}{l} mv_{x}{\dot{\beta }}(t)={F}_{yf}(t)+{F}_{yr}(t)-mv_{x}\varOmega _{z}(t) \\ I_{z}{\dot{\varOmega }}_{z}(t)=l_{f}{F}_{yf}(t)-l_{r}{F}_{yr}(t)+M_{z}(t) \end{array} \right. \end{aligned}$$
(1)

where the FR lateral forces are represented by \({F}_{yf}\) and \({F}_{yr}\), respectively, and they are given by

$$\begin{aligned} {F}_{yi}(t)=\zeta _{ i}\alpha _{i}(t), \quad (i=f,r) \end{aligned}$$
(2)

where \(\zeta _{f}\) and \(\zeta _{r}\) represent the cornering stiffness of FR wheel, respectively. In addition, the FR slip angles can be denoted by \(\alpha _{f}\) and \(\alpha _{r}\), respectively, and they satisfy

$$\begin{aligned} \alpha _{f}(t)&=\delta _{f}(t)-\frac{l_{f}\varOmega _{z}(t)}{v_{x}}-\beta (t) \nonumber \\ \alpha _{r}(t)&=\frac{l_{r}\varOmega _{z}(t)}{v_{x}}-\beta (t). \end{aligned}$$
(3)

By substituting (2) and (3) into (1), the state-space form of vehicle handling dynamic model (1) is deduced as

$$\begin{aligned} {\dot{\chi }}(t)={\mathbb {A}}\chi (t)+{\mathbb {B}}_{1}\omega (t)+{\mathbb {B}}_{2}u(t) \end{aligned}$$

where

$$\begin{aligned} {\mathbb {A}}= & {} \left[ \begin{array}{cc} -\frac{\zeta _{f}+\zeta _{ r}}{mv_{x}} &{} -1-\frac{l_{f} \zeta _{f}-l_{r}\zeta _{r}}{mv_{x}^{2}}\\ -\frac{l_{f}\zeta _{ f}-l_{r}\zeta _{ r}}{I_{z}} &{} -\frac{l_{f}^{2}\zeta _{ f}+l_{r}^{2}\zeta _{r}}{I_{z}v_{x}} \end{array} \right] \\ {\mathbb {B}}_{1}= & {} \left[ \begin{array}{c} \frac{\zeta _{ f}}{mv_{x}}\\ \frac{l_{f}\zeta _{ f}}{I_{z}} \end{array} \right] ,\quad {\mathbb {B}}_{2}=\left[ \begin{array}{c} 0\\ \frac{1}{I_{z}} \end{array} \right] ,\quad \omega (t)=\delta _{f}(t) \\ \chi (t)= & {} \left[ \beta (t)~~\varOmega _{z}(t)\right] ^{T}, \quad u(t)=M_{z}(t) .\end{aligned}$$

2.2 IT2 Fuzzy Vehicle Dynamic Model

The following IT2 fuzzy model depicts the electric vehicle systems with uncertainties.

Rule \(R_{i}\): IF\(\varrho _{1}(\chi (t))\) is \(M_{i1}\), \(\cdots\), and \(\varrho _{\rho }(\chi (t))\) is \(M_{i\rho }\), Then

$$\begin{aligned} {\dot{\chi }}(t)={\mathbb {A}}_{i}\chi (t)+{\mathbb {B}}_{1i}\omega (t) +{\mathbb {B}}_{2i}u(t) \end{aligned}$$

where \(\varrho (\chi (t))=[\varrho _{1}(\chi (t)),\ldots , \varrho _{\rho }(\chi (t))]\) represent the premise variables. \(M_{is}\) denotes the ith fuzzy set, \(s\in \{1,2,\ldots , \rho \}\). \({\mathbb {A}}_{i}\), \({\mathbb {B}}_{1i}\), and \({\mathbb {B}}_{2i}\) are known matrices. The firing strength of the ith rule can be expressed by the following interval sets:

$$\begin{aligned} {\tilde{\xi }}_{i}(\chi (t))&=[{\underline{\xi }}_{i}(\chi (t)),~ {\overline{\xi }}_{i}(\chi (t))],\quad i\in \{1,2,\ldots , \wp \} \end{aligned}$$

where

$$\begin{aligned} {\underline{\xi }}_{i}(\chi (t))&=\prod _{s=1}^{\rho }{\underline{\mu }}_{M_{is}}(\varrho _{s}(\chi (t)))\ge 0 \\ {\overline{\xi }}_{i}(\chi (t))&=\prod _{s=1}^{\rho }{\overline{\mu }}_{M_{is}}(\varrho _{s}(\chi (t)))\ge 0 \\ 0\le {\underline{\mu }}&_{M_{is}}(\varrho _{s}(\chi (t))) \le {\overline{\mu }}_{M_{is}}(\varrho _{s}(\chi (t)))\\ {\underline{\xi }}_{i}(\chi (t))&\le {\overline{\xi }}_{i}(\chi (t)) \end{aligned}$$

then, the IT2 fuzzy vehicle model is obtained:

$$\begin{aligned} {\dot{\chi }}(t)=\sum _{i=1}^{\wp }\xi _{i}(\chi (t))({\mathbb {A}}_{i}\chi (t) +{\mathbb {B}}_{1i}\omega (t)+{\mathbb {B}}_{2i}u(t)) \end{aligned}$$
(4)

where

$$\begin{aligned} {\hat{\xi }}_{i}(\chi (t))&={\underline{\xi }}_{i}(\chi (t)){\underline{\nu }}_{i}(\chi (t))+{\overline{\xi }}_{i}(\chi (t)){\overline{\nu }}_{i}(\chi (t))\\ \xi _{i}(\chi (t))&=\frac{{\hat{\xi }}_{i}(\chi (t))}{\sum _{i=1}^{\wp }{\hat{\xi }}_{i}(\chi (t))}, \quad \sum _{i=1}^{\wp }\xi _{i}(\chi (t))=1 \end{aligned}$$

with the weighting functions \({\underline{\nu }}_{i}(\chi (t))\) and \({\overline{\nu }}_{i}(\chi (t))\) satisfy \(0\le {\underline{\nu }}_{i}(\chi (t))\le 1,~0\le {\overline{\nu }}_{i}(\chi (t))\le 1,~ {\underline{\nu }}_{i}(\chi (t))+{\overline{\nu }}_{i}(\chi (t))=1,\) and \(\xi _{i}(\chi (t))\) represents the normalized MF.

The vehicle mass and moment of inertia actually vary in a given range, i.e., \(m\in [m_{\mathrm{min}},~m_{\mathrm{max}}]\) and \(I_{z}\in [I_{z\text {min}},~I_{z\text {max}}]\). Then, the premise variables \(\frac{1}{m}\) and \(\frac{1}{I_{z}}\) involved in the IT2 fuzzy vehicle model (4) are represented by

$$\begin{aligned} l_{1}=\frac{1}{m}\in [l_{1\text {min}},~l_{1\text {max}}],\quad l_{2}=\frac{1}{I_{z}}\in [l_{2\text {min}},~l_{2\text {max}}] \end{aligned}$$

the LUMFs of IT2 fuzzy systems are listed in Table 1.

Table 1 LUMFs
Full size table

On account of the influence of road conditions and wear of the tires, the cornering stiffness may become a varying parameter. According to [11], the variables \(\triangle \zeta _{\alpha f}\) and \(\triangle \zeta _{\alpha r}\) should be considered, we have

$$\begin{aligned} {F}_{yf}(t)&=(\zeta _{\alpha f}+\triangle \zeta _{\alpha f})\alpha _{f}(t) \\ {F}_{yr}(t)&=(\zeta _{\alpha r}+\triangle \zeta _{\alpha r})\alpha _{r}(t) \ \end{aligned}$$

then, the IT2 fuzzy vehicle model is represented by

$$\begin{aligned} {\dot{\chi }}(t)&=\sum _{i=1}^{\wp }\xi _{i}(\chi (t))[({\mathbb {A}}_{i} +\triangle {\mathbb {A}}_{i})\chi (t)+({\mathbb {B}}_{1i}+\triangle {\mathbb {B}}_{1i})\omega (t) \\&\quad +{\mathbb {B}}_{2i}u(t)] \end{aligned}$$

where \(\triangle {\mathbb {A}}_{i}\) and \(\triangle {\mathbb {B}}_{1i}\) represent the variations of matrices \({\mathbb {A}}_{i}\) and \({\mathbb {B}}_{1i}\), respectively. By adopting the norm-bounded method, the definitions of \(\triangle {\mathbb {A}}_{i}\) and \(\triangle {\mathbb {B}}_{1i}\) are expressed as

$$\begin{aligned}{}[\triangle {\mathbb {A}}_{i}~\triangle {\mathbb {B}}_{1i}]=HF[E_{i}~E_{1i}] \end{aligned}$$

where the matrices \(F=\text {diag}\{\lambda _{1},\lambda _{2},\lambda _{3},\lambda _{4}\}\), H, \(E_{i}\) and \(E_{1i}\) are known constant matrices.

Remark 1

Considering that the road conditions are usually same for FR tyres, we can reasonably assume that the road coherent coefficients are identical, which can reduce the computational complexity. Based on the above analysis, we define \(\lambda _{1}=\lambda _{2}=\lambda _{3}=\lambda _{4}\).

As any actuation mechanisms may be constrained by inherent physical limitations, the control saturation needs to be taken into consideration in the controller design procedure. According to [46], the saturation function \({{sat}(u(t))}\) satisfies

$$\begin{aligned} {sat}(u(t))=\left\{ \begin{aligned}&u(t), \quad \text {if}~~|u(t)|\le \mu _{\mathrm{lim}} \\& {sign}(u(t))\mu _{\mathrm{lim}},\quad {\text {if}}~~|u(t)|>\mu _{\text{lim}} \end{aligned} \right. \end{aligned}$$

where \(\mu _{\mathrm{lim}}>0\) represents the limitation of control input.

Then, the IT2 fuzzy vehicle systems with saturation nonlinearity are expressed by

$$\begin{aligned} {\dot{\chi }}(t)=\sum _{i=1}^{\wp }\xi _{i}(\chi (t))[({\mathbb {A}}_{i}+\triangle {\mathbb {A}}_{i})\chi (t)\nonumber \\ \quad +({\mathbb {B}}_{1i}+\triangle {\mathbb {B}}_{1i})\omega (t) +{\mathbb {B}}_{2i}{\bar{u}}(t)]\nonumber \\=\sum _{i=1}^{\wp }\xi _{i}(\chi (t))\left[ ({\mathbb {A}}_{i} +\triangle {\mathbb {A}}_{i})\chi (t)+({\mathbb {B}}_{1i}+\triangle {\mathbb {B}}_{1i})\omega (t) \right. \nonumber \\\quad \left. +{\mathbb {B}}_{2i}\frac{1+\mathfrak {I}}{2}u(t) +{\mathbb {B}}_{2i}({\bar{u}}(t)-\frac{1+\mathfrak {I}}{2}u(t))\right] \end{aligned}$$
(5)

where \(0<\mathfrak {I}<1\) and \({\bar{u}}(t)={{sat}(u(t))}\).

2.3 Sensor Failures

Due to the wear and overtime operation of machinery, the IT2 vehicle model will inevitably suffer from sensor failure. To handle this problem, the corresponding failure model is adopted here [47]:

$$\begin{aligned} {\tilde{\chi }}_{j}(t)=\beta _{\epsilon j}\chi _{j}(t),\quad j=1,2,\ldots ,k \end{aligned}$$

where

$$\begin{aligned} 0\le {\underline{\beta }}_{\epsilon j} \le \beta _{\epsilon j}\le {\overline{\beta }}_{\epsilon j},\quad 0\le \beta _{\epsilon j} \le 1 \end{aligned}$$

with the variable \(\beta _{\epsilon j}\) quantifies the sensor failures [19]. To this end, we define

$$\begin{aligned} {\tilde{\chi }}(t)=\beta _{\epsilon }\chi (t),\quad \beta _{\epsilon }=\text {diag}\{\beta _{\epsilon 1},\ldots ,\beta _{\epsilon k}\} .\end{aligned}$$

2.4 IT2 Fuzzy Controller

Based on the mismatched MFs, an IT2 fuzzy state-feedback controller is constructed:

Controller Rule\(R_{j}\): IF\(\partial _{1}(\chi (t))\) is \(W_{j1}\) and \(\cdots\) and \(\partial _{\rho }(\chi (t))\) is \(W_{j\rho }\), Then

$$\begin{aligned} u(t)={\mathcal {K}}_{j}{\tilde{\chi }}(t) \end{aligned}$$

where \(\partial (\chi (t))=[\partial _{1}(\chi (t)),\ldots , \partial _{\rho }(\chi (t))]\) represent the premise variables. \(W_{js}\) is the jth fuzzy set, \(s\in \{1,2,\ldots ,\rho \}\). Then, the firing strength of the jth rule is represented by the following interval sets:

$$\begin{aligned} {\tilde{\eta }}_{j}(\chi (t))&=[{\underline{\eta }}_{j}(\chi (t)),~ {\overline{\eta }}_{j}(\chi (t))], \quad j\in \{1,2,\ldots , \wp \} \end{aligned}$$

where

$$\begin{aligned} {\underline{\eta }}_{j}(\chi (t))&=\prod _{s=1}^{\rho }{\underline{\mu }}_{W_{js}}(\partial _{s}(\chi (t)))\ge 0\\ {\overline{\eta }}_{j}(\chi (t))&=\prod _{s=1}^{\rho }{\overline{\mu }}_{W_{js}}(\partial _{s}(\chi (t)))\ge 0 \\ 0\le {\underline{\mu }}_{W_{js}}&(\partial _{s}(\chi (t))) \le {\overline{\mu }}_{W_{js}}(\partial _{s}(\chi (t))) \\ {\underline{\eta }}_{j}(\chi (t))&\le {\overline{\eta }}_{j}(\chi (t)) \end{aligned}$$

then, the IT2 fuzzy controller is designed as

$$\begin{aligned} u(t)=\sum _{j=1}^{\wp }\eta _{j}(\chi (t)){\mathcal {K}}_{j}{\tilde{\chi }}(t) \end{aligned}$$
(6)

where

$$\begin{aligned} {\hat{\eta }}_{j}(\chi (t))&={\underline{\emptyset }}_{j}(\chi (t)){\underline{\eta }}_{j}(\chi (t)) +{\overline{\emptyset }}_{j}(\chi (t)){\overline{\eta }}_{j}(\chi (t))\\ \eta _{j}(\chi (t))&=\frac{{\hat{\eta }}_{j}(\chi (t))}{\sum _{k=1}^{\wp }{\hat{\eta }}_{k}(\chi (t))}\ge 0,\quad \sum _{j=1}^{\wp }\eta _{j}(\chi (t))=1 \end{aligned}$$

with the weighting functions \({\underline{\emptyset }}_{j}(\chi (t))\) and \({\overline{\emptyset }}_{j}(\chi (t))\) satisfy \(0\le {\underline{\emptyset }}_{j}(\chi (t))\le 1,~0\le {\overline{\emptyset }}_{j}(\chi (t))\le 1,~ {\underline{\emptyset }}_{j}(\chi (t))+{\overline{\emptyset }}_{j}(\chi (t))=1,\) and \(\eta _{j}(\chi (t))\) denotes the normalized MF. For brevity, the MFs are defined as \(\xi _{i}(\chi (t))\triangleq \xi _{i}\) and \(\eta _{j}(\chi (t))\triangleq \eta _{j}\).

For electric vehicle systems, the sideslip angle and yaw rate are defined as two control outputs

$$\begin{aligned} z_{1}(t)=&[1~~0]\chi (t)=C_{1}\chi (t) \nonumber \\ z_{2}(t)=&[0~~1]\chi (t)=C_{2}\chi (t) .\end{aligned}$$
(7)

In the lateral stability control, our control objective is to make the actual yaw rate follow its reference value. Then, we define the desired yaw rate [25]:

$$\begin{aligned} \varOmega _{zd}(t)=\frac{v_{x}}{l(1+\kappa _{us}v_{x}^{2})}\delta _{f}(t) \end{aligned}$$

where \(l=l_{f}+l_{r}\) represents the distance between the FR axles and \(\kappa _{us}\) stands for the stability factor.

When the disturbance exists, the \(L_{2}\) gain is regarded as the performance measure to represent the size of the control output signal \(z_{1}(t)\).

$$\begin{aligned} \Vert T_{z1\omega }\Vert _{\infty }= {sup}\frac{\Vert z_{1}(t)\Vert _{2}}{\Vert \omega (t)\Vert _{2}},\quad \Vert \omega (t)\Vert _{2}\ne 0 \end{aligned}$$

and \(\Vert z_{2}(t)\Vert _{\infty }= {sup}_{t\in [0,~\infty )}\sqrt{z_{2}^{T}(t)z_{2}(t)}<\ell \Vert \omega (t)\Vert _{2}\), where \(\ell\) denotes a prescribed scalar.

3 Main Results

The sufficient conditions of system stability and IT2 fuzzy controller design are given in this section, which ensures that the IT2 fuzzy systems in (5) are quadratically stable and the \(L_{2}\) gain \(\Vert T_{z1\omega }\Vert _{\infty }\) is achieved. Before getting the main results, the following lemmas should be introduced.

Lemma 1

[46] For the saturation constraint, if\(\Vert u(t)\Vert\)\(\le \frac{u_{\mathrm{lim}}}{\mathfrak {I}}\)holds, we get

$$\begin{aligned} \Vert {\bar{u}}(t)-\frac{1+\mathfrak {I}}{2}u(t)\Vert \le \frac{1-\mathfrak {I}}{2}\Vert u(t)\Vert \end{aligned}$$

and the above condition is equivalent to

$$\begin{aligned}&{}\left[ {\bar{u}}(t)-\frac{1+\mathfrak {I}}{2}u(t)\right] ^{T} \left[ {\bar{u}}(t)-\frac{1+\mathfrak {I}}{2}u(t)\right] \\&\quad \le \left( \frac{1-\mathfrak {I}}{2}\right) ^{2}\Vert u(t)\Vert ^{2} \Vert u(t)\Vert \end{aligned}$$

where\({0}<{\mathfrak{I}}<{1}\).

Lemma 2

[10] Given any matricesV, FandN, if\(\Vert F\Vert \le I\)holds, then

$$\begin{aligned} VFN+N^{T}F^{T}V^{T}\le \epsilon ^{-1}VV^{T}+\epsilon N^{T}N \end{aligned}$$

where the scalar\(\epsilon >0\).

Theorem 1

Given positive constants\(\ell\), \(\varphi\), \(\mathfrak {I}\), \(\mu _{\mathrm{lim}}\), under the condition\(\eta _{j}-\sigma _{j}\xi _{j}\ge 0\)\((0<\sigma _{j}<1)\), the IT2 fuzzy systems in (5) are quadratically stable and the\(L_{2}\)gain\(\Vert T_{z1\omega }\Vert _{\infty }\)is achieved, there exist matrices\(\varPhi _{i}>0\), \(Q>0\), control gain\(\bar{{\mathcal {K}}}_{j}\), nonsingular matrixWand scalars\(\epsilon _{1}>0\), \(\epsilon _{2}>0\), \(\epsilon _{3}>0\)such that for\(i, j=1,\ldots , 4\):

$$\begin{aligned}&\varPsi _{ij}-\varPhi _{i}<0 \end{aligned}$$
(8)
$$\begin{aligned}&\sigma _{i}\varPsi _{ii}-\sigma _{i}\varPhi _{i}+\varPhi _{i}<0 \end{aligned}$$
(9)
$$\begin{aligned}&\sigma _{j}\varPsi _{ij}-\sigma _{j}\varPhi _{i}+\varPhi _{i}+\sigma _{i}\varPsi _{ji} -\sigma _{i}\varPhi _{j}+\varPhi _{j}\le 0,~~i<j \end{aligned}$$
(10)
$$\begin{aligned}&\left[ \begin{array}{cc} Q &{} QC_{2}^{T} \\ *&{} I \end{array} \right] >0 \end{aligned}$$
(11)
$$\begin{aligned}&\left[ \begin{array}{cc} \left( \frac{\mu _{\mathrm{lim}}}{\mathfrak {I}}\right) ^{2} &{} \bar{{\mathcal {K}}}_{j}\beta _{\epsilon }\\ *&{} Q\varphi ^{-1} \end{array} \right] \ge 0 \end{aligned}$$
(12)
$$\begin{aligned}&\beta _{\epsilon }Q=W\beta _{\epsilon } \end{aligned}$$
(13)

where

$$\begin{aligned} \varPsi _{ij}&= \left[ \begin{array}{ccc} \varPsi _{ij}^{11} &{} \varPsi _{ij}^{12} &{} \varPsi _{ij}^{13} \\ *&{} \varPsi _{ij}^{22} &{} 0 \\ *&{} *&{} -I \end{array} \right] \\ \varPsi _{ij}^{12}&= \left[ \begin{array}{ccc} 0 &{} QE_{i}^{T} &{} \beta _{\epsilon }^{T}\bar{{\mathcal {K}}}_{j}^{T}\\ E_{1i}^{T} &{} 0 &{} 0 \end{array} \right] \\ \varPsi _{ij}^{13}&= \left[ \begin{array}{c} QC_{1i}^{T}\\ 0 \end{array} \right] ,\quad \varPsi _{ij}^{11}= \left[ \begin{array}{cc} {\bar{\varPsi }}_{ij}^{11} &{} {\mathbb {B}}_{1i} \\ *&{} -\ell ^{2}I \end{array} \right] \\ \varPsi _{ij}^{22}&=\text {diag} \left\{ -\epsilon _{3}^{-1}I~-\epsilon _{2}^{-1}I~ -\epsilon _{1}^{-1}\left( \frac{2}{1-\mathfrak {I}}\right) ^{2}I\right\} \\ {\bar{\varPsi }}_{ij}^{11}&=[{\mathbb {A}}_{i}Q]_{s}+\epsilon _{2}^{-1}HH^{T}+\epsilon _{3}^{-1}H_{1}H_{1}^{T}\\&\quad +(1+\mathfrak {I}){\mathbb {B}}_{2i}\bar{{\mathcal {K}}}_{j}\beta _{\epsilon } +\epsilon _{1}^{-1}{\mathbb {B}}_{2i}{\mathbb {B}}_{2i}^{T} \end{aligned}.$$

Moreover, the IT2 fuzzy controller gain is shown as \({\mathcal {K}}_{j}=\bar{{\mathcal {K}}}_{j}W^{-1}\).

Proof

Define the Lyapunov function:

$$\begin{aligned} {\mathcal {V}}(t)=\chi ^{T}(t){\mathcal {P}}\chi (t),\quad {\mathcal {P}}={\mathcal {P}}^{T}>0 \end{aligned}$$
(14)

then, the time derivative of \({\mathcal {V}}(t)\) is obtained as

$$\begin{aligned} \dot{{\mathcal {V}}}(t)={\dot{\chi }}^{T}(t){\mathcal {P}}\chi (t)+\chi ^{T}(t){\mathcal {P}}{\dot{\chi }}(t) \\ =\sum _{i=1}^{4}\xi _{i}\left[ \chi ^{T}(t)({\mathbb {A}}_{i}+\triangle {\mathbb {A}}_{i})^{T}{\mathcal {P}}\chi (t)\right. \\ \left. +\omega ^{T}(t)({\mathbb {B}}_{1i}+\triangle {\mathbb {B}}_{1i})^{T}{\mathcal {P}}\chi (t)\right. \\ \left. +\frac{1+\mathfrak {I}}{2}u^{T}(t){\mathbb {B}}_{2i}^{T}{\mathcal {P}}\chi (t) \right. \\ \left. +\left( {\bar{u}}(t)-\frac{1+\mathfrak {I}}{2}u(t)\right) ^{T}{\mathbb {B}}_{2i}^{T}{\mathcal {P}}\chi (t)\right. \\ \left. +\chi ^{T}(t){\mathcal {P}}({\mathbb {A}}_{i}+\triangle {\mathbb {A}}_{i})\chi (t)\right. \\ \left. +\chi ^{T}(t){\mathcal {P}}({\mathbb {B}}_{1i}+\triangle {\mathbb {B}}_{1i})\omega (t) \right. \\ \left. +\frac{1+\mathfrak {I}}{2}\chi ^{T}(t){\mathcal {P}}{\mathbb {B}}_{2i}u(t) \right. \\ \left. +\chi ^{T}(t){\mathcal {P}}{\mathbb {B}}_{2i} \left( {\bar{u}}(t)-\frac{1+\mathfrak {I}}{2}u(t)\right) \right] \end{aligned}.$$

By adopting Lemmas 1 and 2, together with (6), the following inequality holds

$$\begin{aligned} \dot{{\mathcal {V}}}(t)\le&\sum _{i=1}^{4}\sum _{j=1}^{4}\xi _{i}\eta _{j}[\chi ^{T}(t)({\mathbb {A}}_{i}^{T}{\mathcal {P}}+{\mathcal {P}}{\mathbb {A}}_{i}+\epsilon _{2}E_{i}^{T}E_{i}\\&+\epsilon _{2}^{-1}{\mathcal {P}}HH^{T}{\mathcal {P}}+\epsilon _{3}^{-1}{\mathcal {P}}H_{1}H_{1}^{T}{\mathcal {P}} \\&+\frac{1+\mathfrak {I}}{2}\beta _{\epsilon }^{T}{\mathcal {K}}_{j}^{T}{\mathbb {B}}_{2i}^{T}{\mathcal {P}} +\frac{1+\mathfrak {I}}{2}{\mathcal {P}}{\mathbb {B}}_{2i}\mathcal {{\mathcal {K}}}_{j}\beta _{\epsilon } \\&+\epsilon _{1}^{-1}{\mathcal {P}}{\mathbb {B}}_{2i}{\mathbb {B}}_{2i}^{T}{\mathcal {P}} +\epsilon _{1}\left( \frac{1-\mathfrak {I}}{2})^{2}\beta _{\epsilon }^{T}{\mathcal {K}}_{j}^{T}{\mathcal {K}}_{j}\beta _{\epsilon }\right) \chi (t)\\&+\chi ^{T}(t){\mathcal {P}}{\mathbb {B}}_{1i}\omega (t)+\omega ^{T}(t){\mathbb {B}}_{1i}^{T}{\mathcal {P}}\chi (t)\\&+\epsilon _{3}\omega ^{T}(t)E_{1i}^{T}E_{1i}\omega (t)] \end{aligned}$$

then, we have

$$\begin{aligned} J&=\dot{{\mathcal {V}}}(t)+z_{1}^{T}(t)z_{1}(t)-\ell ^{2}\omega ^{T}(t)\omega (t)\nonumber \\&\le \varGamma ^{T}(t)\left( \sum _{i=1}^{4}\sum _{j=1}^{4}\xi _{i}\eta _{j}\varOmega _{ij}\right) \varGamma (t) \end{aligned}$$
(15)

where

$$\begin{aligned} \varOmega _{ij}&= \left[ \begin{array}{cc} \varOmega _{ij1} &{} {\mathcal {P}}{\mathbb {B}}_{1i} \\ *&{} -\ell ^{2}I+\epsilon _{3}E_{1i}^{T}E_{1i} \end{array} \right] \\ \varGamma ^{T}(t)&= \left[ \begin{array}{cc} \chi ^{T}(t)&\omega ^{T}(t) \end{array} \right] \\ \varOmega _{ij1}&=[{\mathcal {P}}{\mathbb {A}}_{i}]_{s}+\epsilon _{2}E_{i}^{T}E_{i} +\epsilon _{2}^{-1}{\mathcal {P}}HH^{T}{\mathcal {P}}\\&\quad +\epsilon _{3}^{-1}{\mathcal {P}}H_{1}H_{1}^{T}{\mathcal {P}} +\frac{1+\mathfrak {I}}{2}\beta _{\epsilon }^{T}{\mathcal {K}}_{j}^{T}{\mathbb {B}}_{2i}^{T}{\mathcal {P}} \\&~~~+\frac{1+\mathfrak {I}}{2}{\mathcal {P}}{\mathbb {B}}_{2i}{\mathcal {K}}_{j}\beta _{\epsilon }+\epsilon _{1}^{-1}{\mathcal {P}}{\mathbb {B}}_{2i}{\mathbb {B}}_{2i}^{T}{\mathcal {P}}\\&\quad +\epsilon _{1}\left( \frac{1-\mathfrak {I}}{2}\right) ^{2}\beta _{\epsilon }^{T}{\mathcal {K}}_{j}^{T}{\mathcal {K}}_{j}\beta _{\epsilon }+C_{1i}^{T}C_{1i} .\end{aligned}$$

Considering \(\varOmega _{ij}<0\), it follows that \(J<0\). Then, defining \(Q={\mathcal {P}}^{-1}\) and \(\varUpsilon =\text {diag}\{{\mathcal {P}}^{-1}~I\}\), by performing a congruence transformation with \(\varUpsilon\) to the matrix \(\varOmega _{ij}\), the matrix \(\varOmega _{ij}\) is equivalent to

$$\begin{aligned} \varPsi _{ij}&= \left[ \begin{array}{cc} \varPsi _{ij1} &{} {\mathbb {B}}_{1i} \\ *&{} -\ell ^{2}I+\epsilon _{3}E^{T}_{1i}E_{1i}^{T} \end{array} \right] \\ \varPsi _{ij1}&=[{\mathbb {A}}_{i}Q]_{s}+\epsilon _{2}QE_{i}^{T}E_{i}Q+\epsilon _{2}^{-1}HH^{T}+\epsilon _{3}^{-1}H_{1}H_{1}^{-1}\\&\quad +(1+\mathfrak {I}){\mathbb {B}}_{2i}{\mathcal {K}}_{j}\beta _{\epsilon }Q+\epsilon _{1}^{-1}{\mathbb {B}}_{2i}{\mathbb {B}}_{2i}^{T}\\&\quad +\epsilon _{1}\left( \frac{1-\mathfrak {I}}{2}\right) ^{2}Q\beta _{\epsilon }^{T}{\mathcal {K}}_{j}^{T}{\mathcal {K}}_{j}\beta _{\epsilon }Q+QC_{1i}^{T}C_{1i}Q. \end{aligned}$$

To reduce the conservatism of the systems, the slack matrices are introduced. Define \(\sum _{i=1}^{4}\sum _{j=1}^{4}\xi _{i}(\xi _{j}-\eta _{j})\varPhi _{i}=0\), where \(\varPhi _{i}=\varPhi _{i}^{T}\) denotes an arbitrary matrix with appropriate dimensions. Then, it follows that

$$\begin{aligned} \sum _{i=1}^{4}\sum _{j=1}^{4}\xi _{i}\eta _{j}\varPsi _{ij}=&\sum _{i=1}^{4}\sum _{j=1}^{4}[\xi _{i}\xi _{j}(\varPhi _{i}-\sigma _{j}\varPhi _{i}+\sigma _{j}\varPsi _{ij})\\&+\xi _{i}(\eta _{j}-\sigma _{j}\xi _{j})(\varPsi _{ij}-\varPhi _{i})] \\ =&\sum _{i=1}^{4}\sum _{j=i}^{4}\xi _{i}^{2}(\sigma _{i}\varPsi _{ii}-\sigma _{i}\varPhi _{i}+\varPhi _{i})\\&+\sum _{i=1}^{3}\sum _{j=i+1}^{4}\xi _{i}\xi _{j}(\sigma _{j}\varPsi _{ij}-\sigma _{j}\varPhi _{i}+\varPhi _{i} \\&+\sigma _{i}\varPsi _{ji}-\sigma _{i}\varPhi _{j}+\varPhi _{j})\\&+\sum _{i=1}^{4}\sum _{j=1}^{4}\xi _{i}(\eta _{j}-\sigma _{j}\xi _{j})(\varPsi _{ij}-\varPhi _{i}) \end{aligned}.$$

Under the condition \(\eta _{j}-\sigma _{j}\xi _{j}\ge 0\), from the inequalities (8)–(10), we have

$$\begin{aligned} \dot{{\mathcal {V}}}(t)+z_{1}^{T}(t)z_{1}(t)-\ell ^{2}\omega (t)^{T}\omega (t) <0,\quad \omega (t)\in [0,\infty ) \end{aligned}$$
(16)

by integrating both sides of (16), it follows that \(\Vert z_{1}(t)\Vert _{2} <\ell \Vert \omega (t)\Vert _{2}\). According to the conditions in Theorem 1, if \(\omega (t)=0\) holds, we can get \(\dot{{\mathcal {V}}}(t)<0\). Therefore, it is concluded that the IT2 fuzzy systems (5) with \(\omega (t)=0\) are quadratically stable.

In addition, if the following condition holds

$$\begin{aligned} \left[ \begin{array}{cc} {\mathcal {P}} &{} C_{2}^{T} \\ *&{} I \end{array} \right] >0 \end{aligned}$$
(17)

using the Schur complement, we have \(C_{2}^{T}C_{2}<{\mathcal {P}}\). From (14) and (15), the condition \(\chi ^{T}(t){\mathcal {P}}\chi (t)<\ell ^{2}\int _{0}^{t}\)\(\omega ^{T}(s)\omega (s)ds\) holds if \(\varOmega _{ij}<0\). Then, according to (7) and (17), the following condition holds for \(t\ge 0\)

$$\begin{aligned} z_{2}^{T}(t)z_{2}(t)&=\chi ^{T}(t)C_{2}^{T}C_{2}\chi (t)<\chi ^{T}(t){\mathcal {P}}\chi (t)\\&<\ell ^{2}\int _{0}^{t}\omega ^{T}(s)\omega (s)ds\le \ell ^{2}\int _{0}^{\infty }\omega ^{T}(s)\omega (s)ds \end{aligned}$$

then, one can have \(\Vert z_{2}(t)\Vert _{\infty }<\ell \Vert \omega (t)\Vert _{2}\). Defining \(\varUpsilon =\text {diag}\{{\mathcal {P}}^{-1}~I\}\), by performing a congruence transformation with \(\varUpsilon\) to (17), it holds that

$$\begin{aligned} \left[ \begin{array}{cc} {\mathcal {P}}^{-1} &{} {\mathcal {P}}^{-1}C_{2}^{T}\\ *&{} I \end{array} \right] >0. \end{aligned}$$
(18)

Define \(Q={\mathcal {P}}^{-1}\), it can be shown that the inequality (18) is equivalent to (11).

According to the constraint condition \(\Vert u(t)\Vert \le \frac{\mu _{\mathrm{lim}}}{\mathfrak {I}}\), we get

$$\begin{aligned} \left| \sum _{j=1}^{4}\eta _{j}{\mathcal {K}}_{j}\beta _{\epsilon }\chi (t)\right| \le \frac{\mu _{\mathrm{lim}}}{\mathfrak {I}} \end{aligned}$$

then, the inequality \(|{\mathcal {K}}_{j}\beta _{\epsilon }\chi (t)|\le \frac{\mu _{\mathrm{lim}}}{\mathfrak {I}}\) holds.

Considering \(\varOmega ({\mathcal {K}})=\{\chi (t)|\chi ^{T}(t)\beta _{\epsilon }^{T}{\mathcal {K}}_{j}^{T}{\mathcal {K}}_{j}\beta _{\epsilon }\chi (t)|\le (\frac{\mu _{\mathrm{lim}}}{\mathfrak {I}})^{2}\}\), the equivalent condition for an ellipsoid \(\varOmega ({\mathcal {P}},\)\(\varphi )=\{\chi (t)|\chi ^{T}(t){\mathcal {P}}\chi (t)\le \varphi \}\) being a subset of \(\varOmega ({\mathcal {K}})\) is given by [48]

$$\begin{aligned} {\mathcal {K}}_{j}\beta _{\epsilon } \left( \frac{{\mathcal {P}}\mathcal {}}{\varphi }\right) ^{-1} ({\mathcal {K}}_{j}\beta _{\epsilon })^{T}\le \left( \frac{\mu _{\mathrm{lim}}}{\mathfrak {I}}\right) ^{2}. \end{aligned}$$

By employing the Schur complement, the following condition holds

$$\begin{aligned} \left[ \begin{array}{cc} \left( \frac{\mu _{\mathrm{lim}}}{\mathfrak {I}}\right) ^{2}I &{} {\mathcal {K}}_{j}\beta _{\epsilon }\left( \frac{{\mathcal {P}}}{\varphi }\right) ^{-1} \\ *&{} \left( \frac{{\mathcal {P}}}{\varphi }\right) ^{-1}I \end{array} \right] \ge 0. \end{aligned}$$
(19)

Define \(Q={\mathcal {P}}^{-1}\), it can be seen from the condition (12) that the condition (19) holds. The proof is finished. \(\square\)

Based on the above discussion and analysis, the minimization \(\ell\) can be obtained

$$\begin{aligned} \text {minimization}~~\ell ~~&\text {subject}~~\text {to}~~\text {linear matrix inequalities}\nonumber \\&\text {(LMIs)}~~(8)-(12) \end{aligned}$$
(20)

by adopting MATLAB LMI toolbox, and we can solve the convex optimization problem.

Remark 2

It is difficult to solve the equality restrictive condition (13) by MATLAB LMI toolbox, so the constrained condition should be converted into the following form [49, 50]

$$\begin{aligned}{}[\beta _{\epsilon }Q-W\beta _{\epsilon }]^{T}[\beta _{\epsilon }Q-W\beta _{\epsilon }]<\varsigma I \end{aligned}$$

where \(\varsigma\) denotes a small positive constant. By the Schur complement, we obtain

$$\begin{aligned} \left[ \begin{array}{cc} -\varsigma I &{} [\beta _{\epsilon }Q-W\beta _{\epsilon }]^{T}\\ *&{} -I \end{array} \right] <0. \end{aligned}$$
(21)

4 Simulation Results

Table 2 Vehicle parameter values in the simulation
Full size table

To testify the effectiveness of the proposed control scheme, simulation results for vehicle dynamic model are given. The vehicle parameters referred from [7] are listed in Table 2, where the vehicle mass and moment of inertia are assumed as \(20\%\) variations, and the cornering stiffness is considered as \(30\%\) variation. Define \({\underline{\emptyset }}_{j}(t)={\overline{\emptyset }}_{j}(t)=0.5\), and the LUMFs of the IT2 fuzzy controller are defined as

$$\begin{aligned} {\underline{\eta }}_{1}&={\underline{\mu }}_{W_{11}}={\overline{\eta }}_{1}={\overline{\mu }}_{W_{11}}=e^{-\frac{3-\chi _{1}^{2}(t)}{2.5}},\\ {\underline{\eta }}_{2}&={\underline{\mu }}_{W_{21}}={\overline{\eta }}_{2}={\overline{\mu }}_{W_{21}}=e^{-\frac{2-\chi _{1}^{2}(t)}{2.5}}, \\ {\underline{\eta }}_{3}&={\underline{\mu }}_{W_{31}}={\overline{\eta }}_{3}={\overline{\mu }}_{W_{31}}=e^{-\frac{1-\chi _{1}^{2}(t)}{2.5}},\\ {\underline{\eta }}_{4}&={\underline{\mu }}_{W_{41}}={\overline{\eta }}_{4}={\overline{\mu }}_{W_{41}}=1-{\overline{\mu }}_{W_{11}}-{\overline{\mu }}_{W_{21}}-{\overline{\mu }}_{W_{31}} .\end{aligned}$$

It is noted that the electric vehicle systems are controlled to make a single-lane change maneuver. Define \(\mu _{\mathrm{lim}}=7000\text {Nm}\), \(\beta _{\epsilon }=\text {diag}\{0.4,0.6\}\), \(\mathfrak{I}={0.1}\), and \(\varphi =0.05\). By solving the convex optimization problem (20) and (21), under the situation of optimal \(\ell (\ell _{\mathrm{min}}=2.405)\), the controller gains are calculated as

$$\begin{aligned} {\mathcal {K}}_{1}&=10^{4}\times \left[ \begin{array}{cc} 0.8140&-1.6618 \end{array} \right] \\ {\mathcal {K}}_{2}&=10^{4}\times \left[ \begin{array}{cc} 0.7676&-1.6299 \end{array} \right] \\ {\mathcal {K}}_{3}&=10^{4}\times \left[ \begin{array}{cc} 0.8240&-1.6851 \end{array} \right] \\ {\mathcal {K}}_{4}&=10^{4}\times \left[ \begin{array}{cc} 0.8099&-1.6442 \end{array} \right] \end{aligned}$$
Fig. 3
figure 3

Steering input angle

Full size image
Fig. 4
figure 4

The trajectories of sideslip angle

Full size image
Fig. 5
figure 5

The trajectories of yaw rate

Full size image
Fig. 6
figure 6

The trajectory of yaw moment

Full size image
Fig. 7
figure 7

The trajectory of lateral acceleration

Full size image
Fig. 8
figure 8

The trajectories of lateral tyre forces

Full size image

The steering input angle is shown in Fig. 3. Figures 4 and 5 plot the trajectories of the sideslip angle and yaw rate, respectively. From Figs. 4 and 5, we observe that the state trajectories of controlled systems can convergence to 0 faster than the uncontrolled systems. It is noted that the trajectory of the sideslip angle of controlled systems varies within a small range, which means that the corrected linear tire model can meet lots of complicated road conditions. In particular, from Fig. 5, the trajectory of the yaw rate of controlled systems can follow the reference value with a small error. Figure 6 depicts the response of the yaw moment. The trajectories of lateral acceleration and lateral tyre forces are presented in Figs. 7 and 8, respectively. In terms of the above analysis results, we can have that the yaw-moment controller can enhance the vehicle handling and stability.

5 Conclusion

The yaw-moment control issue for uncertain electric vehicle systems with sensor failures and actuator saturation has been investigated. With the LUMFs, the IT2 fuzzy model for uncertain electric vehicle systems has been developed to tackle the uncertainties. By employing a norm-bounded approach, the saturation nonlinear problem has been availably handled. Moreover, the IT2 fuzzy controller has been presented to ensure that the derived IT2 fuzzy systems are quadratically stable and the \(L_{2}\) gain \(\Vert T_{z1\omega }\Vert _{\infty }\) is achieved. Finally, simulation results have illustrated the feasibility of the proposed IT2 fuzzy control strategy. In future work, we will consider the sliding mode control issue [51,52,53] for uncertain electric vehicle systems with actuator failures.