An integrated group FWA-ELECTRE III approach based on interval type-2 fuzzy sets for solving the MCDM problems using limit distance mean

Abstract

The material handling equipment (MHE) has a close connection with layout of machinery and plays the important role in productivity of servicing or manufacturing systems. Since each of MHE has distinct characteristics than the others with respect to conflicting criteria and design experts may state the different subjective judgments with respect to qualitative criteria, the material handling equipment selection problem (MHESP) can be taken into account as a group multi-criteria decision-making (GMCDM) problem. In this paper, a version of type-2 fuzzy sets (T2FSs), named Gaussian interval type-2 fuzzy sets (GIT2FSs), is first used as an alternative to the traditional triangular membership functions (MFs) to weight criteria and sub-criteria and also evaluate of alternatives with respect to sub-criteria. The synthetic value method of GIT2FSs is then carried out to convert the assessments stated as GIT2FSs for each alternative with respect to each sub-criterion and also weights of criteria (sub-criteria) into the single fuzzy rating and weight, respectively. Then, the fuzzy weighted average (FWA) approach is adopted to integrate the single fuzzy ratings of each alternative with respect to sub-criteria and the single fuzzy weights of sub-criteria under each criterion with the aggregated weighted ratings. In next stage, ELECTRE III (ELimination Et Choix Traduisant la Realite´—elimination and choice translation reality) is generalized with GIT2FSs to select the optimal MHE through a new ranking approach. Moreover, some arithmetic operations and properties are extended to GIT2FSs. In addition, to demonstrate its potential applications, the proposed methodology is implemented in a real case study and an illustrative example, and then, the ranking results are compared with those of the others in the literature. Finally, the sensitivity analysis is carried out to show robustness and stability of the obtained results.

Introduction

In the today competition world, one of the managers’ important duties for gaining the greater share of product market is to reduce costs. The considerable section of these costs is related to the material handling. After the stages of production and process design when setting up of the manufacturing or servicing system, the design of material handling equipment (MHE) (including the activities of selection, arrangement, and establishment) should be carried out in stage of operation design. Obviously, the material handling equipment selection problem (MHESP) changes the productivity index, since it depends on the cost of goods manufactured directly. MHE can encompass “30–75% of this cost and the selection of efficient MHE can be responsible for reducing the plant’s operating costs by 15–30%” [1]. The choice of unsuitable MHE not only results in the rearranging costs but also imposes reinvestment for purchasing new MHE. There are different models of MHE for transporting goods or materials. Each of them has distinguished properties as compared to the others, such that solution of the MHESP has transformed with a complex and time-consuming process. Complexity of MHESP has some reasons as follows. These properties are usually categorized into two groups of criteria, namely the quantitative criteria (such as measure of investment, cost of spare parts, capacity, etc.) and subjective or qualitative criteria (such as attainability of spare parts, convenience, maintainability, etc.). On the other hand, some criteria (along with their corresponding sub-criteria) are of benefit type and some criteria (along with their corresponding sub-criteria) are of cost type. In addition, since each criterion consists of several sub-criteria, it is difficult to apply several times of the decision-making technique to each criterion and then calculate the final score. Furthermore, an expert may apply the different probability density functions such as Gaussian, Beta, or etc. distribution instead of triangular or trapezoidal membership functions (MFs). Hence, such a problem can be considered as a multi-criteria decision-making (MCDM) problem in which the qualitative criteria are expressed based on verbal terms or linguistic variables. An MCDM problem can be stated as the process of determining the best alternative among all possible alternatives with respect to the different criteria. One of the important advantages of MCDM problems is that they can take into account both quantitative and qualitative criteria (including crisp and fuzzy data). There are different techniques for solving the MCDM problems according to appraising style of criteria or alternatives. ELimination Et Choix Traduisant la Realite´ (ELECTRE) that was first presented by Roy [2] is one of the most popular techniques of MCDM. The case that distinguishes this method than the others is property of its non-compensatory. It means that bad scores of criteria cannot be compensated by good scores of other criteria. It compares different alternatives as pairwise by considering various indices and determining indifference, veto, and preference thresholds. In the classical ELECTRE method, the measures of appraisals and weights of criteria are determined with crisp values. However, the crisp data are not suitable for managers’ subjective judgments when faced with the real decision-making problems, because these are often expressed as verbal terms. To express the uncertainty in the real-world problems, fuzzy data instead of crisp data have been adopted in many MCDM techniques including ELECTRE. In ELECTRE III, the ratings and weights can state by means of the fuzzy data. However, a decision-maker may have doubt about the measure of MF. In other words, in type-1 fuzzy sets, it is often difficult for an expert to express his/her notions as a specified number at the interval [0, 1] regarding MF. Hence, type-2 fuzzy sets (T2FSs) were presented by Zadeh [3] as a generalization of the concept of type-1 fuzzy sets. T2FSs are depicted in three-dimensional space including finite non-empty set X, secondary grade f_x (u), and the domain of secondary MF $J_{\text{x}}$, where MF is defined by a fuzzy set at the interval [0, 1] [4]. Interval type-2 fuzzy sets (IT2FSs) are a special case of T2FSs characterized by an interval MF, such that decision-makers can have more flexible to represent the ambiguity of MF [5]. In other words, IT2FSs are suitable for situations in which decision-maker not only has indecisive standpoints as compared to measure of a variable on X but also he is uncertain regarding measure of MF. IT2FSs have a greater ability as compared to type-1 fuzzy sets to handle uncertainty and imperfect information coming from judgments of different experts and can motivate more degrees of flexibility to show the vagueness in real applications. Lack of freedom degree for selecting the interval MFs is led to increase the number of experts, such that the solving the MCDM problem will be complicated and time-consuming. Accordingly, many studies have applied IT2FSs to the management and industrial scopes as follows: Hagras [6], Sepulveda et al. [7], Kumbasar and Hagras [8], Lynch et al. [9], and Kumbasar [10] adopted T2FSs to optimize and design intelligent controllers. Similarly, Castillo et al. [11] presented a comparative study of type-2 fuzzy logic systems with respect to interval type-2 and type-1 fuzzy logic systems to show the efficiency and performance of a generalized type-2 fuzzy logic controller. Ontiveros-Robles et al. [12] proposed a comparison regarding the robustness of interval type-2 and generalized type-2 fuzzy logic controllers, to generate criteria to decide which type of controller is better in specific applications. Auephanwiriyakul et al. [13] and Liu and Mendel [14] used T2FSs to obtain data from human sources (linguistic responses) in management studies. Bouchachia and Mittermeir [15] described a fuzzy neural approach for information retrieval where the fuzzy representation was used to reflect the hierarchical nature of texts. Wu and Mendel [16] extended antecedent connector word models to the framework of Mamdani type-1 fuzzy logic system where the uncertainties originating from descriptive words, connector words, and data were modeled simultaneously. Castillo and Melin [17] and also Own et al. [18] adopted type-2 fuzzy logic for achieving adaptive noise cancelation. Particularly, Melin et al. [19] used the neural networks to analyze the sound signal of an unknown speaker, and then, a set of type-2 fuzzy rules were applied to decision-making. Moreover, they utilized genetic algorithms to optimize the architecture of the neural networks. Sanchez et al. [20] introduced the generalized type-2 fuzzy control system for a mobile robot regarding three types of external perturbations, namely band-limited white noise, pulse noise, and uniform random number noise. Liang and Wang [21] and also Shu and Liang [22] applied T2FSs to analyze the lifetime of a wireless sensor network and forecast strength of sensed signal in wireless sensors, respectively. Baguley et al. [23] planned a T2FSs-based model to predict time to market from performance measures, which is a potentially valuable tool for decision-making and continuous improvement. Gu and Zhang [24] suggested the web shopping expert system based on the IT2FSs for online users. Rhee [25] introduced interval type-2 clustering method by modifying the prototype-updating and hard-partitioning procedures in the type-1 fuzzy objective function-based clustering method. Linda and Manic [26] extended interval type-2 fuzzy logic to the fuzzy voting scheme, which constitutes an essential component of many fault tolerant systems. Cervantes and Castillo [27] presented a new approach for complex control combining several simpler individual fuzzy controllers. It is useful when the problem is a multivariable control system. Castillo et al. [28] applied the granular approach for intelligent control using generalized type-2 fuzzy logic in which granularity was used to divide the design of the global controller into several individual simpler controllers. In the scope of MCDM, Rashid et al. [29] extended technique for order preference by similarity to ideal solution (TOPSIS) to generalized interval-valued trapezoidal fuzzy numbers for the selection of a suitable robot. Keshavarz Ghorabaee [30] presented a GMCDM for robot selection where vlsekriterijumska optimizacija i kompromisno resenje (VIKOR) method with interval type-2 fuzzy numbers was handled. Soner et al. [31] integrated analytic hierarchy process (AHP) and VIKOR with IT2FSs for the hatch cover design selection problem, which has utmost importance in structure of bulk carrier ships to prevent water ingress and protect cargo form the external damages. Zhong and Yao [32] extended the ELECTRE I method to interval type-2 fuzzy numbers for electronic materials supplier selection problem. Abdullah et al. [33] handled interval type-2 fuzzy simple additive weighting (SAW) for ambulance location problem, which has an important role for improving the emergency medical services. Deveci et al. [34] developed weighted aggregated sum product assessment (WASPAS)-based TOPSIS to IT2FSs for the car sharing station selection problem.

There are the known versions for IT2FSs such as trapezoidal interval type-2 fuzzy sets (TraIT2FSs), triangular interval type-2 fuzzy sets (TriIT2FSs), and Gaussian interval type-2 fuzzy sets (GIT2FSs) in the literature. Triangular or trapezoidal MFs are the simplest MFs formed using straight lines. MFs of triangular and trapezoidal fuzzy numbers have steep slopes in their reference points. In the real-life problems, however, the decision-maker may consider smoother slope for the MFs in reference points. Hence, “Gaussian MFs are suitable for problems requiring continuously differentiable curves, whereas the triangular and trapezoidal MFs do not posses these abilities” [35]. In this paper, the performance ratings with respect to sub-criteria and also weights of criteria and sub-criteria are first expressed as linguistic variables and Gaussian interval type-2 fuzzy numbers (GIT2FNs) are then defined for them. GIT2FNs are better selection than the others while the MFs are in the curved form.

The goal of this paper is to introduce a generalized hybrid group decision-making methodology based on GIT2FSs for MHESP. Application of fuzzy data as GIT2FNs is more suitable relative to type-1 fuzzy sets according to the reasons described above. The following cases are the main contributions of the present paper:

• Because of MHE’s selection which is a group activity [36], the synthetic value method is implemented in integrating the interval type-2 fuzzy data of an alternative with respect to sub-criteria, interval type-2 fuzzy weights of criteria and sub-criteria, and interval type-2 fuzzy thresholds.

• Several MCDM techniques based on IT2FSs are integrated to solve the MHESP.

• Since each criterion contains a set of sub-criteria with different weights, the authors first utilized the interval type-2 fuzzy weighted average (FWA) technique as a suitable integrating tool for aggregating the synthetic type-2 fuzzy ratings of each alternative with respect to all sub-criteria under each criterion and the synthetic type-2 fuzzy weights of sub-criteria to the aggregated weighted ratings. This approach makes it unnecessary to use several times of the ELECTRE III technique for each criterion.

• The interval type-2 fuzzy ELECTRE III method based on the aggregated weighted ratings is then applied to choose optimal MHE.

• The new proposed methodology is usable to each type of MF (both straight and curve lines). Moreover, it can be applied to rank type-1 fuzzy sets and T2FSs.

• To incorporate GIT2FNs into the MCDM techniques, some arithmetic operations of GIT2FNs are presented.

• In addition to the final orders of alternatives, the proposed ranking methodology is applied to determine thresholds and weight criteria and sub-criteria.

The rest of present paper is organized as follows: Sect. 2 presents the literature review regarding the MCDM techniques, ELECTRE III, and MHESP. In Sect. 3, preliminaries (including ELECTRE III and arithmetic operations of IT2FSs) are reviewed. The suggested ranking approach is introduced in Sect. 4. In Sect. 5, the proposed ranking methodology is incorporated into the ELECTRE III framework. Section 6 includes a real case study and two illustrative examples in which our ranking methodology is extended to the ELECTRE III method, and finally, conclusions and comparisons are studied in Sect. 7.

Literature review

Mardani et al. [37] listed the most famous methods for solving the MCDM problems and then categorized the applications of the MCDM problems into 15 fields. In a more general categorization, the MCDM techniques can be divided into two branches: multi-objective decision-making (MODM) and multi-attribute decision-making (MADM). An MADM problem includes small number of pre-specified alternatives assessed with respect to a set of criteria. In the classical MADM methods, evaluations and weights are stated as precise and crisp, whereas in the real world, decision-making process accommodates with uncertain and doubt. If it is integrated with fuzzy data to deal with the uncertainty, it is named fuzzy MADM (FMADM). Hence, the FMADM-based approaches are applied to resolve the imprecision and vagueness. There are the different FMADM methods [e.g., preference ranking organization method for enrichment evaluations (PROMETHEE), TOPSIS, VIKOR, etc.]. In another comprehensive study, Mardani et al. [38] grouped the applications and methodologies of the fuzzy MCDM (FMCDM) techniques into four main fields as follows: engineering, management and business, science, and technology. Among the classical MCDM methods developed for solving the real-world decision problems, the ELECTRE III method (based on the concept of outranking relations) was introduced to relieve difficulties coming from the existing decision-making solution methods [39, 40].

Lots of applications based on the ELECTRE III method have been introduced in the literature. Roy and Bouyssou [2] compared two decision-aid models for a nuclear power plant sitting problem using ELECTRE III. Siskos and Hubert [41] analyzed the energy alternatives from the social and public health point of view. Karagiannidis and Moussiopoulos [42] used ELECTRE III to decisions in the area of municipal solid-waste management in Greece. Alomoush [43] applied the ELECTRE III method to select the best location of thyristor-controlled phase angle regulator in a competitive energy market. Montazer et al. [44] designed a new mixed expert decision-aid system where fuzzy ELECTRE III method was applied to vendor selection. Rogers [45] evaluated complex civil/structural engineering projects using ELECTRE III. Tam et al. [46] implemented ELECTRE III in evaluating performance of construction plants. Leyva Lopez [47] solved the student selection problem using the ELECTRE III methodology under fuzzy outranking relation. Li and Wang [48] developed a new ranking method to the ELECTRE III method. Zak and Fierek [49] implemented ELECTRE III/IV and AHP in evaluating the generated variants of urban transportation system. Papadopoulos and Karagiannidis [50] implemented ELECTRE III in the optimization of decentralized energy systems. Radziszewska-Zielina [51] handled the ELECTRE III to select the best partner construction enterprise in terms of partnering relations. Giannoulis and Ishizaka [52] adopted a web-based decision support system with ELECTRE III for ranking British universities. Cavallaro [53] used the ELECTRE III method to select production processes of thin-film solar technology. Marzouk [54] formulated ELECTRE III for value engineering applications. Liu and Zhang [55] proposed the entropy weight and the improved ELECTRE-III method for the supplier selection of a supply chain. Cliville et al. [56] deployed the ELECTRE III and MACBETH multi-criteria ranking methods for small and medium enterprises tactical performance improvements. Fancello et al. [57] planned a decision-aid system based on ELECTRE III for safety analysis in a suburban road network. Heracles et al. [58] compared the ELECTRE III and PROMETHEE II methods regarding the choice of alternative investment scenarios for a geothermal field. Shafia et al. [59] ranked scenarios based on fuzzy cognitive map through the ELECTRE III where scenarios help to simulate future events to analyze the outcomes of possible courses.

On the other hand, there are the several extensions of the ELECTRE approach in the literature. Vahdani and Hadipour [60] presented the interval-valued fuzzy ELECTRE method for solving the MCDM problems where the weights of criteria were determined using the concept of interval-valued fuzzy sets. Hatami-Marbini and Tavana [61] developed the ELECTRE I method to consider the uncertain and imprecise assessments based on standpoints of a group of DMs. Vahdani et al. [62] extended the group ELECTRE method to intuitionistic fuzzy sets. Chen [63] first extended the interval-valued intuitionistic fuzzy ELECTRE (IVIF-ELECTRE) method. Next, the concordance and discordance indices were obtained using an aggregated importance weight score function and a generalized distance measurement between weighted evaluative ratings, respectively. Finally, two IVIF-ELECTRE ranking procedures were developed for the partial and complete ranking of the alternatives based on the concordance and discordance dominance matrices. Hashemi et al. [64] proposed the extended version of ELECTRE III under the interval-valued intuitionistic fuzzy environment. Wang et al. [65], Juan et al. [66], and Na et al. [67] provided the hesitant fuzzy environment on the different versions of the ELECTRE method.

Many attempts have been carried out for solving the MHESP during the last 3 decades. In a general classification, these studies can be categorized into the following four classes: (1) decision support systems (expert system for the design of repetitive manual materials handling tasks [68], the material handling expert system [69], the prototype expert system for the selection of industrial truck type, an expert consultant for in-plant transportation equipment [70], and a knowledge-based system for the choice of conveyor equipment [71]); (2) hybrid methods (an intelligent knowledge-based expert system, named intelligent consultant system, for selection and evaluation of material handling equipment, which has been composed of the following four models: equipment and their attributes, a rule-based database for selecting type of equipment, an MCDM technique (AHP) for selection of optimal equipment, and simulators to evaluate the performance of the equipment model [72], a decision support system based on axiomatic design principles [73], and a hybrid fuzzy knowledge-based expert system and genetic algorithm for the selection and assignment of the most appropriate MHE [74]); (3) optimization formulations (an integer programming model for minimizing material handling costs in manufacturing systems or warehousing facilities [75], a hybrid methodology including the integer programming formulation for designing layout and material handling system simultaneously [76], a 0–1 integer programming model to determine operation allocation and selection of material handling system in an flexible manufacturing systems simultaneously [77], a mathematical model to implement problem modeled by radio-frequency identification technology [78], and a multi-objective optimization model for selection of material handling system for large ship [79]); (4) the MCDM problems (fuzzy axiomatic design principles for selecting automated guided vehicles [80], fuzzy AHP (FAHP), and decision-making trial and evaluation laboratory (DEMATEL)-ANP with geographic information system for the selection of the best space for leisure in a blighted urban site [81], FAHP and fuzzy additive ratio assessment for selection of conveyor [82], the fuzzy complex proportional assessment (COPRAS) method for evaluating performance measures of equipment in total productive maintenance [83], the AHP and TOPSIS methods for selecting the most appropriate tomography equipment [84], COPRAS, simple additive weighting, and TOPSIS for analyzing and prioritizing Rotor systems [85], FAHP, fuzzy entropy, fuzzy TOPSIS (FTOPSIS), and multi-objective mixed integer linear programming for the choice of MHE in warehouse [86], FAHP for bulk material handling equipment [87], and comparing the four MCDM methods: combinative distance based assessment, evaluation based on distance from average solution method, weighted aggregated sum product assessment method, and multi-objective optimization on the basis of ratio analysis for selection of automated guided vehicles [88]). Recently, Hadi-Vencheh and Mohamadghasemi [89] introduced an integrated MCDM model for the MHESP. Despite all its advantages, it has some shortcomings as follows: it applies the voting approach to weight criteria and sub-criteria. Unfortunately, the voting method is of compensatory model type, i.e., the value of a significantly weak assessment grade with respect to one criterion could be directly compensated by the measures of other good assessment grades. In addition, note that it uses the linguistic variables as assessment grades, such that it does not consider the shape of their MFs. On the other hand, the application of type-1 fuzzy sets is other limitation of the proposed approach based on the same reasons described in Sect. 1. Lack of more flexibility to choose the interval MFs is caused that cost and time of data collection increase. This methodology adopts the triangular fuzzy numbers with usual arithmetic operations to weight and evaluate. However, other versions such as GIT2FNs are the more suitable than the others as argued in Sect. 1. In addition, the authors obtained a set of compromise solutions. Nevertheless, one may select a unique solution as optimal MHE. Accordingly, the proposed methodology of present paper eliminates all weaknesses stated above.

This paper focuses on the last class where a model among the different commercial models is evaluated based on IT2FSs with respect to a set of criteria and sub-criteria. The constructed MCDM approaches for the MHESP have some shortcomings. Some studies expressed above adopt the traditional AHP with crisp data; the MHESP is solved by one design expert; and/or the equal weights are considered for criteria. On the other hand, type-1 fuzzy sets use a specified MF at interval [0, 1]. However, there are many situations in the real-world decision-makings, which due to further ambiguity, it is better to choose an interval for MF. Thus, to eliminate the difficulties reviewed in the studies mentioned above, this paper structures a new ranking technique for GIT2FNs. Due to the use of GIT2FNs in the ELECTRE III method, this paper is the first work in scope of the MHESPs.

Preliminaries

Basic principles of the ELECTRE III method

The ELECTRE method was first introduced by Benayoun et al. [90]. Later, this method was generalized in its different versions such as ELECTRE I [91], ELECTRE II [92], ELECTRE III [93], ELECTRE IV [94], ELECTRE IS [95], ELECTRE TRI [96], ELECTREGKMS [97], ELECTRE TRI-C [98], and ELECTRE TRI-NC [99]. Among them, the ELECTRE III method has been widely used to solve MCDM problems. ELECTRE III was adopted to relieve drawbacks of ELECTRE II. It can take into account uncertain data.

The following steps are a summary of the ELECTRE III methodology:

Step 1 Construct the crisp decision matrix $D = [x_{ij} ]_{m \times n}$ for the MCDM problem where there are m alternatives $A_{i} (i = 1,\ldots,m)$ undern criteria $C_{j} (j = 1,\ldots,n)$ and $x_{ij}$ represents the assessment measure of equipment i with respect to criterion j. Moreover, let $[w_{j} ]_{1 \times n}$ be the weights of criteria. The above MCDM problem can also be showed in matrix format as follows:

$$ \begin{aligned} \begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}{c}} \ \quad{\mathop {{C_1}}\limits^{{w_1}} }&\quad {\,\mathop {\,{C_2}}\limits^{{w_2}} }&\quad {\,\,\mathop {{C_3}}\limits^{{w_3}} }&\quad\, \ldots &\quad {\,\,\mathop {{C_n}}\limits^{{w_n}} }&\quad {} \end{array}\\ D = \begin{array}{*{20}{c}} {{A_1}}\\ {{A_2}}\\ {{A_3}}\\ \vdots \\ {{A_m}} \end{array}\left[ {\begin{array}{*{20}{c}} {{x_{11}}}&\quad {{x_{12}}}&\quad {{x_{13}}}&\quad \cdots &\quad {{x_{1n}}}\\ {{x_{21}}}&\quad {{x_{22}}}&\quad {{x_{23}}}&\quad \cdots &\quad {{x_{2n}}}\\ {{x_{31}}}&\quad {{x_{32}}}&\quad {{x_{33}}}&\quad \cdots &\quad {{x_{3n}}}\\ \vdots &\quad \vdots &\quad \vdots &\quad \cdots &\quad \vdots \\ {{x_{m1}}}&\quad {{x_{m2}}}&\quad {{x_{m3}}}&\quad \cdots &\quad {{x_{mn}}} \end{array}} \right], \end{array}\ \end{aligned} $$

(1)

Step 2 Obtain the outranking relations using the following three thresholds:

• Indifference threshold ($q_{j}$): If difference of performance measures between alternatives $A_{r}$ and $A_{k}$ under criterion j, namely $x_{rj}$preferred to the alternative.

• and $x_{kj}$, is less than or equal $q_{j} \,$(i.e. $x_{rj} - x_{kj} \, \le \,q_{j} \,{\text{and}}\,\,\,x_{kj} - x_{rj} \le q_{j}$), it is said that alternative $A_{r}$ and alternative $A_{k}$ under criterion j are indifference.

• Veto threshold ($v_{j}$): If difference of performance measures between alternatives $A_{k}$ and $A_{r}$ with respect to criterion j, i.e., $x_{kj}$ and $x_{rj}$, is more than or equal $v_{j}$(or $x_{kj} - x_{rj} \ge v_{j}$), it is said that the alternative $A_{r}$ is not better than the alternative $A_{k}$.

• Preference threshold ($p_{j}$): If difference of performance measures between alternatives $A_{r}$ and $A_{k}$ under criterion j, i.e., $x_{rj}$ and $x_{kj}$, is more than or equal $p_{j}$ (or equivalently, $x_{rj} - x_{kj} \ge p_{j}$), the alternative $A_{r}$ is preferred to the alternative $A_{k}$. If $x_{kj} + q_{j} < x_{rj} \le x_{kj} + p_{j}$, the alternative $A_{r}$ is weakly preferred to the alternative $A_{k}$.

Based on the above descriptions, the following three relations are introduced for determining the level of the decision-makers’ preferences:

$A_{r}$${\text{P}}_{j}$$A_{k}$	$x_{rj}$ is strictly preferred to $x_{kj}$ under criterion j	↔	$x_{rj} - x_{kj} \ge p_{j}$
$A_{k}$${\text{Q}}_{j}$$A_{r}$	$x_{rj}$ is weakly preferred to $x_{kj}$ under criterion j	↔	$x_{kj} + q_{j} < x_{rj} \le x_{kj} + p_{j}$
$A_{k}$${\text{I}}_{j}$$A_{r}$	$x_{rj}$ is indifferent to $x_{kj}$ under criterion j; and $x_{kj}$ is indifferent to $x_{rj}$ under criterion j	↔	$\left| {x_{rj} - x_{kj} } \right| \le q_{j}$

The thresholds $q_{j}$, $p_{j}$, and $v_{j}$ for each criterion are usually determined based on experts’ views, nature of decision-making problem, or (maximum measure − minimum measure) * certain coefficient. By using these thresholds, an outranking relation S as $A_{r}$S$A_{k}$ are constructed for comparing pairs of alternatives $A_{r}$ and $A_{k}$. It means that “$A_{r}$ is at least as good as $A_{k}$” OR “$A_{r}$ is not worse than $A_{k}$” [100].

In order to examine expression $A_{r}$S$A_{k}$, the following two principles should be taken account into:

• The concordance principle: it includes a majority of criteria such that agree with expression $A_{r}$S$A_{k}$, that is the majority principle.

• The non-discordance principle: it includes a minority of criteria such that do not satisfy expression $A_{r}$S$A_{k}$, which is the minority principle.

The final goal is to rank the alternatives based on the outranking relations and the principles described above. For a certain criterion, more concordance and less non-discordance indices indicate stronger superiority.

Step 3 Calculate the concordance index of alternative $A_{r}$ relative to alternative $A_{k}$ (C ($A_{r}$, $A_{k}$)) as follows:

$$ C(A_{r} ,A_{k} ) = \frac{{\sum\nolimits_{j = 1}^{n} {w_{j} *c_{j} (A_{r} ,A_{k} )} }}{{\sum\nolimits_{j = 1}^{n} {w_{j} } }},\,\,\,\quad \,r,k = 1,\ldots,m;\,\,\,r \ne k,\,\, $$

(2)

where $w_{j}$ and $c_{j} (A_{r} ,A_{k} )$ are weight of criterion j and the superior level of alternative $A_{r}$ versus alternative $A_{k}$Calculate the discordance index of alternative, respectively. For benefit (B) and cost (C) criteria, $c_{j} (A_{r} ,A_{k} )$ is calculated, respectively, by the following relations:

$$ c_{j} (A_{r} ,A_{k} ) = \left\{ \begin{array}{lll} 0 &\quad x_{kj} - x_{rj} \ge p_{j}, & \\ \frac{{x_{rj} - x_{kj} + p_{j} }}{{p_{j} - q_{j} }} & \quad q_{j} < x_{kj} - x_{rj} \le p_{j}, &\quad j = 1,\ldots,n,\\ 1 &\quad x_{kj} - x_{rj} \le q_{j} , & \\ \end{array} \right.$$

(3)

and

$$ c_{j} (A_{r} ,A_{k} ) = \left\{ \begin{array}{lll} 0&\quad x_{rj} - x_{kj} \ge p_{j} ,\,\, \hfill \\ \frac{{x_{kj} - x_{rj} + p_{j} }}{{p_{j} - q_{j}}} & \quad{\text{otherwise}},&\quad j = 1,\ldots,n.\,\, \hfill \\ 1&\quad x_{rj} - x_{kj} \le q_{j} , \hfill \\ \end{array} \right. $$

(4)

Step 4 Calculate the discordance index of alternative $A_{r}$ versus alternative $A_{k}$ for criterionj ($d_{j}$($A_{r}$,$A_{k}$)). It shows lack of superiority an alternative versus other alternative with respect to other criteria. The following two expressions show the discordance indices of alternative $A_{r}$ versus alternative $A_{k}$ for B and C criteria, respectively:

$$ d_{j} (A_{r} ,A_{k} ) = \left\{ \begin{array}{lll} 0&\quad x_{kj} - x_{rj} \le p_{j} ,\,\, \hfill \\ \frac{{x_{kj} - x_{rj} - p_{j} }}{{v_{j} - p_{j} }}&\quad p_{j} < x_{kj} - x_{rj} \le v_{j} ,& j = 1,\ldots,n, \hfill \\ 1& x_{kj} - x_{rj} \ge v_{j} , \hfill \\ \end{array} \right. $$

(5)

and

$$ d_{j} (A_{r} ,A_{k} ) = \left\{ \begin{array}{lll} 0&\quad x_{rj} - x_{kj} \le v_{j} ,\,\, \hfill \\ \frac{{x_{rj} - x_{kj} - p_{j} }}{{v_{j} - p_{j} }} &\quad {\text{otherwise}},&\quad j = 1,\ldots,n.\, \hfill \\ 1&\quad x_{rj} - x_{kj} \ge v_{j} , \hfill \\ \end{array} \right. $$

(6)

Step 5 Determine outranking relation by the following credit degree index:

$$\begin{aligned} & S(A_{r} ,A_{k} ) \\ &\quad = \left\{ \begin{array}{lll} C(A_{r} ,A_{k} ),&\quad if\,d_{j} (A_{r} ,A_{k} ) \le \,C(A_{r} ,A_{k} ),&\quad \forall j, \hfill \\ C(A_{r} ,A_{k} ).&\prod\limits_{{j \in J:d_{j} (A_{r} ,A_{k} ){ > }\,C(A_{r} ,A_{k} )}} {\frac{{1 - d_{j} (A_{r} ,A_{k} )}}{{1 - C(A_{r} ,A_{k} )}}} &\quad{\text{otherwise}}, \hfill \\ \end{array} \right.\,\end{aligned} $$

(7)

where $S(A_{r} ,A_{k} )$ and J are the degree of outranking $A_{r}$ relative to alternative $A_{k}$ and the set of criteria for which $d_{j} (A_{r} ,A_{k} ) > \,C(A_{r} ,A_{k} )$, respectively.

Step 6 Calculate the final score and rank alternatives.

There are several approaches to rank alternatives in the ELECTRE III technique. (1) Min max method: in this method, the optimal alternative is the alternative that the largest measure in its corresponding column in credit degree matrix is less than the same measure for other alternatives. (2) Double ranking method: in this method, two distillation procedures are utilized. The first type is descending distillation in which ranking order is from the best to the worst alternatives. In the second type, named ascending distillation, alternatives are prioritized from the worst to the best alternative. The results of above two procedures are then combined to determine the final ranking.

T2FSs and their arithmetic operations

Definition 3.2.1

Let ${{\tilde{\tilde{A}}}}$ be the T2FS in the universe of discourse X as follows [101]:

$$ \begin{aligned} {{\tilde{\tilde{A}}}} &= \left\{ \left( {(x,u),\mu_{{{{\tilde{\tilde{A}}}}}} (x,u)} \right)\,\,\left| \,\,\forall \,x \in X,\right.\right.\\ &\quad \left.\forall \,u \in J_{x} \subseteq [0,1],\,0 \le \mu_{{{{\tilde{\tilde{A}}}}}} (x,u)\, \le 1 \right\},\, \end{aligned} $$

(8)

where X denotes the domain of ${{\tilde{\tilde{A}}}}$, $\mu_{{{{{{\tilde{\tilde{A}}}}}}}}$ refers to the MF (secondary MF) of ${{\tilde{\tilde{A}}}}$, and $J_{x}$ is an sub-interval at [0, 1] and denotes the primary MF. ${{\tilde{\tilde{A}}}}$ can also be expressed as follows:

$$ {{\tilde{\tilde{A}}}} = \int_{x \in X} {} \int_{{u \in J_{X} }} {\mu_{{{{\tilde{\tilde{A}}}}}} (x,u)/(x,u)} ,\,\, $$

(9)

where $J_{x} \subseteq [0,1]$ and $\int {\int_{{}} {} }$ denotes the overall admissible union of x and u.

Definition 3.2.2

For the T2FS ${{\tilde{\tilde{A}}}}$, if all $\mu_{{{{{{\tilde{\tilde{A}}}}}}}} (x,u) = 1$, ${{\tilde{\tilde{A}}}}$ is named IT2FS. An IT2FS ${{\tilde{\tilde{A}}}}$ can be regarded as a special case of a T2FS as follows [101]:

$$ {{\tilde{\tilde{A}}}} = \int_{x \in X} {\int_{{u \in J_{X} }} {{1/ {(x,u)}}} } ,\, $$

(10)

where $J_{x} \subseteq [0,1]$. It is obvious that the upper and the lower MFs of an IT2FS are both type-1 MFs.

Definition 3.2.3

Footprint of uncertainty (FOU) is derived from the union of all primary memberships:

$$ {\text{FOU}}({{\tilde{\tilde{A}}}}) = \int_{x \in X} {J_{X} }. $$

(11)

The FOU can also be represented by the lower and upper MFs [102]:

$$ {\text{FOU}}({{\tilde{\tilde{A}}}}) = \int_{x \in X} {\left[ {\underline{\mu }_{{{{\tilde{\tilde{A}}}}}} (x),\bar{\mu }_{{{{\tilde{\tilde{A}}}}}} (x)} \right]} ,\, $$

(12)

where $\underline{\mu }_{{{{\tilde{\tilde{A}}}}}} (x)\,\;{\text{and}}\;\,\bar{\mu }_{{{{\tilde{\tilde{A}}}}}} (x)$ are the lower and upper MFs of a T2FS. An IT2FS ${{\tilde{\tilde{A}}}}$, is said to be normal if $\underline{\mu }_{{{{{{\tilde{\tilde{A}}}}}}}} (x) = \bar{\mu }_{{{{{{\tilde{\tilde{A}}}}}}}} (x) = 1$. An IT2FS ${{\tilde{\tilde{A}}}}$, is said to be subnormal if $\underline{\mu }_{{{{\tilde{\tilde{A}}}}}} (x)\,\, < \,1\,\,{\text{and }}\,\bar{\mu }_{{{{\tilde{\tilde{A}}}}}} (x) = 1$.

Definition 3.2.4.

Let ${\tilde{\tilde{X}}}^{L}$ and ${\tilde{\tilde{X}}}^{U}$ (L and U are equal to the lower and upper MFs) be two non-negative trapezoidal type-1 fuzzy numbers [101]. In addition, let $H_{{{\tilde{\tilde{A}}}}}^{L}$ and $H_{{{\tilde{\tilde{A}}}}}^{U}$ denote the heights of ${\tilde{\tilde{X}}}^{\text{L}}$ and ${\tilde{\tilde{X}}}^{\text{U}}$, respectively. Let $x_{ 1}^{L} ,\,x_{ 2}^{L} ,\,x_{ 3}^{L} ,\,x_{ 4}^{L} ,\,x_{ 1}^{U} ,\,x_{ 2}^{U} ,\,x_{ 3}^{U} ,\,{\text{and }}x_{ 4}^{U}$ be non-negative real values. Trapezoidal type-t fuzzy numbers (TraIT2FNs) can be represented by (see Fig. 1):

Fig. 1

Subnormal TraIT2FN

$$\begin{aligned} {{\tilde{\tilde{X}}}} &= [{\tilde{\tilde{X}}}^{L} ,{\tilde{\tilde{X}}}^{U} ]\\& = \left[ {\left( {x_{1}^{L} ,\,x_{2}^{L} ,\,x_{3}^{L} ,\,x_{4}^{L} ;H_{{{\tilde{\tilde{X}}}}}^{L} \,} \right),\left( {\,x_{1}^{U} ,\,x_{2}^{U} ,\,x_{3}^{U} , x_{4}^{U} ;H_{{{\tilde{\tilde{X}}}}}^{U} } \right)} \right]. \end{aligned}$$

(13)

Definition 3.2.5.

Let ${{\tilde{\tilde{X}}}}_{1}$ and ${{\tilde{\tilde{X}}}}_{2}$ be two non-negative TraIT2FNs, where ${{\tilde{\tilde{X}}}}_{1} = [{\tilde{\tilde{X}}}_{1}^{L} ,{\tilde{\tilde{X}}}_{1}^{U} ] =$$\,\Big[ \Big( x_{11}^{L} ,\,x_{12}^{L} ,\,x_{13}^{L} ,\,x_{14}^{L} ;H_{{{\tilde{\tilde{X}}}_{1} }}^{L} \, \Big),\Big( \,x_{11}^{U} ,\,x_{12}^{U} ,\,x_{13}^{U} , x_{14}^{U} ;H_{{{\tilde{\tilde{X}}}_{1} }}^{U} \Big) \Big]\,$ and $\,{{\tilde{\tilde{X}}}}_{2} = [{\tilde{\tilde{X}}}_{2}^{L} ,{\tilde{\tilde{X}}}_{2}^{U} ] = \,\Big[ \Big(x_{21}^{L} ,\,x_{22}^{L} ,\,x_{23}^{L} ,\,x_{24}^{L} ;H_{{{\tilde{\tilde{X}}}_{2} }}^{L} \, \Big),\Big( \,x_{21}^{U} ,\,x_{22}^{U} ,\,x_{23}^{U} , x_{24}^{U} ;H_{{{\tilde{\tilde{X}}}_{2} }}^{U} \Big) \Big]$. Arithmetic operations between ${{\tilde{\tilde{X}}}}_{1}$ and ${{\tilde{\tilde{X}}}}_{2}$ are defined as follows:

Addition operation:

$$ \begin{aligned} \,\,\,{{\tilde{\tilde{X}}}}_{1} \oplus {{\tilde{\tilde{X}}}}_{2} & = \left[ \left( x_{11}^{L} + x_{21}^{L} ,\,x_{12}^{L} + x_{22}^{L} ,\,x_{13}^{L} + x_{23}^{L} ,\,x_{14}^{L} + x_{24}^{L} ;\right.\right.\\ &\quad\quad\left.\left.\hbox{min} \left\{ {H_{{{\tilde{\tilde{X}}}_{1} }}^{L} ,H_{{{\tilde{\tilde{X}}}_{2} }}^{L} } \right\}, \right) \right],\,\, \\ \, & \quad \,\left[ \left( x_{11}^{U} + x_{21}^{U} ,\,x_{12}^{U} + x_{22}^{U} ,\,x_{13}^{U} + x_{23}^{U} ,\,x_{14}^{U} + x_{24}^{U} ;\right.\right.\\ &\quad\quad\left.\left.\hbox{min} \left\{ {H_{{{\tilde{\tilde{X}}}_{1} }}^{U} ,H_{{{\tilde{\tilde{X}}}_{2} }}^{U} } \right\} \right) \right]\,\,. \\ \end{aligned} $$

(14)

Subtraction operation:

$$ \begin{aligned} \,{{\tilde{\tilde{X}}}}_{1} \varTheta {{\tilde{\tilde{X}}}}_{2} &= \left[ \left( x_{11}^{L} - x_{24}^{L} ,\,x_{12}^{L} - x_{23}^{L} ,\,x_{13}^{L} - x_{22}^{L} ,\,x_{14}^{L} - x_{21}^{L} ;\right.\right.\\ &\quad\quad\left.\left.\hbox{min} \left\{ {H_{{{\tilde{\tilde{X}}}_{1} }}^{L} ,H_{{{\tilde{\tilde{X}}}_{2} }}^{L} } \right\}\, \right), \right], \hfill \\ &\quad\left[ \left( x_{11}^{U} - x_{24}^{U} ,\,x_{12}^{U} - x_{23}^{U} ,\,x_{13}^{U} - x_{22}^{U} ,\,x_{14}^{U} - x_{21}^{U} ;\right.\right.\\ &\quad\quad\left.\left.\hbox{min} \left\{ {H_{{{\tilde{\tilde{X}}}_{1} }}^{U} ,H_{{{\tilde{\tilde{X}}}_{2} }}^{U} } \right\} \right) \right]\,.\, \hfill \\ \end{aligned} $$

(15)

Multiplication operation:

$$ {{\tilde{\tilde{X}}}}_{1} \otimes {{\tilde{\tilde{X}}}}_{2} = \left[ \begin{aligned} \left( {x_{11}^{L} .x_{21}^{L} ,\,x_{12}^{L} .x_{22}^{L} ,\,x_{13}^{L} .x_{23}^{L} ,\,x_{14}^{L} .x_{24}^{L} ;\hbox{min} \left\{ {H_{{{\tilde{\tilde{X}}}_{1} }}^{L} ,H_{{{\tilde{\tilde{X}}}_{2} }}^{L} } \right\}\,} \right), \hfill \\ \quad \left( {x_{11}^{U} .x_{21}^{U} ,\,x_{12}^{U} .x_{22}^{U} ,\,x_{13}^{U} .x_{23}^{U} ,\,x_{14}^{U} .x_{24}^{U} ;\hbox{min} \left\{ {H_{{{\tilde{\tilde{X}}}_{1} }}^{U} ,H_{{{\tilde{\tilde{X}}}_{2} }}^{U} } \right\}} \right) \hfill \\ \end{aligned} \right]. $$

(16)

Division operation:

$$ {{\tilde{\tilde{X}}}}_{1} \varphi \,{{\tilde{\tilde{X}}}}_{2} = \left[ \begin{aligned} \left( {\frac{{x_{11}^{L} }}{{x_{24}^{L} }},\,\frac{{x_{12}^{L} }}{{x_{23}^{L} }},\,\frac{{x_{13}^{L} }}{{x_{22}^{L} }},\,\frac{{x_{14}^{L} }}{{x_{21}^{L} }};\hbox{min} \left\{ {H_{{{\tilde{\tilde{X}}}_{1} }}^{L} ,H_{{{\tilde{\tilde{X}}}_{2} }}^{L} } \right\}\,} \right), \hfill \\ \left( {\frac{{x_{11}^{U} }}{{x_{24}^{U} }},\,\frac{{x_{12}^{U} }}{{x_{23}^{U} }},\,\frac{{x_{13}^{U} }}{{x_{22}^{U} }},\,\frac{{x_{14}^{U} }}{{x_{21}^{U} }};\hbox{min} \left\{ {H_{{{\tilde{\tilde{X}}}_{1} }}^{U} ,H_{{{\tilde{\tilde{X}}}_{2} }}^{U} } \right\}} \right) \hfill \\ \end{aligned} \right].\,\, $$

(17)

Multiplication by an ordinary number:

$$ {{\tilde{\tilde{X}}}}_{1} .\,r = r.\,{{\tilde{\tilde{X}}}}_{1} = \left\{ \begin{aligned} \left[ {\left( {r.\,x_{11}^{L} ,\,r.\,x_{12}^{L} ,\,r.\,x_{13}^{L} ,\,r.\,x_{14}^{L} ;H_{{{\tilde{\tilde{X}}}_{1} }}^{L} \,} \right),\left( {r.\,x_{11}^{U} ,\,r.\,x_{12}^{U} ,\,r.\,x_{13}^{U} ,\,r.\,x_{14}^{U} ;H_{{{\tilde{\tilde{X}}}_{1} }}^{U} \,} \right)} \right]\,\,{\text{if}}\,\,r \ge 0 \hfill \\ \,\left[ {\left( {r.\,x_{14}^{L} ,\,r.\,x_{13}^{L} ,\,r.\,x_{12}^{L} ,\,r.\,x_{11}^{L} ;H_{{{\tilde{\tilde{X}}}_{1} }}^{L} \,} \right),\left( {r.\,x_{14}^{U} ,\,r.\,x_{13}^{U} ,\,r.\,x_{12}^{U} ,\,r.\,x_{11}^{U} ;H_{{{\tilde{\tilde{X}}}_{1} }}^{U} \,} \right)} \right]\,\,{\text{if}}\,\,r \le 0\, \hfill \\ \end{aligned} \right.. $$

(18)

Definition 3.2.6

Let ${\tilde{\tilde{G}}}$ be a normal GIT2FN as follows (see also Fig. 2):

Fig. 2

Normal GIT2FN

$$ {\tilde{\tilde{G}}} = [\tilde{G}^{L} ,\tilde{G}^{U} ] = \,\left[ {\left( {\,\mu^{L} ;\,\sigma^{L} ;H_{{\tilde{\tilde{G}}}}^{L} \,} \right),\left( {\mu^{U} ;\,\sigma^{U} ;H_{{\tilde{\tilde{G}}}}^{U} \,} \right)} \right]\,,\,\, $$

(19)

where $\mu^{L} ;\sigma^{L} \,{\text{and}}\,\mu^{U} ;\sigma^{U}$ are the mean and standard deviation of the lower and upper Gaussian MFs, respectively, such that $H_{{\tilde{\tilde{G}}}}^{L} = H_{{\tilde{\tilde{G}}}}^{U}$, $\mu^{L} = \mu^{U}$ and $\sigma^{L} \langle \,\sigma^{U}$ [103].

Definition 3.2.7

Aset of all GIT2FNs ${\tilde{\tilde{G}}}_{i}$ is said symmetric if there is no intersection between beginning left reference limits or final right reference limits (see Fig. 3).

Fig. 3

Set of symmetric GIT2FNs (the left, right, minimum, and maximum reference limits)

Definition 3.2.8

The α-cut of ${{\tilde{\tilde{A}}}}$ is presented as follows [104]:

$$ A_{\alpha } = \left\{ {\left( {(x,u} \right)\left| {f_{x} (u) \ge \alpha } \right.} \right\}. $$

(20)

Definition 3.2.9

The α-cut of ${{\tilde{\tilde{A}}}}$ may be represented by the α-cut of its FOU using the extension of α-cut of a type-1 fuzzy set ${\tilde{\tilde{A}}}$ [105] as follows:

$$ A_{\alpha } = \left\{ {x\left| {\underline{\mu }_{{{{\tilde{\tilde{A}}}}}} (x) \ge \alpha ,\bar{\mu }_{{{{\tilde{\tilde{A}}}}}} (x)} \right. \ge \alpha } \right\},\,\, $$

(21)

For a normal GIT2FN, α-cut may be presented as interval as follows (see Fig. 3):

$$ \begin{aligned} &{\text{Normal:}} \hfill \\ &\quad\hat{G}_{i\alpha } = \left[ {\left[ {\bar{x}_{1i\alpha }^{l} ,\underline{x}_{2i\alpha }^{l} } \right],\mu_{i} ,\left[ {\underline{x}_{1i\alpha }^{r} ,\bar{x}_{2i\alpha }^{r} } \right]} \right],\,\, \hfill \\ \end{aligned} $$

(22)

where $\bar{x}_{1i\alpha }^{l} < \underline{x}_{2i\alpha }^{l} < \mu < \underline{x}_{1i\alpha }^{r} < \bar{x}_{2i\alpha }^{r}$, and l and r show the left and right MFs of ${\tilde{\tilde{G}}}$, respectively.

Definition 3.2.10

Let $X = [x_{1} ,x_{2} ]\,$ and $\,Y = [y_{1} ,y_{2} ]$ be two positive interval numbers, such that $x_{1} \le x \le x_{2}$ and $\, y_{1} \le y \le y_{2}$ ($x_{1} ,y_{1}$ and $x_{2} ,y_{2}$ are the infima and the suprema, respectively). Interval arithmetic operations including addition, subtraction, multiplication, and division are defined, respectively, as follows [106]:

Addition operation:

$$ X + Y = [x_{1} + y_{1} ,x_{2} + y_{2} ]. $$

(23)

Subtraction operation:

$$ X - Y = [x_{1} - y_{2} ,x_{2} - y_{1} ]. $$

(24)

Multiplication operation:

$$\begin{aligned} X.\,Y &= [\hbox{min} \,(x_{1} .y_{1} ,x_{1} .y_{2} ,x_{2} .y_{1} ,x_{2} .y_{2} ),\\ &\quad\quad \hbox{max} \,(x_{1} .y_{1} ,x_{1} .y_{2} ,x_{2} .y_{1} ,x_{2} .y_{2} )].\end{aligned} $$

(25)

Division operation:

$$\begin{aligned} &\frac{X}{Y} = [{x_1},{x_2}].\left( {\frac{1}{{[{y_1},{y_2}]}}} \right),\\ &{\rm{where}} \frac{1}{{[{y_1},{y_2}]}} = \left[ {\frac{1}{{{y_2}}},\frac{1}{{{y_1}}}} \right] \quad {\rm{if}} \; 0 \notin [{y_1},{y_2}]. \end{aligned}$$

(26)

Distance between X and Y:

$$ \Delta_{X - Y} = \frac{1}{2}\left| {(x_{1} - y_{2} ) + (x_{2} - y_{1} )} \right|. $$

(27)

Some arithmetic operations of normal GIT2FNs

Let ${\tilde{\tilde{G}}}_{1}$ and ${\tilde{\tilde{G}}}_{2}$ be two non-negative normal GIT2FNs, where ${\tilde{\tilde{G}}}_{1} = [\tilde{G}_{1}^{L} ,\tilde{G}_{1}^{U} ] =$$\,\Big[ \Big( {\,\mu_{1}^{L} ;\,\sigma_{1}^{L} ;H_{{\tilde{G}_{1} }}^{L} \,} \Big),\Big( \,\mu_{1}^{U} ;\,\sigma_{1}^{U} ;H_{{\tilde{G}_{1} }}^{U} \, \Big) \Big]\,$,$\,{\tilde{\tilde{G}}}_{2} = [{\tilde{\tilde{G}}}_{2}^{L} ,{\tilde{\tilde{G}}}_{2}^{U} ] = \,\,\Big[ \Big( \,\mu_{2}^{L} ;\,\sigma_{2}^{L} ;H_{{\tilde{G}_{2} }}^{L} \, \Big),\Big( {\,\mu_{2}^{U} ;\,\sigma_{2}^{U} ;H_{{\tilde{G}_{2} }}^{U} \,} \Big) \Big]\,$, and $H_{{\tilde{G}_{1} }}^{L} = H_{{\tilde{G}_{2} }}^{L} = H_{{\tilde{G}_{1} }}^{U} = H_{{\tilde{G}_{2} }}^{U}$. The arithmetic operations between ${\tilde{\tilde{G}}}_{1}$ and ${\tilde{\tilde{G}}}_{2}$ at level $\alpha$($\alpha = \alpha_{1} ,\ldots,\alpha_{N}$; N is the number of alpha cuts) are calculated using Definition 3.2.9 ($\hat{G}_{i\alpha } = \left[ {\left[ {\bar{x}_{1i\alpha }^{l} ,\underline{x}_{2i\alpha }^{l} } \right],\mu_{i} ,\left[ {\underline{x}_{1i\alpha }^{r} ,\bar{x}_{2i\alpha }^{r} } \right]} \right]$) and extensions of definitions stated by Chen and Lee [101] as follows:

Addition operation:

$$ \begin{aligned} \,\,\,\hat{G}_{1\alpha } \oplus \hat{G}_{2\alpha } &= \left[ \left( \underline{x}_{21\alpha }^{l} + \underline{x}_{22\alpha }^{l} ,\,\mu_{1} + \mu_{2} ,\,\underline{x}_{11\alpha }^{r} + \underline{x}_{12\alpha }^{r} ;\right.\right.\\ &\quad\left.\left.\hbox{min} \left\{ {H_{{\tilde{G}_{1} }}^{L} ,H_{{\tilde{G}_{2} }}^{L} } \right\}\, \right) \right],\,\, \hfill \\ &\quad \left[ \left( \bar{x}_{11\alpha }^{l} + \bar{x}_{12\alpha }^{l} ,\,\mu_{1} + \mu_{2} ,\,\bar{x}_{21\alpha }^{r} + \bar{x}_{22\alpha }^{r} ;\right.\right.\\ &\quad\left.\left.\hbox{min} \left\{ {H_{{\tilde{G}_{1} }}^{U} ,H_{{\tilde{G}_{2} }}^{U} } \right\}\, \right) \right]\,. \hfill \\ \end{aligned} $$

(28)

Subtraction operation:

$$ \begin{aligned} \,\hat{G}_{1\alpha } {{\varTheta }}\hat{G}_{2\alpha } &= \left[ \left( \underline{x}_{21\alpha }^{l} - \underline{x}_{12\alpha }^{r} ,\mu_{1} - \mu_{2} ,\,\underline{x}_{11\alpha }^{r} - \underline{x}_{22\alpha }^{l} ;\right.\right.\\ &\left.\left.\quad\quad\hbox{min} \left\{ {H_{{\tilde{G}_{1} }}^{L} ,H_{{\tilde{G}_{2} }}^{L} } \right\}\, \right) \right],\,\, \hfill \\ &\quad \left[ \left( \bar{x}_{11\alpha }^{l} - \bar{x}_{22\alpha }^{r} ,\,\mu_{1} - \mu_{2} ,\,\bar{x}_{21\alpha }^{r} - \bar{x}_{12\alpha }^{l} ;\right.\right.\\ &\left.\left.\quad\quad\hbox{min} \left\{ {H_{{\tilde{G}_{1} }}^{U} ,H_{{\tilde{G}_{2} }}^{U} } \right\} \right) \right]. \hfill \\ \end{aligned} $$

(29)

Multiplication operation:

$$ \begin{aligned} \hat{G}_{1\alpha } \otimes \hat{G}_{2\alpha } &= \left[ \left( \underline{x}_{21\alpha }^{l} \times \underline{x}_{22\alpha }^{l} ,\,\mu_{1} \times \mu_{2} ,\,\underline{x}_{11\alpha }^{r} \times \underline{x}_{12\alpha }^{r} ;\right.\right.\\ &\left.\left.\quad\quad\hbox{min} \left\{ {H_{{\tilde{G}_{1} }}^{L} ,H_{{\tilde{G}_{2} }}^{L} } \right\}\, \right) \right], \hfill \\ &\quad\left[ \left( \bar{x}_{11\alpha }^{l} \times \bar{x}_{12\alpha }^{l} ,\,\mu_{1} \times \mu_{2} ,\,\bar{x}_{21\alpha }^{r} \times \bar{x}_{22\alpha }^{r} ;\right.\right.\\ &\left.\left.\quad\quad\hbox{min} \left\{ {H_{{\tilde{G}_{1} }}^{U} ,H_{{\tilde{G}_{2} }}^{U} } \right\} \right) \right].\, \hfill \\ \end{aligned} $$

(30)

Division operation:

$$ \begin{aligned}{{\hat{G}_{1\alpha } } / {\hat{G}_{2\alpha } }}\, &= \left[{\left({\frac{{\underline{x}_{21\alpha }^{l} }}{{\underline{x}_{12\alpha}^{r} }},\,\frac{{\mu_{1}}}{{\mu_{2}}},\,\,\frac{{\underline{x}_{11\alpha }^{r}}}{{\underline{x}_{22\alpha }^{l} }};\hbox{min}\left\{{H_{{\tilde{G}_{1} }}^{L} ,H_{{\tilde{G}_{2} }}^{L} }\right\}} \right)\,} \right],\,\, \hfill \\ &\quad \left[ {\left({\frac{{\bar{x}_{11\alpha }^{l} }}{{\bar{x}_{22\alpha }^{r}}},\,\, \frac{{\mu_{1} }}{{\mu_{2} }},\,\frac{{\bar{x}_{21\alpha}^{r} }}{{\bar{x}_{12\alpha }^{l} }};\hbox{min} \left\{{H_{{\tilde{G}_{1} }}^{U} ,H_{{\tilde{G}_{2} }}^{U} } \right\}}\right)} \right].\, \hfill \\ \end{aligned}$$

(31)

Multiplication by an ordinary number:

$$ \hat{G}_{1\alpha } .\,r = r.\,\hat{G}_{1\alpha } = \left\{ \begin{aligned} &\left[ {\left( {r.\,\underline{x}_{21\alpha }^{l} ,\,r.\,\mu_{1} ,\,r.\,\underline{x}_{11\alpha }^{r} ;H_{{\tilde{G}_{1} }}^{L} \,} \right),\left( {r.\bar{x}_{11\alpha }^{l} ,\,r.\,\mu_{1} ,\,r.\,\bar{x}_{21\alpha }^{r} ;H_{{\tilde{G}_{1} }}^{U} \,} \right)} \right]\,\,{\text{if}}\,\,r \ge 0 \hfill \\ &\,\left[ {\left( {r.\,\,\underline{x}_{11\alpha }^{r} ,r.\,\mu_{1} ,\,r.\,\underline{x}_{21\alpha }^{l} ;H_{{\tilde{G}_{1} }}^{L} \,} \right),\left( {r.\bar{x}_{21\alpha }^{r} ,\,r.\,\mu_{1} ,\,r.\bar{x}_{11\alpha }^{l} ;H_{{\tilde{G}_{1} }}^{U} \,} \right)} \right]\,\,{\text{if}}\,\,r \le 0 \hfill \\ \end{aligned} \right.. $$

(32)

Average operation:

Let ${\tilde{\tilde{G}}}_{1} ,\ldots,{\tilde{\tilde{G}}}_{U}$ be U non-negative normal GIT2FNs, where ${\tilde{\tilde{G}}}_{u} = [\tilde{G}_{u}^{L} ,\tilde{G}_{u}^{U} ] =$$\,\Big[ \Big( {\,\mu_{u}^{L} ;\,\sigma_{u}^{L} ;H_{{\tilde{G}_{u} }}^{L} \,} \Big),\Big( \,\mu_{u}^{U} ;\,\sigma_{u}^{U} ;H_{{\tilde{G}_{u} }}^{U} \, \Big) \Big]\,$ and $H_{{\tilde{G}_{u} }}^{L} = H_{{\tilde{G}_{u} }}^{U}$$(u = 1,\ldots,U)$. The average operations $\bar{\hat{G}}_{\alpha } = (\bar{\bar{x}}_{1\alpha }^{l} ,\underline{{\bar{x}}}_{2\alpha }^{l} ,\bar{\mu }_{\alpha } ,\underline{{\bar{x}}}_{1\alpha }^{r} ,\bar{\bar{x}}_{2\alpha }^{r} )$ between ${\tilde{\tilde{G}}}_{1} ,\ldots,{\tilde{\tilde{G}}}_{U}$ at level $\alpha$ ($\alpha = \alpha_{1} ,\ldots,\alpha_{N}$) are calculated as follows:

$$ \bar{\bar{x}}_{1\alpha }^{l} = {{\left( {\sum\limits_{u = 1}^{U} {\bar{x}_{1u\alpha }^{l\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{u = 1}^{U} {\bar{x}_{1u\alpha }^{l\,} } } \right)} U}} \right. \kern-0pt} U},\,\,\,\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\,\,\, $$

(33)

$$ \underline{{\bar{x}}}_{2\alpha }^{l} = \,{{\left( {\sum\limits_{u = 1}^{U} {\underline{x}_{2u\alpha }^{l\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{u = 1}^{U} {\underline{x}_{2u\alpha }^{l\,} } } \right)} U}} \right. \kern-0pt} U},\,\,\quad \,\,\alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\,\,\, $$

(34)

$$ \bar{\mu }_{\alpha } = \,{{\left( {\sum\limits_{u = 1}^{U} {\mu_{u\alpha } } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{u = 1}^{U} {\mu_{u\alpha } } } \right)} U}} \right. \kern-0pt} U},\,\quad \,\alpha = \alpha_{1} ,\ldots,\alpha_{N} , $$

(35)

$$ \underline{{\bar{x}}}_{1\alpha }^{r} = {{\left( {\sum\limits_{u = 1}^{U} {\underline{x}_{1u\alpha }^{r\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{u = 1}^{U} {\underline{x}_{1u\alpha }^{r\,} } } \right)} U}} \right. \kern-0pt} U},\,\,\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\,\,\, $$

(36)

$$ \bar{\bar{x}}_{2\alpha }^{r} = {{\left( {\sum\limits_{{u = \text{1}}}^{U} {\bar{x}_{2u\alpha }^{r\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{u = \text{1}}}^{U} {\bar{x}_{2u\alpha }^{r\,} } } \right)} U}} \right. \kern-0pt} U},\,\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} . $$

(37)

Weighted average operation:

Let ${\tilde{\tilde{G}}}_{ij\alpha } = \left[ {\left[ {\bar{x}_{1ij\alpha }^{l} ,\underline{x}_{2ij\alpha }^{l} } \right],\mu_{ij} ,\left[ {\underline{x}_{1ij\alpha }^{r} ,\bar{x}_{2ij\alpha }^{r} } \right]} \right]$ and ${\tilde{\tilde{w}}}_{j\alpha } = \left[ {\left[ {\bar{w}_{1j\alpha }^{l} ,\underline{w}_{2j\alpha }^{l} } \right],\mu_{j} ,\left[ {\underline{w}_{1j\alpha }^{r},\bar{w}_{2j\alpha }^{r} } \right]} \right]$ be the evaluation of alternative i with respect to criterion j ($j = \text{1,}\ldots\text{,}J$) and the weight of criterion j at level α, respectively, which both of them are normal GIT2FNs. Moreover, let $H_{{\tilde{G}_{ij} }}^{L} = H_{{\tilde{G}_{ij} }}^{U} = 1\,({\text{for}}\,i = 1,\ldots,I,\,j = 1,\ldots,J)$ and $H_{{\tilde{\tilde{w}}_{j} }}^{L} = H_{{\tilde{\tilde{w}}_{j} }}^{U} = 1\,\,({\text{for}} = j = 1,\ldots,J)$. The weighted average of alternative i ($W\hat{A}_{i\alpha }$) at level $\alpha$ is obtained as follows:

$$ \begin{array}{ll} W\hat{A}_{i\alpha } &= {{\sum\limits_{j = 1}^{J} {(\hat{w}_{j\alpha } \times \hat{G}_{ij\alpha } )} } \mathord{\left/ {\vphantom {{\sum\limits_{j = 1}^{J} {(\hat{w}_{j\alpha } \times \hat{G}_{ij\alpha } )} } \,}} \right. \kern-0pt} \,}\sum\limits_{j = 1}^{{_{J} }} {\hat{w}_{j\alpha } } ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i = 1,\ldots I;\,\,\alpha = \alpha_{1} ,\ldots,\alpha_{N} , \\\\ &\quad = \frac{{\sum\nolimits_{j = 1}^{J} {\left( {\left\{ {\left[ {\bar{w}_{1j\alpha }^{l\,} ,\underline{w}_{2j\alpha }^{l\,} } \right]\,\,,\mu_{j\alpha } ,\left[ {\underline{w}_{1j\alpha }^{r\,} ,\bar{w}_{2j\alpha }^{r\,} } \right]} \right\} \times \left\{ {\left[ {\bar{x}_{1ij\alpha }^{l} ,\underline{x}_{2ij\alpha }^{l} } \right]\,\,,\mu_{ij\alpha } ,\left[ {\underline{x}_{1ij\alpha }^{r} ,\bar{x}_{2ij\alpha }^{r} } \right]} \right\}\,} \right)} }}{{\sum\nolimits_{j = 1}^{J} {\left\{ {\left[ {\bar{w}_{1j\alpha }^{l\,} ,\underline{w}_{2j\alpha }^{l\,} } \right]\,\,,\mu_{j\alpha } ,\left[ {\underline{w}_{1j\alpha }^{r\,} ,\bar{w}_{2j\alpha }^{r\,} } \right]} \right\}} }}, \hfill \\\\ & \quad= \frac{{\sum\nolimits_{j = 1}^{J} {\left\{ {\left[ {\underline{w}_{2j\alpha }^{l\,} \times \underline{x}_{2ij\alpha }^{l} ,\mu_{j\alpha } \times \mu_{ij\alpha } ,\underline{w}_{1j\alpha }^{r} \times \underline{x}_{1ij\alpha }^{r} } \right]\,\,,\left[ {\bar{w}_{1j\alpha }^{l\,} \times \bar{x}_{1ij\alpha }^{l} ,\mu_{j\alpha } \times \mu_{ij\alpha } ,\bar{w}_{2j\alpha }^{r} \times \bar{x}_{2ij\alpha }^{r} } \right]} \right\}} }}{{\sum\nolimits_{j = 1}^{J} {\left\{ {\left[ {\bar{w}_{1j\alpha }^{l\,} ,\underline{w}_{2j\alpha }^{l\,} } \right]\,\,,\mu_{j\alpha } ,\left[ {\underline{w}_{1j\alpha }^{r\,} ,\bar{w}_{2j\alpha }^{r} } \right]} \right\}} }}. \\ \end{array} $$

(38)

Property 1

Let ${{\tilde{\tilde{A}}}}_{1}$ and ${{\tilde{\tilde{A}}}}_{2}$ be two non-negative normal TraIT2FNs or triangular interval type-2 fuzzy numbers (TriIT2FNs). Then, all expressions in Sect. 3.3 hold true for them, respectively.

Proof

Since α-cuts can easily be depicted for normal TraIT2FNs or TriIT2FNs and reference points are generated at each level α, one can calculate the expressions calculated above for them.

A new approach for ranking GIT2FNs

The normal GIT2FNs case

Based on Kaufmann and Gupta [107], although ${\tilde{\tilde{A}}}$ and $\tilde{B}$ are triangular fuzzy numbers (as shown in Fig. 4), ${\tilde{\tilde{A}}}.\tilde{B}$ is not a triangular fuzzy number (the left and right MFs are not straight lines). It can challenge the distances between IT2FNs, while the curved MFs are applied to evaluations. The proposed approach is able to calculate distances on the different levels and rank GIT2FNs at interval [0, 1] concurrently. Generally, it considers the maximum and minimum reference limits among all GIT2FNs as reference limits (ideal solutions) and then calculates the limit distance mean (LDM) by subtracting the right and left limits of GIT2FNs from these reference limits.

Fig. 4

${\tilde{\tilde{A}}}.\tilde{B}$ is not a triangular fuzzy number

For this purpose, the left and right MFs of $\mu_{{{\tilde{\tilde{G}}}}} (x,u)$, for a GIT2FN, are partitioned into two MFs $\mu_{l} (x,u)\,({\rm for}\,\,x\langle \mu )\,\,{\text{and}}\,\mu_{r} (x,u)\,{\rm for}\,\,x\rangle \mu$, respectively (as shown in Fig. 3).

Moreover, assume that the minimum reference limit $\mu^{\hbox{min} } (x,u)$ and the maximum reference limit $\mu^{\hbox{max} } (x,u)$ are $\left\{ {\hbox{min} \left\{ {\mu_{l\,i} (x,u)} \right\}\,\,\,i \in all\,\,\,{\text{GIT2FNs}}\,} \right\}$ and $\left\{ {\,\hbox{max} \left\{ {\mu_{r\,i} (x,u)} \right\},\,\,i \in all\,\,\,{\text{GIT2FNs}}\,} \right\}$, respectively, as represented in Fig. 3.

Since the intersection of α-cut with a GIT2FN creates the interval numbers, interval arithmetic operations can be applied to them. As demonstrated in Fig. 3, suppose that the α-cut of the minimum and maximum reference limits $\mu_{\alpha }^{\hbox{min} } (x,u)\,$ and $\mu_{\alpha }^{\hbox{max} } (x,u)\,$ generates intervals $[\bar{x}_{1}^{\hbox{min} } ,\underline{x}_{2}^{\hbox{min} } ]_{\alpha }$ and $[\underline{x}_{1}^{\hbox{max} } ,\bar{x}_{2}^{\hbox{max} } ]_{\alpha }$ on X, respectively, where $\bar{x}_{1}^{\hbox{min} }$ and $\underline{x}_{2}^{\hbox{min} }$ are related to the upper and lower MFs of $\mu^{\hbox{min} } (x,u)$, respectively, and $\underline{x}_{1}^{\hbox{max} } \,{\text{and}}\,\bar{x}_{2}^{\hbox{max} }$ are equal to the lower and upper MFs of $\mu^{\hbox{max} } (x,u)$, respectively. In addition, let α-cut of the left and right MFs of a GIT2FN such as ${\tilde{\tilde{G}}}_{2}$ creates the intervals $[\bar{x}_{1}^{l} ,\underline{x}_{2}^{l} ]_{\alpha }$ and $[\underline{x}_{1}^{r} ,\bar{x}_{2}^{r} ]_{\alpha }$, respectively, where $\bar{x}_{1}^{l}$ and $\underline{x}_{2}^{l}$ are related to the upper and lower MFs of $\mu_{l} (x,u)$ and $\underline{x}_{1}^{r} \,{\text{and}}\,\bar{x}_{2}^{r}$ are equal to the lower and upper MFs of $\mu_{r} (x,u)$. With these assumptions in mind, if the evaluation’s measure of desirable alternative has the shortest distance from the positive ideal (PI) solution, the distance of $\mu_{l} (x,u)$ from $\mu^{\hbox{min} } (x,u)$ and the distance of $\mu_{r} (x,u)$ from $\mu^{\hbox{max} } (x,u)$ should have the shortest distance for C and benefit B criteria, respectively. Hence, LDM can be calculated for the PI solution with respect to C criteria as follows:

$$\begin{aligned}& {\text{LDM}}_{PI,C} ({{\tilde{\tilde{A}}}})= \frac{{\sum\nolimits_{\alpha = 0.1}^{1} {(\mu_{l\alpha } (x,u) - \mu_{\alpha }^{\hbox{min} } (x,u))\alpha } }}{{\sum\nolimits_{\alpha = 0.1}^{1} {(\mu_{l\alpha } (x,u) - \mu_{\alpha }^{\hbox{min} } (x,u))} - \sum\nolimits_{\alpha = 0.1}^{1} {(\mu_{r\alpha } (x,u) - \mu_{\alpha }^{\hbox{max} } (x,u))} }},\,\end{aligned} $$

(39)

where $\alpha = 0,\,0.1,\,0.2,\,0.3,\,0.4,\,0.5,\,0.6,\,0.7,\,0.8,\,{\text{ and 0}} . 9$. Note that $\sum\nolimits_{\alpha = 0.1}^{1} {(\mu_{l\alpha } (x,u) - \mu_{\alpha }^{\hbox{min} } (x,u))}$ and $\sum\nolimits_{\alpha = 0.1}^{1} {(\mu_{r\alpha } (x,u) - \mu_{\alpha }^{\hbox{max} } (x,u)\,)}$ are the positive and negative values. Thus, the negative sign was considered in the denominator. To simplify the calculations, Eq. (39) can be converted into the following equation using notation in Definition 3.2.9:

$$\begin{aligned}& {\text{LDM}}_{PI,C \, } ({{\tilde{\tilde{A}}}}) = \frac{{\sum\nolimits_{\alpha = 0.1}^{1} {[\bar{x}_{1}^{l} ,\underline{x}_{2}^{l} ]_{\alpha } - [\bar{x}_{1}^{\hbox{min} } ,\underline{x}_{2}^{\hbox{min} } ]_{\alpha } } }}{{\sum\nolimits_{\alpha = 0.1}^{1} {[\bar{x}_{1}^{l} ,\underline{x}_{2}^{l} ]_{\alpha } - [\bar{x}_{1}^{\hbox{min} } ,\underline{x}_{2}^{\hbox{min} } ]_{\alpha } } - \sum\nolimits_{\alpha = 0.1}^{1} {[\underline{x}_{1}^{r} ,\bar{x}_{2}^{r} ]_{\alpha } - [\underline{x}_{1}^{\hbox{max} } ,\bar{x}_{2}^{\hbox{max} } ]_{\alpha } } }}.\end{aligned} $$

(40)

Obviously, measures $[\bar{x}_{1}^{l} ,\underline{x}_{2}^{l} ]_{\alpha } - [\underline{x}_{1}^{\hbox{max} } ,\bar{x}_{2}^{\hbox{max} } ]_{\alpha }$ and $[\underline{x}_{1}^{r} ,\bar{x}_{2}^{r} ]_{\alpha } - [\underline{x}_{1}^{\hbox{max} } ,\bar{x}_{2}^{\hbox{max} } ]_{\alpha }$ equal to the negative measures when $(\bar{x}_{1}^{l} < \bar{x}_{2}^{\hbox{max} } ;\underline{x}_{2}^{l} < \underline{x}_{1}^{\hbox{max} } )$ or $(\underline{x}_{1}^{r} < \bar{x}_{2}^{\hbox{max} } ;\bar{x}_{2}^{r} < \underline{x}_{1}^{\hbox{max} } )$. Instead, $LD_{PI,C}$ can be calculated using Eq. (27) as follows:

$$ \begin{aligned} {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{A}}}})&= \frac{{\sum\nolimits_{\alpha = 0.1}^{1} {\frac{1}{2}\left| {(\bar{x}_{1}^{l} - \underline{x}_{2}^{\hbox{min} } )_{\alpha } + (\underline{x}_{2}^{l} - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} }}{{\sum\nolimits_{\alpha = 0.1}^{1} {\frac{1}{2}\left| {(\bar{x}_{1}^{l} - \underline{x}_{2}^{\hbox{min} } )_{\alpha } + (\underline{x}_{2}^{l} - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} + \sum\nolimits_{\alpha = 0.1}^{1} {\frac{1}{2}\left| {(\underline{x}_{1}^{r} - \bar{x}_{2}^{\hbox{max} } )_{\alpha } + (\bar{x}_{2}^{r} - \underline{x}_{1}^{\hbox{max} } )_{\alpha } } \right|} }} \hfill \\ &\quad \times\frac{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| {(\bar{x}_{1}^{l} - \underline{x}_{2}^{\hbox{min} } )_{\alpha } + (\underline{x}_{2}^{l} - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} }}{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| {(\bar{x}_{1}^{l} - \underline{x}_{2}^{\hbox{min} } )_{\alpha } + (\underline{x}_{2}^{l} - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} + \sum\nolimits_{\alpha = 0.1}^{1} {\left| {(\underline{x}_{1}^{r} - \bar{x}_{2}^{\hbox{max} } )_{\alpha } + (\bar{x}_{2}^{r} - \underline{x}_{1}^{\hbox{max} } )_{\alpha } } \right|} }}.\, \hfill \\ \end{aligned} $$

(41)

Similarly, the PI solution for the set of B criteria and the negative ideal (NI) solution for the set of C and B criteria are given, respectively, as follows:

$$ {\text{LDM}}_{{{\text{PI}},B}} ({{\tilde{\tilde{A}}}}) = \frac{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| { (\underline{x}_{1}^{r} - \bar{x}_{2}^{\hbox{max} } )_{\alpha } + (\bar{x}_{2}^{r} - \underline{x}_{1}^{\hbox{max} } )_{\alpha } } \right|} }}{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| { (\underline{x}_{1}^{r} - \bar{x}_{\hbox{max} 2} )_{\alpha } + (\bar{x}_{2}^{r} - \underline{x}_{1}^{\hbox{max} } )_{\alpha } } \right|} + \sum\nolimits_{\alpha = 0.1}^{1} {\left| { (\bar{x}_{1}^{l} - \underline{x}_{2}^{\hbox{min} } )_{\alpha } + (\underline{x}_{2}^{l} - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} }},\,\, $$

(42)

$$ {\text{LDM}}_{{{\text{NI}},C}} ({{\tilde{\tilde{A}}}}) = \frac{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| {(\bar{x}_{1}^{l} - \bar{x}_{2}^{\hbox{max} } )_{\alpha } + (\underline{x}_{2}^{l} - \underline{x}_{1}^{\hbox{max} } )_{\alpha } } \right|} }}{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| {(\bar{x}_{1}^{l} - \bar{x}_{2}^{\hbox{max} } )_{\alpha } + (\underline{x}_{2}^{l} - \underline{x}_{1}^{\hbox{max} } )_{\alpha } } \right|} + \sum\nolimits_{\alpha = 0.1}^{1} {\left| {(\underline{x}_{1}^{r} - \underline{x}_{2}^{\hbox{min} } )_{\alpha } + (\bar{x}_{2}^{r} - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} }},\,\,\,\, $$

(43)

$$ {\text{LDM}}_{{{\text{NI}},B}} ({{\tilde{\tilde{A}}}}) = \frac{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| { (\underline{x}_{1}^{r} - \underline{x}_{2}^{\hbox{min} } )_{\alpha } + (\bar{x}_{2}^{r} - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} }}{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| { (\underline{x}_{1}^{r} - \underline{x}_{2}^{\hbox{min} } )_{\alpha } + (\bar{x}_{2}^{r} - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} + \sum\nolimits_{\alpha = 0.1}^{1} {\left| { (\bar{x}_{1}^{l} - \bar{x}_{2}^{\hbox{max} } )_{\alpha } + (\underline{x}_{2}^{l} - \underline{x}_{1}^{\hbox{max} } )_{\alpha } } \right|} }}. $$

(44)

Obviously, the desirable alternative has the shortest distance from the PI solution and the longest distance from the NI solution based on Eqs. (41)–(42) and (43)–(44), respectively. In other words, in case of the NI solution, the distance of $\mu_{l} (x,u)$ from $\mu^{\hbox{max} } (x,u)$ and the distance of $\mu_{r} (x,u)$ from $\mu^{\hbox{min} } (x,u)$ should have the longest distance with respect to C and B criteria for a desirable alternative, respectively. On the other hand, in the situation of PI solution, the distance of $\mu_{l} (x,u)$ from $\mu^{\hbox{min} } (x,u)$ and the distance of $\mu_{r} (x,u)$ from $\mu^{\hbox{max} } (x,u)$ should have the shortest distance with respect to C and B criteria, respectively.

Moreover, measures $(\underline{x}_{1}^{r} - \bar{x}_{2}^{\hbox{max} } ) + (\bar{x}_{2}^{r} - \underline{x}_{1}^{\hbox{max} } )$ and $(\bar{x}_{1}^{l} - \underline{x}_{2}^{\hbox{min} } ) + (\underline{x}_{2}^{l} - \bar{x}_{1}^{\hbox{min} } )$ are equal to zero when $[\underline{x}_{1}^{r} ,\bar{x}_{2}^{r} ]$ and $[\bar{x}_{1}^{l} ,\underline{x}_{2}^{l} ]$ matches $\mu^{\hbox{max} } (x,u)$ and $\mu^{\hbox{min} } (x,u)$, respectively. Hence, the measures $\frac{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| { (\bar{x}_{2}^{\hbox{max} } - \underline{x}_{1}^{\hbox{max} } )_{\alpha } } \right|} }}{\alpha }$ and $\frac{{\sum\nolimits_{\alpha = 0.1}^{1} {\left| { (\underline{x}_{2}^{\hbox{min} } - \bar{x}_{1}^{\hbox{min} } )_{\alpha } } \right|} }}{\alpha }$ are used to calculate LDMs when the distances of reference limits $\mu^{\hbox{max} } (x,u)$ and $\mu^{\hbox{min} } (x,u)$ are obtained from themselves, respectively.

Some properties of the above LDMs:

Property 2

Neither of the denominators in Eqs. (41)–(44) is zero.

Property 3

All distances obtained by LDMs in Eqs. (41)–(44) include at interval [0, 1].

Property 4

Four LDMs in Eqs. (41)–(44) can be utilized for the MCDM techniques where it is necessary to calculate the PI and NI ideal solutions.

Property 5

Let ${\tilde{\tilde{G}}}_{1}$ and ${\tilde{\tilde{G}}}_{2}$ be two non-negative symmetric normal GIT2FNs in a set of non-negative symmetric normal GIT2FNs, where ${\tilde{\tilde{G}}}_{1} = [\tilde{G}_{1}^{L} ,\tilde{G}_{1}^{U} ] =$$\,\left[ {\left( {\,\mu_{1}^{L} ;\,\sigma_{1}^{L} ;H_{{\tilde{G}_{1} }}^{L} \,} \right),\left( {\,\mu_{1}^{U} ;\,\sigma_{1}^{U} ;H_{{\tilde{G}_{1} }}^{U} \,} \right)} \right]\,$ and $\,{\tilde{\tilde{G}}}_{2} = [{\tilde{\tilde{G}}}_{2}^{L} ,{\tilde{\tilde{G}}}_{2}^{U} ] = \,\,\left[ {\left( {\,\mu_{2}^{L} ;\,\sigma_{2}^{L} ;H_{{\tilde{G}_{2} }}^{L} \,} \right),\left( {\,\mu_{2}^{U} ;\,\sigma_{2}^{U} ;H_{{\tilde{G}_{2} }}^{U} \,} \right)} \right]\,$. In addition, suppose that distance between ${\tilde{\tilde{G}}}_{1}$ and ${\tilde{\tilde{G}}}_{2}$ is showed as $d({\tilde{\tilde{G}}}_{1} ,{\tilde{\tilde{G}}}_{2} ) = LDM({\tilde{\tilde{G}}}_{1} ) - LDM({\tilde{\tilde{G}}}_{2} )$. Then, $\left| {d({\tilde{\tilde{G}}}_{1} ,{\tilde{\tilde{G}}}_{2} )} \right| = \left| {LDM({\tilde{\tilde{G}}}_{1} ) - LDM({\tilde{\tilde{G}}}_{2} )} \right| \ge 0$ for all LDMs.

Property 6

Let ${\tilde{\tilde{G}}}_{1}$ and ${\tilde{\tilde{G}}}_{2}$ be two non-negative symmetric normal GIT2FNs where ${\tilde{\tilde{G}}}_{1} = [\tilde{G}_{1}^{L} ,\tilde{G}_{1}^{U} ] =$$\,\Big[ \Big( \,\mu_{1}^{L} ;\,\sigma_{1}^{L} ;H_{{\tilde{G}_{1} }}^{L} \, \Big),\Big( {\,\mu_{1}^{U} ;\,\sigma_{1}^{U} ;H_{{\tilde{G}_{1} }}^{U} \,} \Big) \Big]\,$ and $\,{\tilde{\tilde{G}}}_{2} = [{\tilde{\tilde{G}}}_{2}^{L} ,{\tilde{\tilde{G}}}_{2}^{U} ] = \,\,\Big[ \Big( {\,\mu_{2}^{L} ;\,\sigma_{2}^{L} ;H_{{\tilde{G}_{2} }}^{L} \,} \Big),\Big( \,\mu_{2}^{U} ;\,\sigma_{2}^{U} ;H_{{\tilde{G}_{2} }}^{U} \, \Big) \Big]\,$. Moreover, suppose that distance between ${\tilde{\tilde{G}}}_{1}$ and ${\tilde{\tilde{G}}}_{2}$ is showed as $d({\tilde{\tilde{G}}}_{1} ,{\tilde{\tilde{G}}}_{2} )$. Then, $\left| {d({\tilde{\tilde{G}}}_{1} ,{\tilde{\tilde{G}}}_{2} )} \right| = \left| {d({\tilde{\tilde{G}}}_{2} ,{\tilde{\tilde{G}}}_{1} )} \right|$.

Property 7

Let ${\tilde{\tilde{G}}}_{1}$, ${\tilde{\tilde{G}}}_{2}$, and ${\tilde{\tilde{G}}}_{3}$ be three non-negative symmetric normal GIT2FNs in a set of non-negative symmetric normal GIT2FNs where ${\tilde{\tilde{G}}}_{1} = [\tilde{G}_{1}^{L} ,\tilde{G}_{1}^{U} ] =$$\,\left[ {\left( {\,\mu_{1}^{L} ;\,\sigma_{1}^{L} ;H_{{\tilde{G}_{1} }}^{L} \,} \right),\left( {\,\mu_{1}^{U} ;\,\sigma_{1}^{U} ;H_{{\tilde{G}_{1} }}^{U} \,} \right)} \right]\,$, $\,{\tilde{\tilde{G}}}_{2} = [{\tilde{\tilde{G}}}_{2}^{L} ,{\tilde{\tilde{G}}}_{2}^{U} ] = \,\,\left[ {\left( {\,\mu_{2}^{L} ;\,\sigma_{2}^{L} ;H_{{\tilde{G}_{2} }}^{L} \,} \right),\left( {\,\mu_{2}^{U} ;\,\sigma_{2}^{U} ;H_{{\tilde{G}_{2} }}^{U} \,} \right)} \right]\,$, and $\,{\tilde{\tilde{G}}}_{3} = [{\tilde{\tilde{G}}}_{3}^{L} ,{\tilde{\tilde{G}}}_{3}^{U} ] = \,\,\left[ {\left( {\,\mu_{3}^{L} ;\,\sigma_{3}^{L} ;H_{{\tilde{G}_{3} }}^{L} \,} \right),\left( {\,\mu_{3}^{U} ;\,\sigma_{3}^{U} ;H_{{\tilde{G}_{3} }}^{U} \,} \right)} \right]\,$. Then, $d({\tilde{\tilde{G}}}_{3} ,{\tilde{\tilde{G}}}_{2} ) + d({\tilde{\tilde{G}}}_{2} ,{\tilde{\tilde{G}}}_{1} ) \ge d({\tilde{\tilde{G}}}_{3} ,{\tilde{\tilde{G}}}_{1} )$.

The interested reader can easily implement this proof in other LDMs in this section.

Property 8

${\text{LDM}}_{{{\text{NI}},B}} ({\tilde{\tilde{G}}}_{{}} ) = {\text{LDM}}_{W} ({\tilde{\tilde{G}}}_{{}} )$ introduced in Eq. (44) can be utilized to weight criteria and rank GIT2FNs.

• If ${\text{LDM}}_{{{\text{NI}},B}} ({\tilde{\tilde{G}}}_{2} ) > {\text{LDM}}_{{{\text{NI}},B}} ({\tilde{\tilde{G}}}_{1} )$, then ${\tilde{\tilde{G}}}_{2}$ is better than ${\tilde{\tilde{G}}}_{1}$.

• If ${\text{LDM}}_{{{\text{NI}},B}} ({\tilde{\tilde{G}}}_{2} ) < {\text{LDM}}_{{{\text{NI}},B}} ({\tilde{\tilde{G}}}_{1} )$, then ${\tilde{\tilde{G}}}_{1}$ is better than ${\tilde{\tilde{G}}}_{2}$.

• If ${\text{LDM}}_{{{\text{NI}},B}} ({\tilde{\tilde{G}}}_{2} ) = {\text{LDM}}_{{{\text{NI}},B}} ({\tilde{\tilde{G}}}_{1} )$, then ${\tilde{\tilde{G}}}_{1}$ and ${\tilde{\tilde{G}}}_{2}$ are the same (indifferent).

IN order to demonstrate the effectiveness of Eqs. (41)–(44), the following two examples are taken into account:

Example 1

Consider the following two GIT2FNs as type-2 fuzzy weights for criteria $C_{1}$ and $C_{2}$, respectively:

$$ {\tilde{\tilde{G}}}_{1} = \left[ {\tilde{G}_{1}^{L} ,\tilde{G}_{1}^{U} } \right] = \left[ {\left( {6,\,1.5,\,;\,1} \right),\left( {6,\,2;1} \right)} \right] $$

and ${\tilde{\tilde{G}}}_{2} = \left[ {\tilde{G}_{2}^{L} ,\tilde{G}_{2}^{U} } \right] = \left[ {\left( {8,\,1.5,\,;\,1} \right),\left( {8,\,2;1} \right)} \right].$

As shown in the Fig. 5, $C_{2}$ is larger than $C_{1}$. Table 1 represents levels of α-cuts for the above two GIT2FNs. According to Table 2, measures ${\text{LDM}}_{W}$ for criteria $C_{1}$ and $C_{2}$ are 0.405 and 0.594, respectively. It proves the graphical representation.

Fig. 5

GIT2FNs of Example 1

Table 1 Levels of α-cuts of two GIT2FNs

Table 2 Measures ${\text{LDM}}_{W}$

Example 2

Let two GIT2FNs are as depicted in Fig. 6. Obviously, the lower limits of two GIT2FNs are equal. Note that $C_{2}$ is larger than $C_{1}$ due to its larger upper limit.

Fig. 6

GIT2FNs of Example 2

Table 3 represents levels of α-cuts for these two GIT2FNs. As shown in last row of Table 4, measures ${\text{LDM}}_{W}$ [Eq. (44)] for criteria $C_{1}$ and $C_{2}$ are 0.411 and 0.500, respectively.

Table 3 Levels of α-cuts of two GIT2FNs

Table 4 Measures ${\text{LDM}}_{W}$

Property 9

Properties 2–8 also hold true for non-negative symmetric normal TraIT2FNs and TriIT2FNs.

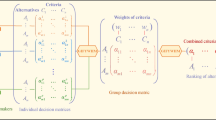
Application of the new ranking method to FWA-ELECTRE III with GIT2FNs

Figure 7 shows the framework of the proposed methodology. The first stage is to define criteria, sub-criteria, and alternatives (different MHE) based on experts’ standpoints or suggestions. In the second stage, the group multi-criteria decision-making (GMCDM) matrix based on GIT2FSs is constructed with GIT2FSs for the MHESP. The weights of criteria and sub-criteria are determined based on GIT2FSs selected by experts in the next stage. The FWA technique based on alpha cuts is then implemented to obtain the aggregated weighted ratings from the Gaussian interval type-2 fuzzy assessments of each alternative with respect to sub-criteria and the Gaussian interval type-2 fuzzy weights of sub-criteria, and finally, the most suitable MHE is chosen using the ELECTRE III approach.

Fig. 7

Framework of the proposed methodology

The following steps are the summary of the integrated algorithm FWA- ELECTRE III based on GIT2FNs for ranking MHE:

Step 1 Assume that I alternatives $A_{i}$ ($i\; = \;1,\ldots,\;I$) are to be evaluated by L experts with respect to J criteria $C_{j}$$(j = 1,\,\ldots,\,J)$. Moreover, let each criterion $C_{j}$ includes k sub-criteria $c_{jk} \, (k = 1,2,\ldots,k_{j} ).$

Step 2 Determine two types of linguistic variables for the MHESP. The first type is adopted to evaluate alternatives with respect to sub-criteria (see Table 5) and the second one is applied to weight criteria and sub-criteria (see Table 6).

Table 5 Linguistic variables for ratings

Table 6 Linguistic variables for weights

Step 3 Apply the data in Table 6 to weight criteria and sub-criteria. There are the following two vectors of weights with respect to criteria ($W$) and their corresponding sub-criteria ($W_{j}$), respectively:

$$ W = (w_{1} ,w_{2} ,\ldots,w_{J} ),\,\, $$

(45)

$$ W_{j} = (w_{j1} ,w_{j2} ,\ldots,w_{{jk_{j} }} ),\,\,\,\,\,\,\,\,\,\,j = 1,\ldots,J. $$

(46)

Step 4 Construct the Gaussian interval type 2 fuzzy MCDM (GIT2FMCDM) matrix (as represented in Table 7) for the MHESP as follows:

Table 7 GIT2FMCDM matrix for the MHESP

where each criterion $C_{j}$ ($j\; = \;1,\ldots,\;J$) includes $k\,(k = 1,2,\ldots,k_{j} )$ sub-criteria ($c_{j1} ,\ldots,\;c_{{jk_{j} }}$) and ${{\tilde{\tilde{X}}}}_{ijk}^{l}$ is a GIT2FN selected by lth expert assessing alternative i ($i\; = \;1,\ldots,\;I$) with respect to $k{\text{th}}\, (k = 1,2,\ldots,k_{j} )$ sub-criterion $(c_{jk} )$ regarding criterion $C_{j}$ ($j\; = \;1,\ldots,\;J$).${{\tilde{\tilde{X}}}}_{ijk}^{l}$ is a GIT2FN as $\left[ {\left( {\,\mu^{L} ;\,\sigma^{L} ;H_{{\tilde{\tilde{G}}}}^{L} \,} \right),\left( {\mu^{U} ;\,\sigma^{U} ;H_{{\tilde{\tilde{G}}}}^{U} \,} \right)} \right]$ (as explained in Definition 3.2.6).

Step 5 Integrate the type-2 fuzzy ratings ${{\tilde{\tilde{X}}}}_{ijk}^{l}$ (for all $l\; = \;1,\ldots,\;L$) for each sub-criterion $(c_{jk} )$ (for each $i\; = \;1,\ldots,\;I$, $j\; = \;1,\ldots,\;J$ and $k = 1,2,\ldots,k_{j}$) with the synthetic type-2 fuzzy rating ${{\tilde{\tilde{X}}}}_{ijk}$ using the following equation:

$$\begin{aligned} {{\tilde{\tilde{X}}}}_{ijk} &= ({1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}) \otimes ({{\tilde{\tilde{X}}}}_{ijk}^{1} \oplus {{\tilde{\tilde{X}}}}_{ijk}^{2} \oplus \ldots \oplus {{\tilde{\tilde{X}}}}_{ijk}^{L} ),\\ &\quad\quad\,i = 1,\ldots,I;\,\,\,j = 1,\ldots,J;\,\,\,\,k = 1,\ldots,k_{j} .\end{aligned} $$

(47)

Indeed, it is the average of the type-2 fuzzy ratings ${{\tilde{\tilde{X}}}}_{ijk}^{l}$ ($l\; = \;1,\ldots,\;L$) selected by L experts. Similarly, integrate the type-2 fuzzy weights ${\tilde{\tilde{w}}}_{j}^{l}$ and ${\tilde{\tilde{w}}}_{jk}^{l}$ (for all $l\; = \;1,\ldots,\;L$) for each criterion and sub-criterion $(c_{jk} )$ (for each $j\; = \;1,\ldots,\;J$ and $k = 1,2,\ldots,k_{j}$) with the synthetic type-2 fuzzy weight ${\tilde{\tilde{w}}}_{j}$ and ${\tilde{\tilde{w}}}_{jk}$, respectively, as follows:

$$ {\tilde{\tilde{w}}}_{j} = ({1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}) \otimes ({\tilde{\tilde{w}}}_{j}^{1} \oplus {\tilde{\tilde{w}}}_{j}^{2} \oplus \ldots \oplus {\tilde{\tilde{w}}}_{j}^{L} ),\quad j = \text{1,}\ldots\text{,}J,\,\,\,\, $$

(48)

$$\begin{aligned} {\tilde{\tilde{w}}}_{jk} &= ({1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}) \otimes ({\tilde{\tilde{w}}}_{jk}^{1} \oplus {\tilde{\tilde{w}}}_{jk}^{2} \oplus \ldots \oplus {\tilde{\tilde{w}}}_{jk}^{L} ),\\ &\quad j = 1,\ldots,J;\,\,\,\,k = 1,\ldots,k_{j} .\end{aligned} $$

(49)

Using the notation described in Definition 3.2.9, GIT2FNs ${{\tilde{\tilde{X}}}}_{{ijk_{\alpha } }}$ at level $\alpha$ (for each $i\; = \;1,\ldots,\;I$, $j\; = \;1,\ldots,\;J$ and $k = 1,2,\ldots,k_{j}$) can be represented as follows:

$$\begin{aligned} \hat{x}_{{ijk_{\alpha } }} &= (\bar{x}_{{1ijk_{\alpha } }}^{l\,} ,\underline{x}_{{2ijk_{\alpha } }}^{l\,} ,\mu_{{ijk_{\alpha } }} \,,\,\underline{x}_{{1ijk_{\alpha } }}^{r\,} ,\bar{x}_{{2ijk_{\alpha } }}^{r\,} ),\\ &\quad \,i = 1,\ldots,I;\,\,\,j = \text{1,}\ldots\text{,}J;\,\,\,k = 1,\ldots,k_{j} ,\,\end{aligned} $$

(50)

where $\mu_{{ijk_{\alpha } }}$ is the mean of GIT2FN when alternative i ($i\; = \;1,\ldots,\;I$) is evaluated with respect to $k{\text{th}}\, (k = 1,2,\ldots,k_{j} )$ sub-criterion $(c_{jk} )$ regarding criterion $C_{j}$($j\; = \;1,\ldots,\;J$) at level $\alpha$.

Similarly, GIT2FN ${{\tilde{\tilde{X}}}}_{{ijk_{\alpha } }}^{l}$ selected by lth expert at level $\alpha$ can be showed as follows:

$$\begin{aligned} \hat{x}_{{ijk_{\alpha } }}^{l} &= (\bar{x}_{{1ijk_{\alpha } }}^{l\,l} ,\underline{x}_{{2ijk_{\alpha } }}^{l\,l} ,\mu_{{ijk_{\alpha } }} \,,\,\underline{x}_{{1ijk_{\alpha } }}^{r\,l} ,\bar{x}_{{2ijk_{\alpha } }}^{r\,l} ), \,\,i = 1,\ldots,I;\\&\quad j = \text{1,}\ldots\text{,}J;\,\,\,k = 1,\ldots,k_{j} ;l = 1,\ldots,L.\end{aligned} $$

(51)

The average (synthesis) of five reference points is obtained for GIT2FNs chosen by L experts as $\bar{\hat{x}}_{{ijk_{\alpha } }} = (\bar{\bar{x}}_{{1ijk_{\alpha } }}^{l\,} ,\underline{{\bar{x}}}_{{2ijk_{\alpha } }}^{l\,} ,\bar{\mu }_{{ijk_{\alpha } }} \,,\,\underline{{\bar{x}}}_{{1ijk_{\alpha } }}^{r\,} ,\bar{\bar{x}}_{{2ijk_{\alpha } }}^{r\,} )$ at level α ($\alpha = \alpha_{1} ,\ldots,\alpha_{N}$;$\,i = 1,\ldots,I;$$j = \text{1,}\ldots\text{,}J;\,{\text{and}}\,\,\,k = 1,2,\ldots,k_{j}$) using extension of Eqs. (33)–(37) as follows:

$$\begin{aligned} &\bar{\bar{x}}_{{1ijk_{\alpha } }}^{l\,} = {{\left( {\sum\limits_{l = 1}^{L} {\bar{x}_{{1ijk_{\alpha } }}^{l\,l} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{l = 1}^{L} {\bar{x}_{{1ijk_{\alpha } }}^{l\,l} } } \right)} L}} \right. \kern-0pt} L}, i = 1,\ldots,I;\,\,\,j = 1,\ldots,J;\\ &\quad k = 1,\ldots,k_{j} ;\alpha = \alpha_{1} ,\ldots,\alpha_{N} , \end{aligned}$$

(52)

$$\begin{aligned} & \underline{{\bar{x}}}_{{2ijk_{\alpha } }}^{l\,} = \,{{\left( {\sum\limits_{l = 1}^{L} {\underline{x}_{{2ijk_{\alpha } }}^{l\,l} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{l = 1}^{L} {\underline{x}_{{2ijk_{\alpha } }}^{l\,l} } } \right)} L}} \right. \kern-0pt} L},\,\quad \,\,i = 1,\ldots,I;\\ &\quad j = 1,\ldots,J;\,\,\,k = 1,\ldots,k_{j} ;\alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(53)

$$ \begin{aligned} &\bar{\mu }_{{ijk_{\alpha } }} = \,{{\left( {\sum\limits_{l = 1}^{L} {\mu_{{ijp_{\alpha } }}^{\,l} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{l = 1}^{L} {\mu_{{ijp_{\alpha } }}^{\,l} } } \right)} L}} \right. \kern-0pt} L},\,\,\quad i = 1,\ldots,I;\\ &\quad\,j = 1,\ldots,J;\,\,\,k = 1,\ldots,k_{j} ;\alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\,\,\,\,\end{aligned}$$

(54)

$$ \begin{aligned} &\underline{{\bar{x}}}_{{1ijk_{\alpha } }}^{r\,} = {{\left( {\sum\limits_{l = 1}^{L} {\underline{x}_{{1ijk_{\alpha } }}^{r\,l} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{l = 1}^{L} {\underline{x}_{{1ijk_{\alpha } }}^{r\,l} } } \right)} L}} \right. \kern-0pt} L},\,\,\,\quad \,\,i = 1,\ldots,I;\\ &\quad\,j = 1,\ldots,J;\,\,\,k = 1,\ldots,k_{j} ;\alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\,\,\,\end{aligned} $$

(55)

$$\begin{aligned} &\bar{\bar{x}}_{{2ijk_{\alpha } }}^{r\,} = {{\left( {\sum\limits_{l = 1}^{L} {\bar{x}_{{2ijk_{\alpha } }}^{r\,l} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{l = 1}^{L} {\bar{x}_{{2ijk_{\alpha } }}^{r\,l} } } \right)} L}} \right. \kern-0pt} L},\,\,\quad i = 1,\ldots,I;\\ &\quad j = 1,\ldots,J;\,\,\,k = 1,\ldots,k_{j} ;\alpha = \alpha_{1} ,\ldots,\alpha_{N} .\end{aligned} $$

(56)

Similarly, the average of five reference points for weights of criteria and sub-criteria $\bar{\hat{w}}_{{j_{\alpha } }} = (\bar{\bar{w}}_{{1j_{\alpha } }}^{l\,} ,\underline{{\bar{w}}}_{{2j_{\alpha } }}^{l\,} ,\bar{\mu }_{{j_{\alpha } }} \,,\,\underline{{\bar{w}}}_{{1j_{\alpha } }}^{r\,} ,\bar{\bar{w}}_{{2j_{\alpha } }}^{r\,} )$ and $\bar{\hat{w}}_{{jk_{\alpha } }} = (\bar{\bar{w}}_{{1jk_{\alpha } }}^{l\,} ,\underline{{\bar{w}}}_{{2jk_{\alpha } }}^{l\,} ,\bar{\mu }_{{jk_{\alpha } }} \,,\,\underline{{\bar{w}}}_{{1jk_{\alpha } }}^{r\,} ,\bar{\bar{w}}_{{2jk_{\alpha } }}^{r\,} )$ are determined at level α, respectively, as follows:

$$\begin{aligned} &\bar{\bar{w}}_{{1j_{\alpha } }}^{l\,} = {{\left( {\sum\limits_{l = 1}^{L} {\bar{w}_{{1j_{\alpha } }}^{ll\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{l = 1}^{L} {\bar{w}_{{1j_{\alpha } }}^{ll\,} } } \right)} L}} \right. \kern-0pt} L},\quad\,j = 1,\ldots,J;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(57)

$$ \begin{aligned} &\underline{{\bar{w}}}_{{2j_{\alpha } }}^{l\,} = \,{{\left( {\sum\limits_{{l = \text{1}}}^{L} {\underline{w}_{{2j_{\alpha } }}^{ll\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\underline{w}_{{2j_{\alpha } }}^{ll\,} } } \right)} L}} \right. \kern-0pt} L},\quad \,j = \text{1,}\ldots\text{,}J;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(58)

$$\begin{aligned}& \bar{\mu }_{{j_{\alpha } }} = \,{{\left( {\sum\limits_{{l = \text{1}}}^{L} {\mu_{{j_{\alpha } }}^{l} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\mu_{{j_{\alpha } }}^{l} } } \right)} L}} \right. \kern-0pt} L},\quad j = \text{1,}\ldots\text{,}J;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N\,} ,\end{aligned} $$

(59)

$$ \begin{aligned} &\underline{{\bar{w}}}_{{1j_{\alpha } }}^{r\,} = {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\underline{w}_{{1j_{\alpha } }}^{rl\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\underline{w}_{{1j_{\alpha } }}^{rl\,} } } \right)} L}} \right. \kern-0pt} L}, \quad j = \text{1,}\ldots\text{,}J;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(60)

$$ \begin{aligned} &\bar{\bar{w}}_{{2j_{\alpha } }}^{r\,} = {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\bar{w}_{{2j_{\alpha } }}^{rl\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\bar{w}_{{2j_{\alpha } }}^{rl\,} } } \right)} L}} \right. \kern-0pt} L}, j = \text{1,}\ldots\text{,}J;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(61)

and

$$\begin{aligned} & \bar{\bar{w}}_{{1jk_{\alpha } }}^{l\,} = {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\bar{w}_{{1jk_{\alpha } }}^{ll\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\bar{w}_{{1jk_{\alpha } }}^{ll\,} } } \right)} L}} \right. \kern-0pt} L},\quad j = \text{1,}\ldots\text{,}J;\\&\quad k = 1,\ldots,k_{j} ;\alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(62)

$$\begin{aligned} & \underline{{\bar{w}}}_{{2jk_{\alpha } }}^{l\,} = \,{{\left( {\sum\limits_{{l = \text{1}}}^{L} {\underline{w}_{{2jk_{\alpha } }}^{ll\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\underline{w}_{{2jk_{\alpha } }}^{ll\,} } } \right)} L}} \right. \kern-0pt} L},\quad \,j = \text{1,}\ldots\text{,}J;\quad k = 1,\ldots,k_{j} ;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(63)

$$ \begin{aligned} &\bar{\mu }_{{jk_{\alpha } }} = \,{{\left( {\sum\limits_{{l = \text{1}}}^{L} {\mu_{{jk_{\alpha } }}^{\,l} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\mu_{{jk_{\alpha } }}^{\,l} } } \right)} L}} \right. \kern-0pt} L},\quad j = \text{1,}\ldots\text{,}J;\,\,\,k = 1,2,\ldots,k_{j} ;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(64)

$$ \begin{aligned} &\underline{{\bar{w}}}_{{1jk_{\alpha } }}^{r\,} = {{\left( {\sum\limits_{l = 1}^{L} {\underline{w}_{{1jk_{\alpha } }}^{rl\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{l = 1}^{L} {\underline{w}_{{1jk_{\alpha } }}^{rl\,} } } \right)} L}} \right. \kern-0pt} L},\quad j = 1,\ldots,J;\,\,\,k = 1,2,\ldots,k_{j} ;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} ,\end{aligned} $$

(65)

$$\begin{aligned} & \bar{\bar{w}}_{{2jk_{\alpha } }}^{r\,} = {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\bar{w}_{{2jk_{\alpha } }}^{rl\,} } } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{{l = \text{1}}}^{L} {\bar{w}_{{2jk_{\alpha } }}^{rl\,} } } \right)} L}} \right. \kern-0pt} L},\quad j = \text{1,}\ldots\text{,}J;\,\,\,k = 1,2,\ldots,k_{j} ;\\&\quad \alpha = \alpha_{1} ,\ldots,\alpha_{N} . \end{aligned}$$

(66)

Step 6 If number of sub-criteria under one criterion are greater than or equal 2 $(k \ge 2)$, integrate the synthetic type-2 fuzzy ratings of each alternative with respect to all sub-criteria under one criterion (calculated by Eqs. (52)–(56)) and the synthetic type-2 fuzzy weights of sub-criteria (obtained by Eqs. (62)–(66)) with the aggregated weighted ratings $\hat{a}_{ij \alpha }$ at level $\alpha$ using the generalization of the FWA approach introduced in Eq. (38):

$$\begin{aligned}&\hat{a}_{ij \alpha } = {\sum \limits_{k = 1}^ {k_{j}}} (\hat{w}_{jk \alpha} \times \hat{x}_{ijk \alpha }) / {\sum\limits_{k = 1}^{k_{j}}} {\hat{w}_{jk \alpha }}, \quad i = 1,\ldots, I; \\&\quad j = 1,\ldots, J; \alpha = \alpha_{1} ,\ldots, \alpha_{N},\end{aligned} $$

(67)

where $\hat{a}_{{ij_{\alpha } }} = \left\{ {\left[ {\bar{a}_{{1ij_{\alpha } }}^{l\,} ,\underline{a}_{{2ij_{\alpha } }}^{l\,} } \right]\,\,,\left[ {\underline{a}_{{1ij_{\alpha } }}^{r\,} ,\bar{a}_{{2ij_{\alpha } }}^{r\,} } \right]} \right\}$.

Thus, the GIT2FMCDM matrix for the MHESP (as presented in Table 7) is transformed with the following aggregated weighted MCDM matrix:

$$\begin{aligned}& \quad\quad\quad\quad\quad\quad\quad\quad{{C_1}}{\, \cdots \,}{{C_J}}\\ &{{\hat A}_{I \times J\alpha }} = \begin{array}{l} {{A_1}}\\ \vdots \\ {{A_I}} \end{array}\left[ {\begin{array}{lll} {{{\hat a}_{11\alpha }}} &\cdots &{{{\hat a}_{1J\alpha }}}\\ \vdots & \cdots & \vdots \\ {{{\hat a}_{I1\alpha }}}& \cdots &{{{\hat a}_{IJ\alpha }}} \end{array}} \right],\\&\quad i = 1,...,I;\,\,\,j = 1,...,J;\alpha = {\alpha _1},...,{\alpha _N},\ \end{aligned}$$

(68)

where $\bar{\hat{w}}_{{j_{\alpha } }} = (\bar{\bar{w}}_{{1j_{\alpha } }}^{l\,} ,\underline{{\bar{w}}}_{{2j_{\alpha } }}^{l\,} ,\bar{\mu }_{{j_{\alpha } }} \,,\,\underline{{\bar{w}}}_{{1j_{\alpha } }}^{r\,} ,\bar{\bar{w}}_{{2j_{\alpha } }}^{r\,} )$ is the average of weights vector for $\,\alpha = \alpha_{1} ,\ldots,\alpha_{N}$ and $j = \text{1,}\ldots\text{,}J$.

Step 7 Calculate three thresholds $q_{j}$, $p_{j}$, and $v_{j}$.

First, the largest and the smallest of evaluations for the quantitative criteria are obtained as follows:

$$ A_{j}^{ + } \,\,\,\, = \left\{ {\max_{i} \,(x_{ij} )} \right\},\,\,\quad \,\,\,j = 1,\ldots,n^{\prime},\,\, $$

(69)

$$ A_{j}^{ - } \,\,\,\, = \left\{ {\max_{i} \,(x_{ij} )} \right\},\,\,\,\quad \,\,\,j = 1,\ldots,n^{\prime}. $$

(70)

Second, measures of thresholds for the quantitative criteria are calculated as follows:

$$ q_{j} = (A_{j}^{ + } \, - A_{j}^{ - } \,)*\beta_{1j} ,\,\,\quad j = 1,\ldots,n^{\prime},\,\, $$

(71)

$$ p_{j} = (A_{j}^{ + } \, - A_{j}^{ - } )*\beta_{2j} ,\,\,\,\,\quad j = 1,\ldots,n^{\prime}, $$

(72)

$$ v_{j} = (A_{j}^{ + } \, - A_{j}^{ - } \,)*\beta_{3j} ,\,\quad j = 1,\ldots,n^{\prime},\, $$

(73)

where $\beta_{1} ,$$\beta_{2} ,$ and $\beta_{3}$ are scalars that their measures are determined by decision-makers.

On the other hand,${{\tilde{\tilde{q}}}}_{j}$,${\tilde{\tilde{p}}}_{j}$, and ${\tilde{\tilde{v}}}_{j}$ are determined using GIT2FNs and then their LDMs are calculated using Eq. (41).

Step 8 Calculate the concordance index of alternative $A_{r}$ relative to alternative $A_{k}$ (C ($A_{r}$ ,$A_{k}$)) by the following formula:

$$ \hat{C}(A_{r} ,A_{k} ) = \frac{{\sum\nolimits_{j = 1}^{{n^{\prime}}} {LDM_{W} ({\tilde{\tilde{w}}}_{j} )*c_{j} (A_{r} ,A_{k} ) + \sum\nolimits_{{j = n^{\prime} + 1}}^{n} {LDM_{W} ({\tilde{\tilde{w}}}_{j} )*\hat{c}_{j} (A_{r} ,A_{k} )} } }}{{\sum\nolimits_{j = 1}^{n} {LDM_{W} ({\tilde{\tilde{w}}}_{j} )} }},\,\,\,\,\,\,\,\,\,\,r,k = 1,\ldots,m;\,\,\,r \ne k,\, $$

(74)

where $LDM_{W} ({\tilde{\tilde{w}}}_{j} )$, $c_{j} (A_{r} ,A_{k} )$, and $\hat{c}_{j} (A_{r} ,A_{k} )$ are weight of criterion j ($j = n^{\prime} + 1,\ldots,n$) by using Eq. (44), the superior level of alternative $A_{r}$ relative to alternative $A_{k}$ for quantitative criteria [Eqs. (3) and (4)], and the superior level of alternative $A_{r}$ relative to alternative $A_{k}$ for qualitative criteria, respectively. For B andC qualitative criteria, $\hat{c}_{j} (A_{r} ,A_{k} )$ is calculated, respectively, by the following relation:

$$ \hat{c}_{j} (A_{r} ,A_{k} ) = \left\{ \begin{array}{ll} 0 &\quad \quad {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{kj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{rj} ) \ge {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{p}}}_{j} ),\,\, \hfill \\ \frac{{{{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{rj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{kj} ) + {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{p}}}_{j} )}}{{{{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{p}}}_{j} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{q}}}}_{j} )}} &\qquad {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{q}}}}_{j} ) < \,{{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{kj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{rj} )\\ &\qquad\quad \le {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{p}}}_{j} ), \hfill \\ 1 &\quad \quad {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{kj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{rj} ) \le {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{q}}}}_{j} ), \hfill \\ \end{array} \right. $$

(75)

and

$$ \hat{c}_{j} (A_{r} ,A_{k} ) = \left\{ \begin{array}{ll} 0 &\quad {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{rj} ) - {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{kj} ) \ge {\text{LDM}}_{{{\text{PI}},C}} ({\tilde{\tilde{p}}}_{j} ),\,\, \hfill \\ \frac{{{\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{kj} ) - {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{rj} ) + {\text{LDM}}_{{{\text{PI}},C}} ({\tilde{\tilde{p}}}_{j} )}}{{{\text{LDM}}_{{{\text{PI}},C}} ({\tilde{\tilde{p}}}_{j} ) - {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{q}}}}_{j} )}}&\quad{\text{otherwise}}, \hfill \\ 1 &\quad {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{rj} ) - {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{kj} ) \le {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{q}}}}_{j} ), \hfill \\ \end{array} \right. $$

(76)

where $LDM^{\prime}_{PI,B} = 1 - LDM_{PI,B}$ and $LDM^{\prime}_{PI,C} = 1 - LDM_{PI,C}$.

Step 9 Calculate the discordance index of alternative $A_{r}$ versus alternative $A_{k}$ ($\hat{d}_{j} (A_{r} ,A_{k} )$) for quantitative criteria ($j = 1,\ldots,n^{\prime}$) using Eqs. (5) and (6) and for B and C qualitative criteria ($j = n^{\prime} + 1,\ldots,n$) as:

$$ \hat{d}_{j} (A_{r} ,A_{k} ) = \left\{ \begin{array}{ll} 0 &\quad\quad{{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{kj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{rj} ) \le {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{p}}}_{j} ),\,\, \hfill \\ \frac{{{{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{kj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{rj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{p}}}_{j} )}}{{{{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{v}}}_{j} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{p}}}_{j} )}},&\quad\quad{{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{p}}}_{j} ) {{ < {\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{kj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{rj} ) \le {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{v}}}_{j} ),\, \hfill \\ 1& \quad\quad{{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{kj} ) - {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({{\tilde{\tilde{X}}}}_{rj} ) \ge {{{\rm LDM}^{\prime}}}_{{{\text{PI}},B}} ({\tilde{\tilde{v}}}_{j} ), \hfill \\ \end{array} \right. $$

(77)

and

$$ \hat{d}_{j} (A_{r} ,A_{k} ) = \left\{ \begin{array}{l@{\quad}l} 0&{\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{rj} ) - {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{kj} ) \le {\text{LDM}}_{{{\text{PI}},C}} ({\tilde{\tilde{p}}}_{j} ),\,\, \hfill \\ \frac{{\,{\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{rj} ) - {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{kj} ) - {\text{LDM}}_{{{\text{PI}},C}} ({\tilde{\tilde{p}}}_{j} )}}{{{\text{LDM}}_{{{\text{PI}},C}} ({\tilde{\tilde{v}}}_{j} ) - {\text{LDM}}_{{{\text{PI}},C}} ({\tilde{\tilde{p}}}_{j} )}}& {\text{otherwise}}, \hfill \\ 1&{\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{rj} ) - {\text{LDM}}_{{{\text{PI}},C}} ({{\tilde{\tilde{X}}}}_{kj} ) \ge {\text{LDM}}_{{{\text{PI}},C}} ({\tilde{\tilde{v}}}_{j} ). \hfill \\ \end{array} \right. $$

(78)

Step 10 Determine credit degree index of alternative $A_{r}$ versus alternative $A_{k}$($\hat{S}(A_{r} ,A_{k} )$) for quantitative criteria ($j = 1,\ldots,n^{\prime}$) using Eq. (7) and for qualitative criteria ($j = n^{\prime} + 1,\ldots,n$) by the following formula:

$$ \hat{S}(A_{r} ,A_{k} ) = \left\{ \begin{array}{ll} \hat{C}(A_{r} ,A_{k} ),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,if\,\hat{d}_{j} (A_{r} ,A_{k} ) \le \,\hat{C}(A_{r} ,A_{k} )&\quad\forall j, \hfill \\ \hat{C}(A_{r} ,A_{k} ).\,\,\prod\limits_{{j \in J:\hat{d}_{j} (A_{r} ,A_{k} ){ > }\,\hat{C}(A_{r} ,A_{k} )}} {\frac{{1 - \hat{d}_{j} (A_{r} ,A_{k} )}}{{1 - \hat{C}(A_{r} ,A_{k} )}}} &\quad{\text{otherwise}}, \hfill \\ \end{array} \right.\,\, $$

(79)

where $\hat{S}(A_{r} ,A_{k} )$ and J are the degree of outranking alternative $A_{r}$ relative to alternative $A_{k}$ and the set of criteria for which $\hat{d}_{j} (A_{r} ,A_{k} ){ > }\,\hat{C}(A_{r} ,A_{k} )$, respectively.

Step 11 Calculate the final scores and rank alternatives:

In addition to cases discussed in Sect. 3.1, in this paper, the net credibility value method [108] is used to determine the final scores. To acquire the net credibility value, the concordance credibility value and the discordance credibility value should be first calculated as follows:

• I. The following concordance credibility value is determined for alternative r:

  $$ \theta_{r}^{c} = \sum\limits_{k = 1,k \ne r}^{m} {\hat{S}(A_{r} ,A_{k} )} ,\,\, \,\,r = 1,\ldots,m. $$

  (80)

• II. The discordance credibility value is determined for alternative r using the following relation:

  $$ \theta_{r}^{d} = \sum\limits_{k = 1,k \ne r}^{m} {\hat{S}(A_{k} ,A_{r} )} ,\,\quad \,r = 1,\ldots,m. $$

  (81)

• III. The following net credibility value is obtained for alternative r:

  $$ \theta_{r} = \theta_{r}^{c} - \theta_{r}^{d} ,\quad r = 1,\ldots,m,\, $$

  (82)

  where $\theta_{r}$ represents the total score of alternative r (the higher the score, the greater the preference level).

Application

Case study

To show the ability of the proposed approach to solve the MHESP, a real case study is considered in this section where five conveyers $A_{i} \,\,$$(i = 1,\,2,\,3,\,4,\,5)$ [pneumatic conveyor (alternative 1), chute conveyor (alternative 2), roller conveyor (alternative 3), flat-belt conveyor (alternative 4), and wheel conveyor (alternative 5)] are evaluated with respect to four criteria $C_{j} \,\,$$(j = 1,\,2,\,3,\,4)$ (characterizations of technical, monetary, operational, and strategic).

Design experts are three experts who select the most suitable conveyor among the different alternatives. Obviously, each kind of MHE has different characterizations. Figure 8 shows the hierarchy structure of optimal MHE selection process with respect to four criteria. Each criterion includes five sub-criteria in the next level. In addition, five types of conveyors are in the lowest level.

Fig. 8

Hierarchical structure of the GIT2FMCDM for the MHESP

First, linguistic variables with their GIT2FNs are applied to weight criteria and sub-criteria in the table. Three experts are then asked to select one of them for determining their importance degree. Table 8 and also Tables 9, 10, 11 and 12 show these variables for criteria and sub-criteria, respectively.

Table 8 Determining the weights of criteria

Table 9 Determining the weights of sub-criteria with respect to technical $(C_{1} )$

Table 10 Determining the weights of sub-criteria with respect to monetary $(C_{2} )$

Table 11 Determining the weights of sub-criteria with respect to operational $(C_{3} )$

Table 12 Determining the weights of sub-criteria with respect to strategic $(C_{4} )$

Assessments of alternatives with respect to sub-criteria have been also presented in Tables 13 and 14 using the data in Table 5. The linguistic variables located in rows and columns are the preference level of experts when appraising the alternatives with respect to sub-criteria. Then, the synthetic type-2 fuzzy weights of criteria, sub-criteria, and the synthetic type-2 fuzzy ratings of alternatives with respect to sub-criteria obtained using Eqs. (57)–(61), Eqs. (62)–(66), and Eqs. (52)–(56) for $\alpha = 0.1,\,0.2,\,0.4,\,0.6,\,0.8,{ 0} . 9$.

Table 13 Subjective evaluations of three experts for each alternative with respect to sub-criteria under $C_{1}$ and $C_{2}$

Table 14 Subjective evaluations of three experts for each alternative with respect to sub-criteria under $C_{3}$ and $C_{4}$

Now, the weights of criteria ($LDM_{W}$) are calculated for $\alpha = 0.1,\,0.2,\,0.4,\,0.6,\,0.8,{ 0} . 9$ using Eq. (44). Table 15 represents the weights of criteria, which are 0.5000, 0.6717, 0.8433, and 0.1569, respectively.

Table 15 Weights of criteria

Aggregated weighted ratings $\hat{a}_{ij \alpha }$ are also calculated using Eq. (67) for $\alpha = 0.1,\,0.2,\,0.4,\,0.6,\,0.8,{ 0} . 9$ (see Tables 16 and 17).

Table 16 Aggregated weighted ratings $\hat{a}_{ij\alpha }$ with respect to criteria $C_{1}$ and $C_{2}$ for $\alpha = 0.1,\,0.2,\,0.4,\,0.6,\,0.8,{ 0} . 9$

Table 17 Aggregated weighted ratings $\hat{a}_{ij\alpha }$ with respect to criteria $C_{3}$ and $C_{4}$ for $\alpha = 0.1,\,0.2,\,0.4,\,0.6,\,0.8,{ 0} . 9$

Table 18 demonstrates thresholds as the linguistic variables with respect to criteria. The linguistic variables are specified based on the preferences of experts using the data in Table 5.

Table 18 Linguistic variables of thresholds with respect to criteria

Based on the data in Tables 18, 19 represents the measures of thresholds for quantitative criteria using Eqs. (71)–(73) and for qualitative criteria using Eq. (41). Table 20 shows measures LDMs with respect to criteria based on Eqs. (41) and (42).

Table 19 Thresholds with respect to different criteria

Table 20 Measures of LDMs of alternatives with respect to criteria

Now, the concordance matrix (Table 21) is constructed based on the comparison of the alternatives, according to Eqs. (74)–(76).

Table 21 Concordance matrix

After calculating the discordance matrices for each criterion based on Eqs. (77) and (78) (for qualitative criteria), the comparisons between the concordance and discordance matrices are carried out, as shown in Table 22 based on Eq. (79).

Table 22 Comparison matrix

Now, the results of credit degree ($S(A_{r} ,A_{k} )$) between alternatives are presented in Table 23 using Eq. (79) (for qualitative criteria). Then, the net credibility matrix is made using Eqs. (80)–(82), as demonstrated in Table 24. Based on the data of this table, the ranking order is as $A_{3} > A_{1} > A_{4} > A_{5} > A_{2}$.

Table 23 Credit degree matrix

Table 24 Net credibility matrix

Sensitivity analysis

In the ELECTRE III approach, the criteria weights and thresholds affect the stability of the obtained orders within a decision-making process. To demonstrate the reliability of the obtained rankings, it is necessary to analyze the sensitivity analysis with respect to different values of the criteria weights and thresholds measures. Accordingly, the authors considered four sets of criteria weights and three sets of thresholds measures to investigate the use of the different weights and measures in the proposed method, respectively. In each set of the criteria weights, there is one criterion with the highest weight (as shown in Fig. 9). The proposed method is then solved with respect to each set, separately. Orders of each set of criteria are represented in Table 25. To check the similarity of the ranking results for all sets of criteria, the authors utilized the Spearman correlation coefficient. Table 26 represents the correlation coefficients between these sets. According to the data of this table, coefficients are greater than 0.9 when calculating relations between sets. It can be inferred that the proposed method has a fairly good stability with respect to the different weights of criteria. Figure 10 and Tables 27, 28, 29, 30 represent the sets of thresholds and rankings of each set, respectively. In each set of thresholds under a certain criterion, only these thresholds change and the thresholds measures of other criteria are fixed. Table 31 shows the correlation coefficients among these sets for different criteria. As represented in this table, the correlation coefficients are greater than 0.9 when calculating coefficients. It concludes that the obtained orders are stable and reliable based on our proposed approach.

Fig. 9

Sets of criteria weights

Table 25 Ranking results with respect to the different sets of the criteria weights

Table 26 Correlation coefficients between the different sets of criteria weights

Fig. 10

Sets of thresholds

Table 27 Ranking results with respect to different sets of thresholds with respect to criterion $C_{1}$

Table 28 Ranking results with respect to different sets of thresholds with respect to criterion $C_{2}$

Table 29 Ranking results with respect to different sets of thresholds with respect to criterion $C_{3}$

Table 30 Ranking results with respect to different sets of thresholds with respect to criterion $C_{4}$

Table 31 Correlation coefficients between the different sets of thresholds with respect to the different criteria

Comparison with other methods

To further illustrate the effectiveness of the proposed methodology, the results obtained by ELECTRE III based on GIT2FSs are compared with some existing approaches in the literature. Table 32 represents the ranking results based on VIKOR with IT2FSs [30], VIKOR with IT2FSs [31], TOPSIS with IT2FSs [109], SAW with IT2FSs [33], and WASPAS with IT2FSs [34]. As represented in this table, $A_{3}$ is the optimal alternative in all approaches. It verifies the effectiveness and robustness of the proposed method with the other MCDM techniques introduced above when determining the optimal alternative. But, the authors obtained the different analysis when the use of the fuzzy VIKOR (FVIKOR) method [89]. The ranking priorities obtained by indices ${\text{DF}}(\tilde{Q}_{r} )$, ${\text{DF}}(\tilde{S}_{r} )$, and ${\text{DF}}(\tilde{R}_{r} )$ have been shown in Table 33 according to descending order, in which ${\text{DF}}(\tilde{Q}_{r} )$,${\text{DF}}(\tilde{S}_{r} )$, and ${\text{DF}}(\tilde{R}_{r} )$ show the measures of defuzzification $\tilde{Q}_{r}$,$\tilde{S}_{r}$, and $\tilde{R}_{r}$, respectively.

Table 32 Comparison of ranking results by other techniques

Table 33 Ranking results by FVIKOR

Illustrative example 1

In this section, to show the effectiveness of our ranking method with, the illustrative example adopted by Rashid et al. [29] is taken into account where three robots $R_{1}$, $R_{2}$, and $R_{3}$ are assessed with respect to six criteria $C_{1}$, $C_{2}$,$C_{3}$, $C_{4}$,$C_{5}$, and $C_{6}$. The authors have decided to eliminate the effect of thresholds using the thresholdless techniques such as TOPSIS and VIKOR. In other words, the authors want to understand that similar results can be achieved among different approaches when thresholds are not used to them. Note that criteria 4 and 6 are of cost type and the other criteria are of benefit type. Tables 34, 35, 36 represent the performance ratings, weights, and normalized measures with respect to different criteria, respectively.

Table 34 Performance ratings of robots with respect to different criteria

Table 35 Weights of criteria

Table 36 Normalized measures

Based on Tables 36, 37 shows the weighted normalized matrix. In addition, Tables 38 and 39 represent PI and NI solutions based on the existence TOPSIS [29] and the interval type-2 fuzzy TOPSIS methods using LDM, respectively.

Table 37 Weighted normalized matrix

Table 38 PI and NI solutions (the existence TOPSIS method [29])

Table 39 PI and NI solutions (interval type-2 fuzzy TOPSIS using LDM)

According to Tables 39, 40 presents ${\text{LDM}}_{\text{PI }}$, ${\text{LDM}}_{\text{NI }}$, ideal separation ($\hat{S}_{i}^{ + }$), anti-ideal separation ($\hat{S}_{i}^{ - }$), and relative closeness (RC). Finally, Table 41 shows the ranking results of different approaches. Obviously, the most desirable alternative is robot 3 based on the different approaches and the ranking results are as $R_{3} > R_{2} > R_{1}$ for all of them. In fact, the obtained results imply that the use of LDMs in the thresholdless techniques can show the effectiveness and reliability of the proposed ranking method.

Table 40 Measures ${\text{LDM}}_{\text{PI }}$, ${\text{LDM}}_{\text{NI }}$, $\hat{S}_{i}^{ + }$,$\hat{S}_{i}^{ - }$, and ${\text{RC}}$ based on interval type-2 fuzzy TOPSIS using LDM

Table 41 Ranking results of different approaches

Illustrative Example 2

In this section, a numerical example introduced by Zhong and Yao [32] is presented to compare the ranking results of extended ELECTRE III method with those of the others in the literature. A high-technology company intends to evaluate five qualified suppliers $A_{1}$, $A_{2}$,$A_{3}$, $A_{4}$, and $A_{5}$ with respect to seven criteria including company reputation ($C_{1}$), technical performance ($C_{2}$), date of delivery ($C_{3}$), service ($C_{4}$), cost control ($C_{5}$), management performance ($C_{6}$), and quality ($C_{7}$), which their weights are $w_{1} = 0. 0 5 6 2$, $w_{2} = 0. 1 2 3 4$, $w_{3} = 0. 0 4 5 2$, $w_{4} = 0. 1 2 4 5$, $w_{5} = 0. 2 3 2 5$, $w_{6} = 0. 1 3 8 0$, and $w_{7} = 0. 2 8 0 1$ based on the entropy method, respectively. Note that the above criteria are of benefit type. Table 42 represents the evaluated decision matrix of alternatives with respect to criteria. Based on Tables 42,  43 shows the PI and NI solutions.

Table 42 Evaluated decision matrix of alternatives with respect to criteria

Table 43 PI and NI solutions

Table 44 presents the concordance matrix based on the different approaches. By calculating the discordance matrices for each criterion based on Eqs. (77) and (78), the comparisons between the concordance and discordance matrices are carried out based on Eq. (79), as shown in Table 45.

Table 44 Concordance matrix

Table 45 Comparison matrix

Now, the results of credit degree ($S(A_{r} ,A_{k} )$) between alternatives are presented in Table 46 using Eq. (79). In the next step, the net credibility matrix is made using Eqs. (80)–(82), as demonstrated in Table 47. In addition, Table 48 presents the ranking results using the different methods. According to the data of this table, the ranking order of alternatives is as $A_{5} > A_{4} > A_{1} > A_{2} > A_{3}$ using the proposed method. Thus, alternative 5 is selected as the optimal alternative which is also the most important alternative based on the last four approaches. On the other hand, the ranking results obtained by the ELECTRE I method [32] are different from those of the others. It implies that the recent approach cannot be the suitable method for ranking alternatives.

Table 46 Credit degree matrix

Table 47 Net credibility matrix

Table 48 Ranking results of different approaches

Conclusion and discussion

In the real world, the selection of the best alternative with respect to conflicting criteria is a difficult and complex work when data are vague and inexact. Although type-1 fuzzy sets could greatly resolve ambiguities in decision problems, it takes into account only a specified measure for MF. Thus, T2FSs are applied to consider an interval at [0, 1] for MF when decision-maker is uncertain about the value of MF. The MFs of a T2FS can take the different versions such as triangular, trapezoidal, and Gaussian. Since GIT2FNs have the smoother MF, the authors adopted them for evaluating alternatives with respect to qualitative criteria. This paper presents a new approach for prioritizing GIT2FNs. The proposed method first depicts alpha cuts and then calculates the distances from reference limits. It generates the distances or ranking measures automatically at interval [0, 1]. It is also able to rank TriIT2FNs, TraIT2FNs, and other curved forms. This approach can be applied to the MCDM techniques such as ELECTRE III needing to rank weights of criteria or determine distances of type-2 fuzzy numbers from ideal solutions. To show the effectiveness of the proposed methodology, it was also implemented in a real case study. The authors proposed an integrated GMCDM approach to solve the MHESP where the judgments of experts were represented by GIT2FNs. In real, the experts ranked a kind of equipment named conveyor with respect to a set of criteria and their corresponding sub-criteria where all criteria and sub-criteria weights were expressed as GIT2FNs. In our suggested methodology, the type-2 fuzzy weights of criteria and sub-criteria and also type-2 fuzzy ratings of alternatives with respect to sub-criteria were first integrated with the synthetic type-2 fuzzy weights and ratings, respectively. The FWA method was then adopted by the authors for incorporating the synthetic ratings of each alternative with respect to all sub-criteria under one criterion and the synthetic weights of sub-criteria to the aggregated weighted ratings and finally, the alternatives were ranked by ELECTRE III. According to the obtained results, the authors have concluded that the alternative 3 is the optimal MHE for all approaches (see Table 32). However, there are a few differences in ranking the other alternatives due to the different nature of compared approaches. In the following, we state them in detailed. As shown in Table 32, there are the similar ranking results as $A_{3} > A_{2} > A_{4} > A_{5} > A_{1}$ between VIKOR with IT2FSs [30], VIKOR with IT2FSs [31], FVIKOR [89], and TOPSIS [109] with IT2FSs approaches, since all of them are based on the closeness to PI solution and the avoidance of NI solution. Although, in the approaches of VIKOR with IT2FSs [30, 31], both conditions C₁ and C₂ were satisfied and only one alternative was chosen as the best MHE. However, the authors obtained a set of the compromise solutions when FVIKOR [89] was applied. Hence, the conditions C₁ and C₂ should be analyzed for obtaining the final ranking results. Since alternative three has the lowest value regarding the above indices, so alternative three has acceptable stability. In addition, condition C1 (i.e., $DF(\tilde{Q}_{2} ) - DF(\tilde{Q}_{3} ) = 0. 1 5 5< 0.25$) is not satisfied. Hence, alternative 4 that has third situation in the ranking list by ${\text{DF}}(\tilde{Q}_{r} )$ should be considered for satisfying the condition C1. Since the obtained expression (i.e., ${\text{DF}}(\tilde{Q}_{4} ) - {\text{DF}}(\tilde{Q}_{3} ) = 0. 5 8 3> 0.25$) holds true, alternatives 2 and 3 are proposed as a set of compromise solutions. Moreover, because of the SAW [33] and WASPAS [34] methods which have the similar ranking programs, the ranking results are almost similar. Note that two last methods have the different ranking structure as compared to the others. As a result, there are the partial ranking differences between them due to the use of weighted product model (WPM) in the WASPAS method. However, they also determined alternative 3 as the most desirable alternative. On the other hand, conveyors 1 and 2 have ranks 2 and 5 based on our proposed method (ELECTRE III with IT2FSs), respectively. In real, lower measure of threshold $p_{1}$ as compared to other criteria and also lower measures of thresholds $v_{j}$ with respect to criteria 1 and 3 as compared to criteria 2 and 4 are the principal reasons of this ranking change. In real-world problems, it may be a situation in which a decision-maker has not any preference with respect to some measures of alternatives. In other words, thresholds can foster better understanding of experts when solving real problems. For example, an investor may have no difference between costs 1000 and 2000 dollar. Thus, the measures of thresholds can help to experts when facing with such situations. These reasons imply that the ELECTRE III method with GIT2FNs is more reliable and more logical for GMCDM problems.

On the other hand, to show effectiveness of the proposed ranking method, LDMs were applied to the thresholdless techniques such as TOPSIS and VIKOR (see illustrative Example 1). Based on Table 41, the results ranked by our method are similar to those of the others. It proves reliability of the proposed ranking method.

Again, the proposed ranking method was integrated with ELECTRE III in the illustrative Example 2. According to Table 48, several conclusions can be obtained as follows:

• The last four approaches (the thresholdless techniques) in this table have the similar ranking results as: $A_{5} > A_{1} > A_{3} > A_{4} > A_{2}$.

• Alternative 5 was selected as the optimal alternative based on the proposed method (ELECTRE III using LDM), TOPSIS with IT2FSs [29], WASPAS with IT2FSs [34], VIKOR with IT2FSs [30], and SAW with IT2FSs [33].

• The results determined by the ELECTRE I method [32] are quite different from those of the others. Alternative 4 was chosen as the most desirable alternative. It implies that the recent approach cannot be the suitable method for ranking alternatives.

Generally, it should be noted that the differences of orders between the ELECTRE III with the others can be arisen from the impact of the threshold values in the ELECTRE III method. In other words, the main reason of these differences is the lack of thresholds in the VIKOR and TOPSIS methods. Moreover, the results obtained by our approach are stable and reliable when changing the criteria weights and thresholds.

Some important directions for further studies are as follows:

• 1. Our methodology was implemented only in a kind of MHE (named conveyor). However, managers can apply it to the others such as cranes, forklift truck, etc.

• 2. Other criteria and sub-criteria may be taken into account in the other manufacturing industries or service organizations.

• 3. In our case study, the distance between alpha cuts was determined 0.1 when LDMs were calculated. To obtain more accurate results, one can adopt the smaller values for them such as 0.05 or 0.01.

• 4. The proposed methodology is efficient for each number of alternatives, qualitative criteria, and quantitative criteria.

• 5. The proposed approach is applicable to other MCDM techniques, in addition to ELECTRE.

• 6. The proposed method can be adopted for other mathematical branches such as data envelopment analysis (DEA) and/or statistical science where probability density functions with different curved forms may be applied.

• 7. The proposed method can be used to other fuzzy environments such as intuitionistic fuzzy sets, spherical fuzzy sets, neutrosophic fuzzy sets, etc.