Abstract
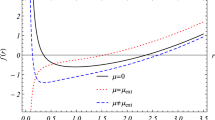
An Ermakov–Pinney-like equation associated with the scalar wave equation in curved space-time is here studied. The example of Schwarzschild space-time considered in the present work shows that this equation can be viewed more as a “model equation,” with interesting applications in black hole physics. Other applications studied involve cosmological space-times (de Sitter) and pulse of plane gravitational waves: in all these cases the evolution of the Ermakov–Pinney field seems to be consistent with a rapid blow-up, unlike the Schwarzschild case where spatially damped oscillations are allowed. Eventually, the phase function is also evaluated in many of the above space-time models.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
Note that a harmonic time dependence leads to a term linear in y and hence corresponds to the \(p \not =0\) case.
Generalizations with \(\alpha \) a complex scalar field are also possible.
We follow the convention according to which Greek indices from the beginning of the alphabet are Lie-algebra indices. When necessary, this index specification is explicitly repeated in the text to avoid confusion.
In general, all our formulae for currents are particular cases of the general expressions
$$\begin{aligned} J=J^{\mu }{\partial \over \partial x^{\mu }}, \; J_{\nu }=J^{\mu }g_{\mu \nu }, \; J^{\flat }=J_{\nu }dx^{\nu }. \end{aligned}$$Note that, as discussed above in the Schwarzschild case, the second term here is obtained from the first by replacing \(f_c\rightarrow -f_c\).
References
Cohen, J.M., Kegeles, L.S.: Electromagnetic fields in curved spaces: a constructive procedure. Phys. Rev. D 10, 1070 (1974)
Treves, F.: Introduction to Pseudodifferential and Fourier Integral Operators. Fourier Integral Operators, vol. 2. Plenum Press, New York (1980)
Esposito, G., Battista, E., Di Grezia, E.: Bicharacteristics and Fourier integral operators in Kasner spacetime. Int. J. Geom. Methods Mod. Phys. 12, 1550060 (2015)
Esposito, G., Minucci, M.: A new perspective on the Ermakov–Pinney and scalar wave equations. Lett. High Energy Phys. LHEP 3, 5 (2019). arXiv:1905.09382 [math.GM]
Ermakov, V.P.: Second-order differential equations: conditions of complete integrability. Univ. Izv. Kiev Ser. III 9, 1 (1880)
Pinney, E.: The non-linear differential equation \(y^{\prime \prime }+p(x)y+cy^{-3}=0\). Proc. Am. Math. Soc. 1, 681 (1950)
Detweiler, S.L., Messaritaki, E., Whiting, B.F.: Selfforce of a scalar field for circular orbits about a Schwarzschild black hole. Phys. Rev. D 67, 104016 (2003). https://doi.org/10.1103/PhysRevD.67.104016. [arXiv:gr-qc/0205079 [gr-qc]]
Ronveaux, A.: Heun’s Differential Equations. Oxford University Press, Oxford (1995)
Stephani, H., Kramer, D., MacCallum, M.A.H., Hoenselaers, C., Herlt, E.: Exact Solutions of Einstein’s Field Equations. Cambridge University Press, Cambridge (2003). https://doi.org/10.1017/CBO9780511535185
Schmidt, B.G., Stewart, J.M.: The scalar wave equation in a Schwarzschild spacetime. Proc. R. Soc. Lond. A 367, 503 (1979)
Casadio, R., Luzzi, M.: The method of comparison equations for Schwarzschild black holes. Phys. Rev. D 74, 085005 (2006)
Tsamparlis, M., Paliathanasis, A.: Generalizing the autonomous Kepler–Ermakov system in a Riemannian space. J. Phys. A 45, 275002 (2012)
Acknowledgements
G. Esposito is grateful to the Dipartimento di Fisica “Ettore Pancini” of Federico II University for hospitality and support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Bini, D., Esposito, G. New solutions of the Ermakov–Pinney equation in curved space-time. Gen Relativ Gravit 52, 60 (2020). https://doi.org/10.1007/s10714-020-02713-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10714-020-02713-y