Clustering method for censored and collinear survival data

Abstract

In this paper we propose a Dirichlet process mixture model for censored survival data with covariates. This model is suitable in two scenarios. First, this method can be used to identify clusters determined by both the censored survival data and the predictors. Second, this method is suitable for highly correlated predictors, in cases when the usual survival models cannot be implemented because they would be unstable due to multicollinearity. The Dirichlet process mixture model links a response vector to covariate data through cluster membership and in this paper this model is extended for mixtures of Weibull distributions, which can be used to model survival times and also allow for censoring. We propose two variants of this model, one with a shape parameter common to all clusters (referred to as a global parameter) for the Weibull distributions and one with a cluster-specific shape parameter. The first satisfies the proportional hazard assumption, while the latter is very flexible, as it has the advantage of allowing estimation of the survival curve whether or not the proportional hazards assumption is satisfied. We present a simulation study and, to demonstrate the applicability of the method in practice, a real application to sleep surveys in older women from The Australian Longitudinal Study on Women’s Health. The method developed in the paper is available in the R package PReMiuM.

1 Introduction

We propose a Dirichlet process mixture model for censored survival data with covariates. This model is most useful in two situations.

First of all, this method can be used to identify clusters determined by censored survival data and explanatory variables. The idea of linking a response vector to covariate data through cluster membership was proposed initially by several authors including Dunson et al. (2008), Bigelow and Dunson (2009), Molitor et al. (2010), Papathomas et al. (2011), and Molitor et al. (2011). We will focus on the latter of these articles, which refers to this idea as profile regression, where a Dirichlet mixture model is used for inference on the clusters. This model was implemented in an R package by Liverani et al. (2015) and it has been employed in a variety of fields (Molitor et al. 2014), including genetics (Papathomas et al. 2012), environmental epidemiology (Papathomas et al. 2011; Pirani et al. 2015; Coker et al. 2016; Liverani et al. 2016) and occupational epidemiology (Hastie et al. 2013; Mattei et al. 2016). In this paper we extend this model to survival outcomes with censoring.

Second, the proposed method is suitable when the explanatory variables are multicollinear. Multicollinearity, or collinearity, is the existence of near-linear relationships among the explanatory variables. The high correlation between explanatory variables can create inaccurate, or unstable, estimates of the regression coefficients, inflate the standard errors, deflate the partial t-tests, give false, nonsignificant, p-values, and degrade the predictability of the model. Hence, one of the first steps in a regression analysis is to determine if multicollinearity is present. Our proposed method is stable when highly correlated predictors are included in the model, making it a powerful tool to explore survival datasets with highly correlated predictors.

The model that we propose is essentially a mixture of Weibull distributions and distributions suitable for the covariates, non-parametrically linking the response and the predictors through cluster membership. Modelling independently the response and the covariates is the idea underpinning profile regression as an exploratory method in the presence of collinearity in the covariates. This modelling choice allows the exploration of the complex relationship between the response and the covariates. Although the response and the covariates are modelled independently, this clustering method can uncover linear and non-linear relationships between covariates and response.

This model includes some cluster specific parameters, which characterise the clusters, and some global parameters, which are shared by all clusters. The Weibull distributions, with cluster-specific scale parameters, can be used to model survival times and also allow for censoring. We propose two models with Weibull distributions for the response, one with a global shape parameter for the Weibull distributions and one with a cluster-specific shape parameter. The first model satisfies the proportional hazard assumption, which allows for comparisons between clusters. On the other hand, the latter model has the advantage of allowing the estimation of the survival curve without having to satisfy the proportional hazards assumption. Therefore, it is a very flexible model. Suitable distributions for the covariates are the Normal distribution in the case of continuous explanatory variables and the multinomial distribution in the case of categorical explanatory variables.

Kottas (2006) did important early work on the Weibull Dirichlet process mixture model for unknown survival distributions, although their model was limited to estimating the survival distribution component only and did not extend to regression. In contrast, our proposed method links the survival outcome to a multivariate profile, and estimates hazard ratios (in the case where a proportional hazards assumption is satisfied) and median survival times. Moreover, the Weibull Dirichlet process mixture by Kottas (2006) involves mixing on both the shape and scale parameters of the Weibull kernel, while we also propose and discuss the reduced model satisfying the desirable assumption of proportional hazards. Another contribution of our paper is the computation of the posterior predictive distribution of survival time to provide interpretable results. Finally, our methods are readily available in the R package PReMiuM using advanced state-of-the-art MCMC algorithms.

In this paper, we apply our model to the analysis of sleep data based on a unique cohort of very old women from The Australian Longitudinal Study on Women’s Health (ALSWH). We are interested in learning about the relationship between sleep difficulty and survival in an Australian cohort of old women (Leigh et al. 2016b). Due to the fact that difficulty in sleeping may be related to additional factors which also affect survival (for example, Body Mass Index (BMI), comorbidity, sleep medication use, physical functioning and vitality, mental health), it is also of interest to model the joint effects of sleep difficulty and these additional covariates on survival, via profile regression. Previous analyses (Leigh et al. 2015, 2016a) utilised latent class analysis (LCA) to identify longitudinal patterns (profiles) of sleep difficulty, and then utilised these classes to predict survival, adjusted for various other factors, as well as the interaction between the sleep classes and disease count. In the present paper, profiles are based on the additional covariates as well as sleep difficulty, and thus may better capture the complex interactions between all covariates of interest. Moreover, only a single model fit is required rather than a procedure in steps, which might be unable to model appropriately certain features of the data.

In Sect. 2 we introduce the formulation of the Dirichlet process mixture model and profile regression. In Sects. 3 and 4 we propose the two new models for censored survival data with global and cluster-specific shape parameters. In Sect. 5 we provide a method for the computation of hazard ratios, expected survival time and predictions. In Sect. 6 we report the results on simulated data and in Sect. 7 the results on the ALSWH dataset. Some concluding remarks are given in Sect. 8.

2 Profile regression

Profile regression is a Dirichlet process mixture model where the response variable and the covariates are modelled jointly (Molitor et al. 2010; Liverani et al. 2015).

The Dirichlet process (DP) is a stochastic process used in Bayesian nonparametric models, particularly in Dirichlet process mixture models. It is a distribution over distributions, so each draw from a Dirichlet process is itself a distribution. For a random distribution G to be distributed according to a DP, its marginal distributions have to be Dirichlet distributed, which is the reason for the name Dirichlet of this process. Specifically, let H be a distribution over $\Theta$ and $\alpha$ be a positive real number. Then for any finite measurable partition $A_1,\ldots ,A_r$ of $\Theta$, the vector $(G(A_1),\ldots ,G(A_r))$ is random since G is random. We say G is Dirichlet process distributed with base distribution H and concentration parameter $\alpha$, written $G \sim DP(\alpha ,H)$, if

$$\begin{aligned} (G(A_1),\ldots ,G(A_r))\sim \text{ Dir } (\alpha H(A_1),\ldots , \alpha H(A_r)) \end{aligned}$$

for every finite measurable partition $A_1,\ldots ,A_r$ of $\Theta$. The draws from a DP satisfy a discreteness property which also implies a clustering property. The discreteness and clustering properties of the DP play crucial roles in the use of DPs for clustering via DP mixture models, as described in Teh (2011). The nonparametric nature of the Dirichlet process translates to mixture models with a countably infinite number of components. We model a set of observations $\{y_1,\ldots ,y_n\}$ using a set of latent parameters $\{\theta _1,\ldots ,\theta _n\}$. Each $\theta _i$ is drawn independently and identically from G, while each $y_i$ has distribution $F(\theta _i)$. Because G is discrete, multiple $\theta _i$’s can take on the same value simultaneously, and the above model can be seen as a mixture model, where $y_i$’s with the same value of $\theta _i$ belong to the same cluster.

Profile regression is a generalisation of the DP mixture model, where the induced mixture model is a mixture of two distributions, one for the response vector y and one for the covariate data ${\mathbf {x}}$. In particular, we define response data $y_i$ and covariate data ${\mathbf {x}}_i$ for each individual i with $i=1,\ldots ,n$. There is also the possibility to include additional data, ${\mathbf {w}}_i$ for each individual, which we will refer to as fixed effects. The fixed effects are constrained to only have a global (i.e., non-cluster specific) effect on the response $y_i$ and the functional relationship between the response and the fixed effects is discussed below for specific response models. The mixture model is then given by

$$\begin{aligned} f({\mathbf {x}}_i,y_i | {\varvec{\phi }},{\varvec{\theta }},{\varvec{\psi }}, {\varvec{\beta }},{\varvec{z}},{\varvec{w}}_i) = \sum _{c=1}^\infty \psi _c f_x({\mathbf {x}}_i | z_i = c,{\varvec{\phi }}_c)f_y(y_i|z_i=c,\theta _c,{\varvec{\lambda }},{\mathbf {w}}_i) \end{aligned}$$

(1)

where ${\mathbf {x}}_i = (x_{i1},\ldots ,x_{iP})$ is the P-dimensional covariate profile and ${\varvec{z}} = (z_1,\ldots ,z_n)$ with $z_i = c$ is the allocation variable indicating the cluster to which individual i belongs. The parameter vectors ${\varvec{\phi }}$ and ${\varvec{\theta }}$ are the cluster specific parameters and are defined in more detail below. The parameter vector ${\varvec{\psi }}=(\psi _1,\psi _2,\ldots )$ are the cluster weights and ${\varvec{\lambda }}$ are the global parameters linking the fixed effects to the response variable. An active cluster is a cluster which contains at least one observation. There are an infinite number of clusters in this model, though a finite data set only exhibits a finite number of active clusters, which are inferred from the data.

The likelihoods $f_y$ and $f_x$ depend upon the choice of response and covariate model, respectively. The covariate model is different depending on the data. For continuous data, we assume a mixture of Gaussian distributions. Under this setting for each cluster c, the cluster specific parameters are given by ${\varvec{\phi }}_c=(\mu _c,\Sigma _c)$, where $\mu _c$ is a mean vector and $\Sigma _c$ is a covariance matrix. Under this setting, it follows that

$$\begin{aligned} f_x({\mathbf {x}}_i|z_i=c,{\varvec{\phi }}_{c})=(2\pi )^{-\frac{J}{2}}|\Sigma _{c}|^{-\frac{1}{2}}\exp \left\{ -\frac{1}{2}({\mathbf {x}}_i-\mu _{c})^\top \Sigma _{c}^{-1}({\mathbf {x}}_i-\mu _{c})\right\} . \end{aligned}$$

(2)

For discrete variables, where for each individual i, ${\mathbf {x}}_i$ is a vector of J locally independent discrete categorical random variables, where the number of categories for covariate j is $K_j$, for $j=1,2,\ldots ,J$. Then we can write ${\varvec{\phi }}_c=\Phi _c=(\Phi _{c,1},\Phi _{c,2}\ldots ,\Phi _{c,J})$ with $\Phi _{c,j} = (\phi _{c,j,1},\phi _{c,j,2},\ldots ,\phi _{c,j,K_j})$ and

$$\begin{aligned} f_x({\mathbf {x}}_i|z_i=c,\Phi _c)=\prod _{j=1}^J\phi _{{c},j,x_{i,j}}. \end{aligned}$$

(3)

Similarly, for the response model we implement models which are suitable for the data under study. One simple case is a continuous response variable, in which case the likelihood for the response model is given by

$$\begin{aligned} f_y(y_i|z_i=c,\theta _{c},{\varvec{\lambda }},{\mathbf {w}}_i)=\frac{1}{\sqrt{2\pi \sigma ^2_y}}\exp \left\{ -\frac{1}{2\sigma ^2_y}(Y_i-\mu _i)^2\right\} , \end{aligned}$$

(4)

where $\mu _i=\theta _{c}+{\varvec{\beta }}^\top {\mathbf {w}}_i$ and ${\varvec{\lambda }}=({\varvec{\beta }},\sigma ^2_y)$. For both $f_y$ and $f_x$ we can also make other modelling choices, like a binary response model, a categorical response model, Poisson or Binomial mixtures for count data. Liverani et al. (2016) also propose an extension of this response model to account for spatial correlation. In this paper we propose a new response model, for censored survival data.

Profile regression as described above is implemented in the R package PReMiuM (Liverani et al. 2015), along with a range of prior distributions. Inference is made in a Bayesian framework using Markov chain Monte Carlo (MCMC) methods. Hastie et al. (2015) provide details on assessing lack of convergence for these models. Additional features are available in the R package, such as two methods for variable selection, which allow us to determine which covariates actively drive the mixture components, and which share characteristics common to all components. One of these variable selection methods is based on the work by Chung and Dunson (2009), a cluster-specific selection approach which is also applied on the ALSWH sleep data in Sect. 7. Each cluster c has an associated vector $\xi _c = (\xi _{c,1},\xi _{c,2},\ldots ,\xi _{c,J})$, where $\xi _{c,j}$ is a binary random variable that determines whether covariate j is important to cluster c. For discrete covariates, we can then define the new composite parameters,

$$\begin{aligned} \phi ^{*}_{c,j,k}:= \xi _{c,j} \phi _{c,j,k} + (1-\xi _{c,j}) \phi _{0,j,k} =\left( \phi _{c,j,k}\right) ^{\xi _{c,j}} \left( \phi _{0,j,k}\right) ^{(1-\xi _{c,j})} \end{aligned}$$

(5)

which replace the cluster specific parameters for discrete covariates defined above. We assume that, given $\rho _{j}$, the $\xi _{c,j}$, $c=1,\ldots ,C$, are independent Bernoulli variables with $\xi _{c,j} \sim \text{ Bernoulli } (\rho _{j})$. To induce variable selection, we consider a sparsity inducing prior for $\rho _{j}$ with an atom at zero, so that

$$\begin{aligned} \rho _{j}&\sim 1_{\{w_{j}=0\}} \delta _{0}(\rho _{j}) + 1_{\{w_{j}=1\}} \text{ Beta } (\alpha _{\rho }, \beta _{\rho }), \end{aligned}$$

(6)

where $w_{j} \sim \text{ Bernoulli }(p_w)$. By examining the posterior distribution of $\rho _j$ we can ascertain the extent of the contribution of variable j to the clustering: if it has mostly mass around zero, it is unlikely to be contributing significantly to the clustering.

The MCMC produces a rich posterior output, with a partition of the observations provided at each iteration. It is therefore necessary to infer a representative partition, as an effective way to convey the output of the clustering algorithm. It is also of interest to assess the uncertainty associated with subgroups of this best partition. Moreover, due to the problem of ‘label switching’, i.e the labels associated with each cluster change during the MCMC iterations, we can not simply assign each observation to the cluster that maximizes the average posterior probability. One solution which has proved useful is to summarise the MCMC output in a dissimilarity matrix, where at each iteration of the sample, we record pairwise cluster membership and construct a score matrix. Averaging these matrices over the whole MCMC run leads to a similarity matrix S, which can then be used to identify an optimal partition. Post-processing methods are also available in the R package PReMiuM and discussed in detail by Liverani et al. (2015). Molitor et al. (2010) include further discussion on the motivation and justification of profile regression models.

3 Survival response Weibull with global shape parameter

We extend the profile regression model described in Sect. 2 for survival data with censoring, using a mixture of Weibull distributions. In this section, we develop the model with a global shape parameter for the Weibull distribution.

For survival data, with a survival or censoring time and a censoring indicator, we have

$$\begin{aligned} f_y(y_i|z_i=c,\theta _c, {\varvec{\lambda }}, {\mathbf {w}}_i) = h(y_i|z_i=c,\theta _{c}, \nu , {\varvec{\beta }}, {\mathbf {w}}_i)^{d_i} S(y_i|z_i=c, \theta _{c}, \nu ,{\varvec{\beta }}, W_i) \end{aligned}$$

(7)

where h is the hazard function, S is the survival function, ${\varvec{\lambda }} = (\nu ,{\varvec{\beta }})$ are the global parameters and y is the lifetime of an individual. The censoring indicator $d_i$ is defined as follows.

$$\begin{aligned} d_i = \left\{ \begin{array}{ll} 0 &{}\quad \text{ if } \text{ the } \text{ individual } \text{ is } \text{ censored } \text{ or } \\ 1 &{}\quad \text{ if } \text{ the } \text{ individual } \text{ experiences } \text{ the } \text{ event } \text{ of } \text{ interest } \end{array} \right. \end{aligned}$$

(8)

with $d = \sum _{i=1}^n d_i$. Survival time has a Weibull distribution if its survival distribution is given by

$$\begin{aligned} S(y_i| z_i=c,\theta _c, \nu ,{\varvec{\beta }}, {\mathbf {w}}_i) = f(y>y_i | \theta _{z_i}, \nu , {\varvec{\beta }}, {\mathbf {w}}_i) = \exp \left( - \gamma _{z_i} y_i^\nu \right) \end{aligned}$$

(9)

and its hazard function is given by

$$\begin{aligned} h(y_i|z_i=c,\theta _c, \nu , {\varvec{\beta }}, {\mathbf {w}}_i) = \nu \gamma _{z_i} y_i^{\nu -1} \end{aligned}$$

(10)

with link function $\gamma _{z_i} = \exp \left( \theta _{z_i} + {\varvec{\beta }}^T {\mathbf {w}}_i \right)$. For this model the baseline risk is constant. When $\nu > 1$ the hazard rate increases as time increases, it is constant for $\nu =1$ and the hazard rate decreases for $\nu < 1$.

The likelihood is given by

$$\begin{aligned} f_y(y|.)= & {} \prod _{i=1}^n h(y_i|z_i=c,\theta _{c}, \nu , {\varvec{\beta }}, {\mathbf {w}}_i)^{d_i} S(y_i|z_i=c, \theta _{c}, \nu ,{\varvec{\beta }}, W_i) \end{aligned}$$

(11)

$$\begin{aligned}= & {} \nu ^d \left( \prod _{i=1}^n \gamma _{z_i}^{d_i} \right) \exp \left( - \sum _{i=1}^n \gamma _{z_i} y_i^\nu \right) \prod _{i=1}^n \left( y_i^{\nu -1}\right) ^{d_i}. \end{aligned}$$

(12)

Therefore, the conditional distribution of $\nu$ is given by

$$\begin{aligned} f(\nu |.)\propto & {} \prod _{i=1}^n h(y_i|z_i=c,\theta _{c}, \nu , {\varvec{\beta }}, {\mathbf {w}}_i)^{d_i} S(y_i|z_i=c, \theta _{c}, \nu ,{\varvec{\beta }}, W_i) \pi _\nu (\nu )\end{aligned}$$

(13)

$$\begin{aligned}\propto & {} \nu ^d \exp \left( - \sum _{i=1}^n \gamma _{z_i} y_i^\nu \right) \prod _{i=1}^n \left( y_i^{\nu -1}\right) ^{d_i} \pi _\nu (\nu ) \end{aligned}$$

(14)

where $\pi _\nu (\nu )$ is the log-concave prior distribution of $\nu$. It can be shown that

which is satisfied if and only if $f(\nu |.)$ is log-concave (Borzadaran and Borzadaran 2011). Given the log concavity of $f(\nu |.)$, we can use an adaptive rejection sampling algorithm to sample from the posterior distribution of $\nu$ (Gilks and Wild 1992). We set the prior distribution for $\nu$, $\pi _\nu (\nu )$, to be a Gamma distribution with parameters $a_\nu$ and $b_\nu$, so we require that $a_\nu \ge 1$ to ensure the log-concavity of $\pi _\nu (\nu )$.

To implement the adaptive rejection sampler (Gilks and Wild 1992), we require the logarithm of a function proportional to the distribution of interest and its derivative. This function and its derivative are given by the following,

$$\begin{aligned} \log f(\nu |.)\propto & {} d \log \nu - \sum _{i=1}^n \gamma _{z_i} y_i^\nu + \nu \sum _{i=1}^n d_i \log y_i + (a_\nu -1) \log \nu - b_\nu \nu \end{aligned}$$

(15)

and

(16)

The model developed in this section has a global shape parameter for each Weibull distribution in the mixture. The advantage of this model is that the assumption of proportional hazards holds and we can compute hazard ratios between different clusters. However, for the cases where the assumption of proportional hazards is untenable, we develop a more flexible model, in the Sect. 4, with cluster-specific shape parameters.

4 Survival response Weibull with cluster-specific shape parameter

Here we propose a mixture of Weibull distributions with cluster-specific scale and shape parameters. This model is more flexible than the model proposed in Sect. 3 because it does not require the assumption of proportional hazards to hold. In this model the shape parameters of the Weibull distributions are now a vector ${\varvec{\nu }} = (\nu _1, \nu _2, \ldots )$ of cluster-specific shape parameters. Therefore, the components of the mixture of Weibull distributions take the following form,

$$\begin{aligned} f_y(y_i|z_i=c,\theta _c,\nu _c, {\varvec{\lambda }}, {\mathbf {w}}_i) = h(y_i|z_i=c,\theta _{c}, \nu _c, {\varvec{\beta }}, {\mathbf {w}}_i)^{d_i} S(y_i|z_i=c, \theta _{c}, \nu _c,{\varvec{\beta }}, W_i) \end{aligned}$$

(17)

where h is the hazard function, S is the survival function, ${\varvec{\lambda }} = {\varvec{\beta }}$ are the global parameters, $\theta _c, \nu _c$ and $\phi _c$ are the cluster-specific parameters and $y_i$ is the lifetime of an individual. It follows that the survival time Y has a Weibull distribution if its survival distribution is now given by

$$\begin{aligned} S(y_i| z_i=c,\theta _c, \nu _{z_i},{\varvec{\beta }}, {\mathbf {w}}_i) = f(y>y_i | \theta _{z_i}, \nu _{z_i}, {\varvec{\beta }}, {\mathbf {w}}_i) = \exp \left( - \gamma _{z_i} y_i^{\nu _{z_i}} \right) \end{aligned}$$

(18)

and its hazard function is as follows

$$\begin{aligned} h(y_i|z_i=c,\theta _c, \nu _{z_i}, {\varvec{\beta }}, {\mathbf {w}}_i) = \nu _{z_i}\gamma _{z_i} y_i^{\nu _{z_i}-1} \end{aligned}$$

(19)

with link function $\gamma _{z_i} = \exp \left( \theta _{z_i} + {\varvec{\beta }}^T {\mathbf {w}}_i \right)$. For this model the baseline risk is constant. The loglikelihood is given by

$$\begin{aligned} \log f_y(y|.)= & {} \sum _{i=1}^n \log \left( \left( \nu _{z_i} \gamma _{z_i} y_i^{\nu _{z_i}-1} \right) ^{d_i} \exp \left( - \gamma _{z_i} y_i^\nu \right) \right) \end{aligned}$$

(20)

$$\begin{aligned}= & {} \sum _{i=1}^n \left( d_i \left( \log \nu _{z_i} + \log \gamma _{z_i} +(\nu _{z_i}-1) \log y_i\right) - \gamma _{z_i} y_i^\nu \right) . \end{aligned}$$

(21)

The conditional distribution of $\nu _c$ depends only on the data in cluster c. We define the indicator $d_{lc}$ for the censored data in cluster c.

$$\begin{aligned} d_{lc} = \left\{ \begin{array}{ll} 0 &{}\quad \text{ if } \text{ the } \text{ individual } l \text{ in } \text{ cluster } c \text{ is } \text{ censored } \\ 1 &{}\quad \text{ if } \text{ the } \text{ individual } l \text{ in } \text{ cluster } c \text{ experiences } \text{ the } \text{ event. } \end{array} \right. \end{aligned}$$

(22)

with $d_{c} = \sum _{l=1}^{n_c} d_{lc}$ and $\sum _{c=1}^C n_c = n$. It follows that the conditional distribution of $\nu _c$, for $z_i=c$ , is given by

$$\begin{aligned} \log f(\nu _c|.)\propto & {} \sum _{l=1}^{n_c}\left( d_{lc} \left( \log \nu _c + \log \gamma _{z_l} +(\nu _c-1) \log y_l\right) - \gamma _{z_l} y_i^{\nu _c} \right) + \log \pi _{\nu _c}(\nu _c)\end{aligned}$$

(23)

$$\begin{aligned}\propto & {} \left( \log \nu _c + \log \gamma _{z_l}\right) d_{c} +(\nu _c-1) \sum _{l=1}^{n_c}d_{lc} \log y_l - \sum _{l=1}^{n_c}\gamma _{z_l} y_i^{\nu _c} + \log \pi _{\nu _c}(\nu _c)\nonumber \\ \end{aligned}$$

(24)

where $\pi _\nu (\nu _c)$ is the log-concave prior distribution of $\nu _c$. It can be easily shown that

which, as before, is satisfied if and only if $f(\nu |.)$ is log-concave. Given the log concavity of $f(\nu |.)$, as for the case of the global shape parameter, it follows that we can use an adaptive rejection sampling algorithm for $\nu$. We set the prior distribution for each shape parameter $\nu _c$ to be a Gamma distribution with parameter $a_\nu$ and $b_\nu$, and require that $a_\nu \ge 1$ to ensure the log-concavity of $\pi _\nu (\nu _c)$. As before, to implement the adaptive rejection sampler, we require the logarithm of a function proportional to the distribution of interest and its derivative, which are given by

$$\begin{aligned} \log f(\nu _c|.)\propto & {} d_{c}\log \nu _c +\nu _c \sum _{l=1}^{n_c}d_{lc} \log y_l - \sum _{l=1}^{n_c}\gamma _{z_l}y_l^{\nu _c} + (a_\nu -1) \log \nu _c - b_\nu \nu _c \end{aligned}$$

(25)

and

(26)

This mixture model with cluster-specific shape parameters can fit the data well in each cluster, but the assumption of proportional hazards does not hold. The additional challenge is how to compare observations in different clusters informatively. A proposal for this is given in the following section.

5 Computing and interpreting the hazard ratios and the expected survival time

The main inferential objective is to compare the clusters identified by profile regression. This is straightforward when the shape parameter is global, but cluster comparisons require careful consideration when the shape parameter is cluster specific. An alternative approach is to compare the clusters using the predicted survival time for individuals that belong to different clusters.

When there is a global shape parameter $\nu$ we can easily compute hazard ratios. The ratio of the hazard functions of two different clusters, with all fixed effects ${\mathbf {w}}_i$ constant, is given by

$$\begin{aligned} \frac{h(y_i|c_1)}{h(y_i|c_2)} = \frac{\nu \gamma _{c_1} y_i^{\nu -1}}{\nu \gamma _{c_2} y_i^{\nu -1}} = \frac{\nu \exp (\theta _{c_1} + {\varvec{\beta }}^T {\mathbf {w}}_i) y_i^{\nu -1}}{\nu \exp (\theta _{c_2} + {\varvec{\beta }}^T {\mathbf {w}}_i) y_i^{\nu -1}} = \frac{\exp (\theta _{c_1} ) }{ \exp (\theta _{c_2})} = \exp (\theta _{c_1} - \theta _{c_2}). \end{aligned}$$

(27)

Moreover, we can compute the hazard ratios for the fixed effects. The ratio of the hazard functions of two different values of $w_j$ in cluster $c_k$ is given by

$$\begin{aligned} \frac{h(y_i|c_k,w_j = x_1)}{h(y_i|c_k,w_j=x_2)} = \frac{\nu \exp (\theta _{c_k} + \beta _1 w_1 + \cdots + \beta _p w_p) y_i^{\nu -1}}{\nu \exp (\theta _{c_k} + \beta _1 w_1 + \cdots + \beta _p w_p) y_i^{\nu -1}} = \exp (\beta _j (x_1-x_2)). \end{aligned}$$

(28)

The fixed effects $\beta _j$ are global parameters, so they take the same value within each cluster. Therefore, we can write

$$\begin{aligned} \frac{h(y_i|c_k,w_j = x_1)}{h(y_i|c_k,w_j=x_2)} = \frac{h(y_i'|c_l,w_j = x_1)}{h(y_i'|c_l,w_j=x_2)} = \exp (\beta _j (x_1-x_2)) \end{aligned}$$

(29)

for any l and k. These ratios are constant proportions that depend only on the covariate $w_j$ and not on time. If $x_1= x_2+1$ then the hazard ratio simplifies to $\exp (\beta _j)$.

In the case of cluster-specific shape parameter $\nu$, first we check whether we can assume proportional hazards. The assumption that the proportional hazards stay constant over time can be inspected by looking at a graph of the logarithm of the estimated cumulative hazard function. This plot is also known as a log-log survival plot. The proportional hazard assumption is evidenced by the difference between the logarithms of the hazards for any two clusters not changing over time, or equally by the difference between the logarithms of the cumulative hazard functions being constant. If proportional hazards are a sensible assumption, we can compute the hazards as above. If the hypothesis of proportional hazards is not tenable, we can interpret the results by computing the mean survival time. The mean survival time for cluster c is given by

$$\begin{aligned} E(Y) = \gamma _c ^{-1/ \nu _c} \Gamma (1+1/\nu _c) \end{aligned}$$

(30)

where $\Gamma (.)$ represents the Gamma function.

5.1 Predictions

Posterior predictive distributions are computed for the survival time and the hazard ratios. At each sweep, the allocation of a predictive profile to a cluster c is sampled from the mixture weights, according to the covariates $x_{pred}$ of the predictive profile. These draws give us a posterior predictive distribution for the ${\hat{\theta }}_s$, which is the predicted value of $\theta _{z_s}$ for the predictive profile s at the r-th iteration of the MCMC.

We can then compute the predicted hazard ratios for each iteration r of the MCMC as

$$\begin{aligned} \frac{\exp ({\hat{\theta }}_s^r)}{\exp ({\hat{\theta }}_1^r)} \end{aligned}$$

(31)

where ${\hat{\theta }}_1$ is the baseline hazard function, for example chosen as corresponding to the lowest values of all risk factors.

We can also compute the posterior predictive distribution of survival time as the expectation of the Weibull distribution, which is given by

$$\begin{aligned} {\hat{y}}_{pred} = \min ({\hat{\gamma }}_{c,r} ^{-1/ {\bar{\nu }}_c} \Gamma (1+1/{\bar{\nu }}_c),T^*) \end{aligned}$$

where $T^*$ is the maximum observed survival time before censoring, ${\bar{\nu }}$ is the posterior mean of $\nu _c$ and ${\hat{\gamma }}^{c,r} =\exp ({\hat{\theta }}_s^r + \hat{{\varvec{\beta }}}^T {\mathbf {w}})$ with $\hat{{\varvec{\beta }}}$ the posterior mean of ${\varvec{\beta }}$.

6 Application to simulated data

First we demonstrate the proposed method on two simulated datasets and then compare the results to ridge regression, a commonly used method to deal with collinearity.

6.1 Clustering censored survival data

We demonstrate the proposed method on two datasets, each with three clusters of 250 observations. We simulated the response variables y from a Weibull distribution and five covariates $x_1$, $x_2$,..., $x_5$ are drawn from multinomial distributions with 2, 2, 3, 3, and 4 categories respectively. There are no fixed effects. The values of the parameters ${\varvec{\theta }}$ and ${\varvec{\phi }}$ for each cluster c are given in Table 1. The shape parameter for the first dataset is $\nu _c=2$ for all clusters $c=1,2,3$. The second dataset has cluster-specific shape parameters, so $\nu _1 = 2$, $\nu _2= 1$ and $\nu _3=3$. There are no missing values but all observations are censored at $y=50$ if the event has not happened yet.

Table 1 Values of the parameter ${\varvec{\theta }}$ and ${\varvec{\phi }}$ for each cluster

We analyse the datasets using the proposed survival profile regression, implemented in the R package PReMiuM (Liverani et al. 2015) with 2000 iterations of burn in period and 2000 iterations after burn in. Good convergence (and mixing) of MCMC output was achieved within a few hundred iterations (based on visual diagnosis of MCMC output for model parameters, not shown).

Fig. 1

The posterior distribution of $\nu$ for the first dataset (left hand side) and ${\varvec{\nu }}$ for the second dataset (right hand side)

Fig. 2

Survival probability for the two simulated datasets. Each survival function corresponds to a different cluster

The first dataset was analysed using the model with global shape parameter, while the second was analysed using a cluster-specific shape parameter. The posterior distributions are consistent with the generating values provided in Table 1 and they are shown in the Appendix. We show here the posterior distribution of $\nu$ for the first dataset and the posterior distribution of ${\varvec{\nu }}$ for the second dataset in Fig. 1. The survival probability over time for the three clusters is given in Fig. 2.

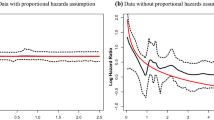
As discussed, we could compute hazard ratios for the first dataset as we have assumed a global shape parameter. However, for the second dataset, generated with cluster-specific parameters, the analysis has allowed the shape parameter to be cluster specific and found that it was different for the three clusters. The log cumulative hazard function, shown in Fig. 3, shows that the assumption of proportional hazards does not hold, and therefore we cannot compute hazard ratios meaningfully. Instead, for example, we can compare the clusters and interpret the results using the posterior survival time.

Fig. 3

Log cumulative hazard for the three clusters of the second dataset

6.2 Comparison with ridge regression

We compare our clustering method to ridge regression (Gray 1992; Xue et al. 2007), a method suitable for collinear survival data. We generated 50 datasets with three 2-dimensional clusters, where the two variables are highly correlated within each cluster. The three clusters, of 300, 400 and 500 observations each, are generated from a bivariate Normal distribution with correlation of 0.95. The survival time is also generated from a Normal distribution. A censoring variable is generated from a Binomial distribution with $p=0.9$, so only about 10

As a measure of accuracy for profile regression and ridge regression, we compare their predictive power using the root mean square error (RMSE) of the predicted values with respect to the observed outcome. This measure of goodness of fit is given by

$$\begin{aligned} RMSE = \sqrt{\frac{\sum _{i=1}^{n}\left( y_i - {\hat{y}}_i\right) ^2}{n}} \end{aligned}$$

(32)

where ${\hat{y}}_i$ denotes the mean of the posterior predictive distribution for the survival time for observation i. Table 2 shows the mean and the standard deviation of the RMSE for the 50 simulated datasets. The precision of the in-sample predicted survival times obtained with profile regression was higher than the one obtained with ridge regression.

Table 2 Mean and standard deviation of the RMSE of the predicted values with respect to the observed outcome when using profile regression and ridge regression

7 Application to the ALSWH sleep data

We apply our two methods to The Australian Longitudinal Study on Women’s Health (ALSWH), a longitudinal study of over 40,000 women, consisting of three cohorts. The women were randomly selected from the Australian national health insurance database (Medicare), with oversampling of women from rural and remote areas to allow adequate numbers for statistical comparisons to be made. At baseline, in 1996, the cohorts, known according to the year the women were born as ‘1973–78’, ‘1946–51’, and ‘1921–26’, were aged 18–23, 45–50, and 70–75. Follow-up omnibus style surveys were mailed out every three years. The ALSWH explores factors that influence health among women who are broadly representative of the entire Australian population, and is the largest project of its kind ever conducted in Australia. The current analysis focuses on data from the oldest cohort, born between 1921–26, who completed the baseline survey in 1996, and who first completed the sleep questionnaire 3 years later at Survey 2 (N = 10076).

We carried out the analysis of the data using the proposed survival profile regression. The response variable of interest is survival, measured in years from Survey 2. Deaths were ascertained from the National Death Index (Powers et al. 2000). The data cover 16 years after the survey and there is significant censoring: 97 women were not followed up in any survey and 5144 were still alive at the last survey. Sleep difficulty was measured using items from the NHP (Nottingham Health Profile) Sleep subscale (Hunt et al. 1981), as follows:

• 1. Do you wake in the early hours of the morning? (early)

• 2. Do you lie awake most of the night? (lying)

• 3. Do you take a long time to get to sleep? (long)

• 4. Do you sleep badly at night? (bad)

We will refer to these sleep items using the words provided in the parenthesis next to each item. The answers to these questions were coded as $no=0$ and $yes=1$. We also surveyed use of sleep medication (meds), first measured at Survey 2 (referred to as ’baseline’ sleep difficulty). Other covariates of interest, measured at baseline, included comorbidity count (comorb, classified as 0, 1–2, and 3 or more¹), marital status (ms, classified as married/de facto, separated/divorced, widowed, never married), area of residence (area, classified as Major Cities of Australia, Inner Regional Australia, Outer Regional Australia, Remote/Very Remote Australia) (Department of Health and Aged Care 2001), highest obtained educational status (edu, classified as none, school/higher school certificate, trade/diploma, higher education), self-rated health (srgood, classified as excellent/very good/good or fair/poor), Short Form Health Survey (SF36) (Ware et al. 1994) measures of physical functioning (pfq), mental health (mhq) and vitality (vtq, classified on its quartiles), and the body mass index (bmi, classified as underweight, normal weight, overweight or obese). Age (years) at baseline was also included as a fixed effect. Due to the fact that the survival profile regression and sleep/disease profiles are estimated simultaneously in the current analysis, we restricted the profiles to baseline data only (as opposed to longitudinal), to avoid the situation where missing data due to death at later surveys might dominate the resultant profiles. However, prior work (Leigh et al. 2015) investigating longitudinal patterns of sleep difficulty has shown that sleep difficulty patterns remain stable over time, and thus the baseline values are fairly representative of the women’s sleep patterns over time.

Fig. 4

Log cumulative hazard function for the clusters

Table 3 Cluster sizes and posterior means for the cluster specific parameters $\varvec{\theta }$ and $\varvec{\phi }$

Fig. 5

Survival probability for the first 5 clusters and the last cluster. The gray area highlights the span of the survival probability for all clusters

Fig. 6

Survival probability for all clusters except the first five. The gray area highlights the span of the survival probability for all clusters

Fig. 7

Posterior distribution of the survival time since Survey 2 for each cluster. The dashed horizontal line is the overall median survival time

Fig. 8

Posterior distribution of the parameter $\rho$ for four covariates: early, lying, ms and area

Fig. 9

Heatmap summary table of the clusters. Each row represents a cluster. The columns represents, respectively, the mean survival time and each covariate included in the analysis. The colour of each cell in the matrix corresponds to a quintile of the distribution for that variable (ie. by column). The clusters are ordered as in Table 3 by survival time, from the shortest to the longest

We obtained fifteen clusters. The credible interval for $\beta$ is (0.14,0.18). Figure 4 shows that the log cumulative hazard function does not support the assumption of proportional hazards and thus a cluster-specific shape parameter was used in the modelling. Therefore we do not compute hazard ratios but analyse the data using survival times. The cluster sizes and the posterior means of the parameters $\varvec{\theta }$ and $\varvec{\phi }$ are given in Table 3, with the clusters ordered according to their estimated mean survival time. Figures 5 and 6 show the posterior survival probabilities for the clusters. It can be seen that the survival functions for the first five clusters are distinct, while they are clustered together and overlapping for the remaining clusters.

Figure 7 shows the boxplots for the posterior survival time for the fifteen clusters. The overall median is also shown in the plot, allowing a comparison with the deviation from the median of the posterior survival time for each cluster.

We also carried out variable selection. Values of $\rho$ close to 1 indicate the variable is significant for the clustering, while values close to zero indicate it is not. The posterior distribution for $\rho$ showed that two of the covariates, ms and area, were not relevant for the clustering model, since the posterior distribution of $\rho$ for these two variables was heavily distributed close to zero. This is demonstrated in Fig. 8, which shows the posterior distribution of $\rho$ for marital status and area, as well as example distributions of $\rho$ for variables which are important for the model (early and lying). The distribution of $\rho$ for these latter two variables is distributed closer to 1.

We propose the use of a heatmap as the most immediate way to visualise the clustering and associated covariate patterns. Figure 9 shows a summary table of the survival time and the posterior distribution of the covariates in each cluster. Each row represents a cluster. The columns represents, respectively, the mean survival time and each covariate included in the analysis. The colour of each cell in the matrix corresponds to a quintile of the distribution for that variable (ie. by column). The clusters are ordered as in Table 3 by survival time, from the shortest to the longest. Note that the colours in the matrix do not become darker (or lighter) in a smooth manner, suggesting a complex relationship between survival time and the covariates considered. For example, we can see that higher levels of physical functioning and vitality are generally associated with longer average survival times. However, there are several exceptions to this, and we can see complex non-linear relationships between survival time and the other covariates (Table 4).

We then exclude the covariates which are not driving the clustering process, as identified by looking at the posterior distribution of $\rho$. Each value in the heatmap gives the quintiles of the distribution, therefore summarising the clusters. It can be noted how the relationships between the covariates are complex and could not have been easily learnt using other methods. We can see that there are three clusters (3, 10 and 15) with overall poor sleep difficulty patterns. Of these clusters, two (10 and 15) correspond to long median survival times, while one of them (3) corresponds to a shorter median survival time. Three other clusters had individuals with greater sleep difficulty patterns in just some of the domains (clusters 5, 9 and 13). Moreover, we can see how these clusters are also associated with other covariates such as medication, high BMI or low levels of vitality and physical activity. The cluster with the lowest survival had a high probability of comorbidities, but reported no sleep difficulty. Cluster 3, which reported sleep difficulty and the 3rd shortest median survival, did not exhibit high probability of comorbidities, however they scored low on all QoL covariates, and were likely to have higher BMIs. The two other clusters with greatest sleep difficulty, 10 and 15, exhibited good self-rated health, low to moderate likelihood of using sleep meds, cluster 10 did not score high on all quality of life (QoL) items but cluster 15 did, and neither exhibited high BMIs. Cluster 13 endorsed ’taking a long time to get to sleep’, and also were likely to use meds, have high QoL, and good self-rated health. Cluster 9 endorsed ’early waking’, had good self-rated health but moderate QoL measures. Many clusters were characterised by low probability of sleep difficulty across all items.

We can thus learn and visualise how the posterior distribution of median survival time changes depending on the values of different covariates. For example, Fig. 10 shows the posterior predictive distributions for three profiles of women who answer yes to the question ‘Do you wake in the early hours of the morning?’ (early = 1). For the first profile the individual is healthy and their sleep patterns are good based on their answers (no) to the other items of the Nottingham Health Profile (lying = 0, long = 0, bad = 0). For the second profile, they did not answer the other sleep questions (lying = NA, long = NA, bad = NA) but they are healthy. For the third profile, we only know that they wake up early. The posterior predictive distributions of these three profiles allow us to make inference on the median survival times for specific individuals, or groups of individuals, and shed light on the potentially complex true relationsips between covariates and survival, as highlighted by the multimodality of the posterior predictive distributions shown in Fig. 10.

Table 4 Posterior mean of the probabilities of ${\varvec{\phi }}$ for the first simulated dataset

Fig. 10

Posterior predictive distributions for three profiles of interest. The three profiles show the posterior distribution for predictive profiles for individuals who replied yes to the question ’Do you wake in the early hours of the morning?’. For the first profile on the left hand side we also know that the individual is healthy and their sleep patterns are good otherwise (lying = no, long = no, bad = no). For the second profile, we have no knowledge of how they answered the other sleep questions (lying = NA, long = NA, bad = NA) but know that they are healthy. For the third profile, we have no knowledge about the individual apart from the fact that they wake up early

Fig. 11

The posterior distribution of ${\varvec{\theta }}$ and the posterior distribution of the survival time for the first simulated dataset

Fig. 12

Posterior distribution of ${\varvec{\theta }}$ and the posterior distribution of the survival time for the second simulated dataset

8 Discussion

We have proposed a mixture model for the survival response and covariates, where the response variable has a Weibull distribution and it allows for censoring. In the model we allow for the shape parameter of the Weibull distribution to be shared by all clusters (therefore satisfying the condition of proportional hazards) but also proposed a more general model with cluster-specific shape parameters. Moreover, we have discussed the challenges of predictive profiles in the context of survival modelling and we have made these methods easily available in the R package PReMiuM.

We have used the latter model to analyse data from The Australian Longitudinal Study on Women’s Health and have demonstrated how useful inference can be drawn using our proposed models. A previous analysis (Leigh et al. 2015), which clustered the women based only on the sleep difficulty questions, found four clusters, corresponding to no sleep difficulty (answered no to all questions on sleep), trouble sleeping (answered yes to all questions on sleep), early wakers, and trouble falling asleep. The current clustering also identified clusters characterised by low sleep difficulty, trouble sleeping, and a cluster defined by taking a long time to get to sleep (those who answered yes to whether they take a long time to get to sleep). In the current analysis, many more clusters were identified as additional covariate data was also allowed to inform the clustering (Figs. 11, 12).

Leigh et al. (2016a, b) found that, unadjusted for covariates, those with mild sleep difficulty had lower hazard of death than those without sleep difficulty, while the most troubled sleepers had higher hazard of death. After adjusting for covariates, the troubled sleepers did not have greater hazard of death, and those with mild sleep difficulty (early wakers and trouble falling asleep) still had lower hazard of death. Also significant in the models were disease count, BMI, education, physical functioning, self-rated health, marital status and area. The effect of those covariates, in conjunction with sleep, led to many more clusters being identified in the current analysis. We observe that greater sleep difficulty can be related to both longer and shorter survival, with different patterns in the covariates. This may be attributable to the difference in the effect of trouble sleeping with and without covariate adjustment in the previous models. Furthermore, a previous analysis (Leigh et al. 2015) could not account for the interaction between sleep and each covariate of interest. The current analysis however takes into account the multivariate relationships between all variables, and leads to interesting insights. For example, previous work Leigh et al. (2016b) found that BMI was significant for survival when modelling as a predictor along side sleep, with underweight related to greater hazard of death, overweight greater hazard of death, and non significant results for obese women. However, BMI may also be interrelated with sleep, for instance obesity is related to sleep apnoea, which can cause sleep disturbance. While we see one class with high BMI and poor sleep and shorter survival (cluster 3), the other clusters with the greatest sleep difficulty do not have higher BMIs, and also have longer survival. It is possible that the relationship between greater sleep difficulty and survival in cluster 3 is explained by the high BMI, whereas the relationship between sleep difficulty and lower hazard of death in clusters 10 and 15 is explained by healthier BMI (and better self-rated health etc.).

Moreover, in previous work clustering was conducted prior to regression on the survival outcome, and thus missing covariate data patterns related to survival may have influenced class membership. Thus, the clusters themselves may have also included information about the survival outcome, and thus possibly biased the subsequent regression results. The current analysis used only baseline data, thus the clusters themselves are not dominated by missing data.

A limitation of our model is that in its present formulation does not incorporate covariate information collected after the baseline, which is the objective for our future work.

Appendix: Additional results from the simulation study

In this Appendix we provide additional plots showing the posterior distribution for some of the parameters for the simulated data in Sect. 6.

Fig. 13

Violin plot of the posterior predictive distribution for four predictive profiles: (0,0,0,0,0), (0,0,0,0,1), (0,1,2,2,0) and (1,1,1,1,3) for the second simulated dataset

We also show in Fig. 13 the posterior predictive distribution for four predictive profiles. These are combinations of values of the covariates for which we compute the posterior predictive distribution of $\theta _c$ or the survival time.