Abstract
We provide an elegant homological construction of the extended phase space for linear Yang–Mills theory on an oriented and time-oriented Lorentzian manifold M with a time-like boundary \(\partial M\) that was proposed by Donnelly and Freidel (JHEP 1609:102, 2016). This explains and formalizes many of the rather ad hoc constructions for edge modes appearing in the theoretical physics literature. Our construction also applies to linear Chern–Simons theory, in which case we obtain the extended phase space introduced by Geiller (Nucl Phys B 924:312, 2017).
Similar content being viewed by others
1 Introduction and summary
The topic of edge modes is a time-honored one in the study of gauge theories on manifolds with boundary. Historically, such edge modes first arose as the (conformal) boundary degrees of freedom of Chern–Simons theory, both in the context of Chern–Simons theory as applied to condensed matter physics (see, e.g., [3, 9]), as well as in the context of (3D) Chern–Simons gravity [14, 36], where the edge modes were shown to be related to the asymptotic symmetries of 3D AdS spacetime [4, 11, 17].
In these early investigations, the motivation for edge modes and the construction of the corresponding boundary action (e.g., the Wess–Zumino–Witten action and its variants) relied heavily on the fact that the theory’s bulk action is not gauge-invariant in the presence of a boundary, and the edge modes can heuristically be understood as boundary degrees of freedom that ‘compensate’ for this failure of gauge invariance. However, Donnelly and Freidel [20] recently showed that one can hope to construct edge modes even in cases where the bulk action is gauge-invariant, e.g., in Yang–Mills theory. One of their main observations is that, even if the bulk action of a gauge theory is gauge-invariant in the presence of boundaries, its presymplectic form (on field space) may fail to be invariant under arbitrary gauge transformations, calling for the introduction of boundary-localized degrees of freedom, the edge modes, to compensate for this lack of invariance. The result of such an analysis is therefore an extended phase space, encoding also the additional edge mode degrees of freedom, that is endowed with a gauge-invariant extension of the naive presymplectic form by terms depending on the edge modes. This has been carried out in the original paper [20] for the cases of Yang–Mills theory and general relativity.
Donnelly and Freidel’s work has inspired a revived and growing interest in gauge and gravity theories on manifolds with boundaries, see, e.g., [10, 21,22,23,24,25,26,27] for some follow-up papers. A particularly noteworthy reaction to their work is [24,25,26,27], which observes that the notion of boundary in [20] is ambiguous between a ‘fiducial’ boundary, meaning a non-physical boundary that does not in any way influence the field content and which disappears upon gluing along the boundary, and a ‘physical’ boundary, meaning a boundary that influences the field content in some way, e.g., by carrying a defect theory or a Higgs field. (This ambiguity is heightened by the fact that [20] do not associate any action to the edge modes.) For pure gauge fields, the study in [25, 27] uses a certain Singer–De Witt connection form on field space, which they interpret as a geometric generalization of ghost fields, to show that fiducial boundaries cannot carry charged edge modes. Furthermore, in the case where matter fields are present, they introduce the notion of a Higgs connection on field space to reproduce the edge modes from [20]. However, we note that they also do not introduce a boundary action for these edge modes.
The goal of this paper is to provide an elegant and rigorous construction of extended phase spaces as in [20] for two simple cases: linear Yang–Mills theory on a globally hyperbolic Lorentzian manifold M with a time-like boundary \(\partial M\) and linear Chern–Simons theory on a three-dimensional product manifold \(M={\mathbb {R}}\times \Sigma \) with boundary \(\partial M = {\mathbb {R}}\times \partial \Sigma \). Our construction employs some basic techniques from homological algebra and the theory of groupoids, which are necessary to describe the higher categorical structures featuring in gauge theory. We refer the reader to [33] for an extensive overview of such techniques and also to [7, Section 3] for a rather non-technical introduction. The main benefit of adopting this more abstract homological perspective is that many of the ad hoc constructions for edge modes in the theoretical physics literature become very natural.
The basic ideas behind our proposed construction are easy to explain in general, without referring to any specific example. Our first input datum is the specification of the gauge fields and gauge transformations in the bulk M, which assemble into a groupoid of bulk gauge fields. As the second input, we choose a boundary condition on \(\partial M\) for the bulk gauge fields, which we implement in a homotopical way by forming a homotopy pullback. As we explain in detail in Remark 2.2, see also Remarks 2.4 and 2.5 for further supporting examples, the appearance of edge modes is a direct consequence of implementing a suitable (topological) boundary condition in this homotopical fashion. This supports the suggestion in [24,25,26,27] that edge modes are associated with physical boundaries. The last input for our construction is a gauge-invariant action functional on the total groupoid of fields (including the edge modes) that is obtained by implementing the boundary condition via a homotopy pullback. We would like to emphasize that this does not only require the choice of a bulk action, but also that of a boundary action, potentially including also terms that depend on the edge modes. From this collection of input data, we construct a homotopical refinement of the solution space, called a derived critical locus, that is associated with our chosen action functional. By the general results of derived algebraic geometry [13, 31, 32], this solution ‘space’ (more precisely, this is a derived stack) carries a canonical \([-1]\)-shifted symplectic structure. From a choice of Cauchy surface \(\Sigma \subset M\), we then determine from the latter data an unshifted symplectic structure on \(\Sigma \) and hence the extended phase space of the theory. Our construction of an unshifted symplectic structure from the canonical \([-1]\)-shifted symplectic structure allows us to carefully distinguish between the different types of ‘boundaries’ that feature in our models of interest, see also (4.2) for a helpful visualization. On the one hand, there is the boundary \(\partial M\) on which we impose a boundary condition, i.e., on which the edge modes are localized, and, on the other hand, there is the Cauchy surface \(\Sigma \subset M\) on which the unshifted symplectic structure is defined.
Even though our proposed construction is relatively easy to sketch in an informal way, there are technical challenges, most notably in the last step where a derived critical locus and its \([-1]\)-shifted (and also unshifted) symplectic structure have to be determined. Unfortunately, the current technology from derived algebraic geometry [13, 31, 32] is rather abstract and involved, so that it is very difficult to apply such techniques to examples of relevance in field theory. In particular, even though derived critical loci always exist in this framework, they are very difficult to describe in explicit terms for examples such as Yang–Mills theory or general relativity. In order to obtain a computationally accessible and feasible framework, we restrict (drastically) our attention to the case of linear gauge theories when discussing derived critical loci and their symplectic structures. In this case, the necessary techniques from derived algebraic geometry reduce to relatively basic homological algebra of chain complexes. We hope that a generalization of this last part of our construction to nonlinear gauge theories becomes available in the future once the necessary technology at the intersection of derived algebraic geometry and field theory has been developed.
The explicit results that we obtain for the simple examples given by linear Yang–Mills and Chern–Simons theory are, however, already very interesting. For both theories, we make the novel observation that their extended phase spaces can be obtained from simple action functionals [see (2.8) and (5.1)] via our homological construction, even though this was thought to be not possible in [20, 23]. We believe that our approach via action functionals is more elegant than the proposal in [20, 23], which is to introduce by hand additional terms to the ordinary symplectic structure in order to restore gauge invariance in the presence of a boundary. As another novel result, our construction leads to an extension of the extended phase spaces and their symplectic structures in [20, 23] to ghost fields and antifields, whose explicit form for linear Yang–Mills theory is given in (4.5) and for linear Chern–Simons theory in (5.5).
We would like to add a few remarks on the comparison between our proposed construction and the BV–BFV formalism for gauge theories on manifolds with boundaries. This framework originated in [15], and it was extended recently toward the description of edge mode phenomena in [30]. At a superficial level, these approaches and ours look similar as they consider, in addition to the gauge fields, ghost fields and antifields, and work with shifted symplectic structures. However, a closer look shows that actual constructions in the BV–BFV formalism are performed in a different order than what we propose. The starting point of [30] is a BV-extended gauge theory on a manifold (possibly with boundaries, corners or a stratification), which, however, does not yet refer to edge modes and their dynamics. The latter are obtained from a choice of polarization functional (via an f-transformation) and an AKSZ-inspired transgression construction, see [30, Theorem 58] for the case of Chern–Simons theory. Interestingly, for appropriate choices of polarization functionals, this construction produces the gauged Wess–Zumino and gauged Wess–Zumino–Witten actions for Chern–Simons edge modes. In contrast to that, the starting point of our construction is very basic and it consists of (1) a gauge theory (not BV-extended) in the bulk M, (2) a boundary condition on \(\partial M\) and (3) a choice of action functional, including possibly also boundary terms on \(\partial M\). The edge modes are then obtained by implementing the boundary condition by a homotopy pullback, and the BRST/BV field content (with differentials and \([-1]\)-shifted symplectic structure) is determined from the derived critical locus construction. We refer to Remarks 4.5 and 5.2 for a more concrete comparison to [15, 30] at the level of explicit examples.
The outline of the remainder of this paper is as follows: In Sect. 2, we introduce our linear Yang–Mills theory model on a Lorentzian manifold M with a time-like boundary \(\partial M\), together with a boundary condition (leading to the edge modes, see Remark 2.2) and the novel action functional (2.8). In Sect. 3, we construct explicitly the (linear) derived critical locus for our model (3.6) and its canonical \([-1]\)-shifted symplectic structure (3.7). In Sect. 4, we derive, from the choice of a Cauchy surface \(\Sigma \subset M\), an unshifted symplectic structure (4.5) and show that the 0-truncation of our homological construction reproduces the extended phase space of [20], see Remark 4.4. In Sect. 5, we apply our techniques to linear Chern–Simons theory and show that the 0-truncation of our construction reproduces the extended phase space of [23]. Appendix A summarizes the relevant background for computing homotopy pullbacks for groupoids and chain complexes that are needed for our work.
Notation and conventions for chain complexes: The main constructions and results in this paper are stated in the category \(\mathbf {Ch}_{\mathbb {R}}\) of (possibly unbounded) chain complexes of vector spaces over the field of real numbers \({\mathbb {R}}\). We use homological degree conventions, i.e., the differentials \(\mathrm {d}: V_n\rightarrow V_{n-1}\) lower the degree by 1. The tensor product \(V\otimes W\) of two chain complexes is given by \((V\otimes W)_n = \bigoplus _{m\in {\mathbb {Z}}} V_m\otimes W_{n-m}\) together with the differential \(\mathrm {d}(v\otimes w) = (\mathrm {d}v)\otimes w + (-1)^{\vert v\vert } \, v\otimes (\mathrm {d}w)\) determined by the graded Leibniz rule, where \(\vert v\vert \in {\mathbb {Z}}\) denotes the degree of v. The tensor unit is \({\mathbb {R}}\in \mathbf {Ch}_{\mathbb {R}}\), regarded as a chain complex concentrated in degree 0 with trivial differentials. Given a chain complex V and an integer \(p\in {\mathbb {Z}}\), the [p]-shifted chain complex V[p] is defined by \(V[p]_n = V_{n-p}\) and \(\mathrm {d}^{V[p]} \,=\, (-1)^p\,\mathrm {d}^V\).
The homology \(H_\bullet (V)\) of a chain complex V is the graded vector space defined by \(H_n(V) := \mathrm {Ker}(\mathrm {d}: V_n\rightarrow V_{n-1}) / \mathrm {Im}(\mathrm {d}: V_{n+1}\rightarrow V_n)\), for all \(n\in {\mathbb {Z}}\). A chain map \(f : V\rightarrow W\) is called a quasi-isomorphism if the induced map \(H_\bullet (f) : H_\bullet (V)\rightarrow H_\bullet (W)\) in homology is an isomorphism. Quasi-isomorphic chain complexes are considered as ‘being the same,’ which can be made precise by endowing \(\mathbf {Ch}_{\mathbb {R}}\) with a model category structure, see, e.g., [29]. We refer to [7, Section 3] for a brief non-technical introduction to model categories in the context of classical and quantum gauge theory.
2 Definition of the Yang–Mills model
Let M be an oriented and time-oriented Lorentzian manifold with a smooth boundary \(\partial M\). Following common practice in hyperbolic PDE theory and Lorentzian (quantum) field theory, we assume that the boundary \(\partial M\) is time-like. In this case, there exists a well-established notion of Cauchy surfaces and of global hyperbolicity, see, e.g., [34] and [1]. These concepts are not only important for developing a theory of solutions for hyperbolic PDEs in the presence of boundaries, see, e.g., [18, 19], but they will also enter explicitly our construction in Sect. 4. (We would like to note that the present section and also Sect. 3 do not require the assumption of a time-like boundary.) We denote by \(\iota : \partial M\rightarrow M\) the boundary inclusion and by \(m=\mathrm {dim}(M)\ge 2\) the dimension of M. The orientation, time orientation and Lorentzian metric on M induce on \(\partial M\) the structure of an oriented and time-oriented Lorentzian manifold (without boundary) of dimension \(\mathrm {dim}(\partial M) = m-1\). We interpret M as a physical spacetime whose boundary is another (Lorentzian) spacetime \(\partial M\).
Let us now introduce the field content of our model of interest. As bulk fields on M, we consider principal \({\mathbb {R}}\)-bundles with connections, together with their gauge transformations. These data are described by the groupoid
whose objects are interpreted as gauge fields and morphisms as gauge transformations between gauge fields. (Recall that every principal \({\mathbb {R}}\)-bundle is isomorphic to the trivial principal \({\mathbb {R}}\)-bundle. Hence, up to equivalence of groupoids, one may consider only the trivial principal \({\mathbb {R}}\)-bundle, as we have done in (2.1).) Take a principal \({\mathbb {R}}\)-bundle on the boundary \(\partial M\), which is described by a map of groupoids (i.e., a functor)
from the point \(\{*\}\) to the groupoid
of principal \({\mathbb {R}}\)-bundles on \(\partial M\) and their gauge transformations. Observe that there is another map of groupoids
which forgets the bulk connection and restricts the bulk principal \({\mathbb {R}}\)-bundle to the boundary \(\partial M\). Concretely, this functor acts on objects as \(A \mapsto *\) and on morphisms as \((\epsilon : A\rightarrow A+\mathrm {d}\epsilon ) \mapsto (\iota ^*\epsilon : *\rightarrow *)\), where \(\iota ^*\epsilon \in \Omega ^0(\partial M)\) denotes the pullback of \(\epsilon \in \Omega ^0(M)\) along the boundary inclusion \(\iota : \partial M\rightarrow M\). We would like to impose a boundary condition that identifies the restriction of the bulk principal \({\mathbb {R}}\)-bundle with the fixed principal \({\mathbb {R}}\)-bundle on \(\partial M\). This is formalized by considering the homotopy pullback (or equivalently a 2-categorical pullback)

in the model category (or 2-category) of groupoids, see Appendix A for some technical details. The resulting groupoid \({\mathfrak {F}}(M)\) plays the role of the groupoid of fields for our model of interest.
Proposition 2.1
A model for the homotopy pullback in (2.5) is given by the groupoid
Proof
This is a direct computation using the explicit description of homotopy pullbacks for groupoids from Appendix A, see, in particular, Proposition A.1. Concretely, an object in the homotopy pullback (2.5) is a pair of objects \((*,A)\in \{*\}\times {\mathbf {B}}{\mathbb {R}}_\mathrm {con}(M)\) together with a \({\mathbf {B}}{\mathbb {R}}(\partial M)\)-morphism \(p(*) = *{\mathop {\longrightarrow }\limits ^{\varphi }} *= \mathrm {res}(A)\). Hence, an object in \({\mathfrak {F}}(M)\) is given by a pair \((A,\varphi ) \in \Omega ^1(M)\times \Omega ^0(\partial M)\). A morphism \((A,\varphi )\rightarrow (A^\prime ,\varphi ^\prime )\) in the homotopy pullback (2.5) is a pair of morphisms \((\mathrm {id}_*: *\rightarrow *, \epsilon : A\rightarrow A+\mathrm {d}\epsilon = A^\prime )\in \{*\}\times {\mathbf {B}}{\mathbb {R}}_\mathrm {con}(M)\) that is compatible with \(\varphi \) and \(\varphi ^\prime \), i.e., the diagram

in \({\mathbf {B}}{\mathbb {R}}(\partial M)\) commutes. Hence, a morphism in \({\mathfrak {F}}(M)\) is given by \((A,\varphi ) {\mathop {\longrightarrow }\limits ^{\epsilon }} (A+\mathrm {d}\epsilon , \varphi + \iota ^*\epsilon )\), where \(\epsilon \in \Omega ^0(M)\). \(\square \)
Remark 2.2
Note that an object of the groupoid \({\mathfrak {F}}(M)\) in (2.6) is a pair \((A,\varphi )\in \Omega ^1(M)\times \Omega ^0(\partial M)\) consisting of a gauge field A in the bulk M and a gauge transformation \(\varphi \) on the boundary \(\partial M\). Hence, the groupoid of fields \({\mathfrak {F}}(M)\) contains both bulk and boundary fields. It is one of the main goals of the present paper to explain that these \(\varphi \) are precisely the edge modes introduced in [20]. As a first piece of evidence for this claim, we note that the morphisms of the groupoid \({\mathfrak {F}}(M)\) in (2.6) are precisely the gauge transformations on bulk and boundary fields in [20].
From our groupoid perspective, the origin of edge modes can be explained very naturally. The groupoid of fields \({\mathfrak {F}}(M)\) is obtained by identifying the restriction of the bulk principal \({\mathbb {R}}\)-bundle with the fixed principal \({\mathbb {R}}\)-bundle on \(\partial M\), i.e., we implement a boundary condition via the homotopy pullback diagram (2.5). We may call this boundary condition topological because, in contrast to the usual Dirichlet or Neumann-type boundary conditions, it only involves the underlying principal bundle and not the connection part of the bulk gauge field. Boundary conditions in a gauge theory are quite subtle because gauge fields are not compared by equality but rather by gauge transformations, i.e., morphisms in the relevant groupoids. Hence, a boundary condition in a gauge theory is not a property of the gauge fields but an additional structure given by gauge transformations acting as witnesses of the boundary condition. The edge modes \(\varphi \) in (2.6) are precisely the witnesses for the statement that the restriction of the bulk principal \({\mathbb {R}}\)-bundle is ‘the same as’ the fixed boundary principal \({\mathbb {R}}\)-bundle.
In the next step, we introduce a gauge-invariant action functional in order to specify the dynamics of our model of interest. This is described by a map of groupoids \(S : {\mathfrak {F}}(M)\rightarrow {\mathbb {R}}\) from our groupoid of fields (2.6) to the real numbers \({\mathbb {R}}\), regarded as a groupoid with only identity morphisms. We define
where \(*_{(\partial )}^{}\) denotes the Hodge operator on \((\partial )M\) and the affine covariant differential is given by
Clearly, the action (2.8) is gauge-invariant because \(\mathrm {d}A\) and \(\mathrm {d}_A\varphi \) are invariant under the gauge transformations in (2.6). (In the physics literature, the quantity \(\mathrm {d}_A \varphi \) is also referred to as a ‘dressing,’ see, e.g., [2].)
Upon varying the action with respect to compactly supported variations \((\alpha ,\psi )\in \Omega ^1_\mathrm {c}(M)\times \Omega ^0_\mathrm {c}(\partial M)\), a straightforward calculation using Stokes’ theorem yields the expression
The corresponding Euler–Lagrange equations are
Remark 2.3
We would like to emphasize very clearly that both the bulk and boundary terms in the action (2.8) are inputs for our construction that one has to choose. Besides its evident simplicity, our choice of action is motivated from the fact that its Euler–Lagrange equations (2.11) include the matching constraint, which has been implemented by hand in the work of Donnelly and Freidel [20]. Of course, it would be possible to choose a different action, for example, by introducing a multiplicative factor \(\lambda \in {\mathbb {R}}\) in front of the boundary term in (2.8), which would lead to different Euler–Lagrange equations, including a different matching constraint between bulk and boundary fields. The constructions that we develop in this paper apply to general gauge-invariant quadratic actions functionals. However, our focus will be on the action (2.8) because our main aim is to reconstruct and interpret the model of [20] from a homological point of view.
Remark 2.4
Up to this point, our construction admits a straightforward generalization to non-Abelian Yang–Mills theory. To simplify the presentation in this remark, let us work locally by assuming that \(M\cong {\mathbb {R}}^{m-1}\times [0,\infty )\) is diffeomorphic to a half-space. Let G be a compact matrix Lie group and denote its Lie algebra by \({\mathfrak {g}}\). As a consequence of our assumptions, there exist no non-trivial principal G-bundles on both M and \(\partial M\); hence, the groupoid of principal G-bundles with connection on M reads as
and the groupoid of principal G-bundles on \(\partial M\) reads as
The two maps in the homotopy pullback diagram (2.5) exist also in the non-Abelian setting. An explicit computation as in Proposition 2.1 yields the groupoid of fields
Recalling the curvature \(F(A) = \mathrm {d}A + A\wedge A\) and introducing the non-Abelian ‘dressing’ \(\mathrm {d}_{A} u := (\mathrm {d}u)\,u^{-1} - u\,(\iota ^*A)\, u^{-1}\), one easily checks that
defines a gauge-invariant action. The Euler–Lagrange equations of this action include the matching constraint \(u^{-1}\,\iota ^*(*F(A)) \,u - *_{\partial } \mathrm {d}_A u =0\) on \(\partial M\), which agrees with the proposal in [20] by introducing the notation \(E:= *_{\partial } \mathrm {d}_A u \in \Omega ^{m-2}(\partial M,{\mathfrak {g}})\). We will not develop this non-Abelian generalization of our model any further, because linearity will be crucial to simplify our constructions in the remainder of this paper.
Remark 2.5
We would like to comment very briefly on the gravity example considered in [20]. The origin of the gravitational edge modes may be understood in terms of a boundary condition too. Let us fix as in [20] an m-dimensional manifold M with smooth boundary \(\partial M\). The bulk fields are given by the groupoid \(\mathbf {Lor}_m(M)\) whose
- (i)
objects are all (Lorentzian) metrics g on M, and
- (ii)
morphisms \(f : (M,g)\rightarrow (M,g^\prime )\) are all diffeomorphisms \(f: M\rightarrow M\) preserving the boundary, i.e., the restriction \(f_\partial := f\vert _{\partial M} : \partial M\rightarrow \partial M\) is a diffeomorphism, and the metrics, i.e., \(f^*(g^\prime ) = g\) holds true.
Let us denote by \(\mathbf {Man}_{m-1}\) the groupoid of \(m-1\)-dimensional manifolds, with morphisms given by diffeomorphisms. There exists an evident functor \(\mathrm {res} : \mathbf {Lor}_m(M)\rightarrow \mathbf {Man}_{m-1}\) acting on objects as \((M,g)\mapsto \partial M\) and on morphisms as \((f : (M,g)\rightarrow (M,g^\prime ) ) \mapsto (f_\partial : \partial M\rightarrow \partial M)\). Choosing any object \(B \in \mathbf {Man}_{m-1}\) that is diffeomorphic to \(\partial M\in \mathbf {Man}_{m-1}\), which we may regard as a functor \(B : \{*\}\rightarrow \mathbf {Man}_{m-1}\), we can form the homotopy pullback

which implements the metric-independent boundary condition that the boundary \(\partial M\) of the bulk manifold M is ‘the same as’ the fixed \(m-1\)-dimensional manifold B. Computing this homotopy pullback via Proposition A.1, we obtain that
- (i)
objects in \({\mathfrak {F}}_{\mathrm {gravity}}(M)\) are pairs (g, X), where g is a metric on M and \(X : B\rightarrow \partial M\) is a diffeomorphism between B and the boundary \(\partial M\), and
- (ii)
morphisms \(f: (g, X )\rightarrow (g^\prime ,X^\prime )\) in \({\mathfrak {F}}_{\mathrm {gravity}}(M)\) are all diffeomorphisms \(f : M\rightarrow M\) preserving the metrics, i.e., \(f^*(g^\prime ) =g\), and satisfying \(f_\partial \circ X = X^\prime \).
The diffeomorphisms \(X:B \rightarrow \partial M\) are the gravitational edge modes from [20]. We currently do not know a gravitational analog of the boundary actions in (2.15) and (2.8), but we believe that it should be possible to design such an action by carefully studying the gravitation matching constraints in [20]. As for the case of non-Abelian Yang–Mills theory from the previous remark, we will not develop this gravity model any further, because our remaining constructions require a linear field theory.
Because our model of interest is a linear gauge theory, we can reformulate it in the language of chain complexes of vector spaces. The key ingredient for this construction is given by the Dold–Kan correspondence between simplicial vector spaces and (non-negatively graded) chain complexes of vector spaces, see, e.g., [8] for an application in the context of gauge theory. Explicitly, the Dold–Kan correspondence assigns to (the nerve of) our groupoid of fields (2.6) the chain complex (denoted with abuse of notation by the same symbol)

concentrated in homological degrees 0 and 1, with differential given by
for all \(C\in \Omega ^0(M)\). From now on, we shall denote gauge transformations by \(C\in \Omega ^0(M)\). This choice of notation is explained in Remark 3.2, where C will be interpreted as a ghost field. Observe that elements \((A,\varphi )\in \Omega ^1(M)\times \Omega ^0(\partial M)\) in degree 0 are the fields of the theory, elements \(C\in \Omega ^0(M)\) in degree 1 are the gauge transformations and the differential Q encodes the action \((A,\varphi )\rightarrow (A,\varphi ) + Q(C) = (A+\mathrm {d}C,\varphi + \iota ^*C)\) of gauge transformations. The variation of the action (2.10) determines a linear differential operator
given by
for all \((A,\varphi )\in \Omega ^1(M)\times \Omega ^0(\partial M)\). The signs in (2.18) are due to the following choice of conventions: The codomain of P is given by the smooth Lefschetz dual
of the degree 0 component \({\mathfrak {F}}_{0,\mathrm {c}}(M)= \Omega ^1_\mathrm {c}(M)\times \Omega ^0_\mathrm {c}(\partial M)\) of the compactly supported analog of the field complex (2.17). The evaluation pairing \(\langle \,\cdot \, ,\,\cdot \,\rangle : {\mathfrak {F}}_{0,\mathrm {c}}(M)^*\times {\mathfrak {F}}_{0,\mathrm {c}}(M)\rightarrow {\mathbb {R}}\) reads as
for all \((A^\dagger , a^\dagger ,\varphi ^\dagger ) \in \Omega ^{m-1}(M)\times \Omega ^{m-2}(\partial M) \times \Omega ^{m-1}(\partial M)\) and \((A,\varphi )\in \Omega ^1_\mathrm {c}(M)\times \Omega ^0_\mathrm {c}(\partial M)\). The linear differential operator P is defined by (2.10) and the equation \(\delta _{(\alpha ,\psi )}S(A,\varphi ) = \langle P(A,\varphi ),(\alpha ,\psi )\rangle \), for all \((A,\varphi )\in \Omega ^1(M)\times \Omega ^0(\partial M)\) and \((\alpha ,\psi )\in \Omega _\mathrm {c}^1(M)\times \Omega _\mathrm {c}^0(\partial M)\). Hence, the signs in (2.18) are a consequence of graded commutativity of the \(\wedge \)-product.
3 Derived critical locus and shifted symplectic structure
Instead of enforcing the Euler–Lagrange equations (2.11) in a strict sense, we consider their homological enhancement given by the (linear) derived critical locus construction. Our motivation and reasons for this are twofold: (1) Enforcing the Euler–Lagrange equations strictly as in (2.11) is in general incompatible with quasi-isomorphisms in the category \(\mathbf {Ch}_{\mathbb {R}}\) of (possibly unbounded) chain complexes, i.e., if one takes two different quasi-isomorphic field complexes, the naive solution complexes assigned to them are, in general, no longer quasi-isomorphic. This is problematic because it violates the main principle of homological algebra that all sensible constructions must respect quasi-isomorphisms. (2) Every derived critical locus carries a canonical \([-1]\)-shifted symplectic structure (see, e.g., [13, 31, 32] for the corresponding results in derived algebraic geometry) which has various physical applications. For instance, in the context of (quantum) field theory, this shifted symplectic structure is the starting point for constructing a factorization algebra [16] or an algebraic quantum field theory [5]. Below, we give a novel application of this \([-1]\)-shifted symplectic structure: It will be used to construct the extended phase space introduced in [20]. We note that in physics terminology, derived critical loci are called the BRST/BV formalism and the shifted symplectic structure is called the antibracket.
Our construction of the (linear) derived critical locus and its shifted symplectic structure is a relatively straightforward generalization of the case of linear Yang–Mills theory on spacetimes without boundaries presented in [5, 7]. To make the present paper self-contained, we shall briefly explain this construction. By analogy with (2.19), we define the smooth Lefschetz dual
of the degree 1 component \({\mathfrak {F}}_{1,\mathrm {c}}(M)=\Omega ^0_\mathrm {c}(M)\) of the compactly supported analog of the field complex (2.17). The evaluation pairing \(\langle \,\cdot \, ,\,\cdot \,\rangle : {\mathfrak {F}}_{1,\mathrm {c}}(M)^*\times {\mathfrak {F}}_{1,\mathrm {c}}(M)\rightarrow {\mathbb {R}}\) reads as
for all \((C^\dagger , c^\dagger ) \in \Omega ^m(M)\times \Omega ^{m-1}(\partial M)\) and \(C\in \Omega ^0_\mathrm {c}(M)\). We denote by
the formal adjoint of the linear differential operator Q in (2.17), which is defined implicitly by \(\langle Q^*(A^\dagger ,a^\dagger ,\varphi ^\dagger ), C \rangle = \langle (A^\dagger ,a^\dagger ,\varphi ^\dagger ), Q(C) \rangle \), for all \((A^\dagger ,a^\dagger ,\varphi ^\dagger )\in \Omega ^{m-1}(M)\times \Omega ^{m-2}(\partial M) \times \Omega ^{m-1}(\partial M)\) and \(C\in \Omega ^0_\mathrm {c}(M)\). A straightforward calculation using Stokes’ theorem then provides the explicit expression
for all \((A^\dagger ,a^\dagger ,\varphi ^\dagger )\in \Omega ^{m-1}(M)\times \Omega ^{m-2}(\partial M) \times \Omega ^{m-1}(\partial M)\). The smooth Lefschetz dual of the compactly supported analog of the field complex (2.17) is thus given by

This chain complex is used to define the total space \(T^*{\mathfrak {F}}(M) := {\mathfrak {F}}(M)\times {\mathfrak {F}}_\mathrm {c}(M)^*\in \mathbf {Ch}_{\mathbb {R}}\) of the cotangent bundle over the field complex (2.17) as a Cartesian product of chain complexes. The variation of the action (2.10), or equivalently, the associated differential operator P in (2.18) defines a section

of the cotangent bundle. The zero section of the cotangent bundle is given by

In order to enforce the dynamics encoded by the action functional (2.8), we intersect \(\delta S\) with the zero section 0 (in the derived sense) by forming the homotopy pullback

in the model category \(\mathbf {Ch}_{\mathbb {R}}\).
Proposition 3.1
A model for the homotopy pullback in (3.5) is given by the chain complex

with differentials defined in (2.17), (2.18) and (3.2).
Proof
This is a direct consequence of the explicit description of homotopy pullbacks for chain complexes from Appendix A, see, in particular, Proposition A.3. In the present scenario, we have that \(V = {\mathfrak {F}}(M)\) is the field complex (2.17), \(W = {\mathfrak {F}}_\mathrm {c}(M)^*\) is the smooth Lefschetz dual (3.2), and \(f_0:V_0\rightarrow W_0\) is the differential operator P in (2.18). Inserting this into (A.6) yields (3.6). \(\square \)
Remark 3.2
The chain complex (3.6) admits an interpretation in terms of the BRST/BV formalism. Elements \(C\in {\mathfrak {S}}_1(M)=\Omega ^0(M)\) in degree 1 are the ghost fields, and elements \((A,\varphi )\in {\mathfrak {S}}_0(M)=\Omega ^1(M)\times \Omega ^0(\partial M)\) in degree 0 are the fields of the theory. Furthermore, elements \((A^\dagger ,a^\dagger ,\varphi ^\dagger )\in {\mathfrak {S}}_{-1}(M)= \Omega ^{m-1}(M)\times \Omega ^{m-2}(\partial M)\times \Omega ^{m-1}(\partial M)\) in degree \(-1\) are the antifields and elements \((C^\dagger ,c^\dagger )\in \Omega ^m(M)\times \Omega ^{m-1}(\partial M)\) in degree \(-2\) are the antifields for ghosts. The differential operator Q encodes the gauge symmetries and P encodes the equation of motion of our model. In particular, the 0th homology \(H_0({\mathfrak {S}}(M))\) of (3.6) is the ordinary vector space of gauge equivalence classes of solutions of the Euler–Lagrange equations (2.11). Note that, in contrast to the usual BRST/BV formalism on manifolds without a boundary, our model of interest (3.6) also contains boundary fields \(\varphi \) and boundary antifields \(a^\dagger \), \(\varphi ^\dagger \) and \(c^\dagger \). It is important to emphasize that this field content is not arbitrary, but it is dictated (up to quasi-isomorphism) by our homological approach, i.e., by the homotopy pullbacks in (2.5) and (3.5).
To conclude this section, we explicitly write out the canonical \([-1]\)-shifted symplectic structure that exists on the (linear) derived critical locus (3.5). Denoting by \({\mathfrak {S}}_\mathrm {c}(M)\) the compactly supported analog of the solution complex \({\mathfrak {S}}(M)\) in (3.6), the \([-1]\)-shifted symplectic structure is the chain map \(\omega _{-1} : {\mathfrak {S}}_\mathrm {c}(M)\otimes {\mathfrak {S}}_\mathrm {c}(M)\rightarrow {\mathbb {R}}[-1]\) defined in terms of the integration pairings (2.19) and (3.1) by
for all \((C^\dagger ,c^\dagger )\in \Omega _\mathrm {c}^m(M)\times \Omega _{\mathrm {c}}^{m-1}(\partial M)\), \(C \in \Omega ^0_\mathrm {c}(M)\), \((A^\dagger ,a^\dagger ,\varphi ^\dagger )\in \Omega _\mathrm {c}^{m-1}(M) \times \Omega _{\mathrm {c}}^{m-2}(\partial M) \times \Omega _{\mathrm {c}}^{m-1}(\partial M)\) and \((A,\varphi )\in \Omega ^1_\mathrm {c}(M)\times \Omega ^0_{\mathrm {c}}(\partial M)\).
4 Construction of the unshifted symplectic structure
From now on, we assume that M is globally hyperbolic in the sense of Lorentzian manifolds with a time-like boundary, see, e.g., [1, 34] and also [6] for a review. Let us choose any Cauchy surface \(\Sigma \subset M\) and note that \(\Sigma \) is a manifold with boundary \(\partial \Sigma \subset \partial M\). The aim of this section is to construct from the datum of a Cauchy surface \(\Sigma \subset M\) and the \([-1]\)-shifted symplectic structure \(\omega _{-1}\) in (3.7) an unshifted symplectic structure \(\omega ^\Sigma _0\). We will then show that the extended phase space proposed by Donnelly and Freidel in [20] is given by the 0-truncation of this homological construction.
Before we can state our definition of the unshifted symplectic structure \(\omega ^\Sigma _0\), we will need to introduce some simple concepts from Lorentzian geometry. Let us denote by
the causal future of the Cauchy surface \(\Sigma \subset M\), which is the set of all points \(p\in M\) that can be reached from \(\Sigma \subset M\) via future-pointing causal curves, including all points \(p\in \Sigma \) in the Cauchy surface. Note that, by definition, \(\Sigma \subset \Sigma _+\) is a subset. We denote by
the intersection of \(\Sigma _+\) with the boundary of M. The following picture visualizes our geometric setup

We observe that \(\Sigma _+\) has two different kinds of boundary components, given by the time-like boundary \((\partial \Sigma )_+\) and the (space-like) Cauchy surface \(\Sigma \), as well as a codimension 2 corner \(\partial \Sigma \).
We now define a map \(\omega _{-1}^{\Sigma } : {\mathfrak {S}}_\mathrm {c}(M)\otimes {\mathfrak {S}}_\mathrm {c}(M)\rightarrow {\mathbb {R}}[-1]\) of graded vector spaces by recalling the definition of the \([-1]\)-shifted symplectic structure in (3.7) and restricting the integrations therein from M to \(\Sigma _+\) and from \(\partial M\) to \((\partial \Sigma )_+\). Explicitly, this gives
for all \((C^\dagger ,c^\dagger )\in \Omega _\mathrm {c}^m(M)\times \Omega _{\mathrm {c}}^{m-1}(\partial M)\), \(C \in \Omega ^0_\mathrm {c}(M)\), \((A^\dagger ,a^\dagger ,\varphi ^\dagger )\in \Omega _\mathrm {c}^{m-1}(M) \times \Omega _{\mathrm {c}}^{m-2}(\partial M) \times \Omega _{\mathrm {c}}^{m-1}(\partial M)\) and \((A,\varphi )\in \Omega ^1_\mathrm {c}(M)\times \Omega ^0_{\mathrm {c}}(\partial M)\). It is important to emphasize that, in contrast to the \([-1]\)-shifted symplectic structure in (3.7), the restricted integrations in (4.3) do not define a chain map, i.e., the pre-composition \(\omega _{-1}^{\Sigma } \circ \mathrm {d}^\otimes \ne 0\) with the differential \(\mathrm {d}^\otimes \) of the tensor product chain complex \({\mathfrak {S}}_\mathrm {c}(M)\otimes {\mathfrak {S}}_\mathrm {c}(M)\) is nonzero. However, we obtain a chain map \(\omega _{-1}^{\Sigma } \circ \mathrm {d}^\otimes : {\mathfrak {S}}_\mathrm {c}(M)\otimes {\mathfrak {S}}_\mathrm {c}(M)\rightarrow {\mathbb {R}}\) to the unshifted real numbers, because the differential \(\mathrm {d}^\otimes \) has degree \(-1\) and the chain map property \(\omega _{-1}^{\Sigma } \circ \mathrm {d}^\otimes \circ \mathrm {d}^\otimes =0 \) is a consequence of nilpotency \({\mathrm {d}^\otimes }^2=0\) of the differential.
We are now in a position to define the unshifted symplectic structure associated with a Cauchy surface \(\Sigma \).
Definition 4.1
The unshifted symplectic structure associated with \(\Sigma \subset M\) is the chain map
Proposition 4.2
The unshifted symplectic structure is explicitly given by
for all \((A,\varphi ), (A^\prime ,\varphi ^\prime ) \in \Omega ^1_\mathrm {c}(M)\times \Omega ^0_{\mathrm {c}}(\partial M)\), \((A^\dagger ,a^\dagger ,\varphi ^\dagger )\in \Omega _\mathrm {c}^{m-1}(M)\times \Omega _{\mathrm {c}}^{m-2}(\partial M) \times \Omega _{\mathrm {c}}^{m-1}(\partial M)\) and \(C \in \Omega ^0_\mathrm {c}(M)\).
Proof
The proof is a straightforward calculation using Stokes’ theorem for manifolds with boundaries and corners, see, e.g., [12]. Thus, we will not write out the details of this calculation. However, for the benefit of the reader, we note that there are two different instances of Stokes’ theorem that enter this calculation. (Consider the picture in (4.2) for a helpful visualization.) First, for any \(\zeta \in \Omega ^{m-1}_\mathrm {c}(\Sigma _+)\) in the bulk \(\Sigma _+\), Stokes’ theorem with corners yields
because \(\partial (\Sigma _+) = (\partial \Sigma )_+ \cup \Sigma \). Second, for any \(\eta \in \Omega ^{m-2}_\mathrm {c}((\partial \Sigma )_+) \) on the time-like boundary component \((\partial \Sigma )_+\), ordinary Stokes’ theorem yields
because \(\partial ((\partial \Sigma )_+) = -\partial \Sigma \) is the boundary of \(\Sigma \) with the opposite orientation. \(\square \)
Corollary 4.3
Using the same formulas as in (4.5), the unshifted symplectic structure from Definition 4.1 and Proposition 4.2 admits an extension to a chain map
where \({\mathfrak {S}}_{\mathrm {sc}}(M)\) is the space-like compactly supported analog of the solution complex (3.6). (Recall that a differential form \(\zeta \in \Omega ^p(M)\) has space-like compact support if \(\mathrm {supp}(\zeta ) \subseteq J^+_M(K) \cup J^-_M(K)\), for some compact subset \(K\subseteq M\).)
Remark 4.4
At first sight, it seems that our unshifted symplectic structure (4.5) is different from the one proposed in [20]. However, upon closer inspection, one finds that this is not the case and that the 0-truncation of our approach reproduces the results of [20]. Let us recall that [20] are not working in a homological approach, which means that they are implementing the Euler–Lagrange equations (2.11) in the strict sense. From our perspective, this means that they are considering 0-cycles in the space-like compactly supported solution complex \({\mathfrak {S}}_{\mathrm {sc}}(M)\). For every two 0-cycles \((A,\varphi ),(A^\prime ,\varphi ^\prime )\in \Omega ^1_\mathrm {sc}(M)\times \Omega ^0_{\mathrm {sc}}(\partial M)\), i.e., \(P(A,\varphi )=0=P(A^\prime ,\varphi ^\prime )\) with P given in (2.18), one can write the unshifted symplectic structure (4.5a) equivalently as
where we used explicitly the matching constraint from the Euler–Lagrange equations (2.11). This equivalent form of the unshifted symplectic structure on 0-cycles coincides with the proposal in [20]. We note that the antifield-ghost component (4.5b) of our unshifted symplectic structure is a novel feature of our homological approach that has no corresponding analog in the 0-truncation studied in [20].
Remark 4.5
We would like to conclude this section with a comparison of our results to the BV–BFV formalism [15, 30]. Because the study of electromagnetism in [15, Section 5.1] does not include edge modes (in contrast to the newer study in [30, Section 4], on which we will comment below), we shall focus first on the case of an empty boundary \(\partial M=\emptyset \). The solution complex (3.6) then simplifies to

and the \([-1]\)-shifted symplectic structure (3.7) simplifies to
Furthermore, the unshifted symplectic structure (4.5) associated with a Cauchy surface \(\Sigma \subset M\) simplifies to
We observe that both the \([-1]\)-shifted and unshifted symplectic structure agree with the ones obtained from the BV–BFV formalism applied to electromagnetism [15, Section 5.1]. Furthermore, we obtain as in [15, Section 5.1.6] a \([+1]\)-shifted symplectic structure in codimension 2 by iterating our construction in Definition 4.1. Concretely, let us choose any codimension 1 submanifold \(S\subset \Sigma \) of the Cauchy surface (i.e., \(S\subset M\) is codimension 2) and cut \(\Sigma \) along S. This defines two submanifolds \(S_+,S_-\subset \Sigma \) with boundary \(\partial (S_{\pm }) = {\pm } S\) which determine \(\Sigma \) by pasting \(\Sigma =S_+ \sqcup _{S} S_- \). Analogously to (4.3), we define \(\omega ^{S}_0\) by restricting the integrations from \(\Sigma \) to \(S_+\subset \Sigma \). The \([+1]\)-shifted symplectic structure can then be defined analogously to Definition 4.1 as \(\omega ^S_{1} := \omega ^{S}_0\circ \mathrm {d}^\otimes : {\mathfrak {S}}_\mathrm {c}(M)\otimes {\mathfrak {S}}_\mathrm {c}(M)\rightarrow {\mathbb {R}}[1]\). By a straightforward calculation using Stokes’ theorem, we obtain
Note that this matches the codimension 2 \([+1]\)-symplectic structure in [15, Section 5.1]. Finally, by a further iteration of our construction in Definition 4.1, one easily shows that the \([+2]\)-shifted symplectic structure in codimension 3 is zero.
The results in [30, Section 4] generalize the BV–BFV formalism for Yang–Mills theory to the case of a boundary \(\partial M\ne \emptyset \) including edge modes. Unfortunately, a direct and explicit comparison to our results in this section seems to be difficult, because the quantities of interest to us, in particular the boundary action in (2.8) and the unshifted symplectic structure (4.5), have not been worked out in [30] for the Yang–Mills example. We refer the reader to Remark 5.2, where we compare the results we obtain by applying our techniques to linear Chern–Simons theory with the results from [30], which are in this case more detailed than for the Yang–Mills example.
5 Linear Chern–Simons theory
In this last section, we shall apply our techniques to investigate edge modes in linear Chern–Simons theory. This will allow us to compare in more depth our approach to the one proposed in [23], which is based on Donnelly and Freidel’s methods [20], and the one in [30], which is a generalization of the BV–BFV formalism [15].
Let us fix a three-dimensional manifold \(M={\mathbb {R}}\times \Sigma \) with smooth boundary \(\partial M = {\mathbb {R}}\times \partial \Sigma \). We assume that both M and the two-dimensional manifold \(\Sigma \) are oriented, and hence, the factor \({\mathbb {R}}\) is oriented too. As an input for our construction, we have to specify in analogy to Sect. 2 the following data: (1) a groupoid of bulk fields on M, (2) a boundary condition on \(\partial M\), and (3) a gauge-invariant action functional on the groupoid of fields satisfying the boundary condition (in the sense of homotopy pullbacks, cf. (2.5) and also Remark 2.2). For our linear Chern–Simons model, we take the groupoid of bulk fields \({\mathbf {B}}{\mathbb {R}}_{\mathrm {con}}(M)\) from (2.1) and implement the same topological boundary condition (2.5) as in the case of linear Yang–Mills theory. Hence, the field groupoid \({\mathfrak {F}}(M)\) is precisely the one of Proposition 2.1, see, in particular, (2.6). Instead of (2.8), we propose now the following action
where \(\lambda \in {\mathbb {R}}\) is a parameter on which we shall comment later. Note that, for defining the third term, we have chosen (the conformal class of) a Lorentzian metric \(g_\partial ^{}\) on the boundary \(\partial M\). This term is necessary to reproduce the well-known chiral currents on \(\partial M\), see, e.g., [9]. The second term in the action (5.1) is needed to compensate for the failure of the usual Chern–Simons action \(\int _M \frac{1}{2} \,A\wedge \mathrm {d}A\) to be gauge-invariant in the presence of a boundary \(\partial M\ne \emptyset \). For any choice of \(\lambda \in {\mathbb {R}}\), the total action (5.1) is invariant under the gauge transformations in \({\mathfrak {F}}(M)\), see (2.6). Varying this action with respect to compactly supported variations \((\alpha ,\psi )\in \Omega ^1_\mathrm {c}(M)\times \Omega ^0_\mathrm {c}(\partial M)\) yields
The corresponding Euler–Lagrange equations are
We observe that the first and third equations imply the second one, and hence, the independent equations of motion for our model are given by (5.3a) and (5.3c). Note that the latter equation specializes to the (anti-) self-duality constraint \(*_\partial \mathrm {d}_A\varphi = {\pm } \mathrm {d}_A \varphi \) for the 1-form \(\mathrm {d}_A \varphi \in \Omega ^1(\partial M)\), provided that we choose \(\lambda = \mp \frac{1}{2}\). For our studies, we shall keep the parameter \(\lambda \) arbitrary.
Because we are dealing with a linear field theory, we can reformulate the Chern–Simons model from above in the language of chain complexes and compute as in Sect. 3 the derived critical locus together with its \([-1]\)-shifted symplectic structure. Since the calculations are completely analogous to the case of linear Yang–Mills theory, we shall present only the final results. The Chern–Simons solution complex is given by

where
and
The \([-1]\)-shifted symplectic structure \(\omega _{-1} : {\mathfrak {S}}_\mathrm {c}(M)\otimes {\mathfrak {S}}_\mathrm {c}(M)\rightarrow {\mathbb {R}}[-1]\) for linear Chern–Simons theory coincides with the one for linear Yang–Mills theory from (3.7).
Let us now choose the datum of a ‘Cauchy’ surface \( \Sigma \subset M\), by which we mean in this case a surface of constant \(t_0\in {\mathbb {R}}\). Using the orientation on the \({\mathbb {R}}\)-factor of \(M={\mathbb {R}}\times \Sigma \), we introduce the ‘future’ \(\Sigma _+\subseteq M\) of this surface and its intersection \((\partial \Sigma )_+ := \Sigma _+\cap \partial M\) with the boundary \(\partial M\). The geometric picture is again as in (4.2), where now the role of time is played by the \({\mathbb {R}}\)-factor of the product manifold \(M={\mathbb {R}}\times \Sigma \). In analogy to Definition 4.1, we define the unshifted symplectic structure associated with the ‘Cauchy’ surface \(\Sigma \subset M\) by \(\omega ^\Sigma _0 := \omega ^{\Sigma }_{-1}\circ \mathrm {d}^\otimes : {\mathfrak {S}}_\mathrm {c}(M)\otimes {\mathfrak {S}}_\mathrm {c}(M)\rightarrow {\mathbb {R}}\), where we recall that \(\omega ^{\Sigma }_{-1}\) is the \([-1]\)-shifted symplectic structure with integrations restricted to \(\Sigma _+\) and \((\partial \Sigma )_+\). By a direct calculation using Stokes’ theorem (see the proof of Proposition 4.2 for some hints and instructions), we obtain
When evaluated on two 0-cycles, i.e., \(P(A,\varphi )=0=P(A^\prime ,\varphi ^\prime )\), one can write the unshifted symplectic structure equivalently as
by using explicitly the matching constraint (5.3c). Let us recall and emphasize that the unshifted symplectic structure is by construction invariant under gauge transformations \((A,\varphi )\rightarrow (A+\mathrm {d}\epsilon ,\varphi +\iota ^*\epsilon )\) and \((A^\prime ,\varphi ^\prime )\rightarrow (A^\prime +\mathrm {d}\epsilon ,\varphi ^\prime +\iota ^*\epsilon )\) of 0-cycles. The first term in (5.6) is the usual symplectic structure for linear Chern–Simons theory and the second term is that of a chiral free boson on \(\partial M\). The third term is the analog for linear Chern–Simons theory of the corner contribution to the linear Yang–Mills symplectic structure by Donnelly and Freidel [20], see also (4.9). Note that our unshifted presymplectic structure (5.6) agrees with the proposal in [23, Eqn. (3.64)]. (The apparent sign differences are due to Geiller’s opposite sign convention \((A,\varphi )\rightarrow (A+\mathrm {d}\epsilon ,\varphi -\iota ^*\epsilon )\) for gauge transformations of the edge modes.)
Remark 5.1
From the expression in (5.6), it seems that our unshifted symplectic structure on 0-cycles is independent of the choice of the free parameter \(\lambda \) in the action (5.1). This is indeed true, provided that we do not set \(\lambda = 0\). In this special case, the matching constraint (5.3c) degenerates to \(\mathrm {d}_A\varphi =0\); hence, the chiral free boson is eliminated from the field content and consequently its contribution to the symplectic structure (5.6) vanishes.
Remark 5.2
We would like to conclude by comparing our results to the ones obtained within the BV–BFV formalism [15, 30], see, in particular, [30, Section 2.7] for the example of interest to us. We first observe that the boundary action in [30, Eqn. (85)], which is obtained by a transgression construction and the choice of polarization functional in [30, Eqn. (83)], is related to our choice of boundary action in (5.1): Using that the Hodge operator \(*_{\partial }^{2} =\mathrm {id}\) squares to the identity on \(\Omega ^1(\partial M)\), we can decompose \(\iota ^*A = A_+ + A_-\) and \(\mathrm {d}\varphi = \mathrm {d}_+\varphi + \mathrm {d}_-\varphi \) into self-dual and anti-self-dual parts. Inserting this decomposition into (5.1), one obtains
which in the self-dual case \(\lambda = -\frac{1}{2}\) and in the anti-self-dual case \(\lambda =\frac{1}{2}\) reduces to boundary actions analogous to [30, Eqn. (85)].
According to our best understanding, the paper [30] does not seem to study unshifted symplectic structures for the edge modes; at least no results were explicitly stated. Hence, a comparison to our unshifted symplectic structure (5.5), whose 0-truncation (5.6) agrees with the proposal by Geiller [23], is not possible at the moment. We however believe that, for practitioners of the BV–BFV formalism, it should be possible to obtain analogous results in the framework proposed in [30].
References
Aké, L., Flores, J.L., Sánchez, M.: Structure of globally hyperbolic spacetimes with timelike boundary. arXiv:1808.04412 [gr-qc]
Attard, J., Francois, J., Lazzarini, S., Masson, T.: The dressing field method of gauge symmetry reduction, a review with examples. In: Kouneiher, J. (ed.) Foundations of Mathematics and Physics one Century After Hilbert, New Perspectives. Springer, Berlin (2018). arXiv:1702.02753 [math-ph]
Balachandran, A.P., Bimonte, G., Gupta, K.S., Stern, A.: Conformal edge currents in Chern–Simons theories. Int. J. Mod. Phys. A 7, 4655 (1992). arXiv:hep-th/9110072
Banados, M., Brotz, T., Ortiz, M.E.: Boundary dynamics and the statistical mechanics of the (2 + 1)-dimensional black hole. Nucl. Phys. B 545, 340 (1999). arXiv:hep-th/9802076
Benini, M., Bruinsma, S., Schenkel, A.: Linear Yang–Mills theory as a homotopy AQFT. Commun. Math. Phys. (to appear) [arXiv:1906.00999 [math-ph]]
Benini, M., Dappiaggi, C., Schenkel, A.: Algebraic quantum field theory on spacetimes with timelike boundary. Ann. Henri Poincaré 19(8), 2401 (2018). arXiv:1712.06686 [math-ph]
Benini, M., Schenkel, A.: Higher structures in algebraic quantum field theory. Fortsch. Phys. 67(8–9), 1910015 (2019). arXiv:1903.02878 [hep-th]
Benini, M., Schenkel, A., Szabo, R.J.: Homotopy colimits and global observables in Abelian gauge theory. Lett. Math. Phys. 105(9), 1193 (2015). arXiv:1503.08839 [math-ph]
Bieri, S., Fröhlich, J.: Physical principles underlying the quantum Hall effect. C. R. Phys. 12, 332 (2011). arXiv:1006.0457 [cond-mat.mes-hall]
Blommaert, A., Mertens, T.G., Verschelde, H.: Edge dynamics from the path integral—Maxwell and Yang–Mills. JHEP 1811, 080 (2018). arXiv:1804.07585 [hep-th]
Brown, J.D., Henneaux, M.: Central charges in the canonical realization of asymptotic symmetries: an example from three-dimensional gravity. Commun. Math. Phys. 104, 207 (1986)
Bruveris, M., Michor, P.W., Parusiński, A., Rainer, A.: Moser’s theorem on manifolds with corners. Proc. Am. Math. Soc. 146(11), 4889–4897 (2018). arXiv:1604.07787 [math.DG]
Calaque, D., Pantev, T., Toën, B., Vaquié, M., Vezzosi, G.: Shifted Poisson structures and deformation quantization. J. Topol. 10(2), 483 (2017). arXiv:1506.03699 [math.AG]
Carlip, S.: The statistical mechanics of the (2 + 1)-dimensional black hole. Phys. Rev. D 51, 632 (1995). arXiv:gr-qc/9409052
Cattaneo, A., Mnev, P., Reshetikhin, N.: Classical BV theories on manifolds with boundary. Commun. Math. Phys. 332, 535 (2014). arXiv:1201.0290 [math-ph]
Costello, K., Gwilliam, O.: Factorization Algebras in Quantum Field Theory. New Mathematical Monographs 31. Cambridge University Press, Cambridge (2017)
Coussaert, O., Henneaux, M., van Driel, P.: The asymptotic dynamics of three-dimensional Einstein gravity with a negative cosmological constant. Class. Quantum Gravity 12, 2961 (1995). arXiv:gr-qc/9506019
Dappiaggi, C., Drago, N., Ferreira, H.: Fundamental solutions for the wave operator on static Lorentzian manifolds with timelike boundary. Lett. Math. Phys. 109(10), 2157 (2019). arXiv:1804.03434 [math-ph]
Dappiaggi, C., Drago, N., Longhi, R.: On Maxwell’s equations on globally hyperbolic spacetimes with timelike boundary. arXiv:1908.09504 [math-ph]
Donnelly, W., Freidel, L.: Local subsystems in gauge theory and gravity. JHEP 1609, 102 (2016). arXiv:1601.04744 [hep-th]
Freidel, L., Livine, E.R., Pranzetti, D.: Gravitational edge modes: from Kac–Moody charges to Poincaré networks. Class. Quantum Gravity 36(19), 195014 (2019). arXiv:1906.07876 [hep-th]
Freidel, L., Pranzetti, D.: Electromagnetic duality and central charge. Phys. Rev. D 98(11), 116008 (2018). arXiv:1806.03161 [hep-th]
Geiller, M.: Edge modes and corner ambiguities in 3d Chern–Simons theory and gravity. Nucl. Phys. B 924, 312 (2017). arXiv:1703.04748 [gr-qc]
Gomes, H.: Gauging the boundary in field-space. Stud. Hist. Philos. Sci. B 67, 89 (2019). arXiv:1902.09258 [physics.hist-ph]
Gomes, H., Hopfmüller, F., Riello, A.: A unified geometric framework for boundary charges and dressings: non-Abelian theory and matter. Nucl. Phys. B 941, 249 (2019). arXiv:1808.02074 [hep-th]
Gomes, H., Riello, A.: Unified geometric framework for boundary charges and particle dressings. Phys. Rev. D 98(2), 025013 (2018). arXiv:1804.01919 [hep-th]
Gomes, H., Riello, A.: The quasilocal degrees of freedom of Yang–Mills theory. arXiv:1910.04222 [hep-th]
Hollander, S.: Characterizing algebraic stacks. Proc. Am. Math. Soc. 136(4), 1465–1476 (2008). arXiv:0708.2705 [math.AT]
Hovey, M.: Model Categories. Mathematical Surveys and Monographs, vol. 63. American Mathematical Society, Providence (1999)
Mnev, P., Schiavina, M., Wernli, K.: Towards holography in the BV–BFV setting. Ann. Henri Poincaré. arXiv:1905.00952 [math-ph]
Pantev, T., Toën, B., Vaquié, M., Vezzosi, G.: Shifted symplectic structures. Publ. Math. Inst. Hautes Études Sci. 117, 271 (2013). arXiv:1111.3209 [math.AG]
Pridham, J.: An outline of shifted Poisson structures and deformation quantisation in derived differential geometry. arXiv:1804.07622 [math.DG]
Schreiber, U.: Differential cohomology in a cohesive infinity-topos. https://ncatlab.org/schreiber/show/differential+cohomology+in+a+cohesive+topos. [arXiv:1310.7930 [math-ph]]
Solis, D.A.: Global properties of asymptotically de Sitter and Anti de Sitter spacetimes. PhD Thesis, University of Miami (2006). arXiv:1803.01171 [gr-qc]
Walter, B.: Rational Homotopy Calculus of Functors. PhD Thesis, Brown University (2005). arXiv:math/0603336 [math.AT]
Witten, E.: (2 + 1)-Dimensional gravity as an exactly soluble system. Nucl. Phys. B 311, 46 (1988)
Acknowledgements
We would like to thank Marco Benini, William Donnelly, Laurent Freidel, Jorma Louko, Pavel Mnev and Konstantin Wernli for useful discussions and comments on this work. We also would like to thank the anonymous referee for their valuable comments and suggestions that helped us to improve this manuscript. L.M. gratefully acknowledges the support of NSF Grant DMS-1547292. A.S. gratefully acknowledges the financial support of the Royal Society (UK) through a Royal Society University Research Fellowship UF150099, a Research Grant RG160517 and an Enhancement Award RGF\(\backslash \)EA\(\backslash \)180270. N.T. gratefully acknowledges the support of NSF Grant STS-1734155.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Homotopy pullback constructions
Homotopy pullback constructions
The aim of this appendix is to provide more details on the homotopy pullback constructions for groupoids and chain complexes that are used in Propositions 2.1 and 3.1. Generally speaking, homotopy pullbacks are higher categorical generalizations of pullbacks from ordinary category theory that are compatible not only with isomorphisms, but also with the appropriate concepts of weak equivalences in these contexts, e.g., categorical equivalences in the category of groupoids \(\mathbf {Grpd}\) or quasi-isomorphisms in the category of chain complexes \(\mathbf {Ch}_{\mathbb {R}}\). A general theory of homotopy limits (and colimits) can be developed in the framework of model category theory [29] by making use of derived functors. For the purpose of our work, however, we do not have to focus too much on these abstract considerations as it will be sufficient to provide and explain explicit models for computing homotopy pullbacks for groupoids and chain complexes.
Let us start with the case of groupoids. Let \(f : {\mathcal {G}} \rightarrow {\mathcal {K}}\) and \(g : {\mathcal {H}}\rightarrow {\mathcal {K}}\) be two functors between groupoids \({\mathcal {G}},{\mathcal {H}},{\mathcal {K}}\in \mathbf {Grpd}\) and consider the homotopy pullback diagram

The following explicit description of the groupoid \({\mathcal {P}}\in \mathbf {Grpd}\) that is determined by this homotopy pullback is well known, see, e.g., [28, Section 2].
Proposition A.1
A model for the homotopy pullback in (A.1) is given by the groupoid \({\mathcal {P}}\) whose
- (i)
objects are triples (x, y, k) with \(x\in {\mathcal {G}}\), \(y\in {\mathcal {H}}\) and \(k : f(x)\rightarrow g(y)\) an isomorphism in \({\mathcal {K}}\), and
- (ii)
morphisms are pairs \((\phi ,\psi ) : (x,y,k)\rightarrow (x^\prime ,y^\prime ,k^\prime )\) with \(\phi : x\rightarrow x^\prime \) a morphism in \({\mathcal {G}}\) and \(\psi : y\rightarrow y^\prime \) a morphism in \({\mathcal {H}}\), such that the diagram
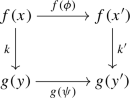 (A.2)
(A.2)in \({\mathcal {K}}\) commutes.
Remark A.2
For illustrative purposes, let us consider the special case where all groupoids \({\mathcal {G}},{\mathcal {H}},{\mathcal {K}}\in \mathbf {Set}\subseteq \mathbf {Grpd}\) are sets, i.e., every morphism in these groupoids is an identity morphism. Then the groupoid \({\mathcal {P}}\) from Proposition A.1 is a set too, namely
Observe that this is the ordinary pullback (also called fiber product) in the category of sets, which consists of pairs of elements \((x,y)\in {\mathcal {G}}\times {\mathcal {H}}\) whose images in \({\mathcal {K}}\) under f and g coincide. The general homotopy pullback for groupoids from Proposition A.1 admits a similar interpretation: Its objects are pairs of objects \((x,y)\in {\mathcal {G}}\times {\mathcal {H}}\) together with an isomorphism\(k : f(x)\rightarrow g(y)\)witnessing thatf(x) andg(y) ‘coincide’ in\({\mathcal {K}}\)in the sense that they are isomorphic. A morphism in \({\mathcal {P}}\) can then be interpreted as a pair of morphisms \(\phi : x\rightarrow x^\prime \) and \(\psi : y\rightarrow y^\prime \) that is compatible with these witnesses.
Let us consider now the case of chain complexes \(\mathbf {Ch}_{\mathbb {R}}\). To simplify our presentation, we shall focus only on the specific class of homotopy pullbacks that is needed for computing linear derived critical loci as in Sects. 3 and 5. We refer to [35, Section 3] for a study of more general types of homotopy pullbacks and also other homotopy (co)limits. Let \(V,W\in \mathbf {Ch}_{\mathbb {R}}\) be two chain complexes. We assume that V is non-negatively graded, i.e., \(V_n=0\) for all \(n<0\), and that W non-positively graded, i.e., \(W_n=0\) for all \(n>0\). (This assumption is always satisfied in applications to derived critical loci for linear gauge field theories, where V is a chain complex encoding the gauge fields and (higher) ghost fields in non-negative degrees, and \(W = V^*\) is the dual of V. We would like to emphasize that, in this context, the antifields are not included in V, but they are a result of the homotopy pullback construction in Proposition A.3.) We regard the projection chain map \(\pi _1 : V\times W \rightarrow V\) on the first factor of the Cartesian product complex as a bundle over V with fiber W and consider two sections, the zero section \((\mathrm {id},0) : V\rightarrow V\times W\) and a generic section \((\mathrm {id},f) : V\rightarrow V\times W\), where \(f :V\rightarrow W\) is any chain map. Because V is by hypothesis non-negatively graded and W is non-positively graded, the chain map f is necessarily of the form

i.e., it is determined by a single linear map \(f_0 : V_0\rightarrow W_0\) in degree 0 that has to satisfy \(f_0 \circ \mathrm {d}^V =0\) and \(\mathrm {d}^W \circ f_0=0\). Our goal is to provide an explicit description of the chain complex \(L\in \mathbf {Ch}_{\mathbb {R}}\) that is determined by the homotopy pullback

Proposition A.3
A model for the homotopy pullback in (A.5) is given by the chain complex

where we indicate in round brackets the homological degrees of L.
Proof
We follow the same strategy as in [7, Proposition 3.21], where a special case of this proposition was proven. In particular, we will compute the homotopy pullback (A.5) in terms of an ordinary pullback by replacing the zero section \((\mathrm {id},0) : V\rightarrow V\times W\) by a weakly equivalent fibration. To construct such a replacement, let us introduce the chain complex

concentrated in degrees 0 and \(-1\). Note that this complex is acyclic, i.e., the unique map \(0 \rightarrow D\) from the zero complex to D is a quasi-isomorphism. Let us consider now the tensor product complex \(D\otimes W\), which is acyclic too, and observe that it is explicitly given by \((D\otimes W)_{n} \cong W_n \oplus W_{n+1} \cong W_n\times W_{n+1}\), for all \(n\in {\mathbb {Z}}\), together with the differential
for all \((w_n,{\widetilde{w}}_{n+1})\in W_n\times W_{n+1}\). We define a chain map \(p: D\otimes W \rightarrow W\), sending \((w_n,{\widetilde{w}}_{n+1}) \mapsto w_n\), and note that this map is degree-wise surjective and hence a fibration in \(\mathbf {Ch}_{\mathbb {R}}\). With these preparations, we obtain a fibration
that is a weakly equivalent replacement of the zero section \((\mathrm {id},0) : V\rightarrow V\times W\). This allows us to compute the chain complex L in (A.5) by the ordinary pullback

Explicitly, the degree \(n\in {\mathbb {Z}}\) component of the chain complex L is given by
where the isomorphism in the last step is given by \((v_n,{\widetilde{w}}_{n+1}) \mapsto \big ((v_n, f(v_n) , {\widetilde{w}}_{n+1}), v_n\big )\). Using (A.8), we can compute the differential \(\mathrm {d}^{L} : L_n\rightarrow L_{n-1}\) and find
for all \((v_n,{\widetilde{w}}_{n+1}) \in V_n\times W_{n+1}\). Recalling that V is by hypothesis non-negatively graded and W is non-positively graded, we find that the chain complex described by (A.11) is isomorphic to the chain complex in (A.6), which completes our proof. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mathieu, P., Murray, L., Schenkel, A. et al. Homological perspective on edge modes in linear Yang–Mills and Chern–Simons theory. Lett Math Phys 110, 1559–1584 (2020). https://doi.org/10.1007/s11005-020-01269-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-020-01269-x
Keywords
- Linear Yang–Mills theory
- Linear Chern–Simons theory
- Edge modes
- Derived critical locus
- Homological algebra
- BRST/BV formalism




