Abstract
We address some usually overlooked issues concerning the use of \(*\)-algebras in quantum theory and their physical interpretation. If \({\mathfrak {A}}\) is a \(*\)-algebra describing a quantum system and \(\omega : {\mathfrak {A}}\rightarrow {\mathbb {C}}\) a state, we focus, in particular, on the interpretation of \(\omega (a)\) as expectation value for an algebraic observable \(a=a^*\in {\mathfrak {A}}\), studying the problem of finding a probability measure reproducing the moments \(\{\omega (a^n)\}_{n\in {\mathbb {N}}}\). This problem enjoys a close relation with the selfadjointness of the (in general only symmetric) operator \(\pi _\omega (a)\) in the GNS representation of \(\omega \) and thus it has important consequences for the interpretation of a as an observable. We provide physical examples (also from QFT) where the moment problem for \(\{\omega (a^n)\}_{n\in {\mathbb {N}}}\) does not admit a unique solution. To reduce this ambiguity, we consider the moment problem for the sequences \(\{\omega _b(a^n)\}_{n\in {\mathbb {N}}}\), being \(b\in {\mathfrak {A}}\) and \(\omega _b(\cdot ):=\omega (b^*\cdot b)\). Letting \(\mu _{\omega _b}^{(a)}\) be a solution of the moment problem for the sequence \(\{\omega _b(a^n)\}_{n\in {\mathbb {N}}}\), we introduce a consistency relation on the family \(\{\mu _{\omega _{b}}^{(a)}\}_{b\in {\mathfrak {A}}}\). We prove a 1-1 correspondence between consistent families \(\{\mu _{\omega _{b}}^{(a)}\}_{b\in {\mathfrak {A}}}\) and positive operator-valued measures (POVM) associated with the symmetric operator \(\pi _\omega (a)\). In particular, there exists a unique consistent family of \(\{\mu _{\omega _{b}}^{(a)}\}_{b\in {\mathfrak {A}}}\) if and only if \(\pi _\omega (a)\) is maximally symmetric. This result suggests that a better physical understanding of the notion of observable for general \(*\)-algebras should be based on POVMs rather than projection-valued measure.
Similar content being viewed by others
Notes
When a new term is introduced and defined, its name appears in boldface style.
The converse does not hold, since \(\ker (\pi _\omega )\) is a two-sided \(*\)-ideal and thus \(\ker (\pi _\omega ) \subsetneq G_{({\mathfrak {A}},\omega )}\) in the general case.
A sufficient condition (by no means necessary!) assuring essential selfadjointness of \(\pi _\omega (a)\) for a fixed Hermitian element \(a\in {{\mathfrak {A}}}\) and every non-normalized state \(\omega \) is that [23] there exist \(b_\pm \in {{\mathfrak {A}}}\) such that \((a\pm i {{\mathbb {I}}})b_\pm = {{\mathbb {I}}}\) (equivalently \(b'_\pm (a\pm i {{\mathbb {I}}}) = {{\mathbb {I}}}\), where \(b'_\pm =b_\mp ^*\)). This is because the written condition trivially implies that \({\text {Ran}}(\pi _\omega (a) \pm iI) \supset {\mathcal{D}}_\omega \) and thus \({\text {Ran}}(\pi _\omega (a) \pm iI)\) is dense, so that the symmetric operator \(\pi _\omega (a)\) is essentially selfadjoint (see, e.g., [15, Thm. 5.18]).
In the non-normalized case, the meaning of expectation value would be actually reserved to \({\widehat{\omega }}(a)=\omega ({{\mathbb {I}}})^{-1}{\omega }(a)\), though, for shortness, we improperly also call \(\omega (a)\) expectation value in the rest of the work.
If \(\omega _b\) is not singular, some \(\mu ^{(a)}_{\omega _b}\) exists due to Proposition 6. If it is singular, the zero measure solves the moment problem.
The creation and annihilation operators \(a,a^\dagger \) appearing in Eq. (3.2.28) in [27] are our \(-ia_{K\varphi }\) and \(ia^+_{K\varphi }\).
The field operators \(\varPhi _S(f)\) used there correspond to our \(2^{-1/2}\pi _\omega (\varPhi [\varphi ])\).
Condition (29) has been verified for the algebra \({\mathfrak {A}}[M,g]\) when (M, g) is 4D Minkowski spacetime and the generators \(\varPhi [\varphi ]\) are smeared with real test Schwartz functions serving as Cauchy data. This is a very special case which is suitable in Minkowski spacetime especially because therein the Cauchy surfaces can be chosen as submanifolds isometrically isomorphic to \({{\mathbb {R}}}^3\). However, we expect that the conclusions (a1), (b1) hold true also for the algebra \({\mathfrak {A}}(M,g)\) (i.e., field operators smeared with Cauchy data in \(C_c^\infty ({{\mathbb {R}}}^3)\)) as the closure of the \(\pi _\omega \)-representation of the generators \(\varPhi (f)\in {\mathfrak {A}}(M,g)\) and \(\varPhi [Ef]\in {\mathfrak {A}}[M,g]\) coincides, though a rigorous proof of this fact is not presented here. Some standard spacetime-deformation argument would probably allow to prove similar conclusions for a number of pure quasifree states in curved spacetimes too, though we refrain to specify the precise set of states. We are grateful to an anonymous referee for drawing our attention on these issues.
With reference to [21, Ch. 6] this implies that for all \(E\in {\mathscr {B}}(\varSigma )\) and for all countable partitions \(E=\cup _{n\in {\mathbb {N}}} E_n\), with \(E_n\in {\mathscr {B}}(\varSigma )\) and \(E_n\cap E_m=\varnothing \) if \(n\ne m\), it holds \(Q_{\psi ,\varphi }(E)=\sum _{n\in {\mathbb {N}}}Q_{\psi ,\varphi }(E_n)\), where the series is absolutely convergent. In particular, the total variation of this measure \(|Q_{\psi , \varphi }|\) is a finite positive \(\sigma \)-additive measure. Notice that \(Q_{\psi ,\psi }\) is a finite positive measure.
In particular, if \(f: {{\mathbb {R}}}\ni \lambda \rightarrow \lambda \in {{\mathbb {R}}}\), we have
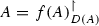 , but the domain of f(A) according to (38) is in general larger than D(A), and \(||f(A)\psi ||^2 = \int _{{\mathbb {R}}} |f(\lambda )|^2 \mathrm{d}Q^{(A)}_{\psi ,\psi }(\lambda )\) is valid for \(\psi \in D(A)\).
, but the domain of f(A) according to (38) is in general larger than D(A), and \(||f(A)\psi ||^2 = \int _{{\mathbb {R}}} |f(\lambda )|^2 \mathrm{d}Q^{(A)}_{\psi ,\psi }(\lambda )\) is valid for \(\psi \in D(A)\).
References
Akhiezer, N.I., Glazman, I.M.: Theory of Linear Operators in Hilbert Space. Dover, New York (1993), two volumes bound as one, translated from Russian by M. Nestell, first published by F. Ungar, New York, in 1961 and 1963
Beneduci, R.: Joint measurability through Naimark’s dilation theorem. Rep. Math. Phys. 79, 197–214 (2017)
Borchers, H.J., Yngvason, J.: Local nets and self-adjoint extensions of quantum field operators. Lett. Math. Phys. 21, 151 (1991)
Brunetti, R., Dappiaggi, C., Fredenhagen, K., Yngvason, J. (eds.): Advances in Algebraic Quantum Field Theory. Springer, New York (2015)
Buchholz, D., Fredenhagen, K.: A \(C^*\)-algebraic approach to interacting quantum field theories. arXiv:1902.06062 [math-ph]
Busch, P., Lahti, P.J., Pellonpää, J.-P., Ylinen, K.: Quantum Measurement. Springer, New York (2016)
Dubin, D., Kiukas, J., Pellonpää, J.-P., Ylinen, K.: Operator integrals and sesquilinear forms. J. Math. Anal. Appl. 413, 250–268 (2014)
Dubois-Violette, M.: A generalization of the classical moment problem on \(*\)-algebras with applications to relativistic quantum theory I. Commun. Math. Phys. 43, 225–254 (1975)
Dubois-Violette, M.: A generalization of the classical moment problem on \(*\)-algebras with applications to relativistic quantum theory II. Commun. Math. Phys. 54, 151–172 (1977)
Fewster, C.J., Verch, R.: Quantum fields and local measurements. arXiv:1810.06512 [math-ph]
Fewster, C.J.: A generally covariant measurement scheme for quantum field theory in curved spacetimes. arXiv:1904.06944 [math-ph]
Haag, R.: Local Quantum Physics. Fields, Particle, Algebras. 2nd Revised and Enlarged Edition. Springer, New York (1996)
Kay, B.S., Wald, R.M.: Theorems on the uniqueness and thermal properties of stationary, nonsingular, quasifree states on spacetimes with a bifurcate killing horizon. Phys. Rep. 207, 49–136 (1991)
Khavkine, I., Moretti, V.: Algebraic QFT in curved spacetime and quasifree Hadamard states: an introduction. In: Brunetti, R., Dappiaggi, C., Fredenhagen, K., Yngvason, J. (eds.) Advances in Algebraic Quantum Field Theory. Springer, New York (2015)
Moretti, V.: Spectral Theory and Quantum Mechanics, 2nd Revised and Enlarged Edition. Springer, New York (2017)
Moretti, V.: Fundamental Mathematical Structures of Quantum Theory. Springer, New York (2019)
Naimark, N.: Self-adjoint extensions of the second kind of a symmetric operator. Izv. Akad. Nauk SSSR 4(1), 53–104 (1940)
Naimark, N.: Spectral functions of a symmetric operator. Izv. Akad. Nauk SSSR 4(3), 277–318 (1940)
Rabsztyn, S.: Deficiency indices for wick powers in one dimension. Rep. Math. Phys. 27, 161–168 (1989)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics. Fourier Analysis, Self-Adjointness, vol. II. Academic Press, New York (1975)
Rudin, W.: Real and Complex Analysis, 2nd edn. McGraw-Hill, New York (1987)
Sanders, K.: Essential self-adjointness of Wick squares in quasi-free Hadamard representations on curved spacetimes. J. Math. Phys. 53, 042502 (2012)
Schmüdgen, K.: Unbounded Operator Algebras and Representation Theory. Springer, New York (1990)
Schmüdgen, K.: Unbounded Self-adjoint Operators on Hilbert Space. Springer, New York (2012)
Schmüdgen, K.: The Moment Problem. Springer, New York (2017)
Streater, R.F., Wightman, A.S.: PCT, Spin and Statistics, and All That. Princeton University Press, Princeton (2000)
Wald, R.M.: Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics. Chicago Lectures in Physics. University of Chicago Press, Chicago (1994)
Acknowledgements
The authors thank C. Capoferri, C. Dappiaggi, S. Mazzucchi and N. Pinamonti for useful discussions. We are grateful to C. Fewster for helpful comments and for pointing out to us reference [3] and to the anonymous referees for their helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Reducing subspaces
Definition 37
If \(D(T) \subset {\mathsf {H}}\) is a subspace of the Hilbert space \({{\mathsf {H}}}\), let \(T : D(T) \rightarrow {\mathsf {H}}\) be an operator and \({\mathsf {H}}_0 \subset {\mathsf {H}}\) a closed subspace with \(\{0\} \ne {\mathsf {H}}_0 \ne {\mathsf {H}}\), \(P_0\) denoting the orthogonal projector onto \({\mathsf {H}}_0\). In this case, \({\mathsf {H}}_0\) is said to reduceT if both conditions are true
- (i)
\(T(D(T) \cap {\mathsf {H}}_0) \subset {\mathsf {H}}_0\) and \(T(D(T) \cap {\mathsf {H}}^\perp _0) \subset {\mathsf {H}}^\perp _0\),
- (ii)
\(P_0(D(T)) \subset D(T)\),
so that the direct orthogonal decomposition holds

The operator  is called the part ofTon\( {\mathsf {H}}_0\). \(\square \)
is called the part ofTon\( {\mathsf {H}}_0\). \(\square \)
Remark 38
(1) It is worth stressing that (i) does not imply (ii). (A counterexample is given by \({\mathsf {H}}:=L^2([0,+\infty ),\mathrm{d}x)\), \(T:=-i\frac{\mathrm{d}}{\mathrm{d}x}\) with \(D(T):= C_c^\infty ((0,+\infty ))\) and \({\mathsf {H}}_0:={\text {span}}\{\varphi \}\), where \(\varphi (x)=e^{-x}\). Here \(D(T)\cap {\mathsf {H}}_0 = \{0\}\) so that the former inclusion in (i) is trivially valid, whereas the latter is valid by integrating by parts. However, it is easy to pick out \(\psi \in D(T)\) such that \(\langle \psi |\varphi \rangle \ne 0\), so that \((P_0\psi )(x)\) has the support of \(\varphi \) itself given by the whole \([0,+\infty )\) and \(P_0\psi \not \in D(T)\).) Moreover, without (ii) the direct orthogonal decomposition (66) cannot take place.
(2) Evidently \({\mathsf {H}}_0\) reduces T iff \({\mathsf {H}}_0^\perp \) reduces T, since \(I-P_0\) projects onto \({\mathsf {H}}_0^\perp \).
(3) A condition equivalent to (i)–(ii) is \(P_0T\subset TP_0\) as the reader immediately proves. \(\square \)
Proposition 39
If the closed subspace \({\mathsf {H}}_0\) reduces the symmetric (selfadjoint) operator T on \({\mathsf {H}}\), then also  and
and  are symmetric (resp. selfadjoint) in \({\mathsf {H}}_0\) and \({\mathsf {H}}_0^\perp \), respectively.
are symmetric (resp. selfadjoint) in \({\mathsf {H}}_0\) and \({\mathsf {H}}_0^\perp \), respectively.
Proof
Direct inspection. \(\square \)
A useful technical fact is presented in the following proposition [24].
Proposition 40
Let T be a closed symmetric operator on a Hilbert space \({{\mathsf {H}}}\). Let \(D_0\) be a dense subspace of a closed subspace \({{\mathsf {H}}}_0\) of \({{\mathsf {H}}}\) such that \(D_0 \subset D(T )\) and \(T(D_0)\subset {{\mathsf {H}}}_0\). Suppose that  is essentially selfadjoint on \({{\mathsf {H}}}_0\). Then \({{\mathsf {H}}}_0\) reduces T and \(\overline{T_0}\) is the part of T on \({{\mathsf {H}}}_0\).
is essentially selfadjoint on \({{\mathsf {H}}}_0\). Then \({{\mathsf {H}}}_0\) reduces T and \(\overline{T_0}\) is the part of T on \({{\mathsf {H}}}_0\).
Proof
See [24, Prop.1.17]. \(\square \)
1.2 More on generalized symmetric and selfadjoint extensions
According to definition 21 we have
where D(B) is dense in \({\mathsf {K}}\) and D(A) is dense in \({\mathsf {H}}\). Generalized extensions B with \(B\supsetneq A\) are classified accordingly to the previous inclusions following [1], in particular:
- (i)
B is said to be of kind I if \(D(A)\ne D(B)\cap {\mathsf {H}}= D(B)\)—that is, if B is a standard extension of A;
- (ii)
B is said to be of kind II if \(D(A)= D(B)\cap {\mathsf {H}}\ne D(B)\);
- (iii)
B is said to be of kind III if \(D(A)\ne D(B)\cap {\mathsf {H}}\ne D(B)\);
Proposition 41
If \(A:D(A) \rightarrow {\mathsf {H}}\) with \(D(A) \subset {\mathsf {H}}\) is maximally symmetric and \(B \supsetneq A\) is a generalized symmetric extension, then B is of kind II.
Proof
The kind I is not possible a priori since A does not admit proper symmetric extensions in \({\mathsf {H}}\). Let us assume that B is either of kind II or III and consider the operator \(P_{{\mathsf {H}}}BP_{{\mathsf {H}}}\), with its natural domain \(D(P_{{\mathsf {H}}}BP_{{\mathsf {H}}})= D(BP_{{\mathsf {H}}})\), where \(P_{{\mathsf {H}}}\in {\mathscr {L}}({\mathsf {K}})\) is the orthogonal projector onto \({\mathsf {H}}\). Since this is a symmetric extension of A in \({\mathsf {H}}\) which is maximally symmetric, we have \(A=P_{{\mathsf {H}}}BP_{{\mathsf {H}}}\), in particular \(D(BP_{{\mathsf {H}}})=D(A)\). As a consequence, if \(x \in D(B)\cap {\mathsf {H}}\), then \(x \in D(BP_{{\mathsf {H}}}) =D(A)\) so that \(D(A) \supset D(B)\cap {\mathsf {H}}\) and thus \(D(A) = D(B)\cap {\mathsf {H}}\) because the other inclusion is true from (67). We have proved that B is of kind II. \(\square \)
We have an important technical result
Theorem 42
A non-selfadjoint symmetric operator A always admits a generalized selfadjoint extension B. Such an extension can be chosen of kind II when A is closed.
Proof
See [1, Thm. 1. p.127 Vol II] for the former statement. The latter statement relies on the comment under the proof of [1, Thm. 1. p.127 Vol II] and it is completely proved in [17, Thm.13].Footnote 11 The fact that the selfadjoint extensions can be chosen in order to satisfy (iii) of Definition 21 is proved in [18, Thm.7]. \(\square \)
1.3 Proof of some propositions
Lemma 43
Referring to (1) in Example 11, \(\psi _\omega \in \mathcal{D}_{\omega _B}\).
Proof
To prove that \(\psi _\omega \in \mathcal{D}_{\omega _B}\) observe that, since A and \(A^*\) are generators of \({\mathfrak {A}}_{\text {CCR},1}\) satisfying \([A,A^*]=I\), we can always rearrange every element \(B \in {\mathfrak {A}}_{\text {CCR},1}\) into the form
where \(A^0:=A^{*0}:=I\) and where only a finite number of coefficients \(c^{(B)}_{n,m} \in {{\mathbb {C}}}\) depending on B are different from 0. Here, (13) implies
where again only a finite number of coefficients \(d^{(B)}_k \in {{\mathbb {C}}}\) depending on B are different from 0 and to pass from the first sum to the second one we took advantage of the standard harmonic oscillator algebra of the Hermite basis where \(A\psi _k=\sqrt{k}\psi _{k-1}\), \(A^*\psi _k=\sqrt{k+1}\psi _{k+1}\) with \(\psi _0:= \psi _\omega \). To conclude, notice that, if \(C \in {{\mathfrak {A}}}_{\text {CCR},1}\), (13) also implies that \(\pi _{\omega _B}(C)\psi _{\omega _B}= \pi _{\omega }(C)\psi _{\omega _B}\). Therefore, if \(k_B\in {{\mathbb {N}}}\) is the largest natural such that \(d^{(B)}_k \ne 0\) in (68), choosing \(C:= \frac{1}{d^{(B)}_{k_B}\sqrt{k_B!}}A^{k_B}\in {{\mathfrak {A}}}_{\text {CCR},1}\), we have
In other words, \(\psi _\omega \in \mathcal{D}_{\omega _B}\) as argued. \(\square \)
Lemma 44
Referring to (2) in Example 11, \(\psi _\omega \in {\mathcal{D}}_{\omega _b}\) if (29) is valid.
Proof
First define the elements of the algebra \({{\mathfrak {A}}}[M,g]\)
We stress that the elements \(A^*_{\varphi } \) and \(A_{\varphi } \) form a set of generators of \({{\mathfrak {A}}}[M,g]\), because the \(\varPhi [\varphi ]\) are generators and the previous relations can be inverted to
By using (26), linearity of \(x \mapsto a_x^+\), antilinearity of \(x \mapsto a_x\) and (29), we immediately find
The algebraic relations reflecting (25) are also valid from (b) and (c) in item (2) of Example 11,
Exploiting the found results, we can prove that \(\psi _\omega \in {\mathcal{D}}_{\omega _b}\) as wanted. The generic element \(b \in {{\mathfrak {A}}}[M,g]\), taking advantage of the generators \(A_{\varphi }\) and \(A^*_{\varphi }\) and their commutation relations, is always of the form (where we adopt the convention that \(\prod _{j=1}^{0} A^{(*)}_{\varphi _j}:= {{\mathbb {I}}}\))
for sets of solutions \(\{\varphi ^{(k)}_{j}\}_{j\in \{1,\ldots , D_k\}}\) and \(\{{\tilde{\varphi }}^{(h)}_{i}\}_{i \in \{1,\ldots , E_h\}}\) in Sol[M, g] and where we adopted Einstein’s summation convention. Obviously, \(N,D_h, E_h\), and the complex coefficients \(c_{k,h}^{j_1\ldots j_k i_1\ldots i_h} \) depend on b and these coefficients are completely symmetric separately in the indices \(j_r\) and in the indices \(i_r\) due to the fact that the elements \(A^*_{\varphi _{j_1}},\cdots , A^*_{\varphi _{j_k}}\) and \(A_{\varphi _{i_1}},\cdots ,A_{\varphi _{i_h}}\) separately pairwise commute. Hence, (69) entails
where \(\psi ^{(k)}_j := K\varphi ^{(k)}_j\) and we henceforth assume that not all coefficients \(c_{N0}^{j_1\ldots j_N}\) vanish and all vectors \(\psi ^{(N)}_j = K\varphi ^{(N)}_j\) for \(j=1,\ldots , D_N\) do not vanish. (Otherwise, the Nth addend in (71) would give no contribution.) Defining
(25) yields, if \(c^{j_1\cdots j_N} := c_{N0}^{j_1\cdots j_N}\) and \(\psi _j := \psi ^{(N)}_j\)
At this juncture we can fix an orthonormal basis \(\{e_l\}_{i=1,\ldots , D}\) in the span of the vectors \(\{\psi _{j}\}_{j=1,\ldots , D_N}\) and we can rearrange the identity above as
where not all the symmetric coefficients \(c'^{j_1\cdots j_N}\) vanish (since they are the components in a new basis of the non-vanishing tensor defined by the components \(c^{j_1\cdots j_N}\)). Expanding the contractions we find, where \(P_N\) denotes the group of permutations of N objects
(In the second line, \(c'^{j_{\sigma ^{-1}(1)}\cdots j_{\sigma ^{-1}(N)}}= c'^{j_1\cdots j_N} \) arises from the symmetry of the coefficients.) That is
Since the coefficient in front of \(\psi _\omega \) in (73) does not vanish, then \(\psi _\omega \in {\mathcal{D}}_{\omega _b}\) as wanted. \(\square \)
Proof of Proposition 22
Let B be a generalized symmetric extension in the Hilbert space \({{\mathsf {K}}}\) of the selfadjoint operator A in the Hilbert space \({{\mathsf {H}}}\) with \({{\mathsf {H}}}\subset {{\mathsf {K}}}\). The closed symmetric operator \(B'= {\overline{B}}\) in \({\mathsf {K}}\) extends A. In view of Proposition 39–40, since  is selfadjoint on \({\mathsf {H}}\), then \({\mathsf {H}}\) reduces \(B'\) and
is selfadjoint on \({\mathsf {H}}\), then \({\mathsf {H}}\) reduces \(B'\) and  , where the two addends are symmetric operators, respectively, on \({\mathsf {H}}\) and \({\mathsf {H}}^\perp \). Requirement (iii) in Definition 21 imposes that \({\mathsf {H}}^\perp = \{0\}\), so that \({\mathsf {K}}= {\mathsf {H}}\) and B is a standard symmetric extension of the selfadjoint operator A which entails \(B=A\). \(\square \)
, where the two addends are symmetric operators, respectively, on \({\mathsf {H}}\) and \({\mathsf {H}}^\perp \). Requirement (iii) in Definition 21 imposes that \({\mathsf {H}}^\perp = \{0\}\), so that \({\mathsf {K}}= {\mathsf {H}}\) and B is a standard symmetric extension of the selfadjoint operator A which entails \(B=A\). \(\square \)
Proof of Theorem 23
(a) and (b). If A is symmetric, for each generalized selfadjoint extension B as in Definition 21 (they exist in view of Theorem 42 and, if A is selfadjoint, \(B:=A\)), one can define a corresponding normalized POVM \(Q^{(A)}:{\mathscr {B}}({\mathbb {R}})\rightarrow {\mathfrak {B}}({\mathsf {H}})\) as follows. Let \(P:{\mathscr {B}}({\mathbb {R}})\rightarrow {\mathscr {L}}({\mathsf {K}})\) be the unique PVM associated with B
(see, e.g., [15, Thm. 9.13]) and let \(P_{{\mathsf {H}}}\in {\mathscr {L}}({\mathsf {K}})\) denote the orthogonal projection onto \({\mathsf {H}}\) viewed as a closed subspace of \({\mathsf {K}}\). A normalized POVM \(Q^{(A)}:{\mathscr {B}}({\mathbb {R}})\rightarrow {\mathfrak {B}}({\mathsf {H}})\) is then defined by setting

The POVM \(Q^{(A)}\) is linked to A by the following identities as the reader easily proves from standard spectral theory:
The above relation implies the following facts, where \(\lambda ^k\) henceforth denotes the map \({{{\mathbb {R}}}} \ni \lambda \rightarrow \lambda ^k \in {{{\mathbb {R}}}} \) for \(k\in {\mathbb {N}} := \{0,1,2, \ldots \}\),

the second equality arising from the identity
which descends from Eq. (75). [1, Thm. 2, p. 129 Vol II] proves that every POVM (it is equivalent to a spectral function used therein, see Remark 14) satisfying (76) arises from a PVM of a generalized selfadjoint extension B of A as above, so that (77) are satisfied. The proof of (a) and (b) is over.
(c) If the selfadjoint operator B extending A as in (b) is a standard extension of A, then \({{\mathsf {H}}}={{\mathsf {K}}}\) so that \(P_{{{\mathsf {K}}}}=I\) and \(Q^{(A)}=P\) so that \(Q^{(A)}\) is a PVM. If \(Q^{(A)}\) is a PVM, \(B := \int _{{\mathbb {R}}}\lambda \mathrm{d}Q^{(A)}(\lambda )\) with domain \(D(B)= \{\psi \in {{\mathsf {H}}}\,|\, \int _{{\mathbb {R}}}\lambda ^2 \mathrm{d}Q^{(A)}_{\psi ,\psi }(\lambda ) <+\infty \}\) is a standard selfadjoint extension of A and the associated trivial dilation triple \({{\mathsf {K}}}:={{\mathsf {H}}}\), \(P_{{\mathsf {H}}}:=I\), \(P:=Q^{(A)}\) trivially generates \(Q^{(A)}\) as in (b).
(d) Referring to the proof of (a) and (b) above, for generalized selfadjoint extensions B of kind II, and this choice for B is always feasible when A is closed in view of Theorem 42, we have \(D(A)=D(B)\cap {\mathsf {H}}\) and therefore

Since (77) is valid for every POVM satisfying (76), we have that the identity \(D(A)=\{\psi \in {\mathsf {H}}|\;\lambda \in L^2({\mathbb {R}},P_{\psi ,\psi })\}\) holds if and only if  , namely B is an extension of type II of A.
, namely B is an extension of type II of A.
(e) and (f). They are established in [1, Thm. 2, p. 135 Vol II], taking Theorem 42 into account and (d) above. \(\square \)
Proof of Theorem 26
Consider Naimark’s dilation triple of Q, \(({\mathsf {K}}, P_{{\mathsf {H}}}, P)\) and define the selfadjoint operator \(B := \int _{{\mathbb {R}}}\lambda \mathrm{d}P(\lambda )\). By hypothesis \(D(A^{(Q)})= D(B)\cap {\mathsf {H}}\). Since D(B) is a subspace of \({\mathsf {K}}\), it also holds that \(D(A^{(Q)})\) is a subspace of \({\mathsf {H}}\) proving (a). A well-known counterexample due to Naimark [1] proves that, in some cases, \(D(A^{(Q)}) =\{0\}\) though Q is not trivial. It is clear that, if an operator \(A^{(Q)}: D(A^{(Q)}) \rightarrow {\mathsf {H}}\) satisfies (39) then it is unique due to the arbitrariness of \(\varphi \in {\mathsf {H}}\). So we prove (b) and (d) simultaneously just checking that  satisfies (39). The proof is trivial since, from standard properties of the integral of a PVM, if \(\psi \in D(A^{(Q)})\subset D(B)\) and \(\varphi \in {\mathsf {H}}\), then
satisfies (39). The proof is trivial since, from standard properties of the integral of a PVM, if \(\psi \in D(A^{(Q)})\subset D(B)\) and \(\varphi \in {\mathsf {H}}\), then
(c) immediately arises with the same argument taking advantage of the fact that \(B=B^*\) and \(P_{{\mathsf {H}}} \psi = \psi \) if \(\psi \in {\mathsf {H}}\). Regarding (e), it is sufficient observing that (see, e.g., [15]), if \(\psi \in D(B)\), then \(||B\psi ||^2 = \int _{{\mathbb {R}}} \lambda ^2 \mathrm{d}P_{\psi ,\psi }(\lambda )\) and next taking advantage of \(D(A^{(Q)})= D(B)\cap {\mathsf {H}}\) and (d) observing, in particular, that \(P_{{\mathsf {H}}}^* P_{{\mathsf {H}}}\varphi = P_{{\mathsf {H}}} P_{{\mathsf {H}}}\varphi = P_{{\mathsf {H}}}\varphi =\varphi \) if \(\varphi \in {\mathsf {H}}\). The fact that \(A^{(Q)}\) is closed immediately follows from the fact that B is closed (because selfadjoint) and \(A= B|_{D(B) \cap {\mathsf {H}}}\) where \({\mathsf {H}}\) is closed. \(\square \)
Proof of Proposition 32
What we have to prove is just that the right-hand side of (54) is a positive semi definite Hermitian scalar product over X. Indeed, with that definition of the scalar product \((\, |\, )_p\), the identity \(p(x) = \sqrt{(x|x)_p}\) is valid (see below) and this fact automatically implies that p is a seminorm. Uniqueness of the scalar product generating a seminorm p is a trivial consequence of the polarization identity. Let us prove that \((\, |\, )_p\) defined in (54) is a positive semidefinite Hermitian scalar product over X. From the definition of \((\,|\,)_p\) and property (i) of \(p:X\rightarrow [0,+\infty )\), it is trivial business to prove the following facts per direct inspection:
- 1.
\((x|x)_p = p(x)^2 \ge 0\),
- 2.
\((x|0)_p=0\),
- 3.
\((x|y)_p= \overline{(y|x)_p}\),
- 4.
\((x|iy)_p = i(x|y)_p\).
With these identities, we can also prove
- 5.
\((x|y+z)_p = (x|y)_p + (x|z)_p\),
- 6.
\((x|-y)_p = -(x|y)_p\),
by exploiting property (ii) of p. Actually, (6) immediately arises form (2) and (5). We will prove (5) as the last step of this proof. Iterating property (5), we easily obtain \((x|ny)_p = n(x|y)_p \) for every \(n\in {\mathbb {N}}\), so that \((1/n) (x|z)_p = (x|(1/n) z)_p \) when replacing ny for z. As a consequence, \(\lambda (x|y)_p = (x|\lambda y)_p\) if \(\lambda \in \mathbb {Q}\). This results extends to \(\lambda \in {\mathbb {R}}\) if the map \({\mathbb {R}} \ni \lambda \mapsto (x|\lambda y)_p\) is right-continuous because, for every \(x\in [0,+\infty )\) there is a decreasing sequence of rationals tending to it. Definition (54) of \((x|y)_p\) proves that map is in fact right-continuous since property (iii) of p implies that, if \(\lambda _0 \in [0, +\infty )\),
We can therefore add the further property
- 7.
\(\lambda (x|y)_p = (x|\lambda y)_p\) if \(\lambda \in [0,+\infty )\).
Collecting properties (1), (3), (5), (7), (6), (4) together, we obtain that \(X\times X \ni (x,y) \mapsto (x|y)_p\) defined as in (54) is a positive semi definite Hermitian scalar product over X whose associated seminorm is p as wanted.
To conclude the proof, we establish property (5) from requirement (ii) on p.
Since, from (i) of the requirements on p,
we can rearrange the found decomposition of \(4(x|y+z)_p\) as
From (ii) of the requirements on p,
The special case \(z=0\) and (2) yield \(2(x/2|y)_p= (x|y)_p\) which, exploited again above, yields the wanted result (5) \(4(x|y+z)_p = 4(x|y)_p + 4(x|z)_p\). \(\square \)
Rights and permissions
About this article
Cite this article
Drago, N., Moretti, V. The notion of observable and the moment problem for \(*\)-algebras and their GNS representations. Lett Math Phys 110, 1711–1758 (2020). https://doi.org/10.1007/s11005-020-01277-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-020-01277-x




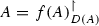 , but the domain of f(A) according to (
, but the domain of f(A) according to (