1 Introduction

Cities all over the world are attracting more and more inhabitants leading to the development of novel as well as reconstructed urban areas. Providing liveable zones in major cities is an important issue, since approximately 70% of the people on the global scale will be living in urban areas by 2050 (Magistrat 2014). This trend can also be observed in Vienna, where a population growth of 22% to more than 2 million people is expected by 2050. Establishing more attractive, sustainable and economically viable urban areas for a growing amount of residents thus becomes a key point high on the agenda of decision makers. Taking into account the aim of providing high and socially balanced quality of living and preserving resources is essential when building and refurbishing residential and working areas, public utilities and infrastructure.

To achieve these aims, the city of Vienna established so-called Smart City objectives, which comprise three pillars: resources, innovation and quality of life (Smart City Wien 2018). Resources focuses on issues such as intelligent construction sites, energy, building standards, and mobility concepts. While green field projects enable the adoption and implementation of novel concepts for more sustainable living through all implementation phases, existing infrastructure and traffic in urban areas limit the extent of refurbishment and construction tasks, such as establishing new residential buildings, expanding train and metro stations, or renovating and reconstructing buildings to improve their functionality and sustainability. These construction projects contribute to more attractive, sustainable and economically viable urban areas once they are finished by improving accessibility, functionality and energy efficiency. However, construction tasks can cause severe negative impact on the surrounding community, to a large extent due to transport activities (Gilchrist and Allouche 2005).

In this work, we aim at optimizing construction logistics operations encountered in the development process of newly built areas, comprising multiple construction sites. More specifically, we present the case study of the new development area Seestadt Aspern in Vienna. Seestadt Aspern is one of Austria’s largest construction areas, where a new city quarter is being constructed in several phases until 2030 on an area of 2.4 million \(\text {m}^2\). This area will provide accommodation for about 20,000 people and about 20,000 workplaces (Wien 3420 Aspern Development AG 2016). All construction tasks in Seestadt Aspern are managed by the consortium ‘Baulogistik & Umweltmanagement Seestadt Aspern’ (BLUM), a construction logistics and environmental management agency. Together with BLUM, the assumptions and input for the case study were derived from their experiences in site logistics.

To avoid negative impacts of construction tasks on the environment, a so-called Environmental Impact Assessment (EIA) of Seestadt Aspern has been performed. As introduced by the European Commission (2017), Environmental assessment is a procedure that ensures that the environmental implications of decisions are taken into account before the decisions are made. Environmental assessment can be undertaken for individual projects, such as a dam, motorway, airport or factory, on the basis of Directive 2011/92/EU (known as EIA Directive) (EIA 2007). The principle is to ensure that plans, programs and projects likely to have significant effects on the environment are made subject to an environmental assessment, prior to their approval or authorization. As a limiting factor for negative environmental effects of construction logistics operations, the EIA of Seestadt Aspern states that a specific number of transport trips per day must not be exceeded.

Besides the reduction of traffic related to construction tasks, we aim at optimizing resource-efficiency, referring to human resources as well as time. According to Ekeskär (2016), in the construction industry, a large part of construction workers’ workdays is spent on non-value adding tasks, such as material handling and waiting (for material to be delivered, for other tasks to be finished, etc.). Less than half of the deliveries in the construction industry are delivered damage free and in the right amount, to the right location and on time (Ekeskär 2016). Coordination helps to free time of construction workers for value adding tasks, otherwise spent on material handling or waiting. Coordination of construction logistics operations leads to improvements in terms of cost reduction, improved quality, reduced lead times, increased productivity and increased sustainability (Ekeskär 2016).

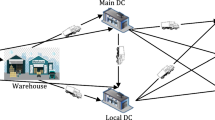
The limited number of transports that are allowed in the construction area, the problem of unproductive time of construction workers due to organizational deficiencies, and the lack of storage facilities on site are main challenges in construction logistics. While the latter two issues might provoke a higher number of transports, these are to be minimized for economic, environmental and societal issues. The number of deliveries to a construction area and disruptions due to material handling on site can be reduced by consolidating material. Deliveries of material can be bundled at a construction consolidation center (CCC) and delivered to multiple construction sites. Figure 1 shows the principles of a CCC. By minimizing transport, residents and businesses already present in the surroundings of the construction area can be protected from nuisance, emissions and shortage of space.

Fig. 1
figure 1

Principles of a construction consolidation center (CCC), adapted from Lundesjo (2015)

Full size image

The contributions of this work are threefold: (1) We introduce a Construction Logistics Optimization Problem (CLOP), which contains characteristics of project scheduling and construction scheduling problems, as well as inventory routing problems (IRPs). To the best of our knowledge, the combination of these issues has not yet been investigated. The present paper aims at filling this gap by considering the interdependence of multi-project scheduling and the related material delivery and storage decisions. By simultaneously optimizing construction schedules and transports, efficiencies in terms of time and cost, as well as related issues such as quality and environmental considerations are addressed. (2) We present a hierarchical modeling approach, which decomposes the CLOP addressed in the present paper into a tactical and an operational planning level. A time schedule of construction tasks for multiple construction sites is determined on the tactical planning level, considering material transports and storage decisions on a weekly basis. Based on this schedule, the daily material transports and storage decisions, modeled as an IRP, are optimized on the operational planning level. We provide a mixed-integer programming formulation of the problem at each level and solve it with CPLEX. (3) The suggested approach is tested on realistic data from the city of Vienna and the results associated with different scenarios are analyzed to illustrate the value of the proposed approach for the design of construction logistics processes.

The remainder of the article is organized as follows. Section 2 reviews relevant literature related to the tactical and the operational planning levels. In Sect. 3 the problem is described in detail and mathematical formulations are provided. Experimental results for a real-world case study are presented in Sect. 4 to show the effectiveness of construction logistics planning. Concluding remarks and managerial implications are provided in Sect. 5.

2 Related literature

This section presents a review of construction optimization, starting with project scheduling in general, followed by construction scheduling problems, and then exploring inventory routing problems for construction-related transport. Finally, the contribution of the present paper beyond the state-of-the-art is presented.

2.1 Project scheduling problems

A project can be defined as a series of tasks, whose executions take time, require resources, and incur costs. Precedence relations may exist between tasks referring to technical or organizational requirements with respect to the order or the timing of the tasks relative to each other. The resources allocated to a project are generally scarce and the time for completion of a project is limited, i.e. has a deadline. Project scheduling means the selection of execution modes and determination of execution time intervals for the tasks of a project. According to the type of constraints taken into account when scheduling a project, time-constrained and resource-constrained project scheduling problems can be distinguished. In time-constrained problems tasks are to be scheduled subject to precedence relations, where the required resources can be provided in the required amount, possibly with higher execution cost. In resource-constrained problems, limited resources have to be taken into account. Time-constrained problems may also include a resource allocation problem, where resources have to be assigned to tasks over time (Demeulemeester and Herroelen 2002; Schwindt and Zimmermann 2015).

Artigues et al. (2015) present (mixed-)integer linear programming formulations for the resource-constrained project scheduling problem. The different formulations are divided into three categories: (i) time-indexed formulations, in which time-indexed binary variables encode the status of a task at the respective point in time (e.g. Kolisch 2000a, b; Kolisch and Hess 2000; Pritsker et al. 1969), (ii) sequencing formulations including two types of variables, continuous natural-date variables representing the start time of the tasks and binary sequencing variables used to model decisions with respect to the ordering of tasks that compete for the same resources (e.g. Olaguibel and Goerlich 1993), (iii) event-based formulations, containing binary assignment and continuous positional-date variables (e.g. Koné et al. 2011).

Decision makers regularly face a time-cost problem (Doerner et al. 2008): carrying out a project on time necessitates crashing certain tasks by exploiting extra resources, which increases the cost of a project. Doerner et al. (2008) develop and evaluate three metaheuristic solution procedures for multi-objective activity crashing. These procedures provide decision support for the selection of appropriate tasks and crashing measures under time and cost considerations. Dodin and Elimam (2001) focus on integrated project scheduling and material ordering. They allow job crashing by treating the task duration as a decision variable and consider rewards (penalties) for project termination ahead of (after) the due date. The authors show that an optimal schedule either starts as early as possible or completes as late as possible and that in case of no rewards (penalties), an optimal solution is obtained by scheduling every job at its latest start time.

Zhang et al. (2006) propose a heuristic algorithm investigating possible combinations of tasks, simultaneously scheduling all tasks in the selected combination to minimize project duration. Kolisch and Padman (2001) investigate the literature focusing on project scheduling problems considering models, data, as well as optimal and heuristic algorithms.

2.2 Construction scheduling problems

Construction scheduling problems are concerned with optimally scheduling tasks over time and allocating resources accordingly for successful completion of construction projects. Construction scheduling problems have been investigated including various features over the last 20 years. Given precedence and/or resource constraints, the aim of construction scheduling optimization is to find a feasible schedule of tasks (with respect to the constraints) with minimum or maximum objective function value, e.g. shortest project duration or lowest cost (Zhou et al. 2013). In construction scheduling problems a trade-off between cost and time exists. The duration of a construction project can be crashed by allocating additional resources, which leads to an increase in direct cost (e.g. material and labor), but a reduction in indirect cost (e.g. project overhead) (Ng and Zhang 2008). Yang (2005) present a piecewise linear time-cost tradeoff analysis under budget uncertainty. The authors show that the time-cost tradeoff problem is of practical interest when a planner has to crash tasks to meet a predefined deadline. A time-cost tradeoff can be beneficial in order to evaluate whether a crash is worth an additional cost or whether some tasks should be lengthened, whereas the extended project duration is still acceptable and the project cost is reduced.

Several articles address the coordination of assembly planning and manufacturing planning, with relevance for construction scheduling. Kolisch (2000a) consider the problem of scheduling multiple, large scale, make-to-order assemblies. In this paper, spatial resource and part availability constraints are taken into account in addition to classical precedence and resource constraints. The objective of the assembly scheduling problem is to place orders on assembly areas, assign parts to operations and schedule operations. The authors do not explicitly assign resources, parts and assembly areas, but they schedule operations subject to aggregated availabilities of resources, assembly area and parts. They present a model with two types of decision variables (indicating when an operation is started and the time span of tardiness of an order, respectively). The authors show how their assembly scheduling problem can be transformed into the resource allocation problem, the assembly area location problem, and the part allocation problem. A list scheduling heuristic is developed to solve the problem and several priority rules are evaluated. Based on that paper, Kolisch and Hess (2000) introduce three efficient heuristic solution methods, a biased random sampling method and two tabu search-based optimization methods with different neighborhoods. Kolisch (2000b) considers make-to-order production in a multi-project environment, where an order consists of jobs interrelated by precedence constraints. Assembly jobs are scheduled and fabrication lotsizes are determined with the objective of providing a production plan which is feasible with respect to time and resources, while minimizing holding and setup cost.

Schultmann and Rentz (2001, 2002) use project scheduling methods for deconstruction projects under resource constraints. Material-flow management for closed-loop recycling of construction materials is addressed and a multi-mode resource-constrained project scheduling model is optimized. The authors investigate different dismantling strategies and evaluate three scenarios compared to the present situation in practice. In addition the effects of a limited net site area for storage and machines in urban dismantling projects are illustrated. Li and Love (1997) focus on the minimization of project cost and duration in a single-objective problem formulation. Said and El-Rayes (2014) provide an optimization framework for material supply and storage management at construction sites. The authors focus on a multi-objective construction logistics optimization problem, minimizing logistics cost and schedule criticality. Caron et al. (1998) develop a stochastic model to plan material delivery to a construction site, enabling a continuous construction process. Zhou et al. (2013) present a recent review of methods and algorithms for optimizing construction scheduling.

2.3 Inventory routing problems

The inventory routing problem (IRP), first addressed by Bell et al. (1983) is a variation of the classical vehicle routing problem (VRP) since it integrates inventory management, vehicle routing and delivery-scheduling decisions (Coelho et al. 2013). Federgruen and Zipkin (1984) show the positive economic effects of the coordination of distribution and inventory decisions. As opposed to individual orders of material in VRPs, the quantity and timing of deliveries are coordinated and determined by the supplier in IRPs (Moin and Salhi 2007). The supplier has to manage product inventory at customers to ensure that customers do not experience a stock-out, while minimizing costs for the distance traveled and inventory holding costs, and respecting limited inventory holding capacity.

Bertazzi et al. (2008) present an overview of IRPs, regarding different formulations and several extensions. IRPs can differ with respect to the planning horizon, which can be finite or infinite. Another characteristic of IRPs are production and consumption rates, which can either be modeled in a deterministic or a stochastic way, can be constant over time or vary over time and can take place at discrete time periods or constantly. Further, inventory holding costs can be incorporated at the supplier or at the customer, apply to both actors or to none. Another characteristic of IRPs concerns the vehicle fleet, which can be homogeneous or heterogeneous and the fleet size can be one, many or unconstrained. Finally, different inventory replenishment policies can be specified (Bertazzi et al. 2008). Under a maximum level policy, for example, the replenishment level is flexible but restricted by the maximum capacity available at each customer, while under an order-up-to-level policy, a customer is delivered up to the maximum inventory capacity whenever visited (Coelho et al. 2013).

Due to its complexity, only few exact algorithms have been developed for the IRP, among those the first branch-and-cut algorithm for a single-vehicle IRP by Archetti et al. (2007). The authors investigated three replenishment policies and used different inequalities to strengthen the formulation for each policy. A multi-vehicle formulation was proposed and solved with branch-and-cut by Coelho et al. (2013). The three-indexed model was compared to a two-index formulation without vehicle index (Adulyasak et al. 2014). Since the number of variables grows with the number of vehicles, routing constraints were replaced by variables without a vehicle index. The authors propose several sets of valid inequalities to strengthen the proposed vehicle index and non-vehicle index formulations, as well as branch-and-cut approaches for subtour elimination.

Federgruen and Simchi-Levi (1995) provide a mathematical formulation of the single-depot single-period IRP. Campbell and Hardin (2005) consider the problem of minimizing the number of vehicles for periodic deliveries, which is motivated by IRPs considering customer demands at a steady rate. Yu et al. (2008) study an IRP with split deliveries, allowing the delivery to each customer in each period to be performed by multiple vehicles. Solyalı et al. (2012) present a robust IRP with uncertain demands. The authors determine the delivery quantities and delivery times, as well as the vehicle routes and they allow backlogging of demand at customers. Campbell et al. (1998) study the IRP as well as the stochastic IRP, where the future demand of a customer is uncertain. The authors introduce a dynamic programming model, considering only transportation and stockout costs, neglecting inventory holding costs.

In many articles, metaheuristics such as adaptive large neighborhood search, variable neighborhood search and genetic algorithms are applied to obtain potentially optimal solutions within reasonable time (Coelho et al. 2012; Hemmelmayr et al. 2010; Nolz et al. 2014). For a recent survey on 30 years of inventory routing, the interested reader is referred to Coelho et al. (2013).

2.4 Contribution beyond state-of-the-art

In the present paper, the following modeling concepts for construction project scheduling on the tactical planning level are applied. We consider (binary) on/off variables from time-indexed formulations, set to 1 if task i is in progress at time t, and 0 otherwise. In addition, we introduce variables indicating the start time of task i. Since the acceleration of a task requires additional resources and, hence, contributes to a higher cost, different decisions as to how the various tasks are performed result in different time-cost realizations for the overall project. In the present paper, a (piecewise) linear time-cost tradeoff is used to identify the sets of decisions that lead to desirable project duration and cost. In order to minimize construction-related transport, the delivery of material from a construction consolidation center to multiple construction sites over a given time horizon, is modeled as an IRP on the operational planning level. We consider a maximum level inventory replenishment policy for deliveries performed with a homogeneous fleet of vehicles.

Table 1 Related literature
Full size table

Table 1 gives an overview of the features provided in the literature as compared to the present paper. It can be seen in which aspects the present paper differs from and extends the literature. Articles are presented in the lines, while the features can be seen in the rows. The combination of project scheduling, inventory management and vehicle routing is treated for the first time in the present paper, which provides a valuable contribution beyond the state-of-the-art.

As Drexl and Kimms (1997) already stated more than twenty years ago, apparently, lot sizing and scheduling interacts with other planning tasks in a firm, e.g. distribution planning, cutting and packing, and project scheduling. The authors claim the coordination of these planning tasks as essential to avoid high transaction costs in the presence of competition, and thus as the most crucial goal for future work. Consequently, in the present paper the hierarchical problem formulation of the tactical and the operational planning problems, where project scheduling and coordinated inventory and routing decisions are made, is addressed.

3 Problem description

We present a hierarchical problem formulation for construction schedules and material transports of multiple construction sites. The first level focuses on tactical construction logistics planning, and the second level focuses on operational construction logistics planning. In order to enable flexibility and reactivity in decision-making, the two levels are solved consecutively, where decisions on the tactical level are taken as constraints for the operational level.

The tactical planning level addresses the entire construction project and focuses on optimizing construction logistics processes a priori. Operational planning is carried out on a bi-weekly rolling horizon (cf. Baker 1997), which means that the operational planning problem is repeatedly solved in a cycle of two weeks. Therefore, the whole time horizon is divided into periods of one week and an iterative procedure is started. The operational planning problem for the coming two weeks is solved but only the schedule for the first week is fixed. Information updates on material availability are incorporated and deliveries can be adapted within the operational planning horizon of 2 weeks. Unforeseen events might occur when construction works are already ongoing reflecting different sources of supply chain uncertainty (e.g. material which is not delivered in the right quantity, at the right time, or at the right place). Therefore, the operational level is dynamically adjusted to handle changes in the a priori plan given by the tactical planning. In this way, project risk and quality are considered, next to the minimization of project duration and cost.

The rolling horizon proceeds in this manner, as illustrated in Fig. 2. This on the one hand allows to incorporate accurate information available at the operational level each week. On the other hand it enables to look ahead and optimize transport and storage decisions. The hierarchical model represents a guideline for the operational planning given by the tactical planning.

Fig. 2
figure 2

Rolling horizon planning procedure

Full size image

3.1 Tactical planning level

The objective of the tactical Construction Logistics Optimization Problem (CLOP) is to determine a schedule for the construction tasks at each construction site within the time horizon and a schedule for transports of construction material to the construction sites, while minimizing total cost. The cost include personnel cost comprising acceleration cost for deploying an additional number of workers to perform construction tasks, penalty cost associated with a milestone delay, and storage cost.

Four decisions have to be made: (1) when to start a construction task, (2) how fast to perform a construction task, (3) when to transport material to each construction site, (4) how much material to transport to each construction site, to minimize total cost. While (1) and (2) are standard decisions known from project scheduling, the planning of transports is a novel contribution of this work.

Table 2 Notation for tactical CLOP
Full size table

Table 2 introduces the notation for the tactical CLOP under investigation.

Each building (i.e. construction site) is constructed by performing a set of typical construction tasks, grouped in different construction phases. Let \({\mathcal {G}} = \left( {\mathcal {V}}, {\mathcal {E}}\right)\) be a complete graph, where \({\mathcal {V}} = \left\{ 0, \ldots , N\right\}\) is the vertex set and \({\mathcal {E}}\) is the edge set. Material is located at a construction consolidation center (CCC) outside the construction area, from where it is transported to the different construction sites. Vertex 0 represents the CCC and vertices \(i = 1, \ldots , N\) represent the set of construction sites.

An earliest start date for constructing each building is specified, as well as a set of milestones indicating the completion time limit for each construction phase. We express by \(t = 1, \ldots , T\) the discrete time periods partitioning the time horizon, by \(u = 1, \ldots , U\) the construction phases, and by \(p = 1, \ldots , P\) the different construction tasks. We denote by \(ES_{ip}\) the earliest start time of task p at construction site i. The variable \(e_{ipt}\) is 1 if task p starts at time t at construction site i, 0 otherwise. Variable \(s_{ip}\) is the start time of task p at construction site i.

Variable \(r_{ipt}\) takes the value 1 if task p is active at construction site i at time t, 0 otherwise. The variable \(g_{ipt}\) determines whether active task p is in process using resources at construction site i at time t. We denote by \(w_{ip}\) the passive processing time, if active task p is in process but not using resources, e.g. for material to dry out. Passive processing time therefore captures the time required to finish a task before the next task can be started, also known as minimal time lag (e.g. in Bartusch et al. 1988; Schwindt 1999).

The milestone of phase u at construction site i is expressed by \(D_{iu}\). We denote by \({\mathcal {P}}_{u}\) the set of construction tasks belonging to construction phase u and by \({\mathcal {Q}}_{p}\) the set of predecessor tasks of task p. Precedence relations are specified for tasks, as shown in the activity-on-node network in Fig. 3.

Fig. 3
figure 3

Activity-on-node network, showing precedence relations and parallel tasks

Full size image

The activity-on-node network indicates tasks which can be performed in parallel. Tasks potentially concluding a construction phase coinciding with a milestone are marked in red / light. Please note, that dummy nodes indicating project start and project end have been omitted in this illustration.

For each task, the minimal, normal, and maximal duration are defined, reached by deploying the maximal, normal, and minimal number of workers, respectively. The normal duration of task p performed at construction site i is expressed by \(\bar{l}_{ip}\), while \(l_{ip}\) gives the actual duration of task p at construction site i.

The duration of a task can be reduced by allocating more resources (deploying an additional number of workers) at certain cost (also known as ‘crash cost: Doerner et al. 2008; Zhou et al. 2013). Not all tasks are eligible to be accelerated, therefore \({\mathcal {A}}\) defines the set of tasks which can be accelerated. \(c^{\mathrm {Pers}}\) are the personnel cost per person for performing a task per time period. We denote by \(F_{ip}\) the personnel factor for task p at construction site i per time period. The personnel factor \(F_{ip}\) equals the number of workers that are required during the execution of task p at site i when the task is performed with normal duration \(\bar{l}_{ip}\), where \(\bar{l}_{ip} \ F_{ip}\) is the regular workload of the task. Augmenting the duration of a task at no cost is also possible (e.g. in order to avoid exceeding the maximum number of allowed transports because of material requirements).

Deceleration does not imply any direct cost, but could lead to additional cost because of milestone delays or material storage. The delay of completion of phase u at construction site i is given by \(k_{iu}\), and the penalty cost per time period of a milestone delay at construction site i are given by \(c_{iu}^{\mathrm {Del}}\).

The speed factor of task p at construction site i is expressed by \(a_{ip}\) and the personnel cost factor for acceleration of task p at construction site i is expressed by \(f_{ip}\):

$$\begin{aligned} \begin{aligned} f_{ip} = {\left\{ \begin{array}{ll} 1 &\quad \text {if} \ a_{ip} \ge 1\\ 2 - a_{ip} &\quad \text {otherwise}, \end{array}\right. } \end{aligned} \end{aligned}$$

where the speed factor \(a_{ip}\) can take a continuous value between 0.5 and 2.

Based on discussions with practitioners, i.e. BLUM, we assume that a task cannot be performed twice as fast as normal, if twice the number of workers as normal are deployed. This is due to the fact that a larger number of workers are hindered from working efficiently, since space at the construction site is limited.

By deploying additional personnel, the duration of task p can be reduced, as illustrated in the following example. The normal duration of task p at construction site i is 4 weeks and the required number of workers is 10, requiring 40 person weeks in total. Then, if the duration is increased to 8 weeks with a speed factor \(a_{ip}\) of 2, the required number of workers is 5, again requiring 40 person weeks in total, since the personnel cost factor \(f_{ip}\) is 1. If the duration is decreased to 2 weeks with a speed factor \(a_{ip}\) of 0.5, the required number of workers is 30 (60 person weeks in total), since the personnel cost factor \(f_{ip}\) is 1.5.

The variable \(y_{ipt}\) gives the amount of material for task p delivered to construction site i at time t. We express the maximum vehicle capacity per transport for task p with \(V_{p}\). For storage purposes, material might be stored in compliance with the construction phase directly inside the constructed buildings. However, for example during the flooring of floating screed, no material can be stored and therefore the storage capacity during the required time interval is set to zero. The set of tasks during which storage is not possible is expressed by \({\mathcal {H}}\). Variable \(h_{it}\) indicates if storage at construction site i is possible at time t.

Variable \(q_{ipt}\) is the amount of material for task p required at construction site i at time t. The amount of material for task p at construction site i is given by \(m_{ip}\). The inventory of material for task p at construction site i at time t is expressed by \(I_{ipt}\). The maximum storage capacity at construction site i is given by \(S_{i}\). Storing material inside the constructed buildings implies cost, since the material might cause inconvenience to the workers at the construction sites. Therefore, \(c^{\mathrm {Stor}}\) are the storage cost per unit stored per time period. A maximal number of transports \(R^{tact}\) allowed to enter and leave the construction area is given for each time period. We therefore face a trade-off between the restriction of transports to be carried out, the amount of material to be stored at the construction sites and the number of workers deployed at the same time to perform a task.

In the following, we provide a mixed-integer programming formulation of the tactical CLOP.

$$\begin{aligned} \min \sum _{i=1}^{N} \sum _{p=1}^{P} c^{\text {Pers}} \ \bar{l}_{ip} \ F_{ip} \ f_{ip} + \sum _{i=1}^{N} \sum _{u=1}^{U} c_{iu}^{\text {Del}} \ k_{iu} + \sum _{i=1}^{N} \sum _{p=1}^{P} \sum _{t=1}^{T} c^{\text {Stor}} \ I_{ipt} \end{aligned}$$
(1)

subject to

$$\begin{aligned}s_{ip} = \sum _{t=1}^{T} t \ e_{ipt}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(2)
$$\begin{aligned}&l_{ip} = a_{ip} \ \bar{l}_{ip}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(3)
$$\begin{aligned}&s_{ij} \ge s_{ip} + l_{ip} + w_{ip}&\forall \ i = 1, \ldots , N, \ j = 1, \ldots , P, \ p \in {\mathcal {Q}}_{j} \end{aligned}$$
(4)
$$\begin{aligned}&s_{ip} \ge ES_{ip}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(5)
$$\begin{aligned}&f_{ip} \ge 2 - a_{ip}&\forall \ i = 1, \ldots , N, \ p \in A \end{aligned}$$
(6)
$$\begin{aligned}&I_{ip0} = 0&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P\end{aligned}$$
(7)
$$\begin{aligned}&I_{ipt} = I_{ip,t-1} + y_{ipt} - q_{ipt}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(8)
$$\begin{aligned}&s_{ip} \le r_{ipt} \ t + M \ (1-r_{ipt})&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(9)
$$\begin{aligned}&r_{ipt} \ t \le s_{ip} + l_{ip} + w_{ip} - 1&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(10)
$$\begin{aligned}&\sum _{t=1}^{T} r_{ipt} = l_{ip} + w_{ip}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(11)
$$\begin{aligned}&h_{it} \le 1 - r_{ipt}&\forall \ i = 1, \ldots , N, \ p \in {\mathcal {H}}, \ t = 1, \ldots , T \end{aligned}$$
(12)
$$\begin{aligned}&h_{it} \ge 1 - \sum _{p \in {\mathcal {H}}} r_{ipt}&\forall \ i = 1, \ldots , N, \ t = 1, \ldots , T \end{aligned}$$
(13)
$$\begin{aligned}&\sum _{p=1}^{P} I_{ipt} \le S_{i} \ h_{it}&\forall \ i = 1, \ldots , N, \ t = 1, \ldots , T \end{aligned}$$
(14)
$$\begin{aligned}&s_{ip} \le g_{ipt} \ t + M \ (1-g_{ipt})&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(15)
$$\begin{aligned}&g_{ipt} \ t \le s_{ip} + l_{ip} - 1&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(16)
$$\begin{aligned}&l_{ip} = \sum _{t=1}^{T} g_{ipt}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(17)
$$\begin{aligned}&q_{ipt} \le g_{ipt} \ \frac{2 m_{ip}}{\bar{l}_{ip}}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(18)
$$\begin{aligned}&q_{ipt} \ge g_{ipt} \ \frac{m_{ip}}{2 \ \bar{l}_{ip}}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(19)
$$\begin{aligned}q_{ip,t+1}\ \ge \ q_{ipt} - M \ (1 - g_{ip,t+1}) &\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T-1 \end{aligned}$$
(20)
$$\begin{aligned}&q_{ipt}\ \ge \ q_{ip,t+1} - M \ (1 - g_{ipt}) &\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T-1 \end{aligned}$$
(21)
$$\begin{aligned}&\sum _{t=1}^{T} q_{ipt} \ = \ m_{ip}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(22)
$$\begin{aligned}&R^{tact} \ge \sum _{i=1}^{N} \sum _{p=1}^{P} \frac{y_{ipt}}{V_{p}}&\forall \ t = 1, \ldots , T \end{aligned}$$
(23)
$$\begin{aligned}&D_{iu} + k_{iu} \ge s_{ip} + l_{ip} + w_{ip}&\forall \ i = 1, \ldots , N, \ u = 1, \ldots , U, \ p \in {\mathcal {P}}_{u} \end{aligned}$$
(24)
$$\begin{aligned}&k_{iu} \ge 0&\forall \ i = 1, \ldots , N, \ u = 1, \ldots , U \end{aligned}$$
(25)
$$\begin{aligned}&s_{ip}, \ l_{ip} \ge 0&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(26)
$$\begin{aligned}&0 \le I_{ipt}, \ y_{ipt}, \ q_{ipt}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(27)
$$\begin{aligned}&0.5 \le a_{ip} \le 2.0&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(28)
$$\begin{aligned}&1.0 \le f_{ip} \le 1.5&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(29)
$$\begin{aligned}&e_{ipt}, \ r_{ipt}, \ g_{ipt} \in {\{0,1\}}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(30)
$$\begin{aligned}&h_{it} \in {\{0,1\}}&\forall \ i = 1, \ldots , N, \ t = 1, \ldots , T \end{aligned}$$
(31)

The objective function of the tactical problem is given by Eq.  (1), representing the sum of personnel cost, penalty cost for milestone delays, and storage cost at construction sites. Personnel cost are determined by the personnel factor under normal duration of a task adapted with the personnel cost factor for acceleration of that task. Penalty cost incur for every time period exceeding the due date of completion of a milestone (i.e. construction phase). Storage cost are calculated per time period of storage of a material at a construction site.

Constraints (2) to (6) are concerned with the schedule and duration of construction tasks. Constraints (2) define the start time of task p at construction site i. Constraints (3) determine the actual duration of task p as the normal duration altered by a speed factor. Constraints (4) guarantee the sequence and potentially necessary passive processing time between predecessor and successor tasks. Task p cannot start before its earliest start time, cf. Constraints (5). Constraints (6) determine the personnel cost factor of task p at construction site i.

Constraints (7) to (22) are concerned with the inventory and completion of construction projects. The inventory level of material for task p at construction site i at the end of period t arises from all deliveries and requirements occurring by time t (Constraints 7 and 8).

Constraints (9) to (11) determine if task p is active at construction site i at time t including passive processing time \(w_{ip}\). The inventory at construction site i must not exceed the maximum storage capacity, if storage is allowed, cf. Constraints (12) to (14). Constraints (15) to (17) determine if task p is in process using resources at construction site i at time t. Constraints (18) to (22) determine the amount of material for task p required at construction site i at time t. Constraints (18) determine the maximal amount of material required for task p at construction site i at time t in case of acceleration. Since the duration of task p can maximally be shortened to half of the normal duration, in Constraints (18) twice the amount of material required for task p is split over the normal duration. For a deceleration of task p to maximally twice the normal duration, the amount of material is divided by twice the normal duration, cf. Constraints (19). Constraints (20) and (21) evenly distribute the amount of material required for task p at construction site i over the time horizon when task p is in process.

Constraints (23) restrict the maximum number of transports per time period. These constraints are inflicted by the EIA, as an obligatory measure against negative environmental impacts of construction tasks. The EIA is performed for large construction projects, such as Seestadt Aspern, and concerns the global construction processes, comprising several building sites. Because of this practically highly relevant restriction, a decomposition of the global problem into several sub problems, addressing each construction site individually, is not possible.

Constraints (24) determine the completion time of phase u. Finally, Constraints (25) to (31) define the ranges of the variables of the problem.

On the tactical level, the model contains \(N(4P+U+3PT) = O(NPT)\) continuous variables, \(N(3PT + T) = O(NPT)\) binary variables and \(7NP + NP\vert Q\vert + N\vert A\vert + 9 NPT + N\vert H\vert T + 2NT + T + NU\vert {\mathcal {P}}\vert = O(NPT+NP^2)\) constraints.

3.2 Operational planning level

The operational CLOP can be described as follows. We aim at determining a set of vehicle routes for the distribution of construction material to construction sites, while minimizing total cost, including transportation cost and storage cost. Three decisions have to be made: (1) when to deliver to each construction site, (2) how much material to deliver to each construction site each time it is served, (3) how to route the vehicles, to minimize total cost.

Table 3 introduces the notation for the operational CLOP under investigation.

Table 3 Notation for operational CLOP
Full size table

Let \({\mathcal {G}} = \left( {\mathcal {V}}, {\mathcal {E}}\right)\) be a complete graph, where \({\mathcal {V}} = \left\{ 0, \ldots , N\right\}\) is the vertex set and \({\mathcal {E}}\) is the edge set. A distance or travel time matrix satisfying the triangle inequality is defined on \({\mathcal {E}}\). We denote by \(c_{ij}^{\mathrm {Trans}}\) the transportation cost between vertices i and j, based on distance or travel time.

We express by \(t = 1, \ldots , T\) the discrete time periods defining the rolling time horizon of the operational level and by \(\tilde{t} = 1, \ldots , T^{tact}\) the discrete time periods from the tactical level.

The following input is transferred from the tactical planning level (variables) to the operational planning level (parameters):

  • \(y_{ip\tilde{t}}\) is the amount of material for task p delivered to construction site i at time \(\tilde{t}\), as determined on the tactical level

  • \(q_{ipt}\) specifies the amount of material for task p required at construction site i at time t, derived from the tactical level per discrete time period \(\tilde{t}\) and equally apportioned among each operational time period t

  • \(h_{it}\) indicates whether storage at construction site i is possible at time t as part of the discrete time periods \(\tilde{t}\) from the tactical level

Vertices \(i = 1, \ldots , N\) represent the set of construction sites, where material for construction processes is delivered. A set of vehicles is located at the CCC, represented by vertex 0. The vehicle capacity for task p is given by \(B_{p}\) and \(K_{pt}\) states the amount of material for task p available at the CCC at time t. The variable \(x_{ijpt}\) indicates whether a vehicle goes from construction site i to j for task p at time t. The variable \(z_{ipt}\) is 1 if construction site i is visited for task p at time t, 0 otherwise. Variable \(d_{ipt}\) determines the amount of material for task p delivered to construction site i at time t on the operational level and \(b_{ipt}\) gives the number of back and forth trips to construction site i at time t delivering material for task p. Back and forth trips are performed if full truck loads of material are brought to a construction site. Less-than-truckload shipments are performed to bundle material for different construction sites to reduce cost and optimally use capacities. The vehicle load of material for task p after leaving construction site i at time t is expressed by \(v_{ipt}\).

The storage cost at construction site i per unit of material stored per time period are given by \(c^{\mathrm {Stor}}\). The maximum storage capacity at construction site i at time t is expressed by \(S_{it}\). The initial inventory for task p at construction site i is given by \(I_{ip0}\) and \(I_{ipt}\) determines the inventory for task p at construction site i at time t on the operational level.

With \(R^{oper}\), we denote the maximum number of vehicle routes allowed per time period.

In the following, we provide a mixed-integer programming formulation of the operational CLOP.

$$\begin{aligned} \min \sum _{i=0}^{N} \sum _{j=0}^{N} \sum _{p=1}^{P} \sum _{t=1}^{T} c_{ij}^{\mathrm {Trans}} x_{ijpt} + \sum _{i=1}^{N} \sum _{p=1}^{P} \sum _{t=1}^{T} (c_{0i}^{\text {Trans}} +c_{i0}^{\text {Trans}}) b_{ipt} + \sum _{i=1}^{N} \sum _{p=1}^{P} \sum _{t=1}^{T} c^{\text {Stor}} I_{ipt} \end{aligned}$$
(32)

subject to

$$\begin{aligned}&R^{oper} \ge \sum _{j=1}^{N} \sum _{p=1}^{P} x_{0jpt} + \sum _{i=1}^{N} \sum _{p=1}^{P} b_{ipt}&\forall \ t = 1, \ldots , T \end{aligned}$$
(33)
$$\begin{aligned}&\sum _{i=0,\ i \ne j}^{N} x_{ijpt} \le 1&\forall j = 1, \ldots , N, \ p = 1, \ldots , P,\,t = 1, \ldots , T \end{aligned}$$
(34)
$$\begin{aligned}&\sum _{j=0,\ i \ne j}^{N} x_{ijpt} \le 1&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P,\,t = 1, \ldots , T \end{aligned}$$
(35)
$$\begin{aligned}&\sum _{i=0,\ i \ne j}^{N} x_{ijpt} = \sum _{i=0,\ i \ne j}^{N} x_{jipt}&\forall \ j = 0, \ldots , N, \ p = 1, \ldots , P,\,t = 1, \ldots , T \end{aligned}$$
(36)
$$\begin{aligned}&z_{jpt} \le \sum _{i=0,\ i \ne j}^{N} x_{ijpt} + b_{jpt}&\forall j = 1, \ldots , N, \ p = 1, \ldots , P,\,t = 1, \ldots , T \end{aligned}$$
(37)
$$\begin{aligned}&d_{ipt} \le M \ z_{ipt}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P,\, t = 1, \ldots , T \end{aligned}$$
(38)
$$\begin{aligned}&d_{ipt} \ge B_{p} \ b_{ipt}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P,\,t = 1, \ldots , T \end{aligned}$$
(39)
$$\begin{aligned} &d_{ipt} \le B_{p} \ \left( \sum _{j=0}^{N} x_{jipt} + b_{ipt}\right)&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P,\,t = 1, \ldots , T \end{aligned}$$
(40)
$$\begin{aligned}&v_{jpt} \le v_{ipt} - d_{jpt} + B_{p} \ b_{jpt}+ (1-x_{ijpt}) M&\forall \ i = 0, \ldots , N, \ j = 1, \ldots , N, p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(41)
$$\begin{aligned}&v_{ipt} \le B_{p}&\forall \ i = 0, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(42)
$$\begin{aligned}&I_{ipt} = I_{ip0} + \sum _{s=1}^{t} d_{ips} - \sum _{s=1}^{t} q_{ips}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P,\,t = 1, \ldots , T \end{aligned}$$
(43)
$$\begin{aligned}&q_{ipt} \le I_{ip0} + \sum _{s=1}^{t} d_{ips} - \sum _{s=1}^{t-1} q_{ips}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P,\,t = 1, \ldots , T \end{aligned}$$
(44)
$$\begin{aligned}&\sum _{p=1}^{P} I_{ipt} \le S_{i} h_{it}&\forall \ i = 1, \ldots , N, \ t = 1, \ldots , T \end{aligned}$$
(45)
$$\begin{aligned}&\sum _{t=1}^{T} d_{ipt} = \sum _{\tilde{t}=1}^{T^{tact}} y_{ip\tilde{t}}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P \end{aligned}$$
(46)
$$\begin{aligned}&\sum _{i=1}^{N} d_{ipt} \le K_{pt}&\forall \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(47)
$$\begin{aligned}&x_{ijpt} \in {\{0,1\}}&\forall \ i,j = 0, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(48)
$$\begin{aligned}&z_{ipt} \in {\{0,1\}}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(49)
$$\begin{aligned}&v_{ipt} \ge 0&\forall \ i = 0, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(50)
$$\begin{aligned}&d_{ipt}, \ I_{ipt} \ge 0&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(51)
$$\begin{aligned}&b_{ipt} \in {\mathbb {N}}&\forall \ i = 1, \ldots , N, \ p = 1, \ldots , P, \ t = 1, \ldots , T \end{aligned}$$
(52)

The objective function of the operational problem is given by Eq. (32), representing the sum of transportation cost for delivery tours as well as back and forth trips, and storage cost at construction sites.

Constraints (33) state that no more than the maximum number of vehicle routes allowed per time period can be performed by delivery tours and back and forth trips. Constraints (34) and (35) make sure that each construction site is only supplied once per task per time period. Constraints (37) determine whether a construction site is visited to deliver material for task p at time t. Constraints (36) guarantee flow conservation. Material for task p can only be delivered to construction site i, when i is visited at time t, cf. Constraints (38). Constraints (39) and (40) define the amount of material for task p delivered to construction site i at time t. While Constraints (39) determine the lower bound of material deliveries by the number of back and forth trips, Constraints (40) determine the upper bound by the sum of back and forth trips plus delivery tours. Constraints (41) balance the continuous decrease of the load of each vehicle along a delivery tour. Through these constraints, subtours are eliminated as well. Constraints (42) are vehicle capacity restrictions. Constraints (43) define the level of inventory at construction site i at time t. Constraints (44) determine the amount of material for task p delivered to construction site i at time t. The inventory at construction site i at time t must never exceed the maximum storable inventory, cf. Constraints (45). If \(h_{i}^{t}\) is 0, storage is not allowed. Constraints (46) transfer the amount of material delivered for task p at construction site i at time t from the tactical to the operational planning phase. Constraints (47) state that the amount of material delivered for task p to construction site i at time t is limited by the amount of material for task p available at the CCC at time t. Finally, Constraints (48) to (52) define the variables of the problem.

On the operational level, the model contains \(3NPT = O(NPT)\) continuous variables, \(NPT = O(NPT)\) integer variables, \(PT(N^2 + N) = O(N^2PT)\) binary variables and \(T + 9NPT + N^2PT + 2NP + NT + PT = O(N^2PT)\) constraints.

4 Case study

We focus on the development phase of 2017 to 2023 in the northern area of Seestadt Aspern. All assumptions are based on data gathered for the first development phase in the southern area of Seestadt Aspern, investigative interviews and consultation with BLUM, and extensive literature research.

4.1 Test scenarios

The hierarchical Construction Logistics Optimization Problem (CLOP) requires data-intensive input with respect to the envisaged construction projects. This data is usually derived via Building Information Modeling (BIM). BIM simulates the construction project in a virtual environment. A building information model characterizes the geometry, spatial relationships, geographic information, quantities and properties of building elements, cost estimates, material inventories, and project schedules Azhar (2011).

We created realistic test scenarios from Seestadt Aspern, comprising 5 construction projects of different sizes (between 4000 and 18,000 m2 gross floor space), as indicated in Fig. 4. Buildings 1 and 2 are residential houses with a gross floor area of 8000 m2, buildings 3 and 4 are commercial types and offices with a gross floor area of 18,000 m2, and building 5 is residential with a gross floor area of 4000 m2. The base setting serves as a starting point for 8 further scenarios, which are described in Table 4.

Fig. 4
figure 4

Test instance representing 5 construction sites in Seestadt Aspern, , adapted from Wien 3420 (2016)

Full size image
Table 4 Scenario description
Full size table

An earliest start date and a latest completion date for each building are specified, as well as a set of milestones indicating the completion time limit for a construction phase. Each building is constructed by performing a set of 10 typical construction tasks, grouped in different construction phases. Personnel cost specify the cost of a worker with average skills per week. Storage cost indicate the inconvenience cost to store an item for a specific task at a construction site per week. Penalty cost incur for each week exceeding a milestone.

Material is located at a construction consolidation center (CCC) outside the construction area. For storage purposes, a very limited area of each building can be used if adequate in the current construction phase. For example during the flooring of floating screed, all storage material has to be removed and the storage capacity during the required time intervals is set to zero. We do not consider any storage capacity during preliminary building works, since in this phase we only start constructing the buildings, so no storage area is available. Vehicles transport material from the CCC to construction sites, where a maximum number of 700 transports entering and leaving the construction area is specified for each week. The number of planning periods in the tactical planning level are 71 weeks.

Table 5 Number of variables and constraints
Full size table

Table 5 indicates the number of binary (bin.), integer (int.), continuous (cont.) variables (v.) and the number of constraints of each of the scenarios, resulting from the tactical and the operational model.

We perform sensitivity analysis on parameters influencing the cost and characteristics of the computed solutions with an important impact on decision making. Table 4 depicts the variations on these parameters in different scenarios. The Base scenario contains the basic setting of cost without specific features. The variation in cost factors (personnel cost, storage cost, penalty cost) reflects the trade-off between time and cost in construction logistics planning and is investigated in scenarios CS1 and CS2. The impact of restrictive and loose milestones for completing a construction phase compared to the base setting is investigated in scenarios MS1 and MS2. In order to cope with supply chain uncertainty, we generate a scenario defining the availability of material in the CCC (scenario MU), where material for a specific task is not available in a specific time period (week). The material unavailability is considered at the operational planning level on a bi-weekly rolling horizon and is hence unknown at the tactical planning level. If necessary, delivery dates at the operational planning level have to be adapted dynamically (within the rolling horizon of two weeks), influencing the cost of the solution. Two policies with respect to ‘crashing’, i.e. reduction of the duration of construction tasks, and storage are examined. We compare the effects of the base scenario, where acceleration is possible to a scenario where acceleration is not possible due to limited work force availability (scenario NoA). Next, we investigate a scenario where storage on site is not possible due to limited working space (scenario NoS), as opposed to the base scenario where storage on site is partially permitted.

Finally, in order to show the applicability and the benefits of the IRP, we analyze a scenario where no coordination of deliveries from different suppliers via bundling of materials at the CCC is performed. As distinct from the Retailer Managed Inventory (RMI) system, in which each customer (e.g. retailer, construction site) manages its own inventory, a Vendor Managed Inventory (VMI) system assigns the inventory control at customers to the vendor. This VMI system is the basis of the IRP, where the cooperation between vendor and customer aims to ensure a winwin situation for both parties. Scenario NoC presents a RMI system without coordination of material supplies, considering only direct deliveries from suppliers to individual construction sites.

4.2 Computational results

All experiments are conducted on a PC equipped with an Intel Core i7-4600 processor paced at 2.7 GHz and with 16 GB of RAM. The mixed-integer linear programs are solved using IBM ILOG CPLEX 12.6 and Concert Technology.

We first solve the tactical model. The solution of the tactical model then serves as parameters for the operational model. Conceptually, the two planning phases could be combined to a global model, solving the problem at once. This would allow to immediately implement the tactical decisions and solve the global model on a rolling-horizon of two weeks, respecting updated parameters and fixed known variables. However, practically the computational effort of this solution approach is not feasible with the current technical equipment.

Table 6 presents the computation time of each of the planning levels for the different scenarios. In addition, it reports the percentage of optimally solved operational problems (optimally solved), as well as the average relative gap of the feasible but not optimally solved operational solutions (average gap). The MIP on the tactical planning level is always solved to optimality. For the operational planning level, a time limit of 600 s is given to each iteration of the rolling horizon procedure. It can be observed that the computation time of the tactical level varies between 17 and 106 min for most of the scenarios. As can be seen from computation times, the tactical problem is more difficult to solve if milestones are restrictive. Scenario MS1, containing restrictive milestones, needs a computation time of 510 minutes to be solved to optimality. The percentage of optimally solved solutions and the average gap of the feasible solutions give an indication that Scenario MS1 is also hard to solve on the operational level with 61% of optimal solutions and an average gap of 4.09% for feasible solutions. The elapsed time of the operational level (which is limited for each iteration) varies in general between 87 and 277 min. Scenario NoS can be solved efficiently within 1 min, since no storage decisions have to be made. Scenario NoC, where only direct deliveries from suppliers to individual construction sites are considered, can as well be solved to optimality within 1 min.

Table 6 Computation time and performance
Full size table

The investigated scenarios are evaluated by means of two groups of performance indicators. The first group refers to solution cost, while the second group elaborates on solution characteristics. Personnel cost, penalty cost, storage cost, transport cost, and total cost represent the cost structure of the different scenarios. Maximum and average number of trips per day, number of accelerated construction tasks, average acceleration of accelerated construction tasks, average speed of execution of construction tasks and average storage duration of material represent the characteristics of the solutions.

Table 7 Experimental results (cost analysis: cost in Euro)
Full size table
Fig. 5
figure 5

Total cost of construction tasks for different scenarios

Full size image

Table 7 shows the cost that incur for each of the scenarios, as illustrated in Fig. 5. While personnel and penalty cost are derived from the tactical model, the operational model determines detailed storage and transport cost. Personnel cost are lowest for scenario CS1 and highest for scenario CS2, which is obviously due to the underlying cost distribution. Instead, personnel cost are only slightly different for scenarios Base, MU and NoS, but rather high for scenario MS1. This is due to the restrictive milestones of this scenario, which force the acceleration of construction tasks in order to avoid penalty cost. The acceleration of tasks requires additional personnel, resulting in higher cost. When acceleration is not possible (scenario NoA) or not necessary due to loose milestones (scenario MS2), personnel cost are thus lower. For most of the scenarios, milestones are respected and penalty cost are saved. When acceleration of construction tasks is not possible (scenario NoA), milestones have to be exceeded and high penalty cost incur. Storage cost of the different scenarios vary only slightly, with two exceptions. Storage cost of scenario CS1 are elevated due to the underlying cost structure, while obviously no storage cost incur for scenario NoS, where storage at the construction site is not permitted. Storage cost are slightly higher when material is unavailable at the CCC (scenario MU) as opposed to the scenario Base, while transport cost are slightly lower. This is due to the fact, that the material which is unavailable in a specific time period, is then scheduled to be transported earlier and stored at the construction site. Transport cost are lowest for scenario MS1, since the restrictive milestones lead to a denser construction schedule, which enables the bundling of material on delivery tours. As a consequence fewer trips are performed and transport cost can be saved. When storage is not possible or storage cost are high, material needs to be delivered just-in-time and more transports are performed to provide material when it is needed. Consequently, high transport cost incur for scenarios NoS, NoC and CS1.

Table 8 Experimental results (solution characteristics for different scenarios)
Full size table

Table 8 depicts the solution characteristics of the investigated scenarios. When acceleration of construction tasks is not possible (scenario NoA), the maximum number of transport trips (max. trips) per day is lower compared to the other scenarios, since transports are spread over the whole time horizon while peaks do not occur. The average number of trips (av. trips) per day is elevated for scenario MS1, where milestones are restrictive and hence more transports need to be performed in a shorter time period. The opposite becomes apparent for scenario MS2, where milestones are loose and hence transports are to be performed over a longer time period. In general, it can be observed, that construction projects start at the earliest possible time in order to respect milestones at the end of construction phases. When these milestones are set loosely (scenario MS2), however, the average start time of construction projects is 2.4 weeks after the earliest possible start time. The number of accelerated tasks (accel.), average acceleration of accelerated tasks (av. accel.) and average speed of execution of tasks (av. speed) provide information about the deviation of construction tasks from their normal duration. The average speed of execution is the average value of accelerations and decelerations applied to tasks. Restrictive milestones (scenario MS1) cause the highest number of accelerated tasks. In scenario MS1, 26 tasks out of 50 are accelerated with an average acceleration value of 1.41, while 16 tasks are performed more slowly than normally, leading to an average speed of 1.00. Loose milestones (scenario MS2) lead to an average speed of construction tasks of 0.83, where only one task is accelerated to half of the normal duration. The average speed of execution of construction tasks is also comparatively slow, when personnel cost are high (scenario CS2), and obviously when no acceleration is allowed (scenario NoA). High storage cost account for a short average storage duration (av. storage) of material, as can be seen in scenario CS1 as opposed to the other scenarios. The average storage duration is slightly higher when material is unavailable at the CCC (scenario MU) as compared to the scenario Base, since delivery dates on the operational planning level have to be adapted to material supply. In general, it can be observed that the supply chain uncertainty does not significantly impact on the construction schedule. When coordination of material supplies is not possible (scenario NoC), only direct deliveries from suppliers to individual construction sites are considered. This leads to an increase in the maximum number of trips and the average number of trips.

Fig. 6
figure 6

Schedule of construction tasks, illustrating the number of transports per week at construction sites 1–5 for the base scenario (Base)

Full size image
Fig. 7
figure 7

Schedule of construction tasks, illustrating the number of transports per week at construction sites 1–5 for scenario MS1 (restrictive Milestones)

Full size image

Figures 6 and 7 present illustrative examples for construction schedules of the base scenario (Base) compared to the scenario where milestones are restrictive (MS1). The schedules show ten groups of construction tasks on the ordinate, performed in 5 construction projects. The associated number of transports, as well as the maximum number of allowed transports are illustrated on top. The time horizon is depicted on the abscissa, where milestones of the construction phases are indicated as well. The charts show the duration of construction tasks, where the color of the tasks represents the speed of execution ranging from green / light (prolonged) to red / dark (accelerated). The focus of the two figures is on the illustration of the number of transports associated to the different scenarios. It can be observed that the maximum number of transports is very restrictive, especially when milestones limit the construction phases to a short period of time (scenario MS1). The maximum number of allowed transports determines the amount of material that can be delivered to each of the construction sites, further influencing the construction schedules including storage plans and personnel utilization. The illustrated construction schedules serve as decision support for companies involved in urban construction processes. They indicate when each of the construction projects should be started, how fast and with how much personnel construction tasks should be performed and how material transports should be organized to respect all restrictions at minimum cost. It can be observed that under scenario MS1, construction tasks are accelerated in order to achieve the restrictive milestones. Thus, the number of transports carried out per week is comparatively high, but still below the maximal number.

5 Conclusion and managerial implications

This work presents a case study from the building industry, focusing on the optimization of construction schedules and material deliveries to reduce total cost and waste of resources. In particular, we investigated a hierarchical construction logistics optimization problem enabling efficient urban construction processes. We addressed the challenges of coordinating workers and the timely delivery and storage of material with the objective of optimizing resource-efficiency as well as reducing traffic related to construction tasks. We formulated a mathematical model for each planning level and solved it with CPLEX. An iterative rolling-horizon procedure applied on the operational planning level allowed to incorporate dynamic information and cope with supply chain uncertainties. We tested the suggested approach on realistic data from Seestadt Aspern in the city of Vienna and analyzed the results associated with different scenarios.

Experimental results make the trade-offs obvious that need to be faced, when planning construction logistics. Tighter project due dates require more personnel to accelerate the completion time of construction phases, thus increasing personnel cost. When storage of material on site is not possible, transports cannot be organized efficiently, i.e. through the bundling of material delivered to several construction sites located close-by. Hence, transport cost increase since all material has to be delivered just-in-time. Distribution can be optimized by combining the deliveries to different construction sites which are located close-by on one route. The number of deliveries to the construction area is reduced by consolidating material and disruptions due to material handling on site are decreased. The results also show that re-planning during project execution might be necessary due to supply chain uncertainties, i.e. when material is known to be unavailable at the operational planning level. Using the proposed hierarchical model, delivery and storage decisions on the operational level can be revised to incorporate dynamic information on material availability, while still following the tactical construction schedule.

The proposed construction logistics planning approach serves as a valuable decision support for the design of construction logistics processes. It can be used as well by municipalities or other stakeholders interested in estimating the number of flows necessary to perform the required construction works for a specific development area. Operations research techniques, such as problem structuring methods and mathematical modeling support practitioners and decision makers. Complex problems can be analyzed effectively and efficient decisions can be made to implement productive and sustainable systems.

On the basis of this study, future research could focus on the explicit minimization of consumed energy and produced emissions. Further, multi-level residential or office buildings could have specific task networks, entailing identical sub-projects for each level which could be processed in a sequential way. The investigation of a scenario where different crafts could be working at different levels at the same time, would be of great interest for future research. This would also allow to incorporate learning effects from one level to the next.