Introduction

The generation of random numbers has applications in a wide range of fields, from scientific research—e.g. to simulate physical systems—to military scopes—e.g. for effective cryptographic protocols—and every-day concerns—like ensuring privacy and gambling. From a classical point of view, the concept of randomness is tightly bound to the incomplete knowledge of a system; indeed, classical randomness has a subjective and epistemological nature and is erased when the system is completely known1. Hence, classical algorithms can only generate pseudo-random numbers2, whose unpredictability relies on the complexity of the device generating them. Besides, the certification of randomness is an elusive task, since the available tests can only verify the absence of specific patterns, while others may go undetected but still be known to an adversary3.

On the other hand, randomness is intrinsic to quantum systems, which do not possess definite properties until these are measured. In real experiments, however, this intrinsic quantum randomness comes embedded with noise and lack of complete control over the device, compromising the security of a quantum random-number generator. A solution to that is to devise quantum protocols whose correctness can be certified in a device-independent (DI) manner. In such a framework, properties of the considered system can be inferred under some causal assumptions, not requiring a precise knowledge of the devices adopted in the implementation. For instance, from the violation of a Bell inequality4,5, under the assumption of measurement independence and locality, one can ensure that the statistics of certain quantum experiments cannot be described in the classical terms of local deterministic models, hence being impossible to be deterministically predicted by any local observer. Moreover, the extent of such a violation can provide a lower bound on the certified randomness characterizing the measurement outputs of the two parties performing the Bell test, as introduced and developed in refs. 6,7,8. Several other seminal works based on Bell inequalities have been developed9,10,11,12,13,14,15,16,17,18,19,20,21,22, advancing the topics of randomness amplification (the generation of near-perfect randomness from a weaker source), randomness expansion (the expansion of a short initial random seed), and quantum key distribution (sharing a common secret string through communication over public channels). In particular, loophole-free Bell tests based on randomness generation protocol have been implemented7,20,23 and more advanced techniques have been developed to provide security against general adversarial attacks19,21,24,25.

From a causal perspective, the non-classical behavior revealed by a Bell test lies in the incompatibility of quantum predictions with our intuitive notion of cause and effect26,27,28. Given that the causal structure underlying a Bell-like scenario involves five variables (the measurement choices and outcomes for each of the two observers and a fifth variable representing the common cause of their correlations), it is natural to wonder whether a different, and simpler, causal structure could give rise to an analogous discrepancy between quantum and classical causal predictions29,30. The instrumental causal structure31,32, where the two parties (A and B) are linked by a classical channel of communication, is the simplest model (in terms of the number of involved nodes) achieving this result33. This scenario has fundamental importance in causal inference, since it allows the estimation of causal influences even in the presence of unknown latent factors31.

In this letter, we provide a proof-of principle demonstration of the implementation of a DI random number generator based on instrumental correlations, secure against general quantum attacks19.

Our protocol is DI, since it does not require any assumption about the measurements and states used in the protocol, not even their dimension. Furthermore, in our case, the causal assumption consists in the requirement that A’s measurement choice does not have a direct influence over B. In practical applications, this premise can be enforced, by shielding A’s measurement station, in order to allow only for the communication of its outcome bit to B and prevent any other unwanted communication. To implement the protocol in all of its parts, we have set up a classical extractor following the theoretical design by Trevisan34. Moreover, we prove that DI randomness generation protocols implemented in this scenario, for high state visibilities, can bring an advantage in the gain of random bits when compared to those based on the simplest two-input-two-output Bell scenario, the Clauser–Horn–Shimony–Holt (CHSH)35. Therefore, this work paves the way to further applications of the instrumental scenario in the field of DI protocols, which, until now, have relied primarily on Bell-like tests.

Results

Randomness certification via instrumental violations

Let us first briefly review some previous results obtained in the context of Bell inequalities4. In a CHSH scenario35, two parties, A and B, share a bipartite system and, without communicating to each other, perform local measurements on their subsystems. If A and B choose between two given operators each, i.e. (A1, A2) and (B1, B2) respectively, and then combine their data, the mean value of the operator \(S=| \left\langle {A}_{1},{B}_{1}\right\rangle -\left\langle {A}_{1},{B}_{2}\right\rangle +\left\langle {A}_{2},{B}_{1}\right\rangle +\left\langle {A}_{2},{B}_{2}\right\rangle |\) should be upper-bounded by 2, for any deterministic model respecting a natural notion of locality. However, as proved in ref. 35, if A and B share an entangled state, they can get a value exceeding this bound, whose explanation requires the presence of non-classical correlations between the two parties. Hence, Bell inequalities have been adopted in ref. 7 to guarantee the intrinsic random nature of A’s and B’s measurements’ outcomes, within a DI randomness generation and certification protocol.

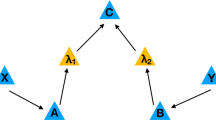
In the instrumental causal model, which is depicted in Fig. 1a, the two parties (Alice and Bob) still share a bipartite state. Alice can choose among l possible d-outcome measurements (\({O}_{A}^{1}\), ..., \({O}_{A}^{l}\)), according to the instrument variable x, which is independent of the shared correlations between Alice and Bob (Λ) and can assume l different values. On the other hand, Bob’s choice y is among d observables (\({O}_{B}^{1}\), ..., \({O}_{B}^{d}\)) and depends on Alice’s outcome a, specifically y = a. In other words, as opposed to the spatially-separated correlations in a Bell-like scenario, the instrumental process constitutes a temporal scenario, with one-way communication of Alice’s outcomes to select Bob’s measurement. This implies, first, that Alice and Bob are not space-like separated, to ensure that the causal structure’s constraints are fulfilled, unlike in Bell-like scenarios. Secondly, due to the communication of Alice’s outcome a to Bob, Bob’s outcome b is not independent of x; however, the instrumental network specifies this influence to be indirect, formalized by the constraint p(b∣x, a, λ) = p(b∣a, λ) and justifying the absence of an arrow from X to B in Fig. 1a. This is the aforementioned causal assumption within our protocol.

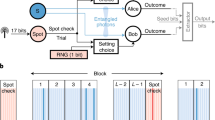
Fig. 1: Randomness generation and certification protocol.
figure 1

a Instrumental causal structure represented as a directed acyclic graph26 (DAG), where each node represents a variable and the arrows link variables between which there is causal influence. In this case, X, A, and B are observable, while Λ is a latent variable. b The plot shows the smooth min-entropy bound for the CHSH (Clauser–Horn–Shimony–Holt) inequality and the instrumental scenario (respectively dashed and continuous curve), in terms of the state visibility v, i.e. considering the extent of violation that would be given by the following state: \(\rho =v\left|{\psi }^{-}\right\rangle \left\langle {\psi }^{-}\right|+(1-v)\frac{{\mathbb{I}}}{4}\). The bounds were obtained through the analysis of ref. 19, secure against general quantum adversaries, which was adapted to our case. The choice of parameters was the following: n = 1012, ϵ = ϵEA = 10−6, \(\delta ^{\prime} =1{0}^{-4}\) and γ = 1. In detail, n is the number of runs, ϵ is the smoothing parameter characterizing the min-entropy \({{\mathcal{H}}}_{\min }^{\epsilon }\), ϵEA is the desired error probability of the entropy accumulation protocol, \(\delta ^{\prime}\) is the experimental uncertainty on the evaluation of the violation \({\mathcal{I}}\) and γ is the parameter of the Bernoulli distribution according to which we select “test” and “accumulation” runs throughout the protocol. c Simplified scheme of the proposed randomness generation and certification protocol (in the case γ = 1): (i) initial seed generation (defining, at each run, Alice's choice among the operators), (ii) instrumental process implementation, (iii) classical randomness extractor. The initial seed is obtained from the random bits provided by the NIST Randomness Beacon42. In the second stage, Alice's and Bob's outputs are collected and the corresponding value of the instrumental violation \({{\mathcal{I}}}^{* }\) is computed. If it is higher than a threshold set by the user, the smooth min-entropy is bounded by inequality (2), otherwise the protocol aborts. The value of the min-entropy indicates the maximum number of certified random bits that can be extracted. At the end, if the protocol does not abort, the output strings are injected in a classical randomness extractor (Trevisan's extractor34) and the final string of certified random bits is obtained. The extractor's seed is as well provided by the NIST Randomness Beacon.

Full size image

Similarly to Bell-like scenarios, the causal structure underlying an instrumental process imposes some constraints on the classical joint probabilities {p(a, b∣x)}a,b,x that are compatible with it31,32 (the so-called instrumental inequalities). In the particular case where the instrument x can assume three different values (1,2,3), while a and b are dichotomic, the following inequality holds32:

$${\mathcal{I}}={\left\langle A\right\rangle }_{1}-{\left\langle B\right\rangle }_{1}+2{\left\langle B\right\rangle }_{2}-{\left\langle AB\right\rangle }_{1}+2{\left\langle AB\right\rangle }_{3}\le 3$$
(1)

where \({\left\langle AB\right\rangle }_{x}={\sum }_{a,b = 0,1}{(-1)}^{a+b}p(a,b| x)\). Remarkably, this inequality can be violated with the correlations produced by quantum instrumental causal models33, up to the maximal value of \({\mathcal{I}}=1+2\sqrt{2}\). Recently, the relationship of the instrumental processes with the Bell scenario has been studied in ref. 36.

In this context, we rely on the fact that if a given set of statistics {p(a, b∣x)}a,b,x violates inequality (1), then the system shared by the two parties exhibits non-classical correlations that impose non-trivial constraints on the information a potential eavesdropper could obtain, represented in the probability distributions {p(a, b, e∣x)}a,b,e,x, where e is the eventual side information of the eavesdropper. Consequently, this restricts the values of the conditional min-entropy, a randomness quantifier defined as \({{\mathcal{H}}}_{\min }=-{\mathrm{log}\,}_{2}[{\sum }_{e}P(e)\mathop{\max }\limits_{a,b}P(a,b| e,x)]\)37. Indeed, it is possible to obtain a lower-bound on the min-entropy, for each x, as a function fx of \({\mathcal{I}}\): \({{\mathcal{H}}}_{\min }\ge {f}_{x}({\mathcal{I}})\) (or, equivalently, of the visibility, see Fig. 1b). For each x and \({\mathcal{I}}\), the lower bound \({f}_{x}({\mathcal{I}})\) can be computed via semidefinite programming (SDP), by maximizing P(a, b∣e, x), under the constraint that the observable terms of the probability distribution are compatible to the laws of quantum mechanics and that the corresponding violation is \({\mathcal{I}}\). The first constraint is imposed by exploiting the NPA hierarchy38. Indeed, such a general method can be applied to any casual model involving a shared bipartite system, on whose subsystems local measurements are performed. Note that, when adopting the NPA method for an instrumental process, no constraints are applied to the untested terms of the form p(a, b∣e, x, y ≠ a) and that the solution of such an optimization will, in general, provide a lower amount of certifiable randomness, with respect to a scenario where all the combinations were tested (for further details, see Supplementary Information note 1). The functions fx are convex and grow monotonically with \({\mathcal{I}}\); so, the higher the violation of inequality (1) is, the higher the min-entropy lower bound will be. Nevertheless, in real experimental conditions, in order to evaluate the quantum violation extent \({{\mathcal{I}}}^{* }\) (or, analogously, the probability distribution p*(a, b∣x)) to compute fx, several experimental runs are necessary. Therefore, unless one makes the “iid assumption” (i.e. all the experimental runs are assumed to be identically and independently distributed, “iid”, so both the state source, as well as Alice’s and Bob’s measurement devices, are supposed not to exhibit time-dependent behaviors), this bound \({f}_{x}({{\mathcal{I}}}^{* })\) will not hold in the presence of an adversary that could include a (quantum) memory in the devices, introducing interdependences among the runs. Several DI protocols have been proposed so far addressing the most general non-iid case13,16,39, but at the cost of a low feasibility. Only very recently feasible solutions have been proposed19,24,25,40. In particular, we will consider the technique developed in ref. 19, resorting to the “Entropy Accumulation Theorem” (EAT), in order to deal with processes not necessarily made of independent and identically distributed runs. Such a method has been recently applied to the CHSH scenario21.

Here we adapt the technique developed in ref. 19 to the instrumental scenario, making our randomness certification, whose scheme is depicted in Fig. 1c, secure against general quantum attacks. According to the EAT, for a category of processes that comprehends also an implemented instrumental process composed of several runs, the following bound on the smooth min-entropy holds:

$${{\mathcal{H}}}_{\min }^{\epsilon }({O}^{n}| {S}^{n}{E}^{n})> nt-\nu \sqrt{n},$$
(2)

where O are the quantum systems given to the honest parties Alice and Bob, at each run, S constitutes the leaked side-information, while E represents any additional side information correlated to the initial state. Then, t is a convex function which depends on the extent of the violation, expected by an honest, although noisy, implementation of the protocol, i.e. in a scenario with no eavesdropper (\({I}_{\exp }\)). On the other hand, ν depends also on the smoothing parameter ϵ, which characterizes the smooth min-entropy \({{\mathcal{H}}}_{\min }^{\epsilon }\), and ϵEA, i.e. the desired error probability of the entropy accumulation protocol; in other words, either the protocol aborts with probability higher than 1 − ϵEA or bound (2) holds (for further detail, see Supplementary Information note 2).

Our protocol is implemented as follows (see Fig. 2): for each run, a random binary variable T is drawn according to a Bernoulli distribution of parameter γ (set by the user); if T = 0, the run is an “accumulation” run, so x is deterministically set to 2 (which guarantees a higher \(f({\mathcal{I}})\), see Supplementary Information note 2); on the other hand, if T = 1, the run is a “test” run, so x is randomly chosen among 1, 2 and 3. After m test runs (with m chosen by the user), the quantum instrumental violation is evaluated from the bits collected throughout the test runs and, if lower than \({I}_{\exp }-\delta ^{\prime}\) (\(\delta ^{\prime}\) being the experimental uncertainty on \({\mathcal{I}}\)), the protocol aborts; otherwise the certified smooth min-entropy is bounded by inequality (2). This lower bound on the certified min entropy represents the maximum certified amount of bits that we can extract from our collected data. Hence, feeding the raw bit string and the \({{\mathcal{H}}}_{\min }^{\epsilon }\) to the classical extractor34, the algorithm will output at most \({{\mathcal{H}}}_{\min }^{\epsilon }({O}^{n}| {S}^{n}{E}^{n})\) certified random bits, the exact value depending on its internal error parameter ϵext. Specifically, we resorted to the classical extractor devised by Trevisan34. This algorithm takes as inputs a “weak randomness source”, in our case the 2n raw bits long string, and a seed, which is poly-logarithmic in the input size (our code for the classical extractor can be found at41 and, for a detailed description of the classical randomness extractor, see Supplementary Information note 3).

Fig. 2: Implementation of the device-independent randomness certification protocol.
figure 2

The implementation of our proposed protocol involves three steps. First of all, an instrumental process is implemented on a photonic platform. Then, for each round of the experiment, a binary random variable T is evaluated. Specifically, T can get value 1 with probability γ, previously chosen by the user (in our implementation, γ = 1). If T = 0, the run is an “accumulation” one, and x is deterministically equal to 2. If T = 1, the run is a “test” run and x is randomly chosen among 1, 2, and 3. Note that, in our case, we only have “test” runs. Secondly, after n runs, through the bits collected in the test runs, we evaluate the corresponding instrumental violation and see whether it is higher than the expected violation for an honest implementation of the protocol, i.e. in a scenario with no eavesdroppers. In our case, we set the threshold to 3.5. If it is lower, the protocol aborts, otherwise, the protocol reaches the third stage, where we employ the Trevisan extractor, to extract the final certified random bit string. The extractor takes, as input, the raw data (weak randomness source), a random seed (given by the NIST Randomness Beacon42) and the min-entropy of the input string. In the end, according to the classical extractor statistical error (ϵext) set by the user (in our case 10−6), the algorithm extracts m truly random bits, with m < n.

Full size image

Experimental implementation of the protocol

The DI random numbers generator, in our proposal, is made up of three main parts, which are seen as black boxes to the user: the state generation and Alice’s and Bob’s measurement stations. The causal correlations among these three stages are those of an instrumental scenario (see Fig. 1a,c) and are implemented through the photonic platform depicted in Fig. 3.

Fig. 3: Experimental apparatus.
figure 3

A polarization-entangled photon pair is generated via spontaneous parametric down-conversion (SPDC) process in a nonlinear crystal. Photon 1 is sent to Alice's station, where one of three observables (\({O}_{A}^{1}\), \({O}_{A}^{2}\), and \({O}_{A}^{3}\)) is measured through a liquid crystal followed by a polarizing beam splitter (PBS). The choice of the observable relies on the random bits generated by the NIST Randomness Beacon42. Detector \({D}_{A}^{0}\) acts as trigger for the application of a 1280 V voltage on the Pockels cell, whenever the measurement output 0 is registered. The photon 2 is delayed 600 ns before arriving to Bob's station by employing a single-mode fiber 125 m long. After leaving the fiber, the photon passes through the Pockels cell, followed by a fixed half waveplate (HWP) at 56.25∘ and a PBS. If the Pockels cell has been triggered (in case of A measurement outcome is 0), its action combined to the fixed HWP in Bob's station allows us to perform \({O}_{B}^{1}\). Otherwise (if A measurement outcome is 1), the Pockels cell acts as the identity and we implement \({O}_{B}^{2}\).

Full size image

Within this experimental apparatus, the qubits are encoded in the photon’s polarization: horizontal (\({\rm{H}}\)) and vertical (\({\rm{V}}\)) polarizations represent, respectively, qubits \(0\) and \(1\), eigenstates of the Pauli matrix σz. A spontaneous parametric down-conversion (SPDC) process generates the two-photon maximally entangled state \(|{\Psi }^{-} \rangle =\frac{|{\rm{HV}}\rangle -|{\rm{VH}}\rangle }{\sqrt{2}}\). One photon is sent to path 1, towards Alice’s station, where an observable among \({O}_{A}^{1}\), \({O}_{A}^{2}\) and \({O}_{A}^{3}\) is measured, applying the proper voltage to a liquid crystal device (LCD). The voltage must be chosen according to a random seed, made of a string of trits (indeed, in our case, we take γ = 1, so x is chosen among (1,2,3) at every run). This seed is obtained from the NIST Randomness Beacon42, which provides 512 random bits per minute. After Alice has performed her measurement, whenever she gets output 1 (i.e. \({D}_{A}^{0}\) registers an event), the detector’s signal is split to reach the coincidence counter and, at the same time, trigger the Pockels cell on path 2. Bob’s station is made of a half waveplate (HWP) followed by this fast electro-optical device. When no voltage is applied to the Pockels cell, Bob’s operator is \({O}_{B}^{1}\) and, when it is turned on, there is a swift change to \({O}_{B}^{2}\) (the cell’s time response is of the order of nanoseconds). In order to have the time to register Alice’s output and select Bob’s operator accordingly, the photon on path 2 is delayed, through a 125 m long single-mode fiber.

The four detectors are synchronized in order to distinguish the coincidence counts generated by the entangled photons’ pairs from the accidental counts. Let us note that our proof of principle is not loophole free, since it requires the fair sampling assumption, due to our overall low detection efficiency. However, such a limitation belongs to this specific implementation and not to the proposed method. The measurement operators achieving maximal violation of \({\mathcal{I}}=1+2\sqrt{2}\), when applied to the state \(|{\psi }^{-}\rangle\), are the following: \({O}_{A}^{1}=-({\sigma }_{{\rm{z}}}-{\sigma }_{{\rm{x}}})/\sqrt{2}\), \({O}_{A}^{2}=-{\sigma }_{{\rm{x}}}\), \({O}_{A}^{3}={\sigma }_{{\rm{z}}}\) and \({O}_{B}^{1}=({\sigma }_{{\rm{x}}}-{\sigma }_{{\rm{z}}})/\sqrt{2}\), \({O}_{B}^{2}=-({\sigma }_{{\rm{x}}}+{\sigma }_{{\rm{z}}})/\sqrt{2}\).

Once the instrumental process is implemented, the threshold \({I}_{\exp }\) is set, corresponding to the violation that is expected by an honest implementation of the protocol. In our case, given that our expected visibility amounts to 0.915, \({I}_{\exp }=3.5\). Then, the desired level of security is imposed by tuning the internal parameters, detailed in the SI, contributing to ν. As next step, according to Eq. (2), one can either fix the number of the desired output random bits and perform the required number of runs or, viceversa, fix the amount of initial randomness to feed the protocol, and hence the number of feasible runs. In the end, the classical randomness extractor is applied to the raw bit strings. Specifically, in our case, we adopted the one devised by Trevisan34. The complete procedure is summarized in Fig. 2.

Theoretical results

The DI random number generation protocol we propose for the instrumental scenario was developed adapting the pre-existing techniques for the Bell scenario19,21, and is secure against general quantum adversaries. The most striking aspect of our protocol, shown in Fig. 4, is that, under given circumstances, our protocol proves to be more convenient than its CHSH-based counterpart. This becomes visible if we compare the amount of truly random bits within Alice’s and Bob’s output strings throughout all the experimental runs (given by \({{\mathcal{H}}}_{\min }^{\epsilon }\)) for our protocol and its CHSH-based counterpart, in the case of a fixed amount of invested bits, for the parties’ inputs and for T. This will result in a different number of feasible runs for the two cases. Such a difference, in the regime of high state visibilities v (~ 0.98), considering a violation extent compatible to the following state \(\rho =v\left|{\psi }^{-}\right\rangle \left\langle {\psi }^{-}\right|+(1-v)\frac{{\mathbb{I}}}{4}\), and large amounts of invested random bits, brings the ratio of the two gains (\({{\mathcal{H}}}_{\min }^{\epsilon \,{\rm{Instr}}}/{{\mathcal{H}}}_{\min }^{\epsilon \,{\rm{CHSH}}}\)), as shown in Fig. 4, to be higher than 1.

Fig. 4: Comparison between Clauser–Horn–Shimony–Holt (CHSH) and Instrumental random bits gain.
figure 4

The plot shows the ratio between the random bits gained throughout all the runs of the proposed protocol (given by \({{\mathcal{H}}}_{\min }^{\epsilon }\)), involving the instrumental scenario, over those gained in its regular CHSH-based counterpart19,21, when fixing the amount of random bits feeding both the protocols. Under these circumstances, given that for each test run the instrumental test requires log2(3) input bits, instead of the 2 of the regular CHSH, the final amounts of random bits in the two cases will differ, due to the different amounts of performed runs, besides their different min-entropies per run. Note that the amount of performed runs depends on the value of γ, i.e. the probability of a test run, which was optimized separately for the two scenarios. In particular, the curves represent different amounts of initially invested random bits, in particular n = 108 (blue, lowest curve), n = 109 (golden, middle curve) and n = 1010 (red, highest curve), in terms of the state visibility v, i.e. corresponding to the extent of violation that would correspond to the following state: \(\rho =v\left|{\psi }^{-}\right\rangle \left\langle {\psi }^{-}\right|+(1-v)\frac{{\mathbb{I}}}{4}\).

Full size image

Experimental results

We implemented the instrumental scenario on a photonic platform and provided a proof of principle of the proposed quantum adversary-proof protocol in our experimental conditions. In particular, for our expected visibility, of 0.915, we put our threshold to \({I}_{\exp }=3.5\), with \(\delta ^{\prime} =0.011\). Furthermore, we set ϵEA = ϵ = 10−1 and fixed the amount of initial randomness to 172,095 experimental runs. Since the registered violation was of 3.516 ± 0.011, compatible to a state \(\rho =v\left|{\psi }^{-}\right\rangle \left\langle {\psi }^{-}\right|+(1-v)\frac{{\mathbb{I}}}{4}\), with v = 0.9186 ± 0.030, our certified smooth min-entropy bound, according to inequality (2), was 0.031125, which allowed us to gain, through the classical extractor, an overall number of 5270 random bits, with an error on the classical extractor of ϵext = 10−6. Note that each experimental run lasted  ~1s and the bottleneck of our implementation is the time response of the liquid crystal,  ~700 ms, that implements Alice’s operator. Hence, in principle, significantly higher rates can be reached on the same platform, adopting a fast electro-optical device also for Alice’s station, with a response time of  ~100 ns.

The length of the seed required by the classical extractor, as mentioned, is poly-logarithmic in the input size and its length also depends on the chosen error parameter ϵext (which is the tolerated distance between the uniform distribution and the one of the final string) and on the particular algorithm adopted. In our case, we used the same implementation of refs. 41,43, which was proven to be a strong quantum proof extractor by De et al. 44. With respect to other implementations of the Trevisan extractor45, ours requires a longer seed, but allows to extract a higher amount of random bits. Let us note that, since the length of the seed grows as log(2n)3, where n is the number of experimental runs, the randomness gain is not modified if we take also into account the bits invested in the classical extractor’s seed. Indeed, the number of extracted bits grows polynomially in n. Hence, if \({H}_{{\min }^{{\rm{Instr}}}}^{\epsilon }> {H}_{{\min }^{{\rm{CHSH}}}}^{\epsilon }\), then \({m}_{{\rm{Instr}}}-{d}_{{\rm{Instr}}}> {m}_{{\rm{CHSH}}}-{d}_{{\rm{CHSH}}}\), where m is the length of the final string (after the classical extraction) and d the length of the required extractor’s seed. For more details about the internal functioning of the classical randomness extractor and its specific parameter settings, see Supplementary Information note 3.

Discussion

In this work we implemented a DI random number generator based on the instrumental scenario. This shows that instrumental processes constitute an alternative venue with respect to Bell-like scenarios. Moreover, we also showed that, in regimes of high visibilities and high amounts of performed runs, the efficiency of the randomness generated by the violation of the instrumental inequality (1) can surpass that of efficiency of the CHSH inequality, as shown in Fig. 4. Indeed, for high visibilities, as it can be seen in Fig. 1b, the min-entropy per run guaranteed in the two scenarios has a similar value and, when the number of runs raises, the advantage brought by the instrumental test, by needing only log2(3) input bits, instead of 2, prevails.

Through the proposed protocol, we could extract an overall number of 5270 random bits, considering a threshold for the instrumental violation of \({I}_{\exp }=3.5\) and 10−1, both as error probability of the entropy accumulation protocol (ϵEA), as well as smoothing parameter (ϵ). The conversion rate, from public to private randomness, as well as the security parameters, could be improved on the same platform, by raising the number of invested initial random bits, or, analogously, the number of runs. To access the regime in which the instrumental scenario is more convenient than the CHSH one, we should invest a number of random bits over 109 and obtain a visibility of  ~0.98 (note that, the more the amount of invested bits grows, the more the threshold for the visibility lowers down).

This proof of principle opens the path for further investigations of the instrumental scenario as a possible venue for other information processing tasks usually associated to Bell scenarios, such as self-testing46,47,48,49,50,51,52,53,54,55 and communication complexity problems56,57,58.

Methods

Experimental details

Photon pairs were generated in a parametric down-conversion source, composed by a nonlinear crystal beta barium borate (BBO) of 2-mm thick injected by a pulsed pump field with λ = 392.5 nm. After spectral filtering and walk-off compensation, photons of λ = 785 nm are sent to the two measurement stations A and B. The crystal used to implement active feed-forward is a LiNbO3 high-voltage micro Pockels Cell—made by Shangai Institute of Ceramics with  < 1 ns risetime and a fast electronic circuit transforming each Si-avalanche photodetection signal into a calibrated fast pulse in the kV range needed to activate the Pockels Cell—is fully described in ref. 59. To achieve the active feed-forward of information, the photon sent to Bob’s station needs to be delayed, thus allowing the measurement on the first qubit to be performed. The amount of delay was evaluated considering the velocity of the signal transmission through a single-mode fiber and the activation time of the Pockels cell. We have used a fiber 125 m long, coupled at the end into a single-mode fiber that allows a delay of 600 ns of the second photon with respect to the first.