A concise nodal-based derivation of the floating frame of reference formulation for displacement-based solid finite elements

Abstract

The Floating Frame of Reference Formulation (FFRF) is one of the most widely used methods to analyze flexible multibody systems subjected to large rigid-body motion but small strains and deformations. The FFRF is conventionally derived via a continuum mechanics approach. This tedious and circuitous approach, which still attracts attention among researchers, yields so-called inertia shape integrals. These unhandy volume integrals, arising in the FFRF mass matrix and quadratic velocity vector, depend not only on the degrees of freedom, but also on the finite element shape functions. That is why conventional computer implementations of the FFRF are laborious and error prone; they require access to the algorithmic level of the underlying finite element code or are restricted to a lumped mass approximation. This contribution presents a nodal-based treatment of the FFRF to bypass these integrals. Each flexible body is considered in its spatially discretized state ab initio, wherefore the integrals are replaced by multiplications by a constant finite element mass matrix. Besides that, this approach leads to a simpler and concise but rigorous derivation of the equations of motion. The steps to obtain the inertia-integral-free equations of motion (in 2D and 3D spaces) are presented in a clear and comprehensive way; the final result provides ready-to-implement equations of motion without a lumped mass approximation, in contrast to the conventional formulation.

1 Introduction

An increasing focus on the optimization of products to higher levels of reliability and efficiency in combination with the growing complexity of our technology-dominated world pushes industry away from physical toward virtual prototyping. That is why advanced engineering simulation tools have become indispensable to master today’s challenges.

Virtually, all engineering devices are composed out of multiple individual components, which are often subjected to (large) motion during operation. The associated forces induce stresses, noise, and vibrations. Hence, the bodies’ flexibility needs to be taken into account to accurately predict a system’s behavior and performance prior production. However, standard geometrically nonlinear finite element (FE) analysis is (presently) limited to a small number of degrees of freedom (DOFs) due to computation resources, and therefore efficient flexible multibody simulations are inevitable.

The well-established floating frame of reference formulation (FFRF) is one of the most widely used methods to simulate flexible multibody systems relevant for industrial applications. The FFRF is suitable for problems characterized by large reference motions, that is, rigid body translations and rotations, but small flexible deformations and strains, which is the case for a wide range of engineering devices. The FFRF equations of motion (EOMs) are conventionally derived for flexible bodies from a continuum mechanics point of view. In this circuitous approach, the system energies are defined for a body using a continuous displacement and the velocity field of the underlying rigid body frame and of the superimposed flexible deformations and therefore not only entail a costly derivation of the EOMs, but also result in a number of drawbacks. However, the continuum-mechanics-based derivation of the FFRF has become a standard in the multibody dynamics literature [14]; recent papers also follow this approach [8, 11, 15, 16], even though it is known from the literature [13, 17] that it is possible to trace single terms of the FFRF back to the FE mass matrix, but so far not without a detour via continuum mechanics.

The additional drawback, beyond the costly and involved derivation, of the conventional continuum-mechanics-based FFRF is the so-called inertia shape integrals arising in the EOMs, which are unhandy volume integrals depending not only on the generalized coordinates but also on the FE shape functions, which make computer implementations of the conventional FFRF laborious, error-prone, and dependent on the algorithmic level of the underlying FE code, where the continuous flexible bodies were discretized. To avoid the evaluation of these integrals, commercial flexible multibody packages like ADAMS (MSC Software Corporation) or RecurDyn (FunctionBay, Inc.) resort to a lumped mass approximation according to [14]; see, for example, [3, 10]. In the (approximate) lumped mass approach, each FE nodal DOF $q_{\mathrm{fe}}^{j}$ is given a so-called nodal mass¹$m_{\mathrm{n}}^{j}$ obtained by, for example, lumping the consistent FE mass matrix via, for example, row-sum lumping [2]. In doing so, the kinetic energy $T$ of a flexible body in the system may be approximated by the sum of all $N$ nodal DOF contributions, where each contribution to the total kinetic energy can be computed according to particle dynamics theory as [10, 14]

$$ T \approx \frac{1}{2} \sum_{j=1}^{N} \dot{q}_{\mathrm{fe}}^{j} \, m _{\mathrm{n}}^{j} \, \dot{q}_{\mathrm{fe}}^{j} , $$

(1)

which is why all inertia integrals are replaced and approximated by sums, a significant simplification. Note that the dot denotes differentiation with respect to (w.r.t.) time. These (approximate) sums are in turn used to calculate the so-called invariants, which are constant “ingredients” required to set up the FFRF EOMs; they can be found in the documentations of commercial flexible multibody codes; see, for example, [3, 10].

The current contribution entirely bypasses the aforementioned shape integrals and also the need for a lumped mass approach, which is commonly used in commercial flexible multibody packages, and presents a concise and novel framework to derive the formulation without any approximations besides the FE discretization. The novelty of this approach lies in the nodal-based derivation of the FFRF EOMs, where each flexible body is considered in its already spatially discretized state ab initio, wherefore the derivation involves linear algebra only. Also, by this means the standard system matrices of the linear FE formulation are extracted only once during preprocessing, and, as already mentioned, the evaluation of inertia shape integrals is no longer required; instead, simple (sparse) matrix multiplications with the consistent FE mass matrix are performed. That is why this new approach is fully decoupled from any FE package, requires just a few lines of code, and therefore holds potential, for example, for the implementation on embedded systems required for real-time applications. Note that the present approach is so far limited to displacement-based finite elements, which is described in detail in Sect. 4.1.

The rest of the paper is structured as follows: Sect. 2 states a few relevant matrix calculus conventions and rules required to derive the nodal-based FFRF EOMs. Then Sect. 3 presents the nodal-based kinematic description of a representative flexible body of the system. Section 4 proposes a concise nodal-based inertia-integral-free derivation of the FFRF EOMs for two- and three-dimensional problems, followed by a conclusion in Sect. 5.

2 Matrix calculus preliminaries

We will use the following matrix calculus conventions and rules to derive the nodal-based and inertia-integral-free FFRF EOMs:

$\square$:

The derivative of a scalar $\alpha$ w.r.t. a column matrix $\boldsymbol{u} \in \mathbb{R}^{n \times 1}$:

$$\frac{\partial \alpha }{\partial \mathit{u}}=\left[\begin{array}{ccc}\frac{\partial \alpha }{\partial u_1}& \dots & \frac{\partial \alpha }{\partial u_n}\end{array}\right]\in {\mathbb{R}}^{1\times n},\text{whereas}\frac{\partial \alpha }{\partial {\mathit{u}}_{}^{\mathrm{T}}}={\left(\frac{\partial \alpha }{\partial {\mathit{u}}_{}^{}}\right)}^{\mathrm{T}}\in {\mathbb{R}}^{n\times 1}.$$

(2)

$\square$:

The derivative of a column matrix $\boldsymbol{v} \in \mathbb{R}^{m \times 1}$ w.r.t. a column matrix $\boldsymbol{u} \in \mathbb{R}^{n \times 1}$:

$$\frac{\partial \mathit{v}}{\partial {\mathit{u}}_{}^{}}=\left[\begin{array}{c}\frac{\partial v_1}{\partial {\mathit{u}}_{}^{}}\\ ⋮\\ \frac{\partial v_m}{\partial {\mathit{u}}_{}^{}}\end{array}\right]\in {\mathbb{R}}^{m\times n},\text{whereas}\frac{\partial \mathit{v}}{\partial {\mathit{u}}_{}^{\mathrm{T}}}={\left(\frac{\partial \mathit{v}}{\partial {\mathit{u}}_{}^{}}\right)}^{\mathrm{T}}\in {\mathbb{R}}^{n\times m}.$$

(3)

$\square$:

The derivative of a (scalar) linear form $\boldsymbol{v}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{w}$ w.r.t. a row matrix $\boldsymbol{u}_{\mathrm{}}^{\mathrm{T}} \! \in \mathbb{R}^{1 \times n}$:

$$ \frac{\partial \boldsymbol{v}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{w}}{ \partial \boldsymbol{u}_{\mathrm{}}^{\mathrm{T}}} = \frac{\partial \boldsymbol{v}_{\mathrm{}}^{\mathrm{}} }{\partial \boldsymbol{u}_{ \mathrm{}}^{\mathrm{T}}} \boldsymbol{w} + \frac{\partial \boldsymbol{w}}{\partial \boldsymbol{u}_{\mathrm{}}^{\mathrm{T}}} \boldsymbol{v}_{\mathrm{}}^{\mathrm{}} \; \in \mathbb{R}^{n \times 1} \quad \text{if } \boldsymbol{v}=\boldsymbol{v}( \boldsymbol{u}) \text{ and } \boldsymbol{w}=\boldsymbol{w}(\boldsymbol{u}) . $$

(4)

$\square$:

The derivative of a (scalar) quadratic form $\boldsymbol{v}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{B} \boldsymbol{v}$ w.r.t. a row matrix $\boldsymbol{u}_{\mathrm{}}^{ \mathrm{T}} \! \in \mathbb{R}^{1 \times n}$:

$$ \frac{\partial \boldsymbol{v}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{B} \boldsymbol{v}}{\partial \boldsymbol{u}_{\mathrm{}}^{\mathrm{T}}} = 2\frac{ \partial \boldsymbol{v}_{\mathrm{}}^{\mathrm{}} }{\partial \boldsymbol{u}_{\mathrm{}}^{\mathrm{T}}} \boldsymbol{B} \boldsymbol{v} \; \in \mathbb{R}^{n \times 1} \quad \text{if } \boldsymbol{B}= \boldsymbol{B}_{\mathrm{}}^{\mathrm{T}}=\text{const. w.r.t. } \boldsymbol{u} . $$

(5)

Note that the derivatives of linear and quadratic forms (see Eq. (4) and Eq. (5)) w.r.t. a column matrix $\boldsymbol{u} \in \mathbb{R}^{n \times 1}$ are given by transposing the results listed in Eq. (4) and Eq. (5), respectively, according to Eq. (2).

3 Nodal-based kinematic description

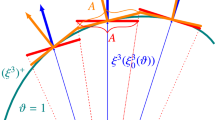
Let ℱ be a global coordinate system, fixed in space and time, and let $\overline{\mathcal{F}}$ be a floating frame attached to the body. The distance and orientation between the two coordinate systems may be described by the translation vector $\boldsymbol{q} _{\mathrm{t}}^{\mathrm{}} \in \mathbb{R}^{3 \times 1}$ and the rotation matrix $\boldsymbol{A}=\boldsymbol{A} ( \boldsymbol{\theta } ) \in \mathbb{R}^{3 \times 3}$ (Fig. 1), depending on a general rotation parameterization $\boldsymbol{\theta }$, such as Euler parameters, Euler angles, and so on.

Fig. 1

FE-discretized body $\varOmega$ with global ℱ and floating $\overline{\mathcal{F}}$ frame, related by the rotation matrix $\boldsymbol{A}$. The position vector $\boldsymbol{r}^{(i)}= \boldsymbol{x}^{(i)}+\boldsymbol{c}^{(i)}$ defines the current position of node $n_{i}$ with corresponding undeformed nodal coordinates $\boldsymbol{x}^{(i)}$ and nodal displacement $\boldsymbol{c}^{(i)}$ (expressed in ℱ). Furthermore, $\varOmega _{e}$ depicts a representative element of the FE mesh

Figure 1 depicts a representative flexible body $\varOmega$ of the system. The body is discretized with solid (continuum) finite elements $\varOmega _{e}$ yielding $n_{\mathrm{n}}$ nodes in total. The fundamental concept of the FFRF, that is, the decomposition of the displacement in its translational, rotational, and flexible parts, is also employed within the present formulation, but on a nodal-based level. This means that we treat the flexible body in its spatially discretized state ab initio, wherefore only a finite number of points—the FE nodes—may be in motion. Therefore the global (discrete) nodal displacement $\boldsymbol{c}_{\mathrm{}}^{\mathrm{(\textit{i})}} \in \mathbb{R}^{3 \times 1}$ of node $n_{i}$ is now decomposed into its translational part $\boldsymbol{c}_{\mathrm{t}}^{ \mathrm{(\textit{i})}} \in \mathbb{R}^{3 \times 1}$, rotational part $\boldsymbol{c}_{\mathrm{r}}^{\mathrm{(\textit{i})}} \in \mathbb{R} ^{3 \times 1}$, and flexible part $\boldsymbol{c}_{\mathrm{f}}^{\mathrm{( \textit{i})}} \in \mathbb{R}^{3 \times 1}$:

$$ \boldsymbol{c}_{\mathrm{}}^{\mathrm{(\textit{i})}}= \boldsymbol{c}_{ \mathrm{t}}^{\mathrm{(\textit{i})}}+\boldsymbol{c}_{\mathrm{r}}^{\mathrm{( \textit{i})}}+ \boldsymbol{c}_{\mathrm{f}}^{\mathrm{(\textit{i})}} . $$

(6)

All FE nodes of the body share the same displacement for a rigid-body translation, that is, the distance $\boldsymbol{q}_{\mathrm{t}}^{ \mathrm{}}$ between global ℱ and local $\overline{ \mathcal{F}}$ frame (Fig. 1), and hence

$$ \boldsymbol{c}_{\mathrm{t}}^{\mathrm{(\textit{i})}}= \boldsymbol{q} _{\mathrm{t}}^{\mathrm{}} . $$

(7)

Similarly, the displacement associated with a rigid-body rotation of node $n_{i}$ is given by the position of node $n_{i}$ after rotation $\boldsymbol{A} \overline{\boldsymbol{x}}^{(i)}$ minus its reference position $\overline{ \boldsymbol{x}}^{(i)}$:

$$ \boldsymbol{c}_{\mathrm{r}}^{\mathrm{(\textit{i})}}= ( \boldsymbol{A}- \boldsymbol{I} ) \boldsymbol{\overline{x}}_{\mathrm{}}^{\mathrm{( \textit{i})}} , $$

(8)

where $\boldsymbol{I} \in \mathbb{R}^{3 \times 3}$ is the identity matrix, and $\boldsymbol{\overline{x}}_{\mathrm{}}^{\mathrm{( \textit{i})}}\in \mathbb{R}^{3 \times 1}$ is the undeformed (reference) nodal coordinates of node $n_{i}$ expressed in $\overline{\mathcal{F}}$.

Finally, the rotation matrix $\boldsymbol{A}$ may be employed to express a local quantity in the global frame ℱ. Hence the global flexible nodal displacement of node $n_{i}$ is given by

$$ \boldsymbol{c}_{\mathrm{f}}^{\mathrm{(\textit{i})}}= \boldsymbol{A} \overline{ \boldsymbol{c}}_{\mathrm{f}}^{(i)} , $$

(9)

where $\overline{\boldsymbol{c}}_{\mathrm{f}}^{(i)}$ denotes the flexible part of the nodal displacement of node $n_{i}$ relative to the floating frame $\overline{\mathcal{F}}$, as used in linear FE analyses.

Combining Eqs. (6) to (9) yields

$$ \boldsymbol{c}_{\mathrm{}}^{\mathrm{(\textit{i})}} = \boldsymbol{q} _{\mathrm{t}}^{\mathrm{}} + (\boldsymbol{A}-\boldsymbol{I} ) \boldsymbol{ \overline{x}}_{\mathrm{}}^{\mathrm{(\textit{i})}} + \boldsymbol{A} \overline{ \boldsymbol{c}}_{\mathrm{f}}^{(i)} , $$

(10)

which may be written in a single block column matrix for all FE nodes as [19]

$$ \boldsymbol{c} = \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \boldsymbol{q}_{\mathrm{t}}^{\mathrm{}} + \left (\boldsymbol{A}_{ \mathrm{bd}}^{\mathrm{}}- \boldsymbol{I}_{\mathrm{bd}}^{\mathrm{}} \right ) \boldsymbol{ \overline{x}}_{\mathrm{}}^{\mathrm{}} + \boldsymbol{A} _{\mathrm{bd}}^{\mathrm{}} \overline{\boldsymbol{c}}_{\mathrm{f}} , $$

(11)

where

$${\mathit{\Phi }}_{\mathrm{t}}^{}={\left[\begin{array}{ccc}\mathit{I}& \dots & \mathit{I}\end{array}\right]}^{\mathrm{T}}\in {\mathbb{R}}^{3n_{\mathrm{n}}\times 3}$$

(12)

applies the translation $\boldsymbol{q}_{\mathrm{t}}^{\mathrm{}}$ to all FE nodes, and

$$ \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}}=\mathrm{diag}(\boldsymbol{A}, \dots ,\boldsymbol{A}) \in \mathbb{R}^{3 n_{\mathrm{n}} \times 3 n _{\mathrm{n}}} $$

(13)

and

$$ \boldsymbol{I}_{\mathrm{bd}}^{\mathrm{}}=\mathrm{diag}(\boldsymbol{I}, \dots ,\boldsymbol{I}) \in \mathbb{R}^{3 n_{\mathrm{n}} \times 3 n _{\mathrm{n}}} $$

(14)

denote the associated block-diagonal matrices with the rotation matrix and the identity matrix on their diagonals, respectively. Note that all herein mentioned block-nodal column matrices, such as $\boldsymbol{c}, \overline{\boldsymbol{x}}, \overline{\boldsymbol{c}}_{\mathrm{f}}, \ldots \in \mathbb{R}^{3n_{\mathrm{n}} \times 1}$, are arranged in the standard FE manner, that is,

$$\mathit{c}=\left[\begin{array}{c}{\mathit{c}}^{(1)}\\ ⋮\\ {\mathit{c}}^{(n_{\mathrm{n}})}\end{array}\right]\in {\mathbb{R}}^{3n_{\mathrm{n}}\times 1}.$$

(15)

Equation (11) defines the mapping

$$ \boldsymbol{c} =\boldsymbol{c} ( \boldsymbol{q} ) $$

(16)

between the global nodal displacements $\boldsymbol{c}$ and the generalized coordinates

$$\mathit{q}={\left[\begin{array}{ccc}{\mathit{q}}_{\mathrm{t}}^{\mathrm{T}}& {\mathit{\theta }}_{}^{\mathrm{T}}& {\bar{\mathit{c}}}_{\mathrm{f}}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}.$$

(17)

Differentiating Eq. (11) w.r.t. time yields the nodal velocities as a function of the generalized coordinates and generalized velocities:

$$ \dot{\boldsymbol{c}}=\dot{\boldsymbol{c}}(\boldsymbol{q}, \dot{ \boldsymbol{q}}) . $$

(18)

Carrying out differentiation and noting that $\boldsymbol{\varPhi } _{\mathrm{t}}^{\mathrm{}}$ and $\boldsymbol{\overline{x}}$ are constant over time yield

$$\begin{aligned} \dot{\boldsymbol{c}} &= \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}}_{\mathrm{t}} + \dot{ \boldsymbol{A}}_{\mathrm{bd}} ( \boldsymbol{\overline{x}} + \overline{ \boldsymbol{c}}_{ \mathrm{f}} ) + \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \dot{\overline{\boldsymbol{c}}}_{\mathrm{f}} \end{aligned}$$

(19)

$$=\left[\begin{array}{ccc}{\mathit{\Phi }}_{\mathrm{t}}^{}& -{\mathit{A}}_{\mathrm{bd}}^{}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& {\mathit{A}}_{\mathrm{bd}}^{}\end{array}\right]\left[\begin{array}{c}{\dot{\mathit{q}}}_{\mathrm{t}}\\ \dot{\mathit{\theta }}\\ {\dot{\bar{\mathit{c}}}}_{\mathrm{f}}\end{array}\right]$$

(20)

$$\begin{aligned} &=\boldsymbol{L} (\boldsymbol{q} ) \dot{\boldsymbol{q}} , \end{aligned}$$

(21)

where the relationship between the time derivative of the rotation matrix and the angular velocity,

$$ \dot{\boldsymbol{A}}=\boldsymbol{A} \widetilde{\overline{ \boldsymbol{\omega }}} \quad \Longrightarrow \quad \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}}= \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}, $$

(22)

and the anticommutativity of the cross product,

$$ {\boldsymbol{\overline{\omega }}} \times \boldsymbol{ \overline{c}} _{\mathrm{}}^{\mathrm{(\textit{i})}} = \widetilde{\boldsymbol{ \overline{\omega }}} \, \boldsymbol{\overline{c}}_{\mathrm{}}^{\mathrm{(\textit{i})}} =- \widetilde{\boldsymbol{\overline{c}}}_{\mathrm{}}^{\mathrm{( \textit{i})}} \boldsymbol{\overline{\omega }} = - \boldsymbol{\overline{c}}_{\mathrm{}}^{\mathrm{(\textit{i})}} \times \boldsymbol{\overline{\omega }} \quad \Longrightarrow \quad \widetilde{ \overline{\boldsymbol{\omega }}}_{\mathrm{bd}} \boldsymbol{ \overline{r}}_{\mathrm{f}}^{\mathrm{}}=- \widetilde{\boldsymbol{ \overline{r}}}_{\mathrm{f}}^{\mathrm{}} \boldsymbol{\overline{\omega }} , $$

(23)

have been transferred to the block-nodal structure of the nodal-based equations presented to simplify the middle term on the right-hand side of Eq. (19) to Eq. (21). Note that

$$ \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}= \mathrm{diag}( \widetilde{\overline{\boldsymbol{\omega }}},\dots , \widetilde{\overline{ \boldsymbol{\omega }}}) \in \mathbb{R}^{3 n_{ \mathrm{n}} \times 3 n_{\mathrm{n}}} $$

(24)

denotes the block-diagonal matrix with the skew-symmetric matrix²$\widetilde{\overline{\boldsymbol{\omega }}} \in \mathbb{R}^{3 \times 3}$ associated with the angular velocity vector $\overline{ \boldsymbol{\omega }}$, that is,

$$\bar{\mathit{\omega }}=\left[\begin{array}{c}{\bar{\omega }}_1\\ {\bar{\omega }}_2\\ {\bar{\omega }}_3\end{array}\right]⟹\widetilde{\bar{\mathit{\omega }}}=\left[\begin{array}{ccc}0& -{\bar{\omega }}_3& {\bar{\omega }}_2\\ {\bar{\omega }}_3& 0& -{\bar{\omega }}_1\\ -{\bar{\omega }}_2& {\bar{\omega }}_1& 0\end{array}\right],$$

(25)

on its diagonal. Furthermore, the matrix $\overline{ \boldsymbol{G}}=\overline{\boldsymbol{G}}(\boldsymbol{\theta })$ depends on the rotation parameters $\boldsymbol{\theta }$ so that

$$ \overline{\boldsymbol{\omega }}=\overline{\boldsymbol{G}} \dot{ \boldsymbol{\theta }} \in \mathbb{R}^{3 \times 1}, $$

(26)

where the generic relationship in Eq. (26) is valid for any set of rotation parameters [14], which means that the presented derivations and equations are valid for any parameterization. The matrix $\widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}$ comprises the $n_{\mathrm{n}}$ skew-symmetric matrices $\widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{(i)} \in \mathbb{R}^{3 \times 3}$ of all FE nodes associated with the nodal position vectors,

$$ \overline{\boldsymbol{r}}_{\mathrm{f}}^{(i)}= \boldsymbol{\overline{x}}^{(i)} + \overline{\boldsymbol{c}}_{ \mathrm{f}}^{(i)} \in \mathbb{R}^{3 \times 1} \quad \Longrightarrow \quad \overline{ \boldsymbol{r}}_{\mathrm{f}}= \boldsymbol{\overline{x}} + \overline{ \boldsymbol{c}}_{\mathrm{f}} \in \mathbb{R}^{3 n_{\mathrm{n}} \times 1} , $$

(27)

after elastic deformation, expressed in the body frame, that is,

$${\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}=\left[\begin{array}{c}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{(1)}\\ ⋮\\ {\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{(n_{\mathrm{n}})}\end{array}\right]\in {\mathbb{R}}^{3n_{\mathrm{n}}\times 3}.$$

(28)

Note that the derived anticommutativity property of the block-nodal quantities stated in the rightmost part of Eq. (23) is also valid for any block-nodal column matrix such as $\overline{\boldsymbol{c}}_{\mathrm{f}}, \, \dot{\overline{\boldsymbol{c}}}_{\mathrm{f}}, \, \overline{ \boldsymbol{x}}, \, \overline{\boldsymbol{r}}_{\mathrm{f}}, \dots$$\in \mathbb{R}^{3 n_{\mathrm{n}} \times 1}$ arranged in the standard FE manner; see Eq. (15).

4 Nodal-based derivation of the equations of motion

4.1 Lagrangian approach

The spatially discretized nodal-based FFRF EOMs are derived via Lagrange’s equation

$$ \frac{\mathrm{d}}{\mathrm{d} t} \biggl( \frac{\partial L}{\partial \dot{\boldsymbol{q}}^{\mathrm{T}}} \biggr) - \frac{\partial L}{ \partial \boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}}= \boldsymbol{0} , $$

(29)

where the modified Lagrangian $L$ for a general mechanical system is given by [7]

$$ L=T-V+W-\boldsymbol{\lambda }_{\mathrm{}}^{\mathrm{\! T}} \boldsymbol{g} $$

(30)

with $W$ representing the work done by applied FE nodal forces, $\boldsymbol{\lambda }$ represents the Lagrange multipliers, and $\boldsymbol{g}=\boldsymbol{0}$ represents the holonomic constraint equations defined in terms of the global FE nodal displacements $\boldsymbol{c}$.

A further key aspect to enable the nodal-based treatment of the FFRF is defining the system energies on a semidiscrete (nodal-based) level. The nodal-based linear elastic strain energy $V$, the nodal-based kinetic energy $T$, and the nodal-based work done by applied forces $W$ are given by

$$\begin{aligned} V &=\frac{1}{2} \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}} \overline{ \boldsymbol{K}} \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{}} , \end{aligned}$$

(31)

$$\begin{aligned} T &=\frac{1}{2} \dot{\boldsymbol{c}}^{\mathrm{T}} \boldsymbol{M}_{ \mathrm{}}^{\mathrm{}} \dot{\boldsymbol{c}}, \quad \text{and} \end{aligned}$$

(32)

$$\begin{aligned} W &=\boldsymbol{c}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{f} , \end{aligned}$$

(33)

where $\boldsymbol{\overline{K}}$ denotes the standard (constant) FE stiffness matrix expressed in the floating frame $\overline{ \mathcal{F}}$, $\boldsymbol{f}$ denotes the applied FE nodal forces expressed in the global frame ℱ, and $\boldsymbol{M}$ is the consistent (constant) FE mass matrix, where

$$ \boldsymbol{M}=\boldsymbol{\overline{M}}, $$

(34)

since the consistent (or lumped) FE mass matrix is rotation invariant and therefore commutes with the block-diagonal rotation matrix, that is,

$$ \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}}=\boldsymbol{M} \quad \Longleftrightarrow \quad \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}}= \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \boldsymbol{M} . $$

(35)

In fact, any matrix composed out of $\alpha _{ij} \boldsymbol{I}$-blocks, where $\alpha _{ij}$ are scalars, such as the consistent and lumped FE mass matrix, commutes with any block-diagonal matrix of appropriate size and is invariant under left- and right-multiplication, in the sense of Eq. (35), if the matrices composing the block-diagonal matrix are orthogonal and of appropriate size.

Note that for the derivation in its present form, we have to require that the FE mass matrix is invariant to rotations; see Eqs. (34) and (35). As already mentioned, this invariance holds if $\boldsymbol{\overline{M}}$ is composed out of $\alpha _{ij} \boldsymbol{I}$-blocks, which is the case for the consistent (and, of course, also for the lumped) mass matrix known from the linear FE theory if the used elements employ only nodal displacements as DOFs or, more generally, as long as all DOFs of a node use the same interpolation shape functions, which is the case for solid continuum finite elements, in contrast to structural elements such as beams, shells, membranes, and trusses. If this requirement is not fulfilled, then the nodal-based framework might be generalized at the expense of a slightly more involved derivation and more complicated EOMs; this generalization—including nodal rotations, where $\boldsymbol{{M}}=\boldsymbol{\overline{M}}$ does not hold—is the subject of future research.

As already mentioned, a key aspect to enable the nodal-based treatment is an appropriate semidiscrete definition of the system energies, which leads to differences between the nodal displacements used to define $T$, $W$, and $V$. On the one hand, only the flexible part of $\boldsymbol{c}$ contributes to the linear elastic strain energy, which is attributed to the fact that rigid-body displacements cannot give rise to stresses and strains (elastic forces), which is why Eq. (31) is stated in terms of $\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{}}$ instead of $\boldsymbol{c}$. On the other hand, rigid-body translations and rotations contribute, of course, to the kinetic energy and to the work done by applied forces of the FE-discretized body, which is why both are expressed in terms of $\boldsymbol{c}$. It is clear that it makes only sense to multiply quantities expressed in the same coordinate system, which is fulfilled here; see Eqs. (31) to (33). This is trivial for $V$ and $W$, but in fact, the consistent FE mass matrix is assembled with respect to the floating frame $\overline{ \mathcal{F}}$ and multiplied with the global nodal displacements expressed in ℱ. However, since $\boldsymbol{{M}}=\boldsymbol{\overline{M}}$ is invariant to translations and rotations, Eq. (32) is valid for the presented geometrically nonlinear formulation under the assumption of large rigid-body translations and rotations, but small flexible deformations and strains.

Combining Eqs. (29) to (33) yields

$$ \underbrace{\frac{\mathrm{d}}{\mathrm{d} t} \biggl( \frac{\partial T}{ \partial \dot{\boldsymbol{q}}_{\mathrm{}}^{\mathrm{T}}} \biggr) - \frac{ \partial T}{\partial \boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}}}_{\substack{ \text{inertia} \\ \text{forces}}} + \underbrace{ \frac{\partial V}{\partial \boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}}}_{\substack{\text{elastic} \\ \text{forces}}} + \underbrace{\frac{\partial \boldsymbol{\lambda } _{\mathrm{}}^{\mathrm{\! T}} \boldsymbol{g}}{\partial \boldsymbol{q} _{\mathrm{}}^{\mathrm{T}}}}_{\substack{\text{constraint} \\ \text{forces}}} = \underbrace{\frac{\partial W}{\partial \boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}}}_{\substack{\text{applied} \\ \text{forces}}} , $$

(36)

since

$$ T=T\left (\dot{\boldsymbol{c}}(\boldsymbol{q},\dot{ \boldsymbol{q}})\right ) $$

(37)

(see Eq. (21) and Eq. (32)),

$$ V=V(\boldsymbol{q}) $$

(38)

(see Eq. (17) and Eq. (31)),

$$ W =W\left (\boldsymbol{c}(\boldsymbol{q}),t\right ) $$

(39)

(see Eq. (11) and Eq. (33)), and

$$ \boldsymbol{g}\left (\boldsymbol{c}(\boldsymbol{q}),t\right )= \boldsymbol{0} . $$

(40)

Note that $\boldsymbol{\lambda }=\boldsymbol{\lambda }(t)$ and $\boldsymbol{f}=\boldsymbol{f}(t)$.

The individual force terms, that is, the contributions of Eq. (36), will be derived in Sects. 4.2–4.5.

4.2 Inertia forces

The inertia forces of the nodal-based FFRF EOMs (see Eq. (36)) can be derived with the help of the chain rule of differentiation and Eq. (37).

Before we derive the inertia forces, it is worth mentioning that Eq. (16), Eq. (21), and $\boldsymbol{q}=\boldsymbol{q}(t)$ imply that

$$ \frac{\partial \dot{\boldsymbol{c}}}{\partial \dot{\boldsymbol{q}}} = \frac{\partial \boldsymbol{c}}{\partial \boldsymbol{q}} = \boldsymbol{L} , $$

(41)

since, by the chain rule of differentiation,

$$ \dot{\boldsymbol{c}} \stackrel{(16)}{=} \frac{\partial \boldsymbol{c}}{\partial \boldsymbol{q}} \dot{\boldsymbol{q}} . $$

(42)

Note that Eq. (41) may be also obtained by differentiating Eq. (11) directly w.r.t. $\boldsymbol{q}$; see Appendix A.

Differentiating the kinetic energy, Eq. (32), w.r.t. $\dot{\boldsymbol{q}}_{\mathrm{}}^{\mathrm{T}}$ and $t$ yields the first term on the left-hand side of Eq. (36):

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d} t} \biggl( \frac{\partial T}{\partial \dot{\boldsymbol{q}}_{\mathrm{}}^{\mathrm{T}}} \biggr) & \stackrel[{(37)}]{(2)}{=} \frac{\mathrm{d}}{\mathrm{d} t} \biggl( \frac{\partial \dot{\boldsymbol{c}}}{ \partial \dot{\boldsymbol{q}}_{\mathrm{}}^{\mathrm{T}}} \frac{\partial T}{\partial \dot{\boldsymbol{c}}_{\mathrm{}}^{\mathrm{T}}} \biggr) \end{aligned}$$

(43)

$$\begin{aligned} &\stackrel{(41)}{=} \frac{\mathrm{d}}{ \mathrm{d} t} \biggl( \boldsymbol{L}_{\mathrm{}}^{\mathrm{T}} \frac{ \partial T}{\partial \dot{\boldsymbol{c}}_{\mathrm{}}^{\mathrm{T}}} \biggr) \end{aligned}$$

(44)

$$\begin{aligned} & \stackrel[{(32)}]{ (5)}{=} \frac{ \mathrm{d}}{\mathrm{d} t} \left ( \boldsymbol{L}_{\mathrm{}}^{ \mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{c}} \right ) \end{aligned}$$

(45)

$$\begin{aligned} &\stackrel{(21)}{=} \frac{\mathrm{d}}{\mathrm{d} t} \left ( \boldsymbol{L}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{L} \dot{\boldsymbol{q}} \right ) \end{aligned}$$

(46)

$$\begin{aligned} &= \dot{\boldsymbol{L}}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{L} \dot{\boldsymbol{q}} + \boldsymbol{L}_{\mathrm{}}^{ \mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{L}} \dot{\boldsymbol{q}} + \boldsymbol{L}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{L} \ddot{\boldsymbol{q}} , \end{aligned}$$

(47)

since $\boldsymbol{M}=\mathrm{const.}$ w.r.t. time, with

$$\dot{\mathit{L}}\underset{\text{(49)}}{\overset{\text{(22)}}{=}}\left[\begin{array}{ccc}\mathbf{0}& -{\mathit{A}}_{\mathrm{bd}}^{}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}+{\dot{\widetilde{\bar{\mathit{c}}}}}_{\mathrm{f}}\bar{\mathit{G}}+{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}})& {\mathit{A}}_{\mathrm{bd}}^{}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}\end{array}\right],$$

(48)

where we have used the same relationships employed to obtain the matrix $\boldsymbol{L}$ itself, and in addition

$$ \dot{{\overline{\boldsymbol{r}}}}_{\mathrm{f}} \stackrel{{ \mathrm{(27)}}}{=} \frac{\mathrm{d} }{ \mathrm{d}t} \left ( \overline{\boldsymbol{c}}_{\mathrm{f}} + \overline{ \boldsymbol{x}} \right ) = \dot{\overline{\boldsymbol{c}}}_{ \mathrm{f}} \quad \Longrightarrow \quad \dot{\widetilde{\overline{\boldsymbol{r}}}}_{\mathrm{f}}= \dot{\widetilde{\overline{\boldsymbol{c}}}}_{\mathrm{f}} \quad \text{since} \ \overline{\boldsymbol{x}}=\mathrm{const.} $$

(49)

has been used.

The next step is to differentiate the kinetic energy, Eq. (32), w.r.t. $\boldsymbol{q}_{\mathrm{}} ^{\mathrm{T}}$ to obtain the second term on the left-hand side of Eq. (36):

$$\begin{aligned} \frac{\partial T}{\partial \boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}} & \stackrel[{(37)}]{ (2)}{=} \frac{ \partial \dot{\boldsymbol{c}}}{\partial \boldsymbol{q}_{\mathrm{}} ^{\mathrm{T}}} \frac{\partial T}{\partial \dot{\boldsymbol{c}}_{ \mathrm{}}^{\mathrm{T}}} \end{aligned}$$

(50)

$$\begin{aligned} & \stackrel[{(32)}]{ (5)}{=} \frac{ \partial \dot{\boldsymbol{c}}}{\partial \boldsymbol{q}_{\mathrm{}} ^{\mathrm{T}}} \boldsymbol{M} \dot{\boldsymbol{c}} \end{aligned}$$

(51)

$$\begin{aligned} &\stackrel{(21)}{=} \frac{\partial \dot{\boldsymbol{c}}}{ \partial \boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}} \boldsymbol{M} \boldsymbol{L} \dot{\boldsymbol{q}} \end{aligned}$$

(52)

$$\begin{aligned} &= \frac{\mathrm{d}}{\mathrm{d} t} \biggl( \frac{\partial \boldsymbol{c}}{\partial \boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}} \biggr) \boldsymbol{M} \boldsymbol{L} \dot{\boldsymbol{q}} \end{aligned}$$

(53)

$$\begin{aligned} &\stackrel{(41)}{=} \dot{\boldsymbol{L}}_{ \mathrm{}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{L} \dot{\boldsymbol{q}} , \end{aligned}$$

(54)

since the order of differentiation does not matter; see Eqs. (52) to (53).

Note that it is also possible to substitute Eq. (21) into Eq. (32) and carry out differentiation directly to obtain the same results as stated in Eq. (47) and Eq. (54) via a more involved but interesting derivation; see Appendix B.

4.3 Elastic forces

The elastic forces of the nodal-based FFRF EOMs (see Eq. (36)) are trivially obtained by differentiating the (symmetric³) quadratic form, Eq. (31), which defines the elastic strain energy w.r.t. $\boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}$:

$$\frac{\partial V}{\partial {\mathit{q}}_{}^{\mathrm{T}}}\underset{\text{(17)}}{\overset{\mathrm{\text{(5)}}}{=}}\left[\begin{array}{c}\mathbf{0}\\ \mathbf{0}\\ {\bar{\mathit{K}}}_{}^{}{\bar{\mathit{c}}}_{\mathrm{f}}^{}\end{array}\right]$$

(55)

$$\begin{aligned} &= {\,\widehat{\boldsymbol{\!K}}} \boldsymbol{q} , \end{aligned}$$

(56)

since $V=V(\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{}})$; see Eq. (31). Note that ${\,\widehat{\boldsymbol{\!K}}}$ is simply the well-known FFRF stiffness matrix containing everywhere zero matrices except on the last diagonal entry, which is the constant stiffness matrix from the linear FE theory.

4.4 Constraint forces

The constraint forces of the nodal-based FFRF EOMs (see Eq. (36)) are obtained by differentiating the linear form $\boldsymbol{\lambda }_{\mathrm{}}^{\mathrm{\! T}} \boldsymbol{g}$ in Eq. (30) w.r.t. $\boldsymbol{q} _{\mathrm{}}^{\mathrm{T}}$:

(57)

$$\begin{aligned} &\stackrel{(40)}{=}\frac{\partial \boldsymbol{c}}{ \partial \boldsymbol{q}_{\mathrm{}}^{\mathrm{T}}} \, \frac{\partial \boldsymbol{g}}{\partial \boldsymbol{c}_{\mathrm{}}^{\mathrm{T}}} \boldsymbol{\lambda } \end{aligned}$$

(58)

$$\begin{aligned} &\stackrel{(41)}{=} \boldsymbol{L}_{\mathrm{}} ^{\mathrm{T}} \boldsymbol{J}_{\mathrm{\! \mathit{{g}}}}^{\mathrm{T}} \boldsymbol{\lambda } , \end{aligned}$$

(59)

where $\boldsymbol{J}_{\mathrm{\! \mathit{{g}}}}^{\mathrm{}}$ is the standard constraint Jacobian obtained by differentiating the constraint equations $\boldsymbol{g}$ defined in terms of the physical FE nodal displacements $\boldsymbol{c}$, w.r.t. $\boldsymbol{c}$:

$$ \boldsymbol{J}_{\mathrm{\! \mathit{{g}}}}^{\mathrm{}}= \frac{\partial \boldsymbol{g}}{\partial \boldsymbol{c}} . $$

(60)

4.5 Applied forces

The applied forces of the nodal-based FFRF EOMs (see Eq. (36)) are obtained by differentiating the linear form, Eq. (33), which defines the work done by applied nodal forces w.r.t. $\boldsymbol{q}_{\mathrm{}}^{ \mathrm{T}}$:

(61)

$$\begin{aligned} &\stackrel{(41)}{=} \boldsymbol{L}_{\mathrm{}} ^{\mathrm{T}} \boldsymbol{f} \end{aligned}$$

(62)

$$\stackrel{\text{(21)}}{=}\left[\begin{array}{c}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{f}\\ -{\bar{\mathit{G}}}_{}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\mathit{f}\\ {\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\mathit{f}\end{array}\right],$$

(63)

where

$$ \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{f} \stackrel{{\mathrm{(12)}}}{=} \sum _{i=1}^{n_{\mathrm{n}}} \boldsymbol{f}_{\mathrm{}}^{\mathrm{(\mathit{i})}} =: \boldsymbol{f} _{\mathrm{res}}^{\mathrm{}} $$

(64)

is the resultant force of all FE nodal forces expressed in the global frame,

$$ \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{f} = \overline{ \boldsymbol{f}} $$

(65)

represents the nodal forces expressed in the body frame, and

$$ - \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{f} = \sum _{i=1} ^{n_{\mathrm{n}}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}} ^{(i)} \boldsymbol{ \overline{f}}_{\mathrm{}}^{\mathrm{(\mathit{i})}} =: \boldsymbol{ \overline{m}}_{\mathrm{res}}^{\mathrm{}} $$

(66)

is the resultant torque generated by all FE nodal forces expressed in the body frame.

4.6 General nodal-based equations of motion

Combining the previously derived force contributions of Eqs. (47), (54), (56), (59) and Eq. (63) according to Lagrange’s equation (36) yields

$$ \boldsymbol{L}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{L} \ddot{\boldsymbol{q}} + \boldsymbol{L}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{L}} \dot{\boldsymbol{q}} + {\,\widehat{\boldsymbol{\!K}}} \boldsymbol{q} + \boldsymbol{L}_{\mathrm{}} ^{\mathrm{T}} \boldsymbol{J}_{\mathrm{\! \mathit{{g}}}}^{\mathrm{T}} \boldsymbol{\lambda } = \boldsymbol{L}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{f} , $$

(67)

where the FFRF mass matrix is given by

$$\begin{aligned} {\,\widehat{\boldsymbol{\!M}}} &=\boldsymbol{L}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{L} \end{aligned}$$

(68)

$$=\left[\begin{array}{ccc}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\mathit{\Phi }}_{\mathrm{t}}^{}& -{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& {\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}\\ & {\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& -{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}\\ \text{sym.}& & {\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}\end{array}\right]$$

(69)

$$=\left[\begin{array}{ccc}m\mathit{I}& -\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& \mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}\\ & {\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& -{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}\\ \text{sym.}& & \mathit{M}\end{array}\right],$$

(70)

and the quadratic velocity vector is given by

$$\begin{aligned} -{\,\widehat{\boldsymbol{\!Q}}}_{\mathrm{v}}^{\mathrm{}} &= \boldsymbol{L} _{\mathrm{}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{L}} \dot{\boldsymbol{q}} \end{aligned}$$

(71)

$$=\left[\begin{array}{c}\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ -{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ \mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\end{array}\right],$$

(72)

since the FE mass matrix is invariant to rotations (see Eq. (35)) and

$$ \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}}=m \boldsymbol{I} , $$

(73)

where $m$ is the mass of the body, which follows directly from the definition of the consistent FE mass matrix and due to the fact that the sum of the FE shape functions is equal to one (partition of unity). Furthermore, Eq. (23) and

$$ \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{A}_{ \mathrm{bd}}^{\mathrm{}} = \boldsymbol{A} \boldsymbol{ \varPhi }_{ \mathrm{t}}^{\mathrm{T}} , $$

(74)

which can be shown by direct calculation, have been used to rearrange the expressions. Hence we can write the nodal-based FFRF EOMs in a similar form as known from the continuum mechanics approach:

$$ {\,\widehat{\boldsymbol{\!M}}} \ddot{\boldsymbol{q}} + {\,\widehat{\boldsymbol{\!K}}} \boldsymbol{q} = {\,\widehat{\boldsymbol{\!Q}}}_{\mathrm{v}}^{\mathrm{}}+ {\,\widehat{\boldsymbol{\!Q}}}_{\mathrm{a}}^{ \mathrm{}}-{\,\,\widehat{\boldsymbol{\! \! J}}}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{\lambda } , $$

(75)

that is,

$$\begin{array}{rl}& \left[\begin{array}{ccc}m\mathit{I}& -\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& \mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}\\ & {\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& -{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}\\ \text{sym.}& & \mathit{M}\end{array}\right]\left[\begin{array}{c}{\ddot{\mathit{q}}}_{\mathrm{t}}\\ \ddot{\mathit{\theta }}\\ {\ddot{\bar{\mathit{c}}}}_{\mathrm{f}}\end{array}\right]+\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \bar{\mathit{K}}\end{array}\right]\left[\begin{array}{c}{\mathit{q}}_{\mathrm{t}}^{}\\ \mathit{\theta }\\ {\bar{\mathit{c}}}_{\mathrm{f}}^{}\end{array}\right]\\ & =\left[\begin{array}{c}-\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ {\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ -\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\end{array}\right]\\ & +\left[\begin{array}{c}{\mathit{f}}_{\mathrm{res}}^{}\\ {\bar{\mathit{G}}}_{}^{\mathrm{T}}{\bar{\mathit{m}}}_{\mathrm{res}}^{}\\ \bar{\mathit{f}}\end{array}\right]-\left[\begin{array}{c}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\\ -{\bar{\mathit{G}}}_{}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\\ {\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\end{array}\right]\frac{\partial \mathit{g}}{\partial {\mathit{c}}_{}^{\mathrm{T}}}\mathit{\lambda },\end{array}$$

(76)

with the generalized applied forces (see Eqs. (62) to (66))

$$ {\,\widehat{\boldsymbol{\!Q}}}_{\mathrm{a}}^{\mathrm{}}= \boldsymbol{L}_{ \mathrm{}}^{\mathrm{T}} \boldsymbol{f} . $$

(77)

Note that [18] derived the nodal-based FFRF EOMs, Eq. (76), through a detour via the absolute coordinate formulation (ACF) [4] at a greater effort but showed that the nodal-based FFRF mass matrix and quadratic velocity vector (see Eq. (76)) may be rearranged to obtain the conventional inertia shape integral terms known from the literature [14, 16], and hence the conventional and nodal-based formulation are equivalent. The equivalence between the nodal-based and conventional FFRFs can be shown by substituting the definition of the standard FE mass matrix into Eq. (76) and by using some relationships stated in the present paper.

4.7 Modal reduction

It is often required to reduce the number of flexible DOFs in Eq. (76) due to limited computation resources. The well-established component mode synthesis (CMS), where the flexible deformation is approximated by a linear combination of component modes, such as vibration eigenmodes, static modes, and so on, is a widely used approach to do so; see, for example, the pioneering works [1, 5, 6, 9, 12]. Within the CMS, it is straightforward to approximate the flexible deformation by a linear combination of component modes, that is, $\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{}} \approx \boldsymbol{\overline{\varPsi }} \boldsymbol{\zeta }$, where $\boldsymbol{\overline{\varPsi }}$ contains columnwise the modes included in the reduction basis, and $\boldsymbol{\zeta }$ are the associated modal coordinates. Therefore the reduction for all generalized coordinates follows:

$$\mathit{q}\approx \mathit{H}\mathit{p}⟺\left[\begin{array}{c}{\mathit{q}}_{\mathrm{t}}^{}\\ {\mathit{\theta }}_{}^{}\\ {\bar{\mathit{c}}}_{\mathrm{f}}\end{array}\right]\approx \left[\begin{array}{ccc}\mathit{I}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{I}}_{\theta }& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \bar{\mathit{\Psi }}\end{array}\right]\left[\begin{array}{c}{\mathit{q}}_{\mathrm{t}}^{}\\ {\mathit{\theta }}_{}^{}\\ \mathit{\zeta }\end{array}\right],$$

(78)

where $\boldsymbol{I}$ and $\boldsymbol{I}_{\! \theta }$ are the identity matrices of proper sizes. Substituting $\boldsymbol{q} \approx \boldsymbol{H} \boldsymbol{p}$ into Eq. (76) and left-multiplying the result with $\boldsymbol{H}_{\mathrm{}}^{ \mathrm{T}}$ yield the nodal-based EOMs in terms of $\boldsymbol{p}$. However, the overall size of the resulting system would be still “large” because of multiplications with “large” matrices involving the generalized coordinates. The aim of a proper model reduction is, however, the reduction of the overall “size” of the governing system of equations, but this is not entirely straightforward within this nodal-based framework. That is why the combination of the nodal-based FFRF and CMS is the scope of a follow-up paper. The purpose of the follow-up paper is to rearrange (without approximations) the EOMs so that all matrix terms of the size of the full FE model are condensed to small constant terms of the size of the number of modes multiplied with the reduced DOFs. This will give us the so-called invariants that commercial flexible multibody packages compute with a lumped mass approach (see Sect. 1) but within the nodal-based framework and without approximations (besides the FE discretization) and a small set of much simpler equations than can be easily implemented on a computer. Also, a follow-up paper will compare test case results with commercial multibody codes to reveal differences caused by the lumped mass approach used in their standard FFRF implementation; see Sect. 1.

4.8 Nodal-based equations of motion for Euler parameters

The nodal-based FFRF EOMs, Eq. (76), may be slightly simplified if Euler parameters are used for the rotational parameterization, that is, $\boldsymbol{\theta }=\boldsymbol{\theta } _{\mathrm{e}}^{\mathrm{}}$ and $\boldsymbol{\overline{G}}= \boldsymbol{\overline{G}}_{\mathrm{e}}^{\mathrm{}}$, since, for Euler parameters [14],

$$ \dot{\overline{\boldsymbol{G}}}_{\mathrm{e}} \dot{\boldsymbol{\theta }}_{\mathrm{e}}=\boldsymbol{0} . $$

(79)

Hence

$$\begin{array}{rl}& \left[\begin{array}{ccc}m\mathit{I}& -\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}{\bar{\mathit{G}}}_{\mathrm{e}}& \mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}\\ & {\bar{\mathit{G}}}_{\mathrm{e}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}{\bar{\mathit{G}}}_{\mathrm{e}}& -{\bar{\mathit{G}}}_{\mathrm{e}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}\\ \text{sym.}& & \mathit{M}\end{array}\right]\left[\begin{array}{c}{\ddot{\mathit{q}}}_{\mathrm{t}}\\ {\ddot{\mathit{\theta }}}_{\mathrm{e}}\\ {\ddot{\bar{\mathit{c}}}}_{\mathrm{f}}\end{array}\right]+\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \bar{\mathit{K}}\end{array}\right]\left[\begin{array}{c}{\mathit{q}}_{\mathrm{t}}^{}\\ {\mathit{\theta }}_{\mathrm{e}}\\ {\bar{\mathit{c}}}_{\mathrm{f}}^{}\end{array}\right]\\ & =\left[\begin{array}{c}-\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}})\\ {\bar{\mathit{G}}}_{\mathrm{e}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}})\\ -\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}})\end{array}\right]+\left[\begin{array}{c}{\mathit{f}}_{\mathrm{res}}^{}\\ {\bar{\mathit{G}}}_{\mathrm{e}}^{\mathrm{T}}{\bar{\mathit{m}}}_{\mathrm{res}}^{}\\ \bar{\mathit{f}}\end{array}\right]\\ & -\left[\begin{array}{c}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\\ -{\bar{\mathit{G}}}_{\mathrm{e}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\\ {\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\end{array}\right]\frac{\partial \mathit{g}}{\partial {\mathit{c}}_{}^{\mathrm{T}}}\mathit{\lambda }.\end{array}$$

(80)

4.9 Nodal-based equations of motion in terms of the angular velocity

It is known that the FFRF may be also derived in terms of the angular velocity $\overline{\boldsymbol{\omega }}$ instead of the rotational parameterization $\boldsymbol{\theta }$, which is also possible within this nodal-based framework. To obtain the desired result, we first differentiate Eq. (26) w.r.t. time:

$$ \dot{\overline{\boldsymbol{\omega }}}=\dot{\overline{\boldsymbol{G}}} \dot{ \boldsymbol{\theta }}+\overline{\boldsymbol{G}} \ddot{\boldsymbol{\theta }} , $$

(81)

and realize that each row of Eq. (76) contains a term including $\overline{\boldsymbol{G}} \ddot{\boldsymbol{\theta }}$, contributed from the FFRF mass matrix times the generalized accelerations, and $\dot{\overline{\boldsymbol{G}}} \dot{\boldsymbol{\theta }}$, contributed from the quadratic velocity vector, premultiplied with the same matrices. These terms may be combined within the product of the mass matrix times the generalized accelerations, which yields

$$\begin{array}{rl}& \left[\begin{array}{ccc}m\mathit{I}& -\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}& \mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}\\ & {\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}& -{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}\\ \text{sym.}& & \mathit{M}\end{array}\right]\left[\begin{array}{c}{\ddot{\mathit{q}}}_{\mathrm{t}}\\ \dot{\bar{\mathit{\omega }}}\\ {\ddot{\bar{\mathit{c}}}}_{\mathrm{f}}\end{array}\right]+\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \bar{\mathit{K}}\end{array}\right]\left[\begin{array}{c}{\mathit{q}}_{\mathrm{t}}^{}\\ \mathit{\theta }\\ {\bar{\mathit{c}}}_{\mathrm{f}}^{}\end{array}\right]\\ & =\left[\begin{array}{c}-\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}})\\ {\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}})\\ -\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}})\end{array}\right]+\left[\begin{array}{c}{\mathit{f}}_{\mathrm{res}}^{}\\ {\bar{\mathit{m}}}_{\mathrm{res}}^{}\\ \bar{\mathit{f}}\end{array}\right]-\left[\begin{array}{c}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\\ -{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\\ {\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\end{array}\right]\frac{\partial \mathit{g}}{\partial {\mathit{c}}_{}^{\mathrm{T}}}\mathit{\lambda }\end{array}$$

(82)

and also shows that the derivation and the result does not depend on the rotational parameterization. Note that the second row of Eq. (82) is initially still premultiplied with $\boldsymbol{\overline{G}}_{\mathrm{}}^{\mathrm{T}}$ after combining the terms involving $\dot{\overline{\boldsymbol{G}}} \dot{\boldsymbol{\theta }}$ and $\overline{\boldsymbol{G}} \ddot{\boldsymbol{\theta }}$, that is,

$$\begin{aligned} \boldsymbol{\overline{G}}_{\mathrm{}}^{\mathrm{T}} & \left [ - \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \boldsymbol{A}_{\mathrm{}}^{\mathrm{T}} \ddot{\boldsymbol{q}}_{ \mathrm{t}} + \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{r}}}_{ \mathrm{f}} \dot{ \overline{\boldsymbol{\omega }}} - \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M}\ddot{\overline{\boldsymbol{c}}}_{\mathrm{f}} \right ] \\ & \quad = \boldsymbol{\overline{G}}_{\mathrm{}}^{\mathrm{T}} \left [ \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \boldsymbol{M} \left ( \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}{\overline{ \boldsymbol{r}}}_{\mathrm{f}} + 2 \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} \dot{{\overline{\boldsymbol{c}}}}_{\mathrm{f}} \right ) + \boldsymbol{\overline{m}}_{\mathrm{res}}^{\mathrm{}}+ \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \frac{\partial \boldsymbol{g}}{\partial \boldsymbol{c}_{\mathrm{}}^{\mathrm{T}}} \boldsymbol{\lambda } \right ] . \end{aligned}$$

(83)

However, Eq. (83) must hold for all orientations/times, and thus the terms in brackets must be equal. Hence $\boldsymbol{\overline{G}}_{\mathrm{}}^{\mathrm{T}}$ has been dropped from Eq. (82).

4.10 Nodal-based equations of motion for 2D problems

The same considerations presented in Sects. 3 to 4.6 are, of course, also applicable for planar (2D) problems, where things become simpler. In two dimensions⁴ the (planar) rotation matrix is given by

$$\underset{\_}{\mathit{A}}=\left[\begin{array}{cc}cos(\vartheta )& -sin(\vartheta )\\ sin(\vartheta )& cos(\vartheta )\end{array}\right]\in {\mathbb{R}}^{2\times 2}$$

(84)

and depends only on one (scalar) rotation parameter, the angle $\vartheta$. Hence

$$ \dot{\underline{\boldsymbol{A}}}= \frac{\partial \underline{\boldsymbol{A}}}{\partial \vartheta } \dot{\vartheta } \quad \Longrightarrow \quad \dot{ \underline{\boldsymbol{A}}}_{\mathrm{bd}} ^{\mathrm{}}= \frac{\partial \underline{\boldsymbol{A}}_{\mathrm{bd}} ^{\mathrm{}}}{\partial \vartheta } \dot{ \vartheta } , $$

(85)

where

$$ _{\vartheta }\!\underline{\boldsymbol{A}}_{\mathrm{}}^{\mathrm{}}:= \frac{ \partial \underline{\boldsymbol{A}}}{\partial \vartheta }=- \underline{\boldsymbol{A}} \,\widetilde{\!\boldsymbol{I}} \quad \Longrightarrow \quad _{\vartheta }\!\underline{\boldsymbol{A}}_{\mathrm{bd}}^{ \mathrm{}} := \frac{\partial \underline{\boldsymbol{A}}_{\mathrm{bd}} ^{\mathrm{}}}{\partial \vartheta }=- \underline{\boldsymbol{A}}_{ \mathrm{bd}}^{\mathrm{}} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{ \mathrm{}} $$

(86)

with

$$\tilde{\mathit{I}}=-{\tilde{\mathit{I}}}_{}^{\mathrm{T}}=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]\in {\mathbb{R}}^{2\times 2}$$

(87)

and the corresponding block-diagonal matrices

$$\begin{aligned} _{\vartheta }\!\underline{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} &= \mathrm{diag}({_{\vartheta }\!\underline{\boldsymbol{A}}},\dots , {_{\vartheta }\!\underline{\boldsymbol{A}}}) \in \mathbb{R}^{2 n_{ \mathrm{n}} \times 2 n_{\mathrm{n}}} , \end{aligned}$$

(88)

$$\begin{aligned} \underline{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} &=\mathrm{diag}( \underline{\boldsymbol{A}},\dots ,\underline{\boldsymbol{A}}) \in \mathbb{R}^{2 n_{\mathrm{n}} \times 2 n_{\mathrm{n}}} , \end{aligned}$$

(89)

$$\begin{aligned} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} &=\mathrm{diag}\left ( \,\widetilde{\!\boldsymbol{I}},\dots ,\,\widetilde{\!\boldsymbol{I}} \right ) \in \mathbb{R}^{2 n_{\mathrm{n}} \times 2 n_{\mathrm{n}}} . \end{aligned}$$

(90)

Note that $\widetilde{\!\boldsymbol{I}}$ and $_{\vartheta }\! \underline{\boldsymbol{A}}$ are orthogonal, that is,

$$\begin{aligned} \widetilde{\!\boldsymbol{I}} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{}}^{ \mathrm{T}}= \,\widetilde{\!\boldsymbol{I}}_{\mathrm{}}^{\mathrm{T}} \,\widetilde{\!\boldsymbol{I}} = \underline{\boldsymbol{I}} \quad &\Longrightarrow \quad \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{T}}= \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{T}} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} = \underline{\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} , \end{aligned}$$

(91)

$$\begin{aligned} {_{\vartheta }\!\underline{\boldsymbol{A}}} \, {_{\vartheta }\! \underline{\boldsymbol{A}}_{\mathrm{}}^{\mathrm{T}}}={_{\vartheta } \! \underline{\boldsymbol{A}}_{\mathrm{}}^{\mathrm{T}}} {_{\vartheta } \! \underline{\boldsymbol{A}}} = \underline{\boldsymbol{I}} \quad & \Longrightarrow \quad {_{\vartheta }\!\underline{\boldsymbol{A}}_{ \mathrm{bd}}^{\mathrm{}}} {_{\vartheta }\!\underline{\boldsymbol{A}} _{\mathrm{bd}}^{\mathrm{T}}}={_{\vartheta } \! \underline{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{T}}} {_{\vartheta } \!\underline{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}}} = \underline{\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} , \end{aligned}$$

(92)

and

$$ \widetilde{\!\boldsymbol{I}} \,\widetilde{\!\boldsymbol{I}} = \,\widetilde{\!\boldsymbol{I}}_{\mathrm{}}^{\mathrm{T}} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{}}^{\mathrm{T}} = - \underline{\boldsymbol{I}}_{\mathrm{}}^{\mathrm{}} \quad \Longrightarrow \quad \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} = \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{T}} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{T}} = - \underline{\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} , $$

(93)

where

$$ \underline{\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}}=\mathrm{diag}( \underline{\boldsymbol{I}},\dots ,\underline{\boldsymbol{I}}) \in \mathbb{R}^{2 n_{\mathrm{n}} \times 2 n_{\mathrm{n}}} $$

(94)

again is the corresponding block-diagonal matrix with the 2D identity matrix $\underline{\boldsymbol{I}}_{\mathrm{}}^{\mathrm{}} \in \mathbb{R}^{2 \times 2}$ on its diagonal.

We now can obtain the $\boldsymbol{L}$ matrix for the planar case in a similar fashion as in the general one (see Eqs. (19) to (21)) with the help of Eqs. (85) and (86):

$$\underset{\_}{\mathit{L}}=\left[\begin{array}{ccc}{\underset{\_}{\mathit{\Phi }}}_{\mathrm{t}}^{}& {}_{\vartheta }\underset{\_}{\mathit{A}}_{\mathrm{bd}}^{}{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}& {\underset{\_}{\mathit{A}}}_{\mathrm{bd}}^{}\end{array}\right].$$

(95)

Furthermore, the time derivative of Eq. (95) is needed to derive the nodal-based 2D FFRF EOMs (see Eq. (67)):

$$\dot{\underset{\_}{\mathit{L}}}\stackrel{\text{(49)}}{=}\left[\begin{array}{ccc}\mathbf{0}& {}_{\vartheta }\underset{\_}{\dot{\mathit{A}}}_{\mathrm{bd}}^{}{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}{+}_{\vartheta }{\underset{\_}{\mathit{A}}}_{\mathrm{bd}}^{}{\dot{\overline{\underset{\_}{\mathit{c}}}}}_{\mathrm{f}}& {\underset{\_}{\dot{\mathit{A}}}}_{\mathrm{bd}}^{}\end{array}\right]$$

(96)

$$\underset{\text{(86)}}{\overset{\text{(85)}}{=}}\left[\begin{array}{ccc}\mathbf{0}& {-}_{\vartheta }{\underset{\_}{\mathit{A}}}_{\mathrm{bd}}^{}{\tilde{\mathit{I}}}_{\mathrm{bd}}^{}{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}\dot{\vartheta }{+}_{\vartheta }{\underset{\_}{\mathit{A}}}_{\mathrm{bd}}^{}{\dot{\overline{\underset{\_}{\mathit{c}}}}}_{\mathrm{f}}& {}_{\vartheta }\underset{\_}{\mathit{A}}_{\mathrm{bd}}^{}\dot{\vartheta }\end{array}\right].$$

(97)

Hence, by analogy to Sect. 4.6,

$$\begin{array}{rl}& \left[\begin{array}{ccc}m\underset{\_}{\mathit{I}}& {}_{\vartheta }\underset{\_}{\mathit{A}}{\underset{\_}{\mathit{\Phi }}}_{\mathrm{t}}^{\mathrm{T}}\underset{\_}{\mathit{M}}{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}& \underset{\_}{\mathit{A}}{\underset{\_}{\mathit{\Phi }}}_{\mathrm{t}}^{\mathrm{T}}\underset{\_}{\mathit{M}}\\ & {\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\underset{\_}{\mathit{M}}{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}& {\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\tilde{\mathit{I}}}_{\mathrm{bd}}^{}\underset{\_}{\mathit{M}}\\ \text{sym.}& & \underset{\_}{\mathit{M}}\end{array}\right]\left[\begin{array}{c}{\ddot{\underset{\_}{\mathit{q}}}}_{\mathrm{t}}\\ \ddot{\vartheta }\\ {\ddot{\overline{\underset{\_}{\mathit{c}}}}}_{\mathrm{f}}\end{array}\right]+\left[\begin{array}{ccc}\mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& 0& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \overline{\underset{\_}{\mathit{K}}}\end{array}\right]\left[\begin{array}{c}{\underset{\_}{\mathit{q}}}_{\mathrm{t}}^{}\\ \vartheta \\ {\overline{\underset{\_}{\mathit{c}}}}_{\mathrm{f}}^{}\end{array}\right]\\ & =\left[\begin{array}{c}{}_{\vartheta }\underset{\_}{\mathit{A}}{\underset{\_}{\mathit{\Phi }}}_{\mathrm{t}}^{\mathrm{T}}\underset{\_}{\mathit{M}}({\tilde{\mathit{I}}}_{\mathrm{bd}}^{}{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}{\dot{\vartheta }}^2-2{\dot{\overline{\underset{\_}{\mathit{c}}}}}_{\mathrm{f}}\dot{\vartheta })\\ {\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\underset{\_}{\mathit{M}}({\tilde{\mathit{I}}}_{\mathrm{bd}}^{}{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}{\dot{\vartheta }}^2-2{\dot{\overline{\underset{\_}{\mathit{c}}}}}_{\mathrm{f}}\dot{\vartheta })\\ {\tilde{\mathit{I}}}_{\mathrm{bd}}^{\mathrm{T}}\underset{\_}{\mathit{M}}({\tilde{\mathit{I}}}_{\mathrm{bd}}^{}{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}{\dot{\vartheta }}^2-2{\dot{\overline{\underset{\_}{\mathit{c}}}}}_{\mathrm{f}}\dot{\vartheta })\end{array}\right]+\left[\begin{array}{c}{\underset{\_}{\mathit{f}}}_{\mathrm{res}}^{}\\ {\overline{\underset{\_}{\mathit{m}}}}_{\mathrm{res}}^{}\\ \overline{\underset{\_}{\mathit{f}}}\end{array}\right]-\left[\begin{array}{c}{\underset{\_}{\mathit{\Phi }}}_{\mathrm{t}}^{\mathrm{T}}\\ {{\overline{\underset{\_}{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}}_{\vartheta }{\underset{\_}{\mathit{A}}}_{\mathrm{bd}}^{\mathrm{T}}\\ {\underset{\_}{\mathit{A}}}_{\mathrm{bd}}^{\mathrm{T}}\end{array}\right]\frac{\partial \mathit{g}}{\partial {\underset{\_}{\mathit{c}}}_{}^{\mathrm{T}}}\mathit{\lambda }\end{array}$$

(98)

by Eq. (86) and Eq. (91), since Eq. (35) is valid for any block-diagonal matrix with an orthogonal matrix (such as ${_{\vartheta }\! \underline{\boldsymbol{A}}}$) placed on its diagonal and Eq. (74) also holds for any block-diagonal matrix (such as ${_{\vartheta }\! \underline{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}}}$). Note that in 2D,

$$\begin{aligned} \overline{\underline{\boldsymbol{m}}}_{\mathrm{res}}^{\mathrm{}} &:= \overline{ \underline{\boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} {_{\vartheta } \! \underline{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{T}}} \underline{ \boldsymbol{f}} \end{aligned}$$

(99)

$$\begin{aligned} & \stackrel[{(87)}]{ (86)}{=} \overline{ \underline{\boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \,\widetilde{\!\boldsymbol{I}}_{\mathrm{bd}}^{\mathrm{}} \overline{\underline{ \boldsymbol{f}}} . \end{aligned}$$

(100)

Equation (98) is the nodal-based counterpart of the conventional 2D FFRF known from the literature [14]; it can be also shown, as already mentioned in Sect. 4.6, by substitution of the definition of the standard FE mass matrix and by using some of the relationships stated in the present paper, that the nodal-based and conventional terms are equivalent.

5 Conclusions

In the present paper, we introduced a nodal-based framework for the floating frame of reference formulation suitable for displacement-based solid finite elements. The novel approach avoids inertia shape integrals ab initio, that is, they arise neither in the derivation nor in the final expression of the equations of motion, which makes the error-prone and tedious computer implementation of the integrals obsolete and avoids the need for a lumped mass approximation, which is commonly employed in commercial flexible multibody codes. Furthermore, the nodal-based/semidiscrete and abstract definition of the system energies enables a very concise but rigorous derivation of the equations of motion, in contrast to the lengthy and involved conventional continuum-mechanics-based derivation of the inertia forces known from the literature, which still attracts attention of researchers. The novel (nodal-based) inertia-integral-free equations of motion are presented for the two- and three-dimensional cases; the final results provide ready-to-implement floating frame equations without inertia shape integrals and lumped mass approximations.

The integration of modal reduction techniques, which is the usual approach in the floating frame of reference formulation to reduce the computational complexity, into the presented nodal-based framework/equations of motion and numerical examples of relevant engineering problems will be the scope of a follow-up paper.

Appendices

Appendix A: Derivative of $\boldsymbol{c}$ with respect to $\boldsymbol{q}$, a direct approach

As already mentioned in Sect. 4.2, it may be shown by differentiating Eq. (11), which states the relationship between the global nodal displacements $\boldsymbol{c}$ in terms of the generalized coordinates $\boldsymbol{q}$, directly w.r.t. $\boldsymbol{q}$ that Eq. (41) holds:

$$\frac{\partial \mathit{c}}{\partial \mathit{q}}\underset{\text{(17)}}{\overset{\text{(3)}}{=}}\left[\begin{array}{ccc}\frac{\partial \mathit{c}}{\partial {\mathit{q}}_{\mathrm{t}}^{}}& \frac{\partial \mathit{c}}{\partial \mathit{\theta }}& \frac{\partial \mathit{c}}{\partial {\bar{\mathit{c}}}_{\mathrm{f}}^{}}\end{array}\right]$$

(101)

$$\underset{\text{(27)}}{\overset{\mathrm{\text{(11)}}}{=}}\left[\begin{array}{ccc}{\mathit{\Phi }}_{\mathrm{t}}^{}& -{\mathit{A}}_{\mathrm{bd}}^{}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& {\mathit{A}}_{\mathrm{bd}}^{}\end{array}\right]$$

(102)

$$\begin{aligned} &\stackrel[{(21)}]{ (20)}{=} \boldsymbol{L} , \end{aligned}$$

(103)

since

$$\frac{\partial {\mathit{A}}_{\mathrm{bd}}^{}{\bar{\mathit{r}}}_{\mathrm{f}}^{}}{\partial \mathit{\theta }}=\left[\begin{array}{c}⋮\\ \frac{\partial \mathit{A}{\bar{\mathit{r}}}_{\mathrm{f}}^{(\mathrm{i})}}{\partial \mathit{\theta }}\\ ⋮\end{array}\right]$$

(104)

$$=\left[\begin{array}{c}⋮\\ -\mathit{A}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{(i)}\bar{\mathit{G}}\\ ⋮\end{array}\right]$$

(105)

$$\begin{aligned} &=- \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{ \overline{\boldsymbol{r}}}_{\mathrm{f}} \overline{ \boldsymbol{G}} , \end{aligned}$$

(106)

where the identity [16]

$$ \frac{\partial \boldsymbol{A} \overline{\boldsymbol{v}} }{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{}}}= - \boldsymbol{A} \widetilde{\overline{ \boldsymbol{v}}}\, \boldsymbol{\overline{G}} , $$

(107)

valid for any vector $\overline{\boldsymbol{v}} \in \mathbb{R}^{3 \times 1}$ that does not explicitly depend on $\boldsymbol{\theta }$, has been applied to the block-nodal structure. Hence Eq. (106) is valid for any block-nodal column matrix such as $\overline{\boldsymbol{c}}_{\mathrm{f}}, \, \dot{\overline{\boldsymbol{c}}}_{\mathrm{f}}, \, \overline{ \boldsymbol{x}}, \, \overline{\boldsymbol{r}}_{\mathrm{f}}, \ldots \in \mathbb{R}^{3 n_{\mathrm{n}} \times 1}$, arranged in the standard FE manner (see Eq. (15)), which does not depend explicitly on $\boldsymbol{\theta }$.

Appendix B: Involved derivation of the inertia forces

2.1 B.1 Preliminary remark

As mentioned in Sect. 4.2, it is also possible to substitute Eq. (21) into Eq. (32) and carry out differentiation directly according to Eq. (29) and Eq. (30) to obtain the inertia forces. This approach is more involved and tedious but exhibits interesting relationships and properties of the involved matrices, which is why it is provided here as well.

Substituting Eq. (21) into Eq. (32) yields $T$ in terms of $\dot{\boldsymbol{q}}$:

$$ T=\frac{1}{2} \dot{\boldsymbol{q}}^{\mathrm{T}} \underbrace{ \boldsymbol{L}_{\mathrm{}}^{\mathrm{T}} \boldsymbol{M}_{\mathrm{}} ^{\mathrm{}} \boldsymbol{L}}_{{\,\widehat{\boldsymbol{\!M}}}} \dot{\boldsymbol{q}} $$

(108)

with the FFRF mass matrix ${\,\widehat{\boldsymbol{\!M}}}$ as before; see Eq. (70). Then the inertia forces arising in the EOMs (see Eq. (36)) are also obtained from

$$ \frac{\mathrm{d}}{\mathrm{d}t} \biggl( \frac{1}{2} \frac{\partial \dot{\boldsymbol{q}}^{\mathrm{T}} {\,\widehat{\boldsymbol{\!M}}} \dot{\boldsymbol{q}}}{\partial \dot{\boldsymbol{q}}^{\mathrm{T}}} \biggr) - \frac{1}{2} \frac{\partial \dot{\boldsymbol{q}}^{ \mathrm{T}} {\,\widehat{\boldsymbol{\!M}}} \dot{\boldsymbol{q}}}{\partial {\boldsymbol{q}}^{\mathrm{T}}}= {\,\widehat{\boldsymbol{\!M}}} \ddot{\boldsymbol{q}} + \underbrace{\,\dot{\widehat{ \boldsymbol{\!M}}} \dot{\boldsymbol{q}} - \frac{1}{2} \frac{\partial \dot{\boldsymbol{q}}^{\mathrm{T}} {\,\widehat{\boldsymbol{\!M}}} \dot{\boldsymbol{q}}}{\partial {\boldsymbol{q}}^{\mathrm{T}}}}_{- {\,\widehat{\boldsymbol{\!Q}}}_{\mathrm{v}}^{\mathrm{}}} $$

(109)

with ${\,\widehat{\boldsymbol{\!M}}}={\,\widehat{\boldsymbol{\!M}}} (\boldsymbol{\theta } ,\overline{\boldsymbol{c}}_{\mathrm{f}} )$ according to Eq. (70). The quadratic velocity vector ${\,\widehat{\boldsymbol{\!Q}}}_{\mathrm{v}}^{\mathrm{}}$ needs further considerations, which is the scope of the following subsections.

2.2 B.2 Involved evaluation of the quadratic velocity vector

2.2.1 B.2.1 Terms involving the derivative w.r.t. the generalized coordinates

Starting with the last term on the right-hand side of Eq. (109), it follows that

$$\frac{\partial {\dot{\mathit{q}}}^{\mathrm{T}}\hat{\mathit{M}}\dot{\mathit{q}}}{\partial {\mathit{q}}^{\mathrm{T}}}=\frac{\partial }{\partial {\mathit{q}}^{\mathrm{T}}}\left[\begin{array}{ccc}{\dot{\mathit{q}}}_{\mathrm{t}}^{\mathrm{T}}& {\dot{\mathit{\theta }}}^{\mathrm{T}}& {\dot{\bar{\mathit{c}}}}_{\mathrm{f}}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{ccc}m\mathit{I}& -{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& {\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}\\ & {\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& -{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}\\ \text{sym.}& & \mathit{M}\end{array}\right]\left[\begin{array}{c}{\dot{\mathit{q}}}_{\mathrm{t}}\\ \dot{\mathit{\theta }}\\ {\dot{\bar{\mathit{c}}}}_{\mathrm{f}}\end{array}\right]$$

(110)

$$\begin{aligned} &\stackrel{\text{{(26)}}}{=} \frac{\partial }{\partial {\boldsymbol{q}}^{\mathrm{T}}} \left ( \dot{\boldsymbol{q}}_{ \mathrm{t}}^{\mathrm{T}} m \dot{\boldsymbol{q}}_{\mathrm{t}}^{ \mathrm{}} - \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \boldsymbol{\overline{\omega }}_{\mathrm{}}^{\mathrm{}} + \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi } _{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}} ^{\mathrm{}} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{\mathrm{}} \right . \\ & \quad {}- \boldsymbol{\overline{\omega }}_{\mathrm{}}^{\mathrm{T}} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} + \boldsymbol{\overline{\omega }}_{ \mathrm{}}^{\mathrm{T}} \widetilde{ \overline{\boldsymbol{r}}}_{ \mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}} \boldsymbol{\overline{ \omega }}_{\mathrm{}}^{\mathrm{}} - \boldsymbol{\overline{\omega }}_{\mathrm{}}^{\mathrm{T}} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{ \mathrm{}} \\ & \quad \left .{} + \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{ \mathrm{T}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{ \varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} - \dot{\boldsymbol{\overline{c}}}_{ \mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}} \boldsymbol{\overline{\omega }}_{\mathrm{}}^{\mathrm{}} + \dot{\overline{\boldsymbol{c}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \dot{\overline{\boldsymbol{c}}}_{\mathrm{f}}^{ \mathrm{}} \right ) \end{aligned}$$

(111)

$$\begin{aligned} &= \frac{\partial }{\partial {\boldsymbol{q}}^{\mathrm{T}}} \left ( \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} m \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} - 2 \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \boldsymbol{\overline{\omega }}_{\mathrm{}}^{\mathrm{}} + 2 \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi } _{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}} ^{\mathrm{}} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{\mathrm{}} \right . \\ & \quad \left .{} + \boldsymbol{\overline{\omega }}_{\mathrm{}}^{ \mathrm{T}} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{r}}}_{ \mathrm{f}} \overline{\boldsymbol{\omega }}_{\mathrm{}}^{\mathrm{}} -2 \overline{\boldsymbol{ \omega }}_{\mathrm{}}^{\mathrm{T}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{ \mathrm{}} + \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{ \mathrm{}} \right ) \end{aligned}$$

(112)

$$\begin{aligned} &=\frac{\partial }{\partial {\boldsymbol{q}}^{\mathrm{T}}} \left ( - 2 \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}} \boldsymbol{\overline{ \omega }}_{\mathrm{}}^{\mathrm{}} + 2 \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi } _{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}} ^{\mathrm{}} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{\mathrm{}} \right . \\ & \quad \left . {}+ \boldsymbol{\overline{\omega }}_{\mathrm{}}^{ \mathrm{T}} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{r}}}_{ \mathrm{f}} \boldsymbol{ \overline{\omega }}_{\mathrm{}}^{\mathrm{}} -2 \boldsymbol{\overline{ \omega }}_{\mathrm{}}^{\mathrm{T}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{ \mathrm{}} \right ) \end{aligned}$$

(113)

$$\begin{aligned} &\stackrel{(23)}{=} 2 \frac{\partial }{\partial {\boldsymbol{q}}^{\mathrm{T}}} \left (\dot{\boldsymbol{q}}_{ \mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{ \mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{\boldsymbol{ \omega }}}_{\mathrm{bd}}{\overline{ \boldsymbol{r}}}_{\mathrm{f}} + \dot{\boldsymbol{q}}_{\mathrm{t}}^{ \mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{}} \right . \\ & \quad {} + \frac{1}{2} {\overline{\boldsymbol{r}}}_{\mathrm{f}} ^{\mathrm{T}} \widetilde{\overline{\boldsymbol{\omega }}}_{ \mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}{ \overline{ \boldsymbol{r}}}_{\mathrm{f}} + {\overline{\boldsymbol{r}}}_{ \mathrm{f}}^{\mathrm{T}} \widetilde{\overline{\boldsymbol{\omega }}} _{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{}} \Bigr) . \end{aligned}$$

(114)

Equation (112) follows from Eq. (111) since a scalar remains unchanged if transposed and $\boldsymbol{M}= \boldsymbol{M}_{\mathrm{}}^{\mathrm{T}}$. Furthermore, Eq. (113) follows from Eq. (112) since both $\dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} m \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{}}$ and $\dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{ \mathrm{}}$ are constant w.r.t. $\boldsymbol{q}$.

None of the terms in Eqs. (110) to (114) depends on $\boldsymbol{q}_{\mathrm{t}}^{\mathrm{}}$, since $T=T(\dot{\boldsymbol{q}},\boldsymbol{\theta }, \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{}})$, that is,

$$ \frac{\partial \dot{\boldsymbol{q}}^{\mathrm{T}} {\,\widehat{\boldsymbol{\!M}}} \dot{\boldsymbol{q}}}{\partial {\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{T}}}=\boldsymbol{0} , $$

(115)

and hence only the partial derivatives of $T$ w.r.t. $\boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}$ and $\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}$ need to be evaluated.

Starting with the partial derivatives w.r.t. $\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}$, we have

$$\begin{aligned} \frac{\partial \dot{\boldsymbol{q}}^{\mathrm{T}} {\,\widehat{\boldsymbol{\!M}}} \dot{\boldsymbol{q}}}{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}} &= \frac{\partial }{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}} \left ( 2 \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi } _{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}} ^{\mathrm{}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} { \overline{\boldsymbol{r}}}_{\mathrm{f}} + {\overline{\boldsymbol{r}}} _{\mathrm{f}}^{\mathrm{T}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \widetilde{\overline{ \boldsymbol{\omega }}}_{ \mathrm{bd}}{\overline{\boldsymbol{r}}}_{\mathrm{f}} + 2 {\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \widetilde{ \overline{\boldsymbol{\omega }}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{ \mathrm{}} \right ) , \end{aligned}$$

(116)

since the second term in brackets on the right-hand side of Eq. (114) is constant w.r.t $\boldsymbol{\overline{c}} _{\mathrm{f}}^{\mathrm{}}$. Differentiating the first term on the right-hand side of Eq. (116), which may be considered as a linear form in $\boldsymbol{\overline{c}}_{\mathrm{f}}^{ \mathrm{}}$, w.r.t. $\boldsymbol{\overline{c}}_{\mathrm{f}}^{ \mathrm{T}}$ yields

$$\begin{aligned} \frac{\partial }{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{ \mathrm{T}}} \left ( 2 \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{\boldsymbol{ \omega }}}_{\mathrm{bd}}{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \right ) & \stackrel{{\mathrm{(4)}}}{=} 2 \frac{\partial \boldsymbol{\overline{r}}_{\mathrm{f}}^{\mathrm{}} }{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{ \varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} \end{aligned}$$

(117)

$$\begin{aligned} & \stackrel{{\mathrm{(120)}}}{=} 2 \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} \end{aligned}$$

(118)

$$\begin{aligned} &\stackrel{{\mathrm{(124)}}}{=} - 2 \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} , \end{aligned}$$

(119)

where

$$ \frac{\partial \boldsymbol{\overline{r}}_{\mathrm{f}}^{\mathrm{}} }{ \partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}} \stackrel{{\mathrm{(27)}}}{=} \frac{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{}} }{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}}=\boldsymbol{I} _{\mathrm{bd}}^{\mathrm{}} \quad \text{since} \ \boldsymbol{\overline{x}}=\mathrm{const.,} $$

(120)

and

$$\begin{aligned} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}^{\mathrm{T}} &= \mathrm{diag}\left (\widetilde{\boldsymbol{\overline{\omega }}}_{\mathrm{}} ^{\mathrm{T}},\dots ,\widetilde{\boldsymbol{\overline{\omega }}}_{ \mathrm{}}^{\mathrm{T}}\right ) \end{aligned}$$

(121)

$$\begin{aligned} &=\mathrm{diag}\left (-\widetilde{\boldsymbol{\overline{\omega }}}_{ \mathrm{}}^{\mathrm{}},\dots ,- \widetilde{\boldsymbol{\overline{ \omega }}}_{\mathrm{}}^{\mathrm{}}\right ) \end{aligned}$$

(122)

$$\begin{aligned} &=-\mathrm{diag}\left (\widetilde{\boldsymbol{\overline{\omega }}}_{ \mathrm{}}^{\mathrm{}},\dots , \widetilde{\boldsymbol{\overline{ \omega }}}_{\mathrm{}}^{\mathrm{}}\right ) \end{aligned}$$

(123)

$$\begin{aligned} &=-\widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}, \end{aligned}$$

(124)

since the transpose of a skew-symmetric matrix is its negative. The derivative of the second term on the right-hand side of Eq. (116), which may be considered as a (symmetric) quadratic form in $\overline{\boldsymbol{r}}_{\mathrm{f}}$, w.r.t. $\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}$ yields

$$\begin{aligned} \frac{\partial }{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{ \mathrm{T}}} \left ( {\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} ^{\mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}{ \overline{ \boldsymbol{r}}}_{\mathrm{f}} \right ) & \stackrel{{\mathrm{ (5)}}}{=} 2 \frac{\partial \boldsymbol{\overline{r}}_{\mathrm{f}}^{\mathrm{}} }{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{\omega }}}_{ \mathrm{bd}} \boldsymbol{\overline{r}}_{\mathrm{f}}^{\mathrm{}} \end{aligned}$$

(125)

$$\begin{aligned} &= - 2 \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{\omega }}}_{ \mathrm{bd}}\boldsymbol{\overline{r}}_{\mathrm{f}}^{\mathrm{}} , \end{aligned}$$

(126)

where again Eq. (120) and Eq. (124) have been used. The derivative of the last term on the right-hand side of Eq. (116), which again may be considered as a linear form in $\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{}}$, w.r.t. $\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}$ yields

$$\begin{aligned} \frac{\partial }{\partial \boldsymbol{\overline{c}}_{\mathrm{f}}^{ \mathrm{T}}} \left ( 2 {\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} ^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{ \mathrm{f}}^{\mathrm{}} \right ) & \stackrel{{\mathrm{(4)}}}{=} 2 \frac{\partial \overline{ \boldsymbol{r}}_{\mathrm{f}}}{\partial \boldsymbol{\overline{c}}_{ \mathrm{f}}^{\mathrm{T}}} \widetilde{\overline{\boldsymbol{\omega }}} _{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{\mathrm{}} \end{aligned}$$

(127)

$$\begin{aligned} &= -2 \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{ \mathrm{}} , \end{aligned}$$

(128)

where, once more, Eq. (120) and Eq. (124) have been used.

Continuing with the partial derivative of $T$ w.r.t. $\boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}$, we have to consider all four terms on the right-hand side of Eq. (114). Differentiating the first term, which may be considered as a linear form in $\dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} {\overline{ \boldsymbol{r}}}_{\mathrm{f}}$, w.r.t. $\boldsymbol{\theta }_{ \mathrm{}}^{\mathrm{T}}$ yields

$$\begin{aligned} \frac{\partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{ \mathrm{T}}} \left (2 \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{\boldsymbol{ \omega }}}_{\mathrm{bd}}{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \right ) & \stackrel{{\mathrm{(22)}}}{=} 2 \frac{\partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}} \left (\dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{ \mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{A}}_{\mathrm{bd}}^{ \mathrm{}} {\overline{\boldsymbol{r}}}_{\mathrm{f}} \right ) \end{aligned}$$

(129)

$$\begin{aligned} &\stackrel{{\mathrm{(4)}}}{=} 2 \frac{\partial \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} {\overline{ \boldsymbol{r}}}_{\mathrm{f}}}{\partial \boldsymbol{\theta }_{ \mathrm{}}^{\mathrm{T}}} \boldsymbol{M} \boldsymbol{\varPhi }_{ \mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{}} \end{aligned}$$

(130)

$$\begin{aligned} &\stackrel{{\mathrm{(135)}}}{=} - 2 \left ( \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\boldsymbol{ \overline{r}}}_{\mathrm{f}}^{\mathrm{}} \boldsymbol{ \overline{G}} + \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\boldsymbol{\overline{r}}}_{\mathrm{f}}^{\mathrm{}} \dot{\boldsymbol{ \overline{G}}} \right )^{\mathrm{T}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} \end{aligned}$$

(131)

$$\begin{aligned} &\stackrel{{\mathrm{(22)}}}{=} - 2 \left ( \boldsymbol{{A}} _{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{ \boldsymbol{\omega }}}_{\mathrm{bd}} \widetilde{\boldsymbol{ \overline{r}}}_{\mathrm{f}}^{\mathrm{}} \boldsymbol{\overline{G}} + \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\boldsymbol{ \overline{r}}}_{\mathrm{f}}^{\mathrm{}} \dot{\boldsymbol{\overline{G}}} \right )^{\mathrm{T}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} \end{aligned}$$

(132)

$$\begin{aligned} &\stackrel{{\mathrm{(124)}}}{=} 2 \left ( \boldsymbol{\overline{G}}_{\mathrm{}}^{\mathrm{T}} \widetilde{\boldsymbol{ \overline{r}}}_{\mathrm{f}}^{\mathrm{T}} \widetilde{\overline{ \boldsymbol{\omega }}}_{\mathrm{bd}}- \dot{\boldsymbol{\overline{G}}}_{\mathrm{}}^{\mathrm{T}} \widetilde{\boldsymbol{\overline{r}}}_{\mathrm{f}}^{\mathrm{T}} \right ) \boldsymbol{{A}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{ \varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} , \end{aligned}$$

(133)

since⁵ [16]

$$ \frac{\partial \dot{\boldsymbol{A}} \overline{\boldsymbol{v}}}{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}}= - \left (\dot{\boldsymbol{A}}\, \widetilde{ \overline{\boldsymbol{v}}} \,\boldsymbol{\overline{G}} + \boldsymbol{A} \widetilde{ \overline{\boldsymbol{v}}}\, \dot{\boldsymbol{\overline{G}}} \right )^{\mathrm{T}} $$

(134)

for any vector $\overline{\boldsymbol{v}} \in \mathbb{R}^{3 \times 1}$ that does not depend explicitly on $\boldsymbol{\theta }$ may be applied to the block-nodal structure, in a similar fashion as it was performed to obtain Eq. (106) (see also Eqs. (104) to (107)), to obtain

$$ \frac{\partial \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} {\overline{ \boldsymbol{r}}}_{\mathrm{f}}}{\partial \boldsymbol{\theta }_{ \mathrm{}}^{\mathrm{T}}}= - \left (\dot{\boldsymbol{A}}_{\mathrm{bd}} ^{\mathrm{}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \, \boldsymbol{\overline{G}} + \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \, \dot{\boldsymbol{\overline{G}}} \right )^{\mathrm{T}} $$

(135)

for any block-nodal column matrix that does not depend explicitly on $\boldsymbol{\theta }$, such as $\overline{\boldsymbol{c}}_{\mathrm{f}}$, $\dot{\overline{\boldsymbol{c}}}_{\mathrm{f}}$, $\overline{ \boldsymbol{x}}$, $\overline{\boldsymbol{r}}_{\mathrm{f}}$, ... $\in \mathbb{R}^{3 n_{\mathrm{n}} \times 1}$, arranged in the standard FE manner (see Eq. (15)). The derivative of the second term on the right-hand side of Eq. (114), which may be considered as a linear form in $\boldsymbol{A}_{\mathrm{bd}}^{ \mathrm{}} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{}}$, w.r.t. $\boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}$ yields

$$\begin{aligned} \frac{\partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{ \mathrm{T}}} \left (2 \dot{\boldsymbol{q}}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{\mathrm{}} \right ) & \stackrel{{\mathrm{ (4)}}}{=} 2 \frac{\partial \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{}}}{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} \end{aligned}$$

(136)

$$\begin{aligned} &\stackrel{{\mathrm{(106)}}}{=}- 2 \boldsymbol{\overline{G}}_{\mathrm{}}^{\mathrm{T}} \dot{\widetilde{\overline{\boldsymbol{c}}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}} \dot{\boldsymbol{q}} _{\mathrm{t}}^{\mathrm{}} , \end{aligned}$$

(137)

since again Eq. (106) is valid for $\dot{\overline{\boldsymbol{c}}}_{\mathrm{f}}$ as well. The derivative of the third term on the right-hand side of Eq. (114), which may be considered as a (symmetric) quadratic form in $\dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} \overline{ \boldsymbol{r}}_{\mathrm{f}}$, w.r.t. $\boldsymbol{\theta }_{ \mathrm{}}^{\mathrm{T}}$ yields

$$\begin{aligned} \frac{\partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{ \mathrm{T}}} \left ( {\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} ^{\mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}{ \overline{ \boldsymbol{r}}}_{\mathrm{f}} \right ) &\stackrel{ (22)}{=} \frac{ \partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}} \left ( {\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{{A}}_{ \mathrm{bd}}^{\mathrm{}} \boldsymbol{M} \boldsymbol{{A}}_{\mathrm{bd}} ^{\mathrm{T}} \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} {\overline{ \boldsymbol{r}}}_{\mathrm{f}} \right ) \end{aligned}$$

(138)

$$\begin{aligned} &\stackrel{(35)}{=} \frac{\partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}} \left ( {\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \dot{\boldsymbol{A}}_{ \mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{A}}_{ \mathrm{bd}}^{\mathrm{}} {\overline{\boldsymbol{r}}}_{\mathrm{f}} \right ) \end{aligned}$$

(139)

$$\begin{aligned} &\stackrel{(5)}{=} 2 \frac{\partial \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} {\overline{ \boldsymbol{r}}}_{\mathrm{f}} }{\partial \boldsymbol{\theta }_{ \mathrm{}}^{\mathrm{T}}} \boldsymbol{M} \dot{\boldsymbol{A}}_{ \mathrm{bd}}^{\mathrm{}} {\overline{\boldsymbol{r}}}_{\mathrm{f}} \end{aligned}$$

(140)

$$\begin{aligned} &\stackrel{(135)}{=} -2 \left (\dot{\boldsymbol{A}} _{\mathrm{bd}}^{\mathrm{}} \widetilde{ \overline{\boldsymbol{r}}}_{ \mathrm{f}} \, \boldsymbol{\overline{G}} + \boldsymbol{A}_{ \mathrm{bd}}^{\mathrm{}} \widetilde{\overline{ \boldsymbol{r}}}_{ \mathrm{f}} \, \dot{\boldsymbol{\overline{G}}} \right )^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} {\overline{ \boldsymbol{r}}}_{\mathrm{f}} \end{aligned}$$

(141)

$$\begin{aligned} &\stackrel{(22)}{=} -2 \left (\boldsymbol{ \overline{G}}_{ \mathrm{}}^{\mathrm{T}} \widetilde{\overline{ \boldsymbol{r}}}_{ \mathrm{f}}^{\mathrm{T}} \widetilde{\overline{ \boldsymbol{\omega }}} _{\mathrm{bd}}^{\mathrm{T}} + \dot{\boldsymbol{ \overline{G}}}^{ \mathrm{T}} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \right ) \boldsymbol{{A}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{{A}}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{ \boldsymbol{\omega }}}_{\mathrm{bd}}{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \end{aligned}$$

(142)

$$\begin{aligned} &\stackrel{(35)}{=} -2 \left (\boldsymbol{\overline{G}} _{\mathrm{}}^{\mathrm{T}} \widetilde{\overline{\boldsymbol{r}}}_{ \mathrm{f}}^{\mathrm{T}} \widetilde{ \overline{\boldsymbol{\omega }}} _{\mathrm{bd}}^{\mathrm{T}} + \dot{ \boldsymbol{\overline{G}}}^{ \mathrm{T}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \right ) \boldsymbol{M} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}{\overline{ \boldsymbol{r}}}_{\mathrm{f}} . \end{aligned}$$

(143)

Finally, the derivative of the fourth term on the right-hand side of Eq. (114), which may be also considered as a linear form, w.r.t. $\boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}$ yields

$$\begin{aligned} \frac{\partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{ \mathrm{T}}} \left (2 {\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} ^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{ \mathrm{f}}^{\mathrm{}} \right ) \stackrel{(22)}{=}& 2 \frac{ \partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}} \left ( {\overline{\boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{A}_{ \mathrm{bd}}^{\mathrm{}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{}} \right ) \end{aligned}$$

(144)

$$\begin{aligned} \stackrel{(35)}{=}& 2 \frac{\partial }{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}} \left ( {\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \dot{\boldsymbol{A}}_{ \mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}} ^{\mathrm{}} \dot{\boldsymbol{ \overline{c}}}_{\mathrm{f}}^{\mathrm{}} \right ) \end{aligned}$$

(145)

$$\begin{aligned} \stackrel{(4)}{=}& 2 \frac{\partial \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} \overline{ \boldsymbol{r}}_{\mathrm{f}} }{\partial \boldsymbol{\theta }_{ \mathrm{}}^{\mathrm{T}}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}} ^{\mathrm{}} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{}}+2 \frac{\partial \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{}}}{\partial \boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}} \boldsymbol{M} \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} \overline{ \boldsymbol{r}}_{\mathrm{f}} \end{aligned}$$

(146)

$$\begin{aligned} \stackrel[{(135)}]{ (106)}{=}& -2 \left ( \dot{\boldsymbol{A}}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \, \boldsymbol{\overline{G}} + \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}} \, \dot{\boldsymbol{\overline{G}}} \right )^{\mathrm{T}} \boldsymbol{M} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{}} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{\mathrm{}} \\ & \quad {} -2 \boldsymbol{\overline{G}}_{\mathrm{}}^{\mathrm{T}} \dot{\widetilde{\overline{\boldsymbol{c}}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{A}_{\mathrm{bd}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{ A}}_{\mathrm{bd}}^{\mathrm{}} \overline{ \boldsymbol{r}}_{\mathrm{f}} \end{aligned}$$

(147)

$$\begin{aligned} \stackrel[{(35)}]{ (22)}{=}& -2 \left (\boldsymbol{\overline{G}} ^{\mathrm{T}} \widetilde{\overline{\boldsymbol{r}}}_{\mathrm{f}}^{ \mathrm{T}} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} ^{\mathrm{T}} + \dot{\boldsymbol{\overline{G}}}^{\mathrm{T}} \widetilde{\overline{ \boldsymbol{r}}}_{\mathrm{f}}^{\mathrm{T}} \right ) \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{ \mathrm{}} \\ & {} -2 \boldsymbol{\overline{G}}_{\mathrm{}}^{\mathrm{T}} \dot{\widetilde{\overline{\boldsymbol{c}}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \widetilde{\overline{\boldsymbol{\omega }}}_{ \mathrm{bd}} \overline{\boldsymbol{r}}_{\mathrm{f}} . \end{aligned}$$

(148)

2.2.2 B.2.2 Terms involving the time derivative of the FFRF mass matrix

Continuing with the middle term on the right-hand side of Eq. (109), which involves the time derivative of the FFRF mass matrix defined in Eq. (70), we have

$$\dot{\hat{\mathit{M}}}=\left[\begin{array}{ccc}{\dot{\hat{\mathit{m}}}}_{\mathrm{tt}}^{}& {\dot{\hat{\mathit{m}}}}_{\mathrm{tr}}^{}& {\dot{\hat{\mathit{m}}}}_{\mathrm{tf}}^{}\\ & {\dot{\hat{\mathit{m}}}}_{\mathrm{rr}}^{}& {\dot{\hat{\mathit{m}}}}_{\mathrm{rf}}^{}\\ \text{sym.}& & {\dot{\hat{\mathit{m}}}}_{\mathrm{ff}}^{}\end{array}\right]$$

(149)

$$=\left[\begin{array}{ccc}\mathbf{0}& -{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}+{\dot{\widetilde{\bar{\mathit{r}}}}}_{\mathrm{f}}\bar{\mathit{G}}+{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}})& {\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}\\ & {\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}+{\dot{\widetilde{\bar{\mathit{r}}}}}_{\mathrm{f}}\bar{\mathit{G}})+({\dot{\bar{\mathit{G}}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}+{\bar{\mathit{G}}}^{\mathrm{T}}{\dot{\widetilde{\bar{\mathit{r}}}}}_{\mathrm{f}}^{\mathrm{T}})\mathit{M}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\bar{\mathit{G}}& -({\dot{\bar{\mathit{G}}}}_{}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}+{\bar{\mathit{G}}}_{}^{\mathrm{T}}{\dot{\widetilde{\bar{\mathit{r}}}}}_{\mathrm{f}}^{\mathrm{T}})\mathit{M}\\ \text{sym.}& & \mathbf{0}\end{array}\right],$$

(150)

since both $\boldsymbol{\varPhi }_{\mathrm{t}}^{\mathrm{}}$ and $\boldsymbol{M}$ are constant. Hence

$$\dot{\hat{\mathit{M}}}\dot{\mathit{q}}=\left[\begin{array}{c}{\dot{\hat{\mathit{m}}}}_{\mathrm{tr}}^{}\dot{\mathit{\theta }}+{\dot{\hat{\mathit{m}}}}_{\mathrm{tf}}^{}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}\\ {\dot{\hat{\mathit{m}}}}_{\mathrm{tr}}^{\mathrm{T}}{\dot{\mathit{q}}}_{\mathrm{t}}+{\dot{\hat{\mathit{m}}}}_{\mathrm{rr}}^{}\dot{\mathit{\theta }}+{\dot{\hat{\mathit{m}}}}_{\mathrm{rf}}^{}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}\\ {\dot{\hat{\mathit{m}}}}_{\mathrm{tf}}^{\mathrm{T}}{\dot{\mathit{q}}}_{\mathrm{t}}+{\dot{\hat{\mathit{m}}}}_{\mathrm{rf}}^{\mathrm{T}}\dot{\mathit{\theta }}\end{array}\right]$$

(151)

$$\begin{array}{rl}& =[\begin{array}{c}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}{\mathit{A}}_{\mathrm{bd}}^{}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ -({\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}^{\mathrm{T}}+{\bar{\mathit{G}}}^{\mathrm{T}}{\dot{\widetilde{\bar{\mathit{c}}}}}_{\mathrm{f}}^{\mathrm{T}}+{\dot{\bar{\mathit{G}}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}){\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\mathit{M}{\mathit{\Phi }}_{\mathrm{t}}^{}{\dot{\mathit{q}}}_{\mathrm{t}}^{}+{\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }}-{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}})\\ -{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}^{\mathrm{T}}{\mathit{A}}_{\mathrm{bd}}^{\mathrm{T}}\mathit{M}{\mathit{\Phi }}_{\mathrm{t}}^{}{\dot{\mathit{q}}}_{\mathrm{t}}^{}+\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}^{}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\end{array}\\ & \begin{array}{c}\\ -({\dot{\bar{\mathit{G}}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}+{\bar{\mathit{G}}}^{\mathrm{T}}{\dot{\widetilde{\bar{\mathit{c}}}}}_{\mathrm{f}}^{\mathrm{T}})\mathit{M}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}-{\dot{\bar{\mathit{G}}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}^{}\\ \\ \end{array}],\end{array}$$

(152)

where Eqs. (23), (26), and (49) have been used; furthermore, the facts that

$$ \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}} \boldsymbol{M} = \boldsymbol{M} \widetilde{\overline{\boldsymbol{\omega }}}_{\mathrm{bd}}, $$

(153)

since $\boldsymbol{M}$ is composed out of $\alpha _{ij} \boldsymbol{I}$-blocks, where $\alpha _{ij}$ are scalars, and therefore commutes with any block-diagonal matrix with $\mathbb{R}^{3 \times 3}$ matrices on its diagonal, and

$$ \dot{\widetilde{\overline{\boldsymbol{c}}}}_{\mathrm{f}}^{\mathrm{T}} \boldsymbol{M} \dot{\boldsymbol{\overline{c}}}_{\mathrm{f}}^{ \mathrm{}} =\boldsymbol{0} $$

(154)

have been employed to simplify Eq. (152). Equation (154) is valid since:

$\square$:

$\boldsymbol{M}=\boldsymbol{M}_{\mathrm{}}^{ \mathrm{T}}$, and $\boldsymbol{M}$ is composed out of $\alpha _{ij} \boldsymbol{I}$-blocks, where $\alpha _{ij}$ are scalars;

$\square$:

the cross product of a vector with itself is zero, that is, $\dot{\boldsymbol{{\overline{c}}}}_{\mathrm{f}}^{\mathrm{( \textit{i})}} \! \times \dot{\boldsymbol{{\overline{c}}}}_{\mathrm{f}} ^{\mathrm{(\textit{i})}} = \dot{\widetilde{\overline{\boldsymbol{c}}}}_{\mathrm{f}}^{(i)} \dot{\boldsymbol{{\overline{c}}}}_{\mathrm{f}}^{\mathrm{(\textit{i})}} = \! \boldsymbol{0}$;

$\square$:

the cross product is anticommutative (see Eq. (23));

$\square$:

the transpose of a skew-symmetric matrix is its negative, that is, $\dot{\widetilde{\overline{\boldsymbol{c}}}}_{ \mathrm{f}}^{(i)^{\mathrm{T}}} \! =- \dot{\widetilde{\overline{\boldsymbol{c}}}}_{\mathrm{f}}^{(i)}$.

2.2.3 B.2.3 Result of the quadratic velocity vector

Summation of all terms from the derivatives of the kinetic energy w.r.t. $\boldsymbol{q}_{\mathrm{t}}^{\mathrm{T}}$, Eq. (115), w.r.t. $\boldsymbol{\overline{c}}_{\mathrm{f}}^{\mathrm{T}}$, Eqs. (119), (126), and (128), and w.r.t. $\boldsymbol{\theta }_{\mathrm{}}^{\mathrm{T}}$, Eqs. (133), (137), (143), and (148), and the time derivative of the FFRF mass matrix times the generalized velocities, Eq. (152), according to Lagrange’s equation (see Eq. (109)) yields the quadratic velocity vector, as given by Eq. (72):

$${\hat{\mathit{Q}}}_{\mathrm{v}}^{}=\left[\begin{array}{c}-\mathit{A}{\mathit{\Phi }}_{\mathrm{t}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ {\bar{\mathit{G}}}^{\mathrm{T}}{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}^{\mathrm{T}}\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\\ -\mathit{M}({\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\bar{\mathit{r}}}_{\mathrm{f}}+2{\widetilde{\bar{\mathit{\omega }}}}_{\mathrm{bd}}{\dot{\bar{\mathit{c}}}}_{\mathrm{f}}-{\widetilde{\bar{\mathit{r}}}}_{\mathrm{f}}\dot{\bar{\mathit{G}}}\dot{\mathit{\theta }})\end{array}\right],$$

(155)

where to simplify the expressions, we have used the commutativity of the FE mass matrix, that is, Eqs. (35), (74), and (153), and the skew-symmetry of the matrix $\widetilde{\overline{\boldsymbol{\omega }}}_{ \mathrm{bd}}$ (Eq. (124)).