Parameter estimation and optimization of multi-objective capacitated stochastic transportation problem for gamma distribution

Abstract

The transportation problem in real life is an uncertain problem with multi-objective decision-making. In particular, by considering the conflicting objectives/criteria such as transportation costs, transportation time, discount costs, labour costs, damage costs, decision maker searches for the best transportation set-up to find out the optimum shipment quantity subject to certain capacity restrictions on each route. In this paper, capacitated stochastic transportation problem is formulated as a multi-objective optimization model along with some capacitated restrictions on the route. In the formulated problem, we assume that parameters of the supply and demand constraints’ follow gamma distribution, which is handled by the chance constrained programming approach and the maximum likelihood estimation approach has been used to assess the probabilistic distributions of the unknown parameters with a specified probability level. Furthermore, some of the objective function’s coefficients are consider as ambiguous in nature. The ambiguity in the formulated problem has been presented by interval type 2 fuzzy parameter and converted into the deterministic form using an expected value function approach. A case study on transportation illustrates the computational procedure.

Introduction

The problem of transportation is a very interesting method of management sciences, which can be conceived and solved as a problem of linear programming (LP). Transport problem (TP) is seen as a logistics issue where the primary aim is to determine how and when to transport goods from distinct sources to distinct destinations with a minimum price or maximum profit. Also, today's decision maker (DM) seeks to reduce the shipping expenses but simultaneously seeks to reduce the distribution system’s transportation time. We have been able to observe in recent years that for many of the real-world situations, a classic mathematical programming model is insufficient. The nature of these problems requires, on the one hand, taking into account multiple goals and, on the other, different types of uncertainty. These uncertainties in the problem is represented by either with fuzziness or multi-choices or by probabilistic variables.

Stochastic programming (SP) discusses situations under which random variables define any or more of the parameters of a computational programming problem, rather than deterministic variables. Although deterministic problems are developed with set parameters, while the real-world problems concerned with the parameters that are almost definitely undefined at the moment a choice is to be taken. If the parameters are unknown but assumed to be in some range of possible values, a solution may be found which is feasible for all specific parameters which helps to optimize a defined objective function. In the recent past, SP has been adhered to problems with various, contradictory and non-commensurable goals where there is usually no single solution capable of optimizing all goals, but there is a set of alternatives from which an “appropriate solution” also known as a “compromise solution” must be identified. In a decision-making problem with several criteria, though, the decision-maker generally follows on requirements compliance rather than optimizing of goals. However, when the parameters are stochastic and fuzzy, these problems become more complicated. It is easy to see from the literature for SP that much work has been done in an uncertain environment. However, in some scenarios, if the sample data are sufficient, we can estimate some parameters as random variables.

The basic concept of solving any SP problem is transitioning the problem into a similarly deterministic form (equal in the context that a solution to the corresponding deterministic problem is a solution to the SP). Many methods have been suggested in the past on SP to address the equivalent deterministic form of the random variables. Some techniques are based on statistical and probabilistic concepts for dealing stochastically with the problem and then finding the corresponding deterministic form. Some prominent work, that can be useful for the present study include, Sinha et al. [1] used Joint Normal distribution; Sahoo and Biswal [2] used Cauchy and Extreme value distribution; Mahapatra et al. [3] used Log-Normal distribution; Barik et al. [4] used Pareto distribution; Roy and Mahapatra [5] used Log-Normal distribution with interval type parameters; Mahapatra et al. [6] used Extreme Value distribution with multi-choice parameters; Roy et al. [7] used Exponential distribution with multi-choice parameters; Biswal and Samal [8] used Cauchy distribution with multi-choice parameters; Samal and Biswal [9] used Exponential distribution; Javaid et al. [10] used Weibull distribution; Mahapatra et al. [11] used Weibull distribution with multi choice parameters; Roy [12] used Weibull distribution with multi-choice parameters; Barik [13] used Pareto distribution; Roy [14] used Logistic distribution with multi-choice parameters; Biswas and De [15] used Joint Extreme value distribution with fuzzy parameters; Barik and Biswal [16] used Normal distribution; Maity et al. [17] used Normal distribution; De et al. [18] used Cauchy and Extreme value distribution with fuzzy parameters; Acharya et al. [19] used three-parameter extreme value distribution for getting the equivalent deterministic form of the uncertain stochastic parameter and also all of them formulated same type of linear TP distribution. Dufuaa and Sultan [20] formulated the maintenance planning problem by considering the schedule reserves scenario with sufficient resources to meet emergency employment when preparing a schedule for on-the-spot employment. Yang and Feng [21] formulated solid bicriteria TP with random parameters and developed three types of models, including the expected value model, the chance-constrained model and the goal programming model. Zhang et al. [22] proposed a fuzzy-robust stochastic model, which integrates LP and SP into a general multi-objective programming framework. The established framework was then implemented to a case study in which petroleum waste-flow-allocation alternatives were planned and associated operations were managed under uncertainty in an integrated petroleum waste management scheme. Beraldi et al. [23] addressed the issue encountered by a number of electricity users in formative the optimum short-term procurement plan and formulated a two-stage problem to assess the optimal quantity of energy to be bought by contractual contracts and from the power market. Díaz-García and Bashiri [24] formulated the multi-response surface problem as multi-objective stochastic optimization and suggested various alternatives to the problem. Mousavi et al. [25] considered multiple cross-docking centers (CDCs) and vehicle routing schedules for logistics companies to make strategic/tactical and operational decisions. They introduced two new methods, i.e., deterministic mixed-integer LP models and fuzzy possibilistic-SP model to integrate CDC place and scheduling of car routing issue with various CDCs. Li et al. [26] considered spare parts for maintenance, repair and operation (MRO) which are vital for machine operations and proposed an improved SP model for MRO spare parts supply chain planning. Before formulating the problem of concern, we realized that under distinct situations, all previous work was formulated for the problem of production and transportation. Samanta et al. [27] formulated multi-objective and multi-item TP with ambiguity, and also implemented the speed of various vehicles and traffic disruption factor for the time minimization for the first time owing to the road conditions on different roads. Kaushal et al. [28] developed a hierarchical design model of fixed charge fractional TP for a food chain business in which the organic cooking oil used for processing. By proposing a new computational method for solving the fuzzy Pythagorean TP, Kumar et al. [29] presented a modern way of treating the uncertainty in the crisp environment. Majumder et al. [30] proposed a profit and time optimization problem that acknowledges the nature of potential indeterminacy by constructing an unpredictable multi-objective solid TP with budget restriction for each destination. Roy and Midya [31] modeled a multi-objective robust TP with component mixing in an intuitionistic vague environment and found various Pareto-optimal solutions from the suggested method, with weight coefficients varying from objective functions. Samanta and Jana [32] developed a method for solving decision-making problems using multi-criteria in order to rate the mode of transportation using the degree of possibility and then used fuzzy goal approach and convex combination method for solving the TP.

From Table 1, we saw that most authors in their formulated models considered the problem of single and multi-objective production and transportation whereas Sinha et al. [1], Biswas and De [15], Barik and Biswal [16] have considered the general formulation of LP. We have also noticed that almost every author hypothetically choose the value of the probabilistic parameter. However, here in the present work, we have used the maximum likelihood estimation (MLE) approach for obtaining the value of the unknown parameter. All the related work has been summarized in Table 1.

Table 1 Summary of related literature

Motivating from such research, we have formulated the multi-objective optimization model for capacitated transportation problem (TP) in a fuzzy and probabilistic environment. From the Table 1, we have found that none of the author has used MLE approach for getting the desired value of the parameters. This is considered to be as the major drawback that we have found in all the previous work. However, in real-world problems, it is often hard for DM to estimate the precise values of parameters to the best of our knowledge. To overcome this issue, we have used MLE approach for getting the desired shape and scale parameter of the considered probabilistic distribution. Following are the key points of this research:

• 1. Earlier, the practitioners regard TP only as a single, multi-objective problem, but we have expanded it to a capacitated problem with the need for time.

• 2. TP with multiple and conflicting objectives is studied for the first time along with interval type 2 parameters among the objective functions.

• 3. SP technique is implemented to address the inequality relationships between different supply and demand constraints.

• 4. The probabilistic random variable for the proposed problem is studied in conjunction with the application of the MLE approach to model the uncertainty in demand and supply parameters.

In this article, we established a Multi-Objective Capacitated Transportation Problem (MOSCTP) model in which the DM is clueless of shipping costs, delivery times, harm costs, labor costs, discounted costs, demand, and supply from a specific source to different destination due to certain inevitable factors. Such unexpected factors contribute to irregularities during the problem development, which are characterized by fuzziness and randomness, and transformed into the corresponding crisp form using the ranking function and SP approach respectively. Uncertainty in demand and supply parameters is assumed to follow the Gamma Distribution (GD), and the MLE approach has been used to determine the scale and location of probabilistic distribution parameters. Finally, to achieve the ideal solution of MOSCTP model, the fuzzy goal-programming technique has been used. To explain the entire model solving procedure; a quantitative case study has been given. The next section, after illustration of the literature review, is related to the problem’s model formulation.

Mathematical model

In this paper, we consider a mathematical model of capacitated TP involving interval type 2 fuzzy number and GD, respectively. TP is considered to be a fundamental problem in networking. TP comprises of a scenario where a product is to be transported from multiple sources (also known as source, supply point) to multiple sinks (also known as location, demand point) with the objective of optimal distribution to minimize transport costs. Today’s DM not only tries to minimize transportation costs but also searches for minimum transportation time at the same time. Sometimes, owing to some budget issue, road security, and consideration of storage, DM specified the cumulative capacity for each path; this provides rise to the growth of capacitated TP that was first researched by Wagner [33]. There was not enough literature available to solve capacitated TP, and a search revealed that there was no unique method available to find an optimal solution to the mixed constraints problem. Let us consider the quantity of the item available at m sources (origins) $O_{i} \,\,(i = 1,2,3,....,m)$ to be delivered to the n location $D_{j} \,\,(j = 1,2,3,.....,n)$ to meet the $b_{j}$ requirement. With this assumption, the three different mathematical model for the multi-objective capacitated TP with mixed constraints is formulated as follows [34, 35]:

Model (1)

$$ \begin{aligned}& {\text{Min}}\,\,\left( {F_{1} = \sum \limits_{i = 1}^{m} {\sum \limits_{j = 1}^{n} {d_{ij} \,x_{ij} } } ,\,\,\,F_{2} = \sum \limits_{i = 1}^{m} {\sum \limits_{j = 1}^{n} {l_{ij} \,x_{ij} } } } \right) \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\,\sum \limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,a_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,b_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij} \hfill \\ \end{aligned} $$

where $r_{ij}$ denote the maximum restriction on the amount of quantity to be shipped from ith source to jth destination i.e. $x_{ij} \le r_{ij} .$ The objective function (1) used to optimizes the damage cost of shipment the aggregate units; and the objective function (2) used to optimizes the labour cost for the aggregate units. Similarly, based on the above-defined assumption, the mathematical model for the multiobjective fractional capacitated TP with mixed constraints is as follows.

Model (2)

$$ \begin{aligned} & {\text{Min}}\,\,\left( {F_{1} = \frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {t_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {t_{{_{ij} }}^{s} \,x_{ij} } } }},F_{2} = \frac{{\sum_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {c_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {c_{{_{ij} }}^{s} \,x_{ij} } } }}} \right) \hfill \\ & {\text{Max}}\,\,F_{3} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {d_{ij}^{s} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {c_{ij}^{a} \,x_{ij} } } }} \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\,\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,a_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,b_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij}. \hfill \\ \end{aligned} $$

A scenario can emerge in several logistical issues when we have to contend with both linear and fractional functions in a single problem. The objective function (3) used to optimize the cumulative fractional transport time for the products to be transported. The objective function (4) used to optimizes cumulative fractional transport cost occurs during product shipment. The objective function (5) used to optimizes the discount per unit provided on transport costs. We also consider the case of multi objective capacitated TP with linear and fractional objective functions with mixed constraints; which may be described as follows.

Notations

$k$ :

index for objectives, for all $k = 1,2,3,4,5, \ldots ,K$

$x_{ij}$ :

is the variable that represents the unknown quantity transported from ith origin to jth destination

$d_{ij}$ :

the cost of damage occur during the transport period

$l_{ij}$ :

the cost of labour for transporting the $x_{ij} > 0$ units

$t_{{_{ij} }}^{a}$ :

the actual time for transporting $x_{ij} > 0$ units

$t_{{_{ij} }}^{s}$ :

the standard time for transporting $x_{ij} > 0$ units

$c_{{_{ij} }}^{a}$ :

the actual cost for transporting $x_{ij} > 0$ units

$c_{{_{ij} }}^{s}$ :

the standard cost of transporting $x_{ij} > 0$ units

$d_{{_{ij} }}^{s}$ :

the discount cost given during the transportation

$r_{ij}$ :

maximum quantity of amount to be transported from ith source to jth destination

Using all the above defined notations, the model has been formulated as

Model (3)

$$ \begin{aligned} & {\text{Min}}\,\,\left( {F_{1} = \sum_{i = 1}^{m} {\sum_{j = 1}^{n} {d_{ij} \,x_{ij} } } \,\,,\,F_{2} = \sum_{i = 1}^{m} {\sum_{j = 1}^{n} {l_{ij} \,x_{ij} } } } \right) \hfill \\ &{\text{Min}}\,\,\left( {F_{3} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {t_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {t_{{_{ij} }}^{s} \,x_{ij} } } }}\,\,,\,F_{4} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {c_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {c_{{_{ij} }}^{s} \,x_{ij} } } }}} \right) \hfill \\ & {\text{Max}}\,\,F_{5} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {d_{ij}^{s} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {c_{ij}^{a} \,x_{ij} } } }} \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\,\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,a_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,b_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij}. \hfill \\ \end{aligned} $$

In the past few years, with the growth of economic globalization, more and more companies and enterprises, particularly many multinational corporations, are focusing on goods TP. Thinking about the different multifaceted nature in real-world business, a few researchers acknowledge that it was typically improper to consider the unit cost of transportation, the demand and supply as real numbers. For instance, the information related to transportation systems, for example, resources, cost, time, demands and supply may not be fixed continuously. Transportation costs depend on fuel price, labour charges, and government taxes, and from time to time, these variables differ. The main reason for the uncertainty in demand and supply is increased cost, and most commonly in the form of excess inventory, excess capacity in production, or the use of faster and more expensive transportation of goods. In view of the possible scenarios discussed above, the fuzzy formulation of the problem by replacing all the deterministic parameters with fuzzy parameters is conventionally expressed as:

Model (1′)

$$ \begin{aligned}& {\text{Min}}\,\,\left( {\tilde{F}_{1} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\tilde{d}_{{_{ij} }}^{{}} \,x_{ij} } } ,\,\,\,\tilde{F}_{2} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\tilde{l}_{{_{ij} }}^{{}} \,x_{ij} } } } \right) & \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\Pr \,\left( {\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,\,a_{i} } \right) \ge 1 - \gamma_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\Pr \left( {\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,\,b_{j} } \right) \ge 1 - \delta_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij} .\hfill \\ \end{aligned} $$

Similarly,

Model (2′)

$$ \begin{aligned} & {\text{Min}}\,\,\left( {\tilde{F}_{1} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{t}_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{t}_{{_{ij} }}^{s} \,x_{ij} } } }},\tilde{F}_{2} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{c}_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{c}_{{_{ij} }}^{s} \,x_{ij} } } }}} \right) \hfill \\ & {\text{Max}}\,\,\tilde{F}_{3} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{d}_{ij}^{s} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{c}_{ij}^{a} \,x_{ij} } } }} \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\Pr \,\left( {\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,\,a_{i} } \right) \ge 1 - \gamma_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\Pr \left( {\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,\,b_{j} } \right) \ge 1 - \delta_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij} .\hfill \\ \end{aligned} $$

Model (3′)

$$ \begin{aligned} & {\text{Min}}\,\,\left( {\tilde{F}_{1} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\tilde{d}_{{_{ij} }}^{{}} \,x_{ij} } } ,\,\,\,\tilde{F}_{2} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\tilde{l}_{{_{ij} }}^{{}} \,x_{ij} } } } \right) \hfill \\ & {\text{Min}}\,\,\left( {\tilde{F}_{3} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{t}_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{t}_{{_{ij} }}^{s} \,x_{ij} } } }},\tilde{F}_{4} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{c}_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{c}_{{_{ij} }}^{s} \,x_{ij} } } }}} \right) \hfill \\ & {\text{Max}}\,\,\tilde{F}_{5} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{d}_{ij}^{s} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{c}_{ij}^{a} \,x_{ij} } } }} \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\Pr \,\left( {\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,\,a_{i} } \right) \ge 1 - \gamma_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\Pr \left( {\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,\,b_{j} } \right) \ge 1 - \delta_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij}. \hfill \\ \end{aligned} $$

In the above-formulated models, input parameters of the objective functions have been represented with vagueness. We have considered $\tilde{d}_{{_{ij} }}^{{}}$, $\tilde{l}_{{_{ij} }}^{{}}$, $\tilde{t}_{{_{ij} }}^{a}$, $\tilde{t}_{{_{ij} }}^{s}$, $\tilde{c}_{{_{ij} }}^{a}$, $\tilde{c}_{{_{ij} }}^{s}$, $\tilde{d}_{ij}^{s}$, and $\tilde{c}_{ij}^{a}$ as interval type-2 trapezoidal fuzzy numbers. The key advantage of type-2 fuzzy sets is their potential to handle the uncertainty more effectively than those of type-1 fuzzy sets. It is so as for type-2 fuzzy sets, a greater number of factors and greater degrees of independence are accessible. More importantly, “A type-1 fuzzy set is characterized by a two-dimensional membership function, whereas a type-2 fuzzy set is characterized by a three-dimensional membership function”. Through type-2 fuzzy set we can interpret the uncertainty more precisely as compared to type-1 fuzzy set. Some essential definitions of these fuzzy parameters are given below:

Definition 1

(Sinha et al. [36]). Let $\tilde{d}_{{_{ij} }}^{{}}$ be a type-2 fuzzy set, then $\tilde{d}_{{_{ij} }}^{{}}$ can be expressed as $\tilde{d}_{{_{ij} }}^{{}}$ = $\left\{ {\left( {(x,u),\mu_{{\tilde{d}_{{_{ij} }}^{{}} }} (x,u)} \right)|\forall x \in X\forall u \in J_{x} \subseteq [0,1],\,0 \le \mu_{{\tilde{d}_{{_{ij} }}^{{}} }} (x,u) \le 1} \right\},$ where X is the universe of discourse and $\mu_{{\tilde{d}_{{_{ij} }}^{{}} }}$ denotes the membership function of $\tilde{d}_{{_{ij} }}^{{}}$. Then, $\tilde{d}_{{_{ij} }}^{{}}$ it can be expressed as $\tilde{d}_{{_{ij} }}^{{}} =$$\int\nolimits_{x \in X} {\int\nolimits_{{u \in J_{x} }} {\mu_{{\tilde{d}_{{_{ij} }}^{{}} }} (x,u)/(x,u)} }$,$u \in J_{x} \subseteq [0,1].[0,1]$$.$

Definition 2

(Sinha et al. [36]). For a type-2 fuzzy set $\tilde{d}_{{_{ij} }}^{{}}$, if all $\mu_{{\tilde{d}_{{_{ij} }}^{{}} }} (x,u) = 1,$ then $\tilde{d}_{{_{ij} }}^{{}}$ is called an interval type-2 fuzzy set, i.e., $\tilde{d}_{{_{ij} }}^{{}}$$\int\nolimits_{x \in X} {\int\nolimits_{{u \in J_{x} }} {1/(x,u)/(x,u)} }$$u \in J_{x} \subseteq [0,1].$

Definition 3

(Sinha et al. [36]). Uncertainty in the primary memberships of a type-2 fuzzy set, $\tilde{d}_{{_{ij} }}^{{}}$ consists of a bounded region that we call the footprints of uncertainty (FOU). It is the union of all primary memberships, i.e.,$FOU(\tilde{d}_{{_{ij} }}^{{}} ) = U_{x \in X} J_{x} .$

FOU is characterized by the upper membership functions (UMF) and the lower membership function (LMF), and are denoted by $\overline{\mu }_{{\tilde{d}_{{_{ij} }}^{{}} }}$ and $\underline{\mu }_{{\tilde{d}_{{_{ij} }}^{{}} }} .$

Definition 4

(Sinha et al. [36]). An interval type-2 fuzzy number is called interval type-2 trapezoidal fuzzy number where the UMF and LMF are both trapezoidal fuzzy numbers, i.e.,

$$ \begin{aligned} \tilde{d}_{{_{ij} }}^{{}} &= \left( {d_{ij}^{U} ,d_{ij}^{L} } \right) \\&= \left( {\left( {\left( {d_{ij}^{U} } \right)_{1} ,\left( {d_{ij}^{U} } \right)_{2} ,\left( {d_{ij}^{U} } \right)_{3} ,\left( {d_{ij}^{U} } \right)_{4} } \right);\,H_{1} (d_{ij}^{U} ),H_{2} (d_{ij}^{U} )} \right), \hfill \\& \quad \quad \left( {\left( {\left( {d_{ij}^{L} } \right)_{1} ,\left( {d_{ij}^{L} } \right)_{2} ,\left( {d_{ij}^{L} } \right)_{3} ,\left( {d_{ij}^{L} } \right)_{4} } \right);\,H_{1} (d_{ij}^{L} ),H_{2} (d_{ij}^{L} )} \right), \hfill \\ \end{aligned} $$

(1)

where $H_{r} (d_{ij}^{L} )$ and $H_{r} (d_{ij}^{U} )$, $(r = 1,2)$ denote membership values of the corresponding elements $\left( {d_{ij}^{L} } \right)_{r + 1}^{{}}$ and $\left( {d_{ij}^{U} } \right)_{r + 1}^{{}}$ respectively.

Definition 5

(Sinha et al. [36]) Defuzzification of Interval Type-2 Trapezoidal Fuzzy Number. Let us consider an interval type-2 trapezoidal fuzzy number $\tilde{d}_{{_{ij} }}^{{}}$, given by Eq. (1). The expected value of interval type-2 trapezoidal fuzzy number $\tilde{d}_{{_{ij} }}^{{}}$ is defined as follows:

$$ \begin{aligned} E(\tilde{d}_{{_{ij} }}^{{}} ) &= \frac{1}{2}\left( {\frac{1}{4}\left( {\sum\limits_{r = 1}^{4} {\left( {\left( {d_{ij}^{L} } \right)_{r} + \left( {d_{ij}^{U} } \right)} \right)_{r} } } \right)} \right) \\ &\quad\times \frac{1}{4}\left( {\sum\limits_{r = 1}^{2} {\left( {H_{r} (d_{ij}^{L} ) + H_{r} (d_{ij}^{U} )} \right)} } \right) \end{aligned} $$

(2)

Similarly, the same definition holds for other fuzzy parameters $\tilde{l}_{{_{ij} }}^{{}}$, $\tilde{t}_{{_{ij} }}^{a}$, $\tilde{t}_{{_{ij} }}^{s}$, $\tilde{c}_{{_{ij} }}^{a}$, $\tilde{c}_{{_{ij} }}^{s}$, $\tilde{d}_{ij}^{s}$, and $\tilde{c}_{ij}^{a}$ respectively. After formulating the model with uncertainty, the next section is related to the crisp transformation of uncertain parameters.

Methodology

Using the above-defined definitions as defined in Sect. 2, the crisp transformation of the fuzzy parameters of objective functions can be presented as:

$$ \begin{aligned} {\text{Minimize}}\,\,\,\tilde{F}_{1} & = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\tilde{d}_{{_{ij} }}^{{}} \,x_{ij} } } \hfill \\ & = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( {d_{ij}^{U} ,d_{ij}^{L} } \right)x_{ij} } } \hfill \\ & =\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( \begin{gathered} \left( {\left( {\left( {d_{ij}^{U} } \right)_{1} ,\left( {d_{ij}^{U} } \right)_{2} ,\left( {d_{ij}^{U} } \right)_{3} ,\left( {d_{ij}^{U} } \right)_{4} } \right);\,H_{1} (d_{ij}^{U} ),H_{2} (d_{ij}^{U} )} \right), \hfill \\ \left( {\left( {\left( {d_{ij}^{L} } \right)_{1} ,\left( {d_{ij}^{L} } \right)_{2} ,\left( {d_{ij}^{L} } \right)_{3} ,\left( {d_{ij}^{L} } \right)_{4} } \right);\,H_{1} (d_{ij}^{L} ),H_{2} (d_{ij}^{L} )} \right) \hfill \\ \end{gathered} \right)x_{ij} } } \hfill \\ & = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( {\frac{1}{2}\left( {\frac{1}{4}\left( {\sum\limits_{r = 1}^{4} {\left( {\left( {d_{ij}^{L} } \right)_{r} + \left( {d_{ij}^{U} } \right)} \right)_{r} } } \right)} \right) \times \frac{1}{4}\left( {\sum\limits_{r = 1}^{2} {\left( {H_{r} (d_{ij}^{L} ) + H_{r} (d_{ij}^{U} )} \right)} } \right)} \right)x_{ij} } ,} \hfill \\ \end{aligned} $$

$$ \begin{aligned} {\text{Minimize}}\,\,\,\tilde{F}_{2} & = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\tilde{l}_{{_{ij} }}^{{}} \,x_{ij} } } \hfill \\ & = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( {l_{ij}^{U} ,l_{ij}^{L} } \right)x_{ij} } } \hfill \\ & = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( \begin{aligned} \left( {\left( {\left( {l_{ij}^{U} } \right)_{1} ,\left( {l_{ij}^{U} } \right)_{2} ,\left( {l_{ij}^{U} } \right)_{3} ,\left( {l_{ij}^{U} } \right)_{4} } \right);\,H_{1} (l_{ij}^{U} ),H_{2} (l_{ij}^{U} )} \right), \hfill \\ \left( {\left( {\left( {l_{ij}^{L} } \right)_{1} ,\left( {l_{ij}^{L} } \right)_{2} ,\left( {l_{ij}^{L} } \right)_{3} ,\left( {l_{ij}^{L} } \right)_{4} } \right);\,H_{1} (l_{ij}^{L} ),H_{2} (l_{ij}^{L} )} \right) \hfill \\ \end{aligned} \right)x_{ij} } } \hfill \\ & = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( {\frac{1}{2}\left( {\frac{1}{4}\left( {\sum\limits_{r = 1}^{4} {\left( {\left( {l_{ij}^{L} } \right)_{r} + \left( {l_{ij}^{U} } \right)} \right)_{r} } } \right)} \right) \times \frac{1}{4}\left( {\sum\limits_{r = 1}^{2} {\left( {H_{r} (l_{ij}^{L} ) + H_{r} (l_{ij}^{U} )} \right)} } \right)} \right)x_{ij} } } , \hfill \\ \end{aligned} $$

$$ \begin{aligned} {\text{Minimize}}\,\,\,\tilde{F}_{3} & = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{t}_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{t}_{{_{ij} }}^{s} \,x_{ij} } } }} \hfill \\ & = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {t_{{_{ij} }}^{aU} ,t_{{_{ij} }}^{aL} } \right)\,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {t_{{_{ij} }}^{sU} ,t_{{_{ij} }}^{sL} } \right)\,x_{ij} } } }} \hfill \\ & = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( \begin{gathered} \left( {\left( {\left( {t_{{_{ij} }}^{aU} } \right)_{1} ,\left( {t_{{_{ij} }}^{aU} } \right)_{2} ,\left( {t_{{_{ij} }}^{aU} } \right)_{3} ,\left( {t_{{_{ij} }}^{aU} } \right)_{4} } \right);\,H_{1} (t_{{_{ij} }}^{aU} ),H_{2} (t_{{_{ij} }}^{aU} )} \right), \hfill \\ \left( {\left( {\left( {t_{{_{ij} }}^{aL} } \right)_{1} ,\left( {t_{{_{ij} }}^{aL} } \right)_{2} ,\left( {t_{{_{ij} }}^{aL} } \right)_{3} ,\left( {t_{{_{ij} }}^{aL} } \right)_{4} } \right);\,H_{1} (t_{{_{ij} }}^{aL} ),H_{2} (t_{{_{ij} }}^{aL} )} \right) \hfill \\ \end{gathered} \right)x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( \begin{gathered} \left( {\left( {\left( {t_{{_{ij} }}^{sU} } \right)_{1} ,\left( {t_{{_{ij} }}^{sU} } \right)_{2} ,\left( {t_{{_{ij} }}^{sU} } \right)_{3} ,\left( {t_{{_{ij} }}^{sU} } \right)_{4} } \right);\,H_{1} (t_{{_{ij} }}^{sU} ),H_{2} (t_{{_{ij} }}^{sU} )} \right), \hfill \\ \left( {\left( {\left( {t_{{_{ij} }}^{sL} } \right)_{1} ,\left( {t_{{_{ij} }}^{sL} } \right)_{2} ,\left( {t_{{_{ij} }}^{sL} } \right)_{3} ,\left( {t_{{_{ij} }}^{sL} } \right)_{4} } \right);\,H_{1} (t_{{_{ij} }}^{sL} ),H_{2} (t_{{_{ij} }}^{sL} )} \right) \hfill \\ \end{gathered} \right)x_{ij} } } }} \hfill \\ & \,\,\,\, = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {\frac{1}{2}\left( {\frac{1}{4}\sum_{r = 1}^{4} {\left( {\left( {t_{{_{ij} }}^{aL} } \right)_{r} + \left( {t_{{_{ij} }}^{aU} } \right)} \right)_{r} } } \right) \times \frac{1}{4}\left( {\sum_{r = 1}^{2} {\left( {H_{r} (t_{{_{ij} }}^{aL} ) + H_{r} (t_{{_{ij} }}^{aU} )} \right)} } \right)} \right)x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {\frac{1}{2}\left( {\frac{1}{4}\sum_{r = 1}^{4} {\left( {\left( {t_{{_{ij} }}^{sL} } \right)_{r} + \left( {t_{{_{ij} }}^{sU} } \right)} \right)_{r} } } \right) \times \frac{1}{4}\left( {\sum_{r = 1}^{2} {\left( {H_{r} (t_{{_{ij} }}^{sL} ) + H_{r} (t_{{_{ij} }}^{sU} )} \right)} } \right)} \right)x_{ij} } } }}, \hfill \\ \end{aligned} $$

$$ \begin{aligned}& {\text{Minimize}}\,\,\,\tilde{F}_{4} = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{c}_{{_{ij} }}^{a} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{c}_{{_{ij} }}^{s} \,x_{ij} } } }} \hfill \\ & \,\,\,\, = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {c_{{_{ij} }}^{aU} ,c_{{_{ij} }}^{aL} } \right)\,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {c_{{_{ij} }}^{sU} ,c_{{_{ij} }}^{sL} } \right)\,x_{ij} } } }} \hfill \\ & \,\,\,\, = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( \begin{gathered} \left( {\left( {\left( {c_{{_{ij} }}^{aU} } \right)_{1} ,\left( {c_{{_{ij} }}^{aU} } \right)_{2} ,\left( {c_{{_{ij} }}^{aU} } \right)_{3} ,\left( {c_{{_{ij} }}^{aU} } \right)_{4} } \right);\,H_{1} (c_{{_{ij} }}^{aU} ),H_{2} (c_{{_{ij} }}^{aU} )} \right), \hfill \\ \,\,\,\left( {\left( {\left( {c_{{_{ij} }}^{aL} } \right)_{1} ,\left( {c_{{_{ij} }}^{aL} } \right)_{2} ,\left( {c_{{_{ij} }}^{aL} } \right)_{3} ,\left( {c_{{_{ij} }}^{aL} } \right)_{4} } \right);\,H_{1} (c_{{_{ij} }}^{aL} ),H_{2} (c_{{_{ij} }}^{aL} )} \right) \hfill \\ \end{gathered} \right)x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( \begin{gathered} \left( {\left( {\left( {c_{{_{ij} }}^{sU} } \right)_{1} ,\left( {c_{{_{ij} }}^{sU} } \right)_{2} ,\left( {c_{{_{ij} }}^{sU} } \right)_{3} ,\left( {c_{{_{ij} }}^{sU} } \right)_{4} } \right);\,H_{1} (c_{{_{ij} }}^{sU} ),H_{2} (c_{{_{ij} }}^{sU} )} \right), \hfill \\ \,\,\,\, \left( {\left( {\left( {c_{{_{ij} }}^{sL} } \right)_{1} ,\left( {c_{{_{ij} }}^{sL} } \right)_{2} ,\left( {c_{{_{ij} }}^{sL} } \right)_{3} ,\left( {c_{{_{ij} }}^{sL} } \right)_{4} } \right);\,H_{1} (c_{{_{ij} }}^{sL} ),H_{2} (c_{{_{ij} }}^{sL} )} \right) \hfill \\ \end{gathered} \right)x_{ij} } } }} \hfill \\ & = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {\frac{1}{2}\left( {\frac{1}{4}\sum_{r = 1}^{4} {\left( {\left( {c_{{_{ij} }}^{aL} } \right)_{r} + \left( {c_{{_{ij} }}^{aU} } \right)} \right)_{r} } } \right) \times \frac{1}{4}\left( {\sum_{r = 1}^{2} {\left( {H_{r} (c_{{_{ij} }}^{aL} ) + H_{r} (c_{{_{ij} }}^{aU} )} \right)} } \right)} \right)x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {\frac{1}{2}\left( {\frac{1}{4}\sum_{r = 1}^{4} {\left( {\left( {c_{{_{ij} }}^{sL} } \right)_{r} + \left( {c_{{_{ij} }}^{sU} } \right)} \right)_{r} } } \right) \times \frac{1}{4}\left( {\sum_{r = 1}^{2} {\left( {H_{r} (c_{{_{ij} }}^{sL} ) + H_{r} (c_{{_{ij} }}^{sU} )} \right)} } \right)} \right)x_{ij} } } }}, \hfill \\ \end{aligned} $$

and lastly,

$$ \begin{aligned} {\text{Maximize}}\,\,\tilde{F}_{5} & = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\tilde{d}_{ij}^{s} \,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {c_{{_{ij} }}^{aU} ,c_{{_{ij} }}^{aL} } \right)\,x_{ij} } } }} \hfill \\ & \,\,\,\, = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {d_{ij}^{sU} ,d_{ij}^{sL} } \right)\,x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {c_{{_{ij} }}^{aU} ,c_{{_{ij} }}^{aL} } \right)\,x_{ij} } } }} \hfill \\ & = \frac{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( \begin{gathered} \left( {\left( {\left( {d_{ij}^{sU} } \right)_{1} ,\left( {d_{ij}^{sU} } \right)_{2} ,\left( {d_{ij}^{sU} } \right)_{3} ,\left( {d_{ij}^{sU} } \right)_{4} } \right);\,H_{1} (d_{ij}^{sU} ),H_{2} (d_{ij}^{sU} )} \right), \hfill \\ \left( {\left( {\left( {d_{ij}^{sL} } \right)_{1} ,\left( {d_{ij}^{sL} } \right)_{2} ,\left( {d_{ij}^{sL} } \right)_{3} ,\left( {d_{ij}^{sL} } \right)_{4} } \right);\,H_{1} (d_{ij}^{sL} ),H_{2} (d_{ij}^{sL} )} \right) \hfill \\ \end{gathered} \right)x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( \begin{gathered} \left( {\left( {\left( {c_{{_{ij} }}^{aU} } \right)_{1} ,\left( {c_{{_{ij} }}^{aU} } \right)_{2} ,\left( {c_{{_{ij} }}^{aU} } \right)_{3} ,\left( {c_{{_{ij} }}^{aU} } \right)_{4} } \right);\,H_{1} (c_{{_{ij} }}^{aU} ),H_{2} (c_{{_{ij} }}^{aU} )} \right), \hfill \\ \left( {\left( {\left( {c_{{_{ij} }}^{aL} } \right)_{1} ,\left( {c_{{_{ij} }}^{aL} } \right)_{2} ,\left( {c_{{_{ij} }}^{aL} } \right)_{3} ,\left( {c_{{_{ij} }}^{aL} } \right)_{4} } \right);\,H_{1} (c_{{_{ij} }}^{aL} ),H_{2} (c_{{_{ij} }}^{aL} )} \right) \hfill \\ \end{gathered} \right)x_{ij} } } }} \hfill \\ & = \frac{{\, = \sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {\frac{1}{2}\left( {\frac{1}{4}\sum_{r = 1}^{4} {\left( {\left( {d_{ij}^{sL} } \right)_{r} + \left( {d_{ij}^{sU} } \right)} \right)_{r} } } \right) \times \frac{1}{4}\left( {\sum_{r = 1}^{2} {\left( {H_{r} (d_{ij}^{sL} ) + H_{r} (d_{ij}^{sU} )} \right)} } \right)} \right)x_{ij} } } }}{{\sum_{i = 1}^{m} {\sum_{j = 1}^{n} {\left( {\frac{1}{2}\left( {\frac{1}{4}\sum_{r = 1}^{4} {\left( {\left( {c_{{_{ij} }}^{aL} } \right)_{r} + \left( {c_{{_{ij} }}^{aU} } \right)} \right)_{r} } } \right) \times \frac{1}{4}\left( {\sum_{r = 1}^{2} {\left( {H_{r} (c_{{_{ij} }}^{aL} ) + H_{r} (c_{{_{ij} }}^{aU} )} \right)} } \right)} \right)x_{ij} } } }}. \hfill \\ \end{aligned} $$

Also, we consider a situation in which demand and supply parameter is random in nature and follows a GD Like most other distributions of probabilities, in many fields GD significance has been found. The GD represents a two-parameter family of continuous probability distributions. The distribution of gamma has been used to model the aggregated volume size of the real world problems. GD has been widely used in many applications such as insurance claims, rainfall prediction, wireless communication, oncology, neuroscience, bacterial gene expression, genomics, and may more. Several authors have worked on this distribution that includes, Harter et al. [37] consider the problem of estimation of parameters for gamma and Weibull populations when samples are complete and censored. Choi and Wette [38] obtained the estimation of parameters with their bias for GD Coit and Jin [39] estimated the parameters of reliability data with missing failure times using GD Zaigraev and Karakulska [40] discussed the estimation of shape parameters when a GD follows samples. The probability density function of GD with shape $\alpha$ and scale $\theta$ parameter is given by:

$$ f(x) = \frac{1}{{\theta^{\alpha } \Gamma \alpha }}x^{\alpha - 1} e^{{ - \frac{x}{\theta }}} ,\quad x \ge 0,\,\,\alpha > 0,\,\,\theta > 0. $$

Since we have considered the problem of MOCSTP with mixed constraint, two different cases happen to be occur for $\left( {a_{i} ,\,\,i = 1,2,...,m} \right)$ when it follows GD and can be presented as:

Case I: When $\Pr \left( {\sum_{j = 1}^{n} {x_{ij} \le a_{i} } } \right) \ge 1 - \gamma_{i} ,$$i = 1,2,...,m$

The probability density function of $a_{i} \,\,(i = 1,2,...,m)$ is given by

$$ f(a_{i} ,\theta_{i} ,\alpha_{i} ) = \frac{1}{{\theta_{i}^{{\alpha_{i} }} \Gamma \alpha_{i} }}a_{i}^{{\alpha_{i} - 1}} e^{{ - \frac{{a_{i} }}{{\theta_{i} }}}} ,\quad a_{i} \ge 0,\,\,\alpha_{i} > 0,\,\,\theta_{i} > 0. $$

(3)

Hence, the probabilistic constraint can be presented as:

$$ \int\limits_{{\sum\limits_{j = 1}^{n} {x_{ij} } }}^{\infty } {f(a_{i} ,\theta_{i} ,\alpha_{i} )\,\,d(a_{i} )\, \ge 1 - \gamma_{i} ,} \quad i = 1,2, \ldots m. $$

(4)

Equation (4) can be expressed in the integral form as:

$$ \int\limits_{{\sum\limits_{j = 1}^{n} {x_{ij} } }}^{\infty } {\frac{1}{{\theta_{i}^{{\alpha_{i} }} \Gamma \alpha_{i} }}a_{i}^{{\alpha_{i} - 1}} e^{{ - \frac{{a_{i} }}{{\theta_{i} }}}} \,d(a_{i} )\, \ge 1 - \gamma_{i} ,} \quad i = 1,2, \ldots m. $$

(5)

Let,

$$ \frac{{a_{i} }}{{\theta_{i} }} = y \Rightarrow \,\,da_{i} = \theta_{i} dy. $$

(6)

Using Eq. (6), the integral can be further presented as:

$$ \int\limits_{{{{\sum\limits_{j = 1}^{n} {x_{ij} } } \mathord{\left/ {\vphantom {{\sum\limits_{j = 1}^{n} {x_{ij} } } {\theta_{i} }}} \right. \kern-\nulldelimiterspace} {\theta_{i} }}}}^{\infty } {\frac{1}{{\theta_{i}^{{\alpha_{i} }} \Gamma \alpha_{i} }}(\theta_{i} y)_{{}}^{{\alpha_{i} - 1}} e^{ - y} \theta_{i} \,dy\, \ge 1 - \gamma_{i} ,} \quad i = 1,2, \ldots m. $$

(7)

On rearranging, we obtain

$$ \frac{1}{{\Gamma \alpha_{i} }}\int\limits_{{{{\sum\limits_{j = 1}^{n} {x_{ij} } } \mathord{\left/ {\vphantom {{\sum\limits_{j = 1}^{n} {x_{ij} } } {\theta_{i} }}} \right. \kern-\nulldelimiterspace} {\theta_{i} }}}}^{\infty } {y_{{}}^{{\alpha_{i} - 1}} e^{ - y} dy\, \ge 1 - \gamma_{i} ,\quad i = 1,2, \ldots m,} $$

(8)

where $\Gamma_{a} (x) = \int\nolimits_{x}^{\infty } {t^{a - 1} } e^{ - t} dt$ an upper incomplete Gamma function.

After simplification, we get

$$ \frac{1}{{\Gamma \alpha_{i} }}\Gamma_{{\alpha_{i} }} \left( {\frac{{\sum\nolimits_{j = 1}^{n} {x_{ij} } }}{{\theta_{i} }}} \right) \ge 1 - \gamma_{i} ,\quad i = 1,2, \ldots m. $$

After rearranging, we get

$$ \frac{{\sum\nolimits_{j = 1}^{n} {x_{ij} } }}{{\theta_{i} }} \ge \Gamma_{{\alpha_{i} }}^{ - 1} \,\left( {\Gamma \alpha_{i} \left( {1 - \gamma_{i} } \right)} \right),\quad i = 1,2, \ldots m. $$

(9)

Thus finally, the probabilistic constraint can be transformed into a deterministic linear constraint as:

$$ \sum\limits_{j = 1}^{n} {x_{ij} } \ge \theta_{i\,\,} \Gamma_{{\alpha_{i} }}^{ - 1} \,\left( {\Gamma \alpha_{i} \left( {1 - \gamma_{i} } \right)} \right) $$

(10)

where $\Gamma_{w}^{ - 1} (u) = \left\{ {x:u = \Gamma_{w} (x)} \right\}$ is an inverse gamma function solved by using R software.

Case II: When $\Pr \left( {\sum_{j = 1}^{n} {x_{ij} \ge a_{i} } } \right) \ge 1 - \delta_{i} ,$$i = 1,2,...,m$ or, $\Pr \left( {\sum\nolimits_{j = 1}^{n} {x_{ij} \le a_{i} } } \right) \le \delta_{i} ,$$i = 1,2,...,m$.

The probability density function of $a_{i} \,\,(i = 1,2,...,m)$ is given by

$$ f(a_{i} ,\theta_{i}^{{\prime}} ,\alpha_{i}^{{\prime}} ) = \frac{1}{{\theta^{\prime}_{i}}^{\alpha_{j}^{\prime}}\Gamma \alpha_{i}^{{\prime}}}b_{i}^{{\alpha_{i}^{{\prime}} - 1}}e^{{ - \frac{{a_{i} }}{{\theta_{i}^{{\prime}} }}}} ,\quad a_{i} \ge 0,\,\,\alpha_{i}^{{\prime}} > 0,\,\,\theta_{i}^{{\prime}} > 0.$$

(11)

Hence, the probabilistic constraint can be presented as:

$$ \int\limits_{{\sum\limits_{j = 1}^{n} {x_{ij} } }}^{\infty } {f(a_{i} ,\theta_{i}^{{\prime}} ,\alpha_{i}^{{\prime}} )\,\,d(b_{i} )\, \le \delta_{i} ,\quad i = 1,2, \ldots m.} $$

(12)

Equation (12) can be expressed in the integral form as:

$$\int\limits_{{\sum\limits_{j = 1}^{n} {x_{ij} } }}^{\infty } \frac{1}{{\theta^{\prime}_{i}}^{\alpha_{j}^{\prime}}\Gamma \alpha_{i}^{\prime}}a_{i}^{\alpha_{i}^{\prime}-1} e^{ - \frac{a_{i}}{\theta_{i}^{\prime}}} \,d(a_{i} )\, \le \delta_{i} ,\quad i = 1,2, \ldots m.$$

(13)

Let,

$$ \frac{{a_{i} }}{{\theta_{i}^{{\prime}} }} = y^{{\prime}} \Rightarrow \,\,da_{i} = \theta_{i}^{{\prime}} dy $$

(14)

Using Eq. (14), the integral can be further presented as:

$$ \int\limits_{\sum\limits_{j = 1}^{n} {x_{ij}/{\theta_{i}^{\prime}}}}^\infty \frac{1}{{\theta^{\prime}_{i}}^{\alpha_{i}^{\prime}}\Gamma \alpha_{i}^{{\prime}}}(y^{{\prime}} \theta_{i}^{{\prime}} ) ^{{\alpha_{i}^{\prime}} - 1}e^{- y^{\prime}} \,\theta_{i}^{\prime} d(y^{\prime})\, \le \delta_{i} , \quad i = 1,2, \ldots m.$$

(15)

On rearranging, we obtain

$$ \frac{1}{{\Gamma \alpha_{i}^{{\prime}} }}\int\limits_{{{{\sum\limits_{j = 1}^{n} {x_{ij} } } \mathord{\left/ {\vphantom {{\sum\limits_{j = 1}^{n} {x_{ij} } } {\theta_{i}^{{\prime}} }}} \right. \kern-\nulldelimiterspace} {\theta_{i}^{{\prime}} }}}}^{\infty } {(y^{{\prime}} )_{{}}^{{\alpha_{i}^{{\prime}} - 1}} e^{{ - y^{{\prime}} }} \,d(y^{{\prime}} )\, \le \delta_{i} ,\quad i = 1,2, \ldots m.} $$

(16)

After simplification, we get

$$ \frac{1}{{\Gamma \alpha_{i}^{{\prime}} }}\Gamma_{{\alpha_{i} }} \left( {\frac{{\sum\nolimits_{j = 1}^{n} {x_{ij} } }}{{\theta_{i}^{{\prime}} }}} \right) \le \delta_{i} ,\quad i = 1,2, \ldots m. $$

After rearranging, we get

$$ \frac{{\sum\nolimits_{j = 1}^{n} {x_{ij} } }}{{\theta_{i}^{{\prime}} }} \le \Gamma_{{\alpha_{i} }}^{ - 1} \left( {\left( {\Gamma \alpha_{i}^{{\prime}} \,\delta_{i} } \right)} \right),\quad i = 1,2, \ldots m. $$

(17)

Thus finally, the probabilistic constraints can be transformed into a deterministic linear constraint as:

$$ \sum\limits_{j = 1}^{n} {x_{ij} } \le \theta_{i}^{{\prime}} \left( {\Gamma_{{\alpha_{i} }}^{ - 1} \left( {\Gamma \alpha_{i}^{{\prime}} \,\delta_{i} } \right)} \right),\quad i = 1,2, \ldots m, $$

(18)

where $\Gamma_{w}^{ - 1} (u) = \left\{ {x:u = \Gamma_{w} (x)} \right\}$ is an inverse gamma function solved by using R software. When $\left( {b_{j} ,\,\,j = 1,2,...,n} \right)$ follows GD, the deterministic form of $\left( {b_{j} ,\,\,j = 1,2,...,n} \right)$ has been obtained as same we did for $\left( {a_{i} ,\,\,i = 1,2,...,m} \right)$. We have also used the likelihood estimation approach for getting the shape and scale parameter of GD The likelihood function of GD can be given as:

$$ L(\alpha ,\theta ) = \prod\limits_{i = 1}^{n} {f(x_{i} ,\alpha ,\theta )} . $$

(19)

It can be further written as:

$$ \ln L(\alpha ,\theta ) = (\alpha - 1)\sum\limits_{i = 1}^{n} {\ln (x_{i} )} - \frac{{\sum\nolimits_{i = 1}^{n} {x_{i} } }}{\theta } - n\alpha \ln (\theta ) - n\ln (\Gamma \alpha ). $$

(20)

Differentiate Eq. (20) with respect to shape and scale parameters, respectively, to get the ML estimate value of parameters, we get the likelihood equations

$$ \frac{{\sum\nolimits_{i = = 1}^{n} {x_{i} } }}{{\theta^{2} }} - \frac{n\alpha }{\theta } = 0, $$

(21)

and,

$$ \sum\limits_{i = 1}^{n} {\ln (x_{i} )} - n\ln (\theta ) - n\phi (\alpha ), $$

(22)

where, $\phi (\alpha ) = \frac{d}{d\alpha }\ln (\Gamma \alpha ) = \frac{{\Gamma^{{\prime}} (\alpha )}}{\Gamma (\alpha )}$.

The (21) and (22) likelihood equations cannot be solved analytically. Here, we use the iterative numerical procedure for each equation, to obtain values of MLEs of parameters. The formulated MOCSTP solution will obviously be the optimum quantity to be transported from source to destination. Since no algorithm is available to effectively solve a multi-objective programming problem, by using some compromise criterion, the problem is to be transformed into a single objective problem. The solution has been obtained by using fuzzy programming approach, which consists of the following steps:

Step 1: to obtain the MOCSTP solution, consider only one objective at a time and ignore the other objective function and obtain the optimum solution as the ideal solution for each objective function.

Step 2: determine the corresponding values for each objective function at each solution obtained from the result of step-1. Let $x_{ij}^{*}$ be the ideal solution for the objective function $f_{1} ,f_{2} ,...,f_{k}$. So $U_{k} = Max\,\left\{ {F_{1} (x_{ij} ),F_{2} (x_{ij} ),....,F_{k} (x_{ij} )} \right\}$ and $L_{k} = Min\,\left\{ {F_{1} (x_{ij} ),F_{2} (x_{ij} ),....,F_{k} (x_{ij} )} \right\},\,\,\,k = 1,2,...,5$, where, $U_{k} \,$ and $L_{k} \,$ be the upper and lower bounds of the $k^{th}$ objective function $F_{k} (x_{ij} ).\,$

Step 3: the membership function for the given problem can be defined as:

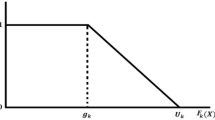
We define the membership function for the k^th objective function (Minimization type) as follows:

$$ \mu_{k} ((F_{k} (x_{ij} )) = \left\{ \begin{aligned} 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,F_{k} (x_{ij} ) \ge \,U_{k} \hfill \\ \frac{{U_{k} (x_{ij} ) - F_{k} (x_{ij} )}}{{U_{k} (x_{ij} ) - L_{k} (x_{ij} )}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,L_{k} \le F_{K} (x_{ij} ) \hfill \\ 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,F_{k} (x_{ij} )\, \le L_{k} \hfill \\ \end{aligned} \right. \le \,U_{k} , $$

where $U_{k} \,\,\,{\text{and}}\,\,L_{k}$ are the upper and lower tolerance limit. Membership function for the k^th objective function (Maximize) is as follows:

$$ \mu_{k} ((F_{k} (x_{ij} )) = \left\{ \begin{aligned} 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,F_{k} (x_{ij} ) \le \,L_{k} \hfill \\ \frac{{F_{k} (x_{ij} ) - U_{k} (x_{ij} )}}{{U_{k} (x_{ij} ) - L_{k} (x_{ij} )}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,L_{k} \le F_{K} (x_{ij} ) \hfill \\ 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{if}}\,F_{k} (x_{ij} )\, \ge U_{k} \hfill \\ \end{aligned} \right. \le \,U_{k} , $$

where $\mu_{k} (F_{k} (x_{ij} ))$ is a strictly monotonic decreasing function with respect to $F_{k} (x_{ij} )$. Therefore, the general aggregation function can be defined as:

$$ \mu_{A} (x_{ij} ) = \mu_{A} \left\{ {\,\mu_{1} (F_{1} (x_{ij} ),\,\,\mu_{2} F_{2} (x_{ij} ),\, \ldots ,\,\,\mu_{k} F_{k} (x_{ij} )} \right\} $$

The fuzzy multi-objective formulation of the problem may be defined as

$$ \begin{aligned} & {\text{Max}} \;\;\mu_{D} (x_{ij} ) \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\Pr \,\left( {\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,\,a_{i} } \right) \ge 1 - \gamma_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\Pr \left( {\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,\,b_{j} } \right) \ge 1 - \delta_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij} \hfill \\ \end{aligned} $$

The problem is to identify the ideal value of $x_{ij}^{*}$ based on addition operator (Tiwari et al. [41]) for this convex fuzzy decision. Therefore, the above problem is rewritten, according to the max-addition operator, as

$$ \begin{aligned} & {\text{Max}} \;\;\mu_{A} (x_{{_{ij} }}^{*} ) = \,\sum\limits_{k = 1}^{K} {\mu_{k} \left( {F_{x} (x_{ij} )} \right)} = \,\sum\limits_{k = 1}^{K} {\frac{{U_{k} - \left( {F_{k} (x_{ij} )} \right)}}{{U_{k} - L_{k} }}} \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\Pr \,\left( {\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,\,a_{i} } \right) \ge 1 - \gamma_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\Pr \left( {\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,\,b_{j} } \right) \ge 1 - \delta_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij} \hfill \\ \end{aligned} $$

The above problem reduces to

$$ \begin{aligned} & {\text{Max}} \mu_{A} (x_{{_{ij} }}^{*} ) = \,\sum\limits_{k = 1}^{K} {\mu_{k} \left( {F_{x} (x_{ij} )} \right)} = \,\sum\limits_{k = 1}^{K} {\left\{ {\frac{{U_{k} }}{{U_{k} - L_{k} }} - \frac{{\left( {F_{k} (x_{ij} )} \right)}}{{U_{k} - L_{k} }}} \right\}} \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\Pr \,\left( {\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,\,a_{i} } \right) \ge 1 - \gamma_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\Pr \left( {\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,\,b_{j} } \right) \ge 1 - \delta_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij} \hfill \\ \end{aligned} $$

The above problem will attain its maxima if the function $Z_{k} (x_{ij} ) = \,\left\{ {\frac{{\left( {F_{k} (x_{ij} )} \right)}}{{U_{k} - L_{k} }}} \right\}$ is to be minimum. Therefore the above problem reduces into the following primal problem given as:

$$ \begin{aligned} & {\text{Min}} Z = \,\sum\limits_{k = 1}^{K} {\left( {Z_{x} (x_{ij} )} \right)} \hfill \\ & {\text{Subject}}\,\,\,{\text{to}}\,\,\Pr \,\left( {\sum\limits_{j = 1}^{n} {x_{ij} } \{ \le / = / \ge \} \,\,\,a_{i} } \right) \ge 1 - \gamma_{i} ,\,\,\,\,\,\,i = 1,2,3, \ldots ,m \hfill \\ & \,\,\,\,\,\,\,\Pr \left( {\sum\limits_{i = 1}^{m} {x_{ij} } \{ \le / = / \ge \} \,\,\,b_{j} } \right) \ge 1 - \delta_{j} ,\,\,\,\,\,\,j = 1,2,3, \ldots ,n \hfill \\ & 0 \le x_{ij} \le r_{ij} \hfill \\ \end{aligned} $$

After defining the transformation process of the uncertain model and their solution procedure; the next section is related to the numerical illustration of the hypothetical case study.

Numerical Illustration

For illustrating the proposed work we considered two numerical examples, which are given below:

Example 1

The following data sets has been used to show case the importance of GD over other distributions. The data represents the exceedances of flood peaks (in m³/s) of the Wheaton River near Carcross in Yukon Territory, Canada. The information is rounded to one decimal point, comprising of 72 exceedances for the years 1958–1984; were 1.6, 2.3, 14.5, 1.2, 0.5, 21.6, 4.2, 0.6, 1.6, 12.9, 11.8, 8.3, 1.2, 16.6, 7.5, 24.4, 12.4, 13.3, 21.3, 1.3, 3.4, 13.3, 1.5, 35.3, 0.5, 2.4, 38.1, 0.4, 14.3, 10.1, 6.3, 20.6, 1.4, 0.3, 0.9, 0.3, 8, 1.5, 6, 19.1, 0.3, 2.4, 12.3, 10.1, 10.2, 10.5, 29, 4.5, 5.3, 29.8, 12.3, 3.2, 24.4, 3.9, 12.6, 22.4, 25.7, 35.5, 3.8, 65, 1.4, 3.4, 37.5, 1.6, 24.3, 21.3, 17.6, 4.4, 10.3, 24.4, 2.4, 31. This data were illustrated by Choulakian and Stephens [42] for testing a Goodness-of-Fit for generalized Pareto distribution and recently analyzed by Merovci and Puka [43] for Transmuted Pareto distribution. Here, for comparison of model, we considered the most efficient criteria used for determining the efficiency of the distribution like AIC (Akaike Information Criterion), introduced by Akaike [44] and BIC (Bayesian information Criterion) introduced by Schwarz [45]. Here, we compared some well-known distributions which is widely used in life scenarios like Weibull Distribution, Pareto Distribution, Generalized Pareto Distribution, Transmuted Pareto Distribution, and Normal Distribution, and the obtained result of the distributions has been compared with the results of GD We obtained the estimate values of parameters as well as standard error of the distributions for the above defined real data set. The obtained result has been arranged according to its rank i.e. the distribution which has the lowest AIC and BIC value, considered as the best distribution among all used distributions. Table 2 show the efficiency of GD over other distributions and it is found better than other considered distributions for this real data set. The Comparison criteria are AIC = 2 k – 2LL and BIC = klog(n) – 2LL, where k is the number of parameters of model, n is sample size of the data set and LL is log likelihood of the model. The obtained results are summarized in Table 2.

Table 2 Comparison of Results

The quantitative information mentioned in the numerical illustrations are not the real evidence; according to the developed concept, it is generated hypothetical.

Example 2

To demonstrate the practical use and the computational details of working out the suggested quantity to be shipped from different sources to a different destination, the following numerical example is provided. Parts of the data are from Gupta et al. [34, 35] in which they considered three origins and three destinations with the objective of how much should they ship from origin to destination to minimize the cost of damage, cost of labouring, total transportation time, total transportation costs and also maximize the discount on shipping costs. The information simulated by DM are summarized below in the Tables 3, 4, 5, 6, 7, 8, 9, and 10.

Table 3 Fuzzy damage cost for the route i to j

Table 4 Fuzzy labour cost for the route i to j

Table 5 Fuzzy transportation time ($t_{{_{ij} }}^{a}$) for the route i to j

Table 6 Fuzzy transportation time ($t_{{_{ij} }}^{s}$) for the route i to j

Table 7 Fuzzy transportation cost $c_{{_{ij} }}^{a}$ for the route i to j

Table 8 Fuzzy transportation cost $c_{{_{ij} }}^{s}$ for the route i to j

Table 9 Fuzzy discount cost for the route i to j

Table 10 Fixed capacitated restriction for the route i to j

Let us assume a situation when there is more than one nature state of availability at the origin and requirement at the destination, respectively. Every time distribution centers are confronted with the issue of assessing the company demand. If the requirements expected from distribution centers are lower than the requirements of his company, then his profit will suffer. On the other side, there will be a marginal loss due to excess demand. Due to the continual market breakdown, the DM intends to supply the distribution centers with more amounts. In the worse business scenario, the DM always wants to understand how much of a product he has to deliver to the distribution centers in order to get rid of his losses. The center does not understand in advance, under this conditional demand and supply risk, the number of lucrative demand units for its company each day. The data given in Table 11 does not tell the DM’s explicitly how many units they should store for tomorrow’s supply to meet the random demand to maximize their profit. The information provided in Table 12 does not tell the distribution centers explicitly how many units they would require each time to maximize their profit. Since there are more than one demand and supply point, and also DM’s have partial demand and supply pattern data, they can treat demand and supply as a random variable and fit it to calculate the expected value of demand and supply through different types of probability distributions.

Table 11 Availability at plants (‘000 units)

Table 12 Requirement at distribution centers (‘000 units)

Deterministic values of the RHS of constraints has been obtained by using the SP approach as defined in Sect. 3. Demand and supply parameters follows GD with specified probability level and MLE approach has been used for obtaining the shape parameters, and scale parameters and calculated values are given below in Table 13.

Table 13 Estimated values of parameters with specified probability level

The method of solving a math problem involves a huge number of equations and thus a machine system is better to use. The software were going to use is named LINGO. LINGO is a powerful and flexible software created by LINDO Systems Inc. The solution is obtained by using LINGO 16.0 software. “LINGO is a comprehensive tool designed to make building and solving linear, nonlinear (convex and non-convex), quadratic, quadratically constrained, stochastic, multi-choice, integer and multi-criteria optimization models faster, easier and more efficiently”. It offers an altogether optimized package that can be used for an effective framework of optimization models for problem solving and more important it helps in getting the solution in minimum time. In short, LINGO’s main aim is to allow a programmer to insert a model formulation easily, solve it, determine the validity or adequacy of the solution, and we can also make a slight adjustments to the formulation easily and repeat the cycle. The primary edition of LINGO includes a “graphical user interface”, but under some specific cases, e.g. operating under Linux (command line functionality) can be used for finding the problem solution.

For Model 1′ which comprises of linear objective functions, the value of membership is unity, which implies that the DM has achieved the full level of aspiration (satisfaction) from the set goal. The formulated mathematical programming model is regarded as a non-LP problem solved by the Lingo 16.0 package. The optimal solution of the MOCSTP is obtained as: x₁₁ = 2, x₁₂ = 2, x₁₃ = 0, x₂₁ = 6, x₂₂ = 3, x₂₃ = 10, x₃₁ = 3, x₃₂ = 6, x₃₃ = 9. From an origin 1, manufacturer can ship around 4 (‘000) units to different destinations; while from an origin 2, the manufacturer can ship around 19 (‘000) units to different destinations; and on the other hand from an origin 3, the manufacturer can ship around 18 (‘000) units to different destinations. The minimum damage cost and labour cost for transporting the optimal units of quantity is 661 and 719 respectively.

For Model 2′ which comprises of fractional objective functions, the value of membership is 0.84, 0.60 and 0.91, which implies that the DM has achieved a level of 84, 60 and 91 percent aspiration (satisfaction) from the set goal. The formulated mathematical programming model is regarded as a non-LP problem solved by the Lingo 16.0 package. The optimal solution of the MOCSTP is obtained as: x₁₁ = 2, x₁₂ = 6, x₁₃ = 0, x₂₁ = 6, x₂₂ = 3, x₂₃ = 10, x₃₁ = 3, x₃₂ = 2, x₃₃ = 13. From an origin 1, manufacturer can ship around 8 (‘000) units to different destinations; while from an origin 2, the manufacturer can ship around 19 (‘000) units to different destinations; and on the other hand from an origin 3, the manufacturer can ship around 18 (‘000) units to different destinations. The minimum per unit transportation time, transportation cost and discount cost for transporting the optimal units of quantity is 1.202, 1.135, and 0.151, respectively.

For the final complicated Model 3′ which is the combination of both linear and fractional objective functions, the value of membership is 0.60, 0.65, 0.84, 0.60 and 0.92 which implies that the DM has achieved a level of 60, 65, 84, 60 and 92 percent aspiration (satisfaction) from the set goal. The formulated mathematical programming model is regarded as a non-LP problem solved by the Lingo 16 package. The optimal solution of the MOCSTP is obtained as: x₁₁ = 2, x₁₂ = 6, x₁₃ = 0, x₂₁ = 6, x₂₂ = 3, x₂₃ = 10, x₃₁ = 3, x₃₂ = 2, x₃₃ = 13. From an origin 1, manufacturer can ship around 8 (‘000) units to different destinations; while from an origin 2, the manufacturer can ship around 19 (‘000) units to different destinations; and on the other hand from an origin 3, the manufacturer can ship around 18 (‘000) units to different destinations. As compared to Origin 2 and 3, from origin 1 minimum number of quantities to be shipped to different destinations because of high transportation cost. The minimum damage cost and labour cost for transporting the optimal units of quantity is 723.50 and 777.50, respectively. While the minimum per unit transportation time, transportation cost and discount cost for transporting the optimal units of quantity is 1.202, 1.135, and 0.151, respectively.

Using AIC and BIC, we used four widely applied continuous distributions on our six parameters of demand and supply to find the best fitting distribution. AIC measures the quality of statistical models for any specific data sets, and BIC is a model selection criterion for a finite set of models; the model with the lowest AIC and BIC is preferred. The obtained results are summarized in Tables 14 and 15.

Table 14 Akaike’s information criteria of data

Table 15 Bayesian information criteria of data

The distribution that gives the least AIC and BIC value is considered to be the best fit distribution for the data set. Among all the used distributions such as Pareto, Weibull, Normal and Gamma, the least value of AIC and BIC has been correspond to the GD that shows the efficiency of our proposed work. The above defined capacitated TP with linear and fractional objective functions was first formulated by Gupta et al. [34] in which they considered the three different types of real life situations in their formulated model. They present the ambiguity in the paper with fuzzy numbers, multi-choices and randomness and used fuzzy goal programming approach for getting the desired result. Later on, Gupta et al. [35] investigated the capacitated TP with multi-choices and LR- fuzzy number parameters, and solved the problem in three stages using goal programming approach. Further, Gupta et al. [46] used different kinds of probabilistic distribution for presenting the randomness in their formulated capacitated TP. Recently Gupta et al. [47] used the concept of linearization of fractional objective functions in their formulated capacitated transportation problem along with $\alpha$-cut approach which was used to present the uncertainty in the formulated model. The obtained results of these papers are listed in Table 16.

Table 16 Comparison of results

These uncertainty scenarios in capacitated TP decision-making were taken because demand and supply are innumerable factors. Because these models are not the same circumstances, assumptions and environment. Therefore, it was not fair to compare the results obtained from these models.

Conclusion

Transportation plays a major role in every supply chain, since goods are seldom manufactured and consumed at the very same place. The product manufactured at one origin has very little interest for the prospective users unless it is transported to the point of use. The effectiveness of every supply chain is directly correlated with the effective usage of transport. Every company makes use of different modes and routes of transportation for maximum profitability. A distribution department uses transportation to reduce the actual expense of the goods to be shipped, thus ensuring a reasonable degree of consumer accessibility.

The problem of capacitated transportation is an essential issue of network optimization and is used in various fields of application-telecommunications networks, production–distribution system, rail and urban road system, and scheduled automated cargo system. In this paper, combination of linear and fractional objective functions under uncertainty have been considered for formulating the capacitated TP. We have also considered a case of uncertainty in capacitated TP in which the objective function’s coefficients are fuzzified, whereas the demand and supply parameter are random in nature. The fuzzy goal programming approach has been used to drive the MOCSTP model’s compromise solution. The research done in this paper may be useful to those researchers and industry practitioners who face the TP in such complicated circumstances. Transportation costs constitute a significant fraction of the overall cost of the supply chain, administrators need a detailed review to choose adequate means of transportation to minimize costs and control the amount of shipment. Supply chain executives ought to leverage the digital technologies at their fingertips to reduce logistics costs and improve performance in their distribution networks. Ambiguity of demand and transit supply will be taken into account when planning transport networks. If one avoids ambiguity in transportation, so the usage of inexpensive and stubborn forms of transportation will becomes greater. This method is very general and can be used in various fields such as supply chain management, portfolio management, inventory management, reliability maintenance, queuing theory etc.

In the future studies, we will extend the work to the different environment such as inventory model [48], stochastic model [49] etc., Apart from it, we will try to build a mathematical model related to (1) Direct distribution—includes the delivery of goods to all the retailers from the manufacturer; (2) Direct delivery of “Milk runs”—a “Milk run” is a path where a truck either sends a commodity to several retailers from a single manufacturer, or goes from multiple vendors to a specific distributor; (3) Deliveries through DC (distribution center)—vendors will not need to deliver products directly to the retailers in this form of transport design network. Distributions chains are split into specific regional areas and for each of those regions a centrally positioned DC is built. Vendors then deliver their supplies to the DC and then the DC passes the related orders to each vendor within its regional area; and (4) Shipping through DC utilizing “Milk Runs”—“Milk runs” can be used from a DC when the lot sizes are low. Milk runs are the most significant as the aggregation of small volumes reduces the expense of freight transport.