A numerical model for simulating the effect of strain rate on eutectic band thickness

Abstract

Large tensile strains acting on the solidifying weld metal can cause the formation of eutectic bands along grain boundaries. These eutectic bands can lead to severe liquation in the partially melted zone of a subsequent overlapping weld. This can increase the risk of heat-affected zone liquation cracking. In this paper, we present a solidification model for modeling eutectic bands. The model is based on solute convection in grain boundary liquid films induced by tensile strains. The proposed model was used to study the influence of strain rate on the thickness of eutectic bands in Alloy 718. It was found that when the magnitude of the strain rate is 10 times larger than that of the solidification rate, the calculated eutectic band thickness is about 200 to 500% larger (depending on the solidification rate) as compared to when the strain rate is zero. In the paper, we also discuss how eutectic bands may form from hot cracks.

1 Introduction

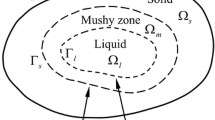
A pure metal has the same solidus and liquidus temperatures. An alloy, on the other hand, has a solidus temperature that is always lower than the liquidus temperature. This results in the formation of a partially melted zone (PMZ) when the alloy is being welded. The PMZ is in the heat-affected zone (HAZ), immediately adjacent to the fusion zone (FZ). In this zone, the base material has only been partially melted. This contrasts with the FZ where all material has been fully melted. The PMZ can be susceptible to HAZ liquation cracking, which is a type of hot crack. HAZ liquation cracking is normally intergranular and is formed by rupture of a grain boundary liquid film (GBLF) [1,2,3]. The rupture occurs at the terminal stage of the solidification and is caused by tensile stresses that are acting on the GBLF.

The susceptibility to HAZ liquation cracking depends on the size of the PMZ and the thickness of the GBLFs in the PMZ. For a polycrystalline alloy, without any particles or eutectic, the outer boundary of the PMZ is traced out by an isotherm that is a few degrees below the solidus temperature of the alloy. This temperature difference is because of the grain boundaries, which are high-energy sites, that slightly lower the melting temperature [1]. However, if the alloy contains particles, melting can start to occur by a eutectic reaction between a particle and the matrix at the eutectic temperature [3]. As the eutectic temperature can be significantly lower than the melting temperature of the matrix, the presence of particles can therefore greatly extend the width of the PMZ.

The presence of grain boundary eutectic in the PMZ can be more detrimental to HAZ liquation cracking than the presence of particles. If the grain boundary eutectic forms long continuous bands, which we call eutectic bands, long continuous GBLFs will rapidly form in the PMZ when the temperature reaches the eutectic temperature. Macroscopic tensile strains can then strongly localize in these GBLFs, which can fracture them and cause HAZ liquation cracking.

A eutectic band forms continuously from the solidifying end (root) of a GBLF which moves with the eutectic temperature isotherm. The thickness of the eutectic band depends on the magnitude of the tensile strains that act on the GBLF that the band forms from. If the strains are large, a large amount of solute can be advected to the root of the GBLF. The excess of solute makes it possible to form a large amount of eutectic when the liquid at the root of the GBLF solidifies. However, if the strains are low, the amount of solute may not be enough to form a continuous band of eutectic along the grain boundary. In this case, the eutectic is primarily located between secondary dendrite arms. This can be seen, for example, in the FZ of single-pass welded Alloy 718 when no load has been applied to the weld during its solidification. However, if an external load is applied to a weld of Alloy 718 (for example with a Varestraint test), eutectic bands can form, which is shown in Fig. 17.

Multi-pass welding processes, such as additive manufacturing and repair welding, may be particularly susceptible to the formation of eutectic bands. In these processes, large residual stresses can form due to the large number of welds. This, together with unfavorable restraining of the weld metal that may arise during the build, can lead to tensile strains that can form eutectic bands.

In this paper, we present a solidification model for studying the effect of tensile strain on the thickness of grain boundary eutectic bands. The model is relatively simple and is limited to alloys whose solidification path can be obtained roughly from a pseudo-binary phase diagram. The model is based on an isolated GBLF where thermodynamic equilibrium at the solid-liquid interface and uniform solute concentration across the thickness of the GBLF are assumed. However, despite these simplifications, the model incorporates several phenomena such as back diffusion, solute advection induced by mechanical straining, solidification shrinkage, and diffusion along the GBLF.

2 Solidification model

In this chapter, we develop a solidification model to estimate the amount of eutectic that forms during the continuous solidification of a GBLF. The model is based on lamellar structure solidification with alternating layers of solid and liquid. The solute concentration in the GBLF is determined by a one-dimensional convection-diffusion model, while the solute concentration in the solid phase, adjacent to the GBLF, is determined by a two-dimensional diffusion model. The solidification of the GBLF is driven by a prescribed temperature field. The solute concentration at the solid-liquid interface of the GBLF is determined from a pseudo-binary phase diagram for a given temperature.

2.1 Process limitations

The presented solidification model is limited to solidification conditions that occur in the FZ of a TIG weld at a low welding speed. The low welding speed is assumed to give rise to a columnar dendritic solidification mode that results in only columnar grains. In this columnar grain structure, it is assumed to exist continuous GBLFs that extend from the liquidus to the solidus isotherm. Furthermore, we assume that the weld is fully penetrating such that the temperature and deformation are uniform in the thickness direction of the weld specimen. Based on these assumptions, we assume that the liquid flow in a GBLF always occurs in the plane of the weld specimen. This is the same approach that the authors were using when they were modeling solidification cracking in the FZ of a TIG weld. More information about this can be found in [4, 5].

2.2 GBLF lamella model

To model the solidification process and the formation of a eutectic band, we consider a GBLF that extends from the liquidus isotherm to the eutectic temperature isotherm. This GBLF is assumed to be located between two large grain clusters, which is shown schematically in Fig. 1. Because the GBLF is weaker than the grain clusters, deformations that occur during the solidification can strongly localize in the GBLF. This has been discussed by the authors in their previous work on solidification cracking [4].

Fig. 1

Schematic of a GBLF between two grain clusters. The grains of the clusters are not shown. Only some of the dendrites that belong to the grains that are closest to the GBLF are shown. A eutectic band that forms at the end of the GBLF is also shown

To simplify the modeling of the solidification of the GBLF, we assume that the GBLF is located between two solid lamellae as shown in Fig. 2. The lamellae extend to infinity in the perpendicular direction to figure. With this approximation, the complex geometries of the dendritic solid-liquid interfaces of the GBLF have been replaced by smooth lines in the xy-plane of the figure.

Fig. 2

Simplified GBLF when no mechanical strain is present. The GBLF is assumed to be symmetric about the y = λ₁/2 plane, and the two opposing solids are assumed to be symmetric about the y = 0 and y = λ₁ planes

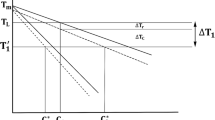
Now, let x be a coordinate along the GBLF, whereas y is a coordinate in the transverse direction of the GBLF. When no mechanical strain is present, the GBLF is assumed to be symmetric about the y = λ₁/2 plane, and the two opposing solids are assumed to be symmetric about the y = 0 and y = λ₁ planes, as shown in Fig. 2. Here, λ₁ is the primary dendrite arm spacing. In the figure, the GBLF thickness of the simplified configuration is denoted by 2h, and the solid-liquid interface position is denoted by Γ. The solidification is assumed to occur with zero undercooling at liquidus (T_l) and to terminate at the eutectic temperature (T_e) with zero undercooling for eutectic formation. In this study, we will restrict to planar liquidus and eutectic isotherms. Thus, the position and speed of the liquidus isotherm are given by $x_{T_{l}}$ and $\dot {x}_{T_{l}}$, respectively, whereas the position and speed of the eutectic isotherm are given by $x_{T_{e}}$ and $\dot {x}_{T_{e}}$, respectively, as shown in Fig. 2.

2.3 Strain localization

The two grain clusters that the GBLF is located between can have a large difference in their crystal directions, i.e., a large misorientation angle. This large misorientation gives rise to an “unstructured” GBLF; that is, the GBLF is thicker than a GBLF associated with a small misorientation. Moreover, even though the opposing secondary primary dendrite arms of a GBLF with a high misorientation come into contact, a significant amount of undercooling may be required to fuse them together [4, 6, 7]. However, if the misorientation angle is small, the dendrite arms can fuse with no undercooling.

As thick liquid films do not withstand tensile loads as well as thin liquid films, and because opposing secondary dendrite arms resist merging, tensile strain localize in the GBLFs that are associated with the large misorientation angles. The degree of localization depends on the number of grains with low misorientation angles that surround a GBLF with a large misorientation angle. These grains form a grain cluster, and owing to the low misorientation angles between them, their secondary dendrite arms can start to merge as soon as they come into contact. Therefore, the grain cluster can start to transmit tensile loads as soon as the temperature approaches the coherent temperature (T_c).

We assume that macroscopic tensile mechanical strain localizes in a GBLF between two grain clusters as is described in [4]. Here, a temperature-dependent length scale, l₀, is used to localize the macroscopic mechanical strain in the GBLF as follows. Given a point in the GBLF, it is assumed that all macroscopic strain within a region of diameter 2h + l₀, and centered at the given point, will localize in the GBLF. The deformation rate of the GBLF can then be written as [4]

$$ \frac{\partial h}{\partial t} = \left( h + \frac{l_{0}}{2} \right)\dot{\varepsilon}^{m}_{\perp} - \frac{\partial {\varGamma}}{\partial t}, $$

(1)

where $\dot {\varepsilon }^{m}_{\perp }$ is the macroscopic strain rate normal to the GBLF. We note that ∂Γ/∂t is the solidification rate in the transverse direction to the GBLF. Furthermore, l₀ represents the amount of surrounding solid phase of the GBLF that can transmit normal tensile loads. The value of l₀ is zero at T_l, the same as the primary dendrite arm spacing at T_c, and as the diameter of a characteristic grain cluster at T_e. Between these temperatures, l₀ is assumed to vary linearly. The characteristic diameter of a grain cluster for Alloy 718 was determined to be 800 μ m in a previous study by the authors [5]. This was obtained by inverse modeling of Varestraint tests for autogenous TIG welding of Alloy 718 at a welding speed of 1 mm/s. The primary dendrite arm spacing in these tests was approximately 20 μ m. Figure 3 shows l₀, as defined above, with the values for Alloy 718.

Fig. 3

l₀ as a function of temperature for Alloy 718

The mechanical strain of the GBLF in Eq. 1 is added to the previously described lamella model by assuming that the solid lamella that is symmetric about the y = 0 plane in Fig. 2 belongs to a grain cluster that is stationary in the xy plane, whereas the lamella that is symmetric about the y = λ₁ plane belongs to a grain cluster that moves at a transverse speed such that the rate of change of the GBLF thickness satisfies Eq. 1. By adding the mechanical straining of the GBLF in this manner, the symmetry of the lamella model about the y = Γ + h surface is destroyed, which is shown in Fig. 4. However, if we consider the displacement caused by the mechanical straining (orders of micrometers) to be much smaller than the length of the GBLF (orders of millimeters), the curvature of the y = Γ + h surface is small. Thus, the lamella model can still be considered to be geometrically symmetric about the y = Γ + h surface, which we will do in the rest of the paper.

Fig. 4

Lamella model with the addition of mechanical straining. The lower solid lamella is stationary with respect to mechanical straining, whereas the upper solid lamella moves with its associated grain cluster so that the GBLF is deformed at a rate satisfying Eq. 1. The box drawn in bold represents a control volume that is used to derive a solute mass balance in the GBLF. The longitudinal and transverse directions are not in proportion in the figure

2.4 Solute mass balance

The transverse solidification rate and the GBLF thickness are now derived from a solute mass balance of a control volume that extends across the GBLF (see Fig. 4). This mass balance is based on the following assumptions. We only consider alloys whose solidification path can be approximately represented by a pseudo-binary phase diagram. Furthermore, we assume thermodynamic equilibrium at the solid-liquid interface. Thus, the solidification of the alloy is determined by considering only one solute element, for which the concentration at the interface is given by a pseudo-binary phase diagram for a given temperature. The transverse solidification rate is then determined by the rate at which the solid phase rejects solute back into the liquid phase (assuming a partition factor less than 1), and by the rate at which the solute can be transported from the solid-liquid interface into the matrix by diffusion. The transverse solidification rate is also determined by the solute diffusion along the GBLF, the solute advection caused by mechanical straining and solidification shrinkage. Furthermore, we assume that the solute concentration is uniform across the GBLF. This and the previous assumption of thermodynamic equilibrium at the solid-liquid interface show that the solute concentration C_l in the whole GBLF can be expressed as a function of the temperature T by

$$ C_{l} = \frac{T-T_{l}}{m} + C_{0}, $$

(2)

where m is the liquidus slope and C₀ is the nominal solute concentration. Furthermore, by the assumption of thermodynamic equilibrium at the interface, the solute concentration $C^{*}_{s}$ at the interface in the solid phase can be determined from

$$ C^{*}_{s} = kC_{l}, $$

(3)

where k is the solute partition coefficient. Both m and k are obtained from the pseudo-binary phase diagram for the alloy under consideration.

We assume that the latent heat that is generated at the solid-liquid interface can diffuse away at a rate significantly larger than the transverse solidification rate. Thus, the temperature in the transverse direction of the GBLF can be considered to be uniform. Furthermore, we assume that the concentration field in the GBLF is symmetric about the y = Γ + h plane (which was discussed in the previous section). Furthermore, the concentration field in the lower solid lamella (see Fig. 4) is assumed to be symmetric about the y = 0 plane. The diffusion of the solute in the longitudinal direction of the solid phase is assumed to be negligible. Thus, there is no solute flux along the end boundary x = x_Te of the solid phase. Along the end boundary x = x_Te of the GBLF, there is an advective flux owing to solidification shrinkage, which is proportional to the longitudinal solidification rate $\dot {x}_{T_{e}}$, as will be discussed later.

Based on the previous assumption of a fully penetrating weld, which gives uniform deformation and temperature through the thickness of the weld specimen, we assume that the liquid flow and the diffusion flux in the GBLF only occur along the x-direction of the GBLF. This means that there is no solute transport in the z-direction. Furthermore, only the average speed of the liquid across the GBLF is considered in the solute advection. Thus, the liquid speed profile across the film is not considered. The domain of the solidification problem can now be reduced to the domain $x_{T_{e}} \leq x \leq x_{T_{l}}, 0 \leq y \leq {\varGamma }+h$. Note that this domain moves in space as solidification progresses.

From the above assumptions, a solute balance across the GBLF can be derived as follows. We consider the control volume CV shown in Fig. 4. By the previous symmetry assumption about the y = Γ + h surface, it suffices to consider only the lower half of the CV, which is shown in Fig. 5. This CV does not move in the x-direction, but its upper and lower boundaries move so that they coincide with the surfaces y = Γ + h and y = Γ, respectively.

Fig. 5

Control volume containing one-half of a cross section slice of the GBLF (see Fig. 4). The control volume is stationary in the x-direction but it is bounded between y = Γ and y = Γ + h which are not stationary. The arrows in the figure indicate solute mass fluxes across the boundaries of the control volume

Now, let C be the mass fraction of solute. At the lower boundary of the CV, solute is leaving the CV with the mass flux $\rho _{s} \partial {{\varGamma }} / \partial {t} C^{*}_{s}$ due to the motion of the solid-liquid interface. Here, ρ_s is the density of the solid phase, which in this study is assumed to be constant. Furthermore, at this boundary, the solute leaves the CV with the flux $\rho _{s} D_{s} \partial {C^{*}_{s}} / \partial {y}$ because of the diffusion of solute from the solid-liquid interface into the solid phase (under the assumption that k < 1). Here, D_s is the diffusion coefficient of the solute in the solid phase, which is assumed to be temperature dependent. Furthermore, owing to the solute gradient in the GBLF, the solute will cross the vertical sides of the CV with the diffusional mass flux ρ_lD_l∂C_l/∂x, where ρ_l and D_l are the density and the diffusion coefficient of the liquid phase, respectively. Both are assumed to be constant. Owing to the solidification shrinkage and the mechanical straining of the GBLF, the solute will enter and leave the CV with mass flux $\rho _{l} \bar {v} C_{l}$, where $\bar {v}$ is the average liquid speed across the GBLF. Based on all these solute fluxes, the solute mass balance for the CV in Fig. 5 can be written as

$$ \begin{array}{@{}rcl@{}} \rho_{l}\frac{\partial (C_{l}h)}{\partial t} &+& \rho_{l}\frac{\partial}{\partial x}\!\left( C_{l} \bar{v}h \right) - \rho_{l}D_{l}\frac{\partial}{\partial x}\!\left( \frac{\partial C_{l}}{\partial x}h\right) + \rho_{s}C^{*}_{s}\frac{\partial {\varGamma}}{\partial t} \\ &+& \rho_{s}D_{s}\frac{\partial C^{*}_{s}}{\partial y} = 0. \end{array} $$

(4)

when Δx goes to zero.

In order to simplify the analysis, we will from now on only consider solidification that occurs along a constant temperature gradient with magnitude G. Then, the ∂C_l/∂x term in Eq. 4 can be written as

$$ \frac{\partial C_{l}}{\partial x} = \frac{G}{m}, $$

(5)

which follows from Eq. 2.

To enhance the robustness of the numerical method that will be used to solve Eq. 4, we use the following length and time scales:

$$ L_{x} = \frac{T_{l} - T_{e}}{G}, \quad L_{y} = \frac{\lambda_{1}}{2}, \quad \tau = \frac{T_{l} - (T_{e} + {\varDelta} T_{s})}{v_{w}G}, $$

(6)

where v_w is the welding speed and ΔT_s is a parameter that is associated with the initial size of the domain for the solid phase (see Section 2.8). These scales are used to define the following nondimensional variables:

$$ \begin{array}{@{}rcl@{}} \tilde{x} &=& \frac{x}{L_{x}},\ \tilde{y} = \frac{y}{L_{y}}, \tilde{t} = \frac{t}{\tau}, \tilde{h} = \frac{h}{L_{y}}, \tilde{{\varGamma}} = \frac{{\varGamma}}{L_{y}}, \dot{\tilde{x}} = \frac{\tau\dot{x}}{L_{x}}, \\ \dot{\tilde{y}} &=& \frac{\tau\dot{y}}{L_{y}}, \dot{\tilde{{\varGamma}}} = \frac{\tau\dot{{\varGamma}}}{L_{y}},\\ \tilde{\bar{v}} &=& \frac{\tau\bar{v}}{L_{x}}, \tilde{l}_{0} = \frac{l_{0}}{L_{y}}, \tilde{C_{s}} = \frac{C_{s}}{C_{0}}, \tilde{C_{l}} = \frac{C_{l}}{C_{0}}, \tilde{D}_{s} = \frac{\tau D_{s}}{{L_{y}^{2}}}, \\ \tilde{D}_{l} &=& \frac{\tau D_{l}}{{L_{x}^{2}}} \end{array} $$

(7)

Substituting these variables into Eq. 4 and using Eqs. 1, 3, and 5 yield

$$ \begin{aligned} &\frac{\partial (\tilde{C}_{l}\tilde{h})}{\partial \tilde{t}} - \frac{\rho_{s}k\tilde{C}_{l}}{\rho_{l}}\frac{\partial \tilde{h}}{\partial \tilde{t}} - \frac{GL_{x}\tilde{D}_{l}}{C_{0}m}\frac{\partial \tilde{h}}{\partial \tilde{x}} + \frac{\partial}{\partial \tilde{x}}\!\left( \tilde{C}_{l} \tilde{\bar{v}}\tilde{h} \right)\\ &+ \frac{\rho_{s}\tau k \dot{\varepsilon}^{m}_{\perp}\tilde{C}_{l}}{\rho_{l}}\tilde{h} + \frac{\rho_{s}\tau k \dot{\varepsilon}^{m}_{\perp}\tilde{C}_{l}}{\rho_{l}}\frac{\tilde{l}_{0}}{2} + \rho_{s}D_{s}\frac{\partial C^{*}_{s}}{\partial \tilde{y}} = 0. \end{aligned} $$

(8)

We note that for a given temperature field, $\tilde {C}_{l}$ is known by Eqs. 2 and 7. Thus, the only unknowns in Eq. 8 are $\tilde {h}$, $\tilde {\bar {v}}$, and $\partial C^{*}_{s} / \partial \tilde {y}$. Furthermore, the only independent variables (except for the given temperature field) in Eq. 8 are $\tilde {x}$ and $\tilde {t}$.

The average liquid speed $\bar {v}$ can be related to h by deriving a total mass balance on the above CV by considering the mass fluxes induced by mechanical straining and solidification shrinkage. This yields

$$ \frac{\partial(\bar{v}h)}{\partial x} = -\left( 1 + \upbeta \right)\frac{\partial {\varGamma}}{\partial t} - \frac{\partial h}{\partial t}, $$

(9)

where β is the solidification shrinkage factor, which is defined by

$$ \upbeta = \frac{\rho_{s} - \rho_{l}}{\rho_{l}}. $$

(10)

The derivation of Eq. 9 is described in more detail in [4].

By substituting Eq. 1 into Eq. 9, and then scaling Eq. 9, and finally integrating Eq. 9 with respect $\tilde {x}$, allows the $\tilde {\bar {v}}\tilde {h}$ term to be expressed in the dependent variable $\tilde {h}$ and the independent variables $\tilde {x}$ and $\tilde {t}$ (see Section 2.6 for more details about the integration). Finally, by substituting this expression for $\tilde {\bar {v}}\tilde {h}$ into Eq. 8 gives an expression for $\tilde {h}$ and $\partial C^{*}_{s} / \partial \tilde {y}$ as the only dependent variables when the temperature field and the strain rate are known.

The back diffusion term $\partial C^{*}_{s} / \partial \tilde {y}$ in Eq. 8 will be treated in the next section. In Section 2.6, we will integrate Eq. 8 to obtain $\tilde {h}$.

2.5 Back diffusion

To determine the solute flux term $\partial C^{*}_{s} / \partial \tilde {y}$ in Eq. 8, we have to determine the concentration field in the entire lower solid lamella in Fig. 4. From the previous approximations of negligible diffusion in the longitudinal direction, symmetry at the y = 0 plane, and local equilibrium at the solid-liquid interface, the concentration field in the solid can be computed from

$$ \begin{cases} \begin{aligned} &\frac{\partial \tilde{C}_{s}}{\partial \tilde{t}} - \tilde{D}_{s} \frac{\partial^{2} \tilde{C}_{s}}{\partial \tilde{y}^{2}} = 0\\ &\tilde{C}_{s}(\tilde{y}=\tilde{{\varGamma}}) = k\tilde{C}_{l}\\ &\frac{\partial \tilde{C}_{s}(\tilde{x}=\tilde{x}_{T_{e}})}{\partial \tilde{x}} = 0\\ &\frac{\partial \tilde{C}_{s}(\tilde{y}=0)}{\partial \tilde{y}} = 0\\ &\end{aligned} &\end{cases} $$

(11)

where Eq. 11 is expressed in terms of the dimensionless variables that are defined in Eq. 7. We determine the C_s field from Eq. 11 by applying a finite difference method. Because the geometry of the solid domain in the $\tilde {x}\tilde {y}$ space is complex and moving, it is difficult to perform the finite difference procedure in this space. Therefore, the solid domain is mapped to the unit square in the ξη space by the inverse of the mapping

$$ \begin{cases} \begin{aligned} \tilde{x} &= (\tilde{x}_{T_{l}} - \tilde{x}_{T_{e}})\xi + \tilde{x}_{T_{e}}, \quad 0\leq \xi \leq 1 \\ \tilde{y} &= \tilde{{\varGamma}}f(\eta), \quad 0\leq \eta \leq 1 \end{aligned} \end{cases} $$

(12)

where f is the stretching function

$$ f(\eta) = \frac{\text{erf}{\left( \eta/\alpha \right)}}{\text{erf}{\left( 1/\alpha \right)}}, $$

(13)

which is used to distribute the grid points more densely at the solid-liquid interface. This enables a better resolution of the large concentration gradient in this region. The erf function in f is the error function, and α is a parameter that is used to control the degree of grid point clustering at the interface.

For the mapping in Eq. 12 to be bijective, we assume that the solidification tip of the solid is flat; that is, ${\varGamma }(x=x_{T_{l}}) = {\varGamma }_{min}$, where Γ_min is a small value. In this study, we used Γ_min = L_y/1000. The inverse of the mapping in Eq. 12 is shown in Fig. 6.

Fig. 6

Mapping of the physical region in the $\tilde {x}\tilde {y}$ space onto the unit square in the ξη space

A structured grid can now easily be constructed on the unit square in the ξη space. However, we must now transform the problem in Eq. 11 into the curvilinear system ξη. The problem can be stated in the ξη system in either a conservative or a non-conservative form. Here, we use the conservative form, which provides telescopic collapse of the flux terms when the difference equations are summed over the field; that is, the summation involves only the boundary fluxes. This favors the conservative form for the numerical representation of the net flux through a volume element [8].

The conservative form of the two-dimensional gradient of a scalar f is given by [8]:

$$ \begin{cases} \begin{aligned} \frac{\partial f}{\partial \tilde{x}} &= \frac{1}{J} \!\left[ \frac{\partial \left( \mathrm{J}_{22} f \right)}{\partial \xi} - \frac{\partial \left( \mathrm{J}_{21} f \right)}{\partial \eta} \right]\\ \frac{\partial f}{\partial \tilde{y}} &= \frac{1}{J}\! \left[ -\frac{\partial \left( \mathrm{J}_{12} f \right)}{\partial \xi} + \frac{\partial \left( \mathrm{J}_{11} f \right)}{\partial \eta} \right] \end{aligned} \end{cases} $$

(14)

where J_ij are the components of the Jacobian matrix

$$ \left[\mathrm{J}_{ij}\right] = \left[\frac{\partial \tilde{x}^{i}}{\partial \xi^{i}}\right], $$

(15)

which is associated with the mapping in Eq. 12, and J is the determinant of the Jacobian matrix. As the grid moves in the physical space, the time derivative should also be transformed. The conservative form of the partial time derivative of a scalar function f on a two-dimensional domain is given by [8]:

$$ \frac{\partial f}{\partial \tilde{t}} = \frac{1}{J} \!\left[ \frac{\partial \left( J f \right)}{\partial \tilde{t}} - \sum\limits_{i=1}^{2} \frac{\partial \left( JfU^{i} \right)}{\partial \xi^{i}} \right], $$

(16)

where Uⁱ is the contravariant grid velocity in the ξⁱ-direction (ξ¹ = ξ,ξ² = η), which is given by

$$ U^{i} = \vec{a}^{i}\bullet\left( -\vec{\dot{\tilde{x}}}\right), $$

(17)

where $\vec {a}^{i}, (i=1,2)$ are the contravariant base vectors of the ξη space, which are given by

$$ \begin{cases} \begin{aligned} \vec{a}^{1} &= \frac{1}{J} \!\left[\mathrm{J}_{22}\hat{\vec{e}}_{\tilde{x}} - \mathrm{J}_{12}\hat{\vec{e}}_{\tilde{y}}\right]\\ \vec{a}^{2} &= \frac{1}{J} \!\left[-\mathrm{J}_{21}\hat{\vec{e}}_{\tilde{x}} + \mathrm{J}_{11}\hat{\vec{e}}_{\tilde{y}}\right], \end{aligned} \end{cases} $$

(18)

and $\vec {\dot {\tilde {x}}}$ is the grid velocity in the $\tilde {x}\tilde {y}$ space. We note that the time derivative on the left side of Eq. 16 is at a fixed point in the physical space, whereas the time derivative on the right side of Eq. 16 is at a fixed point in the transformed space.

We can now transform Eq. 11 into the ξη space. The second-order partial derivative $\partial /\partial \tilde {y}$ in Eq. 11 is obtained by applying Eq. 14(b) twice, with $\tilde {C}_{s}$ instead of f. We note that this expression is simplified by the fact that J₁₂ ≡ 0, which can be seen by applying Eq. (15) to Eq. (12). The transformation of the natural boundary conditions in Eq. 11 is obtained by applying Eq. 14. Furthermore, the grid velocity $\vec {\dot {\tilde {x}}}$ is determined from Eq. 12, which gives

$$ \begin{cases} \begin{aligned} \dot{\tilde{x}} &= (\dot{\tilde{x}}_{T_{l}} - \dot{\tilde{x}}_{T_{s}})\xi + \dot{\tilde{x}}_{T_{s}}\\ \dot{\tilde{y}} &= \dot{\tilde{{\varGamma}}}f(\eta) \end{aligned} \end{cases} $$

(19)

Furthermore, inserting J₁₂ ≡ 0 into Eq. 18 and then inserting Eq. 18 into Eq. 17 yield

$$ \begin{cases} \begin{aligned} U^{1} &= -\frac{\mathrm{J}_{22}}{J}\dot{\tilde{x}} \\ U^{2} &= \frac{1}{J} \!\left[\frac{\mathrm{J}_{21}}{J}\dot{\tilde{x}} - \frac{\mathrm{J}_{11}}{J}\dot{\tilde{y}} \right] \end{aligned} \end{cases} $$

(20)

Finally, by inserting Eq. 19 into Eq. 20, and then inserting Eq. 20 into Eq. 16, the time derivative in Eq. 11 can be computed from Eq. 16 by replacing f with $\tilde {C}_{s}$ in Eq. 16. Thus, the transformation of Eq. 11 into the ξη space can be written as

$$ \begin{cases} \begin{aligned} &\frac{\partial (J\tilde{C}_{s})}{\partial \tilde{t}} + \frac{\partial (q_{1} \tilde{C})}{\partial \xi} + \frac{\partial(q_{2} \tilde{C})}{\partial \eta} + \frac{\partial}{\partial \eta}\!\left[q_{3}\frac{\partial(q_{4} \tilde{C})}{\partial \eta}\right] = 0\\ &\tilde{C}_{s}(\eta=1) = k\tilde{C}_{l}\\ &\tilde{C}_{s}(\xi=1) = k\\ &\frac{\partial \tilde{C}_{s}(\tilde{x}=0)}{\partial \tilde{x}} = \frac{1}{J} \!\left[ \frac{\partial \left( \mathrm{J}_{22} \tilde{C}_{s} \right)}{\partial \xi} - \frac{\partial \left( \mathrm{J}_{21} \tilde{C}_{s} \right)}{\partial \eta} \right] = 0\\ &\frac{\partial \tilde{C}_{s}(\tilde{y}=0)}{\partial \tilde{y}} = \frac{1}{J}\! \left[ \frac{\partial \left( \mathrm{J}_{11} \tilde{C}_{s} \right)}{\partial \eta} \right] = 0 \end{aligned} \end{cases} $$

(21)

where

$$ q_{1} = -\mathrm{J}_{22} \dot{\tilde{x}},\quad q_{2} = -\mathrm{J}_{21} \dot{\tilde{x}} - \mathrm{J}_{11}\dot{\tilde{y}},\quad q_{3} = -\frac{\mathrm{J}_{11}}{J}\tilde{D}_{s},\quad q_{4} = \mathrm{J}_{11}. $$

(22)

This problem is solved by a finite difference method where the space derivatives are approximated by a second-order central difference scheme, and the time derivative by a first-order backward difference scheme. The natural boundary condition along ξ = 0 is implemented by a fifth-order forward difference for ∂/∂ξ and a second-order central difference for ∂/∂η. However, the natural boundary condition along η = 0 is implemented by using the symmetry of the $\tilde {C}_{s}$ field, thus allowing the boundary condition to be implemented by ghost nodes. The Jacobian matrix at the ghost nodes can be computed by an extension of the mapping $\tilde {y} = \tilde {{\varGamma }}f(\eta )$ in Eq. 12 to negative values of η.

The elements of the Jacobian matrix are computed by the same difference representation as in the $\tilde {C}_{s}$ field. Compared with an analytic computation (if possible), this can improve accuracy [8]. Moreover, it is not recommended to compute the Jacobian J as the determinant of the Jacobian matrix because this can lead to spurious source terms; rather, Thompson et al. [8] recommend updating J using the generic conservation equation

$$ \frac{\partial J}{\partial \tilde{t}} - \sum\limits_{i=1}^{2} \frac{\partial \left( JU^{i} \right)}{\partial \xi^{i}}= 0. $$

(23)

Once the concentration field has been determined at a given time, the $\partial C^{*}_{s} / \partial \tilde {y}$ term, which is required for deriving the solute balance, can be computed from

$$ \frac{\partial \tilde{C}^{*}_{s}}{\partial \tilde{y}} = \left.\frac{1}{J}\! \left[ \frac{\partial \left( \mathrm{J}_{11} \tilde{C}_{s} \right)}{\partial \eta} \right]\right|_{\eta=1}, $$

(24)

where the derivative ∂/∂η is calculated by a fifth-order backward difference.

2.6 GBLF thickness

As noted previously, for a given temperature field and strain rate, the combination of the solute mass balance in Eq. 8 and the total mass balance in Eq. 9 yields a PDE with the two dependent variables $\tilde {h}$ and $\partial C^{*}_{s} / \partial \tilde {y}$ and the two independent variables $\tilde {x}$ and $\tilde {t}$. We will now solve this PDE for $\tilde {h}$.

We know from the previous section that $\partial C^{*}_{s} / \partial \tilde {y}$ depends on $\tilde {{\varGamma }}$. $\tilde {{\varGamma }}$ in turn depends on $\tilde {h}$ through Eq. 1. This makes it difficult to express $\partial C^{*}_{s} / \partial \tilde {y}$ as a function of only $\tilde {h}$. Therefore, $\tilde {h}$ will be determined by a fixed-point iteration method, where the $\partial C^{*}_{s} / \partial \tilde {y}$ is determined from a $\tilde {h}$ that lags one iteration. This method is described in the following.

First, we transform the domain $\tilde {x}_{T_{e}}\leq \tilde {x}\leq \tilde {x}_{T_{l}}$ of the GBLF into the domain 0 ≤ ξ ≤ 1 using the inverse of the mapping in Eq. 12(a); that is,

$$ \tilde{x} = (\tilde{x}_{T_{l}} - \tilde{x}_{T_{e}})\xi + \tilde{x}_{T_{e}}, \quad 0\leq \xi \leq 1. $$

(25)

With respect to this transformation, the spatial derivative of a scalar function f is

$$ \frac{\partial f}{\partial \tilde{x}} = \frac{1}{J}\frac{\partial f}{\partial \xi}, $$

(26)

whereas the time derivative with respect to the transformation to the conservative form is

$$ \frac{\partial f}{\partial \tilde{t}} = \frac{1}{J}\left[\frac{\partial(Jf)}{\partial \tilde{t}} - \frac{\partial(\dot{\tilde{x}}f)}{\partial \xi}\right], $$

(27)

where $\dot {\tilde {x}}$ is given by Eq. 19 and J is the Jacobian of the mapping in Eq. 25, given by

$$ J = \frac{\partial\tilde{x}}{\partial \xi} $$

(28)

As was the case for the Jacobian of the mapping in Eq. 12, it is recommended that J is determined from the generic conservation Eq. 23 rather than Eq. 28, which gives

$$ \frac{\partial J}{\partial \tilde{t}} -\frac{\partial\dot{\tilde{x}}}{\partial \xi} = 0 $$

(29)

for the mapping in Eq. 25.

We now transform the solute balance in Eq. 8 using the derivative operators in Eqs. 26 and 27. This yields

$$ \begin{aligned} &\frac{\partial}{\partial \tilde{t}}\! \left( J\tilde{C}_{l}\tilde{h}\right) + p_{1}\frac{\partial(J\tilde{h})}{\partial \tilde{t}} - p_{1}\frac{\partial(\dot{\tilde{x}}\tilde{h})}{\partial \xi} - \frac{\partial}{\partial \xi}\! \left( \dot{\tilde{x}}\tilde{C}_{l}\tilde{h}\right)\\ &+ p_{2}\frac{\partial\tilde{h}}{\partial \xi} + p_{3}\frac{\partial}{\partial \xi}\! \left( \tilde{\bar{v}}\tilde{C}_{l}\tilde{h}\right) + p_{4}\tilde{h} + p_{5}\frac{\tilde{l_{0}}}{2} + p_{5}\frac{\partial\tilde{C}_{s}}{\partial \tilde{y}} = 0, \end{aligned} $$

(30)

where

$$ \begin{array}{@{}rcl@{}} p_{1} &=& -\frac{\rho_{s}k\tilde{C}_{l}}{\rho_{l}}, p_{2} = -\frac{L_{x}G\tilde{D}_{l}}{mC_{0}}, p_{3} = 1, \\ p_{4}&=& \frac{\rho_{s}\tau k \dot{\varepsilon}^{m}_{\perp}J\tilde{C}_{l}}{\rho_{l}}, p_{5} = \frac{\rho_{s}J\tilde{D}_{s}}{\rho_{l}}. \end{array} $$

(31)

Now, we substitute Eq. 1 into Eq. 9, and then also transform Eq. 9. This yields

$$ \begin{array}{@{}rcl@{}} \frac{\partial(\tilde{\bar{v}}\tilde{h})}{\partial \xi} &=& -\tau J(1 + \upbeta)\dot{\varepsilon}^{m}_{\perp}\frac{\tilde{l}_{0}}{2} - \tau J(1 + \upbeta)\dot{\varepsilon}^{m}_{\perp}\tilde{h} - \upbeta\frac{\partial(\dot{\tilde{x}}\tilde{h})}{\partial \xi} \\ &&+ \upbeta\frac{\partial(J\tilde{h})}{\partial \xi}. \end{array} $$

(32)

The transformed domain 0 ≤ ξ ≤ 1 is now discretized using N_i equally spaced grid points, and the time domain $0\leq \tilde {t}\leq \tilde {t}_{e}$ is subdivided into N_k − 1 equal time steps ${\varDelta }\tilde {t}$. Here, $\tilde {t}_{e}$ is the end time. Furthermore, we define ${}^{r,k}_{i}{\tilde {h}}$ as the value of $\tilde {h}$ at the i th grid point, k th time step, and r th iteration of the fixed-point iteration for the current time step. At time step (k − 1), everything is assumed to be known in Eqs. 30 and 32. At the k th time step and r th iteration, everything is assumed to be known from the given temperature field and the given strain rate except $\tilde {h}$ and $\partial \tilde {C}^{*}_{s} / \partial \tilde {y}$. We note that, for example, the variables $\tilde {C}_{l}$, J, and $\dot {\tilde {x}}$ can all be computed directly from the temperature field. We now approximate the time derivatives in Eqs. 30 and 32 by a first-order finite difference. Then, we integrate Eq. 32 over the interval 0 ≤ ξ ≤_iξ at time step k. This yields

$$ \begin{array}{@{}rcl@{}} {~}^{r,k}_{i}(\tilde{\bar{v}}\tilde{h}) \!&=&\! -\upbeta {~}^{k}_{i}{\dot{\tilde{x}}}{~}^{r,k}_{i}{\tilde{h}} + {\int}_{0}^{_{i}\xi}\! \left( \!-\tau {~}^{k}{J} (1 + \upbeta){~}^{k}{\dot{\varepsilon}^{m}_{\perp}} + \frac{\upbeta {~}^{k}{J}}{{\varDelta}\tilde{t}}\right) {~}^{r,k}{\tilde{h}}d\xi\\ &&+ {\int}_{0}^{_{i}\xi} \left( -\tau {~}^{k}{J} (1 + \upbeta){~}^{k}{\dot{\varepsilon}^{m}_{\perp}}\frac{{~}^{k}{\tilde{l}_{0}}}{2} - \frac{\upbeta {~}^{k-1}{}{J}{~}^{k-1}{}{\tilde{h}}}{{\varDelta}\tilde{t}}\right)d\xi, \end{array} $$

(33)

where the boundary condition

$$ {~}^{k}_{1}(\tilde{\bar{v}}) = -\upbeta {~}^{k}_{1}{\dot{\tilde{x}}} $$

(34)

has been used in the integration. This corresponds to the liquid flow at the end of the GBLF owing to solidification shrinkage [4]. We now similarly integrate Eq. 30 and insert Eq. 33. This yields

$$ \begin{array}{@{}rcl@{}} &&{\kern-8.5pt}{\int}_{0}^{_{i}\xi}{~}^{k}{g_{1}}{~}^{r,k}{\tilde{h}}d\xi + p_{3}{~}^{k}_{i}{\tilde{C}_{l}}{\int}_{0}^{_{i}\xi}{~}^{k}{g_{2}}{~}^{r,k}{\tilde{h}}d\xi + {~}^{k}_{i}{g_{3}}{~}^{r,k}_{i}{\tilde{h}} - {~}^{k}_{1}{g_{3}}{r,k}{1}{\tilde{h}}\\ &&= {\int}_{0}^{_{i}\xi}{~}^{r,k}{g_{4}}d\xi + p_{3}{~}^{k}_{i}{\tilde{C}_{l}}{\int}_{0}^{_{i}\xi}{~}^{k}{g_{5}}d\xi, \end{array} $$

(35)

where

$$ \begin{array}{@{}rcl@{}} {~}^{k}_{i}{g_{1}} &=& \frac{{~}^{k}_{i}{J}{~}^{k}_{i}{\tilde{C}_{l}}}{{\varDelta}\tilde{t}} + \frac{{~}^{k}_{i}{p_{1}}{~}^{k}_{i}{J}}{{\varDelta}\tilde{t}} - \frac{\rho_{s}kGL_{x}{~}^{k}_{i}{J}{~}^{k}_{i}{\dot{\tilde{x}}}}{\rho_{l}C_{0}m} + {~}^{k}_{i}{p_{4}}\\ {~}^{k}_{i}{g_{2}} &=& -\tau {~}^{k}_{i}{J}(1 + \upbeta){~}^{k}_{i}{\dot{\varepsilon}^{m}_{\perp}} + \frac{\upbeta{~}^{k}_{i}{J}}{{\varDelta}\tilde{t}}\\ {~}^{k}_{i}{g_{3}} &=& -{~}^{k}_{i}{\dot{\tilde{x}}}{~}^{k}_{i}{\tilde{C}_{l}} + p_{2} - {~}^{k}_{i}{p_{1}}{~}^{k}_{i}{\dot{\tilde{x}}} + p_{3}\upbeta{~}^{k}_{i}{\dot{\tilde{x}}}{~}^{k}_{i}{\tilde{C}_{l}}\\ {~}^{r,k}_{i}{g_{4}} &=& \frac{{~}^{k-1}_{i}{J}{~}^{k-1}_{i}{\tilde{C}_{l}}{~}^{k-1}_{i}{\tilde{h}}}{{\varDelta}\tilde{t}} + \frac{{~}^{k}_{i}{p_{1}}{~}^{k-1}_{i}{J}{~}^{k-1}_{i}{\tilde{h}}}{{\varDelta}\tilde{t}} - {~}^{k}_{i}{p_{4}}\frac{{~}^{k}_{i}{\tilde{l}_{0}}}{2} \\ &&- {~}^{k}_{i}{p_{5}}{r-1,k}{i}{}\frac{\partial \tilde{C}^{*}_{s}}{\partial \tilde{y}}\\ {~}^{k}_{i}{g_{5}} &=& -\tau {~}^{k}_{i}{J}(1 + \upbeta){~}^{k}_{i}{\dot{\varepsilon}^{m}_{\perp}}\frac{{~}^{k}_{i}{\tilde{l}_{0}}}{2} + \frac{\upbeta{~}^{k-1}_{i}{J}{~}^{k-1}_{i}{\tilde{h}}}{{\varDelta}\tilde{t}}. \end{array} $$

(36)

The only unknown in Eq. 35 is now ${~}^{r,k}{\tilde {h}}$. We note that the term ${~}^{r-1,k}_{i}{}\partial \tilde {C}^{*}_{s}/\partial \tilde {y}$ in Eqs. 35 to 36 is known because it is obtained from ${~}^{k-1}_{i}{\tilde {h}}$, which in turn has been determined in the previous iteration.

To determine ${~}^{r,k}{\tilde {h}}$, we approximate the integrals in Eq. 35 with sums by applying the trapezoidal rule. Here, the integration constant can be determined from the following boundary condition

$$ {~}^{r,k}_{N_{i}}{\tilde{h}} = \frac{\lambda_{1}/2 - {\varGamma}_{min}}{L_{y}}. $$

(37)

This boundary condition is given by that no strain is present at $x_{T_{l}}$ and that the thickness of the solid lamella is 2Γ_min at $x_{T_{l}}$.

Now, by varying the integration limit _iξ, we can obtain N_i − 1 linear equations in ${~}^{r,k}_{i}{\tilde {h}}$ from Eq. 35. ${}^{r,k}_{i}{\tilde {h}}$ can then be solved for from this linear system. This yields the fixed-point iteration scheme

$$ \left[{~}^{r,k}_{i}{\tilde{h}}\right] = {\mathbf{A}}{^{-1}}\vec{f}\left( {~}^{r-1,k}_{i}{\tilde{h}}\right);\quad i=1,2,...,(N_{i}-1), $$

(38)

where A is an (N_i − 1) × (N_i − 1) matrix and $\vec {f}$ is an (N_i − 1) × 1 vector. We note that $\vec {f}$ depends on ${}^{r,k}_{i}{\tilde {h}}$ because it contains the terms ${}^{r-1,k}_{i}{}\partial \tilde {C}^{*}_{s}/\partial \tilde {y}$, which in turn depend on the ${}^{r,k}_{i}{\tilde {h}}$ terms. Equation 38 is iterated until

$$ \parallel \!\left[\frac{{~}^{r,k}_{i}{\tilde{h}}}{{~}^{k-1}_{i}{\tilde{h}}}\right] \! \parallel_{_{\infty}} <10^{-8}. $$

(39)

The fixed-point iteration is initiated with the starting value

$$ {~}^{0,k}_{i}{\tilde{h}} = {~}^{k-1}_{i}{\tilde{h}} + {\varDelta}\tilde{t}\left( \frac{{~}^{k-1}_{i}{\tilde{h}} - {is iterated until}^{k-2}_{i}{\tilde{h}}}{{\varDelta}\tilde{t}}\right). $$

(40)

2.7 Transverse solidification rate

Once ${~}^{k}_{i}{\tilde {h}}$ is known, ${~}^{k}_{i}{\tilde {{\varGamma }}}$ can be computed from Eq. 1 as follows. First, Eq. 1 is put in nondimensional form using the variables in Eq. 7 and then is transformed using the mapping in Eq. 25. Subsequently, the time derivative in the transformed form is replaced by finite differences, and the equation is integrated as in the previous section. The integrals are then replaced by sums using the trapezoidal rule, and by varying the upper integration limit, N_i − 1 linear equations in ${~}^{k}_{i}{\tilde {{\varGamma }}}$ are obtained. Finally, ${~}^{k}_{i}{\tilde {{\varGamma }}}$ can be determined from this system using the boundary condition

$$ {~}^{k}_{N_{i}}{\tilde{{\varGamma}}} = \frac{{\varGamma}_{min}}{L_{y}}. $$

(41)

We note that if ${~}^{k}_{i}{\tilde {{\varGamma }}}$ is known, the domain for ${~}^{k}{\tilde {C}_{s}}$ is known, and ${~}^{k}{\tilde {C}_{s}}$ can then be computed by the method described in Section 2.5.

2.8 Longitudinal solidification rate and initial conditions

In addition to the previous assumption of solidification along a constant temperature gradient, we also assume that the liquidus and eutectic isotherms move at the welding speed; that is, $\dot {x}_{T_{l}} = \dot {x}_{T_{e}} = v_{w}$. However, at the beginning of the solidification, $x_{T_{e}}$ is not associated with the location of the eutectic isotherm. At t = 0, the temperature at $x_{T_{e}}$ is set to ΔT_s = 1 ^∘C below T_l, and its location is set to $x_{T_{e}} = 0$. The value of $x_{T_{l}}$ at t = 0 can then be computed from ΔT_s and G. For t > 0, $x_{T_{e}}$, it is assumed to be stationary until the temperature at x = 0 has dropped to T_e, which will occur at $\tilde {t} = 1$ owing to the scaling in Eq. 7. Subsequently, $x_{T_{e}}$ is assumed to move at the same speed as that of $x_{T_{l}}$. This is shown in Fig. 7.

Fig. 7

Scaled positions and velocities of the solidification front and end as functions of the nondimensional time

The initial value of C_s at t = 0 is assumed to be the same as that in equilibrium, and h and Γ at t = 0 are approximated using the lever rule. The initial size of the solid domain for G = 80000 K/m and v_w = 1 mm/s is shown in the left plot in Fig. 8. The right plot shows the size and location of the solid domain at $\tilde {t} = 2$ for the same values of G and v_w as in the left plot. It also shows a size comparison between the domain at $\tilde {t} = 0$ and $\tilde {t} = 2$.

Fig. 8

Left and the right figures show the domains for the C_s field at $\tilde {t} = 0$ and $\tilde {t} = 2$, respectively. Here, G = 80000 K/m and v_w = 1 mm/s. The right figure also shows a size comparison between these two domains

3 Application to Alloy 718

The proposed solidification model was tested on Alloy 718, which is a Ni-based superalloy that is extensively used for high-temperature applications in aerospace engines and gas turbines. It maintains excellent corrosion and oxidation resistance up to 980 ^∘C, as well as excellent resistance to creep and stress rupture up to 700 ^∘C. The composition limits for Alloy 718, given by the Special Metals Corporation [9], are shown in Table 1.

Table 1 Chemical composition limits for Alloy 718 (wt%)

The solidification microstructure of Alloy 718 is similar to that of a binary alloy eutectic system. That is, solidification initiates with the crystallization of the primary proeutectic γ and terminates with the formation of a γ/Laves eutectic constituent [10]. An amount of γ/NbC eutectic is formed during solidification but is small compared with that of the γ/Laves eutectic constituent [10].

To study the solidification of Alloy 718 in the fusion zone of a weld, Knorovsky et al. [10] have developed a pseudo-binary phase diagram using Nb as the primary alloying element compositional variable, as seen in Fig. 9. The important features of the diagram are an austenite γ/Laves phase eutectic that occurs at ≈ 19.1 wt% Nb between austenite containing ≈ 9.3 wt% Nb and a Laves phase containing ≈ 22.4 wt% Nb. Analytical electron microscopy (AEM) has demonstrated that the largest absolute compositional differences between the γ matrix and the Laves phase can be seen for Ni and Nb [10]. Thus, as a first approximation, a weight fraction exchange between Ni and Nb would describe the chemistry difference between the γ matrix and the Laves phase. This was one of the determining factors for Knorovsky et al. to use Nb as the independent variable in their pseudo-binary phase diagram for Alloy 718 [10].

Fig. 9

Pseudo binary phase diagram of Alloy 718. The red line corresponds to a nominal Nb concentration of 5.18 wt%. From [10]

In a multicomponent system such as Alloy 718, a eutectic reaction needs not be temperature invariant. However, DTA performed by Knorovsky et al. has demonstrated that the DTA peak for the γ/Laves reaction is quite narrow [10]. Thus, the approximation in the pseudo-binary phase diagram that the γ/Laves reaction is temperature invariant is assumed to be valid.

Knorovsky et al. [10] used the pseudo-binary phase diagram in Fig. 9 and the Scheil model to calculate the volume fraction of the γ/Laves eutectic. The results were in good agreement with experimental AEM measurements on thin weld foils.

The pseudo-binary phase diagram for Alloy 718 developed by Knorovsky et al. [10] was used in this study to test the solidification model on Alloy 718, with a nominal Nb concentration of C₀ = 5.18 wt%. From the phase diagram, the required solidification model parameters (T_l, T_e, k, and m) can be determined. Their values are given in Table 2. The values of T_c and β were taken from [5], whereas the values of ρ_s and D_l were taken from [11]. ρ_l was calculated from ρ_s and β using Eq. 10. The temperature dependence of D_s was also taken from [11], where it is given by

$$ D_{s} = D_{0s}\exp{\left( \frac{-Q_{s}}{R(T+273)}\right)} $$

(42)

Table 2 Model parameters

We assume that when the temperature reaches T_e, all remaining liquid solidifies into γ/Laves eutectic. Moreover, we assume a G value of 80 × 10³ K/m and a λ₁ value of 20 μ m, which are characteristic for TIG welding of Alloy 718 at a welding speed of 1 mm/s [5].

4 Results and discussion

In this chapter, the previously developed solidification model is going to be used for studying the influence of strain on the thickness of eutectic bands of Alloy 718. This is presented in Section 4.3. However, before that, the effect of back diffusion and the assumption of uniform solute concentration across the GBLF are studied in Sections 4.1 and 4.2, respectively. In Section 4.4, we present some interesting numerical results on how an increase in the magnitude of the strain rate can decrease the liquid permeability in the region of the mushy zone where the temperature is the same as the coherent temperature. In Section 4.5, we present some experimental results of eutectic bands in Varestraint tests of Alloy 718. Finally, in Section 4.6, we discuss some of the major limitations with our solidification model.

4.1 Comparison with equilibrium and Scheil solidification

To test the proposed solidification model, we consider the two limiting cases of complete diffusion and no diffusion in the solid phase. This is done for a closed system without any mechanical strains, i.e., no solute transport in the longitudinal direction.

The former case corresponds to an equilibrium condition that is attained at low solidification rates. Then, for the closed system, the interface position can be approximated from the solid fraction by the lever rule

$$ f_{s} = \frac{C_{0} - C_{l}}{(k-1)C_{l}}, $$

(43)

where f_s is the solid mass fraction and k is the partition coefficient.

The latter case corresponds to high solidification rates. Then, in this case, for the closed system, the interface position can be approximated from the solid fraction given by the Scheil equation

$$ f_{s} = 1 - \left( \frac{C_{l}}{C_{0}}\right)^{\frac{1}{k-1}}. $$

(44)

When no mechanical strain is present, the interface position for the lamella model can be written as

$$ {\varGamma} = \frac{\lambda_{1}}{2}g_{s}, $$

(45)

where g_s is the solid volume fraction. Furthermore, if we neglect solidification shrinkage, that is, β = 0 and ρ_l = ρ_s, we get g_s = f_s. Thus, when ${\dot {\varepsilon }^{m}_{\perp }} = \upbeta = 0$, Γ can be calculated for a given value of g_s for the lever rule or the Scheil equation by inserting Eq. 43 or Eq. 44 into Eq. 45 and setting f_s = g_s.

The closed system condition can be attained in our solidification model by setting ${\dot {\varepsilon }^{m}_{\perp }} = \upbeta = D_{l} = 0$ and ρ_l = ρ_s. Figure 10 shows the interface location calculated by the solidification model under the closed system condition at $\tilde {t} = 1$ for different values of v_w. G = 80 × 10³ K/m was used for all v_w values. The figure also shows the interface location predicted by the lever rule and the Scheil equation.

Fig. 10

Γ profiles at $\tilde {t} = 1$ calculated by the solidification model under the closed system condition for different values of v_w and G = 80 × 10³ K/m. The Γ profiles predicted by the lever rule and the Scheil equation are also plotted. The thin dashed red line shows the temperature variation along the solid-liquid interface

As can be seen from the figure, the interface locations predicted by the solidification model for the various v_w values are all bounded by those predicted by the lever rule and the Scheil equation. When v_w = 10^− 4 mm/s, the Γ calculated by the solidification model almost completely coincides with the Γ calculated by the lever rule, and if v_w ≥ 1 mm/s, the Γ calculated by the solidification model coincides with the Γ calculated by the Scheil equation.

From this test, we can conclude that under the closed system condition, the location of the solid-liquid interface predicted by the solidification model is bounded by those predicted by the lever rule and the Scheil equation. It would be physically unreasonable if this was not the case under the specified system conditions.

4.2 Comparison with 1D solidification model

We further test the solidification model on a closed system by comparing it with a 1D solidification model. The 1D model accounts for solute diffusion in the transverse direction of the GBLF and therefore relaxes the approximation of uniform solute distribution across the GBLF, which is used in the solidification model. Thus, for the closed system, we consider the 1D model to be more accurate than the solidification model. In the 1D model, the interface velocity is governed by the net solute transport by diffusion in the solid and liquid phases through Eq. 46(a), which is stated in Dantzig and Rappaz [12] as follows:

$$ \begin{cases} \begin{aligned} &(1 - k)C^{*}_{l}\frac{\partial {\varGamma}}{\partial t} = D_{s}\frac{\partial C^{*}_{s}}{\partial y} - D_{l}\frac{\partial C^{*}_{l}}{\partial y}\\ &\frac{\partial C_{s}}{\partial t} - D_{s} \frac{\partial^{2} C_{s}}{\partial y^{2}} = 0 ,\quad 0\leq y \leq {\varGamma} ,\quad C_{s}(y = {\varGamma}) = kC^{*}_{l} ,\quad \frac{\partial C_{s}(y = 0)}{\partial y} = 0\\ &\frac{\partial C_{l}}{\partial t} - D_{l} \frac{\partial^{2} C_{l}}{\partial y^{2}} = 0 ,\quad {\varGamma}\leq y \leq L_{y} ,\quad C_{l}(y = {\varGamma}) = C^{*}_{l} ,\quad \frac{\partial C_{l}(y = L_{y})}{\partial y} = 0 &\end{aligned} &\end{cases} $$

(46)

The solute gradient $\partial C^{*}_{s}/\partial y$ at the interface of the solid phase is computed from Eq. 46(b), which is solved by mapping the domain 0 ≤ y ≤Γ to the domain 0 ≤ η ≤ 1, where the solution is obtained by a finite difference method on a stationary grid. Similarly, the solute gradient $\partial C^{*}_{l}/\partial y$ at the interface in the liquid phase is computed from Eq. 46(c) by transforming the domain Γ ≤ y ≤ L_y to the domain 0 ≤ η ≤ 1, where the solution is obtained by a finite difference method. The interface concentration $C^{*}_{l}$ is determined directly from the phase diagram by the equilibrium assumption at the solid-liquid interface. Γ is obtained from Eq. 46(a) by a fixed-point iteration, where both solute gradients are calculated from the Γ value obtained at the previous iteration, as in the fixed point iteration that is used to determine $\tilde {h}$ in Eq. 38. The temperature in the 1D model at time $\tilde {t}$ is determined from

$$ T = T_{l} - (T_{l} - T_{e})\tilde{t}. $$

(47)

The temperature in the 1D model and the temperature at $x_{T_{e}}$ in the solidification model will both reach T_e when $\tilde {t} = 1$. For $\tilde {t} > 1$, the C_s field obtained by the solidification model under the closed system approximation, should reach a quasi steady state condition. Thus, the solute profile at $x_{T_{e}}$ should be the same for $\tilde {t} = 1$ and, for example, $\tilde {t} = 2$. At $\tilde {t} = 2$, the mesh for the solid phase has undergone a substantial translation, which could lead to numerical diffusion if, for instance, spurious source terms are present.

Figure 11 shows the C_s profiles at $x_{T_{e}}$ for different v_w values calculated by the 1D and the solidification model. The C_s profiles were calculated at $\tilde {t} = 1$ for the 1D model, and at $\tilde {t} = 2$ for the solidification model. For v_w = 0.1 mm/s in Fig. 11a and for v_w = 1 mm/s in Fig. 11(b), the C_s profiles calculated by the two models are nearly identical. The relative difference for the calculated Γ value at $x_{T_{e}}$ between the two models is 0.12% for v_w = 0.1 mm/s and 0.64% for v_w = 1 mm/s.

For v_w = 10 mm/s, the C_s profiles calculated at $x_{T_{e}}$ by the two different models start to diverge, as shown in Fig. 11c. The relative difference between the Γ values calculated by the two models has now increased to 5.48%. Furthermore, for v_w = 100 mm/s, there is a large difference in the calculated C_s profiles by the two models, as shown in Fig. 11d. The relative difference between the Γ values calculated by the two models is now more than 60%.

Fig. 11

Nb concentration in the solid phase at $x_{T_{e}}$, calculated by the 1D model at $\tilde {t} = 1$ and by the solidification model under the closed system approximation at $\tilde {t} = 1$ for different v_w values. a v_w = 0.1 mm/s. b v_w = 1 mm/s. c v_w = 10 mm/s. d v_w = 100 mm/s

At this high solidification speed, the solute distribution across the GBLF is not uniform. This becomes apparent in Fig. 12, which shows the solute distribution in the solid and liquid phases calculated at $\tilde {t} = 0.3$ by the 1D model for v_w = 100 mm/s. It can be seen that there is a step solute gradient in the liquid phase at the interface. Thus, the approximation of uniform solute distribution in the GBLF that is used in the solidification model is not valid at solidification speeds of this magnitude.

Fig. 12

Nb concentration in the solid and liquid phase calculated by the 1D model at $\tilde {t} = 0.3$ for v_w = 100 mm/s

By integrating the C_s profiles in Fig. 11 over the cross section, we can estimate the solute loss at $x_{T_{e}}$ that is due to, for example, spurious source terms that may arise by grid transport. For the solidification model under the closed system approximation, the integral

$$ {\int}_{0}^{L_{y}} C dy = {\int}_{0}^{{\varGamma}} C_{s} dy + (L_{y} - {\varGamma})C_{e} $$

(48)

should equal L_yC₀ if no solute is lost. The relative difference between L_yC₀ and the integral, calculated from the C_s curves in Fig. 11, is 0.044% for v_w = 0.1 mm/s, 0.040% for v_w = 1 mm/s, 0.038% for v_w = 10 mm/s, and 0.038% for v_w = 100 mm/s. Thus, the solute loss is small for the solidification model.

4.3 Influence of strain rate on the thickness of eutectic bands

In this section, the closed system approximation is removed, and the effect of strain rate on the thickness of γ/laves eutectic bands in Alloy 718 is studied. Figure 13 shows the calculated Nb concentration in the solid and liquid phases at $\tilde {t} = 2$. Here, v_w = 1 mm/s and ${\dot {\varepsilon }^{m}_{\perp }} = 0.01$ 1/s were used. The domain shown in the figure is bounded by $x_{T_{e}}\leq x \leq x_{T_{l}}, 0\leq y \leq {\varGamma } + h$. It can be seen that h is approximately 2 μ m at $x_{T_{e}}$. Thus, the model predicts that the eutectic band thickness at $x_{T_{e}}$ is 4-μ m thick when $\tilde {t} = 2$.

Fig. 13

Nb concentration in the solid and liquid phases at $\tilde {t} = 2$, and v_w = 1 mm/s, ${\dot {\varepsilon }^{m}_{\perp }} = 0.01$ 1/s

Now, let h_e be the value of h at $x_{T_{e}}$. Figure 14 shows h_e as a function of $\tilde {t}$ for different values of v_w and ${\dot {\varepsilon }^{m}_{\perp }}$. We recall that the temperature at $x_{T_{e}}$ drops to T_e when $\tilde {t} \geq 1$. Thus, for $\tilde {t}\geq 1$, h_e represent half the thickness of the eutectic band at $x_{T_{e}}(\tilde {t})$. Figure 14a, c, and e show h_e for v_w = 0.1,1, and 10 mm/s, respectively, and for several different strain rates. G = 80 × 10³ K/m is used for all cases. Furthermore, Fig. 14 b, d, and f show the relative difference between h_e at a given strain rate and the h_e that results from a strain rate that is zero, for v_w = 0.1,1, and 10 mm/s, respectively. From Fig. 14a, c, and e, it can be seen that h_e ≈ 0.4,0.7,0.8 μ m for v_w = 0.1,1,10 mm/s, respectively, when ${\dot {\varepsilon }^{m}_{\perp }} = 0$ and $\tilde {t} > 1$. Thus, h_e is approximately twice as large when v_w = 10 mm/s as when v_w = 0.1 mm/s. This is because solute diffusion along the GBLF and solute back diffusion from the liquid into the solid phase have more time to occur at a lower longitudinal solidification rate. Thus, there is less amount of Nb to form γ/Laves eutectic at $x_{T_{e}}$ when v_w = 0.1 mm/s than when v_w = 10 mm/s.

When ${\dot {\varepsilon }^{m}_{\perp }}$ has the same magnitude as v_w, h_e is approximately 50, 40, and 20% larger than when $\dot {\varepsilon }^{m}_{\perp } = 0$ for v_w = 0.1,1, and 10 mm/s, respectively, at $\tilde {t} = 1$, as shown in Fig. 14b, d, and f. Thus, at lower longitudinal solidification rates, h_e is more sensitive to the relative strain rate than at higher longitudinal solidification rates.

Fig. 14

h_e vs $\tilde {t}$ for different strain rates and for (a) v_w = 0.1 mm/s, c v_w = 1 mm/s, and e v_w = 10 mm/s. b, d, f The relative difference between h_e for a given strain rate and the h_e given by the zero strain rate for v_w = 0.1,1, and 10 mm/s, respectively

When the magnitude of ${\dot {\varepsilon }^{m}_{\perp }}$ is 10 times as large as that of v_w, h_e is approximately 480, 270, and 200% larger as when $\dot {\varepsilon }^{m}_{\perp } = 0$ for v_w = 0.1,1, and 10 mm/s, respectively, at $\tilde {t} = 1$, as shown in Fig. 14b, d, and f. Figure 14c shows the case where ${\dot {\varepsilon }^{m}_{\perp }}$ is 50 times as large as the magnitude of v_w, in which there is an increase of approximately 1300% in h_e at $\tilde {t} = 1$ compared with the zero-strain case.

As can be seen from Fig. 14a, c, and e, h_e always peaks at $\tilde {t} = 1$, that is, at $x_{T_{e}} = 0$. Subsequently, it decreases until $\tilde {t}$ reaches a value between 1.6 and 2 (depending on ${\dot {\varepsilon }^{m}_{\perp }}$ and v_w), and then it finally attains a constant value. The decrease in h after $\tilde {t}$ reaches 1 can be explained as follows. As the concentration gradient in the GBLF is negative, the liquid flows towards the root of the GBLF, $\bar {v}<0$, which leads to a dilution. To maintain a constant solute concentration, which is required by the thermodynamic equilibrium condition, the transverse solidification rate must increase in order to reject more solute into the liquid from the solid-liquid interface. An increase in the transverse solidification rate will increase the solute concentration in the liquid because the solid cannot dissolve as much solute as the liquid (when k < 1). Thus, the liquid velocity $\bar {v}$ induced by mechanical straining and solidification shrinkage increases the transverse solidification rate. However, at $x_{T_{e}} = 0$ and for $\tilde {t}<1$, we have $\bar {v} = 0$, and therefore $\bar {v} = 0$ does not increase the transverse solidification speed; accordingly, h_e peaks at $x_{T_{e}} = 0$.

Finally, the solidification model is based on a GBLF that is bounded by two solid lamellas separated by the primary dendrite arm spacing when no mechanical strain is present, as shown in Fig. 2. However, for a high-angle grain boundary as that in Fig. 1, the separation of the lamellas bounding the GBLF should be larger than λ₁ because the grain boundary is more unstructured. To test the effect of the separation of the lamellas on h_e, the solid lamella distance was increased by 50%, that is, from 20 to 30 μ m. The effect on h_e for v_w = 1 mm/s is shown in Fig. 15. This figure should be compared with Fig. 14c and d. As can be seen from Fig. 15a and c, increasing the lamella spacing increases the thickness of the eutectic band, as expected.

Fig. 15

a h_e vs $\tilde {t}$ at v_w = 1 mm/s for different strain rates and an undeformed lamella spacing of 30 μ m. b Relative difference between h_e for a given strain rate and the corresponding value for zero strain rate

For all numerical results, a temporal discretization with ${\varDelta } \tilde {t} = 1/1000$ and a space discretization with Δξ = 1/100 and Δη = 1/30 were used for the solidification model. This gives convergence: halving the size of ${\varDelta } \tilde {t}$, Δξ, and Δη only gives a maximum relative change in C_s and Γ of less than 0.1% at $\tilde {t} = 2$.

4.4 Permeability decrease due to increased flow rate

The temperature-dependent length scale l₀ in Fig. 3, which is used to partition macroscopic strain, gives rise to an interesting phenomenon: at high strain rates, the GBLF thickness can become zero at a location in the GBLF where the temperature is much higher than T_e. This is shown in Fig. 16d. Figure 16 shows the half of the GBLF thickness h in the interval $x_{T_{e}}\leq x \leq x_{T_{l}}$ for v_w = 1 mm/s and different values of $\tilde {t}$. In Fig. 16a, h has been calculated using a zero strain rate. The figure shows that h is monotonically decreasing when x tends to $x_{T_{e}}$ for all $\tilde {t}$. Figure 16b shows h for different values of $\tilde {t}$ when ${\dot {\varepsilon }^{m}_{\perp }} = 10^{-3}$ 1/s. Furthermore, in this case, h is monotonically decreasing when x tends to $x_{T_{e}}$ for all $\tilde {t}$; however, it does not decrease as fast as in the previous case. Figure 16c shows h when ${\dot {\varepsilon }^{m}_{\perp }} = 0.5\times 10^{-2}$ 1/s. In this case, h is not monotonically decreasing when x tends to $x_{T_{e}}$. In Fig. 16d, when ${\dot {\varepsilon }^{m}_{\perp }} = 10^{-2}$ 1/s, h can become zero for a $x > x_{T_{e}}$ even if it has a large value at $x = x_{T_{e}}$. This is because a large strain rate gives rise to a high liquid flow rate $\bar {v}$, which results in a higher transverse solidification rate. Furthermore, as l₀ is small at T_c, the mechanical strain does not significantly localize in this temperature region. However, $\bar {v}$ can be large at T_c, resulting in a considerably larger transverse solidification rate than the transverse deformation rate of the GBLF caused by straining in this region. This can result in zero GBLF thickness before the temperature has reached T_e. At lower temperatures, the GBLF can start to open up owing to the large increase in l₀ that occurs when the temperature drops below T_c. Here, as we consider a GBLF with a high grain boundary misorientation angle, we assume that extensive undercooling is required for the two opposing solid interfaces of the GBLF to fuse together [6]; therefore, it is assumed that the GBLF can open up later when the strain localization increases.

Fig. 16

h vs x for v_w = 1 mm/s, and for (a) ${\dot {\varepsilon }^{m}_{\perp }} = 0$, b ${\dot {\varepsilon }^{m}_{\perp }} = 10^{-3}$ 1/s, c ${\dot {\varepsilon }^{m}_{\perp }} = 0.5\times 10^{-3}$ 1/s, and d ${\dot {\varepsilon }^{m}_{\perp }} = 10^{-2}$ 1/s

h cannot become arbitrary small because this would lead to a very high liquid flow rate, which in turn would lead to large heat transport. This would result in melting, which would increase h. The heat transport along the GBLF that is induced by liquid flow is not incorporated into the solidification model. Thus, this model is not accurate for large values of $\bar {v}$, as is the case in Fig. 16d. However, in Fig. 16c, the maximum liquid velocity is $\bar {v} = -2$ mm/s. This results in a thermal Peclet number of Pe = 0.26 for the heat transport in the GBLF. Thus, in this case, the total heat transport is dominated by heat conduction, and therefore the liquid flow is assumed not to cause extensive melting. Hence, the h profiles in Fig. 16c are assumed not to change radically if advection-induced heat transport is added to the solidification model.

Interestingly, an increase in the strain rate can lead to a decrease in the GBLF thickness (in a certain region). A decrease in the GBLF thickness results in a decrease in the GBLF permeability, which in turn reduces the pressure in the GBLF. A low GBLF pressure may increase the risk for pore nucleation and/or pore growth of preexisting pores, which can result in hot cracking [4, 13].

4.5 Study of eutectic bands in Varestraint tests

4.5.1 Eutectic bands

As was discussed in the introduction, eutectic bands may form in multi-pass welding processes such as additive manufacturing and repair welding. However, eutectic bands can also form in weldability tests such as the Varestraint test. Figure 17 shows optical micrographs of eutectic bands that the authors have found in three Varestraint test samples of Alloy 718. These tests were performed with 4% augmented strain, 1 mm/s welding speed, and 10 mm/s ram speed. For more technical details about the Varestraint test, see [5]. At the surface of these tests, a region with large cracks could be found. This region extends across the whole FZ. Adjacent to this region, in the welding direction, there is a region of the FZ with eutectic bands but with no cracks. Numerical simulations performed by the authors in earlier works have shown that this region is less strained in the temperature span T_e < T < T_c than the region with the cracks. Thus, the applied strain in the Varestraint test is not enough to cause cracking in this region. However, the applied strain is much larger than just the thermal strain the region would experience when no bending strain is applied. Thus, although the applied strain is not large enough to cause cracking, it is enough to form eutectic bands.

Fig. 17

Optical micrographs of eutectic bands at the surface of Varestrint tests of Alloy 718 with 4% augmented strain. The light phase in the micrographs corresponds to the γ phase while the dark phase corresponds to the Laves phase

Figure 17a shows an optical micrograph of the weld surface of a Varestraint test where several eutectic bands, roughly 1000 μ m long, can be seen. Figure 17b and c show optical micrographs at the weld surface of a second Varestraint test. In these micrographs, two eutectic bands that are longer than 1000 μ m can be seen. Finally, Fig. 17d shows a roughly 15-μ m-thick eutectic band in a third Varestraint test.

The average thickness of the eutectic bands in the above micrographs varies approximately between 5 and 15 μ m, depending on their locations. Numerical simulations of a Varestraint test with 4% augmented strain predict an average longitudinal macroscopic strain rate of approximately 0.03 1/s in the region where the eutectic bands are located and in the temperature span T_e < T < T_c. It is interesting that our solidification model predicts similar thicknesses for the eutectic bands when the macroscopic strain rates are in the range of 0.01–0.05 1/s. This can be seen in Fig. 14c for the welding speed 1 mm/s, which is the same welding speed as in the Varestraint tests. From the figure, we can see that the predicted eutectic band thickness is 5–20 μ m at $\tilde {t}=1$ when ${\dot {\varepsilon }^{m}_{\perp }} =$ 0.01–0.05 1/s. And at $\tilde {t}=1.7$, the thickness is 2–11 μ m when ${\dot {\varepsilon }^{m}_{\perp }} =$ 0.01–0.05 1/s. Remember that under the simplified solidification conditions that were used to construct Fig. 14, the computed thickness at $\tilde {t}=1$ corresponds to the thickness of a band that forms from a GBLF whose end has always been stationary. The calculated thickness at $\tilde {t}=1.7$ on the other hand corresponds to the thickness that forms from a GBLF whose end moves at the same speed as the liquidus isotherm speed, and that a quasi-steady state condition has been reached. Thus, the calculated band thickness at $\tilde {t}=1$ corresponds to the thickness at the fusion boundary, where the terminal solidification speed along the GBLF is low. While the calculated band thickness at $\tilde {t}=1.7$ corresponds to the thickness at the weld centerline, where the terminal solidification speed is the same as the liquidus speed under quasi steady state conditions. It is interesting to note that our solidification model predicts that eutectic bands located close to the fusion boundary should be thicker than bands located along the weld centerline for the same value of ${\dot {\varepsilon }^{m}_{\perp }}$.

4.5.2 Eutectic bands in hot cracks

Eutectic bands may also be formed in hot cracks and healed hot cracks. This is because large strains can act on the GBLFs that the hot cracks form in. These strains can induce large solute segregations which can lead to the formation of eutectic bands.

Hot cracking normally occurs at the root of the GBLF where the liquid pressure drop in the GBLF is highest. We now assume that a hot crack forms from a void that grows into a crack at the root of a GBLF, as in a previous work by the authors [4, 13]. Once the void has formed, we may consider the following two cases, which concern eutectic bands with regards to hot cracks.

• 1. Non fractured eutectic bands. In this case, the void grows into a crack that continues to grow until the surface tension of the gas-liquid interface of the crack can balance the pressure drop in the GBLF. When the pressure drop is reduced from the value that stationary balance the crack, the crack will start to close. This is because the pressure drop can no longer balance the surface tension of the crack. The closing can be very fast because the liquid phase often wets the solid phase very well. For example, a cylindrical air-liquid interface of a 2-μ m-thick liquid film between two parallel plates can move almost 1 mm in 0.1 s when the balancing pressure drop is instantaneously reduced by 10%. This was calculated by the author by considering a parallel plate Poiseuille flow (see the Appendix). The values for the surface tension, contact angle, and viscosity in the calculation were for Alloy 718.

  Because the crack closing is so fast, the whole crack may be healed even though the root of the crack is at a lower temperature than the terminal eutectic temperature. However, if the temperature at the root of the crack is too low, the liquid will solidify before it can fully heal the whole crack.

  Due to solute accumulation at the gas-liquid interface of the crack, the liquid that flows into the crack and heals it can result in large formations of eutectic when it solidifies. Therefore, a eutectic band can form along the filled crack. This band may extend further from the location where the crack started to close because of continuing straining after the crack closure, which can sustain the solute segregation.

  The solidification model in this paper does not incorporate cracking. However, if the length of the crack is not too long compare to the GBLF length such that not too much solute is lost to the weld pool during the crack growth, and that the crack forms fast and then is closed fast, we may assume that the eutectic band thickness predicted by the solidification model should not be too far from the thickness of the eutectic band that results from the backfilling of the crack.

• 2. Fractured eutectic bands. Multi-component alloy systems can display eutectic reactions which are not invariant. The reaction can then occur over a temperature range instead of at a fixed temperature as for the invariant reaction. For example, for Alloy 718, Scheil-Gulliver simulations with Thermo-Calc predicts that the Laves phase forms during a 20 ^∘C interval. Thus, the γ/Laves eutectic does not form instantaneously at the root of the GBLF at a fixed temperature as we have previously assumed for our solidification model. Instead, the γ/liquid interface can act as a site where the Laves phase can nucleate or grow along. This, in turn, leads to that the γ/Laves eutectic grows from one γ/liquid interface towards the opposing γ/liquid interface of the GBLF. On the opposing γ/liquid interface where will also be eutectic growth. The relative amount of eutectic that forms on the two opposing γ/liquid interfaces depends on the difference in undercooling that is necessary for the Laves phase to grow or nucleate on the opposing γ/liquid interfaces.

  Now, because the eutectic grows from the γ/liquid interfaces, and that the eutectic reaction occurs during a temperature interval, a liquid film will exist between the two growing eutectics from the opposing γ/liquid interfaces. The length of the liquid film depends on the size of the temperature interval that eutectic reaction occurs during. For Alloy 718, we assume that this interval is 20 ^∘C based on the previous Scheil-Gulliver simulations with Thermo-Calc. Furthermore, numerical simulations of a Varestraint test with 1 mm/s welding speed has shown that the temperature gradient at the root of the GBLF can be as low as 40,000 K/m. Thus, a 20/40000 = 500-μ m-long liquid film bounded by eutectic can exist at the root of the GBLF. The length to thickness ratio of this liquid film is large and its interfaces are rather roughed because it is bounded between eutectics. Hence, a large pressure drop can form in this film when it is deformed. If the pressure drop is large enough, a void may form in the film that can grow into a crack. Furthermore, if the pressure drop in the film is large enough to balance and move the surface tension of the void at the same or a large rate than the terminal eutectic solidification rate along the GBLF, then a crack can be continuously frozen into the solid phase. This results in a fractured eutectic band whose thickness depends on the amount of eutectic that was formed before the fracture occurred at the given location of the GBLF.

  The thickness of a fractured eutectic band may be roughly estimated by the solidification model in this paper if the eutectic is not formed during a too large temperature interval. In this case, the formation of the eutectic and the progressive fracture of the GBLF occur close to the end of the GBLF. Thus, the solidification model, which is based on the assumption that the eutectic forms invariantly at the end of the GBLF, may be used to roughly predict the eutectic band thickness in this case.

Figure 18 shows SEM micrographs of a fractured eutectic band at different magnifications. These micrographs were taken at the weld surface in the fusion zone of a Varestraint test of Alloy 718 with 1.1% augmented strain. The darker phase in the micrographs corresponds to the γ phase, whereas the lighter phase corresponds to the Laves phase. Tensile strain, induced by the bending in the Varestraint test, is assumed to be strongly localized in the GBLF. This results in extensive solute segregation which results in the formation of a γ/Laves eutectic band along the grain boundary.

Fig. 18

SEM micrographs at different magnifications of a grain boundary in the fusion zone of Alloy 718. The grain boundary fractured owing to tensile strain induced by a Varestraint test. The γ/Laves eutectic band along the grain boundary is assumed to have been formed owing to segregation caused by the straining. The lamellar structure of the γ/Laves eutectic band can be seen in the higher-magnification micrographs. The dark regions are the γ phase and the light regions are the Laves phase

Numerical simulation of the Varestraint test has shown that the average macroscopic strain rates in the region where the crack in Fig. 18 is formed is in the range of 0.1–0.5 1/s in the temperature interval T_e < T < T_c. With these values in our solidification model, the predicted thickness of the eutectic band is 6–20 μ m (which can be seen in Fig. 14c). This is roughly the same as in the Fig. 18, where the measured band thickness is about 10–15 μ m. Thus, even though the solidification model does not incorporate cracking, it can still roughly estimate the band thickness in this case.

4.6 Model limitations

In this section, we briefly discuss some of the limitations of the proposed solidification model.

The proposed model is only applicable to isolated GBLFs with one-dimensional liquid flow. Furthermore, the model is based on that the solid phase solidifies as lamellae with very smooth interfaces between the solid and the liquid phases. However, in the reality, the solid-liquid interface normally is highly dendritic and therefore highly irregular. Thus, the solid-liquid interface area in the proposed model is smaller than what it is in the reality. This affects back diffusion and solute rejection at the solid-liquid interface. Moreover, because the proposed model cannot resolve secondary dendrite arms, all eutectic that forms will be as continuous bands along grain boundaries, even at low solute advection. In the reality, at low solute advection, the eutectic can form as isolated islands between secondary dendrite arms and not as long continuous bands along grain boundaries.

Another approximation regards the deformation of the GBLF. This is undergone according to a macroscopic strain rate that is localized to the GBLF with a partition length as in Fig. 3. Here, we have neglected the load transmittance of the solid phase, which will alter the strain localization and increase it at higher temperatures.

At large liquid flow rates in the GBLF, solute boundary layers may form at the solid-liquid interfaces. This is not considered in the proposed model where we always assume that the solute concentration is uniform across the GBLF. To investigate the influence of the liquid flow on the solute concentration profile across the GBLF, we calculate the following solutal Peclet number

$$ \mathrm{Pe_{C}} = \frac{Lu}{D}=\frac{h\bar{v}}{D_{l}} $$

(49)

where the characteristic length L has chosen to be the same as h. The solutal Peclet number is a nondimensional number that is defined as the ratio of the rate of advection of solute by the flow to the rate of diffusion of the solute driven by a gradient. Figure 19a shows the calculated Pe_C along the GBLF at $\tilde {t}=2$ and for v_w = 1 mm/s. This was done for the two highest strain rates in Fig. 14c, i.e., ${\dot {\varepsilon }^{m}_{\perp }} = 0.01$ 1/s and ${\dot {\varepsilon }^{m}_{\perp }} = 0.05$ 1/s. From the figure, we can see that Pe_C is close to 1 at the start of the GBLF with ${\dot {\varepsilon }^{m}_{\perp }} = 0.01$ 1/s, while it is only less than 1 at the root of the GBLF with ${\dot {\varepsilon }^{m}_{\perp }} = 0.05$ 1/s. Thus, for these high strain rates, the liquid flow rate is so high so it is difficult for diffusion to keep the solute concentration constant across the GBLF. Hence, the assumption of uniform solute concentration across the GBLF is less valid for these high strain rates.

In the derivation of the proposed solidification model, we have neglected the advection heat transport along the GBLF. We study the implication of this assumption by considering the thermal Peclet number

$$ \mathrm{Pe_{T}} = \frac{Lu}{\alpha} =\frac{L_{x}\bar{v}}{\alpha_{s}} $$

(50)

which is defined as the ratio of the rate of advection of heat by the flow to the rate of diffusion of the heat driven by a gradient. Here, the characteristic length L was chosen as the length of the GBLF, i.e., the same value as L_x. The thermal diffusivity α was chosen to the thermal diffusivity of the solid phase of Alloy 718 at 1100 ^∘C, i.e., about α_s = 6 mm²/s. Figure 19b shows Pe_T along GBLFs for the same values as for Pe_C in Fig. 19a. The strain rate ${\dot {\varepsilon }^{m}_{\perp }} = 0.01$ 1/s is so high such that the GBLF will close in the region there the temperature is about the coherent temperature, which was discussed in Section 4.4. This will result in very high flow rates, which in turn lead to high Pe_T values in this region of the GBLF. In Fig. 19b can it be seen that Pe_T is up to 20 in the region where the GBLF has closed. Thus, the diffusion of heat in the solid phase is not fast enough to transport away the advection heat due to the GBLF flow in this region of the GBLF. Therefore, we can expect that melting of the solid phase occurs in this region. This is not accounted for in our solidification model. When ${\dot {\varepsilon }^{m}_{\perp }} = 0.05$ 1/s, a large part of the GBLF has closed. The maximum Pe_T value can be up 80 in this part of the GBLF, as can be seen in In Fig. 19b. Thus, we can expect large amount of melting of the solid phase. Hence, our model is not likely to be accurate for this very high strain rate.

Fig. 19

a Solutal and b thermal Peclet numbers, calculated along the GBLF at $\tilde {t}=2$ and v_w = 1 mm/s, and for the two different strain rates ${\dot {\varepsilon }^{m}_{\perp }} = 0.01$ 1/s and ${\dot {\varepsilon }^{m}_{\perp }} = 0.05$ 1/s

5 Conclusions

A numerical solidification model for simulating the influence of strain rate on eutectic band thickness has been proposed. The relation between eutectic band thickness, solidification velocity, and mechanical strain rate was studied for Alloy 718. It was found that when the magnitude of the strain rate is 10 times as large as that of the solidification velocity, the predicted eutectic band thickness is increased by 200 to 500% as compared to when the strain rate is zero. It was also found that an increase in strain rate can lead to a decrease in GBLF thickness in the coherent temperature region. This leads to a decrease in permeability, which in turn may increase crack susceptibility. Finally, it was discussed how eutectic bands can form from hot cracks.

Appendix

In this appendix, we derive an expression for the time that it takes for the gas-liquid interface of a crack to move a given distance due to a change in the GBLF pressure. This time was used in Section 4.5 to discuss the rate at which crack healing can occur.

Consider a stationary void in a GBLF whose surface tension is balanced by the external pressure $p_{0}^{*}$. At t = 0, we assume that $p_{0}^{*}$ is instantaneously increased to p₀. Thus, the external pressure can no longer balance the void interface and it will therefore start to move. Now, we greatly simplify the situation by assuming that the gas-liquid interface of the void is located between two parallel plates as is shown in Fig. 20. Furthermore, we assume that the gas-liquid interface is cylindrical and that the void has penetrated through the weld surface so that the pressure inside the void is the same as the atmospheric pressure p_atm.

Fig. 20

A void in a GBLF bounded by two parallel plates. At the time t = t the interface has moved a distance Δs due to a decrease in the pressure drop in the GBLF

The curvature, H, of the cylindrical gas-liquid interface is given by

$$ H = \frac{\cos\theta}{2h} $$

(51)

where 𝜃 is the contact angle. The pressure difference across the void interface is given by Young-Laplace equation

$$ p_{i} - p_{e} = 2 \gamma H $$

(52)

where p_i and p_e are the internal and external void pressures, respectively. γ is the surface tension of the gas-liquid interface of the void. By substituting the previous assumption p_i = p_atm and Eq. 51 into Eq. 52, then the external pressure can be written as

$$ p_{e} = p_{atm} - \frac{\gamma\cos\theta}{2h} $$

(53)

Now, let s₀ be the location of the void interface at the time t = 0 when it is stationary. At t = 0 the liquid pressure at s₀ is increased from p_e to p₀. The void interface will then move a distance Δs = s₀ − s during the time t = t, see Fig. 20, where s is the interface position at t = t. The liquid pressure p_e at s₀ and t = 0 arise because of liquid flow along the GBLF induced by the tensile straining of the GBLF. The sudden change of the liquid pressure at s₀ when t = 0 may be due to an increase in the upstream GBLF permeability caused by the straining (see [4] for a discussion on how the GBLF permeability depends on the straining). For simplicity, we assume that p₀ is constant at s₀ during the short time we are interested to study the interface movement. We defined Δp₀ = p_atm − p₀ as the pressure drop along the GBLF from the weld pool to the location s₀.

Now, we assume that the liquid flow in the GBLF is laminar and is given by a parallel plate Poiseuille flow. The average liquid velocity in a cross section of the GBLF is then given by

$$ \bar{v} = - \frac{h^{2}}{3\mu} \frac{\partial p}{\partial s} $$

(54)

where p is the liquid pressure at s and μ is the dynamic viscosity of the liquid [4]. Furthermore, at the void interface, let $ds/dt = \bar {v}$ be the velocity of the void interface and let ${\varDelta } p = p_{0} - p_{e} = -{\varDelta } p_{0} + \gamma \cos \limits \theta /h$ and Δs = s₀ − s. Substituting this into Eq. 54 and approximating ∂p/∂s by Δp/Δs gives

$$ \frac{ds}{dt} = - \frac{h^{2}}{3\mu {\varDelta} s} \left( -{\varDelta} p_{0} + \frac{\gamma \cos\theta}{h} \right) $$

(55)

Integrating (55) and solving for t finally give

$$ t = \frac{{3\mu{\varDelta} s}^{2}}{2h^{2}\left( -{\varDelta} p_{0} + \frac{\gamma \cos\theta}{h} \right)}, \quad {\varDelta} p_{0} < \frac{\gamma \cos\theta}{h} $$

(56)

Figure 21 shows two plots of t in Eq. 56 with respect to Δp₀ and Δs. h is fixed at 1 μ m in the left plot and at 5 μ m in the right plot. γ = 1.8 J/m², 𝜃 = 10^∘, and μ = 12 mPas, were used for the plots. These values are typical for Alloy 718 [5].

Fig. 21

t as a function of Δp₀ and Δs for (a) h = 1 μ m and (b) h = 5 μ m

It is interesting to note from Fig. 21 that, unless p₀ is very close to p_e, the void interface can move a relatively long distance in a short amount of time.