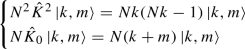Abstract
We present and discuss a formal approach for describing the quantum to classical crossover based on the group-theoretic construction of generalized coherent states. The method was originally introduced by Yaffe (Rev Mod Phys 54:407, 1982) in 1982 for tackling large-N quantum field theories and has been recently used for studying open quantum systems whose environment, while becoming macroscopic, may or may not display a classical behaviour (Liuzzo-Scorpo et al. in EPL (Europhys Lett) 111(4):40008, 2015; Rossi et al. in Phys Rev A 96:032116, 2017; Foti et al. in Quantum 3:179, 2019; Coppo in Schwarzschild black holes as macroscopic quantum systems, Università degli studi di Firenze, Florence, 2019). Referring to these recent developments, in this paper we provide the essential elements of Yaffe’s approach in the framework of standard quantum mechanics, so as to clarify how the approach can be used without referring to quantum field theory. Moreover, we address the role played by a possible global symmetry in making the large-N limit of the original quantum theory to flow into a formally well-defined classical theory, and we specifically consider the quantum-to-classical crossover of angular momentum. We also give details of a paradigmatic example, namely that of N free one-dimensional spinless particles. Finally, we discuss upon the foundational requirement that any classical description should ultimately be derived from an underlying quantum theory, that, however, is not, and should never be confused with, the one obtained via some quantization procedure of the classical description itself.
Similar content being viewed by others
Notes
The Lie group SU(1, 1) is defined as the group of transformations in the two-dimensional complex plane \({\mathbb {C}}^2\) that leave invariant the Hermitian form \({\bar{\psi }}\psi :=\psi ^\dagger \sigma _3\psi =\psi _1^\dagger \psi _1-\psi _2^\dagger \psi _2\), where \(\psi =(\psi _1,\psi _2)\in {\mathbb {C}}^2\) and \(\sigma _3\) is the third Pauli matrix. This group is isomorphic to \(SL(2,{\mathbb {R}})\) and \(Sp(2,{\mathbb {R}})\), and its substantial differences with SU(2) are that it is non-compact and it is not simply connected. We will study an explicit example of a system related to this group in Sect. 3.
This representation is finite-dimensional and hence not Hermitian.
A factor i is needed to define \(\zeta \) because the representation (21) is not Hermitian.
More accurately this is the definition of Hamiltonian classical theory, but not all classical theories are Hamiltonian. Anyway in this paper we only consider these ones.
Notice that the abstract group \({\mathcal {G}}\) and its algebra \({\mathfrak {g}}\) do not depend on \(\chi \), which instead enters \({\mathcal {G}}_\chi \) and its algebra \({\mathfrak {g}}_\chi \) via the \(\chi \)-dependence of the Hilbert space \({\mathcal {H}}_\chi \).
If \({\mathfrak {g}}\) is the Lie algebra defining the theory, we consider the Hamiltonian as an element of the universal enveloping algebra \(U({\mathfrak {g}})=T({\mathfrak {g}})/I\), where \(T({\mathfrak {g}})=K\oplus {\mathfrak {g}}\oplus ({\mathfrak {g}}\otimes {\mathfrak {g}})\oplus ({\mathfrak {g}}\otimes {\mathfrak {g}}\otimes {\mathfrak {g}})\oplus \cdots \) is the tensor algebra of \({\mathfrak {g}}\) (K is the field over which \({\mathfrak {g}}\) is defined) and I is the two-sided ideal over \(T({\mathfrak {g}})\) generated by elements of the form \({\hat{A}}\otimes {\hat{B}}-{\hat{B}}\otimes {\hat{A}}-[{\hat{A}},{\hat{B}}]\) with \({\hat{A}},{\hat{B}}\in {\mathfrak {g}}\). Informally, \(U({\mathfrak {g}})\) is the algebra of the polynomials of \({\mathfrak {g}}\). It is possible to demonstrate (Barut and Raczka 1980) that the representations of \({\mathfrak {g}}\) and \(U({\mathfrak {g}})\) are the same.
In order to avoid explicit rescalings of the coupling constants in the Hamiltonian as \(N\rightarrow \infty \), a factor \(1/\sqrt{N}\) has been included in the definition of \({\hat{q}}_i\) and \({\hat{p}}_i\), as seen from Eq. (41).
Since
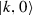 , as reference state (see Sect. 2.5), is a PCS, \(Z(\varOmega )=0\) implies
, as reference state (see Sect. 2.5), is a PCS, \(Z(\varOmega )=0\) implies 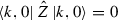 . Then, assuming that
. Then, assuming that (48)
(48)is true when the total number of \({\hat{K}}_-\) plus \({\hat{K}}_+\) is less than n, we must prove the same holds when such number becomes n. Firstly, note that \(Z(\varOmega )=0\) implies
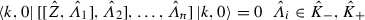 (choose
(choose 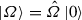 with \({\hat{\varOmega }}=\mathrm {e}^{t_1{\hat{\varLambda }}_1}\mathrm {e}^{t_2{\hat{\varLambda }}_2},\ldots , \mathrm {e}^{t_n{\hat{\varLambda }}_n}\) and differentiate \(Z(\varOmega )\) with respect to each \(t_i\)). Expanding the multiple commutator, we find that only one term contains all \({\hat{K}}_-\) operators to the left and all \({\hat{K}}_+\) operators to the right of \({\hat{Z}}\). Every other term contains at least one \({\hat{K}}_-\) operator which may be pushed right until it annihilates
with \({\hat{\varOmega }}=\mathrm {e}^{t_1{\hat{\varLambda }}_1}\mathrm {e}^{t_2{\hat{\varLambda }}_2},\ldots , \mathrm {e}^{t_n{\hat{\varLambda }}_n}\) and differentiate \(Z(\varOmega )\) with respect to each \(t_i\)). Expanding the multiple commutator, we find that only one term contains all \({\hat{K}}_-\) operators to the left and all \({\hat{K}}_+\) operators to the right of \({\hat{Z}}\). Every other term contains at least one \({\hat{K}}_-\) operator which may be pushed right until it annihilates 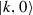 , or one \({\hat{K}}_+\) operator which may be pushed left. This process produces also commutator terms \([{\hat{K}}_-,{\hat{K}}_+]\) which reduce n by two. In the end the vacuum expectation value of a multiple commutator contains a term of the form (48) with n operators plus lower-order terms which vanish for induction. Therefore, Eq. (48) also holds for a number n of \({\hat{K}}_-\) plus \({\hat{K}}_+\) operators.
, or one \({\hat{K}}_+\) operator which may be pushed left. This process produces also commutator terms \([{\hat{K}}_-,{\hat{K}}_+]\) which reduce n by two. In the end the vacuum expectation value of a multiple commutator contains a term of the form (48) with n operators plus lower-order terms which vanish for induction. Therefore, Eq. (48) also holds for a number n of \({\hat{K}}_-\) plus \({\hat{K}}_+\) operators.Notice that, considering the rescaling of the SU(1, 1) commutation rules and of the indices k, m, Eq. (17) assumes the form:
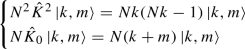
The classical limit of a spin-j system can be naively implemented substituting the spin operators with classical vectors that freely move on a sphere of radius \((j+1/2)\) (Lieb 1973).
Despite the ambiguity of the terminology, in recent literature “closed” systems are defined as quantum non-isolated systems with an environment that enters the analysis as a classical-like agent, such as an external magnetic field, or a classical thermal bath. “Open” quantum systems, instead, are those whose environment is, and must be treated as, a quantum system, which implies having to consider phenomena such as entanglement generation, backflow of information, non-Markovianity, and many others.
This result is clear when considering Eq. (62) for N=1.
Yaffe demonstrates that not only O(N) vector models have a classical limit when \(N\rightarrow \infty \), but also U(N) matrix models and U(N)-lattice gauge theories.
References
Bargmann V (1947) Irreducible unitary representations of the Lorentz group. Ann Math 48:568
Barut A, Fronsdal C (1965) On non-compact groups. II. Representations of the \(2+1\) Lorentz group. Proc R Soc Lond A 287:532
Barut A, Raczka R (1980) Theory of group representations and applications. Polish Scientific Publishers, New York
Biedenharn L, Nuyts J, Straumann N (1965) On the unitary representations of \(SU(1,1)\) and \(SU(2,1)\). Ann Inst Henri Poincaré 3:13
Brandao FGSL, Piani M, Horodecki P (2015) Generic emergence of classical features in quantum Darwinism. Nat Commun 6:7908
Coppo A (2019) Schwarzschild black holes as macroscopic quantum systems. Master thesis, Università degli studi di Firenze, Florence
Foti C, Heinosaari T, Maniscalco S, Verrucchi P (2019) Whenever a quantum environment emerges as a classical system, it behaves like a measuring apparatus. Quantum 3:179
Friedmann T, Hagen C (2012) Group-theoretical derivation of angular momentum eigenvalues in spaces of arbitrary dimensions. J Math Phys 53:122102
Gilmore R (1972) Geometry of symmetrized states. Ann Phys 74:391
Hua LK (1963) Harmonic analysis of functions of several complex variables in the classical domains. Trans Math Monogr 6. https://doi.org/10.1090/mmono/006
Lee J (2012) Introduction to smooth manifolds. Springer, Berlin
Lieb E (1973) The classical limit of quantum spin systems. Commun Math Phys 31:327
Liuzzo-Scorpo P, Cuccoli A, Verrucchi P (2015) Parametric description of the quantum measurement process. EPL (Europhys Lett) 111(4):40008
Novaes M (2004) Some basics of \(Su(1,1)\). Rev Braz Ensino de Fisica 26:351
Perelomov A (1972) Coherent states for arbitrary Lie group. Commun Math Phys 26:222
Perelomov A (1985) Generalized coherent states and their applications. Springer, Berlin
Rossi MAC, Foti C, Cuccoli A, Trapani J, Verrucchi P, Paris MGA (2017) Effective description of the short-time dynamics in open quantum systems. Phys Rev A 96:032116
Yaffe L (1982) Large \(N\) limits as classical mechanics. Rev Mod Phys 54:407
Zhang W, Gilmore R, Feng H (1990) Coherent states: theory and some applications. Rev Mod Phys 62:867
Acknowledgements
Financial support from the Università degli Studi di Firenze in the framework of the University Strategic Project Program 2015 (Project BRS00215) is gratefully acknowledged. PV has worked in the framework of the Convenzione Operativa between the Institute for Complex Systems of the Italian National Research Council (CNR) and the Physics and Astronomy Department of the University of Florence.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Federico Holik.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Coppo, A., Cuccoli, A., Foti, C. et al. From a quantum theory to a classical one. Soft Comput 24, 10315–10325 (2020). https://doi.org/10.1007/s00500-020-04934-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-020-04934-4





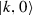 , as reference state (see Sect.
, as reference state (see Sect. 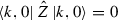 . Then, assuming that
. Then, assuming that
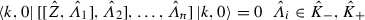 (choose
(choose 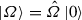 with
with 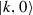 , or one
, or one