1 Introduction

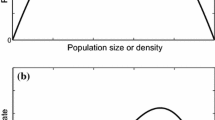
The Allee effect, which is depicted by a relationship between the per capita growth rate and the population size, is a universal biological phenomenon [2, 11, 14]. Allee effects happen while populations rely on cooperation or aggregation to hunt, to prevent capture, or to bring up their young [11, 14]. For instance, the African wild dogs usually form cooperative groups to hunt [4], suricate (Suricata suricatta) and Pacific salmon (Oncorhynchus spp.) form groups to prevent capture [6, 20]. The significance of Allee effects has been admitted in a lot of biological subjects (for example, eco-epidemiology [8], biological invasions [22], and population ecology [7]), and numerous mathematical frameworks have been put forward to dissect the role of Allee effects (see, e.g., [5, 11, 14, 21]). Especially, Takeuchi [21] took advantage of the following equation to test the impacts of Allee effects on the evolution of a population:

$$ \frac{\mathrm{d}\varPsi }{\mathrm{d}t}=\varPsi \biggl[r+ \frac{\mu \varPsi }{1+\lambda \varPsi } - \frac{\varPsi ^{2}}{1+\lambda \varPsi } \biggr], $$
(1)

where \(\varPsi =\varPsi (t)\) means the population size; r indicates the intrinsic growth rate; \(\mu >0\) is the Allee threshold under which the population will become extinct; \(\lambda >0\) depicts the environmental carrying capacity.

All species in natural environments undulate in an essentially random way, and randomness brings a hazard of extinction [19]. Commonly, puny undulations and medium undulations are two classes of usual undulations in the environments [23]. We first appraise the former. Several authors (see, e.g., [1, 9, 10, 15–17]) have proffered that the puny undulations often act on the parameters in a system, and one could take advantage of the white noise to approximately depict the puny undulations. In this way, in model (1)

$$ r\rightarrow r+\eta _{1} \dot{\xi _{1}}(t),\qquad \mu \rightarrow \mu + \eta _{2} \dot{\xi _{2}}(t), $$

and accordingly,

$$ \mathrm{d}\varPsi =\varPsi \biggl[r+\frac{\mu \varPsi }{1+\lambda \varPsi }- \frac{\varPsi ^{2}}{1+\lambda \varPsi } \biggr]\,\mathrm{d}t+\eta _{1} \varPsi \,\mathrm{d}\xi _{1}(t)+\frac{\eta _{2}\varPsi ^{2}}{1+\lambda \varPsi } \,\mathrm{d}\xi _{2}(t), $$
(2)

where \(\eta _{i}^{2}\) means the intensity of the white noise, \(\{\xi (t)\}_{t\geq 0}=\{(\xi _{1}(t), \xi _{2}(t))\}_{t\geq 0}\) indicates a Wiener process defined on a complete probability space \((\varOmega , {\{\mathcal{F}_{t}}\}_{t\geq 0}, \mathrm{P})\) which obeys the usual conditions.

Next we appraise the medium undulations (for instance, the medium variations of rainfall and temperature) which are often encountered by the species. When these medium undulations emerge, the parameter values in a system often jump. For instance, Choristoneura fumiferana (Clemens) reproduces 50% more eggs at 25∘C than at 15∘C [3]. These medium undulations cannot be portrayed by (2) [12, 15–17]. Mathematically, one may employ a finite-state Markov chain to portray these medium undulations [12, 13, 15–17]. Denote by \(\theta =\theta (t)\) a right-continuous irreducible Markov chain which is independent of \(\{\xi (t)\}_{t\geq 0}\). Then we can deduce from Eq. (2) that

$$ \mathrm{d}\varPsi =\varPsi \biggl[r(\theta )+ \frac{\mu (\theta )\varPsi }{1+\lambda (\theta )\varPsi } - \frac{\varPsi ^{2}}{1+\lambda (\theta )\varPsi } \biggr]\,\mathrm{d}t+\eta _{1}( \theta )\varPsi \,\mathrm{d}\xi _{1}(t) + \frac{\eta _{2}(\theta )\varPsi ^{2}}{1+\lambda (\theta )\varPsi } \,\mathrm{d}\xi _{2}(t). $$
(3)

During recent decades, there has been growing interest in extinction, persistence, and stability of population models [23]. However, little research has been conducted to appraise these behaviors of (2) and (3). The present study detects these behaviors of (2): we first dissect the extinction and persistence of model (2) in Sect. 2, and then offer sufficient criteria to ensure that model (3) possesses a unique ergodic stationary distribution (UESD) in Sect. 3; in Sect. 4, we make use of the theoretical outcomes to evaluate the evolution of the African wild dog (Lycaon pictus) in Africa and expose some significant functions of puny undulations and medium undulations.

2 Extinction and permanence

Let \(\varTheta =\{1,\ldots,N\}\) and \(\varGamma =(\gamma _{mj})_{N\times N}\) mean the state space and the generator of \(\theta (t)\), respectively, i.e.,

$$ P\bigl\{ \theta (t+\Delta t)=j|\theta (t)=m\bigr\} = \textstyle\begin{cases} \gamma _{mj}\Delta t+o(\Delta t), & \mbox{if } j\neq m; \\ 1+\gamma _{mm}\Delta t+o(\Delta t), & \mbox{if } j=m, \end{cases} $$

where \(\gamma _{mj}\geq 0\) means the transition rate from state m to state j if \(j\neq m\), and \(\gamma _{mm}=-\sum_{j=1,j\neq m}^{N}\gamma _{mj}\) for \(m=1,2,\ldots,N\), see [18] for more details. Note that \(\theta (t)\) is irreducible, then (see, e.g., [15]) it has a stationary distribution which is denoted by \(\sigma =(\sigma _{1},\ldots,\sigma _{N})\). Let \(\mathbb{R}_{+}^{0}=\{x\in \mathbb{R}|x>0\}\). Define \(f^{u}=\max_{m\in \varTheta }\{f(m)\}\), \(f^{l}=\min_{m\in \varTheta }\{f(m) \}\). By standard procedures (see, e.g., [15]), one can testify the following.

Lemma 1

For any\((\varPsi (0),\theta (0))\in \mathbb{R}_{+}^{0}\times \varTheta \), Eq. (3) possesses a pathwise unique global solution\((\varPsi (t),\theta (t))\in \mathbb{R}_{+}^{0}\times \varTheta \)almost surely (a.s.).

We first offer the criteria for extinction of Eq. (3).

Theorem 1

\(\bar{\chi }+\bar{\varPi }<0\Rightarrow \)\(\lim_{t\rightarrow +\infty }\varPsi (t)=0\), \(a.s\)., namely, \(\varPsi (t)\)becomes extinct, where

$$\begin{aligned}& \bar{\chi }=\sum_{m\in \varTheta }\sigma _{m} \chi (m),\qquad \chi (m)=r(m)- \frac{\eta _{1}^{2}(m)}{2}, \\& \bar{\varPi }=\sum _{m\in \varTheta }\sigma _{m} \biggl[\frac{\mu (m)}{\lambda (m)} - \frac{2(\sqrt{1+\lambda (m)\mu (m)}-1)}{\lambda ^{2}(m)} \biggr]. \end{aligned}$$

Proof

We can deduce from the ergodicity of θ that

$$ \lim_{t\rightarrow +\infty }t^{-1} \int _{0}^{t} \biggl[\chi \bigl( \theta (s) \bigr)+\frac{\mu (\theta (s))}{\lambda (\theta (s))} - \frac{2(\sqrt{1+\lambda (\theta (s))\mu (\theta (s))}-1)}{\lambda ^{2}(\theta (s))} \biggr]\,\mathrm{d}s =\bar{\chi }+\bar{\varPi }.$$
(4)

Notice that

$$ \min_{x>0} \biggl\{ \frac{\mu (\cdot )+\lambda (\cdot )x^{2}}{1+\lambda (\cdot )x} \biggr\} = \frac{2(\sqrt{1+\lambda (\cdot )\mu (\cdot )}-1)}{\lambda (\cdot )}. $$

Then the Itô formula (see, e.g., [18]) implies that

$$ \begin{aligned}[b] \ln \varPsi (t)-\ln \varPsi (0)& = \int _{0}^{t} \biggl[\chi \bigl( \theta (s) \bigr)+ \frac{\mu (\theta (s))\varPsi (s)-\varPsi ^{2}(s)}{1+\lambda (\theta (s))\varPsi (s)} \biggr]\,\mathrm{d}s \\ &\quad {}-\frac{1}{2} \int _{0}^{t} \frac{\eta _{2}^{2}(\theta (s))\varPsi ^{2}(s)}{(1+\lambda (\theta (s))\varPsi (s))^{2}} \,\mathrm{d}s + \sum_{i=1}^{2} L_{i}(t) \\ & = \int _{0}^{t} \biggl[\chi \bigl(\theta (s)\bigr)+ \frac{\mu (\theta (s))}{\lambda (\theta (s))} - \frac{\mu (\theta (s))+\lambda (\theta (s))\varPsi ^{2}(s)}{\lambda (\theta (s)) (1+\lambda (\theta (s))\varPsi (s))} \biggr]\,\mathrm{d}s \\ &\quad {}- \frac{1}{2} \int _{0}^{t} \frac{\eta _{2}^{2}(\theta (s))\varPsi ^{2}(s)}{(1+\lambda (\theta (s))\varPsi (s))^{2}} \,\mathrm{d}s + \sum_{i=1}^{2} L_{i}(t) \\ & \leq \int _{0}^{t} \biggl[\chi \bigl(\theta (s)\bigr)+ \frac{\mu (\theta (s))}{\lambda (\theta (s))} - \frac{2(\sqrt{1+ \lambda (\theta (s))\mu (\theta (s))}-1)}{\lambda ^{2}(\theta (s))} \biggr]\,\mathrm{d}s \\ &\quad {} -\frac{1}{2} \int _{0}^{t} \frac{\eta _{2}^{2}(\theta (s))\varPsi ^{2}(s)}{(1+ \lambda (\theta (s))\varPsi (s))^{2}} \,\mathrm{d}s+ \sum_{i=1}^{2} L_{i}(t), \end{aligned} $$
(5)

where

$$ L_{1}(t)= \int _{0}^{t}\eta _{1}\bigl(\theta (s)\bigr)\,\mathrm{d}\xi _{1}(s),\qquad L_{2}(t)= \int _{0}^{t} \frac{\eta _{2}(\theta (s))\varPsi (s)}{1+\lambda (\theta (s))\varPsi (s)} \,\mathrm{d}\xi _{2}(s). $$

Compute the quadratic variation of \(L_{2}(t)\):

$$ \bigl\langle L_{2}(t),L_{2}(t)\bigr\rangle = \int _{0}^{t} \frac{\eta _{2}^{2}(\theta (s))\varPsi ^{2}(s)}{(1+\lambda (\theta (s))\varPsi (s))^{2}} \,\mathrm{d}s. $$

In accordance with the exponential martingale inequality (see, e.g., [18]), we can deduce that

$$ \mathrm{P} \biggl\{ \sup_{0\leq t\leq k} \biggl[L_{2}(t)- \frac{1}{2} \bigl\langle L_{2}(t),L_{2}(t)\bigr\rangle \biggr]>2\ln k \biggr\} \leq 1/k^{2}. $$

Accordingly, Borel–Cantelli’s lemma (see, e.g., [18]) manifests that, for almost all \(\omega \in \varOmega \), one can find an integer \(k^{\ast }=k^{\ast }(\omega )\) such that, for \(k\geq k^{\ast }\),

$$ \sup_{0\leq t\leq k} \biggl[L_{2}(t)-\frac{1}{2} \bigl\langle L_{2}(t),L_{2}(t) \bigr\rangle \biggr]\leq 2 \ln k. $$

For this reason,

$$ L_{2}(t)\leq 2\ln k+\frac{1}{2}\bigl\langle L_{2}(t),L_{2}(t)\bigr\rangle =2 \ln k+ \frac{1}{2} \int _{0}^{t} \frac{\eta _{2}^{2}(\theta (s))\varPsi ^{2}(s)}{(1+\lambda (\theta (s))\varPsi (s))^{2}} \,\mathrm{d}s,\quad 0\leq t\leq k, k\geq k^{\ast }. $$

Utilizing this inequality to (5) gives that, for \(0\leq t\leq k\), \(k\geq k^{\ast }\),

$$\begin{aligned} \ln \varPsi (t)-\ln \varPsi (0) \leq& \int _{0}^{t} \biggl[\chi \bigl(\theta (s)\bigr)+ \frac{\mu (\theta (s))}{\lambda (\theta (s))} - \frac{2(\sqrt{1+\lambda (\theta (s))\mu (\theta (s))}-1)}{\lambda ^{2}(\theta (s))} \biggr]\,\mathrm{d}s \\ &{}+L_{1}(t)+2 \ln k. \end{aligned}$$

Accordingly, for \(0< k-1\leq t\leq k\), \(k\geq k^{\ast }\),

$$\begin{aligned} t^{-1}\ln \varPsi (t)-t^{-1}\ln \varPsi (0) \leq& t^{-1} \int _{0}^{t} \biggl[ \chi \bigl(\theta (s) \bigr)+\frac{\mu (\theta (s))}{\lambda (\theta (s))} - \frac{2(\sqrt{1+\lambda (\theta (s))\mu (\theta (s))}-1)}{\lambda ^{2}(\theta (s))} \biggr]\,\mathrm{d}s \\ &{}+t^{-1}L_{1}(t) +\frac{2\ln k}{k-1}. \end{aligned}$$
(6)

Obviously,

$$ \lim_{t\rightarrow +\infty }t^{-1}L_{1}(t)=0,\quad \mbox{a.s.}$$
(7)

Utilizing (4) and (7) to (6) causes \(\limsup_{t\rightarrow +\infty }t^{-1}\ln \varPsi (t)\leq \bar{ \chi }+\bar{\varPi }<0\), a.s. As a result, for any \(\epsilon >0\), there is \(T>0\) such that, for any \(t\geq T\),

$$ t^{-1}\ln \varPsi (t)\leq \bar{\chi }+\bar{\varPi }+\epsilon . $$

That is to say,

$$ \varPsi (t)\leq e^{(\bar{\chi }+\bar{\varPi }+\epsilon )t}. $$

Let ϵ be sufficiently small such that \(\bar{\chi }+\bar{\varPi }+\epsilon <0\), then \(\lim_{t\rightarrow +\infty }\varPsi (t)=0\). □

In order to test stochastic permanence (SP) of model (3), we do some preparations. Suppose that \((X(t),\theta (t))\) follows the equation below:

$$ \mathrm{d}X=u_{1} (X,\theta )\,\mathrm{d}t+u_{2} (X, \theta )\,\mathrm{d}\xi _{1}(t) +u_{3} (X,\theta ) \,\mathrm{d}\xi _{2}(t). $$

Let \(U(X,m)\) be a function which is twice continuously differentiable. Define an operator \(\mathcal{L}\) as follows:

$$ \mathcal{L}U(X,m)=U_{X}(X,m)u_{1}(X,m)+ \frac{u_{2}^{2}(X,m)+u_{3}^{2}(X,m)}{2}U_{XX}(X,m)+\sum_{j\in \varTheta } \gamma _{mj}U(X,j). $$

Definition 1

([12])

Model (3) is called SP if, for \(\forall \varepsilon \in (0,1)\), one can find a couple of constants \(f_{1}= f_{1}(\varepsilon )\) and \(f_{2}= f_{2}(\varepsilon )\) such that, for \(\forall (\varPsi (0),\theta (0))\in \mathbb{R}_{+}^{0}\times \varTheta \),

$$ \liminf_{t\rightarrow +\infty }\mathrm{P}\bigl\{ \varPsi (t)\geq f_{1} \bigr\} \geq 1-\varepsilon ,\qquad \liminf_{t\rightarrow + \infty } \mathrm{P}\bigl\{ \varPsi (t)\leq f_{2}\bigr\} \geq 1-\varepsilon. $$
(8)

Lemma 2

([24])

There is a solution to\(\varGamma x=\upsilon \) ⇔ \(\sigma \upsilon =0\), where\(\upsilon \in \mathbb{R}^{N}\).

Theorem 2

\(\bar{\chi }>0\Rightarrow \)model (3) is SP.

Proof

Let

$$ U_{1}(\varPsi )=1/\varPsi ^{2},\quad \varPsi \in \mathbb{R}_{+}^{0}. $$

We can deduce from Itô’s formula that

$$ \begin{aligned} \mathrm{d}U_{1}(\varPsi )& =2U_{1}(\varPsi ) \biggl[ \frac{\varPsi ^{2}}{1+\lambda (\theta )\varPsi }- \frac{\mu (\theta )\varPsi }{1+\lambda (\theta )\varPsi }-r( \theta ) \biggr] \,\mathrm{d}t \\ &\quad {}+3 \biggl(\eta _{1}^{2}( \theta )U_{1}(\varPsi )+ \frac{\eta _{2}^{2}(\theta )}{(1+\lambda (\theta )\varPsi )^{2}} \biggr) \,\mathrm{d}t \\ &\quad {} -2\eta _{1}(\theta )U_{1}(\varPsi )\,\mathrm{d}\xi _{1}(t) -\frac{2\eta _{2}(\theta )}{\varPsi (1+\lambda (\theta )\varPsi )} \,\mathrm{d}\xi _{2}(t). \end{aligned} $$

Examine the equation \(\varGamma x=-2\chi +\bar{\chi }(2,\ldots,2)^{\mathrm{T}}\), where \(\chi =(\chi (1),\ldots,\chi (N))^{\mathrm{T}}\). In accordance with Lemma 2, it possesses a solution which is denoted by \((\alpha _{1},\ldots,\alpha _{N})^{\mathrm{T}}\). Accordingly,

$$ \frac{1}{2}\sum_{j\in \varTheta } \gamma _{mj}\alpha _{j}+\chi (m)=\bar{ \chi }. $$
(9)

Choose sufficiently small \(\varpi \in (0,1)\) which fulfills that, for every \(m\in \varTheta \),

$$ 1-\alpha _{m}\varpi >0,\qquad \bar{\chi }-\varpi \eta _{1}^{2}(m)+ \frac{\alpha _{m}\varpi }{2(1-\alpha _{m}\varpi )}\sum _{j\in \varTheta } \gamma _{mj}\alpha _{j}>0. $$

Then (9) implies that

$$\begin{aligned} \chi (m)-\frac{1}{2(1-\alpha _{m}\varpi )\varpi }\sum _{j\in \varTheta } \gamma _{mj}(1-\alpha _{j} \varpi ) &=\chi (m)+ \frac{1}{2(1-\alpha _{m}\varpi )}\sum_{j\in \varTheta } \gamma _{mj} \alpha _{j} \\ &=\bar{\chi }+ \frac{\alpha _{m}\varpi }{2(1-\alpha _{m}\varpi )}\sum_{j\in \varTheta } \gamma _{mj}\alpha _{j}. \end{aligned}$$
(10)

Let

$$ U_{2}(\varPsi ,m)=(1-\alpha _{m}\varpi ) \bigl(1+U_{1}(\varPsi )\bigr)^{\varpi }. $$

We can deduce from Itô’s formula that

$$ \begin{aligned} \mathrm{d}U_{2}(\varPsi ,\theta )& = \mathcal{L}U_{2}( \varPsi ,\theta )\,\mathrm{d}t-2\eta _{1}( \theta ) (1-\alpha _{m}\varpi )U_{1}( \varPsi ) \bigl(1+U_{1}(\varPsi )\bigr)^{\varpi -1}\,\mathrm{d}\xi _{1}(t) \\ &\quad {} - \frac{2\eta _{2}(\theta )(1-\alpha _{m}\varpi )}{\varPsi (1+\lambda (\theta )\varPsi )}U_{1}( \varPsi ) \bigl(1+U_{1}( \varPsi )\bigr)^{\varpi -1}\,\mathrm{d}\xi _{2}(t), \end{aligned} $$

then taking the expectation gives

$$ \mathbb{E}U_{2}\bigl(\varPsi (t),\theta (t)\bigr)=U_{2} \bigl(\varPsi (0),\theta (0)\bigr)+ \mathbb{E} \int _{0}^{t}\mathcal{L}U_{2}\bigl( \varPsi (s),\theta (s)\bigr) \,\mathrm{d}s, $$

where

$$\begin{aligned}& \mathcal{L}U_{2}(\varPsi ,m) \\ & \quad =2(1-\alpha _{m}\varpi )\varpi \bigl(1+U_{1}(\varPsi ) \bigr)^{ \varpi -2} \\ & \qquad {}\times \biggl\{ \bigl(1+U_{1}(\varPsi )\bigr) \biggl[U_{1}(\varPsi ) \biggl( \frac{\varPsi ^{2}}{1+\lambda (m)\varPsi }- \frac{\mu (m)\varPsi }{1+\lambda (m)\varPsi }-r(m)+3\eta _{1}^{2}(m)/2 \biggr) \\ & \qquad {} + \frac{3\eta _{2}^{2}(m)}{2(1+\lambda (m)\varPsi )^{2}} \biggr]+(\varpi -1) \biggl[\eta _{1}^{2}(m)U_{1}^{2}( \varPsi )+ \frac{\eta _{2}^{2}(m)}{(1+\lambda (m)\varPsi )^{2}}U_{1}(\varPsi ) \biggr] \biggr\} \\ & \qquad {} +\bigl(1+U_{1}(\varPsi )\bigr)^{\varpi }\sum _{j\in \varTheta } \gamma _{mj}(1-\alpha _{j} \varpi ) \\ & \quad =2(1-\alpha _{m}\varpi )\varpi \bigl(1+U_{1}(\varPsi ) \bigr)^{ \varpi -2} \biggl\{ - \bigl[\chi (m)-\varpi \eta _{1}^{2}(m) \bigr]U_{1}^{2}( \varPsi ) \\ & \qquad {} + \biggl(3\eta _{1}^{2}(m)/2-r(m)+ \frac{1}{1+\lambda (m)\varPsi }+ \frac{\eta _{2}^{2}(m)(\varpi +0.5)}{(1+\lambda (m)\varPsi )^{2}} \biggr)U_{1}( \varPsi ) \\ & \qquad {}+ \frac{1}{1+\lambda (m)\varPsi }+ \frac{3\eta _{2}^{2}(m)}{2(1+\lambda (m)\varPsi )^{2}} -\frac{\mu (m)}{\varPsi (1+\lambda (m)\varPsi )} \bigl(1+U_{1}( \varPsi ) \bigr) \biggr\} \\ & \qquad {}+ \bigl(1+U_{1}(\varPsi )\bigr)^{\varpi }\sum _{j \in \varTheta }\gamma _{mj}(1-\alpha _{j} \varpi ) \\ & \quad =2(1-\alpha _{m}\varpi )\varpi \bigl(1+U_{1}(\varPsi ) \bigr)^{ \varpi -2} \biggl\{ - \biggl[ \chi (m)-\varpi \eta _{1}^{2}(m)- \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{2(1-\alpha _{m}\varpi )\varpi } \biggr]U_{1}^{2}( \varPsi ) \\ & \qquad {} + \biggl[3\eta _{1}^{2}(m)/2-r(m)+ \frac{\varPsi }{1+\lambda (m)}+ \frac{\eta _{2}^{2}(m)(\varpi +0.5)}{(1+\lambda (m)\varPsi )^{2}}+ \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{(1-\alpha _{m}\varpi )\varpi } \biggr]U_{1}(\varPsi ) \\ & \qquad {} +\frac{1}{1+\lambda (m)\varPsi }+ \frac{3\eta _{2}^{2}(m)}{2(1+\lambda (m)\varPsi )^{2}} + \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{2(1-\alpha _{m}\varpi )\varpi } \\ & \qquad {}- \frac{\mu (m)}{1+\lambda (m)\varPsi } \varPsi ^{-1} \bigl(1+U_{1}(\varPsi ) \bigr) \biggr\} \\ & \quad =2(1-\alpha _{m}\varpi )\varpi \bigl(1+U_{1}(\varPsi ) \bigr)^{ \varpi -2} \biggl\{ - \biggl[ \bar{\chi }-\varpi \eta _{1}^{2}(m)+ \frac{\alpha _{m}\varpi }{2(1-\alpha _{m}\varpi )}\sum _{j\in \varTheta } \gamma _{mj}\alpha _{j} \biggr]U_{1}^{2}(\varPsi ) \\ & \qquad {} + \biggl[3\eta _{1}^{2}(m)/2-r(m)+ \frac{1}{1+\lambda (m)\varPsi }+ \frac{\eta _{2}^{2}(m)(\varpi +0.5)}{(1+\lambda (m)\varPsi )^{2}} \\ & \qquad {}+ \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{(1-\alpha _{m}\varpi )\varpi } \biggr]U_{1}(\varPsi )+\frac{1}{1+\lambda (m)\varPsi }+ \frac{3\eta _{2}^{2}(m)}{2(1+\lambda (m)\varPsi )^{2}} \\ & \qquad {} + \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{2(1-\alpha _{m}\varpi )\varpi } - \frac{\mu (m)}{1+\lambda (m)\varPsi } \varPsi ^{-1} \bigl(1+U_{1}(\varPsi ) \bigr) \biggr\} . \end{aligned}$$

Choose sufficiently small \(\delta \in \mathbb{R}_{+}^{0}\) which fulfills that, for each \(m\in \varTheta \),

$$ g_{1}=:\bar{\chi }-\varpi \eta _{1}^{2}(m)+ \frac{\alpha _{m}\varpi }{2(1-\alpha _{m}\varpi )}\sum _{j\in \varTheta } \gamma _{mj}\alpha _{j}- \frac{\delta }{2\varpi }>0.$$
(11)

Let

$$ U_{3}(\varPsi ,m)= e^{\delta t}U_{2}(\varPsi ,m). $$

We can deduce from Itô’s formula that

$$ \mathbb{E}U_{3}\bigl(\varPsi (t),\theta (t)\bigr)=U_{2} \bigl( \varPsi (0),\theta (0)\bigr)+\mathbb{E} \int _{0}^{t}\mathcal{L} \bigl[e^{ \delta s}U_{2} \bigl(\varPsi (s),\theta (s)\bigr) \bigr]\,\mathrm{d}s, $$

where

$$ \begin{aligned} &\mathcal{L}\bigl[U_{3}(\varPsi ,m)\bigr] \\ &\quad = 2 e^{\delta t}(1-\alpha _{m}\varpi ) \varpi \bigl(1+U_{1}(\varPsi )\bigr)^{\varpi -2} \\ &\qquad {}\times\biggl\{ - \biggl[ \bar{ \chi }-\varpi \eta _{1}^{2}(m)-\frac{\delta }{2\varpi }+ \frac{\alpha _{m}\varpi }{2(1-\alpha _{m}\varpi )}\sum_{j\in \varTheta } \gamma _{mj}\alpha _{j} \biggr]U_{1}^{2}( \varPsi ) \\ &\qquad {} + \biggl[3\eta _{1}^{2}(m)/2-r(m)+ \frac{1}{1+\lambda (m)\varPsi }+ \frac{\eta _{2}^{2}(m)(\varpi +0.5)}{(1+\lambda (m)\varPsi )^{2}} \\ &\qquad {}+ \frac{1}{(\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )-\alpha _{m}\varpi )\varpi }+ \frac{\delta }{\varpi } \biggr]U_{1}(\varPsi ) \\ &\qquad {} +\frac{1}{1+\lambda (m)\varPsi }+ \frac{3\eta _{2}^{2}(m)}{2(1+\lambda (m)\varPsi )^{2}}+ \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{2(1-\alpha _{m}\varpi )\varpi } \\ &\qquad {}+ \frac{\delta }{2\varpi }-\frac{\mu (m)}{1+\lambda (m)\varPsi } \varPsi ^{-1} \bigl(1+U_{1}(\varPsi ) \bigr) \biggr\} \\ &\quad \leq 2 e^{\delta t}(1-\alpha _{m}\varpi )\varpi \bigl(1+U_{1}( \varPsi )\bigr)^{\varpi -2} \\ &\qquad {}\times\biggl\{ - \biggl[ \bar{ \chi }-\varpi \eta _{1}^{2}(m)- \frac{\delta }{2\varpi }+ \frac{\alpha _{m}\varpi }{2(1-\alpha _{m}\varpi )}\sum_{j\in \varTheta } \gamma _{mj}\alpha _{j} \biggr]U_{1}^{2}( \varPsi ) \\ &\qquad {} + \biggl[3\eta _{1}^{2}(m)/2-r(m)+ \frac{1}{1+\lambda (m)\varPsi }+ \frac{\eta _{2}^{2}(m)(\varpi +0.5)}{(1+\lambda (m)\varPsi )^{2}} \\ &\qquad {}+ \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{(1-\alpha _{m}\varpi )\varpi }+ \frac{\delta }{\varpi } \biggr]U_{1}(\varPsi ) \\ &\qquad {} +\frac{1}{1+\lambda (m)\varPsi }+ \frac{3\eta _{2}^{2}(m)}{2(1+\lambda (m)\varPsi )^{2}}+ \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{2(1-\alpha _{m}\varpi )\varpi } + \frac{\delta }{2\varpi } \biggr\} \\ &\quad =e^{\delta t}(1-\alpha _{m}\varpi )2\varpi \bigl(1+U_{1}( \varPsi )\bigr)^{\varpi -2} \bigl\{ -g_{1}U_{1}^{2}(\varPsi )+g_{2}U_{1}( \varPsi )+g_{3} \bigr\} , \end{aligned} $$

and

$$\begin{aligned}& g_{2}=3\eta _{1}^{2}(m)/2-r(m)+ \frac{1}{1+\lambda (m)\varPsi }+ \frac{\eta _{2}^{2}(m)(\varpi +0.5)}{(1+\lambda (m)\varPsi )^{2}} + \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{(1-\alpha _{m}\varpi )\varpi }+ \frac{\delta }{\varpi }, \\& g_{3}=\frac{1}{1+\lambda (m)\varPsi }+ \frac{3\eta _{2}^{2}(m)}{2(1+\lambda (m)\varPsi )^{2}}+ \frac{\sum_{j\in \varTheta }\gamma _{mj}(1-\alpha _{j}\varpi )}{2(1-\alpha _{m}\varpi )\varpi } +\frac{\delta }{2\varpi }. \end{aligned}$$

Define

$$ Q(\varPsi ,m)= 2\varpi \bigl(1+U_{1}(\varPsi ) \bigr)^{\varpi -2} \bigl\{ -g_{1}U_{1}^{2}( \varPsi )+g_{2}U_{1}(\varPsi )+g_{3} \bigr\} .$$
(12)

According to (11), \(g_{1}>0\), then \(Q(\varPsi ,m)\) is upper bounded on \(\mathbb{R}_{+}^{0}\times \varTheta \), that is to say, \(\sup_{\varPsi \in \mathbb{R}_{+}^{0},m\in \varTheta }\{Q( \varPsi ,m)\}<+\infty \). Define \(\bar{Q}_{1}=\sup_{\varPsi \in \mathbb{R}_{+}^{0},m\in \varTheta }\{Q(\varPsi ,m)\}\). Accordingly,

$$\begin{aligned} \mathbb{E}U_{3}\bigl(\varPsi (t),\varpi (t)\bigr)&=(1-\alpha _{m}\varpi )\mathbb{E}\bigl[e^{ \delta t}\bigl(1+U_{1} \bigl(\varPsi (t)\bigr)\bigr)^{\varpi }\bigr] \\ &\leq (1-\alpha _{m} \varpi ) \bigl(1+U_{1}\bigl( \varPsi (0)\bigr)\bigr)^{\varpi }+(1- \alpha _{m}\varpi )\bar{Q}_{1}\bigl(e^{\delta t}-1 \bigr)/ \delta , \end{aligned}$$

which indicates that

$$ \limsup_{t\rightarrow +\infty }\mathbb{E} \bigl[U_{1}^{\varpi }\bigl( \varPsi (t)\bigr)\bigr]\leq \limsup _{t\rightarrow +\infty }\mathbb{E}\bigl[\bigl(1+U_{1}\bigl( \varPsi (t)\bigr)\bigr)^{\varpi }\bigr]\leq \bar{Q}_{1}/\delta =: \bar{Q}_{2}.$$
(13)

For this reason,

$$ \limsup_{t\rightarrow +\infty }\mathbb{E}\bigl[\varPsi ^{-2\varpi }(t)\bigr] \leq \bar{Q}_{2}. $$

Let \(f_{1}=(\varepsilon /\bar{Q}_{2})^{0.5/\varpi }\). We can deduce from Chebyshev’s inequality (see, e.g., [18]) that

$$ \mathrm{P}\bigl\{ \varPsi (t)< f_{1}\bigr\} =\mathrm{P}\bigl\{ \varPsi ^{-2\varpi }(t)> f_{1}^{-2 \varpi }\bigr\} \leq \mathbb{E} \bigl[\varPsi ^{-2\varpi }(t)\bigr]/ f_{1}^{-2\varpi }= f_{1}^{2 \varpi } \mathbb{E}\bigl[\varPsi ^{-2\varpi }(t) \bigr]. $$

Accordingly,

$$ \limsup_{t\rightarrow +\infty }\mathrm{P}\bigl\{ \varPsi (t)< f_{1} \bigr\} \leq f_{1}^{2\varpi }\bar{Q}_{2}= \varepsilon . $$

For this reason,

$$ \liminf_{t\rightarrow +\infty }\mathrm{P}\bigl\{ \varPsi (t)\geq f_{1} \bigr\} \geq 1-\varepsilon . $$

Now let us test \(\limsup_{t\rightarrow +\infty }\mathrm{P}\{\varPsi (t)> f_{2} \}\leq \varepsilon \). Let

$$ U(\varPsi )=\varPsi ^{\beta },\quad \varPsi >0, \beta \in (0,1). $$

Taking advantage of Itô’s formula results in

$$\begin{aligned} \mathrm{d}U(\varPsi ) =&\beta \varPsi ^{\beta } \biggl[r(\theta )+0.5( \beta -1) \biggl(\eta _{1}^{2}( \theta )+ \frac{\eta _{2}^{2}(\theta )\varPsi ^{2}}{(1+\lambda (\theta )\varPsi )^{2}} \biggr) \\ &{}+\frac{\mu (\theta )\varPsi }{1+\lambda (\theta )\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (\theta )\varPsi } \biggr]\,\mathrm{d}t \\ &{} +\beta \eta _{1}(\theta )\varPsi ^{\beta }\,\mathrm{d}\xi _{1}(t)+ \frac{\beta \eta _{2}(\theta )\varPsi ^{\beta +1}}{1+\lambda (\theta )\varPsi } \,\mathrm{d}\xi _{2}(t) \\ \leq& \beta \varPsi ^{\beta } \biggl[r(\theta )+ \frac{\mu (\theta )\varPsi }{1+\lambda (\theta )\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (\theta )\varPsi } \biggr]\,\mathrm{d}t \\ &{}+\beta \eta _{1}(\theta ) \varPsi ^{\beta }\,\mathrm{d}\xi _{1}(t)+ \frac{\beta \eta _{2}(\theta )\varPsi ^{\beta +1}}{1+\lambda (\theta )\varPsi } \,\mathrm{d}\xi _{2}(t). \end{aligned}$$

For this reason,

$$\begin{aligned} \mathrm{d}\bigl(e^{t} U(\varPsi )\bigr) =&e^{t} U(\varPsi )\,\mathrm{d}t+e^{t} \,\mathrm{d}U(\varPsi ) \\ \leq& e^{t} \varPsi ^{\beta }\,\mathrm{d}t+e^{t} \beta \varPsi ^{\beta } \biggl[r(\theta )+ \frac{\mu (\theta )\varPsi }{1+\lambda (\theta )\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (\theta )\varPsi } \biggr]\,\mathrm{d}t \\ &{}+e^{t}\beta \eta _{1}(\theta )\varPsi ^{\beta }\,\mathrm{d} \xi _{1}(t)+ \frac{e^{t}\beta \eta _{2}(\theta )\varPsi ^{\beta +1}}{1+\lambda (\theta )\varPsi } \,\mathrm{d}\xi _{2}(t) \\ =&\beta e^{t}\varPsi ^{\beta } \biggl[1/\beta +r(\theta )+ \frac{\mu (\theta )\varPsi }{1+\lambda (\theta )\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (\theta )\varPsi } \biggr]\,\mathrm{d}t \\ &{} +e^{t} \beta \eta _{1}(\theta )\varPsi ^{\beta } \,\mathrm{d}\xi _{1}(t)+ \frac{e^{t}\beta \eta _{2}(\theta )\varPsi ^{\beta +1}}{1+\lambda (\theta )\varPsi } \,\mathrm{d}\xi _{2}(t) \\ \leq& \beta e^{t} \varPsi ^{\beta } \biggl[1/\beta +r^{u}+\mu ^{u}/ \lambda ^{l}- \frac{\varPsi ^{2}}{1+\lambda ^{u}\varPsi } \biggr]\,\mathrm{d}t \\ &{}+e^{t} \beta \eta _{1}(\theta )\varPsi ^{\beta }\,\mathrm{d} \xi _{1}(t)+ \frac{e^{t}\beta \eta _{2}(\theta )\varPsi ^{\beta +1}}{1+\lambda (\theta )\varPsi } \,\mathrm{d}\xi _{2}(t) \\ \leq& C e^{t} \,\mathrm{d}t+e^{t} \beta \eta _{1}(\theta ) \varPsi ^{\beta }\,\mathrm{d}\xi _{1}(t)+ \frac{e^{t}\beta \eta _{2}(\theta )\varPsi ^{\beta +1}}{1+\lambda (\theta )\varPsi } \,\mathrm{d}\xi _{2}(t), \end{aligned}$$

where \(C>0\) is a constant. This implies that \(\limsup_{t\rightarrow +\infty }\mathbb{E}[\varPsi ^{\beta }(t)] \leq C \). Then we can deduce from Chebyshev’s inequality that \(\limsup_{t\rightarrow +\infty }\mathrm{P}\{\varPsi (t)> f_{2} \}\leq \varepsilon \). □

3 Stationary distribution

Now we provide sufficient criteria to ensure that model (3) possesses a UESD.

Lemma 3

([24], Theorem 3.13)

Let\(\varLambda (y;t)=(\varPsi (t),\theta (t))\)be an\(\mathbb{R}^{n}\times \varTheta \)-valued stochastic process, where\(y=(\varPsi (0),\theta (0))\). Let\(F \times \varTheta \subset \mathbb{R}^{n}\times \varTheta \)be a domain. Then\(\varLambda (y;t)\)is positive recurrent with respect to\(F \times \varTheta \)if and only if, for arbitrary\(m\in \varTheta \), there is a nonnegative function\(W(\varPsi , m)\): \(F^{c}\rightarrow \mathbb{R} \)such that, for some\(a>0\),

$$ \mathcal{L}W(\varPsi ,m)\leq -a,\quad (\varPsi ,m)\in F^{c}\times \varTheta , $$

where\(F^{c}\)represents the complement ofF.

Lemma 4

([24], Theorems 4.3 and 4.4)

If\(\varLambda (y;t)\)is positive recurrent with respect to a domain, then it has a UESD.

Theorem 3

\(\bar{\chi }>0\Rightarrow \)model (3) possesses a UESD.

Proof

Choose sufficiently small \(\zeta \in (0,1)\) which obeys

$$ 1- \frac{\zeta }{2}\alpha ^{u}>0,\qquad \bar{\chi }- \frac{\zeta }{2}\bigl(\eta _{1}^{2} \bigr)^{u} +\frac{\zeta }{2}\min_{m\in \varTheta } \biggl\{ \frac{\alpha _{m}(\bar{\chi }-\chi (m))}{1-\zeta \alpha _{m}/2} \biggr\} >0,$$
(14)

where \(\alpha _{m}\) abides by (9), \(\alpha ^{u}=\max_{m\in \varTheta }\{\alpha _{m}\}\) and \((\eta _{1}^{2})^{u}=\max_{m\in \varTheta }\{\eta _{1}^{2}(m)\}\). Let

$$ U_{4}(\varPsi ,m)= (1-\zeta \alpha _{m}/2 )\varPsi ^{-\zeta }+\varPsi , \quad \varPsi \in \mathbb{R}_{+}^{0}. $$

We can deduce that

$$ \begin{aligned} &\mathcal{L}U_{4}(\varPsi ,m) \\ &\quad =-\zeta \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr)\varPsi ^{- \zeta } \biggl(r(m)+\frac{\mu (m)\varPsi }{1+\lambda (m)\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (m)\varPsi } \biggr) \\ &\qquad {}+ \frac{\eta _{1}^{2}(m)}{2} \zeta (\zeta +1) \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr)\varPsi ^{- \zeta } \\ &\qquad {} +\frac{\eta _{2}^{2}(m)}{2(1+\lambda (m)\varPsi )^{2}} \zeta (\zeta +1) \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr) \varPsi ^{- \zeta +2} -\zeta \varPsi ^{-\zeta }\sum _{j\in \varTheta } \gamma _{mj} \frac{\alpha _{j}}{2} \\ &\qquad {} +\varPsi \biggl(r(m)+ \frac{\mu (m)\varPsi }{1+\lambda (m)\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (m)\varPsi } \biggr) \\ &\quad =-\zeta \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr)\varPsi ^{- \zeta } \biggl(r(m)-\frac{1}{2}\eta _{1}^{2}(m)- \frac{\zeta }{2}\eta _{1}^{2}(m) \biggr) \\ &\qquad {}- \zeta \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr)\varPsi ^{-\zeta } \biggl(1+ \frac{\zeta \alpha _{m}/2}{1-\zeta \alpha _{m}/2} \biggr)\sum_{j \in \varTheta } \gamma _{mj}\frac{\alpha _{j}}{2} \\ &\qquad {} -\zeta \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr) \varPsi ^{1-\zeta } \biggl( \frac{\mu (m)}{1+\lambda (m)\varPsi }- \frac{\varPsi }{1+\lambda (m)\varPsi }- \frac{\eta _{2}^{2}(m)(\zeta +1)\varPsi }{2(1+\lambda (m)\varPsi )^{2}} \biggr) \\ &\qquad {} +\varPsi \biggl(r(m)+ \frac{\mu (m)\varPsi }{1+\lambda (m)\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (m)\varPsi } \biggr) \\ &\quad =-\zeta \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr)\varPsi ^{- \zeta } \biggl( \chi (m)+\frac{1}{2}\sum_{j\in \varTheta } \gamma _{mj} \alpha _{j}-\frac{\zeta }{2}\eta _{1}^{2}(m)+ \frac{\zeta \alpha _{m}/2}{1-\zeta \alpha _{m}/2}\sum _{j\in \varTheta } \gamma _{mj}\frac{\alpha _{j}}{2} \biggr) \\ &\qquad {} -\zeta \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr) \varPsi ^{1-\zeta } \biggl( \frac{\mu (m)}{1+\lambda (m)\varPsi }- \frac{\varPsi }{1+\lambda (m)\varPsi }- \frac{\eta _{2}^{2}(m)(\zeta +1)\varPsi }{2(1+\lambda (m)\varPsi )^{2}} \biggr) \\ &\qquad {} +\varPsi \biggl(r(m)+ \frac{\mu (m)\varPsi }{1+\lambda (m)\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (m)\varPsi } \biggr) \\ &\quad =-\zeta \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr)\varPsi ^{- \zeta } \biggl( \bar{\chi }-\frac{\zeta }{2}\eta _{1}^{2}(m)+ \frac{\zeta \alpha _{m}/2}{1-\zeta \alpha _{m}/2}\bigl(\bar{\chi }-\chi (m)\bigr) \biggr) \\ &\qquad {} -\zeta \biggl(1-\frac{\zeta \alpha _{m}}{2} \biggr) \varPsi ^{1-\zeta } \biggl( \frac{\mu (m)}{1+\lambda (m)\varPsi }- \frac{\varPsi }{1+\lambda (m)\varPsi }- \frac{\eta _{2}^{2}(m)(\zeta +1)\varPsi }{2(1+\lambda (m)\varPsi )^{2}} \biggr) \\ &\qquad {} +\varPsi \biggl(r(m)+ \frac{\mu (m)\varPsi }{1+\lambda (m)\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (m)\varPsi } \biggr). \end{aligned} $$

Note that

$$\begin{aligned}& \lim_{\varPsi \rightarrow 0^{+}}\zeta \biggl(1- \frac{\zeta \alpha _{m}}{2} \biggr)\varPsi \biggl( \frac{\mu (m)}{1+\lambda (m)\varPsi }-\frac{\varPsi }{1+\lambda (m)\varPsi }- \frac{\eta _{2}^{2}(m)(\zeta +1)\varPsi }{2(1+\lambda (m)\varPsi )^{2}} \biggr)=0, \\& \lim_{\varPsi \rightarrow 0^{+}}\varPsi ^{1+\zeta } \biggl(r(m)+ \frac{\mu (m)\varPsi }{1+\lambda (m)\varPsi }- \frac{\varPsi ^{2}}{1+\lambda (m)\varPsi } \biggr)=0. \end{aligned}$$

Hence

$$ \lim_{\varPsi \rightarrow 0^{+}} \frac{\mathcal{L}U_{4}(\varPsi ,m)}{\varPsi ^{-\zeta }}=-\zeta \biggl(1- \frac{\zeta \alpha _{m}}{2} \biggr) \biggl(\bar{\chi }-\frac{\zeta }{2} \eta _{1}^{2}(m)+\frac{\zeta \alpha _{m}/2}{1-\zeta \alpha _{m}/2}\bigl( \bar{\chi }-\chi (m)\bigr) \biggr)=:-h_{m}. $$

By (14), \(h_{m}>0\), therefore

$$ \lim_{\varPsi \rightarrow 0^{+}} \frac{\mathcal{L}U_{4}(\varPsi ,m)}{h_{m}\varPsi ^{-\zeta }}=-1.$$
(15)

Furthermore,

$$ \lim_{\varPsi \rightarrow +\infty } \frac{\mathcal{L}U_{4}(\varPsi ,m)}{\frac{\varPsi ^{3}}{1+\lambda (m)\varPsi }}=-1.$$
(16)

On the basis of (15) and (16), one can find \(a_{1}<1\) such that, for \(\varPsi \in (0, a_{1}]\cup [1/a_{1},+\infty )\), \(\mathcal{L}U_{4}(\varPsi ,m)\leq -1\). Accordingly, for \(\forall (\varPsi ,m) \in \{(0, a_{1}]\cup [1/a_{1},+\infty )\}\times \varTheta \),

$$ \mathcal{L}U_{4}(\varPsi ,m)\leq -1. $$

We then deduce from Lemma 3 and Lemma 4 that model (3) possesses a UESD. □

4 Real world applications

In this section we employ the theoretical outcomes (i.e., Theorems 1, 2, and 3) to evaluate the evolution of the African wild dog (Lycaon pictus) in Africa. In accordance with prior investigations [4, 9], \(r\in [-0.19,0.49]\), \(\mu =3\), and \(\lambda \in [3,52]\). The present study chooses \(\varTheta =\{1,2\}\), \(r\equiv 0.15\), \(\mu \equiv 3\), \(\lambda \equiv 25\), \(\eta _{1}^{2}(1)=0.6\), \(\eta _{1}^{2}(2)=0.2\), \(\eta _{2}^{2}\equiv 0.16\). Hence

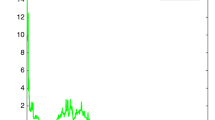
$$\begin{aligned}& \chi (1)=r(1)-\eta _{1}^{2}(1)/2=-0.15,\qquad \chi (2)=0.05, \\& \bar{\varPi }=\varPi (1)=\varPi (2)=\mu /\lambda -2(\sqrt{1+\lambda \mu }-1)/ \lambda ^{2}=0.095. \end{aligned}$$

Due to the fact that \(\chi (1)+\varPi (1)<0\), Theorem 1 implies that the dogs in state 1 become extinct (see Fig. 1(a), which manifests that the extinction happens in about 85 years), and accordingly, state 1 is an extinction state. At the same time, note that \(\chi (2)>0\), Theorem 2 and Theorem 3 indicate that this species in state 2 is SP and possesses a UESD (see Fig. 1(b)), and accordingly, state 2 is a persistence state. Figures 1(a) and 1(b) reflect that the puny undulations on the growth rate bring a hazard of extinction for the dogs. Let us now choose different values of σ.

  1. (i)

    Let \(\sigma =(0.8,0.2)\). Compute that \(\bar{\chi }+\bar{\varPi }=-0.015<0\). Thus Theorem 1 implies that the dogs in system (3) become extinct (see Fig. 1(c), which manifests that the extinction happens in about 105 years).

    Figure 1
    figure 1

    Paths of model (3) with \(\varTheta =\{1,2\}\), \(r\equiv 0.15\), \(\mu \equiv 3\), \(\lambda \equiv 25\), \(\eta _{1}^{2}(1)=0.6\), \(\eta _{1}^{2}(2)=0.2\), \(\eta _{2}^{2}\equiv 0.16\). (a) is a path of the solution of state 1, which manifests that the extinction happens in about 85 years. (b) is a path of the solution of state 2, which manifests that the species is SP. (c) is a path of the solution of model (3) with \(\sigma =(0.8,0.2)\), which manifests that the extinction happens in about 105 years. (d) is a path of the solution of model (3) with \(\sigma =(0.2,0.8)\)

    Full size image
  2. (ii)

    Let \(\sigma =(0.2,0.8)\). Compute that \(\bar{\chi }=0.01>0\). Thus Theorem 2 and Theorem 3 indicate that this species in system (3) is SP and possesses a UESD (see Fig. 1(d)).

Figures 1(c) and 1(d) reflect that if the medium undulations expend much time on the extinction states such that \(\bar{\chi }+\bar{\varPi }<0\), then the dogs are in danger; if the medium undulations expend much time on the persistence states such that \(\bar{\chi }>0\), then the dogs are secure.

5 Conclusions

Evaluating the functions of environmental undulations on the evolution of species is an attractive topic in ecology [19]. The present study has taken advantage of the white noise and the Markovian switching to portray the puny undulations and medium undulations in the environment, respectively, and has put forward a stochastic population model with Allee effects under regime switching. For this model, the criteria for extinction, persistence, and the existence of a UESD have been offered. The findings uncover that these properties of system (3) highly correlate with the environmental undulations.

  • Since

    $$\begin{aligned}& \bar{\chi }=\sum_{m\in \varTheta }\sigma _{m} \chi (m), \qquad \bar{\varPi }= \sum_{m\in \varTheta }\sigma _{m} \biggl[\frac{\mu (m)}{\lambda (m)} - \frac{2(\sqrt{1+\lambda (m)\mu (m)}-1)}{\lambda ^{2}(m)} \biggr], \\& \chi (m)=r(m)-\frac{\eta _{1}^{2}(m)}{2}, \end{aligned}$$

    then for each \(m\in \varTheta \)

    $$ \frac{\mathrm{d}(\bar{\chi }+\bar{\varPi })}{\mathrm{d}\eta _{1}^{2}(m)}=- \frac{\sigma _{m}}{2}\leq 0. $$

    Accordingly, the puny undulations on the growth rate bring a hazard of extinction. This is consistent with the prior studies (see, e.g., [19]).

  • If the Markov chain \(\theta (t)\) expends much time on the persistence states such that \(\bar{\chi }>0\), then model (3) is persistent and possesses a UESD; if \(\theta (t)\) expends much time on the extinction states such that \(\bar{\chi }+\bar{\varPi }<0\), then the species represented by system (3) is dangerous.

At the end of this paper, we would like to mention that we have not examined the case \(\bar{\chi }+\bar{\varPi }>0>\bar{\chi }\). In this case, the results are too complicated to research at the present stage. This issue deserves a fuller treatment in subsequent analyses.