Tailwater gravity currents and their connection to perfectly subcritical flow: laboratory experiments and shallow-water and direct numerical solutions

Abstract

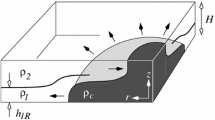
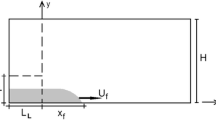
We report upon a series of laboratory experiments and complementary (two-dimensional) direct numerical simulations that explore the lock release of a fixed volume of dense fluid into a two-layer density-stratified ambient. By initial condition, the lock release experiments/simulations fall into one of two categories: full-depth and partial-depth. Our particular focus is on the “tailwaters” limiting case where the lock fluid density matches that of the lower ambient layer. In either case the front speed of the advancing lock fluid is less than that of the excited interfacial disturbances. Consequently, the internal front propagates at constant speed for less time than, say, the downstream-propagating interfacial disturbance, which we term the dense gravity current (or GC1). Complementing GC1, there is an analogue flow of light ambient fluid into the lock, and this we refer to as the light gravity current (or GC2). Measured speeds for GC1, GC2 and the internal front are compared against analogue predictions from shallow water (SW) theory. From this comparison, positive agreement is noted in the case of GC1 and the internal front. Meanwhile, the speed of GC2 post reflection from the lock end wall is under-predicted by 10–20% depending on the initial depth of dense fluid within the lock. This under-prediction is believed to result from a mismatch between where the SW prediction is made (immediately following GC2 reflection from the back of the lock) and where the experimental GC2 speed is measured, usually 0.5–2.5 lock lengths downstream by which point the GC2 height has decreased due to dispersion. Although the GC1 height also undergoes a dispersive decrease in height, generally more positive agreement is noted when comparing measured and predicted gravity current heights. The distance travelled by the internal front prior to being arrested by the reflected GC2 agrees robustly with SW theory. Laboratory and DNS experiments exhibiting a thick ambient interface are also reported upon. We observe that the speed of the internal front and the downstream distance it travels at a constant speed increase with interface thickness. The insights gained from this investigation can be applied to realistic environmental flows such as nocturnal thunderstorm outflows.

Appendices

A Symbols and abbreviations

Symbol/abbreviation	Meaning
a	$h_{Ni}/H$
b	$h_{Ti}/H$
$c_+$,$c_-$	Speed of the characteristics used in SW model solutions
$\delta$	Interface thickness
DNS	Direct numerical simulation
$\eta _i$	GCi height i.e. height of the nose above the tongue
GCi	Gravity current
$g'$	Reduced gravity, $g(\rho _1-\rho _2)/\rho _1$
h	Height of the $\rho _1$ fluid, used especially in the SW model derivation
$h_{\rm{core}}$	Height of the $\rho _1$ fluid located between the GC1 and GC2 fronts
$h_{0i}$	Initial depth of the fluid reservoirs
$h_{\rm{initial}_i}$	Fluid height representing the initial condition in the solution of the shallow water equation (2.3)
$h_{Ni}$	Height of the gravity current nose above the tank bottom
$h_{Ti}$	Initial depth of the fluid tongues
H	Total channel depth
i	Subscript for dense fluid ($i=1$) and light fluid ($i=2$)
$l_i$	Length of the reservoir (which is the lock length when $i=1$)
p	Pressure
Plot symbols (open)	Data from numerical experiments
Plot symbols (closed)	Data from laboratory experiments
$\rho _i$	Fluid density
S	Gravity current density parameter, $(\rho _1-\rho _2)/(\rho _c-\rho _2)$
SW	Shallow water (theory/model)
U	Speed of the internal front
u	Horizontal speed of the $\rho _1$ fluid, used especially in the SW model derivation
$u_{\rm{core}}$	Speed of the $\rho _1$ fluid between the GC1 and GC2 fronts
$u_{\rm{initial}_ i}$	Initial fluid speed representing the initial condition in the solution of the shallow water equation (2.3)
$u_{Ni}$	Speed of the fluid immediately behind the GCi nose
$V_{Ni}$	Speed of the GCi nose
w	Vertical speed of the $\rho _1$ fluid, used especially in the SW model derivation
x	Horizontal distance from the lock gate (into channel)
$x_D$	Distance travelled by the internal front prior to its arrest
z	Vertical distance measured from the bottom of the channel

B Summary of experiments (laboratory and numerical)

A summary of the data relevant to our laboratory and DNS experiments is provided in Tables 2 and 3, respectively.

Table 2 Laboratory experimental data (cgs units)

Table 3 DNS experimental data (cgs units)

C Preparation of the laboratory experiments

Laboratory experiments with a thin interface ($\delta \simeq 2$ cm) were prepared by first adding a layer of salt water to a depth $>h_{T1}$ to the experimental tank with the lock gate in the up position. In cases where $h_{01}<H$, a layer of fresh water (of depth 20 cm$-h_{01}$) dyed orange with food colouring was layered on top of the salt water layer using a sponge float to minimize interfacial mixing. The lock gate was then lowered to a depth of approximately 1 cm from the bottom of the tank. More (orange-dyed) fresh water was then added to the ambient side of the tank. The resulting imbalance of hydrostatic pressures between the outside and inside of the lock pushed down the ambient interface and up the interface inside the lock. Addition of dyed fresh water was continued until the fluid in the lock reached a total depth of 20.0 cm and, simultaneously, $h_{01}$ reached its desired value. Blue food colouring was then injected into the lower, dense, lock fluid layer using a syringe with a long needle. Note that the above technique allowed for an almost exact match between the densities of Reservoir 1 and of Tongue 1. In the simpler cases where $h_{01}=H$, the procedure was identical to the above except that no orange-dyed fresh water was added before the lock gate was lowered to within 1 cm of the tank bottom. All the fresh water was added after this step. Also, a syringe and needle were not required to add the blue dye to the lock fluid.

Laboratory experiments with thick interfaces were prepared using one of three methods. Examples of density profiles measured with the conductivity probe are shown in Fig. 18. For interfaces ranging in thickness from 2 to 10 cm an intrusive gravity current, such as those described in Mehta et al. [17], was used. This technique involved first filling the tank and lock as for a thin interface experiment. A second lock gate was installed at an appropriate distance from the far tank wall, and after filling the tank, this second lock gate was lowered. The salt and fresh water in this secondary lock were then mixed, the secondary lock was released, and the resulting intrusive gravity current propagated through the ambient region of the tank. In turn, this led to a nontrivial broadening of the ambient interface. The main lock-release experiment was conducted a minimum of 20 minutes later. To keep the density variation within the ambient interface as linear as possible, intrusions could also be released in sequence, where the second lock gate, though fixed in terms of its downstream location, was raised and lowered several times over with complete mixing of the secondary lock fluid occurring prior to each release of the secondary lock.

For interfaces 7–15 cm thick, a lock exchange of the type described by Shin et al. [18] was instead performed. This technique involved installing a second lock gate at the approximate midpoint of the ambient region of the tank, then filling one side with salt water and the other side with fresh water. The fresh water was then dyed orange with food colouring. To produce an ambient interface having an approximately linear density profile, the second lock gate was raised in a stepwise fashion, approximately 1 cm at a time. Through this process was produced a rising plume of light fluid that propagated along the top of the dense fluid, while a dense gravity current propagated along the base of the light fluid. Repetition of this procedure eventually produced a layer of continuous stratification throughout the tank.

For interface thicknesses of 15–20 cm the double-bucket technique of Oster [19] was used. We reserved the use of the double-bucket technique to the case of the thickest interfaces because the technique was limited in the overall density difference, $\rho _1-\rho _2$, that it could produce compared to the other two techniques.

When $h_{01}<h_{T1}+\delta /2$, the upper part of the thick interface had to appear inside and outside of the lock. To achieve this, the intrusion and double-bucket techniques began by filling the tank with salt water to a volume $\ge l_1wh_{01}$ (where w is the tank width), after which the remaining combination of salt and fresh water was added as required by the technique in question. This resulted in an overfilled tank having a fluid depth of $>20$ cm. The main lock gate was then lowered to within 1 cm of the tank bottom and an appropriate volume of lock fluid from just below the thick interface was removed by siphon. Simultaneously, lower layer fluid from outside of the lock flowed into the lock. This process continued until the depth, $h_{01}$, of Reservoir 1 reached the desired value.

Fig. 18

Examples of ambient interface density profiles as measured by the conductivity probe. Shown is the profile from laboratory experiment 36 (a), which is typical of a thick interface experiment, the profile from laboratory experiment 41 (b), which is typical of a medium interface experiment, and the profile in experiment 28 (c), which is typical of an experiment with a thin interface

In the case where $h_{01}<h_{T1}+\delta /2$ and lock-exchange was being used to thicken the ambient interface, the second lock gate was placed at a location that resulted in a greater initial volume of salt water than fresh water. Thus, following removal of the second lock gate, the resulting ambient interface was at a greater height than that required for the experiment, which also resulted in an overfilled tank. The primary lock gate was then raised to less than 1 cm from the tank bottom, and fluid was siphoned from the lock as described in the previous paragraph. The hydrostatic balance maintained between the lock and ambient sides of the tank during siphoning resulted in a steady decrease in H, $h_{T1}$, and $h_{01}$. As before, siphoning was terminated once this trio of variables achieved their desired values and $H_{\text{lock}}=20.0$ cm.

D Detailed derivation of the SW model for reflected GC2

The height and speed of GC2 following reflection from the back of the lock are determined using the method described in Section 5.4.2 of Ungarish [9]. Here, we assume that GC2 is either a Type 1 or Type 2 bore. When this is not the case, i.e. GC2 is a Type 3 bore, the incident and reflected disturbance will both be rarefaction waves as noted by Rottman and Simpson [14]. Theoretical examination of this Type 3 case is deferred to future studies.

Figure 4 shows GC2 immediately following reflection from the back of the lock. The upstream conditions were previously determined using the SW analysis detailed in Sect. 2. Only $V_{N2}$ and $h_{N2}$ are unknown. After introducing the ratio $\chi$ in (2.12) and using continuity to obtain an expression for the speed of the bore (2.13), we consider that the reduced hydrostatic pressure to the right of the bore is

$$\begin{aligned} p_r = {\left\{ \begin{array}{ll} h_1-z &{} (0\le z\le h_1) \\ 0 &{} (h_1\le z\le H) \\ \end{array}\right. } \end{aligned}$$

(D.1)

Changing the frame of reference to one where the bore is stationary allows us to consider the increase in pressure along the top boundary in Fig. 4. Bernoulli’s equation gives

$$\begin{aligned} \frac{1}{2}V_{N2}^2+p_L+\Delta =\frac{1}{2}(u_2+V_{N2})^2 \end{aligned}$$

(D.2)

where $\Delta$ denotes the head loss across the bore and $p_L$ is the unknown pressure along the top boundary to the left of the bore. Making the simplifying assumption that $\Delta =0$ (which shows good agreement with more rigorous calculations e.g. Klemp et al. [15]) yields

$$\begin{aligned} p_L=\frac{1}{2}u_2^2+u_2V_{N2} \end{aligned}$$

(D.3)

where $u_2$ is understood to be a negative quantity. This result allows us to calculate the hydrostatic pressure to the left of the bore:

$$\begin{aligned} p_l = {\left\{ \begin{array}{ll} p_L+H-h_{N2}-z &{} (0\le z\le H-h_{N2}) \\ p_L &{} (H-h_{N2}\le z\le H) \\ \end{array}\right. } \end{aligned}$$

(D.4)

A flow-force balance is then applied on the left and right side of the bore (still in the moving frame of reference) as follows:

$$\begin{aligned} \int _{0}^{H} (u^2+p)_l\,{\rm{d}}z = \int _{0}^{H} (u^2+p)_r\,{\rm{d}}z \end{aligned}$$

(D.5)

Using continuity arguments and substituting (2.12), (2.13), (D.1), and (D.4) into (D.5), ultimately yields, after some algebra, the final expression for $\chi$, (2.14).

E Method of solution

As described in Sect. 2.2.1, and in Ungarish et al. [10] when there is one Type 3 nose, (2.3) can be integrated along a characteristic starting from the undisturbed fluid bordering the Type 3 nose; if the Type 3 nose is associated with GC2, then the initial height and speed are chosen as $h_{\rm{initial}_1}=1$ and $u_{\rm{initial}_1}=0$ and integration is along a $c_+$ characteristic. The solution of (2.3) is then used to obtain characteristic speed spectra $c_{\pm }(u,h)$ from (2.4). The range of values for h are used to derive a spectrum of $V_{N1}(h)$ using (2.9) and (2.10). For this purpose, $a=h/H$ and $h_{N1}=h$. Finally, u(h) is used to obtain a second spectrum of $V_{N1}(h)$, this time using (2.8) with $u_{N1}=u$ (and, again, $h_{N1}=h$).

With the above speeds to hand, a composite graph may be constructed as in Fig. 19. We first consider the intersection point of the two curves labelled as $V_{N1}$. If their intersection lies between the $c_+(h)$ and the $c_-(h)$ curves then the solution is valid and the GC1 nose is of Type 1, with height and speed determined by the aforementioned intersection point. This is the scenario that Fig. 19 illustrates. If, instead, the intersection of the two $V_{Ni}(h)$ curves lies above the $c_+(h)$ curve or below the $c_-(h)$ curve, the GC1 nose can be assumed to be of Type 2. However, this scenario was never encountered in this investigation.

In the case when GC1 is a Type 3 nose (instead of GC2), a solution for the GC2 nose can be obtained by inverting the experimental geometry and proceeding as above. Alternately, one may derive a solution by integrating (2.3) along a $c_-$ characteristic having as initial conditions $h_{\rm{initial}_2}=h_{T1}$ and $u_{\rm{initial}_2}=0$. Solving along the $c_-$ characteristic implies that $h \in [h_{T1},1]$.

Fig. 19

(Color online) Sample composite graph showing the variation of u, $c_\pm$, and $V_{N1}$ with h. $V_{N1}(u)$ and $V_{N1}(\text{Fr}_{T})$ are respectively obtained by applying the solution of (3) into (8) and (9)/(10). The non-dimensional initial conditions are $H=2.00$ and $b=0.125$, leading to a Type 3 GC2 nose. The height and speed of the GC1 nose are specified by the intersection of the two $V_{N1}$ curves. Because $c_-(h_{N1})<V_{N1}(h_{N1})<c_+(h_{N1})$ the GC1 nose is of Type 1

In the case when neither GC1 nor GC2 has a nose of Type 3, the method described in Sect. 2.2.2 is used. First it is assumed that both GC1 and GC2 have a nose of Type 2. As a result, (2.3) is integrated twice: both forward along a $c_+$ characteristic and backward along a $c_-$ characteristic. The initial height to use for the integrations is determined using (5.38) from Ungarish [9]: $h_{N1}$ and $h_{N2}$ are determined then the initial heights are $h_{{\rm initial}_1}=h_{N1}$ and $h_{{\rm initial}_2}=H-h_{N2}$ and speeds are as shown in Fig. 3. The intersection of the two resulting u(h) curves gives the height and speed of the dense fluid core.

As further described in Sect. 2.2.2, when the two curves do not intersect it is because either GC1 or GC2 is of Type 1. In this case, (2.3) is still integrated twice, but one of the bores is weakened, i.e. $h_{{\rm initial}_1}$ must be increased or $h_{{\rm initial}_2}$ must be decreased (and $u_{{\rm initial}_i}$ follows from continuity arguments). Figure 20 shows an example solution where the GC1 nose is of Type 2 while the GC2 nose is of Type 1.

Fig. 20

Sample composite graph of u(h) used when the GC1 nose is of Type 2 while the GC2 nose is of Type 1. The curves were obtained by integrating (2.3) both forward along a $c_+$ characteristic (thick line) and backward along a $c_-$ characteristic (thin). The intersection indicates the height and speed of the fluid core between the bores. The parameters are $H=1$ and $h_{T1}=0.202$. $h_{\rm initial_2}$ is obtained by reducing the height calculated by (5.38) from Ungarish [9] by 0.00014 while $h_{\rm initial_1}$ is obtained directly from (5.38)